Abstract
Atmospheric methane concentrations were nearly constant between 1999 and 2006, but have been rising since by an average of ~8 ppb per year. Increases in wetland emissions, the largest natural global methane source, may be partly responsible for this rise. The scarcity of in situ atmospheric methane observations in tropical regions may be one source of large disparities between top-down and bottom-up estimates. Here we present 590 lower-troposphere vertical profiles of methane concentration from four sites across Amazonia between 2010 and 2018. We find that Amazonia emits 46.2 ± 10.3 Tg of methane per year (~8% of global emissions) with no temporal trend. Based on carbon monoxide, 17% of the sources are from biomass burning with the remainder (83%) attributable mainly to wetlands. Northwest-central Amazon emissions are nearly aseasonal, consistent with weak precipitation seasonality, while southern emissions are strongly seasonal linked to soil water seasonality. We also find a distinct east-west contrast with large fluxes in the northeast, the cause of which is currently unclear.
Similar content being viewed by others
Introduction
Methane (CH4) is the second most important greenhouse gas (GHG) causing anthropogenic radiative forcing contributing to climate change1, and it is essential to understand the CH4 budget and possible changes in future emissions to achieve the main goals of the Paris Agreement2. The relative contribution of different sources to the global CH4 budget remains uncertain despite on-going efforts to improve the estimates from the varied sources and sinks3,4,5. Furthermore, the causes of the recent atmospheric CH4 increases and the preceding period of stalled growth are not fully understood. Global mean atmospheric CH4 was nearly constant at 1774 ppb from 1999 to 2006, but rose to 1834 ppb by 2015 and in 2020 its average was 1879 ppb6. With limited measurements, it is not possible to confirm the reasons for this recent increase2. One possible cause of resumed growth since 2007 is tropical South American positive precipitation anomalies during La Niña events, which could increase wetland emissions7,8. Alternatively, increased emissions have been attributed to anthropogenic sources in tropical and temperate regions9. Analysis of 13CH4 suggests substantial biogenic emissions from either agricultural or wetland sources10 may have been an important factor.
Global CH4 emissions estimated by top-down inversions (2008–2017), averaged 576 (range of 550–594, corresponding to the minimum and maximum estimates) TgCH4 y−1 5, with 62% from anthropogenic emissions, 31% from wetlands and 7% from other natural sources (including inland waters)5,11 although aquatic sources have large uncertainty11. Globally, bottom-up emissions are almost 30% larger (average of 737 TgCH4 y−1, with a range of 594–881 TgCH4 y−1) than top-down inversion methods, suggesting that at least some of the bottom-up emissions are overestimated5, highlighting the global uncertainties in methane sources and sinks.
Tropical regions host some of the largest wetlands on Earth, but the paucity of in situ observations, which would allow for accurate regional-scale flux estimation12,13,14,15,16, leads to large emissions uncertainty5. About 20% of Amazonia is permanently or seasonally inundated16, and these aquatic habitats are a major CH4 source17. Significant contributions to Amazonian CH4 emissions include CH4 formed in the anoxic zone of floodplains and released to the atmosphere via the stems of flooded trees18, diffusive and ebullitive fluxes17,19 from inland waters, and lesser emissions from termites20 and upland forests21. Thus, understanding the Amazonian CH4 budget and its regional and temporal variations are essential to determine Amazonia’s contribution to the dramatic increase in global CH4 emissions responsible for the ~100 ppb rise in global atmospheric CH4 in the last 15 years.
Here, we quantify seasonal and annual Amazonian CH4 fluxes, and their changes over time, based on measurements of 590 atmospheric CH4 lower-troposphere (from ~300 m a.s.l. to 4.4 km a.s.l.) vertical profiles using an air column-budgeting technique12,22,23,24 (Methods). The profiles have been collected from 2010 to 2018 at four sites (Fig. 1) using small aircraft. The four sites are ALF (southeast), SAN (northeast), RBA (southwest-central region) and TEF which superseded TAB in 2013 (northwest-central region; hereafter TAB_TEF) (Fig. 1 and Supplementary Fig. 1). Fluxes estimated using the column-budgeting technique (FTOTAL_CH4) result from all sources and sinks within the area traversed by air masses flowing from the Atlantic coast to the site (representative of regional scales, ∼105–106 km2). We refer to the area upwind of each site as the region of influence25 (Fig. 1 and Supplementary Fig. 1).
Mean annual regions of influence (2010–2018) for ALF (8.8°S, 56.7°W; green), SAN (2.8°S, 54.9°W; light blue), RBA (9.3°S, 67.6°W; dark blue), TAB (5.9°S, 70.0°W; yellow) and TEF (3.7°S, 66.5°W; orange) inside the Amazonian mask50 (purple). Coloured circles indicate the aircraft sampling sites, and coloured lines represent 97.5% of the terrestrial regions of influence associated with each site. Land use and cover data are from Mapbiomas32 for Pan-Amazonia up to 2018; wetlands and other inland waters are not well represented.
To estimate surface fluxes we first integrate the difference of vertical profile CH4 mole fraction and a so-called background mole fraction to obtain ∆CH4. By dividing ∆CH4 by the travel time of air parcels from the Atlantic, the background sites, to the vertical profiling site we obtain an average CH4 flux estimate (see “Methods”) according to Eq. 1. Where CH4 is methane concentration in units of (mol m−3), z is the height above sea level (m), and t(z) is air mass travel time (s) from the coast to the site at level z. We estimate background mole fractions based on interpolation of CH4 mole fractions from remote Atlantic Ocean sites (RPB, ASC and CPT; see “Methods”), thus assume that oceanic sources and sinks along air-mass trajectory paths across the Atlantic are negligible compared to fluxes from Amazonia.
Biomass burning is responsible for about 5% of total anthropogenic emissions and results from incomplete combustion5. Biomass burning emissions are mainly concentrated in the tropics and subtropics, where forests may be burned to clear land for agricultural purposes or to maintain pastures5. We use carbon monoxide (CO) measured concomitantly with CH4 to estimate CH4 emissions from biomass burning (FFIRE_CH4) according to Eq. 2. Here FCO is the total CO flux and FCO_Natural is the biogenic CO flux, both in mgCO m−2 d−1 for each vertical profile and rCH4:CO is the ratio of the emission related to each site (see “Methods”). Non-fire fluxes (FNON-FIRE_CH4) were determined as the difference of total CH4 flux (FTOTAL_CH4) and FFIRE_CH4, and are the sum of both natural and non-fire related anthropogenic sources and sinks (Eq. 3).
To help analyse the results we determined, for each of the sites’ quarter-yearly resolved air-mass trajectory density-weighted regions of influence25 (Supplementary Fig. 1b, see “Methods”), the factors possibly influencing CH4 fluxes including air temperature, precipitation, equivalent water thickness (EWT), vapour pressure deficit (VPD), burned area, land use and cover, and anthropogenic emissions from EDGAR (Emissions Database for Global Atmospheric Research) v5.026,27.
Results and discussion
Our data reveal that the annual mean difference (∆CH4) between CH4 at each site and the background mole fraction is enhanced in the planetary boundary layer (PBL; below 1.5 km) in comparison with the free troposphere (above 3.8 km), indicating significant Amazonian emissions (nine-year mean difference of ∆CH4 between the PBL and free troposphere for SAN: 48.4 ± 7.5 ppb, TAB_TEF: 30.4 ± 8.4 ppb, RBA: 28.6 ± 5.4 ppb and ALF: 12.4 ± 3.2 ppb; Fig. 2). Free troposphere mole fractions are similar to the global mean mole fractions (Fig. 2b). There are clear regional differences in annual mean ∆CH4: PBL CH4 enhancements were largest for the SAN region, suggesting the highest emissions from the northeast of Amazonia. Webb et al.28 reported CH4 vertical profiles data measured at a northeastern Brazilian coastal site (SAH, 1.08°S, 48.20°W), with lower concentrations than those at SAN, indicating that SAN PBL CH4 enhancements are due to sources between the Brazilian coast and SAN (Supplementary Fig. 2a and b). These high SAN mole fractions are consistent with previous vertical profile concentration observations at this site measured from 2000 to 201312,24. In contrast, PBL CH4 enhancements were the smallest for the southeastern region (ALF), indicating lower fluxes (Fig. 2b). The difference between Amazonian mean mole fractions in the PBL and free troposphere does not have a significant upward trend between 2010 and 2018, indicating no change in net emissions over this period (Fig. 2b and Supplementary Fig. 3). The annual CH4 atmospheric growth rates observed between 2010 and 2018 at all Amazonian sampling sites (ALF: 7.6 ± 0.6 ppb y−1, RBA: 7.1 ± 0.6 ppb y−1, SAN: 7.9 ± 1.1 ppb y−1 and TAB_TEF: 8.0 ± 1.0 ppb y−1, annual growth rate and s.d.) are similar to the global (7.8 ± 0.1 ppb y−1) and tropical (7.9 ± 0.1 ppb y−1) growth rates29 derived from measurements in the remote marine boundary layer. Also, Amazonian sites have quite similar growth rates to those reported for other tropical GHG observation sites (Supplementary Fig. 4). In turn, this indicates that the positive trend observed for global CH4 after 2010 (and which started in 2007) is probably not a result of an Amazonian emissions increase.
a Annual mean ∆CH4 (profile minus background mole fraction) of vertical profiles measured between 2010 and 2018 (coloured lines) and nine-year mean ∆CH4 (2010–2018; black line). b Mean vertical profiles PBL (red diamonds) and free troposphere (blue diamonds) CH4 at Amazonian sites. Global (black) and tropical Atlantic means (green; mean of NOAA surface sites ASC and RPB located between 17.5°N and 17.5°S). Background CH4 time series from NOAA29.
Amazonian CH4 fluxes
Our data reveal distinct spatial and seasonal CH4 flux patterns (Fig. 3). Northeast Amazonia (SAN) had the largest FTOTAL_CH4 and FNON-FIRE_CH4 fluxes (Tukey test: p < 0.05), with nine-year means of 53.4 ± 6.9 and 41.3 ± 7.2 mgCH4 m−2 d−1, respectively, and a FNON-FIRE_CH4 seasonal pattern with higher fluxes during the beginning of the wet season (February–March) and beginning of the dry season (August–September; Fig. 3 and Supplementary Figs. 5 and 6). Although fluxes upwind of SAN were highest among all sites, their contribution to the Amazonian mean is modest, because of SAN’s relatively small region of influence (~11% of total Amazon area25). Northwest-central Amazonia (TAB_TEF) had the second-highest flux, with nine-year mean FTOTAL_CH4 and FNON-FIRE_CH4 of 16.2 ± 2.8 and 15.0 ± 2.3 mgCH4 m−2 d−1, respectively, and the smallest seasonal amplitude of all sites (Fig. 3 and Supplementary Fig. 6). ALF and RBA (southern regions) had statistically similar (Tukey test: p < 0.05) nine-year means of FTOTAL_CH4, 13.1 ± 2.1 and 14.0 ± 2.5 mgCH4 m−2 d−1, and FNON-FIRE_CH4 of 10.3 ± 2.2 and 11.2 ± 2.6 mgCH4 m−2 d−1, respectively, and their seasonal amplitudes were similar. Both FTOTAL_CH4 and FNON-FIRE_CH4 for ALF, RBA, and TAB_TEF were just 24 to 36% of those for SAN (Table 1). To estimate wetland fluxes (FWTL_CH4) for the regions upwind of each site we subtracted from FNON-FIRE_CH4 anthropogenic (Table 1) and termite fluxes (~0.5 mgCH4 m−2 d−1)20, and added CH4 uptake by upland soils (~1 mgCH4 m−2 d−1)30. Oxidation of CH4 by OH radical over land should impact both observed vertical profile concentrations and background similarly and was ignored.
CH4 flux monthly means for total (grey bars), non-fire (total less fire emissions; dark blue bars), wetlands (non-fire less anthropogenic and termite emissions, plus the CH4 uptake from upland soils; light blue bars) and fire (brown bars), air temperature (green lines), equivalent water thickness (EWT; blue lines) and burned area (black lines) for all regions. Error bars represent the standard deviation of monthly means over the nine years. Note the expanded flux axis for SAN.
In principle, ignoring CH4 oxidation between remote Atlantic sites and the Brazilian coasts should lead to an underestimate of fluxes (by overestimating background). Comparisons between coastal and inland vertical profiles above 2 km height (Supplementary Fig. 2a), reveal a difference of only 4.8 ± 9.2 ppb suggesting that the magnitude of this under-estimate is small. We estimated the magnitude of methane loss from oxidation by OH and Cl reactions while air is travelling from the background location to the Atlantic coast before entering Amazonia (see “Methods”). We find a decrease in air column CH4 of ~1.5 ppb and ~0.03 ppb, respectively, which are small compared to the observed Amazon vertical profile CH4 enhancements (around 30–40 ppb). Finally, the background estimated for the Amazon sites agreed well with the CH4 observations measured at Brazilian coast sites (Supplementary Fig. 2c).
In addition to the potential bias introduced by assuming negligible ocean sources and sinks other biases related to our background estimate based on oceanic observation sites could affect our result that eastern Amazon fluxes upwind of SAN are larger than fluxes from the rest of Amazonia. Therefore, we estimated air-mass CH4 at the Atlantic coast, the background used in our method, with two alternative background methods: using SAN data above 3.8 km a.s.l., and using means of each SAH (Salinópolis) vertical profile interpolated to the time of the SAN profiles. SAH is located at the Atlantic coast a bit to the north of Santarem (Supplementary Fig. 2b). While CH4 fluxes estimates based on these two backgrounds are smaller than the estimate based on the ocean site background estimate, they are still much larger than the fluxes estimated for the upwind regions of the other three sites, confirming high emissions at SAN (Supplementary Fig. 7).
Nine-year mean FWTL_CH4 for ALF, RBA, TAB_TEF and SAN represent 67%, 83%, 94%, and 94%, respectively of FNON-FIRE_CH4 (total CH4 emissions less fire emissions; Table 1), indicating that northern Amazonian regions have a larger relative contribution of wetland emissions than southern regions, which have larger relative contribution from anthropogenic sources in comparison to northern regions.
ALF, SAN and RBA, had the largest biomass burning relative contributions to the total fluxes (FTOTAL_CH4), 22%, 23 and 20% (Tukey test: p < 0.05), respectively, with only 8% at TAB_TEF (Table 1). There is a clear seasonality in FFIRE_CH4 for all regions, with an increase during dry periods (August–December, in general) in each region of influence, when there is less EWT, higher temperatures (0.5–1.5 °C) favouring increased fire occurrence (Fig. 3 and Supplementary Figs. 5, 6 and 8a).
We investigated the possible effects of climate conditions on the inter-annual variability observed in FFIRE_CH4 and FWTL_CH4 emissions. An increase in FFIRE_CH4 was observed during hotter and drier years (Fig. 4 and Supplementary Fig. 9a), mainly during El Niño events (2010 and 2015–16), which had the largest burned areas. In the southern regions (ALF and RBA), annual burned area (ALF: r = 0.97, p = 2.2 × 10−5; RBA: r = 0.66, p = 5.4 × 10−2) and temperature (ALF: r = 0.62, p = 7.6 × 10−2; RBA: r = 0.82, p = 6.4 × 10−3) correlated strongly with FFIRE_CH4 inter-annual variability. For the northern regions (SAN and TAB_TEF) FFIRE_CH4 inter-annual variability also correlates with EWT (SAN: r = 0.67, p = 4.8 × 10−2; TAB_TEF: r = 0.58, p = 1.0 × 10−4; Supplementary Fig. 9a). While, for most sites and variables we did not find a clear relationship between FWTL_CH4 inter-annual variability and climate conditions. Only for the northeast (SAN) was FWTL_CH4 positively correlated with temperature (r = 0.67 and p = 4.6 × 10−2; Fig. 4 and Supplementary Fig. 9b).
Colours and fluxes are defined as in Fig. 3. Annual mean error bars represent the uncertainty estimated by Monte Carlo error propagation (Methods); temperature, burned area and EWT error bars represent the standard deviation of monthly means over 9 years.
We estimated regional mean CH4 fluxes based on each site’s annual regions of influence, and combined them (Methods) to yield a nine-year mean FTOTAL_CH4 of 17.4 ± 3.9 mgCH4 m−2 d−1 for Amazonia, of which 17 ± 3% is from fire emissions (Table 1) and 83 ± 23% from non-fire net emissions. Total CH4 emission of 46.2 ± 10.3 TgCH4 y−1 (Methods) was obtained by extrapolating the mean flux to the entire Amazonian (~7.25 × 106 km²; Amazon Mask in Fig. 1), of which 7.7 ± 1.6 and 38.8 ± 10.7 TgCH4 y−1 came from biomass burning and non-fire emissions (with 87% from wetlands and 13% refers to the difference between anthropogenic and termite emissions, and soil sink), respectively. Our CH4 emissions estimates over our 9-year study period, indicates that Amazonian non-fire, wetland, and biomass burning CH4 emissions did not change significantly: mean non-fire emissions for 2010–2013 and 2014–2018 were 38.4 ± 11.4 and 39.1 ± 10.1 TgCH4 y−1 (t-test: t = −0.26, df = 5, p = 0.81); wetlands were 33.5 ± 12.1 and 33.9 ± 10.8 TgCH4 y−1 (t-test: t = −0.14, df = 5, p = 0.89); and mean fire emissions were 6.7 ± 1.8 and 8.6 ± 1.4 TgCH4 y−1 (t-test: t = −1.37, df = 6, p = 0.22).
CH4 emission seasonality and regional differences
Our results indicate regional differences in CH4 fluxes with the largest non-fire and wetland emissions in the northeast and a south versus north contrast in seasonal patterns. Eastern and southern Amazonia have larger fire emissions than the north-west, which agrees with the larger burned areas observed in these regions (Table 1 and Fig. 3). To understand possible drivers of these spatio-temporal patterns, we investigated climatic conditions and human disturbances in each region of influence on a quarterly basis. Our regions of influence differ regarding human disturbance patterns (Fig. 1, Supplementary Fig. 10 and Supplementary Table 1) and climatic conditions (Table 1). Part of the CH4 flux seasonality for SAN and ALF may result from the region of influence shifting southward to areas with more agriculture (23–26% and 24–25% of the total area, respectively), during the second and third quarters of the year. The western sites, RBA and TAB_TEF, were less affected by these activities, with agriculture influencing 16–18% and 9–11% of the total upwind area, respectively. In addition, atmospheric CH4 increases at ALF, SAN and RBA were influenced by the “Arc of Deforestation”, the Amazon region with the most deforestation31. Although, FFIRE_CH4 intra-annual seasonality correlates strongly with burned area seasonality, annual mean FFIRE_CH4 across sites does not entirely correspond with the mean burned area in each site’s region of influence. For example, FFIRE_CH4 from SAN is highest while it has only the third highest mean burned area (Table 1); although variable or incorrectly specified CO:CH4 emissions ratios could contribute, the reasons for this discrepancy are unclear at this time. Even using the mean CO:CH4 emissions ratios from ALF, RBA and TAB_TEF to estimate SAN FFIRE_CH4 the discrepancy cannot be explained.
The contribution of (non-fire) anthropogenic CH4 fluxes in Amazonia, especially relative to FNON-FIRE_CH4, can be significant. These fluxes are primarily from livestock32 via enteric fermentation (EF) and are more significant in the south and east (Table 1). França et al.33, reported an increase of 680% in the Brazilian Amazonian cattle herds between 1985 and 2019, with 41.81 million animals in 2019. CH4 emissions from full exploitation of coal, gas and oil, in addition to oil refineries and transformation industry account for 12% of total anthropogenic emissions in the whole Amazon region (based on EDGAR v5.026,27 emissions for 2015), but totals only 0.7 TgCH4 y−1. Based on 2010–2015 emissions from EDGAR v5.026,27, we estimate the anthropogenic emissions in our regions of influence, where EF is the mainly anthropogenic source, to contribute 90, 84, 71 and 69% of total (non-fire) anthropogenic emissions at ALF, RBA, TAB_TEF and SAN, respectively. This indicates that the region upwind of ALF is most strongly impacted by agricultural activity, and while EF represents 35% of FNON-FIRE_CH4, total EF upwind of ALF is only 3.5 ± 0.4 mgCH4 m−2 d−1 (Table 1, Supplementary Figs. 10 and 11). At RBA, TAB_TEF, and SAN, EF represents 18%, 6% and 5% of our FNON-FIRE_CH4 estimates, respectively.
The eastern regions (ALF and SAN) had the largest seasonal variations in temperature and precipitation (Fig. 3, Supplementary Figs. 5a and 6), and the highest monthly mean temperatures during the dry season. ALF had the largest reduction in precipitation during the dry season (<30 mm/month during July and August 9-year monthly mean in comparison with ~300 mm/month, considering the mean during the wet season, January to March), and the highest VPD. Lower precipitation and higher temperatures during this period result in lower water availability (Fig. 3, Supplementary Figs. 5 and 6). In contrast, the TAB_TEF had a shorter dry season (just two months with mean precipitation below 100 mm between 2010 and 2018), when total precipitation was higher than 80 mm/month, resulting in a smaller reduction in water availability (Supplementary Figs. 5 and 6).
The southern regions (ALF and RBA) had larger FWTL_CH4 during the period of the year with larger EWT and lower temperature, suggesting that wetland fluxes were sensitive to water availability (Fig. 3 and Supplementary Figs. 5, 6 and 8b). However, flux seasonality is different in the northern Amazonian regions. For instance, the northwest-central region (TAB_TEF) had the least FWTL_CH4 seasonal variability, which may have resulted from low seasonal amplitudes in precipitation, temperature and VPD (Fig. 3 and Supplementary Figs. 5 and 6).
The causes of the FWTL_CH4 seasonality and larger signals in the northeast (SAN) are not fully understood, highlighting the need of more studies to understand the nature of the methane sources in this region. Wetlands CH4 fluxes peaked during the early ascending phase of water level rise (February–March) and again during the beginning of dry season (August–September). Other studies do report higher emissions during low water levels19,34. According to Barbosa et al.19 the higher river emissions during low water season in comparison with the high water season may be explained by the greater dilution of incoming CH4 from sediments and ground waters and greater time for CH4 oxidation in deeper water columns during high water. Also, the increase in hydrostatic pressure during high water season resulted in significantly lower ebullition34. Nonetheless, the mechanisms behind the increase in wetland emissions during the beginning of the dry season remain unclear. A previous study of the SAN region24 reported similar seasonality (higher fluxes during the early ascending phase of water level rise and again during the beginning of the dry season) and emissions, with a mean FNON-FIRE_CH4 of 47.7 ± 4.8 mgCH4 m−2 d−1 (between 2000 and 2013). Based on a global inverse model using satellite data, Wilson et al.15 also found large emissions from eastern Amazonia. Their simulations using satellite data improved the agreement with SAN atmospheric CH4 observations in comparison with simulations of SAN atmospheric CH4 vertical profiles using the Joint UK Land Environment Simulator (JULES) model wetlands flux estimates35,36. One possibility could be that aquatic environments such as flooded forests represent larger areas of influence for the SAN region than for other regions and are not adequately represented in process models. Such aquatic habitats are known to be important biogenic methane sources17,18,19,34. Floodplain fluxes via aerenchyma in trees, in particular, can be considerable18, and regional differences in these fluxes could contribute to the relatively high emissions at SAN. The largest CH4 emission rates from Amazonian floodplains emitted via tree stems (between 2 and 6 times higher than other) were observed in the Tapajos River region, which is directly below the SAN sampling location18. Also, the small VPD seasonal amplitude suggests that the SAN region may be less water-stressed (Supplementary Fig. 5b) compared to the southeast region (ALF). Both the large annual magnitude and double-peaked seasonality of the SAN fluxes suggest that the processes influencing these CH4 emissions are not well understood, highlighting the need for further studies to elucidate the processes responsible for Amazonian emissions.
Trends and inter-annual variability of CH4 emissions
FFIRE_CH4 inter-annual variability correlates with climatic variations and human disturbances. Forest fires are associated with a combination of human activities to provide the ignition source and climatic factors to create drier conditions37. In contrast, agricultural and deforestation fires are more associated with human actions than with climate38. Fluxes are elevated during hotter and drier years, and correlated with the largest burned areas (Supplementary Fig. 9a), with temperature being a stronger predictor of FFIRE_CH4 than EWT for all regions. With more frequent and severe droughts, the increase in climate variability impacts both the Amazonian forest39 and savannah biomes, increase tree mortality40 and ecosystem vulnerability to fire40,41,42. Therefore, without fire-use regulations, more and larger fires are likely41, increasing Amazonian CH4 fire emissions.
Wetland emissions are expected to be larger with warmer and wetter conditions2. However, the impacts of temperature and precipitation may be somewhat cancelling: hotter years may promote methanogenesis, but these years are typically drier; likewise, cooler years may suppress methanogenesis, but these years are typically wetter. Northeast FWTL_CH4 was sensitive to temperature, even with the drier condition during these years. The inter-annual variability observed in FWTL_CH4 flux can be partially explained based both annual mean temperature and precipitation (r = 0.80 and p = 0.05 for multiple linear regression, but appears to be mainly driven by temperature (r = 0.67 and p = 0.05; Supplementary Fig. 12). The temperature effect on microbial activity estimated using a Q10 of 243 is too small to explain the inter-annual variability observed in our FWTL_CH4. An increase in wet season CH4 emissions was reported in the northeast Amazon, suggesting that the emissions were more sensitive to the increase in temperature than to the decrease in wetland fraction15. Meanwhile, the absence of the relationship with the temperature at the other sites could be related to higher water sensitivity of CH4 emissions in southern regions and with the lower climate variability in the northwest, in addition to the potential cancelling effects of precipitation and temperature. Also, Amazonian temperatures have increased, most strongly in the east, over the last 40 years44. Continued positive temperature trends may contribute to CH4 emissions increases in northeastern Amazonia and could represent a positive carbon-climate feedback.
Amazonian CH4 budget
For comparison, we summarize results from previous studies of Amazonian CH4 emissions (Table 2). Melack et al.17 estimated wetland emissions from Amazon lowland area (29 TgCH4 y−1) based on a combination of field measurements of methane fluxes from aquatic environments, and remote sensing of inundated areas and aquatic habitats; however, their study area did not include part of the region upwind of SAN near the mouth of the Amazon, where we found higher CH4 fluxes. The fact of their study is not representative of part of this region could make the results of this study and theirs more similar. Tunnicliffe et al.45 used GOSAT (Greenhouse gases Observing SATellite) data in an inverse model and estimated wetland emissions of 9.2 ± 1.8 TgCH4 y−1 for a portion of the Brazilian Amazon, a value much smaller than our or other estimates (Table 2). Using a combination of CH4 mole fraction data from the surface in situ sites and satellite-based atmospheric column CH4 data from the Scanning Imaging Absorption Spectrometer for Atmospheric Chartography (SCIAMACHY), Bergamaschi et al.46 reported total Amazonian emissions of 47.3–53.0 Tg CH4 y−1 for 2004, with the inversions showing reasonable agreement with vertical profile mole fractions from SAN, although with higher CH4 estimates than ours for the western Amazon. Inverse modelling of the atmospheric CH4 data from the same sites described here14, yielded total Amazonian emissions of 31.0–42.0 Tg CH4 y−1 for 2010–2011, with 0.6–3.1 TgCH4 y−1 from biomass burning. Recently, Wilson et al.15 using GOSAT data in an inverse model estimated an increase in Amazon Basin emissions (natural, agricultural and biomass burning emissions), from 38.2 ± 5.3 (between 2010 and 2013) to 45.6 ± 5.2 TgCH4 (between 2014 and 2017). Based on extensive field measurements, Pangala et al.18 estimated Amazonian CH4 emissions from tree stems and aquatic surfaces between 38.5 ± 6.1 and 45.1 ± 6.4 TgCH4 y−1 (2013–2014) and found good agreement with top-down estimates (2010–2013) of 43.7 ± 5.6 TgCH4 y−1.
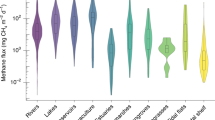
FWTL_CH4 upwind of each site compared to analogous fluxes from the WetCharts wetland model ensemble47 (Fig. 5; see “Methods”) are similar except for the SAN region, where FWTL_CH4 is much higher. WetCharts does show substantial emissions upwind of SAN, but still just 40% of our estimates. The basin-wide annual WetCharts wetland emissions are 39.4 ± 10.3 TgCH4 y−1 (Table 2), while our data-based approach yields a similar value of 33.8 ± 10.9 TgCH4 y−1. This similarity may be an artefact of our column-budgeting approach sensing higher eastern fluxes, while not being sensitive to large emissions in the far west of the Basin simulated by many WetCharts ensemble members (Supplementary Fig. 13a). Basin-wide emissions calculated using fluxes upwind of each site derived from gridded WetCharts fields and each site’s regions of influence (Fig. 5) are ~6 TgCH4 y−1 less than their basinwide total (33.0 ± 11.4 TgCH4 y−1), suggesting that our network configuration leads to a low bias, although across-model variation for far-western fluxes in WetCharts is considerable (Supplementary Fig. 13b). Considering the wide variety of approaches: bottom-up (field measurement, remote sensing and process model) and top-down (both in situ and remote sensing), as well as the different areas considered, we find broadly similar emissions between our top-down estimates and the range of previous Amazonian estimates, with the exception of the high fluxes we calculate for the region upwind of SAN. This highlights regional differences in Amazonian emissions, also observed in CH4 flux seasonality and its drivers.
Boxes show the 25th, median, and 75th percentile of fluxes upwind of each site from the WetCharts model ensemble (see “Methods”); whiskers bound the inner 95% of the distribution and small circles show outliers beyond those limits. Red circles and error bars show the 2010–2018 mean and uncertainty for wetland fluxes upwind of each site based on vertical profile data, after some adjustments (Table 1).
Nine-year mean CH4 emissions constitute ~8% of global emissions (576 TgCH4 y−1 5), demonstrating that Amazonia is an important CH4 source to the atmosphere, and our Amazonian CH4 fire emission estimate represents ~45% of the global fire emissions (17 TgCH4 y−1 5). Our Amazonian CH4 wetland emissions also represent ~23% of the global wetland emissions (149 TgCH4 y−1 5). We observed strong regional variability in non-fire CH4 emissions, with northeastern fluxes 175–300% higher than fluxes from other regions. The reason for these large fluxes and their seasonality is not understood and contrasts strongly with wetland flux patterns from WetCharts model ensemble. The southern regions’ flux seasonality appears to be related to EWT; seasonality in the northwest-central region is nearly absent, and while the northeast exhibits seasonality, it correlates with neither temperature nor EWT. While Amazonia is an important global CH4 source, we observed no significant change in emissions between 2010 and 2018, indicating that Amazonia is not significantly contributing to the strong global CH4 enhancement observed over the same period.
Methods
Air sampling and vertical profile regions of influence
We collected a total of 590 vertical air profiles from January 2010 to December 2018 biweekly at four Brazilian Amazonia sites (Fig. 1). The sites were ALF (8.8°S, 56.7°W) in the southeast, SAN (2.8°S, 54.9°W) in the northeast, RBA (9.3°S, 67.6°W) in the southwest-central region and TAB (5.9°S, 70.0°W) until 2012, replaced by TEF in 2013 (3.7°S, 66.5°W) in the northwest-central region. A sampling gap started in April 2015 at all sites and ended in November 2015 at RBA, February 2016 at ALF, and January 2017 at SAN and TEF. Vertical profiles measured at TAB and TEF were analysed as a single time series (TAB_TEF) due to their similar regions of influence and seasonal patterns44.
Air samples were collected in a descending vertical profile from 4420 m a.s.l. to around 300 m a.s.l., using a two-component portable semi-automatic collection system. The first unit of this system consisted of two compressors and rechargeable batteries, and the second unit contained 17 or 12 borosilicate glass flasks (700 mL), installed on board of small aircraft with one or two engines. Vertical profiles were made between 12:00 and 13:00, local time, a period when the planetary boundary layer tends to be well mixed, such that the profiles integrate gas fluxes from large regions under its region of influence (detailed information in Gatti et al.22; Gatti et al.23; Basso et al.24).
We define regions of influence as those areas covered by the density of back-trajectories integrated over all vertical profiles and altitudes (up to 3500 m) integrated on an annual and a quarterly basis per site25,44 (Supplementary Fig. 1). Individual back-trajectories for each sample for each vertical profile and all flights between 2010 and 2018 were calculated by the Hysplit trajectory model48,49, at a resolution of 1 h using 1˚ × 1˚ Global Data Assimilation System (GDAS) meteorological data. Back-trajectories started from the day, time, and sampling altitude (in metres above sea level) from the central horizontal point of each vertical profile going back 13 days prior to sampling. For each site, all the back-trajectories in a quarter (January–March, April–June, July–September, October–December) or annually were binned, and the number of instances (at hourly resolution) that the back-trajectories passed over a 1˚ × 1˚ grid cell was counted to determine the trajectory density in each grid cell up to an altitude of 3500 m a.s.l.
The annual region of influence is defined by those grid cells with trajectories passing through them within the Amazonia mask and excluding grid cells with the lowest 2.5% trajectory density distribution. The mean annual regions of influence (Fig. 1, limited to Amazonia mask, and Supplementary Fig. 1a) were determined by averaging the nine annual regions of influence for each site, by the sum of the number of points (frequency) within each grid cell integrating all vertical profiles in the year and then averaging all nine years25. The region of influence integrates the back-trajectories quarterly in order to understand the patterns of atmospheric circulations at each location and their seasonality (Supplementary Fig. 1b)25. In order to determine the influence of factors possibly related to CH4 fluxes, we used maps of region of influence based on trajectory density to calculate spatial weighting functions for these factors, which means that grids with higher density of trajectories have a larger influence than the grids with lower density of trajectories.
Our study area (Amazonia mask, about ~7.25 × 106 km²) is the Amazonia limit of Eva and Huber50 and includes the Amazonian subregions of Amazonia sensu stricto, Andes, Guiana, Gurupí (tropical and subtropical moist broadleaf forest) excluding the Planalto region (predominantly tropical and subtropical grasslands, savannas, and shrublands)51.
Measurements
Air samples collected at each site (ALF, SAN, RBA, TAB_TEF) were analysed at the National Institute for Space Research (INPE), Brazil, where a replica of the National Oceanic and Atmospheric Administration (NOAA) GHG analytical system was installed for measuring GHG mole fraction in air. The CH4 analysis system is a gas chromatograph (HP 6890 Plus) with flame ionisation detection, a 198 cm pre-column of silica gel 80/100 mesh, a 106 cm column of molecular sieve 5 A 80/100 mesh, and a 12 mL volume sample loop24.
In order to assess the accuracy and long-term repeatability of the CH4 measurements, a previously calibrated sample is measured as an unknown in the system regularly. These results indicate long-term repeatability (one sigma) of 1.0 ppb. Also, INPE and NOAA weekly measurements at NAT were compared between 2010–2018 (a surface Brazilian northeast coast site; Supplementary Fig. 4a), where the samples were taken simultaneously (with 2 pairs of flask, each pair analysed by one of the laboratories). Analyses by INPE and NOAA had a mean difference of 0.24 ± 2.67 ppb (r = 0.98).
Annual mean ∆CH4 vertical profiles
To calculate the annual mean ∆CH4 vertical profiles for each site and each sample/height, background mole fractions were subtracted from the observed vertical profile concentrations at each sample/height. The means were calculated for individual profiles and then averaged to monthly and annual values (Fig. 2).
CH4 fluxes
We used a column budget technique, which consists of the difference between CH4 concentration measured in the vertical profile and the estimated background concentration (∆CH4) based on the travel time of air parcels along the trajectory from the coast to the site, following the methodology in Miller et al.12, Gatti et al.22, D’Amélio et al.52, Gatti et al.23, Basso et al.24 and Gatti et al.44. Thus, the net methane flux FTOTAL_CH4 along the air mass path is calculated according to Eq. 1.
To apply in Eq. 1 we converted mole fractions [nmol CH4 (mol dry air)−1, i.e., ppb] to concentrations (mol CH4 m−3) using the density of air, where temperature (T) and pressure (P) were measured during the vertical profiles. When T and P were not measured, they were calculated using the equation derived for temperature and pressure based on all measured T and P for each site (Eqs. 4–11 following Gatti et al.44). Then, we integrated the mean concentration between levels by the altitude differences (in metres) to calculate fluxes per m2, and to estimate the vertical profile flux we integrated all the estimates. To estimate the travel time t of air-masses from the coast to each sample site, we used back-trajectories for each altitude of the vertical profile using the Hysplit trajectory model.
We estimated the background concentrations following the Air-Mass Back-Trajectories Method (AMBaM)53. The incoming air has larger or smaller contributions from Northern Hemisphere or Southern Hemisphere depending on the Intertropical Convergence Zone (ITCZ) position. Mixing fractions f between NOAA global stations (RBP, ASC and CPT) were estimated based on the latitude and longitude (geographical position) of back-trajectories calculated for each flask/altitude sampled in the vertical profile. For assigning background concentrations, we use the geographical position of each air-mass back-trajectory where it intersects two virtual limits. One is a line from the equator to the NOAA/GML observation site at RPB, the second is a latitude limit, from the equator southwards at 30° W. The background concentration is related to the position the back-trajectory crosses these virtual lines, and this position is based on the positions (latitude and longitude) and concentrations at the corresponding day at the regional stations (RBP, ASC and CPT)53.
CH4 emissions from biomass burning
CH4 emissions from biomass burning were obtained by using the ratio rCH4:CO in ppbCO/ppbCH4 (or mole/mole). Carbon monoxide (CO) is a product of incomplete combustion and could be used as biomass burning tracer23. To estimate the rCH4:CO ratio, we selected profiles only during the dry season, in which a biomass burning plume was identifiable in the profile after subtraction of CO and CH4 background (Supplementary Fig. 14). The rCH4:CO depends on the nature of fire, enabling an estimation of CH4 fraction from biomass burning as FFIRE_CH4 = rCH4:CO × (FCO – FCO_Natural), where FCO is the total CO flux in mgCO m−2 d−1 estimated analogously to CH4 flux for each vertical profile and rCH4:CO is the ratio of the emission related to each site: TAB_TEF (4.9 ± 2.6 ppbCO/ppbCH4, mean of 7 profiles and 2.6 is one sigma), ALF (5.0 ± 1.8 ppbCO/ppbCH4, 20 profiles mean), RBA (4.7 ± 2.2 ppbCO/ppbCH4, 24 profiles mean) and SAN (3.2 ± 1.3 ppbCO/ppbCH4, 9 profiles mean). To isolate the biomass burning flux from FCO it was necessary to consider the effect of a FCO_Natural as a by-product of isoprene emissions by trees54 and from soil55, which was subtracted from the FCO. We estimated FCO_Natural following Gatti et al.44, where the basin-wide average FCO_Natural between the surface and 600 mbar (the approximate maximum altitude of the vertical profiles) was calculated for 2010 and 2011 starting with output from the Belgian Institute for Space Aeronomy (BIRA) IMAGESv2 chemical transport model (CTM). 2010 fluxes were applied to all the dry years (2010, 2015–2016) and 2011 fluxes were applied to all wet years (2011–2014, 2017–2018). The specification of FCO_Natural as described has a lower impact (in general <10%) in the nine-year annual mean FFIRE_CH4 and its variability. These modelled fluxes were then adjusted on a site-by-site basis with a constant offset each year to match the mean total CO flux observed in the late wet season and the transition to the dry season (period without emissions from biomass burning). This biomass burning CO flux (FCO – FCO_Natural) was converted to FFIRE_CH4 using the rCH4:CO emission ratios on a site by site basis.
CH4 emissions from wetlands
Non-fire CH4 fluxes (FNON-FIRE_CH4) are the difference between FTOTAL_CH4 and the FFIRE_CH4 and represent the result of sources and sinks from all processes, except biomass burning, from the region of influence for a specific vertical profile, expressed as monthly and annual means. To estimate wetland fluxes (FWTL_CH4) for the regions upwind of each site we apply corrections to FNON-FIRE_CH4. The correction comes from anthropogenic fluxes (Table 1) and from termites (~0.5 mgCH4 m−2 d−1)20, both negative, and a positive flux correction from CH4 uptake from upland soils30. Emissions observed at night in the forest canopy (~5 mgCH4 m−2 d−1) reported by do Carmo et al.21 are not accounted for, because of their unknown origin. Oxidation of CH4 by OH over land should impact both vertical profiles observed concentrations and background similarly and is also ignored. Possible methane loss between our background sites and the Brazilian coast from oxidation by OH and Cl reactions was estimated to be of order only 1.5 ppb and 0.03 ppb, respectively, assuming a travel time of 2 days and using the loss rates based on model simulations reported by Hossaini et al.56. Considering the difference between profiles mean concentrations and the background of around 30 and 40 ppb, OH and Cl sinks will not have a significant influence on the fluxes estimates. In addition, Gromov et al.57 using observations of δ13C of CO and Wang et al.58 based on modelling study of global Cl, suggested a very limited role for the CH4 sink due to marine boundary layer Cl.
Precipitation
We compared our CH4 fluxes to the data from the Global Precipitation Climatology Project (GPCP) (http://eagle1.umd.edu/GPCP_ICDR/GPCP_Monthly.html, accessed on 25 January 2019) version 1.359. The GPCP data is a daily data with resolution of 1° × 1° from 2010 to 2018 (Supplementary Figs. 5 and 6).
Temperature
Air temperatures at a height of 2 m from the ERA Interim, monthly means of daily means, obtained from the European Centre for Medium-Range Weather Forecasts (ECMWF), available at (https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era-interim, accessed on January 25, 2019)60 with a resolution of 1° × 1° were used.
Equivalent water thickness (EWT)
The Jet Propulsion Laboratory (JPL) monthly land mass grids that contain land water mass anomaly given as EWT derived from the Gravity Recovery & Climate Experiment (GRACE) time-variable gravity observations at 1° × 1° resolution61 were used. For more details see Landerer and Swenson62.
Vapour pressure deficit (VPD)
The VPD product is a measure of the indirect VPD in kPa (resolution of 2.5 arc-minute) of monthly means of temperature and humidity, provided by Climatic Research Unit (CRU) CRU Ts4.063. VPD is the difference near-surface vapour pressure and saturation vapour pressure and reflects the water demand in the surface available for evapotranspiration and soil moisture, water use efficiency by plants, and seasonal large-scale atmospheric fluxes64. The dataset was resampled to a 1° × 1° spatial resolution using the monthly mean.
Burned area
Evaluation of burned area was obtained from with the Moderate Resolution Imaging Spectroradiometer (MODIS) Collection 6 MCD64A1 burned area product65. Collection 6 provides monthly tiles of burned area with 500 m spatial resolution over the globe with an overall accuracy of 97%65. The algorithm uses several parameters for detecting burned area from the Terra and Aqua satellite products, including daily active fire (MOD14A1 and Aqua MYD14A1), daily surface reflectance (MOD09GHK and MYD09GHK), and annual land cover (MCD12Q1)66,67,68. The burned area product was resampled to 1 × 1° spatial resolution.
CH4 anthropogenic emissions
Anthropogenic emissions (from energy sector, industrial processes and product use, agriculture and waste) were obtained from the European Commission, Joint Research Centre (EC-JRC)/Netherlands Environmental Assessment Agency (PBL), Emissions Database for Global Atmospheric Research (EDGAR) v5.0 (1970–2015)27, open access database available at (https://edgar.jrc.ec.europa.eu/overview.php?v=50_GHG).
Land use and cover change data
We used the land use and cover change (LUCC) dataset (classes included: forest, savanna, mangrove, flooded forest, wetland, grassland, mosaic of agriculture and grass, other non-forest natural formations, non-vegetated area, and river, lake and ocean) covering the Pan-Amazon, Mapbiomas Amazonia collection 232 to estimate the relative contribution of different classes of land use and cover change to each region of influence (Fig. 1, Supplementary Table 1 and Fig. 10). In this study natural non-forest class includes data of three different classes from Mapbiomas32: savannah formation, grass land and other non-forest natural formation, and the class others include data of non-vegetated area. MapBiomas Amazonia is an open access database of annual LUCC product derived from Landsat images classified for 1985 to 2018 at 30 m resolution32. Wetlands and other aquatic environments are not well represented and their temporal variability is not included in this dataset.
Missing data
The FTOTAL_CH4 and FFIRE_CH4 fluxes were missing for months in red in Supplementary Fig. 15 at ALF, SAN, RBA and TAB_TEF due to logistical, laboratory/instrumental and funding issues. We applied “Miss Forest”, a nonparametric missing value approach using Random Forest methodology69 to fill these gaps. Nonparametric methods are used when the population is not large and when the data do not follow a defined distribution. For the imputation of missing data several methods were tested, such as Amelia, MICE, Supporting Vector Machine (SVM), KNN, MNLR (multiple non-linear regression) and MissForest. We used as a metric cross-validation with 15% of the known data, evaluating the NRMSE and machine time. The method that gave the best results was MissForest. It is used for continuous and/or categorical data, mainly when phenomena have complex interactions and nonlinear relations70.
After each interaction, the difference between the input and outputs is assessed in a data matrix. The stop criterion is set when input and output differences become larger than a threshold. We applied Miss Forest to gap fill monthly FTOTAL_CH4 and FFIRE_CH4 values individually71, and used 85% of the following monthly variables with the remaining 15% withheld for cross-validation to train the method for temperature, precipitation, burned area and EWT. FFIRE_CH4, FTOTAL_CH4, and cross-validation calculations were computed 1000 times and the results are mean values. Cross-validation was conducted with 15% of random known data for each site for both FFIRE_CH4 and FTOTAL_CH4 at each site. The normalized root mean squared error (NRMSE) for the cross-validation statistics were 0.03, 0.10, 0.03, and 0.04 for FTOTAL_CH4 and 0.01, 0.03, 0.02, and 0.01 for FFIRE_CH4 at ALF, SAN, RBA, and TAB_TEF, respectively. We used the Miss Forest implementation available in the R Language72.
Uncertainty analysis
We estimated the uncertainty by error propagation with Monte Carlo randomisation. We considered the uncertainty in both background concentrations and in air parcel travel time. Air masses from the coast to each sampling site experience convection promoting vertical mixing between the layers of the atmosphere we sampled and those above it, which could result in loss of some surface flux signal through the top of our measurement domain. To quantify these losses we compared concentrations in the upper troposphere (above 3.8 km) with the mean background concentrations for these levels for CH4 and CO (Supplementary Fig. 16a). For CH4 we observed higher concentrations at the top of profile in comparison with the background concentrations, and to account for these vertical losses we considered the mean differences between top of profile and background as background uncertainties in our Monte Carlo error propagation (for CH4 and CO), using the root-mean-square error (RMSE). To estimate the back-trajectory uncertainties we compared HYSPLIT back-trajectory times for 2010 with two different models23, the FLEXPART Lagrangian particle dispersion model73 and back-trajectories derived from the meso-scale model B-RAMS74. Then we considered the largest difference in mean profile travel time from HYSPLIT and the other two models using the RMSE values as back-trajectory time uncertainties. In order to estimate the FFIRE_CH4 uncertainties we accounted for CO flux (FCO and FCO_Natural) uncertainties as the standard deviation of emissions ratios from each site. FCO uncertainties were estimated with the same methodology used for CH4 total flux and for FCO_Natural we used a 25% uncertainty. A summary of the parameters used in the Monte Carlo error propagation is provided in Supplementary Fig. 16b. The theoretical uncertainty for the nine-year mean fluxes is calculated according to Eq. 12, and this assumes that annual fluxes are uncorrelated. We calculate the nine-year uncertainties as Eq. 13 to be conservative, allowing for significant year to year correlation.
WetCharts flux calculation
WetCharts47,75 is a large ensemble of global process-based wetland model CH4 flux estimates. We used the “Full Ensemble” (324 model variants) which is resolved at 0.5° × 0.5° and monthly resolution for 2009 and 2010. We averaged this product to a quarterly 1° × 1° climatology and applied the Amazonia mask. Each of the 324 quarterly flux maps was weighted by a given sampling site’s quarterly region of influence (and grid cell area) between 2010 and 2018, with the WetCharts flux map repeating every year. This resulted in 36 quarterly estimates of upwind flux for each site, which were then averaged to four quarterly climatological estimates (not shown) and then an annual estimate. The distribution of 324 annual fluxes per site is shown in Fig. 5. Supplementary Fig. 13 also shows the mean spatial distribution of the WetCharts fluxes within the Amazonia mask and the standard deviation, per 1° × 1° pixel across annual means from the 324 model variants. The WetCharts basin-wide flux was calculated by area-weighting each annual mean pixel, summing, and then integrating over time.
Mean Amazon flux and extrapolation to the Amazonia mask
We use the same methodology described by Gatti et al.44 to estimate a mean Amazonia flux, dividing Amazonia into three different regions (Supplementary Fig. 17). Region 1 includes the eastern sites, SAN and ALF, and CH4 flux for this region was estimated using the weighted mean flux of SAN and ALF (Eq. 14). Region 2 includes areas upwind of RBA and TAB (2010–2012) and TEF (2013–2018) regions less the region of overlap with Region 1, calculated on an annual basis (Supplementary Fig. 17). Region 2 flux is the weighted mean fluxes for RBA and TAB (2010–2012) and RBA and TEF (2013–2018; Eq. 15). Region 3 represents the area to the west of TAB_TEF and RBA not covered by Region 2, and we assumed that the mean flux was the same as Region 2 (RBA + TAB_TEF weighted mean) for this region. Finally, for the whole Amazonia mask area we computed a weighted flux of Region 1, Region 2 and Region 3 fluxes (Eq. 16) and then scaled to the Amazonian area (~7.25 × 106 km2).
Data availability
The CH4 vertical profile data that support the findings of this study are available from PANGAEA Data Archiving, at https://doi.pangaea.de/10.1594/PANGAEA.934596.
References
Myhre, G. et al. Anthropogenic and Natural Radiative Forcing. In: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. (2013) doi:978-1-107-05799-1.
Nisbet, E. G. et al. Very strong atmospheric methane growth in the 4 years 2014–2017: implications for the Paris agreement. Global Biogeochem. Cycles 33, 318–342 (2019).
Saunois, M., Jackson, R. B., Bousquet, P., Poulter, B. & Canadell, J. G. The growing role of methane in anthropogenic climate change. Environ. Res. Lett. 11, 120207 (2016).
Kirschke, S. et al. Three decades of global methane sources and sinks. Nat. Geosci. 6, 813–823 (2013).
Saunois, M. et al. The Global Methane Budget 2000–2017. Earth Syst. Sci. Data 12, 1561–1623 (2020).
Dlugokencky, E. Trends in atmospheric methane. NOAA/ESRL www.esrl.noaa.gov/gmd/ccgg/%0Atrends_ch4/ (2020).
Dlugokencky, E. J. et al. Observational constraints on recent increases in the atmospheric CH4 burden. Geophys. Res. Lett. 36, L18803 (2009).
Nisbet, E. G., Dlugokencky, E. J. & Bousquet, P. Methane on the rise-again. Science 343, 493–495 (2014).
Jackson, R. B. et al. Increasing anthropogenic methane emissions arise equally from agricultural and fossil fuel sources. Environ. Res. Lett. 15, 071002 (2020).
Schaefer, H. et al. A 21st-century shift from fossil-fuel to biogenic methane emissions indicated by 13CH4. Science 352, 80–84 (2016).
Rosentreter, J. A. et al. Aquatic ecosystems are highly variable sources contributing half of the global methane emissions. Nat. Geosci. 14, 225–230 (2021).
Miller, J. B. et al. Airborne measurements indicate large methane emissions from the eastern Amazon basin. Geophys. Res. Lett. 34, L10809 (2007).
Bloom, A. A., Palmer, P. I., Fraser, A. & Reay, D. S. Seasonal variability of tropical wetland CH4 emissions: the role of the methanogen-available carbon pool. Biogeosciences 9, 2821–2830 (2012).
Wilson, C. et al. Contribution of regional sources to atmospheric methane over the Amazon Basin in 2010 and 2011. Global Biogeochem. Cycles 30, 400–420 (2016).
Wilson, C. et al. Large and increasing methane emissions from eastern Amazonia derived from satellite data, 2010–2018. Atmos. Chem. Phys. 21, 10643–10669 (2021).
Hess, L. L. et al. Wetlands of the lowland Amazon Basin: extent, vegetative cover, and dual-season inundated area as mapped with JERS-1 synthetic aperture Radar. Wetlands 35, 745–756 (2015).
Melack, J. M. et al. Regionalization of methane emissions in the Amazon Basin with microwave remote sensing. Glob. Chang. Biol. 10, 530–544 (2004).
Pangala, S. R. et al. Large emissions from floodplain trees close the Amazon methane budget. Nature 552, 230–234 (2017).
Barbosa, P. M. et al. Dissolved methane concentrations and fluxes to the atmosphere from a tropical floodplain lake. Biogeochemistry 148, 129–151 (2020).
Martius, C. et al. Methane emission from wood-feeding termites in Amazonia. Chemosphere 26, 623–632 (1993).
Carmo, J. B do et al. A source of methane from upland forests in the Brazilian Amazon. Geophys. Res. Lett. 33, L04809 (2006).
Gatti, L. V. et al. Vertical profiles of CO2 above eastern Amazonia suggest a net carbon flux to the atmosphere and balanced biosphere between 2000 and 2009. Tellus, Ser. B Chem. Phys. Meteorol. 62, 581–594 (2010).
Gatti, L. V. et al. Drought sensitivity of Amazonian carbon balance revealed by atmospheric measurements. Nature 506, 76–80 (2014).
Basso, L. S. et al. Seasonality and interannual variability of CH4 fluxes from the eastern Amazon Basin inferred from atmospheric mole fraction profiles. J. Geophys. Res. Atmos. 121, 168–184 (2016).
Cassol, H. L. G. et al. Determination of region of influence obtained by aircraft vertical profiles using the density of trajectories from the HYSPLIT model. Atmosphere 11, 1073 (2020).
European Comission. EDGAR-Emissions Database for Global Atmospheric Research. https://data.europa.eu/doi/10.2904/JRC_DATASET_EDGAR.
Crippa, M. et al. Fossil CO2 and GHG emissions of all world countries - 2019 Report. https://doi.org/10.2760/655913 (2019).
Webb, A. J. et al. CH4 concentrations over the Amazon from GOSAT consistent with in situ vertical profile data. J. Geophys. Res. Atmos. 121, 11,006–11,020 (2016).
Dlugokencky, E. J., Lang, P. M., Crotwell, A. M., Thoning, K. W. & Crotwell, M. J. Atmospheric Methane Dry Air Mole Fractions from the NOAA ESRL Carbon Cycle Cooperative Global Air Sampling Network. ftp://aftp.cmdl.noaa.gov/data/trace_gases/ch4/flask/surface/ (2017).
Keller, M. et al. Soil–atmosphere exchange of nitrous oxide, nitric oxide, methane, and carbon dioxide in logged and undisturbed Forest in the Tapajos National Forest, Brazil. Earth Interact. 9, 1–28 (2005).
Diniz, F. H., Kok, K., Hott, M. C., Hoogstra-Klein, M. A. & Arts, B. From space and from the ground: Determining forest dynamics in settlement projects in the Brazilian Amazon. Int. For. Rev. 15, 442–455 (2013).
Mapbiomas. Proyecto MapBiomas Amazonía - Colección [2.0] de los mapas anuales de cobertura y uso del suelo. http://amazonia.mapbiomas.org/mapas-de-la-coleccion (2020).
França, F. et al. Reassessing the role of cattle and pasture in Brazil’s deforestation: a response to “fire, deforestation, and livestock: when the smoke clears”. Land Use Policy 108, 105195 (2021).
Sawakuchi, H. O. et al. Methane emissions from Amazonian rivers and their contribution to the global methane budget. Glob. Chang. Biol. 20, 2829–2840 (2014).
Clark, D. B. et al. The Joint UK Land Environment Simulator (JULES), model description – Part 2: carbon fluxes and vegetation dynamics. Geosci. Model Dev. 4, 701–722 (2011).
McNorton, J. et al. Role of regional wetland emissions in atmospheric methane variability. Geophys. Res. Lett. 43, 11,433–11,444 (2016).
Ray, D., Nepstad, D. & Moutinho, P. Micrometeorological and canopy controls of fire susceptibility in a forested Amazon landscape. Ecol. Appl. 15, 1664–1678 (2005).
Berenguer, E. et al. Improving the spatial‐temporal analysis of Amazonian fires. Glob. Chang. Biol. 27, 469–471 (2021).
Anderson, L. O. et al. Vulnerability of Amazonian forests to repeated droughts. Philos. Trans. R. Soc. B Biol. Sci. 373 (2018).
Aragão, L. E. O. C. et al. 21st Century drought-related fires counteract the decline of Amazon deforestation carbon emissions. Nat. Commun. https://doi.org/10.1038/s41467-017-02771-y (2018).
Silva Junior, C. H. L. et al. Fire responses to the 2010 and 2015/2016 Amazonian droughts. Front. Earth Sci. 7 (2019).
Anderson, L. O. et al. Disentangling the contribution of multiple land covers to fire-mediated carbon emissions in Amazonia during the 2010 drought. Global Biogeochem. Cycles 29, 1739–1753 (2015).
Walter, B. P. & Heimann, M. A process-based, climate-sensitive model to derive methane emissions from natural wetlands: Application to five wetland sites, sensitivity to model parameters, and climate. Global Biogeochem. Cycles 14, 745–765 (2000).
Gatti, L. V. et al. Amazonia as a carbon source linked to deforestation and climate change. Nature 595, 388–393 (2021).
Tunnicliffe, L. R. et al. Quantifying sources of Brazil’s CH4 emissions between 2010 and 2018 from satellite data. Atmos. Chem. Phys. 20, 13041–13067 (2020).
Bergamaschi, P. et al. Inverse modeling of global and regional CH4 emissions using SCIAMACHY satellite retrievals. J. Geophys. Res. 114, D22301 (2009).
Anthony Bloom, A. et al. A global wetland methane emissions and uncertainty dataset for atmospheric chemical transport models (WetCHARTs version 1.0). Geosci. Model Dev. 10, 2141–2156 (2017).
Stein, A. F. et al. NOAA’s HYSPLIT atmospheric transport and dispersion modeling system. Bull. Am. Meteorol. Soc. 96, 2059–2077 (2015).
Rolph, G., Stein, A. & Stunder, B. Real-time Environmental Applications and Display sYstem: READY. Environ. Model. Softw. 95, 210–228 (2017).
Eva, H. et al. A Proposal for Defining the Geographical Boundaries of Amazonia; Synthesis of the Results from an Expert Consultation Workshop Organized by the European Commission in Collaboration with the Amazon Cooperation Treaty Organization. Report No. 21808-EN (European Commission, 2005).
Olson, D. M. et al. Terrestrial ecoregions of the world: a new map of life on Earth. Bioscience 51, 933–938 (2001).
D’Amelio, M. T. S., Gatti, L. V., Miller, J. B. & Tans, P. Regional N2O fluxes in Amazonia derived from aircraft vertical profiles. Atmos. Chem. Phys. 9, 8785–8797 (2009).
Domingues, L. G. et al. A new background method for greenhouse gases flux calculation based in back-trajectories over the Amazon Basin. Atmosphere https://doi.org/10.3390/atmos11070734 (2020).
Kuhn, U. et al. Isoprene and monoterpene fluxes from Central Amazonian rainforest inferred from tower-based and airborne measurements, and implications on the atmospheric chemistry and the local carbon budget. Atmos. Chem. Phys. 7, 2855–2879 (2007).
Conrad, R. & Seiler, W. Influence of temperature, moisture, and organic carbon on the flux of H2 and CO between soil and atmosphere: Field studies in subtropical regions. J. Geophys. Res. 90, 5699 (1985).
Hossaini, R. et al. A global model of tropospheric chlorine chemistry: organic versus inorganic sources and impact on methane oxidation. J. Geophys. Res. Atmos. 121, 14,271–14,297 (2016).
Gromov, S., Brenninkmeijer, C. A. M. & Jöckel, P. A very limited role of tropospheric chlorine as a sink of the greenhouse gas methane. Atmos. Chem. Phys. 18, 9831–9843 (2018).
Wang, X. et al. The role of chlorine in global tropospheric chemistry. Atmos. Chem. Phys. 19, 3981–4003 (2019).
Huffman, G. J. et al. Global precipitation at one-degree daily resolution from multisatellite observations. J. Hydrometeorol. 2, 36–50 (2001).
Berrisford, P. et al. Atmospheric conservation properties in ERA-Interim. Q. J. R. Meteorol. Soc 137, 1381–1399 (2011).
Landerer, F. JPL TELLUS GRACE Level-3 Monthly LAND Water-Equivalent-Thickness Surface-Mass Anomaly Release 6.0 in netCDF/ASCII/GeoTIFF Formats. https://doi.org/10.5067/TELND-3AJ06 (2019).
Landerer, F. W. & Swenson, S. C. Accuracy of scaled GRACE terrestrial water storage estimates. Water Resour. Res. 48 (2012).
Abatzoglou, J. T., Dobrowski, S. Z., Parks, S. A. & Hegewisch, K. C. TerraClimate, a high-resolution global dataset of monthly climate and climatic water balance from 1958-2015. Sci. Data 5, 1–12 (2018).
Massmann, A., Gentine, P. & Lin, C. When does vapor pressure deficit drive or reduce evapotranspiration? J. Adv. Model. Earth Syst 11, 3305–3320 (2019).
Giglio, L., Boschetti, L., Roy, D. P., Humber, M. L. & Justice, C. O. The Collection 6 MODIS burned area mapping algorithm and product. Remote Sens. Environ. 217, 72–85 (2018).
Vermote, E. F., El Saleous, N. Z. & Justice, C. O. Atmospheric correction of MODIS data in the visible to middle infrared: First results. Remote Sens. Environ. 83, 97–111 (2002).
Justice, C. O. et al. An overview of MODIS Land data processing and product status. Remote Sens. Environ. 83, 3–15 (2002).
Friedl, M. A. et al. MODIS Collection 5 global land cover: Algorithm refinements and characterization of new datasets. Remote Sens. Environ. 114, 168–182 (2010).
Jiang, N. & Riley, M. L. Exploring the utility of the random forest method for forecasting ozone pollution in SYDNEY. J. Environ. Prot. Sustain. Dev. 1 (2015).
Stekhoven, D. J. & Buhlmann, P. MissForest-non-parametric missing value imputation for mixed-type data. Bioinformatics 28, 112–118 (2012).
Junninen, H., Niska, H., Tuppurainen, K., Ruuskanen, J. & Kolehmainen, M. Methods for imputation of missing values in air quality data sets. Atmos. Environ. 38, 2895–2907 (2004).
R Development Core Team. R: A language and environment for statistical computing. (2017).
Stohl, A., Forster, C., Frank, A., Seibert, P. & Wotawa, G. Technical note: the Lagrangian particle dispersion model FLEXPART version 6.2. Atmos. Chem. Phys. 5, 2461–2474 (2005).
Freitas, S. R. et al. The Coupled Aerosol and Tracer Transport model to the Brazilian developments on the Regional Atmospheric Modeling System (CATT-BRAMS) – Part 1: Model description and evaluation. Atmos. Chem. Phys. 9, 2843–2861 (2009).
Bloom, A. A. et al. CMS: Global 0.5-deg Wetland Methane Emissions and Uncertainty (WetCHARTs v1.0). ORNL DAAC,Oak Ridge, Tennessee, USA https://doi.org/10.3334/ORNLDAAC/1502 (2017).
Acknowledgments
This work was funded by many projects supporting the long term measurements and analyses: State of Sao Paulo Science Foundation - FAPESP (2016/02018-2, 2011/51841-0, 2008/58120-3, 2011/17914-0, 2018/14006-4, 2018/14423-4, 2018/18493-7, 2019/21789-8, 2019/23654-2, 2020/02656-4), UK Environmental Research Council (NERC) AMAZONICA project (NE/F005806/1), NASA grants (11-CMS11-0025, NRMJ1000-17-00431, NNX17AK49G), European Research Council (ERC) under Horizon 2020 (649087), 7FP EU (283080), MCTI/CNPq (2013), CNPq (134878/2009-4). We thank numerous people at NOAA/GML who provided advice and technical support for air sampling and measurements in Brazil and for observations from ASC, RPB, and CPT, and the pilots and technical team at aircraft sites who collected the air samples. We also thank J. F. Mueller for modelled biogenic CO fluxes.
Author information
Authors and Affiliations
Contributions
L.S.B. wrote the first version of the manuscript. L.S.B., L.M., L.V.G., J.B.M., M.G., J.M., H.L.G.C., G.T., A.H.S., S.M.C., L.A. and L.E.O.C.A. participated in commenting and reviewing the manuscript; L.V.G., M.G. and J.B.M. conceived the basin-wide measurement program and approach; L.G.D., A.H.S., L.S.B., H.L.G.C., G.T., L.M. and L.V.G. contributed to the region of influence analysis; L.S.B., H.L.G.C., E.A., L.V.G., S.M.C., G.T., J.B.M., L.A. and L.E.O.C.A. contributed to inclusion of climate and human disturbance data; L.G.D., C.S.C.C., S.P.C. and R.A.L.N. participated in analysis of G.H.G. concentrations; J.B.M. provided WetCharts model ensemble estimates and analysis; J.B.M. and L.V.G. provided estimates of the biogenic CO.; and L.S.B., J.B.M., S.M.C., L.M., L.V.G. and M.G. performed uncertainty estimates.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Communications Earth & Environment thanks the anonymous reviewers for their contribution to the peer review of this work. Primary Handling Editors: Joshua Dean and Clare Davis. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Basso, L.S., Marani, L., Gatti, L.V. et al. Amazon methane budget derived from multi-year airborne observations highlights regional variations in emissions. Commun Earth Environ 2, 246 (2021). https://doi.org/10.1038/s43247-021-00314-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-021-00314-4
This article is cited by
-
Dissolved greenhouse gas (CO2, CH4, and N2O) emissions from highland lakes of the Andes cordillera in Northern Ecuador
Aquatic Sciences (2024)
-
Methane-cycling microbial communities from Amazon floodplains and upland forests respond differently to simulated climate change scenarios
Environmental Microbiome (2024)
-
Andean headwater and piedmont streams are hot spots of carbon dioxide and methane emissions in the Amazon basin
Communications Earth & Environment (2023)
-
Global termite methane emissions have been affected by climate and land-use changes
Scientific Reports (2023)
-
Increased Amazon carbon emissions mainly from decline in law enforcement
Nature (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.