Abstract
Future projections of global mean sea level change are uncertain, partly because of our limited understanding of the dynamics of Greenland’s outlet glaciers. Here we study Nioghalvfjerdsbræ, an outlet glacier of the Northeast Greenland Ice Stream that holds 1.1 m sea-level equivalent of ice. We use GPS observations and numerical modelling to investigate the role of tides as well as the elastic contribution to glacier flow. We find that ocean tides alter the basal lubrication of the glacier up to 10 km inland of the grounding line, and that their influence is best described by a viscoelastic rather than a viscous model. Further inland, sliding is the dominant mechanism of fast glacier motion, and the ice flow induces persistent elastic strain. We conclude that elastic deformation plays a role in glacier flow, particularly in areas of steep topographic changes and fast ice velocities.
Similar content being viewed by others
Introduction
The Greenland Ice Sheet has experienced increased mass loss due to global warming over the past decades1. Warmer air and ocean temperatures continue to destabilise outlet glaciers and enhance ice mass loss2. Projecting their future contribution to sea level changes under different climate scenarios has become one of the most fundamental questions for coastal regions3,4,5. While much progress has been made in large-scale ice sheet models, the behaviour and accurate modelling of fast-flowing ice streams remain a high priority for simulating future ice mass changes6,7. The ice discharge of these fast-flowing outlet glaciers into the ocean is a fundamental process in the ice sheet mass-balance8,9. Up to now, little is known on how short-term stress changes control outlet glacier dynamics and hence ice discharge. To model the effect of short-term stress changes, an appropriate material model needs to be employed to represent viscous long-term ice flow and elastic short-term fluctuations of the stress distribution. Current ice flow models discard the elastic part in the underlying material model due to its higher computational demand and complexity10. The obvious question is to what extent elastic deformation is crucial for glacier motion and in which areas elastic quantities become important.
In fast-flowing ice streams, sliding is a major component that determines the amount of ice discharge11,12 and an improved understanding of basal processes is needed to obtain better estimations of the ice outflow13,14. Our current understanding of basal conditions and their parameterisation in ice sheet models limits the ability to model the evolution of ice sheets over the next century15. The subglacial hydrological system is an important factor controlling the stress at the ice base, as a higher water pressure lubricates the base and enhances sliding speeds16,17,18,19. For marine terminating glaciers, a connection between the subglacial hydrological system and the ocean water exists. Ocean tides modulate the water pressure at the grounding line resulting in short-term changes of basal stress. These short-term stress changes are likely transmitted inland and impact the ice dynamics upstream20. As direct observations at the base are sparse, numerical models are valuable tools to investigate the variation of stresses.
While it is widely accepted that ocean tides induce non-negligible elastic strains, other potential sources for short-term changes in stresses exist. Most likely steep slopes or steps in bed topography, where ice moving across bed undulations experiences changing stresses, a prerequisite for developing elastic strains. However, it remains unclear whether and where elastic strains exist within the ice for longer times or decline such that the viscous glacier flow prevails. The impact of elastic contributions related to abrupt stress changes on ice dynamics has not been quantified yet, either numerically or through observations. These elastic strains are related to stresses based on the constitutive equation and are commonly used to indicate material failure (e.g., crevasses, damage, cracks). Interestingly, extensive crevasse fields occur in fast-flowing outlet glaciers in Greenland, which exert an important control on ice discharge towards the ocean. Approaches of linear elastic fracture mechanics are promising to represent rapid failure and crevasse formation in large-scale ice sheet models21. With increasing tensile stresses above a threshold, brittle failure sets in22. Based on these considerations, several logical questions arise: Are the crevasse fields located in regions in which elastic strains and stresses do not decline due to stress changes? Could a viscoelastic model provide novel insights into the role of elastic strains and stresses in Greenland’s outlet glaciers?
So far, observations of the elastic effects have primarily been focusing on tides: In Antarctica, it has been shown that tides can alter glacier flow up to 80 km upstream of the grounding line of large ice streams20,23,24,25,26,27. The tidally-induced vertical motion of ice shelves and floating ice tongues cause changes in the stress distribution and contributes to the variability of glacier flow near the grounding line26,28. A case study of Rutford Ice Stream showed that only a combination of a viscoelastic material model and a non-linear friction law describes observed fortnightly glacier speed modulation appropriately24. The viscoelastic flowline simulation of Bindschadler Ice Stream, West Antarctica, indicated basal motion consistent with flow dominated by basal sliding over a relatively weak till (determined by higher exponents in sliding laws) and not by internal deformation25. These findings suggest a tidal modulation of the glacier motion facilitated by basal sliding. Despite the broad impact of tides on Antarctic ice streams, only a few studies have considered tidally modulated glacier motion on the Greenland Ice Sheet (GrIS)29,30. Observed bending of the ice tongue at Jakobshavn Glacier (at that time 8 km long) reflected elastic and viscous deformation, while fatigue failure caused by tidal flexure results in deep basal and surface cracks along the grounding line29. Although tidal stresses only affected the glacier terminus at Helheim Glacier, observations after a calving event showed changes at least 12 km upstream of the grounding line30. The tidal range around Greenland varies between 0 and 6 m26 with a magnitude that is similar to the tides around the Antarctic Ice Sheet. Observations at a marine-terminating glacier of the Qaanaaq ice cap revealed semi-diurnal speed peaks coinciding with low tides31. Near the calving front of Bowdoin Glacier, tidal forcing and surface speed were in anti-phase. An underprediction of the amplitude of the semi-diurnal variability is presumably related to either inaccuracy in the surface and bedrock topographies or mechanical weakening due to crevassing32.
We employ a viscoelastic model underpinned by an accurate radar-derived ice geometry to investigate the elastic contribution along the central flowline of Nioghalvfjerdsbræ (79°NG), northeast Greenland. The parameters for the simplest homogeneous isotropic viscoelastic material are the viscosity, determining the rate-dependent viscous behaviour, and two elastic constants, namely Young’s modulus, affecting the stiffness, and Poisson’s ratio, specifying the lateral contraction (see “Methods” section). We rely on observed displacements of GPS stations (see “Methods” section) to assess the accuracy of simulated displacements and validate the material rheology. To model basal sliding we have to know the effective water pressure of the subglacial hydrology and an inferred friction coefficient field (see “Methods” section). The effective pressure is the difference between the ice overburden pressure and the subglacial water pressure and results from the confined-unconfined aquifer system (CUAS) model33. Inversion of observed surface velocities provides the friction coefficient field. Based on these results, we show that ocean tides change the ice flow only a few kilometres upstream of the grounding line at 79°NG. Crevasse fields further upstream thus require another mechanism that sustains elastic deformations. A simulation without tides enables us to evaluate the elastic contribution to the glacier flow at 79°NG. We show that sharp bed undulations and glacier motion cause elastic deformations, which do not decline over time. From the gained insights focusing on 79°NG, we discuss how this study sheds light on the elastic deformation of other fast-flowing outlet glaciers of the GrIS (viscous model) as the applied viscoelastic Maxwell model demands that elastic and viscous stresses are the same. In the end, we propose ideas for future modelling work.
Results and discussion
Tidal modulation of glacier flow
For the 79°NG, an outlet glacier of the Northeast Greenland Ice Stream (NEGIS), we first analyse the influence of tides on glacier flow (Fig. 1). In the summer of 2017, we deployed four GPS receivers along a central flowline to measure the tidal influence on glacier flow. The instruments were positioned on the floating part of the ice tongue (GPS-shelf), on the ~4 km wide hinge zone (GPS-hinge) that experiences bending with tides (see “Methods” section), and some 14 km (GPS-GL-14) and 45 km (GPS-GL-45) upstream of the grounding line (defined as the upper limit of the hinge zone in 2017, Supplementary Fig. 1). The measured flow velocities of the GPS stations positioned along a flowline (Fig. 1 and Supplementary Data 1) show an increasing trend towards the grounding line from 290 m a−1 at GPS-GL-45 over 950 m a−1 at GPS-GL-14 to 1460 m a−1 at GPS-hinge and slightly decreases to 1310 m a−1 at GPS-shelf34. These observed velocities are mean values measured over a 14 day period during the summer that are potentially about 10% above winter velocities35, but fit to the simulated surface velocities of the flowline. We recorded three-dimensional surface movements simultaneously over several tidal cycles.
The underlying background map shows the bed elevation hb. Yellow lines represent contours of the basal friction coefficient field k2. White lines denote the simulated water pressure difference Δpw (high tide minus low tide) in the hydrological system. The flowline profile (red line) is used for a flowline model of glacier motion. The grounding line, where the ice becomes afloat is at 0 km. The hinge zone, the zone in which the ice tongue deforms due to bending, is shown by two black lines, one at its upper limit directly at the grounding line and one at the lower limit 4 km downstream the grounding line. The inset shows the CUAS domain that encompasses the NEGIS catchment including the 79°NG catchment as a solid black polygon. The red rectangle marks the area close to the grounding line shown in the figure.
The processed data (see “Methods” section) reveal a tidal signal only in the floating part at GPS-hinge and GPS-shelf (Fig. 2). At 79°NG, we observe no tidal signal at the grounded GPS stations GPS-GL-14 and GPS-Gl-45, which indicates rapid attenuation within a few kilometres upstream of the hinge zone. Though it is not directly comparable, this is in contrast to observations on large ice streams in Antarctica20,23 where the tidal signal is transmitted tens of kilometres upstream of the grounding line. Inspired by the processes occurring in Antarctica, we deployed the GPS stations and were surprised to see no tidal signal 14 km upstream the grounding line. Besides the tidal signal, a superimposed signal was simultaneously recorded by the GPS receivers (Fig. 2b–d). We link this to supraglacial lake drainage35.
a–d Detrended measured and simulated displacements in horizontal (solid lines) and vertical direction (dashed lines) versus time at GPS-GL-45 (a), GPS-GL-14 (b), GPS-hinge (c), and GPS-shelf (d). The locations of the GPS stations are shown in Fig. 1. Black lines present measured GPS displacements, while green lines show simulated displacements obtained with COMice-ve. Blue lines display displacements for a pure viscous model.
We set up a numerical model and compare the simulated displacements with observations. The momentum balance of this simulation is solved for a viscoelastic Maxwell rheology36 (labelled COMice-ve, details see “Methods” section). This viscoelastic model allows us to simulate and distinguish short-term elastic and long-term viscous responses to external loads like ocean tides37,38,39. For the floating ice tongue of 79°NG, we account for observed ocean tides of GPS-shelf in the basal boundary condition. Additionally, we include this tidal signal in the hydrological model CUAS.
The simulated glacier response using a viscoelastic material model reveals an excellent agreement with the observations. We choose elastic constants for Young’s modulus of E = 1 GPa and Poisson’s ratio of ν = 0.325, which are consistent with other studies in Antarctica37,39. Without further tuning, the correspondence of model results and observations is high with differences less than 1% in the horizontal and vertical direction over large parts of the considered time interval (Fig. 2 and Supplementary Data 2). The free-floating ice tongue moves up and down caused by ocean tides and the simulated detrended horizontal and vertical displacement coincide with the observations (Fig. 2d). At both grounded GPS stations GPS-GL-14 and GPS-GL-45 the simulations show no measurable tidal modulation, which agrees with the observations (Fig. 2a, b). We inferred that the high agreement at GPS-hinge solely arises from the elastic contribution in COMice-ve. Horizontal and vertical displacements computed with purely viscous rheology are not capable of reproducing the observed amplitudes or phase responses (Fig. 2c). Although we varied viscosity and basal sliding parameters (Supplementary Discussion 1), those simulation results cannot reproduce the displacements accurately. That means that the bending and modulation of flow speeds in the hinge zone are a result of the viscoelastic nature of ice. Hence, at least a viscoelastic Maxwell material model (two parameter fluid) is required on the lower part of the glacier to match the observations.
The question arises of how a viscoelastic material model and tides influence basal sliding. To what extent are these findings (elasticity influences the glacier flow) only applicable to tidally modulated flow? Other numerical studies also discussed the influence of elastic deformations caused by short-term variations. For instance, large calving events in Greenland cause first a reversal of flow and elastically compress the ice front as large icebergs rotate40. The reversal of the ice flow typically lasts for a few minutes and is then followed by a flow acceleration, increased longitudinal strain rates and enhanced responses to tidal forcing30. Hence, sudden short-term changes like calving events or lake drainage will induce an additional elastic response, which should be investigated in future work and could be the explanation for flow deceleration and acceleration.
Effect of tides on sliding
We intend to get a complete picture between GPS-GL-14 and the grounding line to estimate how far tides reach inland at 79°NG and influence its basal sliding behaviour. Different basal friction laws exist and need to be handled carefully as basal friction is a crucial boundary condition11,41. The applied friction law is Budd-like and non-linear12,42 and relates basal shear stress τb to basal velocity vb, the friction coefficient field k2 and the effective pressure N (see “Methods” section, Eq. 2). As we assume the inferred friction coefficient field to be constant in time for our study (see “Methods” section), changes in the basal shear stress originate from tidal changes in effective pressure and basal velocities. To disentangle the role of each component in the friction law, we analyse the response of the simulated subglacial hydrology to tides resulting in time-dependent effective pressure fields (see “Methods” section). The simulated vertical movement of the floating base caused by tides result in time-dependent displacement and hence velocity changes.
With this tidally modulated setting along the flowline, we show a comprehensive analysis of the glacier system for all quantities included in the basal boundary condition (Fig. 3 and Supplementary Data 3 and 4). Please note that results are shown point-wise relative to a control run (CTRL) without tidal forcing in the subglacial hydrology system (grounded part) and the water pressure (floating part). The simulated head along the flowline (the corresponding elevation of the water level in a hypothetical borehole connecting glacier surface to bed) is very smooth (Fig. 3b) and spatial variations of the effective pressure primarily originate from the ice overburden pressure and thus ice thickness variations. In the hinge zone (from 0 to 5 km), the simulation reveals a tidal influence on the basal velocity where the highest differences to the CTRL run occur at the transition between low to high tide. The amplitude in the basal velocity behaves similar to the displacements (Fig. 2 and Supplementary Fig. 2), where smaller amplitudes appear for the purely viscous or a stiffer material (dashed and dotted lines in Fig. 3d). Simulated velocities and displacements show a tidal dependency that drops from ±10% at the grounding line to ±0.2% at GPS-GL-14 (Fig. 3d) to none for GPS-GL-45 (not shown). For the grounded part, the transition from low to high tides and vice versa induces the largest changes compared to the spatial evolution for all other tidal states.
a Ocean tidal forcing with four coloured points: blue at low tide, yellow at high tide and red, purple at their transition. The gradual decrease is mainly due to the lunar fortnightly tidal signal. b The green line displays the time-independent friction coefficient k2 (left axis); the black lines shows the dimensions of the ice domain and the position of the hydraulic head (right axis). c–e, Ratio of basal shear stress (c), basal flow velocity (d), and effective pressure (e) relative to the control run without tidal forcing ((⋅)rel = (⋅)/(⋅)CTRL). The grey lines of the relative values in panel c–e depict numerous simulation results computed with changing observed tidal variations (a) every 1.5 h. Certain tidal states are highlighted by coloured lines that match the coloured points of panel a. Note that the grounded part is shown on the left axis (black vertical line highlights the position of GPS-GL-14) and the floating part on the right axis (different axis scale in d). d Solid lines show the viscoelastic (ve) simulation with E = 1 GPa, dashed lines depict the purely viscous response and dotted lines represent a viscoelastic simulation for a stiffer elastic material with E = 9 GPa.
Why occur the lowest or highest basal velocities not at high or low tide but the transition points (Fig. 3d)? Although we expect the tidal effects on the hydrological system to be relevant for glacier flow, we conduct a further simulation without tidal modulation to disentangle the effect of tides on the friction law and the rheology. Hence, the effective pressure in the subglacial water system is kept constant (CTRL run) and only the basal boundary condition at the floating tongue experiences tidal modulation. The velocity variations induced by the vertical tidal movement of the floating tongue reaches around 10 km upstream the grounding line. The bending of the floating tongue influences the basal velocity and high tide leads to lower velocities at the base of the grounded ice, while low tide causes higher velocities (Supplementary Fig. 3). This scenario highlights that the tidally dependent change of the hydrological system alters the flow behaviour: the envelopes of the velocity changes occur for the transition between low and high tides (Fig. 3d). If we include tides in the hydrological system, the effective pressure reacts with a decrease in magnitude and a phase shift to tidal forcing depending on the distance to the grounding line (Supplementary Discussion 2). We find the effect of tidal forcing on the hydrological system is limited to a small band up to 20 km upstream the grounding line where the amplitude of the tidal signal decays to only 10% of the signal at the grounding line (Supplementary Figs. 4 and 5). Caused by tidal forcing, relative changes in the effective pressure are small, except at the grounding line (Fig. 3e and Supplementary Figs. 4 and 6). Additionally, tidal-related changes in the simulated basal velocity are only visible over a distance of less than 14 km upstream the grounding line (Fig. 3d), which is consistent with the observations at GPS-GL-14 (Fig. 2). To validate a non-linear friction law at 79°NG similar to the previous work done in Antarctica37, we have to consider grounded GPS stations closer to the grounding line that record tidal modulations.
Previous observations of radio-echo sounding data from NEGIS suggested that upstream areas of the ice stream are controlled by variations in basal lubrication while downstream regions are confined by basal topography43. The observation of the downstream region fits the simulation results of the central flowline model for 79°NG shown here. In the basal shear stress, we see impacts of tides with changes up to 40% to the CTRL run near the steep increase in the bed slope at −9 km, where also the subglacial hydrology reveals tidal effects (Fig. 3c, e). In the last ~5 km upstream the grounding line, the friction coefficient is small and damps changes in the basal shear stress due to tides (Fig. 3b). Low friction coefficients facilitate the fast response of glacier speeds to changes in the basal water pressure, which is in line with areas of seasonal speedup and short pulses of acceleration arising from supraglacial meltwater input modulating basal frictional stresses35. The tidal variation of the hydrology causes a superposed variation in the basal velocity and consequently a larger change in basal shear stress than neglecting ocean tides in the hydrological system. Overall, ocean tides alter the glacier flow in our case not as far inland as in Antarctica20. In our simulations, the area of high transmissivity at 79°NG (Supplementary Fig. 6b) is confined by the steep basal topography −9 km upstream of the grounding line. Large gradients in the bed or surface topography lead to large gradients in ice overburden and effective pressure. These increase channel wall melt rates17 and therefore transmissivity33. The simulated low aquifer transmissivity at ~10 km and further upstream the grounding line hinders the pressure wave to travel further inland at 79°NG (Supplementary Discussion 2). This matches very well with our measurements at GPS-GL-14 where no tidal signal was observed.
What governs glacier motion
Ice sheet models typically neglect the elastic deformation and compute ice sheet flow based on a viscous model. To estimate elastic contributions to glacier flow, it is necessary to get better insights into processes influencing glacier motion. We analyse the role of sliding and vertical shear deformation independent of tides for 79°NG. Based on this analysis, we aim to derive implications for the entire ice sheet of Greenland. The analysis in this section uses (i) a viscoelastic simulation along the flowline of 79°NG and (ii) a continental scale ice sheet simulation. For the latter, we rely on a viscous model since a viscoelastic simulation is unavailable. The overarching goal is to identify regions where the consideration of elasticity is recommended for a better understanding of outlet glacier dynamics.
We analyse vertical profiles of velocity ratios determined by the velocity v = ∣v∣ at each point relative to its basal velocity vb = ∣vb∣ (Fig. 4a). The simulated velocity field differs from a sliding dominated plug flow (grey area) in regions where the contribution of vertical shear deformation is enhanced. Topographic bed changes seem to induce these higher contributions (e.g., at distances of −18 and −9 km). Slightly before the bed bump peak at −9 km, simulated vertical shear deformation is highest and topographic changes slow down the ice at the base (velocity at the surface is larger than at the base). At this location, we find a maximum of 25% higher velocities at the surface. At some locations, the velocity is even lower at the surface than at the base. Such a feature is known from viscoelastic flow over an undulated bed44,45. The surface velocity is up to 5% lower than the basal velocity. In general, plug flow is the dominant mechanism and vertical shear deformation is small. The simulation results fit radar and seismic observations indicating deformable subglacial sediment in the far upstream part of NEGIS, which facilitates sliding46,47. At 79°NG, the simulation results support that fast-moving outlet glaciers flow mainly by basal sliding30.
a Cross-section of 79°NG along ice flow profile (left axis) with the velocity point-wise related to the basal velocity v/vb (colour bar). Blueish colours depict velocities that are more than 2% smaller than its basal velocities, while reddish colours show domains in which v is at least 2% higher than vb. The blue lines (right axis) depict the simulated surface velocities compared to MEaSUREs velocity64,65. b The reddish lines show the normalised friction coefficient and effective pressure along the grounded part of the flowline while the blueish curves present the contribution of viscous to total strain \({M}_{{{{{{\rm{e}}}}}}/{{{{{\rm{v}}}}}}}^{{{{{{\rm{v}}}}}}}\) and the measure of vertical deformation to sliding \({M}_{{{{{{\rm{d}}}}}}/{{{{{\rm{s}}}}}}}^{{{{{{\rm{a}}}}}}}\) that reacts with a slight horizontal delay to the normalised slope of the base shown in grey. All those quantities correspond to one year of simulation time.
To get better insights into the role of deformation in glacier motion, we first analyse the ratio of vertical shear deformation (d) to sliding (s) and second the amount of viscous to total strain (Fig. 4b and Supplementary Data 5). We introduce a measure \({M}_{{{{{{\rm{d}}}}}}/{{{{{\rm{s}}}}}}}^{{{{{{\rm{a}}}}}}}\in [0,1]\) representing the absolute contribution of vertical shear deformation to sliding
with the ice thickness H, the surface and bed elevations hs, hb, respectively. This depth-integrated measure is zero for a sliding dominated plug flow and allows us to identify regions in which shear deformation of the vertical ice column is pronounced. Overall, the magnitude of \({M}_{{{{{{\rm{d}}}}}}/{{{{{\rm{s}}}}}}}^{{{{{{\rm{a}}}}}}}\) is higher near steeper bed slopes (Fig. 4b). Vertical shear deformation does not exceed 22% along the entire flow line, although this profile contains a rather steep basal topography. The visualisation of this measure shows a horizontal shift to the downstream side of the slopes (Fig. 4b). This offset occurs as vertical shear deformation is highest at the end of steep topographic changes indicated by declining slope values. If the friction coefficient reaches low values (near the grounding line or at a distance of −35 km), vertical shear deformation to sliding \({M}_{{{{{{\rm{d}}}}}}/{{{{{\rm{s}}}}}}}^{{{{{{\rm{a}}}}}}}\) is small (Fig. 4b). The reduction of friction facilitates plug-flow. In the remaining regions, a deformation dependency on slope and friction coefficient is apparent. For a viscous simulation of GrIS motion48, we also consider the contribution of vertical shear deformation to sliding (Fig. 5a). Sliding is dominant in all fast-moving areas but also in the interior of Greenland. Vertical shear deformation occurs up to 35% in the interior or at thin margins where ice is presumably frozen to ground49.
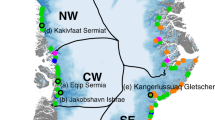
a The contribution of vertical deformation to sliding \({M}_{{{{{{\rm{d}}}}}}/{{{{{\rm{s}}}}}}}^{{{{{{\rm{a}}}}}}}\) where the blue colour means that sliding dominates glacier flow. b–e Changes in first principal stress dσ1/dt in flow direction (darker red colour means higher stress change) superimposed by elastic first principal strain ε1e (darker blue colour means higher elastic strain) for four glacier basins b Jakobshavn Isbræ, c 79°NG and Zacharias Isbræ with the considered flowline in white, d Helheim Glacier, and e Kangerlussuaq Glacier. The black line surround areas of massive crevasse fields.
The remaining question is whether bed undulations can induce elastic responses that persist and consequently contribute to glacier motion. The viscoelastic Maxwell model for the flowline of 79°NG allows us to distinguish between the viscous and elastic strain contribution as both sum up to the total strain36. We exploit this property and quantify the ratio of viscous to total strain. We define the number \({M}_{{{{{{\rm{e}}}}}}/{{{{{\rm{v}}}}}}}^{{{{{{\rm{v}}}}}}}\in [0,1]\) based on Euclidean matrix norms of the viscous (ϵv) and elastic (ϵe) strain
This measure \({M}_{{{{{{\rm{e}}}}}}/{{{{{\rm{v}}}}}}}^{{{{{{\rm{v}}}}}}}\) reaches the value 1 for vanishing elastic strains. Without short-term changes of tides, the amount of viscous relative to total strain consists of 6% elastic strain on average to a maximum above 30% for the grounded part (Fig. 4b difference of \({M}_{{{{{{\rm{e}}}}}}/{{{{{\rm{v}}}}}}}^{{{{{{\rm{v}}}}}}}\) to 1, Supplementary Fig. 7). The ratio of viscous to total strain is close to 1 at the free-floating ice tongue, meaning that the viscous flow dominates as no short-term changes happen. Once elastic strains caused by transient initialisation vanish, the partition of viscous to total strain \({M}_{{{{{{\rm{e}}}}}}/{{{{{\rm{v}}}}}}}^{{{{{{\rm{v}}}}}}}\) remains similar for long simulation times (Fig. 4b for 1a, Supplementary Fig. 7 for up to 10a). However, the ice flow over undulated beds induces unexplored time-independent elastic deformations occurring at grounded parts of the fast-flowing 79°NG.
So far, large ice sheet models did not consider elastic contributions. The implication to neglect this component is not clear yet. For a glacier motion above undulated beds, the elastic strain increases and kinematics lead to higher displacements (integral of the strain), which enhance the flow velocity of the glacier (Supplementary Fig. 8). The results of the viscoelastic flowline simulation reveal the existence of elastic strain for changing bed slopes (Fig. 4b). At 79°NG, bed slopes are too fluctuating for the elastic strain to vanish (which is due to fluctuating stresses), except near −4 or −40 km where \({M}_{{{{{{\rm{e}}}}}}/{{{{{\rm{v}}}}}}}^{{{{{{\rm{v}}}}}}}\) is almost 1. Consequently, a rougher bed fosters more elastic deformation. For a viscoelastic Maxwell model, the total strain is the sum of elastic and viscous strain (see “Methods” section). The elastic strain is around one order of magnitude smaller than the viscous strain (Supplementary Methods 1 and Supplementary Fig. 9). For instance, a constant elastic strain of 2‰ over 50 km induces an additional elastic elongation of 100 m. In the end, a viscoelastic simulation reveals a higher velocity for a fast-flowing outlet glacier than a viscous one caused by the additional elastic deformation.
We aim to transfer local insights at 79°NG to Greenland by determining regions in which elastic deformations may be crucial for understanding outlet glacier dynamics. To deal with the lack of a viscoelastic simulation for entire ice sheets, we leverage the fundamental character of a Maxwell rheology: elastic and viscous stresses are equal. Simulated stresses obtained by a viscous model (initialisation experiment48) can be used to compute principal (i.e., largest) elastic strains (see “Methods” section) on the entire surface of the GrIS (Fig. 5b–e and Supplementary Fig. 10). Without short-term fluctuations, we would expect that the elastic strain declines with time and vanishes. The largest elastic strain is found in fast-moving outlet glaciers and reaches at most 1.14‰. As the elastic strain does not vanish for Greenland (Fig. 5b–e and Supplementary Fig. 10), we analyse the change in first principal stress with respect to time (see “Methods” section). Changing first principal stress over time often coincide with regions of large elastic strains in the fast-moving parts of outlet glaciers (Fig. 6 and Supplementary Fig. 10). In these areas, elastic strains did not decline as changing stresses prevent this. The estimated occurrence of elastic strains at 79°NG (Fig. 5c) matches with the spatial extent of time-independent elastic strain from the viscoelastic flowline simulation (Fig. 4b). This agreement indicates that slope change and viscous flow above 250 m a−1 cause stress changes inducing elastic strains. For assessing the area of Greenland’s ice affected by an elastic contribution arising from bed undulations, we use the BedMachine bedrock topography50 and compute the directional slope (Supplementary Fig. 11). A slope larger than 5% is present in around 10% of the grounded ice of GrIS. For the flowline simulation of 79°NG, the mean slope of the last 45 km upstream the grounding line is 4.7% where at least in this region the elastic strain is not negligible (Fig. 4b).
Areas of massive crevasse fields based on the DEM-residual product are displayed in yellow, superimposed on the MEaSUREs velocity field64,65 in purple colour and stress changes due to glacier motion in red colour for a the northwestern part, b the northern part, c the northeastern part, d the southeastern part, and e the southwestern part of Greenland. The given values in the overview figure denote changes in water pressure caused by a tidal range for some prominent outlet glaciers in Greenland. Areas of crevasses are consistent with areas of high changes in stress.
How does this time-independent elastic strain compare in magnitude to tidal forcing? We first estimate the stress change caused by ocean tides ranging from 0 to 6 m around Greenland (Fig. 6). For the three floating tongues glaciers, tides span from ~0.5 m for Ryder Glacier, ~1.0 m for 79°NG to ~2.2 m for Petermann Glacier. Due to hydrostatic equilibrium, a diurnal tidal range induce 5–20 kPa d−1 stress change at the floating tongues. At 79°NG, the estimated stress change is 10 kPa d−1 = 3650 kPa a−1 at the glacier tongue. Independent of tides, we reach one third of this stress change magnitude at the grounded part of outlet glaciers for Jakobshavn Isbræ, 15% at Kangerlussuaq Glacier and 10% at Helheim Glacier (Fig. 6). We find in other outlet glaciers close to the grounding line about 10% of this value declining to 1% over some tens of kilometres. In the flowline simulation of 79°NG, elastic strains occur in sliding dominated flow and in regions with higher vertical deformation (Fig. 4). In the end, faster flow over rougher beds induces higher elastic strains caused by higher stress changes. Caused by the motion of fast-flowing outlet glaciers over undulated beds, the stress changes are lower of those due to tides. While tides force an elastic elongation and compression on daily time scales, the motion of fast-flowing outlet glaciers induces an elastic elongation independent of time.
As there is no way to conduct in-situ observations of stress, we relate elastic deformation to the occurrence of cracks. Cracks are a representation of the solid nature of a material. Brittle failure is determined by a small process zone in which local elastic quantities causes a fracture, not viscous ones51. The extensive crevasse fields that we observe in outlet glaciers in Greenland are illustrative proofs of this elastic contribution (Supplementary Figs. 10 and 12). Furthermore, crevasse fields in ablation zones facilitate surface meltwater discharge to the ice base. This contributes to seasonal speed-up via lubrication, which increases elastic deformation. Damage in the lower tens kilometres of tidewater glaciers also controls calving dynamics of tidewater glaciers and thus ice discharge rates as feedback22. Taking into account that Jakobshavn Isbræ and Kangerlussuaq Glacier contributed to an estimated 8 mm of global sea-level rise over the last century2, understanding their future response is crucial. All ice discharge of the GrIS and in particular Jakobshavn Isbræ and Kangerlussuaq Glacier (Fig. 5b, d and Supplementary Fig. 13) takes place in a settings where the bed is lubricated52, sliding speeds are high (Fig. 5a)53,54,55,56,57, surfaces are crevassed (Fig. 5b–e and Supplementary Data 6)21,35,58,59,60. In regions where sliding is dominant, the surface velocity is similar to the basal velocity and areas of high surface velocities fit areas of massive crevasse fields (Supplementary Methods 2 and Supplementary Fig. 12). Crevasses also occur in slow-moving outlet glaciers in which the basal topography will lead to necessary stress changes (Fig. 6) and to time-independent elastic strains (Supplementary Fig. 10). The extensive match of massive crevasse fields with areas of large stress change supports the claim that glacier flow over undulated beds induces persistent (time-independent) elastic strains.
Conclusion
By comparing GPS observations with numerical modelling, we demonstrated the need to describe tidal effects on ice by a viscoelastic Maxwell model to reproduce glacier dynamics in the lower part of the 79°NG. The tidal influence, not captured by a viscous model, is limited to the hinge (bending) zone downstream the grounding line and up to 10 km upstream the grounding line. For the grounded ice, the subglacial hydrological system is relevant as it causes a phase delay in basal velocities. In the absence of tides, we found sliding to be the dominant mechanism of fast-moving glacier motion, and a absolute contribution of vertical shear deformation to sliding of less than 22% for the viscoelastic simulation of 79°NG up to 35% for the viscous simulation of Greenland. Deducing from our viscoelastic modelling, the ice flow induces a persistent elastic to total strain of 6% on average up to a maximum of 30% for the considered flowline of 79°NG.
Based on the viscoelastic simulation of 79°NG, we developed a new perspective on deformation in outlet glaciers by transferring our findings from the flowline model to a continental scale simulation. We demonstrated that elastic deformation additionally contributes to the motion of outlet glaciers. Independent of tides, elastic deformation plays a role in areas of non-steady stress fields, such as near steep changes in topography or as ice flow speeds up. These new insights are a step forward to better understand the motion of glaciers since the identified regions are currently poorly constrained in ice flow models. In future works, improving the fidelity of ice flow models by considering the elastic contribution may capture the behaviour of fast-moving outlet glaciers. Under the overarching goal of narrowing uncertainties in sea-level projections, it is arguably important to assess how ice discharge to the ocean is affected by including an elastic deformation in the overall ice flow.
Methods
Viscoelastic modelling
The simulations COMice-ve were conducted with the finite element programme COMSOL applying a viscoelastic Maxwell material model that solves for the unknown displacements (along-flow and in thickness direction)36. We prescribe the ice geometry along the flowline from a high-resolution basal topography obtained from airborne ultra wide-band radar measurements. All simulation results are obtained using this high-resolution geometry subject to a non-linear Budd-like friction law42. The position of the grounding line is the lowest position of the landward limit of the hinge zone defined from SAR interferometry. We show that this landward limit (upper flexure limit) does not move more than 500 m in the time period of observations. Such small changes make no difference in the simulation results, and for simplicity we assume a fixed grounding line at the lowest position of the upper flexure limit derived by SAR interferometry.
COMice-ve solves the underlying viscoelastic Maxwell equations in a small strain setting that is valid for simulation times up to few years. We discretise the model domain with a triangular mesh with a horizontal resolution of 100 m. This fine spatial resolution is necessary to get rid of the mesh discretisation error (Supplementary Fig. 14). The shape functions for the unknown displacements are quadratic Lagrange polynomials. The viscous strain components are additional internal variables for the Maxwell rheology and we use shape functions of linear discontinuous Lagrange type to save computational effort. The viscous and elastic stress of a Maxwell material are the same while the strain is the sum of elastic and viscous strain. The material relation of the volume-preserving deviatoric stress (\({{{{{{{{\boldsymbol{\sigma }}}}}}}}}^{{{{{{\rm{D}}}}}}}={{{{{{{\boldsymbol{\sigma }}}}}}}}-1/3\ {{{{{{{\rm{tr}}}}}}}}({{{{{{{\boldsymbol{\sigma }}}}}}}}){{{{{{{\boldsymbol{I}}}}}}}}\)) to elastic strain \({{{{{{{{\boldsymbol{\varepsilon }}}}}}}}}_{\,{{\mbox{e}}}\,}^{{{{{{\rm{D}}}}}}}\) or viscous strain rate \({\dot{{{{{{{{\boldsymbol{\varepsilon }}}}}}}}}}_{\,{{\mbox{v}}}\,}^{{{{{{\rm{D}}}}}}}\) is given by the constitutive equation
with the elastic material constant μ = E/(1 + ν)10. The viscosity η is non-linear and based on Glen’s flow law using a temperature field from previous modelling61. We choose the same model parameters as used in previous work36. The major difference to previous applications investigating calving of ice shelves36,62 is the incorporation of a friction law. The general friction power law (Budd-like) relates the basal shear stress (τb) to the sliding velocity vb
with the stress exponent m. This exponent is positive and unequal to 1 for a non-linear realisation of the friction law. We choose m = 3 and adjust the unknown friction coefficient field k2 (see section “Inversion for basal friction coefficient” in “Methods” section) to result in a modelled flow velocity that best matches the observed surface velocity37,63. For the effective pressure N = pi − pw, the difference of ice overburden pressure pi and the subglacial water pressure pw, and the friction coefficient field k2 we rely on external products. The effective pressure is obtained from a subglacial hydrology model. The output is used to perform a one-way coupling by feeding the resulting spatial and temporal distribution of the effective pressure of the subglacial system along the flowline back into the friction law (basal boundary condition for grounded ice in the viscoelastic model). The friction coefficient field is inferred by solving an inverse problem for the nonlinear friction law. The inferred friction coefficient \({k}_{{{{{{{{\rm{inv}}}}}}}}}^{2}\) is related to a simpler effective pressure parameterisation Ninv applied for the inversion. Consequently, we adjust the unknown k2 to include in the friction law of the viscoelastic model by the following rule:
This re-scaling ensures that the basal shear stress fed to COMice-ve is comparable to the basal shear stress, which is derived from inversion. The boundary condition at the ice-atmosphere interface is traction-free and at the inflow boundary, we take a constant velocity based on the MEaSUREs velocity data-set64,65. Given the observed vertical displacements of the GPS-shelf, we can compute the tidal pressure field perturbation at the base of the ice tongue. The floating ice mass is subject to a hydrostatic water pressure field normal to the submerged ice-ocean boundary line, depending on tide height (e.g., high tide leads to larger water pressure).
We put much effort in reproducing the observed velocities in the grounded part simulated by COMice-ve. However, the 2D flowline model lacks lateral resistance exerted by the fjord side-walls at the floating tongue. As this effect is inherently not covered we rely on a buttressing formulation66. The lateral resistance is accounted for over the whole floating tongue area (i.e., x > xgl) by adding a body force f in the momentum balance equation, such that
with vx the velocity in horizontal direction. In the grounded part, the lateral resistance coefficient K is zero, while on the floating tongue K > 0. The exponent mlr is set equal to m. Here, we tune the lateral resistance coefficient spatially to obtain a reasonable decline of flow velocities downstream from the grounding line.
We conducted the benchmark experiments ISMIP-HOM B and D for verification of the long-term viscous response of the applied viscoelastic model (Supplementary Methods 3 and Supplementary Figs. 8 and 15). The simulated short-term elastic response with the applied model was already verified62.
Global positioning system (GPS) processing
The GPS data were processed using the GIPSY-OASIS software package including high-precision kinematic data processing methods67 with ambiguity resolution using Jet Propulsion Laboratory (JPL)’s orbit and clock products, constraint on kinematic position solution. We use the GIPSY-OASIS version 6.4 developed at JPL, and released in January 202068. We use JPL final orbit products which include satellite orbits, satellite clock parameters and Earth orientation parameters. The orbit products take the satellite antenna phase centre offsets into account. The atmospheric delay parameters are modelled using the Vienna Mapping Function 1 (VMF1) with VMF1grid nominals69. Corrections are applied to remove the solid Earth tide and ocean tidal loading. The amplitudes and phases of the main ocean tidal loading terms are calculated using the Automatic Loading Provider (http://holt.oso.chalmers.se/loading/) applied to the FES2014b70 ocean tide model including correction for centre of mass motion of the Earth due to the ocean tides. The site coordinates are computed in the IGS14 frame71. We convert the Cartesian coordinates at 5 min intervals to local up, north and east for each GPS site monitored at the surface of the 79°NG. In addition, we use Waypoint GravNav 8.8 processing software. We applied kinematic precise point positioning (PPP) processing using precise satellite orbits and clocks. The site coordinates are computed in the IGS14 frame and converted to WGS84 during data export at 15 s interval. To avoid jumps between daily solutions of the Waypoint PPP product, as the data is recorded in daily files, we merged three successive files prior to processing to enable full day overlaps. In a second step, the 3-day solutions are combined using relative point to point distances. To avoid edge effects, we combined the files in the middle of each 1-day overlap and removed outliers. To estimate the vertical and horizontal displacements we detrended the vertical, northing and easting components of the data after mapping into a polar-stereographic projection and alignment in the ice flow direction. Finally, the detrended data was low pass filtered to suppress signal frequencies larger than 1/3600 Hz and re-sampled to 5 min interval to match the GIPSY-OASIS product. A comparison of both processing software products revealed very similar results, with slightly less noise observed in the GIPSY-OASIS product (Supplementary Figs. 16 and 17). The PPP processing with the GIPSY-OASIS software Package of the GPS-shelf data was used as input for the simulation.
Modelling of subglacial hydrology
We applied CUAS to compute the effective pressure N = pi − pw at the ice base. The model uses an equivalent porous medium (EPM) approach and accounts for efficient and inefficient drainage. A Darcy-type groundwater flow equation for the EPM is used to evolve the hydraulic head h, where the transmissivity T locally adjusts based on channel and cavity evolution. Areas of high transmissivity represent efficient (channelised) flow, whereas low transmissivity is interpreted as inefficient (distributed) flow.
We used a new version of the BedMachine geometry for Greenland50 including the latest AWI airborne data72. In addition to ice sheet basal melt from the Parallel Ice Sheet Model (PISM) output73, we updated and extended the domain outline. We have interpolated the data sets onto a 1.2 km resolution grid (coarse) for the entire NEGIS area and a 300 m resolution grid (fine) covering the area around the 79°NG (Supplementary Fig. 18). We manually set the domain outlines guided by the BedMachine ice mask, the pressure-adjusted basal temperature contour of 0.1 °C of the PISM output, digitised ice front and grounding line positions, and ice flow velocities (≥10 m a−1). We used no-flux boundary conditions at lateral margins (homogeneous Neumann boundary conditions for the head) and Dirichlet boundary conditions (zero head) at grounding lines. At the ocean boundary the transmissivity was set to \({T}_{\max }=100\ {{{{{{{{\rm{m}}}}}}}}}^{2}\ {{{{{{{{\rm{s}}}}}}}}}^{-1}\) while the initial value was 0.2 m2 s−1 elsewhere. We chose the subglacial water pressure to be equal to the ice overburden pressure as initial condition for the head. We choose the same model parameters as used in previous work33.
The output of a 50 years long steady-state run on the coarse grid (Supplementary Fig. 18) was used to run a 1 year long simulation on the fine grid in the 79°NG nested sub-domain to let the model adjust to the changes in grid resolution. The effective pressure at the end of this spin-up was used to adjust the friction coefficient (Eq. 3). We run the model for additional 19 days with and without tidal forcing at the grounding line with hourly output to provide time series of N along the profile shown in Fig. 1 as input for COMice-ve (Eq. 2). We applied the tidal forcing as a time dependent Dirichlet boundary condition for the head at the 79°NG grounding line.
The simulated subglacial drainage system (Supplementary Fig. 18a, b) shows relatively low effective pressure and transmissivity at the land terminating ice margin, indicating less efficient drainage. Observations indicate that efficient channels can form in the ablation area at the ice sheet margin74. At the margin, the ice is usually thin (decreased creep-closure rates), the surface slope is steep and thus, the gradient of the hydraulic potential is large (enhanced channel wall melt). A sufficient amount of water from surface runoff or lake drainage is available at the glacier base via surface-to-bed hydrological connections (e.g., crevasses or moulins) to allow efficient channel formation. In the model, only ice sheet basal melt is considered as the supply for the hydrological system33. At the land terminating margin, basal melt from the PISM simulation is low or absent and thus efficient drainage is inhibited in our simulations. The transmissivity is high in the vicinity of the grounding line indicating efficient (channelised) water transport and declines with distance upstream. In this area, N is close to zero and increases towards GPS-GL-14.
Inversion for basal friction coefficient
The viscoelastic NEGIS ice flow model setup makes use of a basal friction coefficient field \({k}_{{{{{{{{\rm{inv}}}}}}}}}^{2}\) that is retrieved by an inversion method. For the inversion of the basal friction coefficient, we operate the Ice-Sheet and Sea-level System Model75,76, an open source finite element flow model appropriate for continental-scale and outlet glacier applications. The modelling domain is the flowline profile (Fig. 4) and the ice flow is modelled by the full-Stokes equations. Model calculations are performed on a structured finite element grid with a horizontal resolution along-flow of 0.2 km. The domain is vertically extruded with 15 layers refined to the base. A thermo-mechanical coupling is not performed, but a realistic ice rigidity is prescribed based on thermal spin-up77. We performed the inversion for the two different bed geometries: (1) BedMachine geometry for Greenland50 including the latest AWI airborne data72 and (2) the high-resolution basal topography from airborne ultra wide-band radar measurements.
Within the inverse problem a cost function (J), that measures the misfit between observed, vobs, and modelled horizontal velocities, vx, is minimised. We use the observed velocities from the MEaSUREs project64,65 as target within the inversion. This data-set composes a long-term mean (20a) from several remote sensing products and is independent of our GPS measurements. Please note that vobs is the velocity in the curvilinear coordinate system along the flowline. The cost function is composed of two terms which fit the velocities in fast- and slow-moving areas. A third term is a Tikhonov regularisation to avoid oscillations due to over fitting. The cost function is defined as follows:
where ε is a minimum velocity used to avoid singularities and Γs and Γb are the ice surface and ice base, respectively. An L-curve analysis was performed to pick the Tikhonov parameter γt (Supplementary Fig. 19a). We obtained a good agreement to the observed velocities by choosing γ1 = 10, γ2 = 1 and γt = 1 × 10−8.
The inverse problem is run for the non-linear friction law (Eq. (2)), but uses a simple parameterisation of the effective pressure78 with \(N={\varrho }_{{{{{{\rm{i}}}}}}}\ g\ h+\min (0,{\varrho }_{{{{{{{{\rm{w}}}}}}}}}\ g\ {z}_{{{{{{{{\rm{b}}}}}}}}})\), where h is the ice thickness, hb the glacier base and ϱi = 910 kg m−3, ϱw = 1000 kg m−3 the densities for ice and fresh water, respectively. The parameterisation accounts for full water-pressure support from the ocean wherever the ice sheet base is below sea-level, even far into its interior where such a drainage system may not exist. With this parameterisation of the effective pressure, the inferred friction coefficient field is independent in time. The obtained results for the inferred friction parameters \({k}_{{{{{{{{\rm{inv}}}}}}}}}^{2}\) and simulated surface velocities are shown in Supplementary Fig. 19b, c.
Hinge zone by means of interferometry
We applied Synthetic Aperture Radar Interferometry (InSAR) on Sentinel-1 TOPS SAR data to detect the upper and lower limit of tidal flexure. Interferograms are formed from interferometric wide swath single look complex data acquired at times t1 and t2 separated by a temporal baseline of 6 days. Assuming constant horizontal ice flow within a 6 day time period we subtracted another interferogram with data acquired at times t2 and t3 to isolate vertical displacements due to ocean tides61,79,80. This way we were able to produce 26 double differential interferograms from which we manually delineated the upper and lower flexure limit (Supplementary Fig. 1). To minimise the effect of inter annual grounding line migration when compared to the model results we focus on the year 2017. Along the profile used for the viscoelastic modelling we found a maximum variation of 520 m and 880 m for the upper and lower flexure limit, respectively. These variations result from two main reasons (1) the timing between satellite pass and tide level is always different and (2) the horizontal ice flow is not constant within 6 days and hence residua remain in the double differential interferograms81.
Changes of first principal stress for Greenland
The elastic deformation of a Maxwell material is non-negligible when subject to short-term changes in stress, such as those caused by calving events or ocean tides. As a Lagrangian ice parcel passes over an undulating bed, the stress experienced might, however, also change enough to induce non-negligible elastic deformation. Caused by such stress changes (Fig. 6), we considered areas where time-independent elastic strains might occur caused by the viscous glacier flow (Supplementary Fig. 10). Elastic stresses are proportional to elastic strains and viscous stresses are related to viscous strain rates based on their constitutive equations. The elastic strain exists wherever viscous strain rate is present—hence in any regions of non-zero velocity gradients. To sustain elastic strain, the temporal change of stresses is necessary as the long-term stress response of a Maxwell model corresponds to the one of a viscous fluid (Supplementary Fig. 8).
Based on the MEaSUREs velocity field64,65 we generate a set of more than 60,000 flowlines with a point to point spacing of 200 m. The seed points of the flowlines were distributed every 5 km across Greenland, where the surface elevation exceeded 500 m. Along each flowline, we estimate the change of first principal stress over time using a raster with 500 m pixel resolution interpolated from the simulated first principal stress data set. We choose the pixel spacing to preserve the finer mesh used in the simulation in areas of fast flow. In total, we interpolate the stress change of more than 100 million points back to the initial input stress field using the same inverse distance weighting interpolation scheme.
To estimate the change in water pressure over a tidal cycle around Greenland, we used the Arctic Ocean Tidal Inverse Model82,83. We apply the model to a 5 km grid covering Greenland’s coastline (including a buffer zone of 50 km towards the ocean) in a temporal resolution of 10 min for a tidal cycle (one month). Finally, the tidal range is given by the difference of the tide level extrema within each Pixel. This allows us to get a rough idea of the change in water pressure and its regional variation around Greenland (Supplementary Fig. 10).
Data availability
Processed GPS data (https://doi.org/10.1594/PANGAEA.928940) are available at the World Data Center PANGAEA. The new BedMachine data-set is available through NSIDC (https://nsidc.org/data/IDBMG4). Source data for Figs. 1–5 are provided as Supplementary data.
Code availability
The mph file of the finite element software COMSOL Multiphysics (Version 5.6) of COMice-ve used for this study is available via AWI’s gitlab (https://gitlab.awi.de/jchristm/viscoelastic-79ng-greenland) and zenodo (https://doi.org/10.5281/zenodo.5507115). The hydrology model CUAS is available via zenodo (https://doi.org/10.5281/zenodo.5506953).
References
Shepherd, A. et al. Mass balance of the Greenland Ice Sheet from 1992 to 2018. Nature 579, 233–239 (2020).
Khan, S. A. et al. Centennial response of Greenland’s three largest outlet glaciers. Nat. Commun. 11, 5718 (2020).
Larour, E., Ivins, E. R. & Adhikari, S. Should coastal planners have concern over where land ice is melting? Sci. Adv. 3, 11 (2017).
Goelzer, H. et al. The future sea-level contribution of the Greenland ice sheet: a multi-model ensemble study of ISMIP6. Cryosphere 14, 3071–3096 (2020).
Seroussi, H. et al. ISMIP6 Antarctica: a multi-model ensemble of the Antarctic ice sheet evolution over the 21st century. Cryosphere 14, 3033–3070 (2020).
IPCC. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (eds Stocker, T. F. et al.) (Cambridge University Press, 2013).
Oppenheimer, M. et al. Sea level rise and implications for low-lying islands, coasts and communities. In IPCC Special Report on the Ocean and Cryosphere in a Changing Climate (eds Pörtner, H.-O. et al.) (In press, 2019).
Mouginot, J. et al. Forty-six years of Greenland Ice Sheet mass balance from 1972 to 2018. Proc. Natl. Acad. Sci. 116, 9239–9244 (2019).
Choi, Y., Morlighem, M., Rignot, E. & Wood, M. Ice dynamics will remain a primary driver of Greenland ice sheet mass loss over the next century. Commun. Earth Environ. 2, 26 (2021).
Darby, R. Viscoelastic Fluids: An Introduction to their Properties and Behavior, vol. 9 (Marcel Dekker, Inc., 1976).
Brondex, J., Gagliardini, O., Gillet-Chaulet, F. & Durand, G. Sensitivity of grounding line dynamics to the choice of the friction law. J. Glaciol. 63, 854–866 (2017).
Brondex, J., Gillet-Chaulet, F. & Gagliardini, O. Sensitivity of centennial mass loss projections of the Amundsen basin to the friction law. Cryosphere 13, 177–195 (2019).
Iverson, N. R., Helanow, C. & Zoet, L. K. Debris-bed friction during glacier sliding with ice-bed separation. Ann. Glaciol. 60, 30–36 (2019).
Zoet, L. K. & Iverson, N. R. A slip law for glaciers on deformable beds. Science 368, 76–78 (2020).
Franke, S. et al. Complex basal conditions and their influence on ice flow at the onset of the Northeast Greenland Ice stream. J. Geophys. Res. Earth Surf. 126, e2020JF005689 (2021).
Lliboutry, L. General theory of subglacial cavitation and sliding of temperate glaciers. J. Glaciol. 7, 21–58 (1968).
Röthlisberger, H. Water pressure in intraglacial and subglacial channels. J. Glaciol. 11, 177–203 (1972).
Gimbert, F., Tsai, V. C., Amundson, J. M., Bartholomaus, T. C. & Walter, J. I. Subseasonal changes observed in subglacial channel pressure, size, and sediment transport. Geophys. Res. Lett. 43, 3786–3794 (2016).
Smith-Johnsen, S., de Fleurian, B., Schlegel, N., Seroussi, H. & Nisancioglu, K. Exceptionally high heat flux needed to sustain the Northeast Greenland Ice Stream. Cryosphere 14, 841–854 (2020).
Anandakrishnan, S., Voigt, D. E., Alley, R. B. & King, M. A. Ice stream D flow speed is strongly modulated by the tide beneath the Ross Ice Shelf. Geophys. Res. Lett. 30, 7 (2003).
Colgan, W. et al. Glacier crevasses: observations, models, and mass balance implications. Rev. Geophys. 54, 119–161 (2016).
Benn, D. I. & Åström, J. A. Calving glaciers and ice shelves. Adv. Phys. 3, 1048–1076 (2018).
Bindschadler, R. A., Vornberger, P. L., King, M. A. & Padman, L. Tidally driven stick-slip motion in the mouth of Whillans Ice Stream, Antarctica. Ann. Glaciol. 36, 263–272 (2003).
Gudmundsson, G. H. Tides and the flow of Rutford Ice Stream, West Antarctica. J. Geophys. Res. Earth Surf. 112, F4 (2007).
Walker, R. T., Christianson, K., Parizek, B. R., Anandakrishnan, S. & Alley, R. B. A viscoelastic flowline model applied to tidal forcing of Bindschadler Ice Stream, West Antarctica. Earth Planet. Sci. Lett. 319-320, 128 – 132 (2012).
Padman, L., Siegfried, M. R. & Fricker, H. A. Ocean tide influences on the Antarctic and Greenland Ice Sheets. Rev. Geophys. 56, 142–184 (2018).
Rosier, S. H. R. & Gudmundsson, G. H. Exploring mechanisms responsible for tidal modulation in flow of the Filchner–Ronne Ice Shelf. Cryosphere 14, 17–37 (2020).
Fricker, H. A. & Padman, L. Ice shelf grounding zone structure from ICESat laser altimetry. Geophys. Res. Lett. 33, 15 (2006).
Lingle, C., Hughes, T. & Kollmeyer, R. Tidal flexure of Jakobshavns Glacier, West Greenland. J. Geophys. Res. 86, 3960–3968 (1981).
de Juan, J. et al. Sudden increase in tidal response linked to calving and acceleration at a large Greenland outlet glacier. Geophys. Res. Lett. 37, 12 (2010).
Sugiyama, S., Sakakibara, D., Tsutaki, S., Maruyama, M. & Sawagaki, T. Glacier dynamics near the calving front of Bowdoin Glacier, northwestern Greenland. J. Glaciol. 61, 223–232 (2015).
Seddik, H. et al. Response of the flow dynamics of Bowdoin Glacier, northwestern Greenland, to basal lubrication and tidal forcing. J. Glaciol. 65, 225–238 (2019).
Beyer, S., Kleiner, T., Aizinger, V., Rückamp, M. & Humbert, A. A confined–unconfined aquifer model for subglacial hydrology and its application to the Northeast Greenland Ice Stream. Cryosphere 12, 3931–3947 (2018).
Zeising, O. et al. GNSS measurements at 79∘N Glacier in 2017. PANGAEA (2021).
Neckel, N., Zeising, O., Steinhage, D., Helm, V. & Humbert, A. Seasonal observations at 79∘ N Glacier (Greenland) from remote sensing and in-situ measurements. Front. Earth Sci. 8, 142 (2020).
Christmann, J., Mueller, R. & Humbert, A. On nonlinear strain theory for a viscoelastic material model and its implications for calving of ice shelves. J. Glaciol. 65, 212–224 (2019).
Gudmundsson, G. H. Ice-stream response to ocean tides and the form of the basal sliding law. Cryosphere 5, 259–270 (2011).
Wild, C. T., Marsh, O. J. & Rack, W. Unraveling InSAR observed Antarctic ice-shelf flexure using 2-D elastic and viscoelastic modeling. Front. Earth Sci. 6, 28 (2018).
Humbert, A. et al. On the link between surface and basal structures of the Jelbart Ice Shelf, Antarctica. J. Glaciol. 61, 975–986 (2015).
Murray, T. et al. Reverse glacier motion during iceberg calving and the cause of glacial earthquakes. Science 349, 305–308 (2015).
Åkesson, H., Morlighem, M., O’Regan, M. & Jakobsson, M. Future projections of Petermann Glacier under ocean warming depend strongly on friction law. J. Geophys. Res. Earth Surf. 126, e2020JF005921 (2021).
Budd, W. F., Keage, P. L. & Blundy, N. A. Empirical studies of ice sliding. J. Glaciol. 23, 157–170 (1979).
Keisling, B. et al. Basal conditions and ice dynamics inferred from radar-derived internal stratigraphy of the Northeast Greenland Ice Stream. Ann. Glaciol. 55, 127–137 (2014).
Herbert, C. M., Alexander, J. & Martínez de Álvaro, M. J. Back-flow ripples in troughs downstream of unit bars: formation, preservation and value for interpreting flow conditions. Sedimentology 62, 1814–1836 (2015).
Pettas, D., Karapetsas, G., Dimakopoulos, Y. & Tsamopoulos, J. Viscoelastic film flows over an inclined substrate with sinusoidal topography. I. Steady state. Phys. Rev. Fluids 4, 083303 (2019).
Christianson, K. et al. Dilatant till facilitates ice-stream flow in northeast Greenland. Earth Planet. Sci. Lett. 401, 57–69 (2014).
Bagshaw, E. A. et al. Prototype wireless sensors for monitoring subsurface processes in snow and firn. J. Glaciol. 64, 887–896 (2018).
Rückamp, M., Goelzer, H. & Humbert, A. Sensitivity of greenland ice sheet projections to spatial resolution in higher-order simulations: the Alfred Wegener Institute (AWI) contribution to ISMIP6 Greenland using the ice-sheet and sea-level system model (ISSM). Cryosphere 14, 3309–3327 (2020).
Rückamp, M., Greve, R. & Humbert, A. Comparative simulations of the evolution of the Greenland ice sheet under simplified Paris agreement scenarios with the models SICOPOLIS and ISSM. Polar. Sci. 21, 14–25 (2019).
Morlighem, M. et al. BedMachine v3: Complete bed topography and ocean bathymetry mapping of Greenland from multibeam echo sounding combined with mass conservation. Geophys. Res. Lett. 44, 11051–11061 (2017).
Gross, D. & Seelig, T. Fracture Mechanics with an Introduction to Micromechanics, vol. 3 (Springer, 2018).
MacGregor, J. A. et al. A synthesis of the basal thermal state of the Greenland Ice Sheet. J. Geophys. Res. Earth Surf. 121, 1328–1350 (2016).
Lüthi, M., Funk, M., Iken, A., Gogineni, S. & Truffer, M. Mechanisms of fast flow in Jakobshavn Isbræ, West Greenland: part III. Measurements of ice deformation, temperature and cross-borehole conductivity in boreholes to the bedrock. J. Glaciol. 48, 369–385 (2002).
Ryser, C. et al. Sustained high basal motion of the Greenland ice sheet revealed by borehole deformation. J. Glaciol. 60, 647–660 (2014).
Doyle, S. H. et al. Physical conditions of fast glacier flow: 1. measurements from boreholes drilled to the bed of store Glacier, West Greenland. J. Geophys. Res. Earth Surf. 123, 324–348 (2018).
Maier, N., Humphrey, N., Harper, J. & Meierbachtol, T. Sliding dominates slow-flowing margin regions, Greenland Ice Sheet. Sci. Adv. 5, 7 (2019).
Maier, N., Gimbert, F., Gillet-Chaulet, F. & Gilbert, A. Basal traction mainly dictated by hard-bed physics over grounded regions of Greenland. Cryosphere 15, 1435–1451 (2021).
Nolin, A. W. & Payne, M. C. Classification of glacier zones in western Greenland using albedo and surface roughness from the multi-angle imaging spectroradiometer (MISR). Remote Sens. Environ. 107, 264–275 (2007).
Colgan, W. et al. An increase in crevasse extent, West Greenland: hydrologic implications. Geophys. Res. Lett. 38, 18 (2011).
Chudley, T. R. et al. Controls on water storage and drainage in crevasses on the Greenland Ice Sheet. J. Geophys. Res. Earth Surf. 126, e2021JF006287 (2021).
Rückamp, M., Neckel, N., Berger, S., Humbert, A. & Helm, V. Calving induced speedup of Petermann glacier. J. Geophys. Res. Earth Surf. 124, 216–228 (2019).
Christmann, J., Plate, C., Müller, R. & Humbert, A. Viscous and viscoelastic stress states at the calving front of antarctic ice shelves. Ann. Glaciol. 57, 10–18 (2016).
Joughin, I., Smith, B. E. & Schoof, C. G. Regularized Coulomb friction laws for ice sheet sliding: application to Pine Island Glacier, Antarctica. Geophys. Res. Lett. 46, 4764–4771 (2019).
Joughin, I., Smith, B., Howat, I. & Scambos, T. MEaSUREs Multi-year Greenland Ice Sheet Velocity Mosaic, Version 1. (NASA National Snow and Ice Data Center Distributed Active Archive Center, 2016).
Joughin, I., Smith, B. E. & Howat, I. M. A complete map of Greenland ice velocity derived from satellite data collected over 20 years. J. Glaciol. 64, 243 (2018).
Gagliardini, O., Durand, G., Zwinger, T., Hindmarsh, R. C. A. & Le Meur, E. Coupling of ice-shelf melting and buttressing is a key process in ice-sheets dynamics. Geophys. Res. Lett. 37, 14 (2010).
Nettles, M. et al. Step-wise changes in glacier flow speed coincide with calving and glacial earthquakes at Helheim Glacier, Greenland. Geophys. Res. Lett. 35, 24 (2008).
Bertiger, W. et al. GipsyX/RTGx, a new tool set for space geodetic operations and research. Adv. Space Res. 66, 469–489 (2020).
Boehm, J., Niell, A., Tregoning, P. & Schuh, H. Global mapping function (GMF): a new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 33, 7 (2006).
Lyard, F., Lefevre, F., Letellier, T. & Francis, O. Modelling the global ocean tides: modern insights from FES2004. Ocean Dyn. 56, 394–415 (2006).
Altamimi, Z., Rebischung, P., Métivier, L. & Collilieux, X. ITRF2014: a new release of the International terrestrial reference frame modeling nonlinear station motions. J. Geophys. Res. Solid Earth 121, 6109–6131 (2016).
Franke, S. et al. Bed topography and subglacial landforms in the onset region of the Northeast Greenland Ice Stream. Ann. Glaciol. 61, 143–153 (2020).
Aschwanden, A., Fahnestock, M. A. & Truffer, M. Complex Greenland outlet glacier flow captured. Nat. Commun. 7, 10524 (2016).
Davison, B. J., Sole, A. J., Livingstone, S. J., Cowton, T. R. & Nienow, P. W. The influence of hydrology on the dynamics of land-terminating sectors of the Greenland Ice Sheet. Front. Earth Sci. 7, 10 (2019).
Morlighem, M. et al. Spatial patterns of basal drag inferred using control methods from a full-Stokes and simpler models for Pine Island Glacier, West Antarctica. Geophys. Res. Lett. 37, 14 (2010).
Larour, E., Seroussi, H., Morlighem, M. & Rignot, E. Continental scale, high order, high spatial resolution, ice sheet modeling using the Ice Sheet System Model (ISSM). J. Geophys. Res. Earth Surf. 117, F1 (2012).
Rückamp, M., Falk, U., Frieler, K., Lange, S. & Humbert, A. The effect of overshooting 1.5 ∘C global warming on the mass loss of the Greenland ice sheet. Earth Syst. Dyn. 9, 1169–1189 (2018).
Huybrechts, P. A 3-D model for the Antarctic ice sheet: a sensitivity study on the glacial-interglacial contrast. Clim. Dyn. 5, 79–92 (1990).
Joughin, I., Shean, D. E., Smith, B. E. & Dutrieux, P. Grounding line variability and subglacial lake drainage on Pine Island Glacier, Antarctica. Geophys. Res. Lett. 43, 9093–9102 (2016).
Hogg, A. E., Shepherd, A., Gourmelen, N. & Engdahl, M. Grounding line migration from 1992 to 2011 on Petermann Glacier, North-West Greenland. J. Glaciol. 62, 1104–1114 (2016).
Rack, W., King, M. A., Marsh, O. J., Wild, C. T. & Floricioiu, D. Analysis of ice shelf flexure and its InSAR representation in the grounding zone of the southern McMurdo Ice Shelf. Cryosphere 11, 2481–2490 (2017).
Padman, L. & Erofeeva, S. A barotropic inverse tidal model for the Arctic Ocean. Geophys. Res. Lett. 31, 2 (2004).
Padman, L., Erofeeva, S. & Howard, S. AOTIM5: Arctic Ocean Inverse Tide Model, on 5 Kilometer Grid, Developed in 2004 (Arctic Data Center, 2004).
Acknowledgements
This project is part of the GROCE project and is funded by BMBF under the grant 03F0778A. N.N. has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 689443 via project iCUPE (Integrative and Comprehensive Understanding on Polar Environments). S.A.K. acknowledges support from the INTAROS GA No. 727890 funded by European Union’s Horizon 2020 Research and Innovation Programme. The authors would like to thank Emerson E&P Software, Emerson Automation Solutions, for providing licenses in the scope of the Emerson Academic Program. We acknowledge support in the field campaign iGRIFF by Graham Niven, Jens Köhler and Mirko Scheinert. We would also like to thank Malte Thoma and Natalja Rakowsky for maintaining excellent computing facilities at AWI. We thank the chief editor Heike Langenberg, two anonymous reviewers, and Basile de Fleurian for careful reading and very helpful suggestions.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
J.C. conducted the viscoelastic simulations. A.H., R.M., and J.C. developed the concept for the viscoelastic simulations and evaluated the results. T.K. conducted the CUAS simulations, A.H. and T.K. planned and analysed the CUAS simulations. M.M. developed a new BedMachine dataset. M.R. conducted Ice-Sheet and Sea-level System Model simulations, the ISMIP-HOM experiments with COMice-ve and provided basal friction and buttressing. A.H. has designed the study and planned the field expeditions and airborne campaign. D.S., O.Z., N.N., V.H., and S.A.K. conducted the field study. V.H., S.A.K., and O.Z. processed the GPS data. N.N. processed interferograms. V.H. conducted the airborne campaign and supported the base detection. All authors discussed the results and contributed to writing.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Communications Earth & Environment thanks Tun Jan Young, Basile De Fleurian and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editor: Heike Langenberg.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Christmann, J., Helm, V., Khan, S.A. et al. Elastic deformation plays a non-negligible role in Greenland’s outlet glacier flow. Commun Earth Environ 2, 232 (2021). https://doi.org/10.1038/s43247-021-00296-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-021-00296-3
This article is cited by
-
Ice acceleration and rotation in the Greenland Ice Sheet interior in recent decades
Communications Earth & Environment (2024)
-
Extensive inland thinning and speed-up of Northeast Greenland Ice Stream
Nature (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.