Introduction

Calcium (Ca), the fifth most abundant element in the Earth’s crust1, plays a key role in regulating climate over geologic timescales2,3 and is essential for biological processes, such as biomineralization, plant growth, and cellular regulation4,5. Due to the ubiquitous occurrence of Ca in Earth and extraterrestrial materials, as well as major geochemical cycles, stable Ca isotope ratios have emerged as a promising tool for investigating processes in geochemistry, cosmochemistry, biology, and archaeology6,7. Calcium isotope ratios are reported in delta notation as δ44/40Casmp (‰) = [(44Ca/40Ca)smp/(44Ca/40Ca)std − 1] × 1000, where smp refers to the sample and std refers to the normalizing standard, which in this study is OSIL Atlantic Seawater or ASW (δ44/40CaASW = 0‰).

In the ongoing effort to develop and apply the δ44/40Ca tracer, research has focused on quantifying mechanisms that fractionate isotopes according to their masses and produce isotopic offsets (Δ) between related Ca-bearing reservoirs, i.e., Δ44/40Caa − b = δ44/40Caa − δ44/40Cab. Differentiating between kinetic and equilibrium isotope effects during mineral formation is particularly essential for implementing Ca isotopes as paleoenvironmental or temperature proxies8,9,10. Most studies aimed at understanding Ca isotope fractionation during mineral precipitation have focused on calcite (CaCO3) formation at low temperatures (<30 °C) characterizing the Earth’s surface. Here, kinetic isotope effects11,12,13,14,15,16,17 cause calcite to preferentially incorporate lighter Ca isotopes from solution with Δ44/40Cacal–sol on the order of –1‰ to –2‰6. Theory predicts that higher temperatures should promote equilibrium effects and minimize isotopic offsets (Δ44/40Cacal–sol ≈ 0‰) during calcite formation13,16,18; however, only a handful of natural calcites precipitated at elevated temperatures have been measured19,20,21,22. In parallel, some studies examining silicate mineral formation at high temperatures characterizing the solid Earth have attributed δ44/40Ca variability to equilibrium isotope partitioning23,24, driven by differences in Ca–O bonding conditions9,10. However, discrepancies between measured inter-mineral Δ44/40Ca of high-temperature silicates and ab initio model predictions of equilibrium Ca isotope offsets have been interpreted as evidence for mostly kinetic control25,26.

Missing from Ca isotope fractionation theory is an understanding of mechanisms that produce δ44/40Ca variability during mineral formation at temperatures bridging the surface and solid Earth. Intermediate temperatures in the range of ~30–200 °C characterize many hydrothermal systems, which represent key interfaces linking surficial geochemical cycles and solid Earth processes. Studies have used Ca isotopes to examine mid-ocean ridge hydrothermal systems19,27,28, seafloor weathering and oceanic lithosphere subduction22, continental hydrothermal systems20, and water–rock interactions in pilot studies of mineral carbonation of basalt, which is a leading carbon capture and storage (CCS) strategy29,30. Application of the Ca isotope tracer to these and other intermediate temperature systems requires a thorough examination of all secondary minerals that may fractionate Ca isotopes and contribute to the δ44/40Ca values of circulating waters. In addition, a better understanding of both equilibrium and kinetic effects on Ca isotope fractionation at intermediate temperatures is essential for improving knowledge about Ca isotope cycling and identifying novel applications for the δ44/40Ca tracer.

Hydrothermal alteration commonly leads to the formation of zeolites31,32. Zeolite mineral structures comprise frameworks of linked Si- or Al-O tetrahedra, creating voids and channels that contain H2O, Ca, and other cations, which are readily exchangeable33,34,35. The minerals serve as sizeable Ca2+ sinks during low-grade metamorphism36,37,38,39,40,41,42. In basaltic settings such as Iceland, equilibrium-controlled ion-exchange reactions with zeolites strongly regulate Ca2+ concentrations in natural hydrothermal waters43,44, as well as those produced in CCS experiments45,46,47,48. Calcium cycling during basalt weathering in subsurface hydrothermal systems also plays a major role in regulating Earth’s long-term carbon cycle49,50,51. Moreover, owing to their properties as ion-exchangers, absorbents, molecular sieves, and catalysts52, zeolites have numerous environmental, industrial, and medical applications, including drinking water purification53,54,55, nuclear waste management56,57, contaminant transport mitigation58,59,60, automotive emission reduction61, and cancer treatment62.

Nonetheless, despite the widespread occurrence and applicability of zeolites, their Ca isotope geochemistry has been neglected. Only one study has reported Ca isotope data for zeolites21. Coexisting heulandite and stilbite from Iceland are isotopically lighter and heavier, respectively, relative to basalt. Icelandic hydrothermal water and calcite also have δ44/40Ca values higher than basalt21. Heavy calcite is highly unusual because most carbonate minerals form kinetically and incorporate lighter isotopes relative to their Ca source reservoir13,17,63. Uptake of lighter Ca isotopes during zeolitization may elevate the relative abundance of heavier Ca isotopes in hydrothermal waters from which calcite precipitates21, but no systematic understanding has been established.

To better understand the Ca isotope geochemistry of zeolites, we used a high-precision thermal ionization mass spectrometry (TIMS) method to measure δ44/40Ca values of six zeolite mineral species. We also analyzed bulk basalt, primary mineral separates, and calcite. Specimens were collected from the Berufjörður–Breiðdalur region of East Iceland, which is a typelocality for the zeolitization of basaltic lava flows due to burial metamorphism64. Here, increasing temperature with depth below the surface of the lava pile has generated distinct zeolite zones where two zeolite mineral types, referred to as coindex mineral pairs64, distinctly form and thus are diagnostic of each depth zone (Fig. 1). Depth-controlled zeolite zones have been identified worldwide in active geothermal systems37,44,65, as well as extinct systems now exposed at the surface32,38,41,66,67. We report a large range of zeolite δ44/40Ca values, which is best explained by equilibrium isotope partitioning, given a strong observed correlation with Ca–O bond lengths. Our findings point the way for developing entirely new tools for investigating low-grade basalt alteration. They also broadly illustrate how future efforts focused on the Ca isotope geochemistry of zeolites could have implications for numerous other topics, such as understanding the compositional evolution of hydrothermal waters, quantifying elemental cycling in the oceans, and improving CCS strategies.

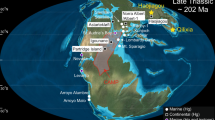
Fig. 1: Map of Iceland showing sample locations.
figure 1

a Mineral separates were obtained from basalts sampled throughout Iceland. The Berufjörður–Breiðdalur region of East Iceland is outlined. b Sampling locations of bulk rocks, calcite, and zeolites collected from the main region of study. c Zeolite sampling locations correspond to different elevations or depths below the original surface of the lava pile. Depth-controlled zeolite zones, adapted from Walker (1960), are overlain on a photograph of the Berufjörður volcanic sequence taken from the north.

Full size image

Geologic setting

Iceland is an exposed section of the Atlantic mid-ocean ridge overlying a mantle plume, which has caused extensive rifting and volcanism over the past 50–60 Myr68. Rocks increase in age away from the active rift zone, with the oldest rocks at the edges of Iceland dating to ~16 Ma69. Samples analyzed in this study were collected from Berufjörður–Breiðdalur region described in detail by Walker (1960) (Fig. 1). Successive eruptions of a Tertiary volcano supplied lava that piled to a minimum total thickness of ~2000 m at the eastern end64,70,71. The central volcano comprises highly altered rhyolite, while the flows are predominantly tholeiitic basalt, with lesser amounts of olivine basalt64,71. Within ~1 Myr after the eruptions ceased, heat from burial, as well as the volcanic center and associated dike swarms, extensively zeolitized the lava pile, filling up to 90% of the primary porosity38,64,70,72. Pleistocene glacial erosion carved deep valleys and fjords into the lava pile and exposed the top ~1000 m of the altered sequence, where the depth-controlled zeolite zones are clearly delineated and accessible above sea level (Fig. 1). The shallowest zone studied here is the chabazite–thomsonite zone (~30–70 °C), followed by the mesolite–scolecite zone (~70–90 °C) and the stilbite–heulandite zone (~90–150 °C), which reaches a maximum depth of ~1500 m below the top of the lava pile31,39,64,73.

Results

Bulk basalt and primary minerals

Table 1 presents elemental and Ca isotope data for bulk basalt and primary mineral separates. Bulk basalt samples from the Berufjörður–Breiðdalur region yield an average δ44/40Ca of −1.04 ± 0.08‰ (2σSD, n = 5), which agrees well with the average of −1.06 ± 0.02‰ (2σSD, n = 6) for basalt sampled from other regions throughout Iceland21. The primary minerals have a narrow range of δ44/40Ca values, which bracket those for bulk basalt. Olivine has the highest average δ44/40Ca (−1.02 ± 0.14‰, 2σSD, n = 3), followed by clinopyroxene (−1.05 ± 0.06‰, 2σSD, n = 3), apatite (−1.12 ± 0.06‰, 2σSD, n = 3), and plagioclase (−1.14 ± 0.04‰, 2σSD, n = 3).

Table 1 Elemental and Ca isotope data for bulk basalt, primary mineral separates, and calcite.
Full size table

Calcite

Table 1 presents elemental and Ca isotope data for calcite samples. The average δ44/40Ca equals −0.80 ± 0.20‰ (2σSD, n = 4), which is similar to the average of −0.79 ± 0.34‰ (2σSD, n = 13) for zeolite–zone calcite reported in Jacobson et al. (2015). Calcite consistently has higher δ44/40Ca than basalt and primary minerals.

Zeolites

Table 2 provides elemental and Ca isotope data for bulk zeolites. Stilbite has the highest average δ44/40Ca (−0.72 ± 0.24‰, 2σSD, n = 3), followed by scolecite (−0.84‰, n = 1), thomsonite (−0.94 ± 0.18‰, 2σSD, n = 3), chabazite (−1.58 ± 0.22‰, 2σSD, n = 4), mesolite (−1.78‰, n = 1), and heulandite (−1.81 ± 0.28‰, 2σSD, n = 5). δ44/40Ca for stilbite and heulandite agree with previously reported values21.

Table 2 Elemental and Ca isotope data for bulk zeolite minerals.
Full size table

Discussion

Controls on zeolite δ44/40Ca: kinetic isotope effects

A striking observation is that for each zeolite zone64, coindex pairs have contrasting δ44/40Ca that bracket basalt, with one mineral lower and the other higher (Fig. 2). Relative to basalt, the zeolites chabazite, mesolite, and heulandite have low δ44/40Ca, while their respective pairs (thomsonite, scolecite, and stilbite) have high δ44/40Ca. Chabazite, mesolite, and heulandite represent some of the isotopically lightest minerals thus far measured6,26,74, neglecting those that host appreciable 40Ca additions from the radioactive decay of 40K75. The data provide good evidence that zeolites fractionate Ca isotopes, as bulk basalt and primary mineral separates show effectively no isotopic variability (Fig. 3).

Fig. 2: Zeolite δ44/40Ca versus burial depth.
figure 2

δ44/40Ca of bulk zeolites versus approximate burial depth in the Berufjörður–Breiðdalur region64. The orange line shows the average value for all basalts analyzed here and by Jacobson et al. (2015), with the width encompassing the standard deviation (−1.05 ± 0.06‰, 2σSD, n = 11). Error bars show external reproducibility (±0.05‰, 2σSD).

Full size image
Fig. 3: δ44/40Ca versus Sr/Ca for primary minerals, bulk basalt, calcite, and zeolites.
figure 3

a Ca isotope measurements of all samples. Symbol size is larger than the external reproducibility (±0.05‰, 2σSD). b Inset from panel (a) includes basalt from the Berufjörður–Breiðdalur region (dark blue triangles), as well as basalt from previous studies (light blue triangles)21.

Full size image

Many studies have shown that kinetic fractionation during mineral precipitation causes preferential uptake of lighter Ca isotopes relative to the main Ca reservoir11,74. Other minerals measured thus far with low δ44/40Ca values similar to zeolites are mainly carbonates, which have experienced kinetic fractionation due to either variable precipitation rates13,14 or biogenic vital effects during mineral growth74. Kinetic effects resulting in low δ44/40Ca have also been observed in some high-temperature silicate minerals25,76,77. However, unlike carbonates and primary rock-forming silicate minerals, all Ca in zeolites is exchangeable34; therefore, it cannot be assumed a priori that kinetic fractionation mechanisms identified for the former minerals apply to zeolites. Kinetic isotope fractionation during mineral precipitation from solution mainly occurs due to incomplete exchange of ions or molecules, when transfer from solution to the solid proceeds more quickly than the reverse reaction9,11,78. Calcium ion exchange in zeolite minerals is equilibrium-controlled34,43, thus implying that forward and backward reaction rates are equal. Nevertheless, we consider below potential transport-related kinetic isotope effects.

Zeolites consist of an aluminosilicate tetrahedral framework, where cations occupy specific exchange sites within void channels33. Isomorphic substitution of Al3+ for Si4+ in the tetrahedra creates a net negative charge in the zeolite framework, which is balanced by the uptake of mono- and divalent cations, including Ca2+, from the coexisting solution33. Thus, coulombic forces related to charge density could in theory kinetically fractionate Ca isotopes due to variable mass-dependent diffusion rates occurring at the mineral–fluid interface or within the zeolite framework itself11,79,80,81. Charge density and distribution, as well as framework topology, control the ease and rate of Ca uptake and diffusion through zeolite frameworks34,58,82. Commonly a proxy for charge density, and thus cation-exchange capacity, zeolite Si/Al ratios reflect the anionic field strength that attracts cations into the structure. In general, zeolites with lower Si/Al ratios have higher charge densities and more readily take up cations relative to those with higher Si/Al ratios and lower charge densities34,83. If kinetic effects related to rates of Ca uptake or diffusion fractionated Ca isotopes, then a trend between zeolite Si/Al ratios and δ44/40Ca values should exist. However, we observe no trend for the present dataset, suggesting that charge density does not elicit kinetic isotope effects for these minerals (see Fig. S1).

One key point is that basalt represents the initial source of Ca in this system37,38. If the occurrence of zeolites with δ44/40Ca higher than basalt was the result of a kinetic fractionation mechanism during mineral formation, then this would require that zeolites with lower δ44/40Ca either precipitate faster or form first, thereby creating an isotopically enriched solution from which zeolites with higher δ44/40Ca later precipitate, as no kinetic fractionation mechanism could result in the preferential uptake of heavier Ca isotopes. Calculations and experiments employing solution chemistry and thermodynamic conditions have been used to predict the progression of zeolitization84,85,86,87, and while petrographic evidence in some locations points to possible chronologic sequences of zeolites32,40,88,89, studies in Iceland indicate that the coindex pairs form simultaneously under similar conditions37,38,41,90. Furthermore, some coindex zeolite pairs analyzed here were intergrown and collected from a single amygdule,  suggesting simultaneous precipitation. The absence of clear evidence for kinetically controlled reservoir effects is unsurprising, as all zeolite-bound Ca is extra-framework, with ion-exchange reactions between zeolites and fluids continuing after initial growth of the aluminosilicate frameworks43,66. Calculated equilibrium elemental compositions of zeolites, as well as those produced experimentally under equilibrium conditions, agree with geochemical analyses of natural Icelandic zeolites, which strongly indicates that the ion-exchange reactions are equilibrium-controlled43,44,66. Because zeolites with identical formation conditions have contrasting δ44/40Ca and the ion-exchange processes governing Ca uptake are equilibrium-controlled, kinetic effects are unlikely to contribute to the δ44/40Ca variations observed here.

Another interesting observation is that zeolites with lower δ44/40Ca also have higher Sr/Ca (Fig. 3). During calcite precipitation, rate-dependent shifts in Ca isotope fractionation and Sr partitioning produce linear correlations between δ44/40Ca values and Sr/Ca ratios13; however, the pattern observed in Fig. 3 for zeolites is nonlinear. In general, the understanding achieved for simple ionic solids does not immediately apply to more complex minerals, such as zeolites. Each zeolite studied here has a unique aluminosilicate framework. Incorporation of Sr into chabazite and heulandite, for example, is widely documented to reflect underlying structural characteristics, where zeolite framework topology and local bonding conditions give rise to larger exchange sites that prefer Sr relative to Ca33,43,91,92,93. The trend shown in Fig. 3 provides evidence that structural properties known to control Sr incorporation may also discriminate Ca isotopes as well.

Controls on zeolite δ44/40Ca: equilibrium isotope effects

We deduce that a fractionation mechanism related to mineral-specific Ca bonding conditions likely explains zeolite δ44/40Ca variability. Previous research has shown that Ca isotope fractionation varies as a function of coordination number (CN)63,94,95,96,97, and relationships between δ44/40Ca and Ca–O bond length have been identified for carbonates, phosphates, hydrous minerals, silicates, and aqueous calcium25,95,96,97,98. Both a function of bond length and CN, bond strength (stiffness) determines isotope fractionation, where stronger bonds preferentially concentrate heavier isotopes9,99.

The CN of Ca in zeolites can vary widely within each mineral because the minerals support a variety of exchange sites with unique Ca–O bonding conditions33. For example, Ca in chabazite could have a CN of 6 or 12 depending on which exchange site Ca occupies (Table 3)100. Moreover, within a given zeolite exchange site, Ca can coordinate to either framework oxygens (Ofmwk), those composing molecular water also contained within the framework (Ow), or some combination thereof. In general, Ca–Ofmwk bonds are considerably longer than Ca–Ow bonds at a given site; thus, Ca–O bond lengths can vary greatly within one individual site, as well as between sites within a single mineral (Table 3). The effect of CN on bond strength is documented for mineral systems where most of the bonds contributing to the CN of Ca have nearly equal lengths, relative to zeolites, which support highly different Ca–O bond lengths25,95,96,97. As the average CN of Ca per zeolite cannot take into account nonuniform bond lengths, the average Ca–O bond length per zeolite likely better approximates bond strength for this particular mineralogical system. Therefore, we calculated an average Ca–O bond length for each unique Ca site and used this as a proxy for the average Ca–O bond length per mineral, assuming Ca is evenly distributed across all potential sites (Table 3).

Table 3 Compilation of mineral data used for estimating average mineral Ca–O bond lengths.
Full size table

When zeolite δ44/40Ca values are plotted versus average Ca–O bond length per mineral (Fig. 4), five of the six zeolites studied generate a significant correlation (R2 = 0.93, p < 0.001). In general, zeolites with lower δ44/40Ca have longer approximate Ca–O bond lengths, while zeolites with higher δ44/40Ca have shorter approximate Ca–O bond lengths, consistent with equilibrium isotope fractionation theory9,10. While CN can adequately predict bond strength for many mineral systems26,63,74,94,95,97, the observation that stilbite (CN = 8) and scolecite (CN = 7) have nearly identical average Ca–O bond lengths and δ44/40Ca values supports our assumption that bond length better approximates the effect of bond strength on Ca isotope fractionation for zeolites. We suggest that differences in zeolite Ca–O bond energies underlie the trend between δ44/40Ca and bond length shown in Fig. 4, which we interpret as evidence for equilibrium isotope partitioning.

Fig. 4: Zeolite δ44/40Ca versus estimated average Ca–O bond length.
figure 4

Symbol size encompasses the external reproducibility (±0.05‰, 2σSD). Also shown are δ44/40Ca data for calcite from this study and zeolite-zone calcite from Jacobson et al. (2015), as well as the average of natural groundwaters21 and pre-injection groundwaters from the CarbFix1 site29, which circulate through active zeolite zones analogous to the extinct system studied here65. Calcite106,136 and groundwater96 Ca-O bond lengths are approximate. The black dashed line shows the average value for Icelandic basalt (−1.05‰) determined from this study and Jacobson et al. (2015). Average Ca–O bond lengths and δ44/40Ca values of bulk zeolites strongly correlate (R2 = 0.93, p < 0.001), when mesolite is excluded from the regression. The grey shading represents the confidence interval of this regression (see Supplementary information (S1) for details of the statistical model).

Full size image

In the context of isotope fractionation between solution and mineral, it is important to consider Ca–O bonding dynamics in the surrounding fluid. Aqueous Ca2+ coordinates to water O atoms in coordination or hydration spheres, which have shorter Ca–O bond lengths than zeolites96. Icelandic groundwater has higher δ44/40Ca values than zeolites (Fig. 4), consistent with predictions from equilibrium fractionation theory that stronger bonds preferentially concentrate heavier isotopes8,9,10. The exchange of Ca between groundwater and zeolite frameworks involves breaking a certain number of Ca–Ow bonds in the hydration spheres (desolvation) to create Ca–Ofmwk bonds82. Theoretical studies focusing on calcite have argued that desolvation can elicit kinetic isotope effects due to faster bond breaking of hydration spheres containing lighter Ca isotopes80,101. If such a mechanism is applied here, then minerals requiring more bond breaking of hydration spheres (i.e., those comprising fewer Ca–Ow bonds) should preferentially incorporate lighter Ca isotopes. However, this pattern is not observed. For example, heulandite and thomsonite only need to break three to four hydration sphere bonds but show greater apparent fractionations than calcite, which must break at least six hydration sphere bonds, as the mineral supports no Ca–Ow bonds. Stilbite has only Ca–Ow bonds (Table 3), implying an absence of desolvation, yet Icelandic calcite and stilbite have similar δ44/40Ca (Table 2). In addition, chabazite has the least Ca–Ow bonds of all zeolites studied here, but shows higher δ44/40Ca than heulandite. In parallel, heulandite and thomsonite have the same proportions of Ca–Ow bonds relative to total Ca–O bonds, suggesting that these two minerals should desolvate hydration spheres identically, but heulandite has much lower δ44/40Ca values than thomsonite. While more research is needed to constrain relationships between zeolite structural characteristics, desolvation kinetics, and Ca isotope fractionation, our present observations better support an equilibrium isotope effect related to mineral Ca–O bond lengths.

Mesolite is the only exception to the relationship shown in Fig. 4. This zeolite and scolecite support identical Ca-site structures, but the mesolite framework also comprises alternating channels of Ca and Na sites102,103. Our bond length estimate assumes that all Ca in mesolite resides in the Ca channel; however, Ca can substitute into the Na channel, where it coordinates to Ofmwk with much longer bonds than in the Ca channel104,105. For this particular sample, it is possible that a substantial proportion of the Ca occupies the Na channel, where Ca–Ofmwk bond lengths are longer than our calculation estimates. Thus, the accumulation of lighter Ca isotopes in the Na channel could explain the sample’s lower δ44/40Ca value. Similar observations of bond lengths varying with elemental substitutions have been made for calcite and other silicates, where Mg/Ca ratios discernably correlate with δ44/40Ca23,26,106.

An alternative explanation is that mesolite experienced kinetic isotope effects. The Ca sites in mesolite and scolecite have identical framework topologies, Ca–O bond lengths, and CNs. Theory for this scenario dictates that contrasting Ca isotope ratios could reflect kinetic isotope effects26. However, because precipitation rate effects observed for other types of minerals do not apply to zeolites, which participate in equilibrium-controlled ion exchange after initial precipitation43,44,66, the exact mechanism that would produce kinetic isotope effects is uncertain. Nevertheless, the data imply that mesolite is the most likely candidate of all zeolites examined here to have experienced kinetic fractionation. If correct, then our observation that mesolite plots off the line in Fig. 4 only supports equilibrium isotope partitioning for the other minerals.

Barring the one mesolite sample, bulk zeolite δ44/40Ca values inversely vary with approximate Ca–O bond lengths. While we interpret this pattern to reflect inter-mineral equilibrium isotope partitioning, more research is needed to better constrain zeolite fractionation mechanisms. The correlation between zeolite Ca–O bond lengths and δ44/40Ca values reported here is consistent with theoretical23,96,97,98,107, laboratory63,95,108, and field studies of other mineral types24,25,26,27,109. To the best of our knowledge, our study is the first to report such effects for zeolites, as few studies have investigated δ44/40Ca variability in minerals that form in nature at intermediate temperatures. Zeolites with low δ44/40Ca values incorporate more Sr relative to Ca (Fig. 3). As Sr2+ has a larger ionic radius than Ca2+, these minerals presumably support larger exchange sites, consistent with Ca isotope evidence that the minerals have longer Ca–O bond lengths. We also note that zeolites appear to fractionate Sr isotopes, with heulandite and stilbite bracketing the composition for bulk basalt50. Our overall interpretation is further consistent with an early investigation reporting that fractionation of Li and K isotopes by zeolites during ion exchange is largely equilibrium-controlled110.

While structural differences between zeolite frameworks adequately explain δ44/40Ca variability, we do note that Ca isotope offsets between the coindex pairs increases with depth (Fig. 2), which counters the expectation that higher temperatures diminish equilibrium isotope fractionation10. This only underscores the first-order control of the mineral structure. Each zeolite has a unique framework structure, which gives rise to the positive correlation between the magnitudes of isotopic contrast and Ca–O bond-length differences between the coindex pairs. Zeolite δ44/40Ca values may indirectly relate to formation temperature, as temperature determines which frameworks crystallize as a function of depth38,64 and structural properties appear to control Ca isotope fractionation (Fig. 4). However, the Ca isotope geochemistry of the minerals could more directly relate to the temperature of coexisting groundwater, as zeolites participate in equilibrium-controlled ion-exchange reactions after formation38,43,44. Thus, calcium isotopes could be developed as a proxy for circulating fluid temperature; however, more studies are needed to better elucidate equilibrium versus kinetic controls on fractionation and fully quantify fractionation factors for each mineral relative to solution. Nevertheless, our present findings illustrate the potential for developing an entirely new geothermometer for investigating low-grade basalt metamorphism, as well as probing a diverse range of other environments where zeolites form111,112.

Controls on hydrothermal water δ44/40Ca

Primary minerals display limited Ca isotope contrast and bracket δ44/40Ca values of bulk basalt (Fig. 3). This confirms previous suggestions that the limited Ca isotope variability of Icelandic basalt is due to a narrow range of primary mineral δ44/40Ca21. The source of fluid in the system studied here is meteoric37,43,72, which implies that its initial δ44/40Ca value is rock-dominated (~−1‰). No evidence exists for preferential Ca isotope release during primary silicate mineral dissolution for any silicate rock type. Therefore, hydrothermal waters and calcite in Iceland must be driven heavy as a byproduct of secondary light Ca sinks. During hydrothermal alteration of basalt, Ca-bearing zeolites and calcite are the two main sinks of aqueous Ca2+ 45,113, with zeolites forming distinctly prior to calcite38,45,48,90,114. Smectite and mixed layer clays form before zeolites, but they incorporate little Ca by comparison38,41,45,65,115. The low δ44/40Ca values of chabazite, mesolite, and heulandite indicate that fractionation by zeolites overshadows any effects due to Ca2+ adsorption onto clays. If an appreciable amount of clay with low δ44/40Ca values formed prior to zeolites, then all zeolites would have elevated δ44/40Ca values, due to a reservoir effect, which is not the observed pattern. Thus, either clays are negligible Ca sinks or they have negligible Ca isotope fractionation factors. Recent research has attributed elevated δ44/40Ca values in CCS waters to the formation of isotopically light calcite29, but no such calcite, whether anthropogenic or natural, has been measured in the Icelandic system. However, similar to natural hydrothermal waters65,116,117,118,119, CCS waters are supersaturated with respect to zeolites after periods of CO2 injection45,48,90. While some zeolites do show higher δ44/40Ca than basalt, the depth trend presented here is clearly asymmetric, where negative fractionations are larger (Fig. 2). Thus, it follows that progressive ion exchange with zeolites would elevate groundwater δ44/40Ca, supporting previous suggestions that uptake of lighter Ca isotopes by zeolites enriches hydrothermal waters in heavier isotopes21,50,120.

Studies of other groundwater systems have suggested that preferential uptake of lighter Ca isotopes by anhydrite or calcite elevates water δ44/40Ca values relative to source rocks19,20,121,122. Zeolites form ubiquitously at temperatures ranging from ~30 to 150 °C during the hydrous alteration of silicates in many diverse environments31,123. Our results emphasize a need to consider Ca uptake by zeolites in studies aimed at understanding the geochemical evolution of natural groundwater, as well as CCS waters monitored during mineral carbonation of basalt26,29,122,124.

Controls on calcite δ44/40Ca

The overlapping range of calcite and hydrothermal water δ44/40Ca values in Iceland suggests that Δ44/40Cacal–sol is close to 0‰21, similar to patterns documented in other natural systems, where calcite slowly forms about the state of chemical equilibrium125,126. Equilibrium isotope effects appear to control the Ca isotope composition of zeolites, given the strong linear correlation between zeolite Ca–O bond lengths and δ44/40Ca (Fig. 4). Many hydrothermal calcite samples also have δ44/40Ca values that closely approach this line, suggesting a similar control by Ca–O bond length. We, therefore, propose that the unusually high δ44/40Ca of Icelandic hydrothermal calcite reflects the influence of zeolites on hydrothermal water δ44/40Ca. Because calcite samples display a range of δ44/40Ca values (Fig. 4), it is possible that the lighter calcite samples may have precipitated from hydrothermal waters that isotopically evolved to differing degrees. Alternatively, kinetic isotope effects due to variable precipitation rates may have contributed to the lower δ44/40Ca of some calcites relative to hydrothermal water. Regardless, it is likely that many Icelandic hydrothermal calcites have δ44/40Ca values consistent with equilibrium isotope control.

While several studies have identified how variable Ca coordination controls inter-mineral equilibrium isotope partitioning63,108, few have determined the effects of CN on mineral–fluid Ca isotope partitioning during natural calcite growth127. Calcite supports only one Ca site having Ca–O bonds of uniform length;97,128,129,130 therefore, unlike zeolites, the CN for calcite adequately approximates bond strength and related isotopic effects. Calcium in calcite coordinates to six O atoms128. Thus, calcite has a lower CN than any of the zeolites examined in this study, as well as shorter Ca–O bond lengths. It follows that calcite should have higher δ44/40Ca than zeolites, which is the relationship observed in Fig. 4. Experimental results and calculations have demonstrated that Ca isotope fractionation during mineral precipitation depends on the CN of mineral Ca, as well as the CN of aqueous Ca2+, which can range from six to ten80,95,96,97,131. Because Icelandic calcite appears to imprint the δ44/40Ca of hydrothermal waters and plot near the equilibrium-controlled zeolite Ca–O bond-length line, we suggest that aqueous Ca2+ in this system likely has a CN of six. Calcite, which has a known CN and a well-constrained Ca–O bond length, shows similar δ44/40Ca and bond length to Icelandic groundwater; thus, it follows that these reservoirs likely have similar CN. The isotopic offset between water and zeolites further implies that the CN of aqueous Ca2+ must be lower than those of zeolites (lowest CN = 7) and more similar to that of calcite (CN = 6). The apparent offset between Ca–O bond lengths for calcite and hydrothermal water (Fig. 4) is likely a consequence of our assumptions, as bond lengths in calcite vary with impurities97,98, and bond lengths for sixfold coordinated aqueous Ca2+ vary with temperature, ion pairing, and fluid ionic strength among other factors80,95,96,131,132.

Our results suggest that equilibrium-controlled calcite δ44/40Ca values could be used to identify the CN of aqueous Ca2+, and that laboratory studies able to control the CN of aqueous Ca2+ could better constrain equilibrium isotope effects in synthesized calcites. In this context, the equilibrium isotopic offset between calcite and water (Δ44/40Cacal–sol), which is generally accepted to be ~0‰ given small Δ44/40Cacal–sol observed in natural settings where calcite precipitates at or near chemical equilibrium15,125,126, could be interpreted not only as an absence of kinetic isotope effects but also as an indication that aqueous Ca2+ and calcite Ca both have a CN of six. This potentially has implications for various applications of the Ca isotope tracer, as the CN of aqueous Ca2+ can vary with ionic strength and temperature131,133, which could theoretically impact the equilibrium isotope fractionation factor between calcite and water. For example, if fluid Ca2+ was coordinated to eight oxygens instead of six (likely resulting in longer bond lengths in the hydration sphere134), Δ44/40Cacal–sol at equilibrium would be nonzero and positive, resulting in calcite that is enriched in heavier Ca isotopes95,96,97. Further work is needed to explore these ideas; however, our findings provide a valuable perspective on mineral–fluid isotope equilibrium, which could have implications for interpreting the δ44/40Ca values of marine carbonates deposited throughout geologic history.

Conclusions

This study reports Ca isotope data for natural zeolite minerals from Iceland, as well as hydrothermal calcite, bulk basalt, and primary mineral separates. Zeolite minerals display a δ44/40Ca range of ~1.4‰, which is on the order of the range exhibited by all igneous rocks thus far measured6,26. Zeolite δ44/40Ca values strongly correlate with average Ca–O bond lengths, which we interpret to reflect equilibrium isotope partitioning. The bond-length hypothesis presented here also provides some evidence that equilibrium isotope effects control Δ44/40Ca between hydrothermal calcite and waters, given that these reservoirs support similar Ca–O bond lengths and display small isotopic offsets. As equilibrium isotope fractionation factors strongly depend on temperature10, our findings suggest that the Ca isotope geochemistry of zeolite minerals could be developed into an entirely new geothermometer for investigating low-grade basalt metamorphism. Moreover, zeolites should be considered in Ca isotope studies of other continental and oceanic hydrothermal systems where the minerals pervasively occur. Calcium isotopes hold particular promise for quantifying the mineralization of injected CO2 during mineral carbonation of basalt, which is a leading CCS strategy29,30. Our study characterizes the composition of key mineral reservoirs necessary for interpreting and modeling Ca isotope variations in both field and theoretical CCS studies. More research dedicated to the Ca isotope geochemistry of zeolites could help improve numerous environmental, industrial, and medical applications of the minerals.

Methods

Field collection

During the summer of 2017, zeolites, bulk basalt, and calcite were collected from various outcrops in the Berufjörður–Breiðdalur region of East Iceland. No permissions were required for sampling in this location. Mineral types were identified in the field and later confirmed by X-ray diffraction (XRD), as described below. Where possible, coindex zeolite pairs were collected from a single outcrop for every depth-zone described by Walker (1960), and calcite samples were collected from all zones. Rock samples for primary mineral separates were collected from basaltic flows throughout Iceland (Fig. 1).

Sample preparation

Heavy liquids (Apatite-to-Zircon Inc., Viola, ID, USA) were used to separate mostly pure fractions of plagioclase, clinopyroxene, olivine, and apatite from three basalt samples with different ages and geologic histories. Intergrown zeolite samples from the same amygdule were physically separated. All basalt and mineral specimens, including primary minerals, calcite, and zeolites, were washed with MilliQ water and sonicated to remove excess sediment and impurities. Samples were dried in an oven at 50 °C and powdered by hand using a Diamonite mortar and pestle. Zeolites fundamentally differ from typical rock-forming silicate minerals, as their frameworks only comprise Al, Si, and O, that is, the minerals do not contain structurally bound Ca. All Ca is extra-framework, as it occurs in voids and channels created by the frameworks. Therefore, bulk measurements are most appropriate for characterizing the Ca isotope geochemistry of zeolites. Subsamples of basalt, primary mineral, and zeolite powders were completely digested using HF and HNO3 acids. No insoluble residues were observed. Calcite powders were completely dissolved in 5% HNO3. To further interrogate the Ca isotope geochemistry of zeolites, a sequential leaching and digestion procedure was applied. Supplementary information (S2) more completely describes this experiment, and the results are summarized in Table S3 and Fig. S2. The leaching solution clearly fractionated Ca isotopes, as indicated by correlations between δ44/40Ca values and elemental ratios (Fig. S3), as well as fractions of Ca leached (Fig. S4); therefore, leachate and residual digest δ44/40Ca values were excluded from the main interpretations of this study.

X-ray diffraction

The identities of zeolite specimens collected in the field were confirmed by XRD in the Integrated Molecular Structure Education and Research Center at Northwestern University. Powder XRD data were collected at room temperature on an STOE-STADI-P powder diffractometer equipped with an asymmetrically curved germanium monochromator (CuKα1 radiation, λ = 1.54056 Å) and a one-dimensional silicon strip detector (MYTHEN2 1K from DECTRIS). The line focused Cu X-ray tube was operated at 40 kV and 40 mA. Intensity data from 2θ ranges of 1°–100° were collected over a period of 30 min. The instrument was calibrated against a NIST Si standard (640d) prior to measurement.

Elemental analysis

Sample solutions were diluted with 5% HNO3 and analyzed for concentrations of Ca, Na, Mg, K, and Sr using a Thermo Scientific iCAP 6500 ICP-OES at Northwestern University. The concentrations have an uncertainty of ±5% (relative standard deviation), as determined by repeated analyses of NIST SRM 1643f. Concentrations of Si and Al were measured using a lithium metaborate fusion procedure and an Enviro II ICP-AES (Activation Laboratories, Ancaster, ON). These data have an uncertainty of ±5%.

Ca isotope ratios

Calcium isotope ratios (44Ca/40Ca) were measured with a Thermo Fisher Triton MC-TIMS in the Radiogenic Isotope Laboratory at Northwestern University, using an optimized 43Ca–42Ca double-spike procedure135. Samples containing 50 μg of Ca were equilibrated with the spike, and the solutions were eluted through Teflon columns packed with Bio-Rad AG MP-50 cation-exchange resin. Approximately 12.5 μg of purified Ca was loaded onto outgassed, single Ta filament assemblies together with 0.5 μL of 10% H3PO4. Total procedural blanks (n = 4) determined with a 42Ca isotope dilution method were negligible (65–117 ng). Reported δ44/40Ca have an internal precision of ±0.02–0.03‰ (2σSEM). The double spike was frequently recalibrated by analyzing at least 8 OSIL ASW standards and 2 NIST 915b standards every 30 or fewer samples. During the period of study, repeated analyses of the standards yielded δ44/40CaASW = 0.000 ± 0.005‰ (2σSEM, n = 68) and δ44/40Ca915b = −1.147 ± 0.012‰ (2σSEM, n = 17). These data correspond to a short-term external reproducibility (2σSD) of ±0.045‰ for OSIL ASW and ±0.049‰ for NIST 915b. Long-term records for the laboratory yield δ44/40CaASW = 0.000 ± 0.002‰ (2σSEM, n = 661) and δ44/40Ca915b = −1.135 ± 0.003‰ (2σSEM, n = 263). These data point to a 2σSD of ±0.044‰ for OSIL ASW and ±0.048‰ for NIST 915b. Based on all standard measurements, we adopt a 2σSD of ±0.05‰ for the present dataset. As shown in the data tables, duplicate analyses of sample unknowns are better than ±0.02‰. Long-term records for the laboratory yield an SRM915a value of δ44/40Ca915a = −1.86 ± 0.01‰ (2σSEM, n = 68) relative to ASW; therefore, data reported here can be converted to the SRM915a scale using the following equation: δ44/40Ca (‰, SRM915a) = δ44/40Ca (‰, ASW) + 1.86‰.

Bond-length calculation

The weighted average bond length per zeolite mineral (L) was approximated by compiling published data on lengths for the two types of bonds (either Ca–Ow or Ca–Ofmwk) specific to each exchange site containing Ca (Table S2). For some zeolites, Ca occupying a given exchange site can coordinate to both water O atoms and framework O atoms (Table 3). Because, in general, bond lengths differ depending on whether Ca coordinates to water O or framework O atoms, we calculated weighted average, site-specific bond lengths (ls), which account for differences in Ca–Ow bond lengths (lw) and Ca–Ofmwk bond lengths (lfmwk) according to the number of water O atoms (Nw) and framework O atoms (Nfmwk) available for coordination.

The equations are:

$$L=({f}_{{{{{{\mathrm{C}}}}}}{{{{{\mathrm{a}}}}}}_{1}}\times {l}_{{{{{{\mathrm{s}}}}}}_{1}})+({f}_{{{{{{\mathrm{C}}}}}}{{{{{\mathrm{a}}}}}}_{2}}\times {l}_{{{{{{\mathrm{s}}}}}}_{2}})\cdots +({f}_{{{{{{\mathrm{C}}}}}}{{{{{\mathrm{a}}}}}}_{i}}\times {l}_{{{{{{\mathrm{s}}}}}}_{i}})$$
(1)
$${l}_{{{{{\mathrm{s}}}}}}=\left({l}_{{{{{\mathrm{w}}}}}}\times \frac{{N}_{{{{{\mathrm{w}}}}}}}{{{{{{\mathrm{C}}}}}}{{{{{\mathrm{N}}}}}}_{{{{{\mathrm{s}}}}}}}\right)+\left({l}_{{{{{\mathrm{fmwk}}}}}}\times \frac{{N}_{{{{{\mathrm{fmwk}}}}}}}{{{{{{\mathrm{C}}}}}}{{{{{\mathrm{N}}}}}}_{{{{{\mathrm{s}}}}}}}\right)$$
(2)
$${{{{{\mathrm{C}}}}}}{{{{{\mathrm{N}}}}}}_{{{{{\mathrm{s}}}}}}={N}_{{{{{\mathrm{w}}}}}}+{N}_{{{{{\mathrm{fmwk}}}}}}$$
(3)

where L is the estimated bond length per mineral (Å), fCa is the fraction of Ca occupying each site (1, 2,…i), ls is the weighted average site-specific bond length (Å), lw is the average Ca–Ow bond length in a given site (Å), lfmwk is the average Ca–Ofmwk bond length in a given site (Å), Nw is the number of Ca–Ow bonds in a given site, Nfmwk is the number of Ca–Ofmwk bonds in a given site, and CNs is the coordination number of Ca in a given site.

The calculations adopted for Fig. 4 assume even distribution of Ca across all potential Ca-bearing sites (Table 3). Sensitivity to this assumption was tested by changing fCa to values that produce the minimum and maximum possible estimates of L for each mineral. The correlation remains significant for all scenarios (R2 > 0.80, p < 0.001). See Supplementary information (S1) for more details on statistical analysis (Table S1).