Abstract
Long term, global records of urban extent can help evaluate environmental impacts of anthropogenic activities. Remotely sensed observations can provide insights into historical urban dynamics, but only during the satellite era. Here, we develop a 1 km resolution global dataset of annual urban dynamics between 1870 and 2100 using an urban cellular automata model trained on satellite observations of urban extent between 1992 and 2013. Hindcast (1870–1990) and projected (2020–2100) urban dynamics under the five Shared Socioeconomic Pathways (SSPs) were modeled. We find that global urban growth under SSP5, the fossil-fuelled development scenario, was largest with a greater than 40-fold increase in urban extent since 1870. The high resolution dataset captures grid level urban sprawl over 200 years, which can provide insights into the urbanization life cycle of cities and help assess long-term environmental impacts of urbanization and human–environment interactions at a global scale.
Similar content being viewed by others
Introduction
Global urban extent, i.e., the land surface that is dominated by man-made materials such as roads and houses, with long temporal spans (e.g., hundred years) is crucial to understanding the impacts of anthropogenic activities on natural and human environments1. Due to different levels of socioeconomic development, the process of urbanization was uneven across the world, both temporally and geographically. For example, during the century 1850–1950, rapidly and extensively urbanization occurred in currently developed regions, such as Europe, Americas, and Australia. In the late 20th century, the process of urbanization in developing countries began to accelerate, especially India and China. By 2050, the trends of urbanization in developing regions will be stronger than that in developed regions. The rapid global urbanization has become a rising public concern due to its wide impacts on sustainability issues including agriculture and deforestation2,3,4, urban ecological and environmental change5,6,7,8,9, energy consumption and emissions10,11,12,13, air pollution and public health14,15. A spatially explicit dataset of global urban extent with long temporal spans is needed to provide the whole life cycle of urbanization (e.g., urbanized, steadily urbanizing, and rapid urbanization16) in both developed and developing regions. With the help of this dataset, researchers can better comprehend the environmental impacts of global urbanization, and urban planning authorities can better address sustainability issues with evidence-based planning.
Remote sensing technology has shown considerable potential for mapping worldwide expansion of urban extent (hereafter, urban sprawl) over past decades17,18,19, but the temporal span of satellite observations (e.g., decades) are much shorter than that of the whole life cycle of urbanization (e.g., hundred years). Consequently, model-based approaches are helpful to project future urban sprawl or reconstruct urban sprawl before remote sensing observations and became available. To capture the urbanization process from past to future, urban sprawl models have gained popularity over the past few decades, including the commonly known cellular automata (CA) model20,21, the GEOMOD model22, the SLEUTH model23, and the conversion of land use and its effects (CLUE) model24,25. In general, there are two components in urban sprawl models. The first component is the estimation of pathway of urban extent (i.e., urban demand), which determines the increment of urban extent in different regions and years. Socioeconomic factors (e.g., such as population and gross domestic product (GDP)) and different approaches (e.g., panel-data analysis26,27, system dynamics (SD)28, and integrated modeling29,30) have been commonly used to estimate the urban demand22,27,31. The second component of urban sprawl models is the allocation of urban demand to spatially explicit grids. The CA model is one type of frequently used tool, in which different factors (e.g., terrain, land cover, roads, and urban infrastructure) are considered to simulate the process of urban sprawl. A variety of urban CA models have been developed32, such as the constraint CA16, the patch CA33, and the Markov CA34.
However, there are several limitations in current urban sprawl models to capture the whole life cycle of urbanization in different regions across the world. First, most of urban sprawl modeling studies focused on national35,36, metropolitan37,38, and city scales39,40, and only a few studies have attempted to simulate urban dynamics at the global scale at coarse spatial resolutions (e.g., 1 km or 8 km)29,30,41,42. Second, less attention has been paid to reconstruct historical urban sprawl, although the historical urban extent is of great help to understand the whole life cycle of urbanization in developed regions. Third, the differences of urban demand across regions under different urbanization stages were not well considered in previous studies. For example, panel data analysis is a commonly used approach for estimating urban demand, which essentially characterizes a linear relationship between per capital urban area and socioeconomic variables (e.g., per capital GDP and the urbanization rate) of all spatial units26. Such a relationship could be too simple to capture discrepancies of urban demand in different urbanization stages and differences of urban sprawl pathways in different regions42,43,44. Fourth, recent studies found that the newly developed lands play a more important role in urban sprawl compared to the early urbanized areas37. Thus, an urban sprawl model with a spatially explicit consideration of the temporal effect of urbanized pixels can better capture the complex urban sprawl at the global scale. Finally, production of global urban extent dynamics spanning hundred years is still lacking, although such a dataset is of great importance to global environmental change studies.
In this paper, we developed a modeling framework to hindcast and project global urban sprawl at a 1 km resolution from 1870 to 2100. First, we calibrated a global urban CA (i.e., the Logistic-Trend-CA) model with the consideration of the temporal effect of urbanized pixels using a longer than two decades of urban extent dataset from nighttime light (NTL) satellite observations. Next, we hindcasted urban shrink from 1992 back to 1870 using the calibrated Logistic-Trend-CA model. Similarly, we projected future global urban sprawl until 2100 under the five shared socioeconomic pathways (SSPs) scenarios45. The SSPs describe five alternative ways in which societal factors such as demographics, human development (for example, health and education), economic growth, inequality, governance, technological change, and policy orientations might evolve in the future45. Finally, we combined urban extent from observations, hindcast, and projection and generated the long-term dataset of urban extent from 1870 to 2100.
Results
Long-term dynamics of global urban extent
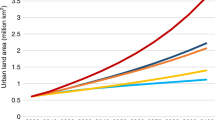
To the best of our knowledge, our product of urban extent for the first time presents a view of urban sprawl across the world for more than 200 years (Fig. 1). Temporally, the growth rate of global urban extent during the hindcast period is 3,230 km2 per year, which is about one sixth (20,000 km2) of the growth rate in the historical period (1992–2013) observed by satellites. Under five SSPs, the growth rates of global urban extent fall into the range of 10,000–240,000 km2 per year. Urban sprawl under SSP3 (regional rivalry) and SSP4 (inequality) is notably slower than that in the past two decades, while urban sprawl under SSP5 (fossil-fueled development) is higher44,45. Under SSP2 (middle of the road), there is a distinctive shift of urban sprawl hotspots from North America and Europe in earlier periods (i.e., before 1990s) to Asia and Africa in the future (i.e., after 2050s), particularly in China and India as well as other countries in west Africa. The presented spatiotemporal dynamics of global urban extent are consistent with the findings reported in the “World Urbanization Prospects”46. Both developing countries in Asia and Africa and developed countries in the North America and Europe will experience notable urban growth under SSP5 due to the projected rapid economic development in this scenario. It is worth to note that the harmonization between HYDE and NTL derived urban extents was conducted based on observations in 1992, which led to a slightly abrupt change around 1990 in the overall trend.
Change of global urban extent from 1870 to 2100 under five SSPs (a). Urban extent in representative years of historical and SSP2 scenario (i.e., Middle of the Road) (b). The urban extent was aggregated from 1 km to 1 degree as a percentage as represented in the maps. Maps in b were generated by ArcGIS Pro software (https://www.esri.com/en-us/arcgis/products/arcgis-pro/overview).
Urban area changes at the continental scale
Our results of urban extents, from hindcast, projection, and remote sensing observations, provide a continuous and harmonized record of global urban dynamics spanning from the 1870s to 2100 (Fig. 2). A notable difference in urban growth patterns across continents was observed. Urban area is largest in Asia among all continents in 2010, and this trend will continue although urban area will grow in all continents through 2100. Africa will be a new engine of urban growth in the second half of the century (i.e., after 2050) in SSP1, SSP2, and SSP5, though the urban proportion of Africa is relatively low17. In other continents (e.g., North America, South America, Europe, and Australia), there is moderate urban growth with a plateau stage albeit there are variations across SSPs. In general, our projection of urban extents under SSP2 (i.e., Middle of the Road) is in agreement with the United Nations’ projections46, which projected that almost 90% of urban population growth would likely occur in Asia and Africa by 2050.
Changes in urban extent at the country scale
Our results of urban extent with a temporal span of more than 200 years reveal pathways of urbanization across countries (Fig. 3). As such, the life cycle of urbanization (or city development) can be approximately characterized. It is crucial to consider the stage (i.e., initial, middle, and mature) of urbanization when analyzing the trend of urban growth. For example, as observed by satellites, the US is a developed country with a relatively low pace of urban growth22,26,41,42,46. From its pathway of urbanization during 1900–1990, we found a significant growth of urban areas (i.e., middle stage of the urbanization process) (Supplementary Fig. 1). Such urban growth is similar to that in China over the past two decades (Supplementary Fig. 1). Country-specific trends of urban growth can be derived from our product and can be used to understand their different stages of urbanization.
Hindcast: 1870, 1990, 1950, and 1990; Observation: 2000; Projection (SSP2: Middle of the Road): 2020, 2050, and 2100. Maps were generated by ArcGIS Pro software (https://www.esri.com/en-us/arcgis/products/arcgis-pro/overview).
In general, among the five SSPs, the growth of urban extent under SSP5 (fossil-fueled development) and SSP4 (inequality) is the highest and lowest, respectively, at the global scale (Supplementary Fig. 2). The primary difference among these SSPs is their trends of future population and the per capita urban area44. For example, the two most populated countries in Asia, China and India, exhibit notably different trends of urban growth due to the different population and per capita urban area pathways in the future. That is, the urban growth in China is anticipated to reach a plateau after 2050, while in India, urban growth under all scenarios show consistent trends of increase (Supplementary Fig. 1), which is driven by the continuous increases of both population and per capita urban area in India44. In some countries in the middle of Africa, future urban extent is still low because these countries are at the initial stage of urbanization before 2050 (Supplementary Fig. 2).
Dynamics of urban extent under different SSPs
Our urban sprawl dataset with a moderate spatial resolution clearly shows the evolution of urban extent over a long period in a spatially explicit way, as shown in a selected example of the Yangtze River Delta in China (Fig. 4), where a significant expansion of urban extent has been observed by satellite observations17. Obviously, there was only one isolated urban cluster (i.e., the main city of Shanghai) in the Yangtze River Delta of China in 1870. In the 1900s, there are only small settlements and the urban sprawl was slow. Over past two decades (1990–2010), this region experienced rapid urban sprawl due to the rapid migration of population from rural to urban areas. During this process, cities with different sizes grew and some of them were merged due to the development of traffic networks and the expansion of built-up areas47. Under SSPs, the continuous increase of population and economy drives the expansion of cities around Shanghai. The differences of spatial pattern in urban sprawl under the five SSPs are mainly driven by urban demand in these scenarios. Consistent with the growth of urban extent in China across the five SSPs, urban growth is largest under the SSP5, while it is smallest under the SSP4.
Maps were generated by ArcGIS Pro software (https://www.esri.com/en-us/arcgis/products/arcgis-pro/overview) (Basemap data © 2021 Esri).
The long-term dynamics of urban extent vary across metropolitan areas under the SSPs (Supplementary Fig. 3). We compared urban sprawl under SSP4 (i.e., inequality), SSP2 (i.e., middle of the road), and SSP5 (i.e., fossil-fueled development), which correspond to low, middle, and high growth rates, respectively44, across five metropolitan areas (Supplementary Fig. 3). In general, we observed a dramatic growth of urban area from 1870 to 2100 in these five regions. The initially sparely distributed and small urban patches grew and merged, resulting in notably enlarged urban clusters. The growth pattern of urban extent varies significantly across these metropolitan areas (Supplementary Fig. 3). For metropolitan areas in the US and UK, there is no significant urban growth between 2050 and 2100 under SSPs. However, for other three metropolitan areas in China, Egypt, and Brazil, we observed noticeable urban sprawls during the period of 2050–2100.
Discussion
Information of urban dynamics, especially at the global scale and over a long time period, is of great importance to deepen our understanding of the urbanization process. The life cycle of cities generally spans over multiple decades or even longer, while available observations and records of urban land for cities are limited43,48. Hence, existing theories about urban land growth could be limited due to the lack of data. Although satellite observations have been extensively used to monitor the urban environmental change over past decades, global records of urban dynamics are still limited due to challenges such as data availability and computational capacity49. Moreover, satellite observations may only cover a short period of the life cycle of cities. These factors hindered the use of temporal contexts in urban growth studies. Urbanization in cities under different stages (i.e., initial, middle, and mature)44 can be well captured from our long-term dataset of urban extent from 1870 to 2100.
Although there are some consistencies between our results and the other two relevant studies (Chen et al.26 and Gao and O’Neill42), trends of future global urban sprawl vary under different SSPs and across regions. Both, Chen et al.26 and Gao and O’Neill42 modeled global urban land change under the five SSPs scenarios through 2100 (Fig. 5). It is worth noting that urban extent in our study was derived from NTL data, which are not the same as the global human settlement layer used in Chen et al.26 and Gao and O’Neill42, in terms of the spatial distribution and total urban areas. Hence, we compared the ratio between urban extent in the future and base year. We found that there are some consistencies between our results and the other two studies. For example, the global urban area growth under the SSP5 (fossil-fueled development) is largest, while the growth under the SSP3 (regional rivalry) is relatively small. However, there are some differences as well. First, global urban areas under different SSPs in Gao and O’Neill42 are not fully consistent with the urbanization processes observed from existing highly urbanized cities (e.g., the US cities in Supplementary Fig. 4), as reflected in our results. Urban areas in Gao and O’Neill42 show consistent increases through 2100, especially for SSP5, SSP2, and SSP4. In fact, satellite observations revealed the growth of urban areas in North America and Europe already slowed down over past decades17, and this historical trend was well captured in our projection model44. Second, our model for urban area estimation is more theoretically based compared to data-driven approaches (e.g., Monte Carlo) in Gao and O’Neill42. In our model, the growth of urban areas is driven by economic development, population growth, and the historical pathway of urban area growth captured by the sigmoid-growth model, which was calibrated for each country using the observed time series of urban extent and historical socioeconomic data (i.e., population and GDP)44. For example, the urban area in China shows a continuous increase through 2100 in most SSP scenarios in Gao and O’Neill42, which is notably different from the trends revealed in our result and Chen et al.26 (Supplementary Fig. 5), given that the population in China was anticipated to decline in 2030. Third, the growth of urban area in Chen et al.26 is relatively low compared to our results and Gao and O’Neill42 (Supplementary Figs. 4 and 5), especially in rapidly developing countries (e.g., China). This is mainly because the spatial differences and temporal dynamics of per capita urban area in different regions were used in the panel data analysis in Chen et al.26. As a result, the derived per capita urban area showed small changes over years, which is not fully consistent with satellite derived results (i.e., per capita urban area in China shows a noticeable increment over past decades). Nevertheless, the historical trends with distinct increment of per capital urban area and the growth rate of urban areas in China were considered in our data and Gao and O’Neill42. Fourth, it is worth to note that the growth of urban extents under SSPs in current studies may not reflect the narrative as it is in literal meaning. For example, there is a large amount of urban area growth under SSP1 (sustainability) in some rapidly developing countries (e.g., China) because the predictions of future urban area growth only consider horizontal expansion. Due to the availability of urban heights data, especially at the global scale, urban vertical growth, which would result in a compact and sustainable urban development under SSP144, was not considered. Although Gao and O’Neill42 manually assigned a trajectory with a relatively low urban expansion rate under SSP1 to realize sustainable land use, the vertical growth of urban extent was not considered either, like most studies23,26,41,42,50. The absences of global urban height datasets and vertical urban growth models are primary barriers for modeling compact and sustainable urban growth. The advent of regional built-up height dataset51 provides the possibility to simulate the vertical growth of urban areas in future studies.
The comparison with other publicly available datasets indicates our historical modeling performs well in capturing temporal trends and spatial variations of urban extents (Supplementary Fig. 6). We selected the US in this experiment using the most available recorded (i.e., historical settlement data compilation; HISDAC-US)50,52 and modeled (i.e., forecasting scenarios of land use change; FORE-SCE)53 historical urban extent data. Although the definition and spatial extent of base maps used to generate historical modeling vary among these datasets, the temporal trends of urban area growth relative to 1940 are similar (Supplementary Fig. 6). The relatively large magnitude of urban area and growth rate in HISDAC-US data is mainly attributed to the definition of urban area in each 250 m grid, in which urban area was defined if one record of built-up properties was found. It is worth to note that we regarded the built-up area in HISDAC-US as urban areas for comparison, and many isolated built-up pixels away from cities were not included in FORE-SCE and our data. The temporal trends of urban growth between the FORE-SCE and our results are similar, although the used approaches are notably different. That is, historical trends of urban area in our data mainly came from the HYDE dataset29, which is notably different from the estimated growth rates in multiple historical years (i.e., 1973, 1980, 1986, and 1992) using change detection in the FORE-SCE model. In addition, the dynamics of urban extent in our data are relatively consistent with those from the FORE-SCE model and HISDAC-US data, despite their differences in definition and base map. It worthy to note that this comparison was conducted in the US, and more diverse comparisons are required in future to accounting for the uncertainty of historical urban sprawl in other regions54,55.
The integration of hindcast and projection of global urban dynamics, with a long temporal coverage (i.e., 230 years) and a moderate spatial resolution (1 km), can contribute to a variety of studies that are relevant to urbanization. For the climate change and sustainability communities, such long-term global urban extent dataset can be used as inputs to climate models to investigate the impacts of global urbanization (e.g., urban heat island) on global climate changes41,56. The expansion of urban extent also resulted in population redistribution, accompanied by different spatial patterns of emitted anthropogenic heat flux from different sectors (e.g., industry, traffic, building, and human metabolism), further influencing the global carbon cycle and climate change12,57,58. Our dataset can also be used to explore the impact of urban expansion on habitat and biodiversity loss7, particularly in those rapidly developing regions, where the urban CA model can also be implemented using fine spatial resolution (e.g., 30 m) urban extent data59,60. Moreover, this product can serve as important inputs for improving representation of urban dynamics in multisector human-Earth systems models.
Methods
Overall framework
We developed a framework by combining hindcasting and projecting urban sprawl as well as satellite observations to generate a product of global urban dynamics from 1870 (i.e., the second industrial revolution) to 2100 under different SSPs (Supplementary Fig. 7). There are four components in this framework. The first is data preparation, including the collection of country-specific socioeconomic data (e.g., population and GDP), spatially explicit proxies (e.g., terrain and traffic), and remotely sensed global urban extent time series17 (Supplementary Fig. 7a). Then, we estimated urban demands in two periods (i.e., 1870–1992 and 2013–2100), using socioeconomic data and an urban area growth model (Supplementary Fig. 7b). After that, we calibrated the Logistic-Trend-CA model37 and evaluated its performance using satellite derived urban extent from 1992 to 2013 (Supplementary Fig. 7c). Finally, we hindcasted historical (1870–1992) and future scenarios (2013–2100) of global urban extent in a spatially explicit manner and developed the dataset of global urban extent from 1870 to 2100 by integrating hindcasted, satellite-derived, and project urban extent (Supplementary Fig. 7d). Details of each component are presented in the following sections.
Data preparation
We collected country-specific socioeconomic (i.e., population and GDP) data to estimate urban demand changes in different countries. Historical population and GDP data were obtained from the World Bank database (http://databank.worldbank.org/). The country-specific urban area growth model can be developed from the population and GDP data combined with the urban extent time series. To project future urban demand change, we collected these two socioeconomic variables with changes under five SSPs until 210045.
Historical urban extent (1992–2013) was derived from the Defense Meteorological Satellite Program/Operational Linescan System (DMSP/OLS) stable nighttime light (NTL) data with a spatial resolution of 1 km17,61. The urban extent was defined as the region that has the largest change of NTL luminance along the urban–rural gradient, and this is consistent with high-resolution built-up area. It is worth to note this definition of urban extent is not same as that in census mainly based on urban population, in which the criteria to define urban areas could vary significantly across regions. Here, we used the NTL-derived urban extent time series data with an annual interval because other global urban extent data with finer spatial resolutions, such as the built-up maps of Global Human Settlement Layer (GHSL)60, are generally only available at coarse temporal resolutions. The NTL-derived global urban extent data are spatially and temporally consistent by using the same approach globally17,62, and are reliable according to the evaluation using finer spatial resolution land cover data. The urban boundaries derived from NTL also agree well with the finer resolution built-up map of GHSL (Supplementary Fig. 8). It worthy to note that some small settlements with size less than 5 km2 were not included in the NTL-derived urban extents (Supplementary Fig. 8). Indeed, the impact of removal smaller urban clusters is tiny (Supplementary Table 1), because these omitted small towns and settlements in NTL-derived urban extent data have relatively low growth rates. More details of the global urban extent data can be found in Zhou et al.17.
We built a global dataset of spatially explicit proxies to evaluate the suitability of urban sprawl at the pixel level. These spatial proxies include terrain, land, and urban infrastructures globally consistent and widely used in other studies59 (Table 1). For those proxies such as major cities and traffic, we calculated each pixel’s Euclidean distance to the nearest cities and roads. Given that these spatial proxies have different units and a wide range of magnitudes, we normalized them from 0–1.
Urban demands
We estimated country-specific urban demands before 1992 and after 2013 under five SSPs using different methods. For urban demand before 1992, given that there are limited socioeconomic data at the country level (e.g., population and GDP) before the 1990s, we used the temporal trend of urban area growth (1870–1992) from the History Database of the Global Environment (HYDE) database63. The HYDE data span from 10,000 BC to AD 2000, of which the built-up areas were estimated from demographic drivers (e.g., total and urban population) based on survey data of cities from literatures31. Because of the difference between urban areas from satellite observations and HYDE, a harmonized strategy using a ratio calculated in 1992 was implemented (Eq. (1)). Historical urban areas during the period 1870–1992 were estimated by multiplying urban area in the HYDE by a ratio.
where i indicates country, \(NT{L}_{i}^{1992}\) and \(HYD{E}_{i}^{1992}\) are derived urban areas in country i from NTL observations and HYDE, respectively.
For urban demand after 2013, we estimated country-specific urban demand using the urban area growth model44. Urban area growth in the future was determined by its historical pathways and the growth of future population and GDP. Using more than 20-year time series data of urban extent17 and the records of population and GDP change from the World Bank database, we developed the urban area growth model for each country44. Thus, we projected urban area growth of global countries under different SSP narratives. Details of these SSPs and the resulting country-specific urban areas can be found in Li et al.44.
Logistic-Trend-CA model
We calibrated the Logistic-Trend-CA model using the global urban extent time series data from 1992 to 2000. The Logistic-Trend-CA model is an improved CA model that considers the temporal effect of urbanized pixels on the spatial expansion of urban land37. That is, there is a relatively higher probability of urban development for pixels that were surrounded by more recently developed urban pixels. This improved model can notably reduce errors generated and propagated during the modeling process64. Hence, we used the Logistic-Trend-CA model to simulate the urban sprawl in this study.
The Logistic-Trend-CA model was built upon the widely used framework of the urban CA model, which has been extensively used in urban growth simulations65. In general, there are three components in the urban CA model, including transition rules, neighborhood, and land constraint21. These components represent different influential factors during urban sprawl, resulting in the development probability Pdev of conversion from non-urban to urban (Eq. (2)). We iteratively allocated derived urban areas to spatially explicit grids based on the development probability Pdev within a given region and period.
where Pdev is the development probability; Psuit, Ω, and Land are three components representing suitability surface, neighborhood, and land constraint, respectively.
We derived the suitability surface (i.e., transition rules) via calibrating the Logistic-Trend-CA model for each country using the global urban extent time series. The suitability surface represents the probability of urban development in an area with consideration of the socioeconomic and biophysical status (e.g., infrastructures, land surface, and terrain). First, we determined urbanized and persistent regions between 1992 and 2000. Then, we randomly generated training samples in urbanized and persistent areas with a sample rate of 20%. Next, we extracted spatial proxies of these samples and generated the suitability surface using the Logistic Regression (LR) model (Eqs. (3) and (4)),
where Psuit is the derived suitability of urban development, b0 is the intercept, bi and xi are the i th coefficient and spatial proxy (Table 1), respectively. The value of bi can be referred to as the contribution of each spatial proxy to the urban sprawl.
We improved the neighborhood component in the CA model by adding a weight factor to represent the trend of urban sprawl. The neighborhood represents the impact of surrounding neighbors on the central pixel, which is likely to be urbanized with urbanized pixels surrounding it. Here, we used the neighborhood that considers the urbanized year of neighbors, based on the widely used Moore configuration66 (Eqs. (5) and (6)).
where Ω denotes the influence of neighborhood with the consideration of the trend of urban sprawl using a weight factor of \({W}_{ij}^{ts}\). \({N}_{ij}^{u}\) is the accumulated year of cell (i, j) with the status as urban from the annual urban time series data with a temporal period of N. Thus, pixels that were urbanized more recently have relatively larger weights in calculating the neighborhood density Ω. m is the window size (set as 3), and Con() is a conditional function and returns 1 when the status of cell (i, j) is urban. In addition, water and protected areas were regarded as land constraints and are not allowed for conversion to urban in the Logistic-Trend-CA model21.
Hindcast and projection
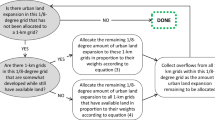
We reconstructed global urban extent back to the 1870s using the calibrated Logistic-Trend-CA model. Different from projection in which the newly developed urban areas expand from the urban core to fringe areas, the hindcast excludes pixels with lower development probabilities from the initial urban areas in 1992 (Supplementary Fig. 9). First, original urban pixels in the period T0 were ranked based on their developed probabilities. Then, urban pixels with relatively lower development probabilities during the period (T0 to T-1) were eroded from urban extent in the period T0. This process was iteratively implemented from 1992 to 1870.
We projected future global urban sprawl from 2013 to 2100 under five SSP scenarios by using the calibrated Logistic-Trend-CA model. The differences of SSPs are mainly reflected in the projected urban demands, which would be spatially allocated in a spatially explicit manner. Within each country, we used the Logistic-Trend-CA model to allocate increased urban demand to each 1-km grid. Finally, we combined hindcasting and projecting urban sprawl results and generated the long-term global urban extent product from 1870 to 2100.
Performance of the Logistic-Trend-CA model
The performance of the calibrated model was evaluated from two aspects. First, we assessed the suitability surface calibrated from the time series of urban extent data during 1992–2000 using the Receiver Operating Characteristic (ROC) approach59. The ROC approach evaluates the performance of the LR model by setting different thresholds over the whole domain of predicted probabilities, forming a continuous curve. The area under the curve (AUC) is commonly used as a quantitative indicator for assessment, and a higher value of AUC indicates better performance of the derived suitability surface. Second, we evaluated the simulated urban extent during 2000–2013 using two metrics: overall accuracy (OA) and figure of merit (FOM). The OA depicts the overall agreement of the modeled and observed urban maps, and the FOM characterizes the agreement between modeled and observed maps on changed pixels relative to the initial year of 2000 (Supplementary Fig. 10) (Eq. (7))67. The FOM (also called the Jaccard index or the Intersection-over-Union indicator in computer sciences) can provide a relatively comprehensive evaluation of model performance, and it has been widely used for model assessment in urban sprawl modeling.
where FOM is the figure of merit, B is the number of pixels that were observed and simulated as urban; A is the number of pixels that were observed as urban but simulated as non-urban; C is the number of pixels that were observed as non-urban but simulated as urban.
The Logistic-Trend-CA model performs well in simulating urban sprawl in most countries (Supplementary Fig. 11). Overall, the mean of AUC for all global countries is 0.89, suggesting a good performance of the calibrated logistic regression model (Supplementary Fig. 11a)68. That is, the generated suitability surface can adequately characterize the difference of urbanized and persistent regions from these spatial proxies. AUCs for countries in Asia and Africa are higher than in other regions, indicating the calibrated model can capture the rapid growth of urban sprawl in developing countries. Besides, the dominant factor of urban sprawl (i.e., the spatial proxy with the largest weight derived from the LR model) varies among countries. Infrastructures (e.g., the distance to city centers, highways, and major roads) are the dominant factors for most countries in the world (Supplementary Fig. 11b). Variations of the dominant spatial proxies across countries reflect different sprawl patterns of urban areas. Such patterns are essentially related to factors such as development levels and urban planning47.
The Logistic-Trend-CA model distinctively outperforms the traditional Logistic-CA model (Supplementary Fig. 12) according to the indicator of FOM. The mean FOM in the Logistic-Trend-CA model is 43%, which is about 10% increase compared to the Logistic-CA model. All settings in the Logistic-Trend-CA and Logistic-CA models are the same, except for the neighborhood, where the Logistic-Trend-CA model considers the temporal effect of urbanized neighbors. Comparison of these two urban CA models suggests the impact of urbanized neighbors at different years on urban sprawl is noticeable, especially for urban sprawl spanning a long period37. For example, we examined the trend of accuracy measures (i.e., OA and FOM) from 2000–2013 in three representative countries (i.e., the US, China, and India) (Supplementary Fig. 13). In each year within the validation period (2001–2013), we compared the FOM with urban extent in 2000. Overall, we observed an opposite trend of OA and FOM with the increase of modeling years. That is, the OA shows a consistent decreasing trend while the FOM is increasing during the modeling period. This phenomenon was caused by error generation and propagation of the urban CA model69. The decrease of OA was caused by the error accumulation during the modeling, while the increase of FOM suggests the neighborhood plays a crucial role in selecting those urbanized pixels around the initial urban extent. In addition, we observed that the FOM derived from the Logistic-Trend-CA model is higher than that from the Logistic-CA model, particularly for years after 2010. This is mainly driven by the significantly increased urban areas in recent years, i.e., the mean growth rate during 2010–2013 in China (13,002 km2/y) is about 2.3 times faster than that during 2000–2010 (5643 km2/y). In addition, it is worth to note that it is difficult to quantify the model accuracy for the far-range prediction and hindcasting results due to the availability of observations. Instead, it is more useful to explore the diverse urban sprawl scenarios in the future, mainly driven by the unique trend of urban area growth in different regions and socioeconomic and climate pathways26,42.
Data availability
Historical country-specific urban area data before 1992 were obtained from the History Database of the Global Environment (HYDE) database63 (https://www.pbl.nl/en/image/hyde). The projected country-specific urban area data after 2013 under five Shared Socioeconomic Pathways were available at the Figshare repository (https://doi.org/10.6084/m9.figshare.7817624.v1)44. The generated long-term global urban extent dataset includes the hindcasted urban extent (1870–1990); satellite-derived urban extent (1992–2013); and the projected urban extent (2020–2100) under the five SSPs. The spatial resolution of this dataset is 30 arc-second (~1000 m at the equator). The uploaded data are in GEOTIFF file format at the Figshare repository (https://doi.org/10.6084/m9.figshare.9696218)70.
Code availability
Code used in the analysis is available on request from the corresponding author.
References
Schneider, A., Friedl, M. A. & Potere, D. Mapping global urban areas using MODIS 500-m data: new methods and datasets based on ‘urban ecoregions’. Remote Sens. Environ. 114, 1733–1746 (2010).
Foley, J. A. et al. Global consequences of land use. Science 309, 570–574 (2005).
DeFries, R. S., Rudel, T., Uriarte, M. & Hansen, M. Deforestation driven by urban population growth and agricultural trade in the twenty-first century. Nat. Geosci. 3, 178–181 (2010).
Seto, K. C. & Ramankutty, N. Hidden linkages between urbanization and food systems. Science 352, 943–945 (2016).
Meng, L. et al. Urban warming advances spring phenology but reduces the response of phenology to temperature in the conterminous United States. Proc. Natl Acad. Sci. USA 117, 4228–4233 (2020).
Li, X. et al. Response of vegetation phenology to urbanization in the conterminous United States. Glob. Chang. Biol. 23, 2818–2830 (2017).
Alberti, M. et al. Global urban signatures of phenotypic change in animal and plant populations. Proc. Natl Acad. Sci. 114, 8951–8956 (2017).
Li, X., Zhou, Y., Asrar, G. R., Imhoff, M. & Li, X. The surface urban heat island response to urban expansion: a panel analysis for the conterminous United States. Sci. Total Environ. 605-606, 426–435 (2017).
Wang, S. et al. Urban−rural gradients reveal joint control of elevated CO2 and temperature on extended photosynthetic seasons. Nat. Ecol. Evol. 3, 1076–1085 (2019).
Güneralp, B. et al. Global scenarios of urban density and its impacts on building energy use through 2050. Proc. Natl Acad. Sci. USA 114, 8945–8950 (2017).
Seto, K. C. et al. in Climate Change 2014: Mitigation of Climate Change (eds Edenhofer, O. et al.) 927–1000 (Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge, United Kingdom and New York, NY, USA, 2014).
Xi, F. et al. Substantial global carbon uptake by cement carbonation. Nat. Geosci. 9, 880 (2016).
Li, X. et al. Urban heat island impacts on building energy consumption: a review of approaches and findings. Energy 174, 407–419 (2019).
Zhang, Q., He, K. & Huo, H. Policy: cleaning China’s air. Nature 484, 161–162 (2012).
Gong, P. et al. Urbanisation and health in China. Lancet 379, 843–852 (2012).
Yeh, A. G.-O. & Li, X. I. A. Sustainable land development model for rapid growth areas using GIS. Int. J. Geogr. Inf. Sci. 12, 169–189 (1998).
Zhou, Y., Li, X., Asrar, G. R., Smith, S. J. & Imhoff, M. A global record of annual urban dynamics (1992–2013) from nighttime lights. Remote Sens. Environ. 219, 206–220 (2018).
Gong, P. et al. Annual maps of global artificial impervious areas (GAIA) between 1985 and 2018. Remote Sens. Environ. 236, 111510 (2020).
Liu, X. et al. High-spatiotemporal-resolution mapping of global urban change from 1985 to 2015. Nat. Sustain. 3, 564–570 (2020).
Li, X. & Yeh, A. G.-O. Neural-network-based cellular automata for simulating multiple land use changes using GIS. Int. J. Geogr. Inf. Sci. 16, 323–343 (2002).
Li, X., Liu, X. & Yu, L. A systematic sensitivity analysis of constrained cellular automata model for urban growth simulation based on different transition rules. Int. J. Geogr. Inf. Sci. 28, 1317–1335 (2014).
Seto, K. C., Güneralp, B. & Hutyra, L. R. Global forecasts of urban expansion to 2030 and direct impacts on biodiversity and carbon pools. Proc. Natl Acad. Sci. USA 109, 16083–16088 (2012).
Zhou, Y., Varquez, A. C. G. & Kanda, M. High-resolution global urban growth projection based on multiple applications of the SLEUTH urban growth model. Sci. Data 6, 34 (2019).
Veldkamp, A. & Fresco, L. O. CLUE: a conceptual model to study the conversion of land use and its effects. Ecol. Model. 85, 253–270 (1996).
Verburg, P. & Overmars, K. Combining top-down and bottom-up dynamics in land use modeling: exploring the future of abandoned farmlands in Europe with the Dyna-CLUE model. Landsc. Ecol. 24, 1167–1181 (2009).
Chen, G. et al. Global projections of future urban land expansion under shared socioeconomic pathways. Nat. Commun. 11, 537 (2020).
Dong, N., You, L., Cai, W., Li, G. & Lin, H. Land use projections in China under global socioeconomic and emission scenarios: utilizing a scenario-based land-use change assessment framework. Glob. Environ. Chang. 50, 164–177 (2018).
He, C. et al. Developing land use scenario dynamics model by the integration of system dynamics model and cellular automata model. Sci. China Ser. D 48, 1979–1989 (2005).
Klein Goldewijk, K., Beusen, A., Doelman, J. & Stehfest, E. Anthropogenic land use estimates for the Holocene – HYDE 3.2. Earth Syst. Sci. Data 9, 927–953 (2017).
Hurtt, G. et al. Harmonization of land-use scenarios for the period 1500–2100: 600 years of global gridded annual land-use transitions, wood harvest, and resulting secondary lands. Clim. Chang. 109, 117–161 (2011).
Klein Goldewijk, K., Beusen, A. & Janssen, P. Long-term dynamic modeling of global population and built-up area in a spatially explicit way: HYDE 3.1. Holocene 20, 565–573 (2010).
Li, X. & Gong, P. Urban growth models: progress and perspective. Sci. Bull. 61, 1637–1650 (2016).
Chen, Y., Li, X., Liu, X. & Ai, B. Modeling urban land-use dynamics in a fast developing city using the modified logistic cellular automaton with a patch-based simulation strategy. Int. J. Geogr. Inf. Sci. 28, 234–255 (2014).
Shafizadeh Moghadam, H. & Helbich, M. Spatiotemporal urbanization processes in the megacity of Mumbai, India: a Markov chains-cellular automata urban growth model. Appl. Geogr. 40, 140–149 (2013).
Liu, X. et al. Simulating urban dynamics in China using a gradient cellular automata model based on S-shaped curve evolution characteristics. Int. J. Geogr. Inf. Sci. 32, 73–101 (2018).
Sohl, T. & Sayler, K. Using the FORE-SCE model to project land-cover change in the southeastern United States. Ecol. Model. 219, 49–65 (2008).
Li, X., Zhou, Y. & Chen, W. An improved urban cellular automata model by using the trend-adjusted neighborhood. Ecol. Process. 9, 28 (2020).
He, C., Tian, J., Shi, P. & Hu, D. Simulation of the spatial stress due to urban expansion on the wetlands in Beijing, China using a GIS-based assessment model. Landsc. Urban Plan. 101, 269–277 (2011).
Liu, Y. & Feng, Y. A logistic based cellular automata model for continuous urban growth simulation: a case study of the Gold Coast City, Australia. Agent-based models of geographical systems, 643–662 (2012).
Li, X., Gong, P., Yu, L. & Hu, T. A segment derived patch-based logistic cellular automata for urban growth modeling with heuristic rules. Comput. Environ. Urban. 65, 140–149 (2017).
Huang, K., Li, X., Liu, X. & Seto, K. C. Projecting global urban land expansion and heat island intensification through 2050. Environ. Res. Lett. 14, 114037 (2019).
Gao, J. & O’Neill, B. C. Mapping global urban land for the 21st century with data-driven simulations and shared socioeconomic pathways. Nat. Commun. 11, 1–12 (2020).
Klein Goldewijk, K., Beusen, A., Doelman, J. & Stehfest, E. J. E. S. S. D. New anthropogenic land use estimates for the Holocene: HYDE 3.2. Earth Syst. Sci. Data Discuss. 9, 927–953 (2017).
Li, X., Zhou, Y., Eom, J., Yu, S. & Asrar, G. R. Projecting global urban area growth through 2100 based on historical time‐series data and future shared socioeconomic pathways. Earth’s Future 7, 351–362 (2019).
Riahi, K. et al. The shared socioeconomic pathways and their energy, land use, and greenhouse gas emissions implications: an overview. Glob. Environ. Chang. 42, 153–168 (2017).
United Nations. World Urbanization Prospects: the 2018 Revision (UN, 2019).
Liu, J., Zhan, J. & Deng, X. Spatio-temporal patterns and driving forces of urban land expansion in China during the economic reform era. AMBIO 34, 450–455 (2005).
Batty, M. Rank clocks. Nature 444, 592–596 (2006).
Gong, P. et al. A new research paradigm for global land cover mapping. Annals GIS 22, 87–102 (2016).
Uhl, J. H. et al. Fine-grained, spatiotemporal datasets measuring 200 years of land development in the United States. Earth Syst. Sci. Data 13, 119–153 (2021).
Li, X., Zhou, Y., Gong, P., Seto, K. C. & Clinton, N. Developing a method to estimate building height from Sentinel-1 data. Remote Sens. Environ. 240, 111705 (2020).
Leyk, S. et al. Two centuries of settlement and urban development in the United States. Sci. Adv. 6, eaba2937 (2020).
Sohl, T. et al. Modeled historical land use and land cover for the conterminous United States. J. Land Use Sci. 11, 476–499 (2016).
Ostafin, K., Kaim, D., Siwek, T. & Miklar, A. Historical dataset of administrative units with social-economic attributes for Austrian Silesia 1837–1910. Sci. Data 7, 208 (2020).
Reba, M., Reitsma, F. & Seto, K. C. Spatializing 6,000 years of global urbanization from 3700 BC to AD 2000. Sci. Data 3, 160034 (2016).
Chen, F. et al. The integrated WRF/urban modelling system: development, evaluation, and applications to urban environmental problems. Int. J. Climatol. 31, 273–288 (2011).
McDonald, R. I. et al. Water on an urban planet: urbanization and the reach of urban water infrastructure. Glob. Environ. Chang. 27, 96–105 (2014).
Zhou, Y., Weng, Q., Gurney, K. R., Shuai, Y. & Hu, X. Estimation of the relationship between remotely sensed anthropogenic heat discharge and building energy use. ISPRS J. Photogramm. Remote Sens. 67, 65–72 (2012).
Li, X. et al. A cellular automata downscaling based 1 km global land use datasets (2010–2100). Sci. Bull. 61, 1651–1661 (2016).
Pesaresi, M. et al. GHS built-up grid, derived from Landsat, multitemporal (1975, 1990, 2000, 2014). (2015).
Li, X. & Zhou, Y. A stepwise calibration of global DMSP/OLS stable nighttime light data (1992–2013). Remote Sens. 9, 637 (2017).
Li, X., Gong, P. & Liang, L. A 30-year (1984–2013) record of annual urban dynamics of Beijing City derived from Landsat data. Remote Sens. Environ. 166, 78–90 (2015).
Klein Goldewijk, K., Beusen, A., van Drecht, G. & de Vos, M. The HYDE 3.1 spatially explicit database of human-induced global land-use change over the past 12,000 years. Glob. Ecol. Biogeogr. 20, 73–86 (2011).
Li, X., Zhou, Y. & Chen, W. An improved urban cellular automata model using trend adjusted neighborhood. Ecol. Process. 9, (2020).
Santé, I., García, A. M., Miranda, D. & Crecente, R. Cellular automata models for the simulation of real-world urban processes: a review and analysis. Landsc. Urban Plan. 96, 108–122 (2010).
Kocabas, V. & Dragicevic, S. Assessing cellular automata model behaviour using a sensitivity analysis approach. Comput. Environ. Urban 30, 921–953 (2006).
Pontius, R. Jr. et al. Comparing the input, output, and validation maps for several models of land change. Ann. Reg. Sci. 42, 11–37 (2008).
Hosmer, D. W., Lemeshow, S. & Sturdivant, R. X. Interpretation of the fitted logistic regression model. Appl. Logist. Regres., Third Edition, 49–88 (2013).
Li, X. et al. Critical role of temporal contexts in evaluating urban cellular automata models. GIScience Remote Sens. https://doi.org/10.1080/15481603.2021.1946261 (2021).
Li, X. & Zhou, Y. High resolution mapping of global urban extents from 1870 to 2100 by integrating data and model driven approaches. figshare. Dataset. https://doi.org/10.6084/m9.figshare.9696218 (2020).
Jarvis, A., Reuter, H. I., Nelson, A. & Guevara, E. J. a. f. t. C.-C. S. m. D. Hole-filled SRTM for the globe Version 4. 15, 25–54 (2008).
Man, U. World Database on Protected Areas WDPA. (2011).
ESRI. (ed ArcGIS Hub) (2018).
ESRI. (ed ArcGIS Hub) (2018).
Acknowledgements
This research was supported by the US Department of Energy, Office of Science, as part of research in MultiSector Dynamics, Earth and Environmental System Modeling Program and the National Science Foundation (2041859). The Pacific Northwest National Laboratory is operated for DOE by Battelle Memorial Institute under contract DE-AC05-76RL01830. We would like to thank the editor and three anonymous reviewers for their constructive comments and suggestions, and the many colleagues and organizations that shared the data used in this project. The views and opinions expressed in this paper are those of the authors alone.
Author information
Authors and Affiliations
Contributions
Y.Z. and X.L. designed the research; X.L. performed experiments and computational analysis; X.L. and Y.Z. drafted the manuscript; M.H., M.W., C.V., G.I. and W.C. revised the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Communications Earth & Environment thanks the anonymous reviewers for their contribution to the peer review of this work. Primary Handling Editor: Clare Davis.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, X., Zhou, Y., Hejazi, M. et al. Global urban growth between 1870 and 2100 from integrated high resolution mapped data and urban dynamic modeling. Commun Earth Environ 2, 201 (2021). https://doi.org/10.1038/s43247-021-00273-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-021-00273-w
This article is cited by
-
An Integrated Multi-Source Dataset for Measuring Settlement Evolution in the United States from 1810 to 2020
Scientific Data (2024)
-
Impacts of climate change-related human migration on infectious diseases
Nature Climate Change (2024)
-
Modelling volumetric growth of emerging urban areas around new transit stations
npj Urban Sustainability (2024)
-
Dynamic urban land extensification is projected to lead to imbalances in the global land-carbon equilibrium
Communications Earth & Environment (2024)
-
An assessment of WRF-urban schemes in simulating local meteorology for heat stress analysis in a tropical sub-Saharan African city, Lagos, Nigeria
International Journal of Biometeorology (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.