Abstract
The Arctic Ocean is of central importance for the global climate and ecosystem. It is a region undergoing rapid climate change, with a dramatic decrease in sea ice cover over recent decades. Surface advective pathways connect the transport of nutrients, freshwater, carbon and contaminants with their sources and sinks. Pathways of drifting material are deformed under velocity strain, due to atmosphere-ocean-ice coupling. Deformation is largest at fine space- and time-scales and is associated with a loss of potential predictability, analogous to weather often becoming unpredictable as synoptic-scale eddies interact and deform. However, neither satellite observations nor climate model projections resolve fine-scale ocean velocity structure. Here, we use a high-resolution ocean model hindcast and coarser satellite-derived ice velocities, to show: that ensemble-mean pathways within the Transpolar Drift during 2004–14 have large interannual variability and that both saddle-like flow structures and the presence of fine-scale velocity gradients are important for basin-wide connectivity and crossing time, pathway bifurcation, predictability and dispersion.
Similar content being viewed by others
Introduction
Ever since Fridtjof Nansen identified the Transpolar Drift (TPD) by joining up occasional observations of surface debris (Siberian driftwood; the wreckage of another expedition ship, Jeannette) in the Arctic in the 1890s and used it to plan the route of the Fram Expedition1, it has been assumed that this surface drift pathway is a relatively steady and clearly identifiable feature, connecting the East Siberian Arctic Shelf (ESAS) to east Greenland/Fram Strait, passing close to the North Pole (Fig. 1). However, as Nansen discovered when the Fram only came within ~670 km of the pole (84° N, 102° 27’ E), predicting the actual TPD is not necessarily so simple. Surprisingly, since then, there have been relatively few updates to the commonly accepted view of this rather steady, persistent, canonical picture of the TPD. Previous studies examined buoys drifting in sea ice within the TPD2 and showed that the velocity may occasionally reverse and also that there was substantial temporal variability associated with atmospheric synoptic circulation. A more recent study using satellite and buoy observations linked substantial variability of the TPD and Beaufort Gyre, and the interplay between their strength and shifting position, to the patterns of atmospheric circulation3. There is a link between decadal atmospheric variability in the Arctic Oscillation (AO) and the strength and orientation of the TPD due to the gyre-scale ocean response of the circulations of the Beaufort Gyre and Eurasian Basin, which straddle the TPD as a counter-rotating dipole4,5,6,7,8,9. When the Beaufort High is relatively weak and the Icelandic Low is relatively strong (positive AO index), there is anomalous cyclonic drift in the Eurasian Basin and the TPD diverts towards the Canadian Basin. When the situation is reversed, the Beaufort Gyre expands and there is a more direct TPD path from the ESAS towards Fram Strait (Fig. 1).
Schematic of the envelope of variability of the Transpolar Drift (TPD) and areas of the major Arctic expeditions, relevant to this study. The climatological path of the TPD from the East Siberian Arctic Shelf towards Greenland/Fram Strait (white arrow) is aligned with the seafloor topography of the Lomonosov Ridge. The particle release patch for this study (magenta box) encloses the start location of the Polarstern, the central observatory of the MOSAiC expedition. The start and endpoints of the drift of the Polarstern and the Fram are shown by yellow and green circles, respectively. The variation of the TPD associated with positive/negative phases of the decadal variability of the Arctic Oscillation/vorticity index are shown by red/blue arrows, respectively. Figure adapted from a version provided by GRID-Arendal (See Acknowledgments), with drift arrows inspired by Mysak7.
Since the late 19th century, there have been many drifting Arctic expeditions, including the drifts of the US T-1, T-2, T-3, Arctic Research Laboratory Ice Station I and II, ALPHA-I and II and Arctic Ice Dynamics Joint Experiment sea ice camps (1950s–1970s), the Soviet Union and Russian North Pole (Северный Полюс) stations (1937 and 1954–2010)10,11, the Sea Ice Mechanics Initiative and Surface Heat Budget of the Arctic Ocean experiments in the 1990s with annual or longer occupation12, International Polar Year missions and drifting buoy deployments under the International Arctic Buoy Programme13,14 and Ice Tethered Profilers 2004-present15,16. There were other short-time dedicated sea ice camps, partly supported by sea ice floe-moored research vessels, FRAM I-IV, Marginal Ice Zone Experiment, Coordinated Eastern Arctic Experiment, Leads Experiment12, etc. In 2006–2008 the Tara schooner attempted to repeat the drift of Fram under the umbrella of the International Polar Year17. In October 2019 the largest polar expedition yet undertaken, the international MOSAiC expedition (Multidisciplinary drifting Observatory for the Study of Arctic Climate; https://mosaic-expedition.org) was launched, partly seeking to repeat the Fram expedition drift, (although starting at higher latitude due to the recent reduction in sea ice cover). MOSAiC was designed to monitor the state of the Arctic physical and biological systems over a full year, drifting freely with the surface flow. Expeditions such as MOSAiC are likely to be repeated in future in order to observe the rapidly changing Arctic. Understanding the characteristics of surface drift and advective connectivity across the Arctic basin is clearly of interest, both for planning future fieldwork and for interpreting past observations.
The surface advective pathways studied here are important for transporting material around the Arctic basin, connecting the Pacific and Atlantic via coastal boundary currents, and connecting shallow shelf seas to the deep interior. Of particular interest is the ESAS, which comprises the Laptev Sea, the East Siberian Sea and the western part of the Chukchi Sea, and is the largest shelf sea region in the world. The ESAS stores a vast amount of carbon in the subsea permafrost, with annual release rates equal to that over the entire pelagic area of the global oceans; recent data also indicates release of methane in the ESAS area18. Siberian rivers not only transport organic carbon and freshwater from Eurasia to the ESAS, but also terragenic minerals19, radioisotopes20, lead contamination21 and, potentially, a large amount of microplastics22. Understanding the advective pathways of such is important for determining whether their ultimate fate is within the Arctic or whether they exit into the Atlantic over a period of time.
It is important to consider whether this decadal- and gyre-scale view of the TPD is still sufficient for understanding Arctic Ocean surface drift pathways, especially in the context of the surface transport of material from the ESAS to Fram Strait and elsewhere, or for the predictability of the path of a drifting ship, scientific autonomous instruments, pollutant or, more generally, a surface particle advected within the sea ice or ocean. Are smaller-scale flow structures and variability important too? We know that there is also substantial synoptic and monthly variability in ice advection, which is largely wind-driven23. There are typically larger lateral gradients of velocity at smaller scales in geophysical flows24, so it might be expected that particle paths or patches of material could be deformed more if they encounter rapidly varying jet boundaries or eddies. The representation of such features either in observations or models is key to representing the advection of material.
Furthermore, it is clear that the Arctic is undergoing considerable changes6. Observations from submarine sonar and satellites show that between 1958 and 2018, the average sea ice thickness near the end of the melt season decreased by 2.0 m or 66%25. The same study shows that the area of multi-year Arctic sea ice lost more than 2 × 106 km2 or 50% between 2002 and 2017. Due to this anomalous ice decline, exposure of the underlying ocean to the atmosphere may lead to regional changes in ocean circulation and new ocean-atmosphere interaction processes. For example, in the eastern Eurasian Arctic basin reduced sea-ice cover has been associated with a weakening of the halocline, accompanied by the shallowing of the warm Atlantic Intermediate water and enhanced winter ventilation, thus potentially providing a positive feedback to local warming in the atmosphere26. More generally, for the whole Arctic, it has been shown that sea ice reduction plays a central role in Arctic surface air temperature amplification, with a positive feedback due to increased northern hemisphere extratropical atmospheric water vapour content, partly in response to reduced sea ice, correlating with enhanced warming in the lower atmosphere of the Arctic in summer and early autumn27. There is evidence that loss of Arctic summer sea ice can affect large-scale Northern Hemisphere atmospheric circulation via amplification of the Arctic Dipole meridional pattern28. Another example identifies a connection between reduced sea ice extent and a change to both the path and formation sites of drifting sea ice, as well as ice-rafted material formed in the shallow ESAS and advected through Fram Strait29. Identifying the TPD variability is an important first step in attributing and predicting any response to the changes in Arctic sea ice cover, ocean circulation and understanding key feedbacks in the Arctic coupled system.
Characterisation of advective pathways of ‘surface drift’ - due to combined surface ocean currents and sea ice (see Methods) may be analysed using two approaches: an Eulerian method (named after Leonhard Euler, a Swiss mathematician, physicist and polymath) to measure fluid properties at a fixed location, and a Lagrangian method (developed by an Italian-French mathematician and astronomer Joseph-Louis Lagrange) that measures fluid properties following a particle advected with the flow. Lagrangian particle tracking is a powerful method for capturing the time-history of changes experienced by particles driven by a time-varying flow to diagnose advective pathways and coherent flow structures defined by particle trajectories. Prediction of surface drift is often driven by a flow field that does not fully represent the energetic ocean dynamics at the mesoscale, a.k.a. the scale of geophysical turbulence. In the Arctic, the mesoscale (typical spatial and temporal scale of <20 km, <1 month respectively)6 is characterised by underlying flow structures with large velocity gradients, which may result in splitting (bifurcation) of surface drift pathways and stretching/shearing (deformation) of fluid parcels. The surface drift depends on the complex dynamics of the underlying ocean and sea ice and of the overlying atmosphere.
In this study, we use a fine-scale ocean model hindcast (with the horizontal resolution order of kilometres) and coarser-scale satellite-derived ice velocities, combined with Lagrangian particle tracking to explore advective pathways of surface drift emanating from the ESAS region and captured within the typical envelope of the TPD towards Fram Strait. We investigate the coherence of the pathways, their connection to the large-scale circulation and the role of the fine-scale surface flow. Fine-scale flow structure impacts both the basin crossing time and the predictability of drift pathways over annual timescales. Stagnation points, where the flow is locally zero, are identified and their neighbouring streamlines are shown to separate distinct regions with different advective properties. These flow separatrices influence pathway bifurcations and related sudden changes to pathway predictability, which we formally link to a measure of particle (tracer) spread (dispersion). Similar to the climatological-mean pattern of the TPD and the adjacent gyres, the most likely drift pathways are predominantly governed by large-scale, slowly-varying atmospherically-forced flow. However, in contrast to this view, our study highlights substantial interannual variability, with dramatic deviations of drift pathways and variations in their source regions.
Results
Here the basic details of the experimental setup are presented. In order to characterise the typical drift of material particles released at a location and time, due to the presence of nonlinear dynamics it is necessary to explore sensitivity of each drift trajectory to initial condition uncertainty (ICU) - spatiotemporal errors due to observations or forecasts. The particles are released in a 25 × 25 grid across 134–136 E, 84–86 N at evenly-spaced lon-lat intervals (equivalent to ~5 km separation), shown by the magenta box in Fig. 1, starting at midday on same date, 6 October (time t = t0), during each of the last 10 full years covered by the ocean model hindcast, 2005–2014. There are further particle releases at midday for each of 10 days before (26 September–5 October) and 10 days after (7–16 October) (21 days total). The release region is designed not only to capture flow from the ESAS, but also to enclose the starting location of the research icebreaker Polarstern, the central observatory of the MOSAiC expedition. Given our interest in the role of fine-scale flow and the lack of comparable ocean hindcasts with such high spatial resolution, the study is constrained to the timespan 2005–2014, which permits an examination of recent interannual variability but not a direct comparison with MOSAiC. It allows us to study the envelope of drift pathways and their relationship to coherent flow structures within this period and to put the MOSAiC drift in the context of the TPD and the surface circulation structure, rather than seeking to recreate a single drift trajectory. With this in mind, our goal is that the envelope of results can be interpreted for future expeditions or for release of tracers or dispersal of pollutants. The time of year chosen for the release is typically when there is a large production of sea ice and the TPD is strong. This also coincides with the approximate start time of year of observational expeditions − 5 October for Fram and 4 October for MOSAiC. The surface velocity field from the hindcast is used by the ARIANE offline Lagrangian particle tracking tool to advect particles for later statistical analysis. See the Methods for details.
Estimating surface drift pathways and their potential predictability
Climate models suggest that a large component of Arctic variability is due to unforced, intrinsic processes in the system30, so it is plausible that skilful prediction of particular drift pathways for a given year may remain elusive, i.e., that there may be variability in system components unrelated to changes in external forcing that are inherently chaotic and unpredictable. Therefore, each year of simulation is treated as an independent estimate of typical future state, under a ‘perfect model’ assumption, thus we assume no errors in the driving velocity field, but use the hindcast to dynamically generate a range of one-year states, each beginning at the same time of year. ARIANE permits us to efficiently simulate advection offline, using many particles to explore sensitivity to chaotic dynamics and predictability.
Lagrangian particle statistics may provide further useful insights31. At a given instant, the ensemble mean across the 25 × 25 = 625 particles represents the best location estimate of the drift, for the given spatial component of ICU. The ‘cloud dispersion’ is based on the second moment of particle displacements and is the square of the root-mean-square particle pair separation31 (RPPS). An increase in RPPS indicates the average relative spreading of the particle patch as it is advected and deformed by the flow, therefore changes to RPPS may also be used as a measure of the evolution of ICU. In addition, cloud dispersion, hence RPPS, provides a formal link to the concentration statistics of a continuous cloud of tracer31, so may indicate processes relevant to the dispersion of freshwater, nutrients, etc. If the cloud dispersion did not change over a given time period following the start of drift, the ICU would not grow and the potential predictability of drift would be perfect.
We next explore these measures of drift and predictability in the context of large- and fine-scale flow variability.
Substantial interannual variability of drift pathways
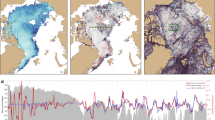
Figure 2 shows the drift pathways for each year for a single chosen start time of t = t0 (6 October).
NEMO model-based drift, showing evolution of the ten annual ensembles of 625 surface drift pathways starting at t = t0 = 6 October in each year, advected for 12 months. Colours represent the elapsed time after the start of the drift and black circles show the ensemble mean position at 0.5, 1.5, …, 11.5 months.
There is substantial interannual variability, both in the ensemble-mean pathway (‘best estimate’ of drift) and in the spread of particles (change in ICU, i.e. estimate of error associated with drift prediction) and in the seasonal sea-ice extent (Supplementary Fig. 1). The key feature in Fig. 2 is the bifurcations in the pathways: near Svalbard in 2005, 2008, 2009 and 2013; north of Greenland in 2007 and 2011 (when the ensemble-mean pathway reverses direction after 11 months) and in 2014 (when some pathways pass through Nares Strait).
In 2006 and 2010, the pathways followed the long-term mean position of TPD, passing through Fram Strait and southwards along eastern Greenland. The time for the ensemble-mean of the particles to reach Fram Strait varies between the years: from 7.5–8.5 months in 2008 to 8–9 months, 9–10 months and 10–11 months in 2010, 2006 and 2013 respectively with the longest transient time of 11–12 months being in 2009. 2012 is atypical, because the particles cover a relatively short distance and drift towards the Canadian Arctic Archipelago (CAA), with the spreading of the patch remaining small throughout the whole drift. 2007, 2011 and 2013 also show initial drift of particles towards the CAA, but ultimately their trajectories cross the basin to reach the East Greenland Current in varying locations.
Although the advection of particles is driven by the local flow structure in a given moment in time, here it is also useful to consider the relation of drift pathways to the large-scale annual-mean flow, shown in Fig. 3. Stokes’ Drift is most familiar as being related to wind-driven surface waves, but its original derivation was actually more general (see p208 and preceding in Stokes32) - it is simply the difference between Lagrangian and Eulerian averages of the flow (see van den Bremer and Breivik33 for a review and Andrews and McIntyre34 for a more mathematical treatment). In this study, we use a general Stokes’ Drift definition. An equivalent kinematic interpretation is that the Stokes’ Drift is the net velocity due to any time-varying advection that causes particles to cross the Eulerian time-mean streamlines. Simply by comparing the Lagrangian drift trajectories and the Eulerian time-mean streamlines, it may be seen that, in certain places there is a crossover due to Stokes’ Drift (due to strong, time-varying advective processes in the velocity field, including wind-driven and eddying flow), otherwise the pathways largely follow the streamlines. An example of the presence of Stokes’ Drift is seen in 2007 (Fig. 3) in the central Arctic, 2–5 months after initialisation.
Ensemble-mean drift pathway for initial condition 6 October in each year, plotted daily over the following 12 months (colours). Streamlines show time-mean surface flow for the 12 month period, with line thickness proportional to flow speed (max. 0.2 m/s). In regions of strong currents, where streamlines converge and obscure the underlying drift pathways, a zoomed view may be beneficial and Fig. 2 should also be used for reference. Inset are examples of saddle points near land (red star) and in the open ocean (blue star) and associated streamline topology (flow direction may be reversed without altering the type of saddle point). Streamlines in the vicinity of saddle point examples are also coloured red and blue, respectively.
In order to classify types of flow structure, fixed-point analysis in dynamical systems theory provides a useful framework: “stagnation points”35, where the velocity becomes zero, are seen as “centres” within gyres and are the “saddle points” in the flow between gyres and currents. A more objective definition of these structures depends on the eigenvalues of the spatial velocity gradient - in the case of a saddle point, defined where the eigenvalues are real, with opposite signs - but this also highlights a practical challenge. The multifractal nature of the sea ice velocity field14,36,37 on geophysical scales features higher velocity gradients within shorter averaging time scales. This means that the velocity gradient thresholds in the saddle point analysis would be dependent on the temporal and spatial scales under consideration. As smaller spatiotemporal scales are examined, yet more saddle points and centres may be observed - (see also Haller38 - their Fig. 5, for example). For the purpose of the present examination, here we use the eigenvalue definition, with a focus on the large-scale, annual-mean flow (marked in Fig. 3). These examples include near-coastal and open-ocean saddle points. We also highlight critical streamlines (separatrices) in the vicinity of the saddle points, which separate distinct regions of the annual-mean flow.
The saddle point in the surface circulation near the coast of northern Greenland changes its location along the shelf break from year to year within an envelope covering approximately 460 km in extent, with extreme western and eastern positions in 2006 and 2008 respectively (red star marker in Fig. 3). In 2014, two saddle points were identified either side of Nares Strait. To identify the critical streamlines separating the pan-Arctic flow (a.k.a., separatrices) and highlight their interannual variability throughout the period under the analysis, we construct a set of streamlines associated with the saddle points in the region and closest neighbouring streamlines (solid red lines in Fig. 3). Although the “terminating” saddle point near northern Greenland (hereafter “terminus”), where the flow terminates with a singularity and is stagnant, does not vary substantially in its position, O(100 km), the starting point of the corresponding separatrix (hereafter “source”) of the flow connecting the Siberian and Greenland limits of the Arctic Ocean varies dramatically from year to year. This variation in the source presents us with varying degrees of this streamline curvature. The relative curvature of a streamline can be approximated by a relative departure of the streamline length from the corresponding shortest distance on the Earth’s surface (here, spherical geometry is used, so this is an arc of a great circle) and, thus, defined by the ratio of the length of the streamline from the source of the separatrix to its terminus, to the length of the corresponding great circle arc, joining the source and the terminus. The exception is the year 2014, for which we define the midpoint for the terminus pair to obtain the endpoint of the separatrix. We define positive curvature for the flow along the streamline as being anticlockwise on the large scale from the source to terminus, and negative - vice versa. The two limiting cases should be noted for this definition: if the streamline follows the great circle exactly, then the curvature is zero; if the terminus coincides with the source, the curvature is undefined. The other limitation occurs when the streamline has a large number of alternating clockwise and anticlockwise departures from the great circle - in this rare case the sign of the curvature is not well defined. The separatrix curvature index (SCI) gives a clear definition of the separation of the surface flow across the Arctic Ocean and the TPD, and also a way to quantify connectivity between the Siberian shelves and regions of the Arctic outflows (Table 1). Following the above analysis, we have noticed clustering of the flow patterns for years with negative SCI (2006, 2007, 2009, 2010) and for years with positive SCI (2005, 2008, 2011, 2012, 2013), and when the sign of the SCI is indeterminate (2014). This gives us the two contrasting multi-annual periods: the period 2006–2010 features the clockwise separatrix streamlines (negative SCI) and the years 2011–2013 are with anti-clockwise streamlines (positive SCI). Years 2008 and 2014 fall outside of the pattern. The positive SCI for 2005 can be attributed to the presence of an open-ocean saddle point and weak circulation on the shelves (see below). We emphasise here that these indices and years refer to the period starting 6 October until 5 October the following year - therefore, when comparing with other indices in the literature for a given year spanning, e.g. Jan-Dec., any offset should be considered.
The interpretation of these periods’ dynamics is as follows. When the SCI is positive, the ESAS is dynamically connected with the Amerasian Arctic and the Beaufort Gyre; when the SCI is negative, the ESAS is connected with the Eurasian Arctic, the TPD and Fram Strait. However, we note that the separatrix streamlines and the TPD (as defined by the strong current shown by tightly-packed black streamlines across the central Arctic in Fig. 3) do not necessarily coincide. In particular, the separatrix streamlines bound the TPD from the Amerasian side of the Arctic Ocean and also the positions of these streamlines are more spatially variable than the position of the TPD itself (Fig. 3). The shift from negative to positive SCI corresponds to a similar anomalous change, but of opposite sign, in the Arctic Ocean Oscillation index (AOO), with a sudden reduction from a large positive AOO index (mean of 2.66 for Jan.–Dec. 2007–11) to a small positive index (mean of 0.90 for Jan.–Dec. 2012–3)39. Transitions in the overall sign of the AOO are dominated by decadal variability, but variability on shorter time scales adds an additional imprint. The AOO reflects the dynamical response of the BG, measured by the difference in sea surface height (SSH) from the BG centre to the outermost closed SSH contour, so is a measure of the geostrophic circulation, whereas the SCI expresses the surface flow structure, which may differ due to ageostrophic dynamics, and includes the BG and adjacent flow, potentially involving the circulation in the ESAS, the TPD and Eurasian gyre. That said, there is a good correspondence between the SCI and the size and position of the BG40, where 2006–10 (negative SCI) matches the period where the BG exhibits a sudden and rapid expansion in extent (especially noticeable in the years Jan-Dec. 2007 and 2010–11) and an area-mean increase in dynamic ocean topography (order 20 cm), which correlates with regional changes in sea level pressure. In contrast, the period 2011–13 (positive SCI) corresponds to a sudden contraction in extent and decrease in area-mean dynamic ocean topography (order 20 cm) in the BG during the years Jan-Dec. 2012–14). This suggests a link between the forcing and dynamics of the BG and the SCI. Although the relationship between decadal variability of the TPD and the Arctic Oscillation (AO) index41 is well established, we find no clear relationship of the AO with the SCI on sub-decadal timescales.
It is noteworthy that both 2005 and 2011 have open-ocean saddle points (blue stars in Fig. 3), so the inclusion/exclusion of the weak circulation on the shelves can make a difference for the size of the gyres, sign of the SCI and the location of the source regions. Indeed, the involvement of the shelf dynamics distinguishes the separatrix streamlines from the closed dynamic ocean topography contours that are used to characterise the BG variability in the study40. Neutral (close to ±1) SCI during 2008 and 2014 suggests that, generally, separatrix streamlines and TPD are almost straight in these years, although the details of the connectivity between the ESAS and Fram Strait/BG may vary. It should further be noted that the curvature index, SCI, gives a direct simple and clear measure of the saddle point streamline (transport barrier) structure and of the flow dynamics; in terms of the surface advection and connectivity, it has more physical meaning than the traditional AO and AOO. The separatrix streamlines highlight the variable connectivity of the ESAS with very distinct regions within the Arctic basin. This has implications for the advection of the freshwater anomalies, geochemical tracers and terragenic material and allows us to investigate the role of shelf sea physics in the pan-Arctic oceanic variability on interannual timescales.
To summarise, we assert that drift pathway depends on i) where the particle is initialised with respect to separatrix streamlines; ii) local Stokes’ Drift; iii) the local velocity of the particle and velocity gradient; with the relative order depending on the magnitude of each effect for the particular evolution of the drift scenario in question. The satellite-based observations of the dynamic ocean topography show that the BG has extended and expanded towards the northwest during the period 2003–2014, covered by the study40, which includes interannual variability. This agrees with our findings on the variations in the surface flow, including the transition in BG properties around Jan. 2012, which match a change from negative to positive SCI beginning in October 2011. However, subtle changes in the BG shape and therefore position of the separatrix streamline adjacent to the TPD appear to play an important role in determining the ensemble-mean particle drift. 2012 is an outlier due to an expanded BG and because the patch of particles is initialised so close to the location of the separatrix streamline at that time. It appears that Stokes’ Drift towards the CAA also played a role and has led to the patch deviating from the TPD and getting entrained into the separated flow of the BG.
Existence and role of fine-scale flow structures
We define fine-scales as spanning the range of variability from that of Arctic mesoscale eddies near the Rossby deformation radius (~5–15 km)42 and ~weeks, up to flow structures that characterise the annual-mean gyre-scale pattern of BG and TPD. The gyre-scale flow in the upper Arctic Ocean is typically driven by atmospheric forcing over the preceding 3 months40. Dynamically, the gyre-scale circulation and the mesoscale are connected. Although the mesoscale is more nonlinear and random, mesoscale eddies are organised by gyre-scale waveguides43,44. The eddies may both draw their energy from shear instability of the gyre-scale flow, as well as feeding back energy and momentum to gyre-scales and larger43,44,45,46,47. Geophysical turbulence theory includes eddies near the gyre scale down to the mesoscale and smaller, and implies that the rate of spatial deformation in the velocity field (strain) increases with decreasing lengthscale24. Larger rate of strain typically leads to a larger deformation of a patch of particles released in the fluid flow.
We argue that the nonlinear mesoscale dynamics are evident in the flow structure, because there is a sensitivity to the start time, particularly in 2005 (also see Supplementary Fig. 2). In this year the patches’ spread is large from the very beginning, except for releases closer to the time t0 + 10. This reflects the presence of a flow in the release region that is highly variable, being strong and with strong lateral shear during the period t0 − 10 to t0, but becoming weaker towards t0 + 10. In 2011 and 2012, there is only negligible sensitivity to start time, and in the other years, the sensitivity emerges later during the drift of particles. For a given start time, e.g. t = t0 (black line), there is typically an increase in RPPS with time, reflecting the accumulated effect of the flow on deformation of the patch and reduced potential predictability of the particles’ pathways. However, as well as periods when RPPS increases, there are also periods when RPPS may locally decrease with time or exhibit negligible change (Fig. 4, pairs of vertical blue lines). Examining the changes to the patches of particles during these periods, it is clear that the rapid variability on the order of weeks, predominantly due to changes in the gyre-scale flow, may be occasionally be quite distinct from the annual-mean streamline patterns in Fig. 3, due to atmosphere-forced synoptic variability. Some examples of deformation of the particle patches occur at times when the patch reaches either a coastal saddle point or an open-ocean saddle point. In the vicinity of these flow structures, the velocity gradient may be relatively large over fine scales, leading to rapid changes in RPPS. Periods when RPPS remains constant or decreases are typically when the patch is being slowly advected by the gyre-scale flow and either continues without deformation or enters a region of converging flow, associated with an open-ocean saddle, where the particles within the patch coalesce for a period of time. Typically, these periods are limited though, because eventually, the patch reaches a coastal saddle point, associated with a rapid increase in RPPS. In the vicinity of coastal boundaries, velocity gradients due to coastal currents with large lateral shear rapidly deform the patch. Patch bifurcation may also occur at a near-coastal saddle point, such as that near northern Greenland, further increasing RPPS. Examples of such bifurcations are seen in Fig. 2.
Root-mean-squared particle pair separation (km) for the 25 × 25 particle patch as a function of time after the start of drift. Each of the 21 coloured lines shown each year represents one-day increment time offsets from t0 = 6 October in that year. Thick lines represent the extreme and central times. At any instant, for a given time offset, the statistics are based on 195,000 particle pairs. Vertical blue lines, which span 1.5 months, highlight example periods for a variety of changes in RPPS, which are discussed in the text, using Fig. 2 for reference, with the black line being the relevant comparator.
Presently, there is no calibrated observational baseline to provide fine-scale constraints of the surface flow covering spatial scales and areas needed by gridded particle tracking algorithms. Gridded observational data from satellite altimeters and surface drifters does not resolve the smaller end of these fine-scales. Neither, yet, do models used for climate projections. However, the ensemble-mean drift structures seen in our fine-resolution model hindcast study (Figs. 2 and 3) broadly compare with that of recent observational estimates (Supplementary Fig. 3), although the basin crossing times are typically many months faster when fine-scales are included. We conclude by emphasising the importance of saddle points and their associated separatrices that straddle distinct advective pathways. These critical regions of streamlines and flow topology, between gyres and boundary currents, which exhibit interannual variability, are important for the predictability of drift for a given initial condition. In the presence of a tracer gradient, saddle points may also act to enhance lateral tracer mixing, because they are associated with changes to RPPS (which we have used to define potential predictability) and which we have related to the so-called cloud dispersion of Lagrangian particle statistics. Regions where material or tracers would be mixed strongly, therefore, correspond to a loss of potential predictability of a surface drift pathway (where RPPS becomes large). These findings are therefore highly relevant for considering a) the transport and mixing of nutrients, freshwater, carbon and contaminants originating from the ESAS source, as outlined in the Introduction; and b) the planning of future drifting Arctic expeditions or instrument deployments. Generally, the existence and importance of saddle points and their connectivity have been demonstrated by this present analysis. In particular, relevant to the coastal saddle point near northern Greenland, the definition of an index, SCI, provides an additional insight into surface flow connectivity and how that varies from year to year.
Methods
There are two surface velocity datasets and two-particle tracking algorithms used in this paper. The majority of the paper is based on surface velocity simulated with a global 1/12° resolution ocean- sea ice dynamical model, NEMO (Nucleus for European Modelling of the Ocean), forced by atmospheric reanalysis, with offline particle tracking using ARIANE, which has been used extensively with NEMO model data48,49,50,51,52,53,54,55,56,57,58,59. Supplementary Fig. 3 is based on ice drift velocity from three sets of satellite observations combined with particle tracking from IceTrack, which is specifically configured to work with the observational data. These are detailed below.
NEMO ocean + sea ice model
The NEMO model framework60 used in the study employs a quasi-uniform ‘ORCA’ orthogonal tripolar grid with two Northern Hemisphere poles placed on land in Siberia and Canada to overcome the North Pole singularity in the ocean61. The model version is 3.6, at a nominal 1/12° horizontal resolution (~4 km in the Arctic), discretized on an Arakawa C-grid and with 75 vertical z-coordinate levels. Within NEMO, the ocean general circulation model OPA (Ocean Parallélisé)62 is coupled to the Louvain-la-Neuve sea-ice model version 2 (LIM2)63,64, which includes Semtner thermodynamics, viscous-plastic rheology, Prather advection and ice ridging and rafting schemes63,65; the ice model is also configured on a C-grid65.
The sea-ice model dynamics depend on two-category ice cover (consolidated ice plus leads), expressed as a two-dimensional compressible linear viscous-plastic continuum, driven by winds and ocean currents. Sea-ice resists deformation with a compressive strength that increases monotonically with ice thickness and concentration. The lateral momentum balance in LIM2 includes the air–ice and ice-ocean stresses, the Coriolis force, the force due to the local horizontal tilt of the ocean surface and ice internal forces caused by ice deformations. The air-ice and ice-ocean stresses are weighted by the ice concentration. The thermodynamics use a three-layer model for vertical heat conduction within snow and ice. The ice-ocean heat and salt fluxes provide a further coupling between LIM2 and OPA. For a more detailed description of the thermodynamic processes, see Fichefet and Morales Maqueda63 and Bouillon et al.65.
The global model simulation, identified as ORCA0083-N06, has been used for many other studies50,66,67,68, and specifically for the Arctic69, where it has also been validated against observations48,49,50. The model is forced by Drakkar Forcing Set 5.2, for the full model run covering 1958–201570. In this study, we make use of data from 2005–15. For further details of the forcing, bathymetry and initial conditions, we refer to Moat et al.66. Here we use the 5-day-mean surface velocity output for the period 2005–2015 for offline calculations with ARIANE.
We define “surface velocity”, Vsurface, as a weighted combination:
Vsurface = Aice × Vice + (1 − Aice) × Vocean(k = 1), where Vice and Vocean are horizontal vectors representing the ice and ocean velocity, respectively. Aice is the ice area fraction (dimensionless).
In addition, a threshold is used for the model sea-ice momentum balance. Where the ice volume per unit area, equal to the area-mean of (ice concentration × ice thickness) in each gridcell, is less than 5 × 10−2 m, the sea-ice velocity in the model sea-ice momentum balance is set equal to the ocean velocity at the top model gridcell (k = 1). The top gridcell is 1 m thick and the ocean velocity is uniform throughout the depth of this cell, so Vsurface is the combined ice-ocean surface velocity taken at the ice-ocean interface at zero metres depth.
The aim of this study is to look at the large-scale motion of surface flow (sea ice and ocean) using off-line tracking with surface velocity output, Vsurface. In the sense of the behaviour described in the preceding paragraph, particles are advected completely with the ice when the ice area fraction approaches 1 and when the ice volume per unit area threshold is met or exceeded. However, offline particle tracking does not capture the whole complexity of ice physics of LIM2 (e.g. particles freezing-in or melting-out from ice; evolution due to snow or metamorphic ice; embedded in the ice brine channels or frozen in the ice lattice, etc.) This requires on-line tracking and would be a very complicated code to create, outside the scope of this study.
ARIANE offline particle tracking
There is a range of general offline Lagrangian particle tracking codes available, each with their own strengths and shortcomings, as described in, e.g. Table 1 of van Sebille et al.71. ARIANE was initially developed to efficiently compute a large number of particle trajectories offline, following the model conservation laws, using supplied velocity data. The efficiency comes from employing an analytical solution for the trajectory within each model grid cell, based on the discretised form of the volume conservation equation for that grid structure72,73. Here, we follow the approach of previous studies48,49,50 and use ARIANE on the 5-day-mean output of NEMO/ORCA0083-N06. Note that all the explicit subgrid-scale diffusive parameterisations cited in LIM2 and OPA contribute to the 5-day-mean velocity but that ARIANE is purely advective and does not add any additional subgrid-scale effects, such as simulated diffusion. Subsequently, from the ARIANE calculations, the particle positions are output every day. A separate study examining the sensitivity of trajectories calculated with ARIANE to the spatiotemporal sampling/averaging of the velocity has been performed using a similar 1/12° NEMO/ORCA model of the North Atlantic74. That study found that there was only notable sensitivity when combined spatiotemporal scales smaller than ½ deg. and 6 days are suppressed. Therefore, we consider the use of 1/12° and 5-day-mean velocity sufficient in our application of ARIANE.
Satellite-based sea ice drift trajectories
Satellite-based Lagrangian sea ice drift trajectories were determined with a drift analysis system called IceTrack that traces sea ice forward in time using a combination of satellite-derived, low-resolution drift products29,75. In summary, IceTrack uses a combination of three different, ice drift products for the tracking: i) motion estimates based on a combination of scatterometer and radiometer data provided by the Center for Satellite Exploitation and Research (CERSAT76, 62.5 × 62.5 km grid spacing), ii) the OSI-405-c motion product from the Ocean and Sea Ice Satellite Application Facility (OSI SAF77, 62.5 × 62.5 km grid spacing), and iii) Polar Pathfinder Daily Motion Vectors (v.4) from the National Snow and Ice Data Center (NSIDC78, 25 × 25 km grid spacing). The contributions of individual products to the used motion field are weighted based on their accuracy and availability which vary with seasons, years, and study region. The IceTrack algorithm first checks for the availability of CERSAT motion data, since CERSAT provides the most consistent time series of motion vectors starting from 1991 to present and has shown good performance on the Siberian shelves75. During summer months (June–August) when drift estimates from CERSAT are missing, motion information is bridged with OSISAF (2012 to present). Prior to 2012, or if no valid OSISAF motion vector is available within the search range, NSIDC data is applied. The tracking approach works as follows: All 625 parcels are traced forward in time on a daily basis starting on October 6th (2005–2014). Tracking is discontinued if ice concentration at a specific location along the trajectory drops below 50% and we assume the ice to be melted. By reconstructing the pathways of 56 GPS buoys using IceTrack, Krumpen et al.29 found that within the first 200 days the displacement between real and virtual buoys was on average 36 ± 20 km.
Lagrangian particle statistics
The ensemble mean position, P, of a set of N particles at a given instant, t, is defined as:
The root-mean-squared particle pair separation (RPPS), equivalent to the square-root of cloud dispersion31, is a measure of the variation about the mean position:
Data availability
The Lagrangian particle track data and statistics produced in this study are available for download from the Zenodo repository: https://doi.org/10.5281/zenodo.4868752.
References
Nansen, F. Farthest North: Being the Record of a Voyage of Exploration of the Ship Fram, 1893–96, and of a Fifteen Months’ Sleigh Journey. 1 (Cambridge University Press, 2011).
Serreze, M. C., McLaren, A. S. & Barry, R. G. Seasonal variations of sea ice motion in the transpolar drift stream. Geophys. Res. Lett. 16, 811–814 (1989).
Volkov, V. A., Mushta, A. & Demchev, D. Sea ice drift in the Arctic. in Sea Ice in the Arctic: Past, Present and Future (eds Johannessen, O. M., Bobylev, L. P., Shalina, E. V. & Sandven, S.) 301–313 (Springer International Publishing, 2020). https://doi.org/10.1007/978-3-030-21301-5_7.
Kwok, R., Spreen, G. & Pang, S. Arctic sea ice circulation and drift speed: decadal trends and ocean currents. J. Geophys. Res. Oceans 118, 2408–2425 (2013).
Armitage, T. W. et al. Arctic Ocean surface geostrophic circulation 2003–2014. Cryosphere 11, 1767–1780 (2017).
Timmermans, M. & Marshall, J. Understanding Arctic Ocean circulation: a review of ocean dynamics in a changing climate. J. Geophys. Res. C Oceans 125, C04S02 (2020).
Mysak, L. A. Patterns of Arctic circulation. Science 293, 1269–1270 (2001).
Steele, M. et al. Circulation of summer Pacific halocline water in the Arctic Ocean. J. Geophys. Res. Oceans 109, C02027 (2004).
Haine, T. W. N. et al. Arctic freshwater export: status, mechanisms, and prospects. Global Planet. Change 125, 13–35 (2015).
Untersteiner, N. AIDJEX review. in Sea ice processes and models (ed. Pritchard, R. S.) 3–11 (University of Washington Press, 1980).
Hakkinen, S., Proshutinsky, A. & Ashik, I. Sea ice drift in the Arctic since the 1950s. Geophys. Res. Lett. 35, L19704 (2008).
Beaufort Gyre Exploration Project. Modern Scientific Expeditions https://www2.whoi.edu/site/beaufortgyre/history/modern-scientific-expeditions-1970s-2000s/(1970s-2000s).
Polyakov, I. V. et al. Variability and trends of air temperature and pressure in the maritime Arctic, 1875–2000. J. Climate 16, 2067–2077 (2003).
Rampal, P., Weiss, J., Marsan, D. & Bourgoin, M. Arctic sea ice velocity field: general circulation and turbulent-like fluctuations. J. Geophys. Res. Oceans 114, C10014 (2009).
Krishfield, R., Toole, J., Proshutinsky, A. & Timmermans, M.-L. Automated ice-tethered profilers for seawater observations under pack ice in all seasons. J. Atmospheric Oceanic Technol. 25, 2091–2105 (2008).
Toole, J., Krishfield, R., Timmermans, M.-L. & Proshutinsky, A. The ice-tethered profiler: Argo of the Arctic. Oceanog. 24, 126–135 (2011).
Gascard, J.-C. et al. Exploring Arctic transpolar drift during dramatic sea ice retreat. EOS Trans. Am. Geophys. Union 89, 21–22 (2008).
Shakhova, N. et al. Geochemical and geophysical evidence of methane release over the East Siberian Arctic Shelf. J. Geophys. Res. Oceans 115, C08007 (2010).
Schoster, F., Behrends, M., Müller, C., Stein, R. & Wahsner, M. Modern river discharge and pathways of supplied material in the Eurasian Arctic Ocean: evidence from mineral assemblages and major and minor element distribution. Int. J. Earth Sci. 89, 486–495 (2000).
Abrahamsen, E. P. et al. Tracer-derived freshwater composition of the Siberian continental shelf and slope following the extreme Arctic summer of 2007. Geophys. Res. Lett. 36, L07602 (2009).
Gobeil, C., Macdonald, R. W., Smith, J. N. & Beaudin, L. Atlantic Water flow pathways revealed by lead contamination in Arctic Basin sediments. Science 293, 1301–1304 (2001).
Kanhai, L. D. K., Gardfeldt, K., Krumpen, T., Thompson, R. C. & O’Connor, I. Microplastics in sea ice and seawater beneath ice floes from the Arctic Ocean. Sci. Rep. 10, 5004 (2020).
Barry, R. G., Serreze, M. C., Maslanik, J. A. & Preller, R. H. The Arctic Sea ice-climate system: observations and modeling. Rev. Geophys. 31, 397–422 (1993).
Vallis, G. K. Atmospheric and oceanic fluid dynamics: fundamentals and large-scale circulation. (Cambridge University Press, 2006).
Kwok, R. Arctic sea ice thickness, volume, and multiyear ice coverage: losses and coupled variability (1958–2018). Environ. Res. Lett. 13, 105005 (2018).
Polyakov, I. V. et al. Greater role for Atlantic inflows on sea-ice loss in the Eurasian Basin of the Arctic Ocean. Science 356, 285–291 (2017).
Screen, J. A. & Simmonds, I. The central role of diminishing sea ice in recent Arctic temperature amplification. Nature 464, 1334–1337 (2010).
Overland, J. E. & Wang, M. Large-scale atmospheric circulation changes are associated with the recent loss of Arctic sea ice. Tellus A: Dyn. Meteorol. Oceanogr. 62, 1–9 (2010).
Krumpen, T. et al. Arctic warming interrupts the Transpolar Drift and affects long-range transport of sea ice and ice-rafted matter. Sci. Rep. 9, 5459 (2019).
Stroeve, J. C. et al. Trends in Arctic sea ice extent from CMIP5, CMIP3 and observations. Geophys. Res. Lett. 39, L16502 (2012).
LaCasce, J. H. Statistics from Lagrangian observations. Prog. Oceanogr. 77, 1–29 (2008).
Stokes, G. G. On the theory of oscillatory waves. Trans. Cambridge Philos. Soc. 8, 441–455 (1847).
van den Bremer, T. S. & Breivik, Ø. Stokes drift. Philos. Trans. R. Soc. A 376, 20170104 (2018).
Andrews, D. G. & Mcintyre, M. E. An exact theory of nonlinear waves on a Lagrangian-mean flow. J. Fluid Mech. 89, 609–646 (1978).
Strogatz, S. H. Nonlinear dynamics and chaos: with applications to physics, biology, chemistry, and engineering. (CRC Press, 2018).
Mandelbrot, B. B. The fractal geometry of nature. (W.H. Freeman, 1982).
Schertzer, D. & Lovejoy, S. Multifractals, generalized scale invariance and complexity in geophysics. Int. J. Bifurcat. Chaos 21, 3417–3456 (2011).
Haller, G. Lagrangian coherent structures. Annu. Rev. Fluid Mech. 47, 137–162 (2015).
Proshutinsky, A., Dukhovskoy, D., Timmermans, M.-L., Krishfield, R. & Bamber, J. L. Arctic circulation regimes. Philos. Trans. R. Soc. A 373, 20140160 (2015).
Regan, H. C., Lique, C. & Armitage, T. W. K. The Beaufort Gyre extent, shape, and location between 2003 and 2014 from satellite observations. J. Geophys. Res. C Oceans 124, 844–862 (2019).
Armitage, T. W. K., Bacon, S. & Kwok, R. Arctic sea level and surface circulation response to the Arctic Oscillation. Geophys. Res. Lett. 45, 6576–6584 (2018).
Nurser, A. J. G. & Bacon, S. The Rossby radius in the Arctic Ocean. Ocean Sci. 10, 967–975 (2014).
Williams, R. G., Wilson, C. & Hughes, C. W. Ocean and atmosphere storm tracks: the role of eddy vorticity forcing. J. Phys. Oceanogr. 37, 2267–2289 (2007).
Waterman, S. & Hoskins, B. J. Eddy shape, orientation, propagation, and mean flow feedback in western boundary current jets. J. Phys. Oceanogr. 43, 1666–1690 (2013).
Hughes, C. W. & Ash, E. R. Eddy forcing of the mean flow in the Southern Ocean. J. Geophys. Res. C Oceans 106, 2713–2722 (2001).
Liu, Y., Wilson, C., Green, M. A. & Hughes, C. W. Gulf Stream transport and mixing processes via coherent structure dynamics. J. Geophys. Res. C Oceans 123, 3014–3037 (2018).
Waterman, S. & Jayne, S. R. Eddy-mean flow interactions in the along-stream development of a western boundary current jet: an idealized model study. J. Phys. Oceanogr. 41, 682–707 (2011).
Kelly, S. J., Proshutinsky, A., Popova, E. K., Aksenov, Y. K. & Yool, A. On the origin of water masses in the Beaufort Gyre. J. Geophys. Res. C Oceans https://doi.org/10.1029/2019JC015022 (2019).
Kelly, S., Popova, E., Aksenov, Y., Marsh, R. & Yool, A. Lagrangian modeling of Arctic Ocean circulation pathways: impact of advection on spread of pollutants. J. Geophys. Res. C: Oceans 123, 2882–2902 (2018).
Kelly, S. J., Popova, E., Aksenov, Y., Marsh, R. & Yool, A. They came from the Pacific: how changing Arctic currents could contribute to an ecological regime shift in the Atlantic Ocean. Earth’s Future 8, e2019EF001394 (2020).
Gary, S. F., Susan Lozier, M., Böning, C. W. & Biastoch, A. Deciphering the pathways for the deep limb of the Meridional Overturning Circulation. Deep Sea Res. Part II 58, 1781–1797 (2011).
Gary, S. F., Fox, A. D., Biastoch, A., Roberts, J. M. & Cunningham, S. A. Larval behaviour, dispersal and population connectivity in the deep sea. Sci. Rep. 10, 10675 (2020).
Gary, S. F., Lozier, M. S., Biastoch, A. & Böning, C. W. Reconciling tracer and float observations of the export pathways of Labrador Sea Water. Geophys. Res. Lett. 39, 8 (2012).
Wagner, P., Rühs, S., Schwarzkopf, F. U., Koszalka, I. M. & Biastoch, A. Can Lagrangian tracking simulate tracer spreading in a high-resolution ocean general circulation model? J. Phys. Oceanogr. 49, 1141–1157 (2019).
Gillard, L. C., Hu, X., Myers, P. G. & Bamber, J. L. Meltwater pathways from marine terminating glaciers of the Greenland ice sheet. Geophys. Res. Lett. 43, 10873–10882 (2016).
Beuvier, J. et al. Spreading of the Western Mediterranean Deep Water after winter 2005: Time scales and deep cyclone transport. J. Geophys. Res. Oceans 117, C07022 (2012).
Schulze Chretien, L. M. & Frajka-Williams, E. Wind-driven transport of fresh shelf water into the upper 30 m of the Labrador Sea. Ocean Sci. 14, 1247–1264 (2018).
Koch-Larrouy, A., Morrow, R., Penduff, T. & Juza, M. Origin and mechanism of Subantarctic Mode Water formation and transformation in the Southern Indian Ocean. Ocean Dyn. 60, 563–583 (2010).
Biastoch, A., Lutjeharms, J. R. E., Böning, C. W. & Scheinert, M. Mesoscale perturbations control inter-ocean exchange south of Africa. Geophys. Res. Lett. 35, L20602 (2008).
Madec, G. NEMO ocean engine (France, Institut Pierre-Simon Laplace, IPSL, 2008) 300 pp.
Madec, G. & Imbard, M. A global ocean mesh to overcome the North Pole singularity. Clim. Dyn. 12, 381–388 (1996).
Madec, G., Delecluse, P., Imbard, M. & Lévy, C. OPA 8.1 Ocean General Circulation Model reference manual (France, Institut Pierre-Simon Laplace, IPSL, 1998) 91 pp.
Fichefet, T. & Morales Maqueda, M. A. Sensitivity of a global sea ice model to the treatment of ice thermodynamics and dynamics. J. Geophys. Res. Oceans 102, 12609–12646 (1997).
Goosse, H. & Fichefet, T. Importance of ice-ocean interactions for the global ocean circulation: a model study. J. Geophys. Res. Oceans 104, 23337–23355 (1999).
Bouillon, S., Morales Maqueda, M. Á., Legat, V. & Fichefet, T. An elastic–viscous–plastic sea ice model formulated on Arakawa B and C grids. Ocean Model. 27, 174–184 (2009).
Moat, B. I. et al. Major variations in subtropical North Atlantic heat transport at short (5 day) timescales and their causes. J. Geophys. Res. C Oceans 121, 3237–3249 (2016).
Hirschi, J. J.-M. et al. Loop current variability as trigger of coherent Gulf Stream transport anomalies. J. Phys. Oceanogr. 49, 2115–2132 (2019).
Blaker, A. T. et al. Historical analogues of the recent extreme minima observed in the Atlantic meridional overturning circulation at 26° N. Clim. Dyn. 44, 457–473 (2015).
Bacon, S., Aksenov, Y., Fawcett, S. & Madec, G. Arctic mass, freshwater and heat fluxes: methods and modelled seasonal variability. Philos. Trans. R. Soc. A 373, 20140169 (2015).
Brodeau, L., Barnier, B., Treguier, A.-M., Penduff, T. & Gulev, S. An ERA40-based atmospheric forcing for global ocean circulation models. Ocean Model. 31, 88–104 (2010).
van Sebille, E. et al. Lagrangian ocean analysis: fundamentals and practices. Ocean Model. 121, 49–75 (2018).
Blanke, B. & Raynaud, S. Kinematics of the Pacific equatorial undercurrent: an Eulerian and Lagrangian approach from GCM results. J. Phys. Oceanogr. 27, 1038–1053 (1997).
Döös, K. Interocean exchange of water masses. J. Geophys. Res. C Oceans 100, 13499–13514 (1995).
Blanke, B., Bonhommeau, S., Grima, N. & Drillet, Y. Sensitivity of advective transfer times across the North Atlantic Ocean to the temporal and spatial resolution of model velocity data: Implication for European eel larval transport. Dyn. Atmospheres Oceans 55–56, 22–44 (2012).
Krumpen, T. et al. The MOSAiC ice floe: sediment-laden survivor from the Siberian shelf. Cryosphere 14, 2173–2187 (2020).
Girard-Ardhuin, F. & Ezraty, R. Enhanced Arctic Sea ice drift estimation merging radiometer and scatterometer data. IEEE Trans. Geosci. Remote Sens. https://doi.org/10.1109/TGRS.2012.2184124 (2012).
Lavergne, T. Validation and monitoring of the OSI SAF low resolution sea ice drift product (v5). 35 http://osisaf.met.no/docs/osisaf_cdop2_ss2_valrep_sea-ice-drift-lr_v5p0.pdf (2016).
Tschudi, M., Meier, W. N., Stewart, J. S., Fowler, C. & Maslanik, J. Polar pathfinder daily 25 km EASE-grid sea ice motion vectors, version 4. https://doi.org/10.5067/INAWUWO7QH7B (2019).
Acknowledgements
This work resulted from the Advective Pathways of nutrients and key Ecological substances in the Arctic (APEAR) project (NE/R012865/1, NE/R012865/2, #03V01461), part of the Changing Arctic Ocean programme, jointly funded by the UKRI Natural Environment Research Council (NERC) and the German Federal Ministry of Education and Research (BMBF). This work has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement no. 820989 (project COMFORT, Our common future ocean in the Earth system – quantifying coupled cycles of carbon, oxygen, and nutrients for determining and achieving safe operating spaces with respect to tipping points). The work reflects only the authors’ view; the European Commission and their executive agency are not responsible for any use that may be made of the information the work contains. This work also used the ARCHER UK National Supercomputing Service and JASMIN, the UK collaborative data analysis facility. Satellite-based sea ice tracking was carried out as part of the Russian-German Research Cooperation QUARCCS funded by the German Ministry for Education and Research (BMBF) under grant 03F0777A. This study was carried out as part of the international Multidisciplinary drifting Observatory for the Study of the Arctic Climate (MOSAiC) with the tag MOSAiC20192020 (AWI_PS122_1 and AF-MOSAiC-1_00) and the NERC Project “PRE-MELT” (Grant NE/T000546/1=). We also acknowledge funding support received from the NERC National Capability programmes LTS-M ACSIS (North Atlantic climate system integrated study, grant NE/N018044/1) and LTS-S CLASS (Climate–Linked Atlantic Sector Science, grant NE/R015953/1). The schematic of the ESAS in Fig. 1 was adapted with permission granted by GRID-Arendal from a version downloaded on 11 Feb 2020 (see https://www.grida.no/resources/6617; persistent archived version at https://web.archive.org/web/20191018051919/http://www.grida.no/resources/6617). The authors would like to acknowledge the contribution of Maria Luneva to the discussions about the initial idea of the paper and for highlighting the historical importance of observations from the Russian North Pole drifting stations. Sadly, Maria passed away suddenly in 2020 before the draft of the paper was written.
Author information
Authors and Affiliations
Contributions
All authors contributed to the writing of the manuscript. C.W., Y.A., S.R. and S.K. contributed to the design of the ARIANE particle tracking experiments. T.K., C.W., Y.A. and S.R. contributed to the design of the IceTrack experiments. C.W. performed the ARIANE experiments and diagnostics and produced the figures. S.K. assisted C.W. in setting up ARIANE and troubleshooting. T.K. performed the IceTrack experiments. A.C.C. performed the NEMO/ORCA0083-N06 experiments.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Communications Earth & Environment thanks the anonymous reviewers for their contribution to the peer review of this work. Primary Handling Editors: Jan Lenaerts, Heike Langenberg
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wilson, C., Aksenov, Y., Rynders, S. et al. Significant variability of structure and predictability of Arctic Ocean surface pathways affects basin-wide connectivity. Commun Earth Environ 2, 164 (2021). https://doi.org/10.1038/s43247-021-00237-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-021-00237-0
This article is cited by
-
The Transpolar Drift current: an ocean-ice-wind complex in rotating, spherical coordinates
Monatshefte für Mathematik (2024)
-
Typical and anomalous pathways of surface-floating material in the Northern North Atlantic and Arctic Ocean
Scientific Reports (2022)
-
Deep water pathways in the North Pacific Ocean revealed by Lagrangian particle tracking
Scientific Reports (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.