Abstract
More than one teramole of carbon per year is subducted as carbonate or carbonaceous material. However, the influence of carbonation/decarbonation reactions on seismic activity within subduction zones is poorly understood. Here we present field and microstructural observations, including stable isotope analyses, of carbonate veins within the Higuchi serpentinite body, Japan. We find that the carbon and oxygen isotope compositions of carbonate veins indicate that carbonic fluids originated from organic materials in metasediments. Thermodynamic calculations reveal that carbonation of serpentinite was accompanied by a solid volume decrease, dehydration, and high magnesium mobility. We propose that carbonation of the mantle wedge occurs episodically in a self-promoting way and is controlled by a solid volume contraction and fluid overpressure. In our conceptual model, brittle fracturing and carbonate precipitation were followed by ductile flow of carbonates and hydrous minerals; this might explain the occurrence of episodic tremor and slip in the serpentinized mantle wedge.
Similar content being viewed by others
Introduction
Subduction zones transport surface materials deep into Earth’s interior. Metamorphism of subducted lithosphere releases water and CO2 to the overlying accretionary prism or mantle wedge1,2,3,4,5,6. Subduction zone fluids contain various chemical species and have a wide range of pH that varies in response to P–T conditions7,8,9. Large gradients in temperature and chemical potential along the subduction interface generate ideal conditions for mineral dissolution, precipitation, and metasomatism4,10,11,12. Such chemical reactions can change mechanical strength, permeability, and fluid pressure, and thus influence the rheological and seismological characteristics of subduction zones10. For example, silica precipitation may control the recurrence periods of ordinary earthquakes13 and slow earthquakes within subduction zones14.
Along the slab–mantle interface below the forearc Moho, hydration of mantle peridotite forms serpentine minerals and hydrous metasomatic minerals such as talc, amphibole, phlogopite, and chlorite4,10,15,16,17,18. Hydration can lower fluid pressure, and the plastic flow or frictional sliding of hydrous minerals result in steady-state slip18. Therefore, the downdip limit of large earthquakes (seismogenic zone) can be defined either by the brittle–ductile transition in crustal rocks (i.e., 350–400 °C) or the intersection of the subduction thrust and the forearc Moho10,19. Slow slip events (SSEs) are observed at depths corresponding to the transition between the seismogenic zone and the deeper stably sliding zone20,21,22,23. Slow slip events include long-term slip events that occur in relatively shallow parts of the subduction interface, and episodic tremor and slip (ETS) in relatively deep parts. In warm subduction zones such as Nankai and northern Cascadia, ETS is abundant in the corner of the mantle wedge20,21,22,23, a region that could be dominated by serpentinite formed by fluids released from the subducting slab. Several geological models involving chemical reactions have been proposed to explain ETS, including those that involve silica precipitation14,24 and the formation of serpentine–brucite assemblages25, and dehydration-induced heterogeneity within eclogitic oceanic crust26. Metasomatic reaction between ultramafic rocks and crustal rocks has been proposed as a mechanism to explain ETS27. Because most metasomatic reactions that occur in serpentinized mantle release liquid water10,12,27, mechanical instabilities might be generated by fluid overpressure. However, the build-up of fluid overpressure is controlled by various factors including the relative rates of fluid generation, pore generation, and pore collapse28,29, and the geological mechanisms controlling the interplay between these factors in the ETS source region remain debated.
Estimates of the carbon budget in subduction zones suggest that more than one teramole of carbon is subducted each year as carbonates or carbonaceous materials1,2,30. The nature of carbon-bearing fluids (e.g., carbon dioxide, methane) and their interaction with rocks are highly sensitive to redox conditions31. Graphite has been considered as a sink of carbon within the subducting slab due to its low solubility in fluids31. However, recent experimental and thermodynamic modeling studies have revealed that graphite solubility is enhanced by pH and dissolved silica32, and that the dissolution of carbonaceous materials in sediments plays an essential role in generating carbon-bearing fluids in subduction zones33. Carbon-bearing fluids are also produced by the decomposition of carbonates via infiltration of H2O-rich fluids1,2,5 and by fluid-induced dissolution of carbonate minerals coupled with precipitation of silicate minerals11. In particular, mantle peridotite has the potential to influence deep carbon cycling by acting as a voluminous sink of CO2. Carbonation of exhumed oceanic mantle and carbon storage within ophicarbonate rocks are commonly reported34, whereas the behavior of carbon-bearing fluids in subduction-related serpentinites is more complex35,36,37,38,39. When carbonates are in contact with serpentinite, graphite is often formed due to the relatively reducing conditions associated with serpentinite35,36. In contrast, reports of high-pressure carbonated serpentinites related to subduction zones37,38,39 highlight the potential for long-term CO2 sequestration in the subducting slab and mantle wedge, even although some studies suggest that most subducted carbonate is recycled back to the surface5. In addition, carbonation and decarbonation reactions can induce changes to the mechanical properties of mantle rocks. For example, infiltration of reducing fluids can promote strain localization in carbonated serpentinites, implying that carbonic fluids could have an influence on earthquake processes in subduction zones36. Experiments involving in situ carbonation of antigorite indicate volume contraction during this reaction40. These results indicate that carbonation of mantle wedge potentially have effects on the behavior of subduction zone thrusts. However, our understanding of carbonation processes in the mantle wedge is limited by a lack of well-characterized examples from ancient exhumed subduction zones. Carbonated serpentinites from the high-pressure (HP) Sanbagawa metamorphic belt in Japan, which represents part of an exhumed Cretaceous subduction zone, provide an unique opportunity to understand the mechanisms of carbonation within a mantle wedge corner under P–T conditions similar to those at which active ETS is reported.
Results and discussion
Carbonation of serpentinite associated with brittle fracturing
The Sanbagawa belt is a HP metamorphic belt that extends ~800 km along the Median Tectonic Line from the Kanto Mountains in the east to Kyushu in the west along Japan (Supplementary Fig. 1)41. It is composed mainly of metasediments and metabasalts that formed during Cretaceous subduction of an oceanic plate. The metamorphic belt also contains meter- to kilometer-scale ultramafic blocks including mantle peridotites, serpentinites, and tremolite-rich rocks42. The mineral compositions and restricted distribution of these ultramafic blocks to regions higher than chlorite zone indicate that they originated in the mantle wedge25,42,43. The Higuchi serpentine body (15 × 8 m; Fig. 1a) is located in the Kanto Mountains near the boundary between the garnet and chlorite zones (36°07′30.7″N 139°07′00.0″E; Supplementary Fig. 1). Raman analysis of carbonaceous materials indicates peak temperatures of 400–450 °C in this area44, and mineral phase equilibria suggest peak pressures of ~0.5–0.9 GPa45. The long axis of the serpentinite body is subparallel to a mineral lineation in the surrounding pelitic schists. The Higuchi body is composed of massive or foliated antigorite (Fig. 1b, c) that is cut by dense networks of multi-generational carbonate(s) + talc veins (Fig. 1a–e and Supplementary Fig. 2), including magnesite (Fig. 1c, d), dolomite (Fig. 1a, b), and dolomite + calcite (Fig. 1e). The carbonate veins propagate from the margin to the center of the body in a branching network (Supplementary Fig. 2). Along contacts with serpentinite (Fig. 1f), the pelitic schists are progressively converted to layers of chlorite rock ~50 cm wide that preserve bands containing primary metamorphic graphite, and then to lenses of actinolite + chlorite schist up to ~30 cm wide (Supplementary Fig. 3).
a Drone photograph and schematic illustration (at right) of the Higuchi serpentinite body with carbonate veins. Open rectangles indicate the locations of b, f, and e, respectively. b Dolomite veins cut through massive serpentinite blocks. c Layered dolomite veins that have experienced shear deformation. d Magnesite + talc veins. e Thick dolomite + calcite veins associated with fragments of serpentinite blocks. f Chlorite rock and actinolite–chlorite schist at the boundary between pelitic schist and the Higuchi serpentinite body. Yellow and pink arrows indicate relict bands of graphite and quartz-rich material, respectively. Mgs magnesite, Dol dolomite, Cal calcite, Chl chlorite, Act actinolite.
Blocks of massive serpentinite (Fig. 1b) are composed of randomly oriented antigorite grains (Fig. 2a, b) with minor amounts of Cr-rich spinel. Olivine, pyroxenes, and brucite are absent. Cr-rich spinel is commonly altered to magnesiochromite (Fig. 2c and Supplementary Table 1), but some Cr-rich spinel grains in the serpentinite and actinolite–chlorite schists retain unaltered cores with XCr (= Cr/Cr+Al) = 0.52–0.58 and XMg (= Mg/Mg+Fe) = 0.55–0.64. Such depleted spinel compositions in the Higuchi serpentinite are similar to those in forearc peridotites46 and those of other ultramafic bodies in the Sanbagawa belt43,47 (Fig. 2c). Carbonate veins in the Higuchi body are composed mainly of dolomite and magnesite, with lesser amounts of calcite. Magnesite commonly occurs as patches 0.2–2.0 mm in size within antigorite blocks (Fig. 2a, d, e), often accompanied by networks of talc veins <1 mm thick. Magnesite–talc layers also occur along foliation surfaces (Fig. 2a), and infill the spaces between asymmetric antigorite blocks produced by brittle shear deformation (Fig. 2e). Dolomite + talc veins are the most distinct veins in the serpentinite body because they are relatively thick (>2 cm) and can be >3 m long (Figs. 1b, c and 2f). Talc occurs along the margins of these veins (Fig. 2f). Some thick dolomite veins show a layered structure including enclaves of serpentinite (Fig. 1b, c, e). The asymmetry of serpentine fragments, the presence of asymmetric folds (Fig. 1c), and the presence of several layers composed of dynamically recrystallized dolomite grains cutting coarse-grained dolomite veins (Fig. 2g), indicate that vein formation and development of localized shear zones was a repetitive process. In some relatively thick veins, euhedral dolomite crystals grew in the center of the veins, and anhedral calcite crystals filled the intervening pore spaces (Fig. 2h). The dolomite crystals in contact with calcite have higher-Fe rims (Supplementary Fig. 4), suggesting that such dolomite rims were in equilibrium with calcite (Supplementary Table 1). Application of calcite–dolomite solvus thermometry48 to these veins indicates a carbonation temperature of 380–400 °C (Supplementary Fig. 4).
a Photomicrograph (crossed polarized light) showing massive antigorite and magnesite patches associated with talc vein networks. b Detail of antigorite showing random grain orientations. c XCr (= Cr/(Cr+Al)) vs. XMg (= Mg/Mg+Fe2+) for Cr-rich spinel in the serpentinite body (OY, 04C) and actinolite–chlorite schist (03B), compared with data from abyssal peridotites and Mariana forearc peridotites46. Serpentinized peridotites in the Sanbagawa belt, central Shikoku43,47 (references therein): SH Shiraga body, HA Higashi Akaishi body, IM Imono body. d Mineral map of magnesite patches rimed by talc. Location of map shown in a. e Asymmetric antigorite blocks infilled by magnesite + talc produced by brittle shear deformation. f Dolomite veins with talc rims from the outcrop in Fig. 1b. g Dynamically recrystallized dolomite grains within a localized shear zone from a coarse-grained dolomite vein shown in Fig. 1c. h BSE image of a thick dolomite–calcite vein. Euhedral dolomite crystals with bright rims occur along the margin of the vein, and anhedral calcite occurs in the center of the vein. The compositional profile of dolomite along line A-B is shown in Supplementary Fig. 3. i Isotopic compositions (δ13CPDB and δ18OSMOW) of carbonates (magnesite, dolomite, and calcite) in veins from the Higuchi serpentinite, compared with marbles from central Shikoku and the compositions of calcite in basic schists and pelitic schists, and associated veins in the Nagatoro area50.
Sources and compositions of carbonic fluids
Carbonic fluids in subduction zones are commonly sourced from carbonates in seafloor sediments, hydrothermal alteration of basaltic oceanic crust1,2,30, or organic materials in sediments30,33. In the Sanbagawa belt, the rare marbles have \({\delta }^{13}C\) values of 0.4–2.8‰, typical of marine limestones49 (Fig. 2i). The stable isotope compositions of calcite in pelitic and basic schists, and related veins, have relatively constant \({\delta }^{18}O\) values (15–17‰) and a large variation in \({\delta }^{13}C\) (−12–2‰), reflecting multiple sources of CO2 including oxidation of in situ biogenic carbonaceous material and metasomatic processes50. In contrast, carbonates in the Higuchi serpentinite body show a relatively narrow range of \({\delta }^{13}C\) (–10.3‰ to –9.3‰), with the exception of one dolomite sample (–7.6‰), and a wide range of \({\delta }^{18}{O}\) between 17.0‰ and 20.2‰. These C–O isotope data indicate that (1) CO2 in the fluids that carbonated the Higuchi serpentinite body was not derived from limestones, but from the degradation of organic material or carbonates derived from methanotrophic processes within the pelites, and (2) carbonic fluids were probably mixed with H2O produced by dehydration of serpentinite during carbonation reactions, such as:51,52
Possible tectonic setting of carbonation and serpentinization
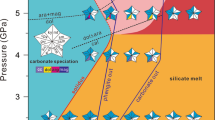
Geological field relationships, including the chemical compositions and P–T conditions recorded by HP metamorphic rocks, indicate that the Higuchi body experienced serpentinization and carbonation at depths of 20–35 km, comparable to conditions in the corner of the mantle wedge in active warm subduction zones such as the Nankai subduction zone in SW Japan22 (Fig. 3a). Our observations suggest that the toe of the forearc mantle was initially serpentinized without macroscopic fracturing (Fig. 3b), followed by local carbonation associated with intense fracturing (Fig. 3c). The metasomatic sequences observed in the Higuchi body progress from the pelitic schists to the interior of the serpentinites as follows: Chl (after pelitic schist)/Act + Chl/Cal + Dol/Dol + Talc/Mgs + Talc (after serpentinite) (Fig. 3c). Mass balance analyses reveal that chloritization of the pelitic schists was characterized by gains in MgO and FeO, and losses of SiO2 and H2O at nearly constant Al2O3, resulting in an overall ~35% reduction in solid volume (Supplementary Table 2 and Supplementary Fig. 5). In contrast, although the quantitative mass balance analysis of the carbonation of the serpentinite body is difficult due to the heterogeneous distribution of carbonate veins, the carbonation reactions were characterized by the formation of carbonates (magnesite, dolomite, or calcite) + talc at the expense of antigorite, and accompanied by gains in CO2, SiO2, and CaO, and losses of H2O and MgO (Fig. 3c).
a Subduction zone setting at the leading edge of the mantle wedge. b Pervasive serpentinization at the leading edge of the mantle wedge is associated with the release of H2O from the subducting slab. c Localized carbonation of serpentinized mantle wedge and serpentinite blocks associated with production of carbonic fluids.
Progress of carbonation assisted by reaction-induced fracturing and Mg-mobility
We conducted thermodynamic modeling of the interactions between pelite-derived fluids and serpentinite at 400 °C and 0.5 GPa with variable fluid–rock ratios (F/R ratio; see Methods section). The initial fluids were assumed to be in equilibrium with the graphite-bearing pelitic schists at various oxygen fugacities, fO2 (Supplementary Fig. 6). Given graphite saturated fluids, the atomic fraction of oxygen to oxygen + hydrogen in initial fluid, XO, is determined for each fO253.
At 400 °C and 0.5 GPa, graphite-bearing assemblages appear at high F/R ratios when antigorite reacts with relatively reducing fluids (Fig. 4a). This is because the solubility of graphite decreases slightly with the addition of antigorite to reducing fluids, as the precipitation of clinopyroxene and tremolite reduces the concentration of Ca-bearing carbonic aqueous complexes, such as Ca(HCOO)+, Ca(HCO3)+, and CaCO3,aq. In cases with initial fluids at around the quartz–fayalite–magnetite (QFM) buffer (fO2 = –28.1, XO = 0.337), relatively common metasomatic minerals (tremolite, chlorite, talc)12 appear along the interfaces between ultramafic rocks and metasediments at log [F/R] of 1.5–2.5.
a Stable mineral assemblage as a function of fluid/rock mass ratio (F/R) and oxygen fugacity, fO2 and the atomic fraction of oxygen to oxygen + hydration, XO, of the initial solution. Pale blue and pink shaded regions indicate carbonate- and graphite-bearing assemblages, respectively. Red dashed lines indicate QFM + 0 (XO = 0.337) and QFM +0.3 (XO = 0.344) of the initial solution. b–f Results in the case of log fO2 = –27.8 (QFM+0.3, XO = 0.344) of the initial solution as a function of log [F/R]. b Mole percent of product minerals. c Schematic illustration showing the relationship between the F/R ratio and mineralogical evolution of the Higuchi serpentinite body. d Change in moles of H2O (\(\triangle\)H2O) and CO2 (\(\triangle\)CO2) in rock before and after reaction. e Total concentration (mol/kg) of individual elements (Si, Al, Fe, Mg, Ca, Na, K) in fluids. f Solid volume ratio (Vsolid/Vsolid,0) and total volume ratio (Vtotal/Vtotal,0) before and after reaction. Kfs K-feldspar, Bt biotite, Cpx clinopyroxene, Tr tremolite, Chl chlorite, Qtz quartz, Cal calcite, Dol dolomite, Mgs magnesite, Gr graphite, Pl plagioclase, Pa paragonite, Mag magnetite.
Typical carbonate-bearing mineral assemblages are found in cases with initial fluids at around QFM + 0.3 (fO2 = –27.8, XO = 0.344; Fig. 4a, b). At log [F/R] > ~2.5, plagioclase, calcite, chlorite, and quartz appear, which are typical minerals in veins within the Sanbagawa pelitic schists54. With an increase in the proportion of antigorite, the mineral assemblage evolves as follows: Chl ± Qtz ± Cpx/Chl + Tr/Cal + Talc/Dol + Talc/Mgs + Talc/Mgs + Talc + Atg (Fig. 4b, c). Such a mineralogical sequence reflects the fluid-dominated system at the boundary of the serpentinite body and close to the large veins, and the rock-dominated system in the interior of the serpentinite body with a fine vein network (Fig. 4c) observed within the Higuchi serpentinite body (Figs. 1–2). At log [F/R] < 2.0, H2O is released by tremolite, and talc and carbonates form at the expense of antigorite, while CO2 is consumed (Fig. 4d). Carbonaceous material in sedimentary rocks is initially poorly crystalline, and its crystallinity increases during prograde metamorphism in subduction zones. Therefore, relatively disordered graphite exists in the metapelites around the Higuchi body44. In the presence of disordered graphite, the CO2 concentration in the input solution could have been greater than those estimated by our thermodynamic calculations (Fig. 4d), which assumed the presence of crystalline graphite33. This could result in the formation of larger amounts of carbonates at the same fO2 conditions in the initial solution.
With a decrease in the F/R ratio (log [F/R] < 1.5; i.e., representative of the interior of the serpentinite body), carbonates + talc form by consumption of antigorite. pH increases and fO2 slightly decreases (Supplementary Fig. 7), as reported in previous studies35,36,55. Si is the dominant component in the initial fluid, as it is saturated with quartz (Fig. 4e). The aqueous CO2 species dominantly exists as the MgOSi(OH)2(HCO3)+ complex (Supplementary Fig. 7). Such effects of SiO2 on the enhancement of carbon solubility have been inferred from dissolution experiments on forsterite + enstatite + graphite32. As the amount of antigorite increases, the concentration of Si decreases and the concentration of Mg increases (Fig. 4e). For example, at log [F/R] = 1.0, the overall mass balance for the carbonation of serpentinite is:
In reaction 3, a small amount of chlorite is formed. Chlorite is not found in the Higuchi serpentinite, but Al-rich antigorite often occurs with talc. Interestingly, the Mg concentration at low log [F/R] (<~1.5), which exists dominantly as Mg(OH)2,aq (Supplementary Fig. 7), is higher than the Si concentration in the initial fluid, implying relatively high mobility of Mg in the mantle wedge. Moreover, at low F/R where talc + carbonates are formed (Fig. 4f), the solid volume decreases (Vsolid/Vsolid,0 = 0.7–1.0), whereas the total volume (solid + fluid) increases (Vtotal/Vtotal,0 = 1.000–1.004). Observations from recent laboratory experiments conducted under forearc mantle conditions40 support our modeling and field observations, suggesting that the progressive formation of magnesite + talc is associated with a solid volume decrease. Although the fluid-mineral equilibria and volume changes were computed for isobaric condition (Fig. 4f), the values of Vtotal/Vtotal,0 > 1 at low F/R suggest that carbonation reactions of serpentinized mantle tend to result in a fluid pressure rise when the system is undrained.
Fracturing induced by volume-changing reactions
To understand the effects of the solid volume change and fluid pressure increase on fracturing, we conducted numerical simulations of coupled fracturing, reaction, fluid flow, and element diffusion using a distinct element method56 (see Methods section). We consider a simple metasomatic dehydration reaction between a serpentinite body and a matrix of pelitic schist (Fig. 5a), in the cases of dilation (Fig. 5b) and contraction (Fig. 5c). In the model, the reaction proceeds along the margins and fractures within the serpentinite body in response to diffusive flux of metasomatic agents (i.e., CO2 species or silica), which is saturated in the pelitic schist. In both cases of dilation and contraction, fluid pressure increases within the serpentinite body, but different fracture patterns are produced depending on the volume change. In the case of dilation, radial cracks develop preferentially within the surrounding matrix (Fig. 5b, d and Supplementary Fig. 10a). In contrast, fracture networks are preferentially developed within the serpentinite body in the case of contraction (Fig. 5c, d and Supplementary Fig. 10b), and the fracture networks develop from the margin with branching-out structure, which shows a similar geometry as the carbonate veins in the Higuchi body (Fig. 1a–e and Supplementary Fig. 2). These contrasting fracture patterns are consistent with previous numerical simulations56,57,58,59 and laboratory experiments28,40,58. Similar fracture patterns are also reproduced (Supplementary Fig. 11) even when fracturing is simulated in models of metasomatic reaction with dilation or contraction but without fluid flow and dehydration. The thermodynamic calculations (Fig. 4) and DEM simulations (Fig. 5) indicate that volume contraction is likely to be the main cause of fracturing during carbonation. Euhedral dolomite grains that are interpreted to have grown in open space (Fig. 2i) indicate that fluid overpressures sustained open cracks, and could have assisted the propagation of fractures. Fluid overpressure could be built up when the rate of fluid production is greater than that of fluid escape through the pelitic schist60. The permeability of the pelitic schist in the Sanbagawa belt is estimated to be 2.1 × 10−20 m2 under a confining pressure of 200 MPa61, and the porosity of the pelitic schist could be low and similar to that of chlorite schist in subduction zones (0.01%–0.2%)62. Such low porosity and permeability in the pelitic schist and the relatively high reaction rate of carbonation with dehydration (several [tens of] percent of carbonation from an antigorite block in a few days)40 could result in fluid overpressure within the serpentinite body, as discussed in dehydration of serpentinite60. The volume contraction produces tensile cracks at an isotropic effective confining stress (Fig. 5), but mechanical instabilities associated with volume changes and fluid overpressure during reaction can trigger earthquake ruptures at high differential stresses60,63.
a Boundary conditions used in the model. b, c Snapshots of the reaction ratio (left), fluid pressure distribution (Pf−Pmin) with the fracture pattern (middle) and the concentration of species S (right) during reaction progress. b Metasomatic dehydration with dilation at an average reaction ratio, ξAv = 17.3%, and a volume strain εv = 0.0076; and c metasomatic dehydration with contraction at ξAv = 5.5%, and the volume strain εv = –0.005. d The crack density (percentage of broken bonds with respect to total bonds) in the reactive material domain and non-reactive matrix for dilation and contraction reactions, respectively.
Consequences of heterogeneous and episodic carbonation in the mantle wedge
In the Sanbagawa belt, carbonation of some ultramafic blocks has occurred47, but the distribution and extent of carbonation reactions are restricted40,47. In the Higuchi body, carbonates were not formed during the initial stages of serpentinization (to form antigorite). These features suggest that in contrast to the relatively homogeneous serpentinization process (Fig. 3b), carbonation in the mantle wedge may involve rupturing that is heterogeneous in time and space (Fig. 3c). The reactions involving carbonic fluids are influenced by redox conditions. It is well known that peridotite has a high reducing potential64,65, but the redox conditions in a fully serpentinized body could be modified by fluid–rock interactions after serpentinization66. In the case of the Higuchi body, carbonation did not occur in the initial stage of serpentinization (massive antigorite; Fig. 2a, b), and chloritized pelitic schists at the boundary were not significantly depleted in graphite (Supplementary Figs. 3a and 5). Therefore, it is unlikely that the CO2 fluid was produced only near the serpentinite body under oxidizing conditions. Based on analysis of the Higuchi body, we infer that carbonation of the mantle wedge can be induced by episodic ingress of carbonic fluids that may be created by oxidation of carbonaceous materials with fluids passing through subducted oxidized layers, including hematite-bearing mafic schists and bedded manganese deposits67,68. In addition, we emphasize that once carbonic fluids reach the mantle wedge, carbonation can proceed in a self-promoting way via positive feedbacks between the reaction, volume contraction, fracturing, and transport of elements and CO2–H2O fluids (Figs. 3–5)40,56.
In the Nankai subduction zone in Shikoku, SW Japan, ETS is observed at the slab–mantle interface near the corner of the mantle wedge20,21,22,23,69. The frictional behavior of serpentine, as well as metasomatic products such as talc, chlorite, and tremolite, is characterized by stable slip related to strain hardening70. A notable feature of carbonation within the Higuchi body is that networks of millimeter- to meter-scale carbonate–talc veins developed during the carbonation of serpentinized mantle (Figs. 1–2 and Supplementary Fig. 2). The total volume increase (fluid + solid) suggested by the thermodynamic modeling of carbonation (Fig. 4f) might cause non-double coupled earthquakes, as reported in swarm seismicity in volcanic zones71. However, the signal of ETS is consistent with shear slip on the plate interface69, and non-double coupled components are not clear due to the large signal-to-noise ratio. The high fluid pressure observed in the Higuchi body (Fig. 2) and suggested by the modeling (Fig. 4f) is consistent with high Vp/Vs ratios associated with the ETS region21,22. The DEM modeling reveals that volume contraction in the presence of high fluid pressures tends to generate tensile fractures (Fig. 5 and Supplementary Fig. 10b), which may subsequently transform (or develop) into shear fractures under differential stress. The brittle shear failures observed in thin-sections and outcrops (Figs. 1b, c and 2e) are consistent with the mechanism of low-frequency earthquakes related to shear slip on the plate interface21,69. Following sealing of void spaces by carbonates, localized shear is concentrated within the talc-rich layers (Figs. 1b and 2a, e) and dolomite veins (Figs. 1c and 2f). We speculate that this kind of repeated brittle failure, followed by viscous flow, may represent an analog for the ETS that is observed within the relatively cold nose of the mantle wedge.
Methods
Measurements of stable isotope compositions of carbonate minerals
The chemical compositions of minerals were analyzed using an electron microprobe analyzer (EPMA, JEOL8200) at Tohoku University. The acceleration voltage was 15 kV, and the current was 12 nA or 120 nA for quantitative analyses and elemental mapping, respectively. Identification of serpentine and other minerals was performed using a Raman spectrometer (Horiba XploRa) equipped with an Olympus BX51 microscope at Tohoku University.
Oxygen (\({\delta }^{18}O\)) and carbon (\({\delta }^{13}C\)) isotope analyses were conducted on selected carbonate samples from the Higuchi serpentinite body. For comparison, we also analyzed the stable isotope compositions of marble samples from the Sanbagawa belt in central Shikoku. Samples were extracted from cut and polished slabs using a sharp knife, and then stained with Alizarin red-S to distinguish between calcite and dolomite. Staining with Alizarin red-S does not affect the C and O isotope ratios49. Sample powders for C–O isotope analyses were taken from different portions of each slab. Carbonate mineral (dolomite, magnesite, or calcite) powders were placed in small stainless steel thimbles and dropped into a reaction vessel containing pyrophosphoric acid at 60 °C (calcite) or 100 °C (for dolomite and magnesite) in vacuum to produce CO2 gas. Released CO2 gas was cleaned to remove impurities like H2O by using pentane slush and collected by using liquid nitrogen cold traps. Stable isotope measurements were carried out with a Thermofischer MAT-253 mass spectrometer at Niigata University. Results are reported in conventional per mil (‰) notation with respect to V-SMOW (Vienna-Standard Mean Ocean Water) for oxygen and V-PDB (Vienna-Peedee Belemnite) for carbon. The precision of δ13C and δ18O for the laboratory standard CO2 gas were 0.04‰ and 0.06‰, respectively72.
Thermodynamic model of fluid–rock interaction
Thermodynamic calculations were carried out in the system Na–K–Ca–Fe–Mg–Al–Si–Cl –C–O–H using the Deep Earth Water (DEW) model73,74 and software EQ3/675 with a modified Berman thermodynamic dataset76. This updated thermodynamic dataset includes H2CO30, HCO3–, and various complexes related to bicarbonic acid (Na(HCO3)0, Ca(HCO3)+, and MgOSi(OH)2(HCO3)+). For this reason, thermodynamic calculations are not restricted to the H2O-rich system but also model CO2-rich fluids involving carbonation74. We treated solid solutions as ideal mixing between Mg and Fe endmembers for chlorite, talc, tremolite, biotite, and clinopyroxene, and between albite and anorthite for plagioclase. We first created an input solution using EQ3, in equilibrium with the observed mineral assemblage in the pelitic schists: muscovite + chlorite (XMg = 0.6) + quartz + albite + clinozoisite + calcite + graphite, at 400 °C and 0.5 GPa54,77. This mineral assemblage represents the most likely fluid source or the metasomatic and carbonation reactions within the serpentinite. The pressure of carbonation in the Higuchi serpentinite was not determined, but probably ranges between 0.5 and 0.9 GPa based on the P–T conditions in the chlorite and garnet zones45. At 400 °C, there is no miscibility of CO2–H2O fluids below 1 GPa78. The log oxygen fugacity of the input solutions, log[fO2], ranged from –29.0 to –27.5, corresponding to ΔQFM (deviation from quartz–fayalite–magnetite buffer) from –0.8 to +0.7 in log units79. Based on the compositions of each initial solution calculated by EQ3, XO is obtained as follows:
where nO and nH are the number of moles of oxygen and hydrogen in the fluids, respectively53. The log[fO2] range of the initial solution corresponds to Xo from 0.318 to 0.354. EQ6 was then used to model the interactions (thermodynamic equilibria) between the input solution and serpentinite composed of 100% antigorite (Fig. 4). We calculated log fluid/rock mass ratios from –2.0 to 4.0. To create the stable mineral assemblage at various F/R and fO2 conditions for the input solution (Fig. 4a and Supplementary Fig. 6), a shell script was written to automatically generate EQ3/6 run input files with various fO2 conditions, and the output files generated by EQ3/6 were further processed with an author-generated MATLAB® script.
The changes in CO2 and H2O during the reactions (Fig. 4d) are calculated by determining changes in hydrous minerals and carbonates. The volume change ratio of the solids (Vsolid/Vsolid,0; Fig. 4f) was calculated by using the volumes of product minerals and consumed antigorite. The volume change ratio of solid and fluids (Vtotal/Vtotal,0) was calculated by the volumes of product minerals, consumed antigorite, and changes in the amount of fluid. The molar volume of fluids was obtained based on the sum of the concentration of carbonic species. With decreasing log [F/R], the XCO2 values decreases from 2.30 × 10–2 to 1.88 × 10–2.
We also undertook the same calculation at 400 °C and 1.0 GPa (Supplementary Fig. 8). We found that the topography of the stable mineral assemblage in a plot of log [fO2] vs. log [F/R] is largely similar to the case at 400 °C and 0.5 GPa (Fig. 4a), except that aragonite is stable instead of calcite. The chemistry of the initial solution calculated by EQ3 is also largely consistent with that calculated by Perple_X version 6.9.1.80 with thermodynamic data of Holland and Powell81 (Supplementary Fig. 9).
Distinct element method to model metasomatic dehydration reactions
We conducted two-dimensional distinct-element numerical simulations to investigate fracture patterns induced by volume-changing dehydration reactions, following the methods of Okamoto & Shimizu56 with slight modifications to incorporate element diffusion. Okamoto & Shimizu56 treated coupled processes of reaction (dehydration/hydration), fluid flow, and fracturing. The model consists of an aggregate of circular elements connected by elastic bonds. When the external force exceeds the tensile or shear strength of the bond, the bond is broken to form a microcrack. To treat fluid flow, we calculate the fluid pressure in each domain, which is defined by the regions surrounded by connected elements. The fluid flow in a channel is calculated by the Poiseuille equation and includes the crack aperture (w), fluid viscosity (\(\mu\)), the length of the flow channel, and the fluid pressure gradient between adjacent domains (\(\triangle\)Pf). Okamoto & Shimizu56 considered a simple hydration/dehydration reaction as Mineral A + H2O = Mineral B, and the reaction rate is assumed to be a linear function of fluid pressure. They showed that contrasting fracture patterns are produced in response to solid volume changes rather than fluid pressure as similar to the other studies56,57,58,59. Here, as a simplification of the carbonation of serpentinite, we consider a simple metasomatic dehydration reaction:
where aqueous species S represents metasomatic agents such as CO2 species and SiO2. The reaction is characterized by the volume change factor (the volumetric ratio of 100% reacted particle to unreacted particle), the ratio of the changes in fluid and particle volume (fluid volume factor), and the ratio of the changes in the amount of species S with respect to the particle volume change (solute factor). For this study, we used volume factors of 1.1 (dilation) or 0.9 (contraction), a fluid factor of –0.1, and a solute factor of 1.0. The reaction rate, Z, is defined as a function of the concentration of CS as follows:
Cs,max and Cs,min represent maximum and minimum concentrations of the species S in the system: the reaction rate is greatest (Zmax) at Cs = Cs,max, and the reaction stops at Cs = Cs,min. In addition to advective transport with H2O, we consider diffusional transport of aqueous species S as a function of the concentration gradient of S in each domain.
The values of the parameters used in this study are summarized in Supplementary Table 3. This study used a 10 × 10 m square rock model that contains 4357 particles with diameters of 50–100 mm. This rock specimen initially contains a reactive mineral domain composed of antigorite (analogous to serpentinized mantle) and an non-reactive matrix composed of quartz (analogous to metasediment). Here we consider that the species S is saturated within the non-reactive matrix. The physical properties (particle density, ρ, and Young’s modulus, E) of the matrix material are based on quartz (ρ = 2650 kg/m3; E = 140 GPa), whereas the reactive mineral properties change from antigorite (ρ = 2600 kg/m3; E = 115 GPa) to a mixture of dolomite (95%) + talc (5%) (ρ = 2830 kg/m3; E = 110 GPa), following the data of Mavko et al.82 and Abers & Hacker83 (Supplementary Table 3). There are no experimental data on the tensile and shear strengths of these minerals, but the tensile strength of rock typically ranges from ~1 to 40 MPa, and compressive strengths are typically ~10 times the tensile strengths84. Here, we set the tensile and shear strengths in the rock model to be 10 and 100 MPa, respectively, regardless of the minerals in the model. Based on these strength data, we performed preliminary simulations of uniaxial compression and tension tests to adjust microscopic input parameters85, and decided to use a tensile spring strength of 30 MPa and a shear spring strength of 118 MPa. The effective confining pressure was set to be 1 MPa. The initial and fluid pressures outside the rock model were set to Pmin, and when dehydration reaction proceeds fluid pressure, Pf, inside the rock increases and fluid flows toward outside. The fluid physical properties (viscosity of 1.0 × 10–4 Pas and bulk modulus of 3.5 GPa) were assumed to be the same as those of water at temperatures of ~400 °C and pressures of 0.5 GPa. The concentration of species S, Cs, is assumed to be a maximum value (Cs,max = 1.0) in the non-reactive matrix (saturated), and Cs in the reactive mineral domain is set to be Cs,min (=0) at the initial stage. The apparent diffusion coefficient (=diffusion coefficient/average particle size) was set to 0 s−1 in unbroken rocks, and 10 s−1 along fractures. As the diffusive flux of species is large with respect to the fluid flow, the concentration of S is nearly equal to Cs,max.
Reporting summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Data availability
The data of this study are available in methods and supplementary tables. The input and output files for EQ3 and EQ6 for representative cases (Fig. 4), and animations of the DEM simulation results are available in the online repository (https://doi.org/10.6084/m9.figshare.13336850).
Code availability
The DEM code used in this study is available from the corresponding author upon request with the approval of A.O. and H.S.
References
Kerrick, D. M. & Connolly, J. A. D. Metamorphic devolatilization of subducted oceanic basalts: implications for seismicity, arc magmatism and volatile recycling. Earth Planet. Sci. Lett. 189, 19–29 (2001).
Kerrick, D. M. & Connolly, J. A. D. Metamorphic devolatilization of subducted marine sediments and the transport of volatiles into the Earth’s mantle. Nature 411, 293–296 (2001).
Hacker, B. R., Peacock, S. M., Abers, G. A. & Holloway, S. D. Subduction factory 2. Are intermediate–depth earthquakes in subducting slabs linked to metamorphic reactions? J. Geophys. Res. Solid Earth 108, 2030 (2003).
Hyndman, R. D. & Peacock, S. M. Serpentinization of the forearc mantle. Earth Planet. Sci. Lett. 212, 417–432 (2003).
Stewart, E. M. & Ague, J. J. Pervasive subduction zone devolatilization recycles CO2 into the forearc. Nat. Commun. 11, 6220 (2020).
Schmidt, M. & Poli, S. Experimentally based water budgets for dehydrating slabs and consequences for arc magma generation. Earth Planet. Sci. Lett. 163, 361–379 (1998).
Manning, C. E. The chemistry of subduction–zone fluids. Earth Planet. Sci. Lett. 223, 626 (1994).
Galvez, M. E., Connolly, J. A. D. & Manning, C. E. Implications for metal and volatile cycles from the pH of subduction zone fluids. Nature 359, 420–424 (2016).
Scambelluri, M., Cannao, E. & Gilio, M. The water and fluid–mobile element cycles during serpentine subduction. A review. Eur. J. Mineral. 31, 405–428 (2019).
Peacock, S. M. & Hyndman, R. D. Hydrous minerals in the mantle wedge and the maximum depth of subduction thrust earthquakes. Geophys. Res. Lett. 26, 2517–2520 (1999).
Ague, J. J. & Nicolescu, S. Carbon dioxide released from subduction zones by fluid–mediated reactions. Nat. Geosci. 7, 355–359 (2014).
Manning, C. E. Phase–equilibrium controls on SiO2 metasomatism by aqueous fluid in subduction zones: reaction at constant pressure and temperature. Int. Geol. Rev. 37, 1074–1093 (2015).
Saishu, H., Okamoto, A. & Otsubo, M. Silica precipitation potentially controls earthquake recurrence in seismogenic zones. Sci. Rep. 7, 13337 (2017).
Audet, P. & Bürgmann, R. Possible control of subduction zone slow–earthquake periodicity by silica enrichment. Nature 510, 389–392 (2014).
Fumagalli, P. & Poli, S. Experimentally determined phase relations in hydrous peridotites to 6.5 GPa and their consequences on the dynamics of subduction zones. J. Petrol. 46, 555–578 (2005).
Fumagalli, P., Zanchetta, S. & Poli, S. Alkalis in phlogopite and amphibole and their effects on phase relations in metasomatized peridotites: a high-pressure study. Contrib. Mineral. Petrol. 158, 723–737 (2009).
Tumiati, S., Fumagalli, P., Tiraboschi, C. & Poli, S. An experimental study on COH-bearing peridotite up to 3.2 GPa and implications for crust–mantle recycling. J. Petrol. 54, 453–479 (2013).
Hirauchi, K., Katayama, I., Uehara, S., Miyahara, M. & Takai, Y. Inhibition of subduction thrust earthquakes by low–temperature plastic flow in serpentine. Earth Planet. Sci. Lett. 295, 349–357 (2010).
Oleskevich, D. A., Hyndman, R. D. & Wang, K. The updip and downdip limits to great subduction earthquakes: thermal and structural models of Cascadia, south Alaska, SW Japan, and Chile. J. Geophys. Res. Solid Earth 14, 14965–14991 (1999).
Beroza, G. C. & Ide, S. Slow earthquakes and nonvolcanic tremor. Annu. Rev. Earth Planet. Sci. 39, 271–296 (2011).
Shelly, D. R., Beroza, G. C., Ide, S. & Nakamula, S. Low-frequency earthquakes in Shikoku, Japan, and their relationship to episodic tremor and slip. Nature 442, 188–191 (2006).
Kato, A. et al. Variations of fluid pressure within the subducting oceanic crust and slow earthquakes. Geophys. Res. Lett. 37, L14310 (2010).
Gao, X. & Wang, K. Rheological separation of the megathrust seismogenic zone and episodic tremor and slip. Nature 543, 416–419 (2010).
Ujiie, K. et al. An explanation of episodic tremor and slow slip constrained by crack–seal veins and viscous shear in subduction mélange. Geophys. Res. Lett. 45, 5371–5379 (2019).
Mizukami, T. et al. Two types of antigorite serpentinite controlling heterogeneous slow–slip behaviors of slab–mantle interface. Earth Planet. Sci. Lett. 401, 148–158 (2014).
Behr, W. M., Kotowski, A. J. & Ashley, K. T. Dehydration-induced rheological heterogeneity and the deep tremor source in warm subduction zones. Geology 46, 475–478 (2018).
Tarling, M. S., Smith, S. A. F. & Scott, J. M. Fluid overpressure from chemical reactions in serpentinite within the source region of deep episodic tremor. Nat. Geosci. 12, 1034–1042 (2019).
Miller, S. A., van der Zee, W., Olgaard, D. L. & Connolly, J. A. D. A fluid–pressure feedback model of dehydration reactions: experiments, modeling, and application to subduction zones. Tectonophysics 370, 241–251 (2003).
Connolly, J. A. D. Devolatilization-generated fluid pressure and deformation-propagated fluid flow during prograde regional metamorphism. J. Geophys. Res. 102, 18149–18173 (1997).
Kelemen, P. B. & Manning, C. E. Reevaluating carbon fluxes in subduction zones, what goes down, mostly comes up. Proc. Natl. Acad. Sci. USA 112, E3997–E4006 (2014).
Galvez, M. E., Manning, C. E., Connolly, J. A. D. & Rumble, D. The solubility of rocks in metamorphic fluids: a model for rock-dominated conditions to upper mantle pressure and temperature. Earth Plant. Sci. Lett. 430, 486–498 (2015).
Tumiati, S. et al. Silicate dissolution boosts the CO2 concentrations in subduction fluids. Nat. Commun. 8, 16 (2017).
Tumiati, T. et al. Dissolution susceptibility of glass-like carbon versus crystalline graphite in high-pressure aqueous fluids and implications for the behavior of organic matter in subduction zones. Geochim. Cosmochim. Acta 273, 383–402 (2020).
Kelemen, P. B. & Matter, J. In situ carbonation of peridotite for CO2 storage. Proc. Natl. Acad. Sci. USA 105, 17295–17300 (2008).
Galvez, M. E. et al. Graphite formation by carbonate reduction during subduction. Nat. Geosci. 6, 473–477 (2013).
Giuntoli, F., Brovarone, A. V. & Menegon, L. Feedback between high–pressure genesis of abiotic methane and strain localization in subducted carbonate rocks. Sci. Rep. 10, 9848 (2020).
Peacock, S. M. Serpentinization and infiltration metasomatism in the Trinity peridotite, Klamath province, northern California: implications for subduction zones. Contrib. Mineral. Petrol. 95, 95–70 (1987).
Scambelluri, M. et al. Carbonation of subduction–zone serpentinite (high–pressure ophiocarbonate; Ligurian Western Alps) and implications for the deep carbon cycling. Earth Planet. Sci. Lett. 441, 155–166 (2016).
Peng, W. et al. Multistage CO2 sequestration in the subduction zone: insights from exhumed carbonated serpentinites, SW Tianshan UHP belt, China. Geochim. Cosmochim. Acta 270, 218–243 (2020).
Sieber, M. J., Yaxley, G. M. & Hermann, J. Investigation of fluid–driven carbonation of a hydrated, forearc mantle wedge using serpentine cores in high–pressure experiments. J. Petrol. 61, egaa035 (2020).
Wallis, S. R. & Okudaira, T. in The Geology of Japan. (eds T. Moreno, T., Wallis, S. R., Kojima, T. & Gibbons W.) 101–124. (Geological Society of London, 2016).
Aoya, M., Endo, S., Mizukami, T. & Wallis, S. R. Paleo–mantle wedge preserved in the Sambagawa high–pressure metamorphic belt and the thickness of forearc continental crust. Geology 41, 451–454 (2013).
Hattori, K., Wallis, S., Enami, M. & Mizukami, T. Subduction of mantle wedge peridotites: evidence from the Higashi–Akaishi ultramafic body in the Sanbagawa metamorphic belt. Isl. Arc 19, 192–207 (2010).
Inui, M. & Takefuji, A. Spatial distribution of garnet indicating control of bulk rock chemistry in the Sanbagawa metamorphic rocks, Kanto Mountains, Japan. J. Mineral. Petrol. Sci. 113, 181–189 (2018).
Enami, M., Wallis, S. R. & Banno, Y. Paragenesis of sodic–pyroxene–bearing quartz schists: implications for the P–T history of the Sanbagawa belt. Contrib. Mineral. Petrol. 116, 182–198 (1994).
Ishii, T., Robinson, P. T., Maekawa, H. & Fiske, R. Petrological studies of peridotites from diapiric serpentinite seamounts in the Izu–Ogasawara–Mariana forearc, Leg 125. In Proc. Proceedings of the Ocean Drilling Program, Scientific Results, College Station, TX (Ocean Drilling Program). (eds. Fryer P., Pearce J. A., Stokking L. B., et al.) 445–85 (1992).
Kawahara, H. et al. Brucite as an important phase of the shallow mantle wedge: evidence from the Shiraga unit of the Sanbagawa subduction zone, SW, Japan. Lithos 254–255, 53–66 (2016).
Powell, R., Condliffe, D. M. & Condliffe, E. Calcite–dolomite geothermometry in the system CaCO3–MgCO3–FeCO3: an experimental study. J. Metamorph. Geol. 2, 33–41 (1984).
Wada, H., Enami, M. & Yanagi, T. Isotopic studies of marbles in the Sanbagawa metamorphic terrain, central Shikoku, Japan. Geochem. J. 18, 61–73 (1984).
Morohashi, K., Okamoto, A., Satish–Kumar, M. & Tsuchiya, N. Variations in stable isotope compositions (δ13C, δ18O) of calcite within exhumation–related veins from the Sanbagawa metamorphic belt. J. Mineral. Petrol. Sci. 105, 361–365 (2008).
Menzel, M. D. et al. Carbonation of mantle peridotite by CO2-rich fluids: the formation of listvenites in the Advocate ophiolite complex (Newfoundland, Canada). Lithos 323, 238–261 (2018).
Hansen, L. D. & Dipple, C. M. Carbonated serpentinite (listwanite) at Atlin, British Columbia: a geological analogue to carbon dioxide sequestration. Can. Mineral. 43, 225–239 (2005).
Connolly, J. A. D. Phase diagram methods for graphitic rocks and application to the system C-O-H-FeO-TiO2-SiO2. Contrib. Mineral. Petrol. 119, 94–116 (1995).
Okamoto, A., Kikuchi, T. & Tsuchiya, N. Mineral distribution within polymineralic veins in the Sanbagawa belt, Japan: implications for mass transfer during vein formation. Contrib. Mineral. Petrol. 156, 323–336 (2008).
Brovarone, A. V. et al. Subduction hides high–pressure sources of energy that may feed the deep subsurface biosphere. Nat. Commun. 11, 3880 (2020).
Okamoto, A. & Shimizu, H. Contrasting fracture patterns induced by volume–increasing and –decreasing reactions: implications for the progress of metamorphic reactions. Earth Planet. Sci. Lett. 415, 9–18 (2015).
Jamtveit, B., Malthe–Sørenssen, A. & Kostenko, O. Reaction enhanced permeability during retrogressive metamorphism. Earth Planet. Sci. Lett. 267, 620–627 (2008).
Kuleci, H., Ulven, O. I., Rybacki, E., Wunder, B. & Abart, R. Reaction–induced fracturing in a hot pressed calcite–periclase aggregate. J. Struct. Geol. 94, 116–135 (2017).
Yoshida, K., Okamoto, A., Shimizu, H., Oyanagi, R., Tsuchiya, N. & Oman Drilling Project Phase 2 Science Party. Fluid infiltration through oceanic lower crust in response to reaction-induced fracturing: Insights from serpentinized troctolite and numerical models. J. Grophys. Res. 125, e2020JB020268 (2020).
Ague, J. J., Park, J. & Rye, D. M. Regional metamorphic dehydration and seismic hazard. Geophys. Res. Lett. 25, 4221–4224 (1998).
Wibberley, C. A. J. & Shimamoto, T. Internal structure and permeability of major strike-slip fault zones: the Median Tectonic Line in Mie Prefecture, Southwest Japan. J. Struct. Geol. 25, 59–78 (2003).
Ganzhorn, A. C., Pilorge, H. & Reynard, B. Porosity of metamorphic rocks and fluid migration within subduction interfaces. Earth Planet. Sci. Lett. 522, 107–117 (2019).
Kirby, S. H., Durham, W. B. & Stern, L. A. Mantle phase changes and deep–earthquake faulting in subducting lithospheres. Science 252, 216–225 (1991).
Klein, F. & Bach, W. Fe–Ni–Co–O–S phase relations in peridotite–seawater interactions. J. Petrol. 50, 37–59 (2009).
Piccoli, F. et al. Subducting serpentinites release reduced, not oxidized, aqueous fluids. Sci. Rep. 9, 19573 (2019).
Malvoisin, B., Chopin, C., Brunet, F. & Galvez, M. E. Low-temperature wollastonite formed by carbonate reduction: a marker of serpentinite redox conditions. J. Petrol. 53, 159–176 (2012).
Nakagawa, M., Santosh, M. & Maruyama, S. Manganese formations in the accretionary belts of Japan: implications for subduction–accretion process in an active convergent margin. J. Asian Earth Sci 42, 208–222 (2011).
Tumiati, S., Godard, G., Matrin, S., Malaspina, N. & Poli, S. Ultra-oxidized rocks in subduction mélanges? Decoupling between oxygen fugacity and oxygen availability in a Mn-rich metasomatic environment. Lithos 226, 116–130 (2015).
Ide, S., Shelly, D. R. & Beroza, G. C. Mechanism of deep low frequency earthquakes: Further evidence that deep non-volcanic tremor is generated by shear slip on the plate interface. Geophys. Res. Lett. 34, L03308 (2007).
Hirauchi, K., den Hartog, S. A. M. & Spiers, C. J. Weakening of the slab–mantle wedge interface induced by metasomatic growth of talc. Geology 41, 75–78 (2013).
Hrubcová, P., Doubravová, J. & Vavryˇcuk, V. Non-double-couple earthquakes in 2017 swarm in Reykjanes Peninsula, SW Iceland: sensitive indicator of volcano-tectonic movements at slow-spreading rift. Earth Planet. Sci. Lett. 563, 116875 (2021).
Satish-Kumar, M., Kiran, S. & Abe, M. A new inlet system for microscale carbon and oxygen isotope analysis using dual inlet isotope ratio mass spectrometer at Niigata University, Japan. Science Reports of Niigata University. Vol. 35 (2021) (in press).
Sverjensky, D. A., Harrison, B. & Azzolini, D. Water in the deep Earth: The dielectric constant and the solubilities of quartz and corundum to 60kb and 1200°C. Geochim. Cosmochim. Acta 129, 125–145 (2014).
Huang, F. & Sverjensky, D. A. Extended deep earth water for predicting major element mantle metasomatism. Geochim. Cosmochim. Acta 254, 192–230 (2019).
Wolery T. J. EQ3NR, A Computer Program For Geochemical Aqueous Speciation–solubility Calculations: Theoretical Manual, User’s Guide, And Related Documentation (version 7.0). (Lawrence Livermore National Laboratory, 1992).
Berman, R. G. Internally-consistent thermodynamic data for minerals in the system Na2O-K2O-CaO-MgO-FeO-Fe2O3-Al2O3-SiO2-TiO2-H2O-CO2. J. Petrol. 29, 445–522 (1988).
Goto, A., Kunugiza, K. & Omori, S. Evolving fluid composition during prograde metamorphism in subduction zones: a new approach using carbonate–baring assemblages in the pelitic system. Gondwana Res. 11, 166–179 (2007).
Abramson, E. H., Bollengier, O. & Brown, M. The water–carbon dioxide miscibility surface to 450 °C and 7GPa. Am. J. Sci. 317, 967–989 (2017).
Miozzi, F. & Tumiati, S. Aqueous concentration of CO2 in carbon-saturated fluids as a highly sensitive oxybarometer. Geochem. Perspect. Lett. 16, 30–34 (2020).
Connolly, J. A. D. Computation of phase equilibria by linear programming: a tool for geodynamic modeling and its application to subduction zone decarbonation. Earth Planet. Sci. Lett. 236, 524–5412 (2005).
Holland, T. & Powell, R. An improved and extended internally consistent dataset for phases of petrological interest, involving a new equation of state for solid. J. Metamorph. Geol. 29, 333–383 (2011).
Mavko, G., Mukerji, T. & Dvorkin, J. The Rock Physics Handbook (Cambridge University Press, 2009)
Abers, G. A. & Hacker, B. R. A MATLAB toolbox and excel workbook for calculating the densties, seismic wave speeds, and major element composition f minerals and rocks at pressure and temperature. Geochem. Geophys. Geosyst. 17, 616–624 (2016).
Pollard, D. D. & Fletcher, R. C. Fundamentals of Structural Geology (Cambridge University Press, 2006)
Shimizu, H. & Okamoto, A. The roles of fluid transport and surface reaction in reaction–induced fracturing, with implications for the development of mesh textures in serpentinites. Contrib. Mineral. Petrol. 171, 1–18 (2016).
Acknowledgements
We thank Kenichi Hirauchi and Mutsuki Aoya for useful discussions, and Shinichi Yamasaki and Otgongayar Dandar for XRF analyses. Fang Huang kindly introduced us to the DEW modeling. Discussion with J.A.D. Connolly helped in clarifying the relation between oxygen fugacity and carbonation reactions. The authors acknowledge constructive comments from two anonymous reviewers that substantially improved this manuscript. This work was financially supported by JSPS KAKENHI Grant Numbers JP 16H06347, 18KK0376, and 17H02981 to A.O., and JP15H05831 and 20KK0081 to M.S.-K, and by Earthquake Res. Inst., the University of Tokyo, Joint Research program 2021-B-01 and 2018-B-01.
Author information
Authors and Affiliations
Contributions
A.O., R.O., K.Y., and M.U. carried out field work. A.O. carried out the petrological analyses. R.O. carried out the thermodynamic calculations on fluid–rock interaction, M.U. performed mass balance analyses. K.Y. and H.S. developed the DEM model and carried out simulations. M.S. and K.Y. performed the isotope analyses of carbonates. A.O. wrote the paper with inputs from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Communications Earth & Environment thanks the anonymous reviewers for their contribution to the peer review of this work. Primary Handling Editors: Maria Luce Frezzotti, Joe Aslin, Heike Langenberg.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Okamoto, A., Oyanagi, R., Yoshida, K. et al. Rupture of wet mantle wedge by self-promoting carbonation. Commun Earth Environ 2, 151 (2021). https://doi.org/10.1038/s43247-021-00224-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-021-00224-5
This article is cited by
-
Subducted carbon weakens the forearc mantle wedge in a warm subduction zone
Nature Communications (2024)
-
Methane-hydrogen-rich fluid migration may trigger seismic failure in subduction zones at forearc depths
Nature Communications (2024)
-
Multiscale off-fault brecciation records coseismic energy budget of principal fault zone
Scientific Reports (2024)
-
Si- versus Mg-metasomatism at the crust–mantle interface: insights from experiments, natural observations and geochemical modeling
Progress in Earth and Planetary Science (2023)
-
Recycled carbonates elevate the electrical conductivity of deeply subducting eclogite in the Earth’s interior
Communications Earth & Environment (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.