Abstract
Future changes of regional precipitation are of great scientific and societal interests. Large uncertainties still exist in their projections by models. Mechanistic understanding is therefore necessary. Here we demonstrate robust features of the percentage change of precipitation normalized to surface temperature change (%/K) under global warming, referred to as scaling of precipitation with temperature in East Asia. We find that land precipitation in the summer scales at ~3%/K, well below the scaling rate of the Clausius-Clapeyron relationship for atmospheric water vapor content, but the scaling in winter is comparable to the Clausius-Clapeyron scaling at ~7%/K. By using moisture budget analysis of model simulations, we show that this scaling and the seasonal contrast can be clearly attributed to the robust climate changes of steeping moisture gradient, weakening westerly jets, and increasing hydrological amplitude of atmospheric eddies.
Similar content being viewed by others
Introduction
Anthropogenic greenhouse emissions have caused global warming that is expected to continue in the 21st Century1,2,3. Associated with the warming are changes of precipitation that affect critical water resources for many sectors in the society2,4,5,6,7. For the Earth as a whole, the scaling of precipitation with temperature is constrained by the rate of atmospheric radiative cooling at about 2–3%/K8,9. On regional scales, however, model projections of future changes in precipitation display large inter-model differences with much larger spatial variations than the warming. Regional dynamics has been shown to play an important role in these variations10, but details of specific processes causing regional precipitation changes are still not well understood. Confidence is therefore low in these projections2,3. More insights into the physical mechanisms are needed10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28.
In this article, we first report robust precipitation scaling with temperature in East Asia by using the Large-Ensemble Simulations (LES) from the Community Earth System Model (CESM1-LES RCP8.5 simulations)29 and those from Phase 6 of the Coupled Model Intercomparison Project (CMIP6) (Supplemental Table 1). We then explain the underlying physical mechanisms, which is simplified by focusing on the deviation from the Clausius-Clapeyron scaling (CCS) of local thermodynamics. The theory is built upon the robust climate change features of steepening moisture gradient16,24,30,31,32 and weakening of westerly jet15,25,33,34,35,36,37,38, which have been extensively reported in the literature, and separation of dynamical and hydrological amplitudes of atmospheric eddies, the latter of which can be also interpreted as larger discharge of moisture in a warmer climate during precipitation events.
Results
Scaling of precipitation change with temperature
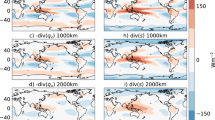
Surface warming in East Asia is projected to be stronger at higher latitudes, more over land than over the ocean, and larger in the winter (December to February, DJF) than in the summer (June to August, JJA) (see red contour lines in Fig. 1a, b for the CESM1-LES. Here and below, the corresponding figures from the CMIP6 ensemble are shown in the Supplemental Information (SI)). These are all consistent with well-established understandings on the polar amplification of global warming and relatively weak evaporation and small heat capacity of the land2. Normalized by these temperature changes, the scaled percentage change of projected precipitation is found to display sharper contrasts in the two seasons and between land and the sea (see color shading in Fig. 1a, b, and Methods in SI). In JJA, the response of land precipitation to warming is scaled to be about 3%/K, but it is above 10% over the subtropical ocean. As a reference, the scaling rate of water vapor content is 7.3%/K in the region (denoted by the black contour in the figure). In DJF, the precipitation scaling is about 7% over land, but nearly zero over the subtropical ocean. The scaling rate of water vapor content is 5.9%/K in the winter due to lower temperature and small change in relative humidity over land. These seasonal and land-ocean contrasts are also confirmed by using two additional large ensembles of model simulations from the Max Plank Institute Grand Ensemble39 (MPI-GE) and the Model for Interdisciplinary Research40 (MIROC6-LES) that are available to us (Figs. S2 and S3).
a, b Future changes of surface temperature in the CESM1-LES RCP8.5 simulations (red contours, unit in degrees K) and percentage change of precipitation scaled by unit temperature change (color shading, unit in %/K) in JJA and DJF. The changes are calculated as the differences between the two periods of 2070–2099 and 1975–2004. The thick black contour is the 7.3%/K scaling of atmospheric water vapor content in JJA. Stippling represents statistical significance at 5% level in student t test with respect to the 40 ensemble variances. c, d Same as above, but for the scaling of the total moisture flux divergence (convergence) in JJA and DJF.
On average, precipitation is balanced by atmospheric moisture convergence and surface evaporation15,32. The seasonal and land-ocean contrasts in the precipitation scaling are closely mirrored by those in the moisture convergence change (Fig. 1c, d). We therefore use the moisture convergence to deconvolute the roles of thermodynamical and dynamical processes in the precipitation scaling. We separate these processes into local thermodynamics, spatial thermodynamics, dynamics of the time mean (stationary) circulation, and transient eddy transport described by the following equation (see Methods in SI). This separation is not merely a mathematical decomposition, but rather a useful approach to decipher precipitation change and its physical causes that vary greatly in space and time. The local thermodynamics describes the impact of the holding capability change of water vapor in the atmosphere on precipitation. The spatial thermodynamics portrays the impact of this capacity change in neighboring regions. The dynamics represents the change of wind divergence. The eddy contribution characterizes the degree of atmospheric transience. Previous studies have used local thermodynamics and dynamics to demonstrate the regional impact of the dynamics10. Here, we have included the additional processes from the spatial variation of the thermodynamics and eddies that will be shown as necessary to explain the precipitation scaling in East Asia. The scaling of the local thermodynamics follows the CCS at about 7%/K. If it is the sole source of precipitation or if its ratio with the other sources remains the same in climate change, precipitation would scale at the same rate as that of the local thermodynamics. It is the basis of the theory of “wet gets wetter, dry gets drier (WWDD)”8,11,12,13,17. This study will focus on the deviations from the CCS depicted in Fig. 1a, b that are contributed by the other three processes.
We find that the changes in the three processes from spatial thermodynamics, dynamics of the mean circulation, and transient eddy transport all act to dry over the land in the summer (Fig. 2a, c and e), leading to the muted scaling of summer precipitation over land. The impact of the first process—the spatial thermodynamics—is caused by the enhanced moisture gradient from land to the ocean in the warmer climate that is collocated with the prevailing climatological westerly (see shading and vectors in Fig. 3a). Without changes in the circulation and mean specific humidity, the change in spatial gradient alone will lead to more moisture divergence and thus drying over land. This process does not necessarily follow the WWDD role since the collocation of the mean winds and changes in moisture gradient does not always coincide with the regions of large precipitation, such as in the present case when summer precipitation over East Asia is “rich” and “wet”. The impact of the second process—the dynamics of the mean circulation—is explained by larger subsidence over the land in this region associated with the anticyclonic motion due to weakening of the westerly jet in the warmer climate (see vectors in Fig. 3c). This weakening is consistent with the reduction of meridional temperature gradient in the lower troposphere and expansion of the subsiding branch of the Hadley circulation in climate change41. The impact of the third process—the moisture transport by transient eddies—is consistent with the reduction of eddy dynamical strength associated with the reduction of westerly jet, despite the increased magnitude of moisture eddy amplitude, which is further discussed later.
a, b Changes of column water vapor content (color shading, unit in kg/m2) overlayed on its climatology (contours) and the climatological vertically integrated winds weighted by specific humidity (vector, unit in m/s) for JJA and DJF. The panels below are the same as (a, b) except for different fields. c, d Changes of tropospheric winds at 300 hPa (vector) and percentage changes of the magnitude of the vertical wind shear (color shading, unit in %, blue color represents larger value to denote the relationship with precipitation). e, f Percentage changes of the dynamical amplitude of eddies in the upper troposphere at 300 hPa (unit in %, blue color represents larger value). g, h Percentage changes in the eddy amplitude of precipitable water (unit in %/K). i, j Percentage changes scaled by unit temperature change in the discharge rate of precipitable water during the extreme precipitation events at 99% threshold (unit in %/K) (see Methods in SI). Stippling represents statistical significance at 5% level in student t test.
The above interpretations can be directly applied to the summer precipitation scaling over the subtropical ocean. The scaling is increased by the positive contributions from both the spatial thermodynamics and dynamics changes of the mean circulation. The prevailing climatological winds over the subtropical ocean is southwesterly as part of the East Asia monsoon that blows down the enhanced moisture gradient, creating larger moisture convergence in a warmer climate even if winds do not change. The region of the subtropical ocean is also under the influence of an anomalous cyclonic circulation to the south of the weakened westerly jet. Hence, there is anomalous wind convergence in the mean circulation. The change in the dynamical circulation dominates the enhanced scaling of summer precipitation over the ocean.
Winter offers additional insights into the separate roles of the three processes (Fig. 2b, d, f). Because the prevailing climatological westerly and northwesterly winter monsoon blow toward a steeper moisture gradient from the land to the ocean (Fig. 3b), the effect of the spatial thermodynamics is to dry the region both over land and ocean, reducing the precipitation scaling. The change of the dynamics in mean circulation also acts to dry the region because the anomalous anticyclonic motion associated with the weakening of the westerly jet is displaced further south in the winter (Fig. 3d). Over the land, these two drying effects are, however, greatly opposed, and more than compensated, by the increased scaling due to enhanced eddy moisture convergence. The effect of eddy transport over the subtropical ocean is nearly zero due to the weakened eddy dynamics as a result of the jet weakening in the region.
What is the cause of the increase of eddy moisture convergence in winter over land? We approach this question from two complemental perspectives. The first is aided by distinguishing the dynamical and hydrological eddy strengths, with the former reflecting changes in the velocity perturbation; the latter in the perturbation of specific humidity or precipitable water in eddies. The dynamical eddy amplitude in the winter is larger in the warmer climate over land (shading in Fig. 3f, blue color denotes larger value) because of the stronger vertical wind shear (shading in Fig. 3d) associated with smaller meridional temperature gradient near the surface but larger gradient in the upper troposphere. The eddy amplitude in moisture is increased even more because it contains the additional contribution of the CCS rate of water vapor (Fig. 3h). This is in contrast to the summer, when the dynamical eddy amplitude is weaker due to the reduced wind shear that offsets the change in the moisture amplitude (Fig. 3c, e and g). A second perspective is to track eddies as cyclones. The scaling of precipitation following a cyclone includes the local thermodynamical contribution. It additionally has the larger moisture discharge (the negative time tendency) in the warmer climate (Fig. 3i, j, see Methods in SI)—having more moisture to store and then be squeezed out—thus adding positively to the precipitation scaling. The larger storage of moisture during precipitation events is consistent with reduction of the mean relative humidity over land in the warmer climate42,43.
While the above three processes account for the seasonal and land-sea contrasts of precipitation scaling, surface evaporation contributes ~2%/K in the summer (Supplemental Fig. S6a). In the winter, surface evaporation is found to play a subtle role contributing to the large precipitation scaling over land. It reaches the CCS in two regions (see Supplemental Fig. S6b). One is over the coastal waters, which is attributed to the winter monsoon blowing cold and dry continental air mass over the relatively warm water near the coast. The second region is located to the north of the Tibet Plateau where the climatological precipitation in the winter is very small. Evaporation from the accumulated snow on the ground into dry air mass is likely to scale according to CCS over ice, which could be amplified by the snow-albedo feedback of more melting and wetter surface in the warmer climate. Additional research is warranted about the evaporation scaling since it should be highly dependent on land surface properties of the specific regions.
We note that the scaling results described above are intended to interpret precipitation response to climate change. The scaling could be different for other types of atmospheric variabilities, such as diurnal or sub-diurnal and seasonal variations44. This is because the systematic changes in the spatial thermodynamics and dynamics will be different and the role of the transience can be also different.
Schematics of the conceptual model
The atmospheric processes responsible for the deviation of precipitation scaling from CCS under climate change and the summer-winter/land-sea contrasts in East Asia can be schematically summarized (Fig. 4). The effect of spatial thermodynamics, with enhanced spatial moisture gradient in a warmer climate, depends on the orientation of the prevailing climatological winds relative to the moisture gradient change. For East Asia, in JJA the prevailing westerly over land and the southwesterly monsoon over the ocean determine the drying effect over land and moistening effect over the ocean, respectively; in DJF the prevailing westerly and northwesterly winter monsoon over both land and the ocean cause drying in a warmer climate (Fig. 4a, b). The effect of the change in the mean circulation is expected to change greatly from one region to another. In East Asia, it is typified by the weakening of the westerly jet centered around 40°N in JJA and 30°N in DJF in a warmer climate. The anomalous anticyclonic circulation north of the weakened jet enhances subsidence to reduce precipitation scaling in the region; the anomalous cyclonic circulation south of the weakened jet enhances upward motion to increase precipitation scaling (Fig. 4c, d). The effect of the eddy moisture transport on the scaling can be understood by separating the eddy strengths in wind and precipitable water. The moisture amplitude of eddies increases in a warmer climate; the wind amplitude depends on the change of the vertical wind shear. For East Asia in JJA, eddy velocity is weakened because of the weakened westerly shear, compensating the increased eddy amplitude in moisture. In DJF, the amplitudes of both eddy dynamics and moisture increase in the warmer climate, resulting in large increase of precipitation scaling (Fig. 4e, f).
a, c, e For JJA; b, d, f for DJF. a, b Changes in spatial thermodynamics, depicting the orientation of the climatological winds over the change of moisture gradient. c, d Changes in mean circulation, depicting jet weakening and the accompanied anomalous anticyclonic circulation to its north, anomalous cyclonic circulation to its south. e, f Changes in eddy transport, depicting responses of the hydrological and dynamical eddy amplitudes to warming, and moisture discharge during precipitation events using the size of the mock cloud representing the dynamical amplitude and the color intensity representing specific humidity.
Conclusions
East Asia provides a clear case to demonstrate the different roles of atmospheric local thermodynamics, spatial thermodynamics, dynamics of the mean circulation, and eddies in causing the scaling of precipitation with temperature, leading to larger scaling of land precipitation in the winter and smaller scaling in the summer in East Asia. These four processes can operate independently of each other. The separation of these processes, including the strengths of eddy dynamics and eddy moisture, provides a useful tool to understand future changes of precipitation in other regions with their specific settings of climatology and circulation changes. It can also help to better discern what model projections of the future precipitation changes are more trustworthy and where priorities should be placed to further improve the climate models45.
Methods
Precipitation scaling
Seasonal means of temperature and precipitation rate are calculated by using the ensemble mean of the 40 member CESM LES simulations, with 1975–2004 in the historical simulation as present-day climate, 2070–2099 in future scenario (RCP85) simulation as future climate. Precipitation scaling is obtained by using the percentage change of precipitation scaled by surface temperature change. The scaling is calculated at each grid point by using the local seasonal means. The reference scaling of water vapor in Fig. 1a, b are calculated by using percentage changes of precipitable water scaled by surface temperature change. For CMIP6 results in the Supplemental Information, we selected 18 CMIP6 models based on the availability at the time of the analysis. Only one ensemble is downloaded for each model. For future climate in the CMIP6 simulations, we used the SSP585 scenario. As a supplement, we used MPI-GE 100 ensembles and MIROC6-LES 50 ensembles, with the former using the RCP85 future scenario, the latter using the SSP585 scenario.
Moisture budget calculation
The basic equation of moisture budget is a balance between precipitation and moisture flux convergence, precipitable water change, and evaporation.
For climatological steady state, Eq. (2) becomes32:
where \(-\nabla \cdot {\overline{\overrightarrow{F}}}_{q}\) is the moisture flux convergence. For future changes of mean precipitation, we have:
The total moisture flux convergence (divergence) can be decomposed into contributions from the mean state (seasonal mean) and transient eddies32:
The first term of the right-hand side in Eq. (5) can be decomposed into thermodynamic change (THE), dynamic change (DYN). They are written as:
The nonlinear term −δ(THE)δ(DYN) in Eq. (6) can be neglected as it is diagnosed to be small. The second and third terms in the right-hand side of Eq. (8) are also small. These three minor terms are treated as residual terms δR in Eq. (1). Combining and reorganizing Eqs. (6), (7), and (8) lead to Eq. (1). Monthly fields are used to calculate all terms in Eqs. (7) and (8). The eddy term is calculated as the residual from Eq. (5).
Moisture discharge during transient events
We use the CESM1-LES 6-hourly output to track extreme precipitation events and consider them as from cyclones (either mid-latitude or tropical). For 6-hourly output, only 1990–2005 is available for the historical simulation, and 2071–2080 for the RCP8.5 scenario. We select 99th percentile of 6-hourly precipitation events at each grid. Using the 99th percentile precipitation index we perform transient moisture budget analysis at each grid point separately because different regions have different extreme events. To maintain spatial structure of extreme events, we calculate the moisture gradient and wind convergence on the whole field and then perform the composition grid-by-grid based on the 99th percentile extreme precipitation index. The basic equation for transient moisture budget is as follows after neglecting the evaporation16:
\(-\frac{\partial }{\partial t}\int _{0}^{{P}_{s}^{e}}{q}^{e}\frac{dp}{g}\) implicates that there is moisture recharge–discharge before, during, and after the extreme precipitation events. For future change, we have:
The last term is shown in Fig. 3i, j.
Data availability
Data used in this study are available at the CMIP6 archive https://esgf-node.llnl.gov/search/cmip6/.
Code availability
Analysis codes used in the study can be accessed at https://github.com/wenguiliang/Scripts.
References
Gillett, N. P. et al. Attribution of polar warming to human influence. Nat. Geosci. 1, 750–754 (2008).
Stocker, T. (ed.). Climate Change 2013: the Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (Cambridge Univ. Press, 2014).
Bock, L. et al. Quantifying progress across different CMIP phases with the ESMValTool. J. Geophys. Res. Atmos. 125, e2019JD032321 (2020).
Bates, B., Kundzewicz, Z. & Wu, S. Climate Change and Water (IPCC Secretariat, 2008).
Schewe, J. et al. Multimodel assessment of water scarcity under climate change. Proc. Natl Acad. Sci. USA 111, 3245–3250 (2014).
Mekonnen, M. M. & Hoekstra, A. Y. Four billion people facing severe water scarcity. Sci. Adv. 2, e1500323 (2016).
Djehdian, L. A., Chini, C. M., Marston, L., Konar, M. & Stillwell, A. S. Exposure of urban food–energy–water (FEW) systems to water scarcity. Sustain. Cities Soc. 50, 101621 (2019).
Held, I. M. & Soden, B. J. Robust responses of the hydrological cycle to global warming. J. Clim. 19, 5686–5699 (2006).
Pendergrass, A. G. & Hartmann, D. L. Changes in the distribution of rain frequency and intensity in response to global warming. J. Clim. 27, 8372–8383 (2014).
Pfahl, S., O’Gorman, P. A. & Fischer, E. M. Understanding the regional pattern of projected future changes in extreme precipitation. Nat. Clim. Change 7, 423–427 (2017).
Chou, C. & Neelin, J. D. Mechanisms of global warming impacts on regional tropical precipitation. J. Clim. 17, 2688–2701 (2004).
Chou, C. et al. Increase in the range between wet and dry season precipitation. Nat. Geosci. 6, 263–267 (2013).
Liu, C. & Allan, R. P. Observed and simulated precipitation responses in wet and dry regions 1850–2100. Environ. Res. Lett. 8, 034002 (2013).
Meehl, G. A., Arblaster, J. M. & Tebaldi, C. Understanding future patterns of increased precipitation intensity in climate model simulations. Geophys. Res. Lett. 32, https://doi.org/10.1029/2005GL023680 (2005).
Seager, R. & Vecchi, G. A. Greenhouse warming and the 21st century hydroclimate of southwestern North America. Proc. Natl Acad. Sci. USA 107, 21277–21282 (2010).
Norris, J., Chen, G. & Neelin, J. D. Thermodynamic versus dynamic controls on extreme precipitation in a warming climate from the Community Earth System Model Large Ensemble. J. Clim. 32, 1025–1045 (2019).
Yang, T., Ding, J., Liu, D., Wang, X. & Wang, T. Combined use of multiple drought indices for global assessment of dry gets drier and wet gets wetter paradigm. J. Clim. 32, 737–748 (2019).
Chadwick, R. & Good, P. Understanding nonlinear tropical precipitation responses to CO2 forcing. Geophys. Res. Lett. 40, 4911–4915 (2013).
Greve, P. et al. Global assessment of trends in wetting and drying over land. Nat. Geosci. 7, 716–721 (2014).
Roderick, M. L., Sun, F., Lim, W. H. & Farquhar, G. D. A general framework for understanding the response of the water cycle to global warming over land and ocean. Hydrol. Earth Syst. Sci. 18, 1575–1589 (2014).
Byrne, M. P. & O’Gorman, P. A. The response of precipitation minus evapotranspiration to climate warming: Why the “wet-get-wetter, dry-get-drier” scaling does not hold over land. J. Clim. 28, 8078–8092 (2015).
Scheff, J. & Frierson, D. M. Terrestrial aridity and its response to greenhouse warming across CMIP5 climate models. J. Clim. 28, 5583–5600 (2015).
Emori, S. & Brown, S. J. Dynamic and thermodynamic changes in mean and extreme precipitation under changed climate. Geophys. Res. Lett. 32, L17706 (2005).
O’Gorman, P. A. Precipitation extremes under climate change. Curr. Clim. Change Rep. 1, 49–59 (2015).
Trenberth, K. E., Fasullo, J. T. & Shepherd, T. G. Attribution of climate extreme events. Nat. Clim. Change 5, 725–730 (2015).
Vautard, R. et al. Attribution of human-induced dynamical and thermodynamical contributions in extreme weather events. Environ. Res. Lett. 11, 114009 (2016).
Lu, J. X. et al. Enhanced hydrological extremes in the western United States under global warming through the lens of water vapor wave activity. Npj Clim. Atmos. Sci 1, 1–9 (2018).
Hu, H., Leung, L. R. & Feng, Z. Observed warm‐season characteristics of MCS and non‐MCS rainfall and their recent changes in the Central United States. Geophys. Res. Lett. 47, e2019GL086783 (2020).
Deser, C. et al. Insights from Earth system model initial-condition large ensembles and future prospects. Nat. Clim. Change 10, 277–286 (2020).
Donat, M. G., Lowry, A. L., Alexander, L. V., O’Gorman, P. A. & Maher, N. More extreme precipitation in the world’s dry and wet regions. Nat. Clim. Change 6, 508–513 (2016).
Bao, J., Sherwood, S. C., Alexander, L. V. & Evans, J. P. Future increases in extreme precipitation exceed observed scaling rates. Nat. Clim. Change 7, 128–132 (2017).
Ting, M., Seager, R., Li, C., Liu, H. & Henderson, N. Mechanism of future spring drying in the southwestern United States in CMIP5 models. J. Clim. 31, 4265–4279 (2018).
Zhang, M. & Song, H. Evidence of deceleration of atmospheric vertical overturning circulation over the tropical Pacific. Geophys. Res. Lett. 33, L12701 (2006).
Chang, E. K., Guo, Y. & Xia, X. CMIP5 multimodel ensemble projection of storm track change under global warming. J. Geophys. Res. Atmos. 117, D23118 (2012).
Seneviratne, S. et al. Changes in Climate Extremes and Their Impacts on the Natural Physical Environment (Cambridge Univ. Press, 2012).
Chang, E. K. CMIP5 projection of significant reduction in extratropical cyclone activity over North America. J. Clim. 26, 9903–9922 (2013).
Shepherd, T. G. Atmospheric circulation as a source of uncertainty in climate change projections. Nat. Geosci. 7, 703–708 (2014).
Yang, D. et al. Role of tropical variability in driving decadal shifts in the Southern Hemisphere summertime eddy-driven jet. J. Clim. 33, 5445–5463 (2020).
Maher, N. The Max Planck Institute Grand Ensemble: enabling the exploration of climate system variability. J. Adv. Model Earth Syst. 11, 2050–2069 (2019).
Tatebe, H. Description and basic evaluation of simulated mean state, internal variability, and climate sensitivity in MIROC6. Geosci. Model Dev. 12, 2727–2765 (2019).
Watt‐Meyer, O., Frierson, D. M. & Fu, Q. Hemispheric asymmetry of tropical expansion under CO2 forcing. Geophys. Res. Lett. 46, 9231–9240 (2019).
Byrne, M. P. & O’Gorman, P. A. Understanding decreases in land relative humidity with global warming: Conceptual model and GCM simulations. J. Clim. 29, 9045–9061 (2016).
Byrne, M. P. & O’Gorman, P. A. Trends in continental temperature and humidity directly linked to ocean warming. Proc. Natl Acad. Sci. USA 115, 4863–4868 (2018).
Ghausi, S. A. & Ghosh, S. Diametrically opposite scaling of extreme precipitation and streamflow to temperature in South and Central Asia. Geophys. Res. Lett. 47, e2020GL089386 (2020).
Bony, S. et al. Clouds, circulation and climate sensitivity. Nat. Geosci. 8, 261–268 (2015).
Acknowledgements
We wish to thank the National Center for Atmospheric Research (NCAR), sponsored by the National Science Foundation, for making the CESM LES available to us and providing computing time. We also thank other modeling groups participating in CMIP6 for making their simulations available to us. This research is partially supported by the US National Science Foundation under grant 1633299 to Stony Brook University.
Author information
Authors and Affiliations
Contributions
W.L. and M.Z. contributed equally to the conceptualization of the study and writing of the manuscript. W.L. carried out the data analysis.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Communications Earth & Environment thanks Subimal Ghosh and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editor: Heike Langenberg. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Liang, W., Zhang, M. Summer and winter precipitation in East Asia scale with global warming at different rates. Commun Earth Environ 2, 150 (2021). https://doi.org/10.1038/s43247-021-00219-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-021-00219-2
This article is cited by
-
Sea–air coupling leads to a decrease in precipitation in East Asia under present day conditions that is partially alleviated in future simulations
npj Climate and Atmospheric Science (2023)
-
Seasonal variations in the dynamic and thermodynamic response of precipitation extremes in the Indian subcontinent
Climate Dynamics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.