Abstract
Fully accounting for the climate impact of aviation requires a process-level understanding of the impact of aircraft soot particle emissions on the formation of ice clouds. Assessing this impact with the help of global climate models remains elusive and direct observations are lacking. Here we use a high-resolution cirrus column model to investigate how aircraft-emitted soot particles, released after ice crystals sublimate at the end of the lifetime of contrails and contrail cirrus, perturb the formation of cirrus. By allying cloud simulations with a measurement-based description of soot-induced ice formation, we find that only a small fraction (<1%) of the soot particles succeeds in forming cloud ice alongside homogeneous freezing of liquid aerosol droplets. Thus, soot-perturbed and homogeneously-formed cirrus fundamentally do not differ in optical depth. Our results imply that climate model estimates of global radiative forcing from interactions between aircraft soot and large-scale cirrus may be overestimates. The improved scientific understanding reported here provides a process-based underpinning for improved climate model parametrizations and targeted field observations.
Similar content being viewed by others
Introduction
Aviation contributes to anthropogenic radiative forcing (RF) by changing cirrus cloudiness, thereby affecting Earth’s energy budget and climate1. Aircraft-induced clouds (AIC) that originate from emitted soot particles include young, line-shaped contrails and the older, irregular-shaped contrail cirrus evolving from them2. AIC yield the largest aviation-induced RF, and effective RF, followed by aviation carbon dioxide emissions2,3. Significant progress has been made in quantifying AIC RF from process-based representations of these man-made ice clouds in global climate models, with a best estimate of 111 mW m−2 for air traffic in the year 2018 3. This estimate does not include the impact of contrails forming within already-existing cirrus4 and is expected to increase strongly in the next decades5, assuming that aviation activity reverts to projected growth rates after the COVID-19 pandemic6. By contrast, the role of aircraft soot particles in the formation of new cirrus proves difficult to establish with confidence. Estimates of RF from aircraft soot–cirrus interactions are highly varied with large positive and negative values of magnitudes that can exceed the total aviation RF best estimate of 149.1 mW m−2 (ref. 3), because a detailed understanding of how aircraft soot particles nucleate ice crystals is lacking. If one of these large RF values were to be substantiated, the perception of the role of aviation in the climate system would be substantially altered.
An extensive field campaign did not detect a unique aviation signature in cirrus formation, but could not rule out that cirrus formed on nuclei originating from aircraft exhaust7. Aircraft measurements ascribed cirrus ice crystal number concentrations (ICNCs) and depolarisation ratios to aircraft soot impacts, but only provided correlational evidence8,9. A cloud model study suggested that aircraft-emitted soot particles present in number concentrations below 100 L−1 modify cirrus ICNCs and coverage under the assumption that they are efficient ice-nucleating particles (INPs)10. Global climate model studies have led to a wide range of RF estimates for aircraft soot–cirrus interactions, currently from approximately −330 to 287 mW m−2 normalised to 2018 air traffic3. This range persists despite some older estimates being superseded3. Some models assume that aircraft-emitted soot particles frozen in contrails act as good INPs in large-scale cirrus formation, while others, assuming that only a small fraction of all aircraft soot particles is capable of nucleating ice, led to much smaller RF values of 11–13 mW m−2 (ref. 3). Consequently, best RF estimates remain undetermined. This represents a severe gap in the knowledge of how aviation contributes to climate change.
While soot particles are poor INPs at mixed-phase cloud temperatures (>238 K)11,12, some studies showed enhanced ice nucleation activity at cirrus temperatures (<233 K)13,14. This behaviour has been explained by pore condensation and freezing, PCF15,16. Contrail processing—the formation of contrail ice crystals on aircraft-emitted soot particles followed by full ice crystal sublimation and release of the soot particles to the atmosphere—results in compacted soot aggregates. A recent laboratory study demonstrated that the ice activity of soot particles is significantly enhanced upon contrail processing17. This enhancement was attributed to increased porosity of soot aggregates after compaction, facilitating PCF.
Contrail processing occurs in long-lived and short-lived AIC. Long-lived AIC evolve over many hours in ice-supersaturated regions2. The formation of long-lived AIC is constrained by the occurrence frequency of upper tropospheric ice supersaturation with a multi-year average of about 20–30% over the North Atlantic region18. Short-lived contrails dissipate a few minutes past formation and are mainly found in low latitudes19. They appear more frequently than long-lived AIC as they form in ice-subsaturated air, and are usually not considered in global climate models because their contribution to AIC RF is negligible2.
The wide range of values and the resulting low confidence attributed to RF estimates from aircraft soot–cirrus interactions3 underscores the importance to critically assess how aircraft soot emissions impact cirrus formation. Here we employ a state-of-the-art, high-resolution cirrus column model20 and combine it with a novel, PCF-based parametrization describing the ice nucleation activity of contrail-processed soot particles21. Clarifying the ice nucleation activity of aircraft-emitted soot particles resolves a long-standing knowledge gap and allows us to unravel the microphysical mechanisms underlying associated cirrus perturbations on the process level. We intentionally overestimate factors controlling aircraft soot–cirrus interactions to establish an upper-limit impact that may serve to constrain the magnitude of associated RF estimates.
Results
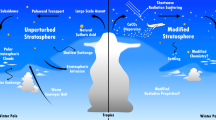
Figure 1 illustrates our conceptual framework. A contrail dissipates at plume age td, defined as the time elapsed after formation (lifetime), releasing the processed soot particles upon which it originally formed. Number concentrations of soot particles and ice crystals decrease with increasing plume dilution caused by entrainment of ambient air. We distinguish between cases where the soot particles participate in the formation of either a new contrail at time tp > td or contrail cirrus at a later time tb > tp. We define cirrus perturbations as plume scenarios (Plume), if the exhaust plume containing these particles is relatively close to the source aircraft and therefore still line-shaped, and if the number concentration of ice-active soot particles exceeds that of INP in the background upper troposphere, which amounts to some 10 L−1 (ref. 22). Otherwise, we define cases as background scenarios (Background). Setting tp = 0.5 h and tb = 5 h, we derive soot particle number concentrations of 5448 and 458 L−1 (Supplementary Table 1), and associated upper-limit estimates of ice-active soot particle number concentrations of 54 and 5 L−1 for scenarios Plume and Background, respectively (see ‘Methods’ section and Supplementary Figs. 1–3).
Contrail ice crystals form in aircraft exhaust plumes closely behind the jet engines at cruise altitudes. Plume dilution decreases soot particle and ice crystal number concentrations over time. The contrail dissipates completely after time td and full sublimation of all ice crystals releases all contrail-processed soot particles. After a timespan (tp − td) or (tb − td), the air is lifted (red arrows), generating ice supersaturation. Ice crystals form via soot-PCF (green arrows and upper inset) in addition to homogeneous freezing of liquid solution droplets (lower inset), modulating ice formation in a new line-shaped cirrus cloud similar to a contrail (scenario Plume) or an irregularly shaped cirrus cloud similar to contrail cirrus (Background). The scenarios consider the number concentrations of ice-active aircraft soot particles that encompass the range of INP values observed in the background upper troposphere. In the unperturbed scenario (Base), new cirrus forms solely by homogeneous freezing. All clouds form in the same meteorological conditions and with the same constant updraught speed enhanced by ubiquitous mesoscale gravity waves (wavy arrows).
In scenario Background, the total soot particle number concentrations approximately quantify the aviation contribution to the large-scale atmospheric particle background (see ‘Methods’ section). As entrainment rates diminish with plume age, the effect of dilution is stronger in scenario Plume than in Background. We describe the baseline against which the soot perturbation scenarios are compared by a simulation of unperturbed cirrus formation via homogeneous freezing of aqueous solution droplets (scenario Base). Using an updraught speed of 0.15 m s−1 to drive cirrus formation in all scenarios is representative of widespread mesoscale gravity wave activity23 (see ‘Methods’ section) and allows us to isolate and determine the characteristics of microphysical mechanisms underlying aircraft soot–cirrus interactions.
Although ice activity measurements of size-selected soot particles with mobility diameters <100 nm are not available, the theoretical underpinning of our soot-PCF parametrization builds strong confidence in applying it to such small particle sizes21. We find that only a fraction of contrail-processed soot particles is ice-active via soot-PCF depending on ice supersaturation and soot particle size on the premise that real aircraft soot particles have properties that are similar to the laboratory soot surrogates. Analysis of pore structures within soot aggregates reveals that high ice supersaturation near the homogeneous aerosol freezing limit (s ≈ 0.5) is required for significant ice activity to occur (see ‘Methods’ section). Microphysical and optical properties of unperturbed and soot-perturbed cirrus differ to the extent soot-derived ice crystals affect the evolution of ice supersaturation during cirrus formation.
We analyse the temporal evolution of the unperturbed cirrus from a scenario Base by focussing on key variables determining cloud radiative effects (Fig. 2). We use the short-wave (solar) cirrus optical depth as a measure of RF24. Ice nucleation occurs in an ICNC burst about 43 min after model initialisation when homogeneous freezing conditions are first met (at peak ice supersaturation). Thereafter, ice crystals continue to form homogeneously at the cloud top due to sustained cooling, but at a reduced rate (Supplementary Fig. 4), causing the ice water path to increase further with time. The maximum ICNC averaged over the cirrus column (≈500 L−1) slightly decreases due to plume dilution, adiabatic cooling and sedimentation. Ice crystal growth due to water vapour (H2O) deposition causes the column-averaged, mean ice crystal diameter to increase rapidly to about 20 μm and then gradually towards 30 μm. Optical depth increases accordingly and reaches a value of 0.3. Cirrus with low optical depth (<0.3) similar to AIC2 are most susceptible to INP perturbations. Column-averaged ice crystal size distributions reveal diameters up to about 20 μm at 45 min and 40 μm at 75 min (Fig. 3). ICNC and mean diameter, as well as ice water content and ice supersaturation, develop significant vertical structure resulting from the interplay between ice crystal nucleation, growth and sedimentation (Supplementary Fig. 4).
Shown are a, e, i ice water path, b, f, j column-average total ice crystal number concentration, c, g, k column-average number-weighted mean ice crystal diameter and d, h, l short-wave cirrus optical depth versus time past ice saturation initially reached at 10 km altitude. The top panel shows the homogeneous freezing-only reference scenario Base and corresponding results for the soot-perturbed scenarios Background and Plume are presented in the middle and bottom panel, respectively. The light grey curves repeat the Base results to facilitate comparison.
Column-averaged results taken at (dashed) 45 min and (solid) 75 min for a the reference scenario and b, c the cirrus perturbation scenarios. Size distribution refers to number concentrations of ice crystals with diameters Di in the range [Di − ΔDi, Di + ΔDi] divided by the grid size resolution ΔDi/Di = 0.0235.
In scenarios Background and Plume, ice crystals already start to form on the subset of ice-active soot particles about 6 min earlier than in scenario Base (Fig. 2). The ice water paths of the maturing soot-perturbed cirrus exceed that of Base, because the soot-generated ice crystals settle into ice-supersaturated air and take up relatively large amounts of water vapour. The onset of homogeneous freezing is slightly delayed, associated ICNCs decrease by ≈150 L−1 (Background) and ≈300 L−1 (Plume) and ice crystal diameters increase. Adding a small number of INPs reduces the number concentrations of homogeneously produced ice crystals for two reasons: growth of soot-derived ice crystals lowers the ice supersaturation resulting from the updraught owing to initially high deposition coefficients (>0.1) and homogeneous freezing rates are very sensitive to even small changes in supersaturation. In addition, turbulent diffusion lowers homogeneously nucleated ICNCs in scenario Plume by flattening vertical supersaturation gradients20. Soot particles and ice crystals dilute faster and the latter achieve larger sizes in scenario Plume than in Background due to faster entrainment of ice-supersaturated air (Supplementary Table 1). As in scenario Base, optical depth is dominated by homogeneous freezing, decreasing only slightly by 0.08 in Plume and increasing by 0.06 in Background. The perturbed size distributions reveal a small number of ice crystals originating from soot with diameters of about 50 µm (Background) and 60–80 µm (Plume) that are absent in Base (Fig. 3). Liquid aerosol particles freeze within and above the soot layer (Supplementary Figs. 5 and 6), showing that aircraft soot is capable of modifying, but not preventing, homogeneous freezing.
Soot particles form significant amounts of ice crystals only around the time and location of peak ice supersaturation. In an ~250-m-thick layer, the highest soot-derived ICNCs are reached shortly before homogeneous freezing commences, namely 4.5 L−1 (Background) and 22 L−1 (Plume) (Supplementary Fig. 7). These values are lower than the upper-limit estimates of 5 and 54 L−1, respectively, reflecting the effect of plume dilution. Outside the ice supersaturation maximum, soot-derived ICNCs diminish rapidly reducing the peak column-integrated values further to 2.5 L−1 (Background) and 13.5 L−1 (Plume) (Fig. 2). Apart from the nonlinearities inherent to ice nucleation and growth processes across vertically inhomogeneous ice supersaturation profiles, dilution and diffusion prevent simple scaling of these results with total soot particle number concentrations.
Discussion
The generation of few large ice crystals by aircraft soot particles and the reduction of ICNCs relative to Base is significant in both scenarios. However, changes in optical depth, a proxy of RF, are minor (≈20%), as it is dominated by homogeneous freezing in all scenarios. We include an additional sensitivity simulation Background—performed using a much lower (synoptic) updraught speed of 0.01 m s−1—to illustrate the competition between homogeneous and heterogeneous ice formation in weak forcing conditions, where INPs generally exert a greater impact. In this case, soot suppresses the initial ICNC burst, but homogeneous freezing still occurs at the cloud top and the resulting cirrus develops only low optical depth (<0.06) (Supplementary Fig. 8). As the vertical wind field is affected by rapid (few minutes) variabilities of ever-present mesoscale gravity wave activity superimposed onto synoptic motions, mean updraught speeds below 0.15 m s−1 are rarely observed in the upper troposphere and lower stratosphere23. Mean updraught speeds above 0.15 m s−1 strongly enhance the homogeneous freezing contribution, leading to optically thicker cirrus clouds and reducing the impact of ice-active soot particles. The use of a single updraught in simulations of cirrus ice formation does not capture the full variability in ICNCs. However, adding wave-induced temporal variability in vertical wind speeds leads to a massive broadening of ICNC frequency distributions due to multiple homogeneous freezing events25. Because this broadening would make it difficult to separate the effect of aircraft soot from wave-induced variability in ICNC, we did not represent such temporal variations in our simulations. Using a higher mean updraught speed or including updraught speed variability would diminish the impact of aircraft soot.
Our approach overestimates the soot impact, as we prescribe: a soot particle population with a high emission index, large modal size and size spread; a soot particle layer encompassing the peak supersaturation region; and a contact angle at the soot-liquid water interface representing bare (uncoated) soot particles with relatively high PCF activity (effects of atmospheric soot ageing processes relevant for aviation emissions beyond tb do not significantly increase their PCF activity). In addition, we assume the absence of coagulation and scavenging processes diminishing number concentrations of fresh soot particles over time26; efficient INPs from sources other than aviation competing with soot particles and overriding the soot impact; and, as detailed above, high mean updraught speeds or wave-induced temporal variability.
Relaxing any of these assumptions would lead to predictions with smaller or negligible soot-induced cirrus perturbations in our simulations. To illustrate this point, we performed sensitivity studies (see ‘Methods’ section and Supplementary Fig. 2), where either a lower-limit soot particle number-size distribution (PSD) or an increased contact angle was used. In both cases, ice-active soot particle number concentrations decrease more than tenfold, rendering ice activity practically negligible. Ozone oxidation can decrease contact angles on bare soot particle surfaces. However, gas-phase oxidation becomes increasingly hampered by condensation and coagulation processes that may lead to thick coatings as soot particles age. In the case of aircraft soot, contact angles decrease only slightly and therefore ice activity is not changed significantly (see ‘Methods’ section). More importantly, we expect aircraft soot particles to coexist with more efficient INPs, especially in the Northern Hemisphere. These INPs include mineral dust particles, which become ice-active already at low ice supersaturation27, where ice activity of aircraft soot particles as predicted by soot-PCF is basically absent (Supplementary Figs. 1 and 2). Aerosol particles emitted from ground sources were observed to be a common feature at cruise altitudes over the Central and Western USA7. Another field study revealed median concentrations of about 35,000 L−1 of refractory particles over the Eastern North Atlantic28, exceeding the total aircraft soot concentrations (Supplementary Table 1) in scenarios Plume (Background) by a factor of 6 (76). Together with the low ice activity of aircraft soot, this strongly suggests that aircraft-emitted soot particles cannot compete in cirrus formation with insoluble aerosol particles from other sources.
Our results challenge the prevailing notion of a large RF from aircraft soot–cirrus interactions. In a global climate model study addressing RF due to soot-perturbed, large-scale cirrus, soot particles released from long-lived AIC were assumed to act as good INPs already at moderate ice supersaturation, based solely on contrail formation and persistence criteria, unless they have collected multilayer sulphate coatings29. Positive RF values were obtained in sensitivity tests assuming low concentrations of ambient sulphate and dust aerosol particles. RF values were found to be negative when processed soot particles were added in areas where homogeneous freezing dominates cirrus formation. More recent studies based on the same global model30,31 suggest lower RF estimates, brought about by accounting for effects of waves on updraught speeds, changes in background aerosols and modifications of the underlying ice nucleation scheme, superseding the largest RF estimates3. Other global model studies32,33 calculated statistically insignificant RF when ascribing a small ice nucleation efficiency (0.1%) to all aircraft-emitted soot particles.
We identify a number of issues causing large negative RF values due to interactions between aircraft soot particles and large-scale cirrus to be overestimated in the global model studies. Firstly, the size-dependence of ice activity of soot particles processed in long-lived AIC due to soot-PCF is much stronger than predicted by parametrizations based on, e.g., immersion freezing34 and leads to lower soot-derived ICNCs. Scenario Background—intentionally overestimating the soot impact—yields a number concentration of ice-active soot particles of 5 L−1, significantly below the values of up to 100–300 L−1 of contrail-processed aircraft soot particles in regions with highest flight activities29. Inclusion of processing of soot emissions in short-lived contrails and Plume-type scenarios that both were not considered in the global model study would partially offset this decrease. Secondly, the parametrization employed in ref. 29 to represent cirrus ice formation reduces the homogeneous freezing contribution too strongly, because processed soot particles, either bare or with minimal coatings, were assumed to act as INPs already at moderate ice supersaturation (0.35, see ref. 30); and the effect of vertically inhomogeneous supersaturation on ice activation and nucleated ICNC as well as homogeneous aerosol freezing at cloud tops was not represented.
Ideally, targeted field measurements would be used to confirm the limited effect of aircraft soot on cirrus. In planning such observations, it is important to analyse the large-scale meteorological situation leading to cirrus formation after AIC dissipation. Emphasis should be placed on the time spans (t − td), since they indicate whether Plume-type (t → tp) or Background-type (t → tb) scenarios are realised. AIC lifetimes (td) and duration and extent of ice-supersaturated areas (affecting both tp and tb) in which AIC evolve show considerable latitudinal and seasonal variations18,35. To enable meaningful comparisons with results from detailed cloud models, airborne measurements should characterise soot PSDs and mixing state before and after contrail processing, and provide number concentration and chemical composition of INPs along with ice supersaturation, cloud ice microphysical properties and vertical air motion variability during cirrus formation. However, it will be challenging to identify aircraft soot-induced changes due to ubiquitous gravity wave activity and because INP other than aircraft soot particles might produce similar or larger perturbations.
Our study is based on an improved physical understanding that grew out of a process-based evaluation of laboratory measurements and by itself presents a major step forward in quantifying aircraft soot–cirrus interactions, although atmospheric conditions and aerosol particle properties are more variable than representable in cloud models. The simulations of a prototype cirrus cloud field experiment will guide the development of global model parametrizations of soot effects as well as future observational studies, enabling a more robust quantification of the associated RF. The results show that cirrus perturbations in optical depth, hence RF, from aircraft soot are minor due mainly to the small size of the soot particles, which severely limits their ice activity. It is likely that the magnitude of RF from aircraft soot–cirrus interactions is much smaller than AIC RF and may even be insignificant because our process-oriented analysis of soot–cirrus interactions using representative upper tropospheric conditions does not reveal a significant impact on cirrus optical depth despite changes in cloud structure. In view of the great difficulty in acquiring conclusive results from airborne measurements, our study provides a major constraint for improved simulations of aircraft soot effects on cirrus in the short term: at most one out of hundred emitted soot particles is ice-active after processing in contrails or contrail cirrus.
Methods
Cirrus cloud model
We employ a numerical model to predict the meteorological and microphysical evolution of an ice cloud column for a given vertical wind field20. Because processes controlling aerosol–cirrus interactions unfold on vertical scales of tens of metres and smaller, we use a one-dimensional model framework with a grid resolution of 1 m in the computational domain (altitude 9.5–12 km). The model simulates vertical advection of potential temperature, H2O and size-resolved aerosol particles across a fixed altitude grid. The non-equilibrium water content in aqueous solution droplets is predicted based on size- and composition-dependent hygroscopic and condensational growth rates. In addition, the model treats homogeneous freezing of these droplets and depositional growth of spherical ice crystals by deposition of H2O, and tracks ice crystals (advection and sedimentation). Aircraft soot PSDs are included based on in situ measurements as detailed below. All types of aerosol particles are transported separately for each size category and form ice crystals when the specific particle size and ice supersaturation conditions are met. To estimate short-wave cirrus optical depth, Mie scattering cross-sections are evaluated at a wavelength of 0.55 μm for non-absorbing ice crystals with a refractive index of 1.311. Turbulent diffusion of H2O and heat as well as entrainment of cloud-free air into the cloud column is additionally considered for AIC simulations. Vertical diffusivity is enhanced in young contrails due to decaying aircraft wake turbulence, approaching small ambient values over time. The entrained environmental air is simulated based on the same dynamical evolution as the cloud column, but without ice crystal formation.
Homogeneously nucleated ICNCs in cirrus depend on vertical wind speeds, which are strongly influenced by mesoscale gravity waves. In our simulations, the air is lifted with a constant updraught speed of 0.15 m s−1, exceeding synoptic values and driving cirrus formation far away from strong wave sources such as steep mountains or deep convection. The imposed updraught corresponds to a mean wave-driven enhancement representing the low end of measured values23. Molecular deposition coefficients control the efficiency of ice crystal growth from the vapour. Growth by uptake of H2O is governed by deposition coefficients depending on ice supersaturation, with additional dependencies on ice crystal size, temperature and pressure36. Deposition coefficients reduce to values <0.01 as growing ice crystals quench the ice supersaturation; the resulting slowdown of deposition growth feeds back on ice supersaturation and impacts the vertical distribution of cloud ice. More than 100,000 (10,000) simulation ice particles37, derived from the liquid (soot) aerosol and each containing a number of real ice crystals, are tracked through their lifecycles in each simulation.
Model initialisation
Initial temperature (230 K at the domain base with a constant lapse rate of −7 K km−1) and relative humidity profiles (Gaussian moist layer with a standard deviation of 350 m peaking at ice saturation at 10 km) are prescribed guided by airborne dropsonde and lidar measurements across flight levels (10–11 km) over the North Atlantic38, representing a typical midlatitude situation with regard to air traffic volume and contrail occurrence. Fully soluble aerosol particles with a hygroscopicity parameter of 0.3, typical for continental accumulation mode aerosols39, are distributed log-normally with a total number concentration of 500,000 L−1 (500 cm−3), modal dry radius of 20 nm and geometric standard deviation of 1.5. Midlatitude upper tropospheric aqueous solution droplet concentrations typically lie in the range 200–2000 cm−3, encompassing large-scale areas where accumulation mode aerosol particles age by coagulation and localised regions where new particles form via gas-to-particle conversion40. Our simulations do not capture variability in ICNCs induced by variations in soluble aerosol properties. However, the susceptibility of homogeneously nucleated ICNCs to soluble aerosol particle properties is weak for updraught speeds and temperatures relevant for the conditions in our simulations41,42,43. The choice of soluble aerosol parameters within reasonable bounds is not crucial for our upper-limit estimates of soot-induced cirrus perturbations. For the given updraught speed, homogeneous freezing of particles across this size distribution occurs in a narrow range around an ice supersaturation of 0.5 at temperatures near 220 K. PSDs are evenly spread in a 300 (400) m deep layer centred at 10 km altitude around the peak supersaturation in scenario Plume (Background). The layer depths are estimated using upper tropospheric vertical diffusivities. The total number emission index, EI = 1015 (kg-fuel)−1, lies in the upper range of most measurements2 and model predictions covering a wide range of aircraft and emission conditions44,45.
Soot particle properties
While most in-flight measurements show that number-size distributions of freshly emitted soot particles in dry exhaust plumes (no contrail processing) are monomodal46, some show a second, large particle mode in both, near-field contrails47 and dry plumes48,49. The origin of the large mode is unclear. In young plumes (age ≈ 1 s), coagulation rates among soot particles diminish rapidly due to plume dilution, preventing the formation of a large mode by collisions26. This suggests that bimodality in soot PSDs does not result from compaction after contrail processing or from coagulation, but can already be a feature of fresh (unprocessed) jet engine emissions. More research is needed to resolve this issue.
PSDs in fresh aircraft exhaust plumes may be approximated by log-normal functions. We employ upper-limit values for the modal dry mobility diameter, Dm = 35.7 nm, and geometric standard deviation, σ = 1.8, of a large number of PSDs inferred from measurements behind a commercial aircraft equipped with turbofan jet engines burning conventional jet fuel at cruising thrust conditions46. In sensitivity studies, we employ a PSD using measured lower-limit values from the same study, Dm = 22.8 nm and σ = 1.65. We note that a reduction in Dm, or EI, replicates the effect of burning pure biofuel or blends of kerosene and biofuel46,50. The measured upper-limit parameters are close to average values predicted by a global aircraft soot emission inventory in cruise conditions44, while the lower-limit values are only rarely found in this inventory. Bimodal PSDs48 are also used in sensitivity studies.
We estimate total soot particle number concentrations to initialise the simulation scenarios Background and Plume at the respective times, tb and tp, based on a single plume dispersion model51. Values taken at a jet engine’s nozzle exit plane scale with the soot emission index, c · EI, with c = 2.43 × 10−6 (kg-fuel) L−1. To account for plume dilution after a typical jet mixing timescale, τ = 0.01 s, the exit plane concentration diminishes over time, t, by the dilution factor d = (τ/t)β, which derives from the entrainment rate, β/t, and together with β = 1.075 represents average conditions. We estimate total particle number concentrations, ntot = c · EI · d(t), to be on the order of 1000 L−1 for plume ages of several hours. Values taken at t = tb and tp and those of other model parameters are summarised in Supplementary Table 1.
These estimates do not account for multiple overlapping plumes enhancing number concentrations. The likelihood of plumes overlapping increases with time as plume widths increase due to wind shear; therefore, ongoing dilution reduces ntot-values in individual plumes. This particularly applies to potentially wide plumes in scenario Background. In the atmosphere, both effects can offset each other, so that ntot = 458 L−1 in scenario Background taken at tb = 5 h approximately represents large-scale number concentrations of aircraft soot particles resulting from mixing of plumes older than 5 h. The impact of dilution on ice microphysics in this scenario is small, as the entrainment-mixing timescale of about 5 h (inferred from Supplementary Table 1) is much longer than the timescales of processes governing the cirrus ice formation event.
Ice activity of contrail-processed soot particles
We assume that ice forms on bare aircraft soot particles via PCF, with homogeneous freezing of pure, supercooled liquid pore water in soot aggregates15,16. Because temperatures are low at cirrus levels and pore water is under increasingly high tension with decreasing ice supersaturation, pore water freezes almost instantly once the pore volume is large enough to host a critical ice germ52. The resulting nanoscopic pore ice can then grow into a macroscopic ice crystal at sufficient ice supersaturation to overcome the Kelvin energy barrier. The main factors controlling the ability of a pore to take up liquid water are its diameter and opening angle, and the contact angle between the pore wall material and water. The pore structure of soot aggregates is complex and comprises a range of different pore types53. We have shown that three-membered and four-membered ring pores, consisting of three and four primary particles in contact with each other, are frequent features in soot aggregates and explain the ability of soot particles to form ice via soot-PCF21. In the same study, we have demonstrated that the ice supersaturation required for soot-PCF to occur in such ring pores is linked to a small set of physical properties of the soot particles that can be readily quantified experimentally: the size of and overlap between primary particles, aggregate size and fractal dimension and the contact angle at the soot/liquid water interface. The fractal dimension is a measure for the number of contacts between primary soot particles and increases with compaction.
We apply the soot-PCF framework, developed based on ice nucleation measurements of well-characterised soot particles using a continuous flow diffusion chamber, to particles with properties characteristic for aircraft soot. The probability of a soot particle to contain a ring pore with N members depends on the number of spherical primary particles making up a soot aggregate, Np, which in turn depends on the primary particle diameter, Dp, the gyration diameter, Dg, and the aggregate fractal dimension, δ:
where D is the dry mobility diameter and k0 is a scaling factor. For diffusion-limited cluster-cluster aggregation, k0 = 1.3 and δ = 1.78 54. Sizes of primary aircraft soot particles depend on the engine thrust level and the type of fuel burnt. We choose Dp = 20 nm to calculate Np as a function of D, which reflects the predominant primary size of soot particles emitted at cruising thrust50. The fraction of soot aggregates with a given mobility diameter D that activates at ice supersaturation s, the s-cumulative ice-active fraction (AF), depends on Np, on the ice-active site probability function, PN, denoting the probability of a primary particle to be part of a ring pore inducing PCF at s, and on the number of neighbouring particles, N, of each primary particle:
The exponent α quantifies the probability that a soot aggregate contains a primary particle within a ring structure21; subtracting N from Np avoids overcounting ring structures. We choose N = 2, reflecting the minimum number of three primary particles to form a three-membered ring pore. The fact that AF is cumulative in s reflects laboratory measurements in which the ice nucleation activity of an aerosol sample is often probed at successively increasing supersaturation.
Knowledge of PN is sufficient to describe the ice activity of soot aggregates with different sizes from the same emission source, assuming the same contact angle21. To represent contrail-processed aircraft soot, PN is compatible with the primary particle size distribution measured at 65% thrust level when burning standard Jet A-1 fuel50. The PN covers supersaturation-dependent activation probabilities by three-membered and four-membered ring pores with primary soot particle diameters and overlaps ranging from 5 to 40 nm and 0.01 to 0.2, respectively, and is fitted as:
with a = 0.378 and b = −0.462 for a soot-water contact angle, θ, of 60°.
Role of soot particle ageing
Ice-active soot particle fractions exhibit a marked dependence on θ, which can be affected by atmospheric ageing processes. Ageing of soot particles impacts their ability to influence clouds and climate55 and predominantly occurs via (i) condensation of semi-volatile compounds, (ii) coagulation with ambient aerosol particles and (iii) oxidation from the gas phase56. While monolayer sulphuric acid (H2SO4) coatings have little effect for heterogeneous ice nucleation on soot particles57, the ability of PCF is significantly reduced if soot pores are filled with H2SO4 or organic carbon58,59 via processes (i) and (ii). If soot particles obtain thick (multilayer) coatings, the ice nucleation mode shifts from PCF to immersion freezing, where soot is an inefficient INP11,57,59. Therefore, only the ageing process (iii) is capable of enhancing PCF efficiency by decreasing θ.
Data of experimentally determined contact angles relating to aircraft soot are scarce. We first discuss soot-water contact angles associated with unaged soot particles. Persiantseva et al.60 produced soot particles in a gas-turbine combustion chamber setup by burning propane-butane mixtures, mimicking aircraft cruise combustion conditions, and found θ = 63°. The same study reported higher values (70°–80°) when burning the aviation fuels TC1 (fuel sulphur content > 0.11 wt%), T6 (0.05 wt%) and kerosene in an oil lamp setup. Contact angles were found to decrease for TC1 and kerosene soot only after heating and outgassing, processes that are not relevant for the upper troposphere. Using the same technique, Popovicheva et al.61 found θ = 59° ± 4° and 69° ± 4° when burning freshly prepared TC1 and long-time stored (oxidised) TC1 kerosene, respectively. A value of 59° was found for TS1 kerosene fuel using the same approach62. Shonija et al.63 found the contact angle of fresh TC1 soot to be 69°. Significantly higher values (≈ 97°–107°) were reported for unaged kerosene soot64.
We now address how ageing via gas-phase oxidation (process (iii)) might affect θ. Wei et al.64 found θ to decrease by ≈5–10° after exposing kerosene soot to ozone mixing ratios of 40 ppb over a period of ten days, which is at the high end of tropospheric soot particle lifetimes of ≈3–11 d 56. Following ref. 64 and doubling the ozone mixing ratio to 80 ppbv to account for mixing of upper tropospheric and lower stratospheric air masses, θ might decrease by ≈15–20° over 10 d. Lifetimes in the upper troposphere and tropopause region can be longer, especially for particles emitted at high altitudes as in the case of aircraft emissions. Doubling the lifetime to 20 d with 40 ppbv of ozone would lead to the same decrease. However, ageing of aircraft-emitted soot particles already occurs in evolving exhaust plumes26 via condensation of H2SO4 formed by oxidation of SO2 vapour from the exhaust (process (i)) and coagulation with liquid ambient and plume aerosol particles (process (ii)). Sulphuric acid hardly oxidises soot surfaces65; therefore, exposure to H2SO4 has next to no effect on θ. Moreover, a H2SO4 coating shields the soot surface preventing oxidation from ozone66. Overall, this limits the time available to reduce θ via ozone oxidation to 1–2 days depending on jet fuel sulphur content and ambient aerosol load26; the above rough estimates for reductions in θ reduce to a few degrees. In summary, our default value of 60° for unaged aircraft soot, which is already at the low end of data, would decrease only slightly.
Some fraction of aircraft soot emissions are emitted above the tropopause with residence times that can be longer than the 10–20 days assumed here. Contrails form less frequently in the dry lowermost stratosphere2, so that soot particles emitted there do not frequently get ice-active to begin with. The contribution of stratospherically aged soot particles to ice formation via PCF is likely negligible due to condensation of H2SO4 and coagulation with particles in aircraft exhaust plumes and from the H2SO4/H2O background aerosol. Additional work is needed to better constrain the lifetime and properties of soot particles depending on the location of emissions. This will ultimately allow to fully establish the ice-active contribution of aged soot particles from aviation to cirrus formation.
Since AF depends strongly on soot aggregate size, PSDs play a crucial role. Supplementary Fig. 1 shows that most aircraft soot aggregates are not significantly larger than typical primary particles (20 nm) and only some exceed mobility diameters of 200 nm (panel a). Ice activity is negligible (AF < 0.001) for θ = 60° and soot particles with diameters up to about 40 nm. Full activation (AF → 1) is predicted for D > 200 nm only at high ice supersaturation (panel b). The ice-active PSDs, obtained by multiplying AF with the soot PSD (normalised to unity), show that PCF maximises for D ≈ 90 nm (panel c). Integrating over all sizes, we find that only a minor fraction, f, of emitted soot particles can become ice-active, depending on s (panel d). Values larger than f = 0.01 are not achieved owing to homogeneous ice nucleation and growth.
Ice activity spectra
The dependence of ice-active soot particle fractions on ice supersaturation is given by integrating the ice-active PSDs shown in Supplementary Fig. 1c over all sizes:
using normalised PSDs. Results of sensitivity studies with several observed size distributions using the default contact angle of 60° show that the bimodal PSDs from refs. 47,48 cause much fewer ice-active particle fractions across all supersaturations as compared to our default upper-limit monomodal PSD due to smaller abundances of large particles (Supplementary Fig. 2). Clearly, PSDs are crucial for accurately representing soot–cirrus interactions in models.
Results of sensitivity studies with different contact angles are also shown. Increasing θ by 10° to a value of 70° renders ice activity negligible for both monomodal PSDs. We also show results of an extreme case with θ decreased by 15° to a value of 45°, greatly overestimating the effect of large-scale soot ageing via ozone oxidation by dismissing the possibility of turning externally mixed soot emissions into internally mixed particles already on the plume scale. As a result, the ice activity spectra peak at 5.5 (0.6)% for the upper-limit (lower-limit) PSD. More frequently observed aircraft soot PSDs, characterised by average parameters46, Dm ≈ 29 nm and σ ≈ 1.7, would yield peak ice activity fractions near 1%, similar to our simulation scenarios. We conclude that the effects of atmospheric ageing on the ice activity of aircraft soot particles are most likely negligible and that our conclusions hold true for both unaged and aged particles.
Total ice-active soot particle number concentrations
To obtain analytical estimates of soot particle number concentrations that are ice-active at ice supersaturation s at a given time past emission, we multiply f(s) with ntot(t). For Dm = 35.7 nm, σ = 1.8, θ = 60° and s = 0.5, this results in f = 0.01 (Supplementary Figs. 1d and 2), i.e. at most 1% of the emitted soot particles are ice-active. When taken at tp = 0.5 h and tb = 5 h, values f · ntot indicate the magnitude of the largest possible perturbation in scenarios Plume (≈54 L−1) and Background (≈5 L−1), respectively (Supplementary Fig. 3). As the numerical simulations start at ice saturation, additional dilution of soot particles until homogeneous freezing commences is not included in these analytical estimates.
A note on pre-activation
Porous particles such as soot can potentially also form cloud ice crystals via pre-activation. Pre-activation occurs when ice from a previous ice nucleation event is retained in aggregates within nanometre-sized pores at temperatures below the bulk melting point and below ice saturation. The ice phase may then grow upon re-encountering sufficiently high ice supersaturation. Hence, pre-activation describes an ice growth process circumventing the freezing nucleation step. Since homogeneous freezing rates of liquid pore water are high at cirrus temperatures, PCF is constrained either by water condensation into wider pores or ice growth out of narrower pores. Therefore, pre-activation is not relevant when ice growth limits PCF, as is the case for the narrow three-membered and four-membered ring pores that occur when the overlap between primary particles is large. Moreover, when PCF is limited by water condensation, pore ice sublimates already at slight ice subsaturation (s < 0). We, therefore, consider the effect of pre-activation negligible for the pore types that dominate ice formation via PCF in aircraft soot aggregates21.
Implementation of ice-active fractions in the cirrus model
In the numerical simulations, soot particle number concentrations as small as 0.1 (0.01) L−1 are resolved in scenario Plume (Background) and converted to simulation ice particles once they become ice-active. These low threshold number concentrations ensure that ice crystal formation is simulated in soot particles with mobility diameters as low as about 40 nm.
We would overestimate soot-derived ICNCs significantly in our numerical simulations when using the s-cumulative AF parametrization, Eq. (2), because soot particles are depleted from the PSD after previous ice formation events. Instead, we estimate the number fraction of particles that activate during a small increase in ice supersaturation (determined by the model time step that is subject to accuracy constraints) in a given size range (determined by the soot PSD that is discretised with fine size resolution, ΔD/D = 0.135) from a parametrization of differential AF, dAF, consistent with the cumulative AF.
To derive dAF, it is convenient to view the s-cumulative AF as the probability to activate aircraft soot particles of size D, resulting from the statistical outcome of many identically prepared laboratory measurements. Defining Δsj = sj − sj−1, with s0 = 0 and AF(s0) = 0, dropping D from the argument list and noting that dAF(sj) shall describe the fraction of soot particles frozen only within Δsj, the total fraction frozen at sj is given by those particles that did not activate into ice (with probability 1 − dAF(sj)) in every interval Δsj prior to sj:
With dAF(s1) = AF(s1), dAF(sj)-values for j > 1 are obtained by recursion. In the simulations, we used constant intervals, Δsj = 0.01.
Data availability
The data that support the findings of this study are available in Zenodo with the identifier https://doi.org/10.5281/zenodo.4709994.
Code availability
A full description of the cirrus cloud model employed in this study is available at https://doi.org/10.1029/2019JD031847. The source code is not publicly available.
References
Fahey, D. W. & Schumann, U. in Aviation and the Global Atmosphere. A Special Report of IPCC Working Groups I and III. Intergovernmental Panel on Climate Change (ed. Penner, J. E.) (Cambridge University Press, 1999).
Kärcher, B. Formation and radiative forcing of contrail cirrus. Nat. Commun. 9, https://doi.org/10.1038/s41467-018-04068-0 (2018).
Lee, D. S. et al. The contribution of global aviation to anthropogenic climate forcing for 2000 to 2018. Atmos. Environ. 244, https://doi.org/10.1016/j.atmosenv.2020.117834 (2021).
Tesche, M., Achtert, P., Glantz, P. & Noone, K. J. Aviation effects on already-existing cirrus clouds. Nat. Commun. 7, https://doi.org/10.1038/ncomms12016 (2016).
Bock, L. & Burkhardt, U. Contrail cirrus radiative forcing for future air traffic. Atmos. Chem. Phys. 19, https://doi.org/10.5194/acp-19-8163 (2019).
Le Quéré, C. et al. Temporary reduction in daily global CO2 emissions during the COVID-19 forced confinement. Nat. Clim. Chang. 10, https://doi.org/10.1038/s41558-020-0797-x (2020).
Toon, O. B. & Miake-Lye, R. C. Subsonic Aircraft: Contrail and Cloud Effects Special Study (SUCCESS). Geophys. Res. Lett. 25, https://doi.org/10.1029/98GL00839 (1998).
Ström, J. & Ohlsson, S. In situ measurements of enhanced crystal number densities in cirrus clouds caused by aircraft exhaust. J. Geophys. Res. 103, https://doi.org/10.1029/98JD00807 (1998).
Urbanek, B. et al. High depolarization ratios of naturally occurring cirrus clouds near air traffic regions over Europe. Geophys. Res. Lett. 45, https://doi.org/10.1029/2018GL079345 (2018).
Jensen, E. J. & Toon, O. B. The potential impact of soot particles from aircraft exhaust on cirrus clouds. Geophys. Res. Lett. 24, https://doi.org/10.1029/96GL03235 (1997).
Kanji, Z. A., Welti, A., Corbin, J. C. & Mensah, A. A. Black carbon particles do not matter for immersion mode ice nucleation. Geophys. Res. Lett. 47, https://doi.org/10.1029/2019GL086764 (2020).
Schill, G. P. et al. The contribution of black carbon to global ice nucleating particle concentrations relevant to mixed-phase clouds. Proc. Natl. Acad. Sci. USA 117, https://doi.org/10.1073/pnas.2001674117 (2020).
Mahrt, F. et al. Ice nucleation abilities of soot particles determined with the Horizontal Ice Nucleation Chamber. Atmos. Chem. Phys. 18, https://doi.org/10.5194/acp-18-13363-2018 (2018).
Nichman, L. et al. Laboratory study of the heterogeneous ice nucleation on black-carbon-containing aerosol. Atmos. Chem. Phys. 19, https://doi.org/10.5194/acp-19-12175-2019 (2019).
Marcolli, C. Deposition nucleation viewed as homogeneous or immersion freezing in pores and cavities. Atmos. Chem. Phys. 14, https://doi.org/10.5194/acp-14-2071-2014 (2014).
David, R. O. et al. Pore condensation and freezing is responsible for ice formation below water saturation for porous particles. Proc. Natl. Acad. Sci. USA 116, https://doi.org/10.1073/pnas.1813647116 (2019).
Mahrt, F. et al. The impact of cloud processing on the ice nucleation abilities of soot particles at cirrus temperatures. J. Geophys. Res. 124, https://doi.org/10.1029/2019JD030922 (2020).
Petzold, A. et al. Ice-supersaturated air masses in the northern mid-latitudes from regular in situ observations by passenger aircraft: vertical distribution, seasonality and tropospheric fingerprint. Atmos. Chem. Phys. 20, https://doi.org/10.5194/acp-20-8157-2020 (2020).
Burkhardt, U., Bock, L. & Bier, A. Mitigating the contrail cirrus climate impact by reducing aircraft soot number emissions. npj Clim. Atmos. Sci. 1, https://doi.org/10.1038/s41612-018-0046-4 (2018).
Kärcher, B. Process-based simulation of aerosol-cloud interactions in a one-dimensional cirrus model. J. Geophys. Res. 125, https://doi.org/10.1029/2019JD031847 (2020).
Marcolli, C., Mahrt, F. & Kärcher, B. Soot-PCF: pore condensation and freezing framework for soot aggregates. Atmos. Chem. Phys. Discuss. https://doi.org/10.5194/acp-2020-1134 (2020).
DeMott, P. J. et al. Measurements of the concentration and composition of nuclei for cirrus formation. Proc. Natl. Acad. Sci. USA 100, https://doi.org/10.1073/pnas.253267710 (2003).
Kärcher, B. & Podglajen, A. A stochastic representation of temperature fluctuations induced by mesoscale gravity waves. J. Geophys. Res. 124, https://doi.org/10.1029/2019JG030680 (2019).
Meerkötter, R. et al. Radiative forcing by contrails. Ann. Geophys. 17, https://doi.org/10.1007/s00585-999-1080-7 (1999).
Kärcher, B., Jensen, E. J. & Lohmann, U. The impact of mesoscale gravity waves on homogeneous ice nucleation in cirrus clouds. Geophys. Res. Lett. 46, https://doi.org/10.1029/2019GL082437 (2019).
Kärcher, B., Möhler, O., DeMott, P. J., Pechtl, S. & Yu, F. Insights into the role of soot aerosols in cirrus cloud formation. Atmos. Chem. Phys. 7, https://doi.org/10.5194/acp-7-4203-2007 (2007).
Hoose, C. & Möhler, O. Heterogeneous ice nucleation on atmospheric aerosols: a review of results from laboratory experiments. Atmos. Chem. Phys. 12, https://doi.org/10.5194/acp-12-9817-2012 (2012).
Minikin, A. et al. Aircraft observations of the upper tropospheric fine particle aerosol in the Northern and Southern Hemispheres at midlatitudes. Geophys. Res. Lett. 30, https://doi.org/10.1029/2002GL016458 (2003).
Zhou, C. & Penner, J. E. Aircraft soot indirect effect on large-scale cirrus clouds: is the indirect forcing by aircraft soot positive or negative? J. Geophys. Res. 119, https://doi.org/10.1002/2014JD021914 (2014).
Penner, J., Zhou, C., Garnier, A. & Mitchell, D. L. Anthropogenic aerosol indirect effects in cirrus clouds. J. Geophys. Res. 123, https://doi.org/10.1029/2018JD029204 (2018).
Zhu, J. & Penner, J. E. Radiative forcing of anthropogenic aerosols on cirrus clouds using a hybrid ice nucleation scheme. Atmos. Chem. Phys. 20, https://doi.org/10.5194/acp-20-7801-2020 (2020).
Gettelman, A. & Chen, C. The climate impact of aviation aerosols. Geophys. Res. Lett. 20, https://doi.org/10.1002/grl.5052 (2013).
Pitari, G. et al. Impact of coupled NOx/aerosol aircraft emissions on ozone photochemistry and radiative forcing. Atmosphere 6, https://doi.org/10.3390/atmos6060751 (2015).
Liu, X. & Penner, J. E. Ice nucleation parameterization for global models. Meteorol. Z. 14, https://doi.org/10.1127/0941-2948/2005/0059 (2005).
Irvine, E. A., Hoskins, B. J. & Shine, K. P. A Lagrangian analysis of ice-supersaturated air over the North Atlantic. J. Geophys. Res. 119, https://doi.org/10.1002/2013JD020251 (2013).
Harrington, J. Y., Moyle, A. & Hanson, E. On calculating deposition coefficients and aspect ratio evolution in approximate models of ice crystal vapor growth. J. Atmos. Sci. 76, https://doi.org/10.1175/JAS-D-18-0319.1 (2019).
Sölch, I. & Kärcher, B. A large-eddy model for cirrus clouds with explicit aerosol and ice microphysics and Lagrangian ice particle tracking. Q. J. Roy. Meteorol. Soc. 136, https://doi.org/10.1002/qj.689 (2010).
Schäfler, A. et al. The North Atlantic waveguide and downstream impact experiment. Bull. Amer. Meteor. Soc. 99, https://doi.org/10.1175/BAMS-D-17-0003.1 (2018).
Petters, M. D. & Kreidenweis, S. M. A single parameter representation of hygroscopic growth and cloud condensation nucleus activity. Atmos. Chem. Phys., 8, https://doi.org/10.5194/acp-7-1961-2007 (2008).
Schröder, F., Kärcher, B., Fiebig, M. & Petzold, A. Aerosol states in the free troposphere at northern midlatitudes. J. Geophys. Res. 107, https://doi.org/10.1029/2000JD000194 (2002).
Kärcher, B. & Lohmann, U. A parameterizationof cirrus cloud formation: Homogeneous freezing of supercooled aerosols. J. Geophys. Res. 107, https://doi.org/10.1029/2001JD000470 (2002).
Hoyle, C. R., Luo, B. P. & Peter, T. Theorigin of high ice crystal number densities in cirrus clouds. J. Atmos. Sci. 62, https://doi.org/10.1175/JAS3487.1 (2005).
Kay, J. E. & Wood, R. Timescale analysis ofaerosol sensitivity during homogeneous freezing and implications for uppertropospheric water vapor budgets. Geophys. Res. Lett. 35, https://doi.org/10.1029/2007GL032628 (2008).
Zhang, X., Chen., X. & Wang, J. A number-based inventory of size-resolved black carbon particle emissions by global civil aviation. Nat. Commun. 10, https://doi.org/10.1038/s41467-019-08491-9 (2019).
Teoh, R. et al. A methodology to relate black carbon particle number and mass emissions. J. Aerosol Sci. 132, https://doi.org/10.1016/j.jaerosci.2019.03.006 (2019).
Moore, R. H. et al. Biofuel blending reduces particle emissions from aircraft engines at cruise conditions. Nature 543, https://doi.org/10.1038/nature21420 (2017).
Petzold, A., Ström, J., Ohlsson, S. & Schröder, F.-P. Elemental composition and morphology of ice crystal residual particles in cirrus clouds and contrails. Atmos. Res. 49, https://doi.org/10.1016/S0169-8095(97)00083-5 (1998).
Petzold, A., Döpelheuer, A., Brock, C. A. & Schröder, F. In situ observations and model calculations of black carbon emission by aircraft at cruise altitude. J. Geophys. Res. 104, https://doi.org/10.1029/1999JD900460 (1999).
Hagen, D. E., Whitefield, P. D. & Schlager, H. Particulate emissions in the exhaust plume from commercial jet aircraft under cruise conditions. J. Geophys. Res. 101, https://doi.org/10.1029/95JD03276 (1996).
Liati, A. et al. Electron microscopic study of soot particulate matter emissions from aircraft turbine engines. Environ. Sci. Technol. 48, https://doi.org/10.1021/es501809b (2014).
Kärcher, B., Burkhardt, U., Bier, A., Bock, L. & Ford, I. J. The microphysical pathway to contrail formation. J. Geophys. Res. 120, https://doi.org/10.1029/2015JD023491 (2015).
Marcolli, C. Technical note: fundamental aspects of ice nucleation via pore condensation and freezing including Laplace pressure and growth into macroscopic ice. Atmos. Chem. Phys. 20, https://doi.org/10.5194/acp-20-3209-2020 (2020).
Rockne, K. J., Taghon, G. L. & Kosson, D. S. Pore structure of soot deposits from several combustion sources. Chemosphere 41, https://doi.org/10.1016/S0045-6535(00)00040-0 (2000).
Sorenson, C. M. The mobility of fractal aggregates: a review. Aerosol Sci. Technol. 45, https://doi.org/10.1080/02786826.2011.560909 (2011).
Lohmann, U. et al. Future warming exacerbated by aged-soot effect on cloud formation. Nat. Geosci. 13, https://doi.org/10.1038/s41561-020-0631-0 (2020).
Bond, T. C. et al. Bounding the role of black carbon in the climate system: A scientific assessment. J. Geophys. Res. 118, https://doi.org/10.1002/jgrd.50171 (2013).
DeMott, P. J., Chen, Y., Kreidenweis, S. M., Rogers, D. C. & Sherman, D. E. Ice formation by black carbon particles. Geophys. Res. Lett. 26, https://doi.org/10.1029/1999GL900580 (1999).
Zhang, C. et al. The effects of morphology, mobility size and SOA material coating on the ice nucleation activity of black carbon in the cirrus regime. Atmos. Chem. Phys. 20, https://doi.org/10.5194/acp-2020-809 (2020).
Crawford, I. et al. Studies of propane flame soot acting as heterogeneous ice nuclei in conjunction with single particle soot photometer measurements. Atmos. Chem. Phys. 11, https://doi.org/10.5194/acp-11-9549-2011 (2011).
Persiantseva, N. M., Popovicheva, O. B. & Shonija, N. K. Wetting and hydration of insoluble soot particles in the upper troposphere. J. Environ. Monit. 6, https://doi.org/10.1039/B407770A (2004).
Popovicheva, O. et al. Effect of soot on immersion freezing of water and possible atmospheric implications. Atmos. Res. 90, https://doi.org/10.1016/j.atmosres.2008.08.004 (2008).
Kireeva, E. D., Popovicheva, O. B., Persiantseva, N. M., Khokhlova, T. D. & Shonija, N. K. Effect of black carbon particles on the efficiency of water droplet freezing. Colloid J. 71, https://doi.org/10.1134/s1061933x09030090 (2009).
Shonija, N. K., Popovicheva, O. B., Persiantseva, N. M., Savel’ev, A. M. & Starik, A. M. Hydration of aircraft engine soot particles under plume conditions: Effect of sulfuric and nitric acid processing. J. Geophys. Res. 112, https://doi.org/10.1029/2006JD007217 (2007).
Wei, Y., Zhang, Q. & Thompson, J. E. The wetting behavior of fresh and aged soot studied through contact angle measurements. Atmos. Clim. Sci. 7, https://doi.org/10.4236/acs.2017.71002 (2017).
Zhang, D. & Zhang, R. Laboratory investigation of heterogeneous interaction of sulfuric acid with soot. Environ. Sci. Technol. 39, https://doi.org/10.1021/es050372d (2005).
Ray, D. et al. Hygroscopic coating of sulfuric acid shields oxidant attack on the atmospheric pollutant benzo(a)pyrene bound to model soot particles. Sci. Rep. 8, https://doi.org/10.1038/s41598-017-18292-z (2018).
Acknowledgements
We thank Andreas Schäfler and Christoph Kiemle for providing us with in situ measurements of vertical profiles of moisture and temperature. We gratefully acknowledge David Fahey for commenting on the manuscript. F.M. received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant Agreement No. 890200.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
B.K. designed the research, carried out the simulations and wrote the original manuscript. F.M. composed the storyline graphic. C.M. and F.M. devised and developed the parametrization of aircraft soot-induced ice formation and growth. All authors jointly discussed the overall concept and methods, interpreted the simulation results and contributed to the final writing.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Primary handling editor: Heike Langenberg.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kärcher, B., Mahrt, F. & Marcolli, C. Process-oriented analysis of aircraft soot-cirrus interactions constrains the climate impact of aviation. Commun Earth Environ 2, 113 (2021). https://doi.org/10.1038/s43247-021-00175-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-021-00175-x
This article is cited by
-
High-precision standard enthalpy of formation for polycyclic aromatic hydrocarbons predicting from general connectivity based hierarchy with discrete correction of atomization energy
Frontiers of Chemical Science and Engineering (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.