Introduction

The largest repository of fresh water on the planet, equivalent to 58 m global sea-level rise, is locked up in the Antarctic Ice Sheet, with a mass balance governed by the processes at the interface between ice, atmosphere, ice-sheet bed, and ocean1. Remote sensing has greatly improved observational records over the last decades, and concomitant advances in numerical modelling now provide plausible predictions on the response of the ice sheet to climate change2. Whereas the large-scale atmospheric and oceanographic drivers affecting ice-sheet dynamics appear well constrained, large uncertainties still remain in parametrizing the small-scale processes at the boundary between the ice, the ice-sheet bed, and the ocean3, such as the presence and movement of liquid subglacial water and the feedbacks of subglacial hydrology, temperature, and pressure on basal sliding at the ice-bed interface4. Observational data are needed to improve our understanding of these critical processes, reduce the uncertainties in the models, and achieve better predictions. However, groundtruthing is a logistical challenge because the base of the ice sheet is buried under hundreds to thousands of metres of ice, and for much of the Antarctic, extensive ice shelves impede access to the grounding zone5. Major drilling expeditions have been carried out to access the base of the ice sheet and the grounding zone in some of the large ice shelves and glaciers. They yielded ice cores with laminated ice facies6,7, samples of subglacial water8 as well as remotely operated vehicle (ROV)9, and borehole camera images of the seafloor showing a strong biological connection between the glacial and the open-water marine environment10,11,12.

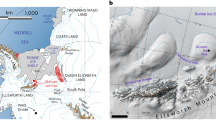
Grounding zones are located up-ice of the calving front along ice shelves, but in areas with low ice-flow rates relative to rates of marine melting and calving, the grounded ice sheet ends abruptly as a vertical cliff or tidewater terminus13. Whereas tidewater cliffs offer direct access to the grounding zone, ice fall from an unstable calving front is a threat that has so far discouraged ice- or ship-based explorations. During RV Polarstern cruise PS111, we were able to approach to less than 50 m of the Coats Land coast (Fig. 1), one of the few sectors in the Weddell Sea that features a tidewater ice cliff, providing a rare opportunity to explore the grounding zone. Here, we combine ROV observations of the ice cliff and seafloor, hydrographic measurements, and available ice sheet and topography data to provide an integrated glacio-marine and ecological perspective of the grounding zone of an Antarctic tidewater ice cliff.

Fig. 1: Study area in the Weddell Sea sector of Antarctica.
figure 1

a Ice shelves fringe most of the coast with the exception of Coats Land and Berkner Island where the ice sheet terminates in a grounded tidewater ice cliff. Red dot marks the ROV dive site in this and the following panels. b Basal ice-sheet topography59 of Coats Land showing the land barrier (brown colours) buttressing the flow of the ice sheet (black arrows) into the ocean (blue colours). The calving front is indicated by the white line. c, d Close-ups of the study area. c Ice-flow field with underlying bathymetry. Depth-contour intervals (black lines) are 50 m and flow velocities are colour coded. CTD station and Parasound sub-bottom acoustic profiles are indicated by green and brown symbols, respectively (see also Supplementary Fig. 6). d Ice front (IF) at the time of the study (greyscale satellite image), 2 yr before (white line), and extrapolated (eIF) from white line and ice flow (blue line). In the southern part of the image, the modelled ice front (blue line) is nearly identical with the calving front encountered during the study, while part of the northern section has been lost by calving. The grounded iceberg off the calving front and its likely former position in the calving front are shown (orange contour). e ROV track along the grounding zone and offshore showing the stages of benthic recolonization in colour. Richer communities were found outside the calving front 2 yr before (white line). Arrows indicate direction of scour marks. See the main text for details and data sources23,24,25,59,61,62,63. For the digitized ice fronts and extrapolation, see also Supplementary Data 3 and 4.

Full size image

Results and discussion

Grounding zone

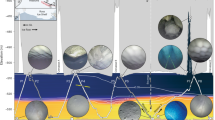
A ROV, equipped with high-definition cameras and oceanographic sensors, was deployed along a tidewater ice cliff. The entire face of the white meteoric ice showed the typical scalloped melt cups14. At a depth of 148 m, we reached the base of the cliff marking the grounding zone—the junction between the grounded ice, the seafloor, and the ocean15 (Fig. 2a). Photogrammetric reconstruction of a 4 × 1 × 1 m section of the grounding zone showed a 0.3–0.5 m gap between the base of the ice and the seafloor (Figs. 2 and 4b).

Fig. 2: Grounding zone image and model.
figure 2

a Still image of the ice-cliff base and adjacent seafloor showing the white meteoric ice underlain by a transparent facies of basal ice. The seafloor is barren with compacted till and thin sediment drape. Adult fish (Pagothenia borchgrevinki, foreground) were common, sessile fauna extremely scarce. b Digital model of the grounding zone revealing the dimensions of basal facies thickness and gap height. An interactive 3D-model is available in Supplementary Data 7.

Full size image

A striking discovery was a 0.4 m facies of transparent ice frozen to the base of the white meteoric ice (Fig. 2). Video close-ups showed it was bubble-free and largely devoid of debris (Supplementary Movie 1). The abrupt transition and absence of bubbles clearly identifies the basal ice as being derived from freeze-on16. The lack of debris in the clear facies indicates a subglacial hydraulic system providing sufficient pressure to separate the ice from the bed. Its homogeneity and thickness implies that water supply and pressure were sustained for prolonged periods of time. Transparent ice facies, albeit of lesser thickness, have been found in slow-16 and fast-moving ice streams17,18. However, an important difference in our study is the lack of multilayered basal ice: we found only the transparent facies but no alternating facies of clear and debris-laden ice7,19. The only incidence of debris in 90 m of inspected ice front is a small spot in the meteoric ice, i.e., above the transparent facies (Supplementary Fig. 5).

The base of the transparent ice was square-edged, and its surface on the underside and side lacked the scalloped melt cusps of the meteoric ice. The interface separating the meteoric from the transparent ice facies showed undulations that could be the line of contact between the meteoric ice and the bed, prior to freeze-on (Fig. 2a). In contrast to the undulations in the interface between the ice facies, the bottom of the basal ice was level, causing a total reflection of the seafloor like a mirror (Supplementary Fig. 2). The flat surface and absence of melt cusps suggests that the basal ice is harder than the meteoric ice and/or is less affected by turbulent flow14.

Dynamics of the calving front

Coats Land bed topography acts like a barrier buttressing the ice sheet, with mountains at the coast (Fig. 1b). Ice-flow velocities are extremely low: inverse modelling shows that it takes the ice more than 3500 yr to travel the final 18 km to the calving front (Fig. 3b and Supplementary Data 5). The observed increase in velocity toward the terminus causes thinning of the terminal 6–7 km of the ice sheet to about half of its former thickness (Fig. 3a). For a tidewater ice cliff in hydrostatic equilibrium at a seawater density of 1028 kg m−3 (Supplementary Fig. 3), a thickness of 170 m, and a freeboard of 20.8 ± 0.7 m (Supplementary Fig. 4), we calculate an average density of meteoric ice of 901 kg m−3. This is much more than the average density of tabular icebergs in the Weddell Sea (845 kg m−3; n = 24, ref. 20) and implies compaction of the ice in this slow-moving part of the ice sheet. If the reported ice density value20 is correct, however, the difference between ice thickness and floatation thickness suggests that the ice front can accommodate non-hydrostatic water pressures and was depressed below hydrostatic equilibrium. Finite element analysis (FEA) of ice sheet deflection (Supplementary Fig. 8) shows a maximum spring tidal flexure at the calving front of only 2 mm—much less than the observed gap beneath the ice (0.3–0.5 m) and the high tide at the time of our study (0.54 m), as determined from the Tide Model Driver (TMD 2.5)21,22 (Supplementary Fig. 1 and Supplementary Data 6). Unless the integrity of the ice sheet is compromised by fracture, we thus expect no tidal variations in grounding line position and, hence, no tidal pumping, at the tidewater terminus. The final kilometre features deep crescent shaped crevasses parallel to the ice front (Fig. 1c, d). We propose calving of ice bands according to the spacing of crevasses (~150 m) in the terminal section of the ice sheet (Fig. 1d). As the ice front advances 29.8 m yr−1 (Fig. 1c), calving is triggered, on average, every 5 yr. Figure 1d shows the satellite image acquired on 24 February 2018, 5 days prior to our study, with (i) the position of the ice front, digitized from a satellite image taken roughly 2 yr before on the 31 December 2015 (white line) and (ii) the modelled ice front at the time of our study, derived from the 31 Dec 2015 position and the ice flow data (blue line)23,24,25 (Supplementary Data 3 and 4). The blue line shows a near perfect fit with the calving front in the southern two thirds of Fig. 1d, showing that the advance of the calving front is predicted very well by the flow model. The upper section of the figure shows that the calving front trails the blue line by 300 m. This part of the tidewater terminus must have disintegrated in the period between the two satellite images. The 300-m-wide grounded iceberg off the calving front is likely to have originated north-east of our study site (orange contour, Fig. 1d).

Fig. 3: Coats Land ice sheet model.
figure 3

a The block model showing the ice sheet on a seaward slope ending in a tidewater ice cliff, where the ROV dive was carried out (buoy and flag symbol). Note the inflection point (Ip) on the surface of the ice sheet marking the transition between the terrestrial and marine portion of the ice sheet. As the ice sheet is buoyed up it tapers out. b Satellite image with flow lines (red) showing the time period it took the ice to complete its trajectory to the study site. Note that the ice speeds up almost fivefold in the marine portion of the ice sheet (see text for details and data sources23,24,25,59,64,65 and Supplementary Data 5 for the model). c Relation between friction (grey line), ice velocity (black line), and ice accretion (blue line) along the flow line from the upper catchment (−17 km) to the study area (origin), showing initiation of ice accretion near the subglacial shoreline (vertical dash-dot line 6 km from the calving front) 400 yr ago. Twofold differences in friction between the terrestrial and the marine portions of the ice sheet (dark grey horizontal lines left and right of the subglacial shoreline) entail corresponding increases in ice velocities. Basal ice grows to 400 mm, assuming a conservative accretion rate of 1 mm yr−1.

Full size image

Basal ice origin

Two preconditions have to be met for basal freeze-on to occur: the availability of subglacial meltwater and temperatures below the pressure-melting point. We derive a maximum ice-sheet thickness along the path of the ice flow of 510 m (red line in Fig. 3b), corresponding to a −0.34 ∘C change in melting point26. Ice flow (~10 m yr−1, Fig. 1c) and associated deformation stress were assumed to be too low to have a significant effect on internal temperature increase27. Whether clean or dirty ice facies is formed depends on the relation between hydrostatic pressure of the meltwater and ice load: If the effective stress \(p^{\prime}\) (i.e. the difference between ice and water pressure) is lower than the regelation criterion (ζ = 100 kPa), clean facies is formed at rates of 1–4 mm yr−1 (ref. 19). If we discount the unknown portion of clean facies that was lost through melting in the grounding zone, the 0.4 m facies of clean ice we encountered corresponds to up to 400 yr of accretion, suggesting a groundwater source feeding the subglacial water system at a pressure allowing sustained freeze-on. We used an ice-sheet model to determine whether there is a sufficient large basal zone below the freezing point to produce the observed basal freeze-on layer. Friction was calculated as a function of shear stress, normal stress, and ice velocity, assuming ice density as a function of ice thickness (vertically homogeneous), and a linear friction law, where the friction factor was determined as a function of slope angle and ice velocity28. Cumulative ice growth (blue line in Fig. 3c) was calculated assuming an accretion rate of 1 mm yr−1. As the ice descends the seaward slope and reaches the ocean, it is buoyed up and loses friction with the seabed. We find that freeze-on was initiated about 6.5 km upstream, corresponding to the subglacial bed at sea level (Fig. 3c). Our model assumes the availability of subglacial meltwater in the marine portion of the ice sheet, which could be due to a dynamic equilibrium between a groundwater head supplied by meltwater and static seawater29.

Temperatures in the water column near the ice cliff are well above the freezing temperature of −1.93 ∘C for the range of salinities and pressures in our study, and we see that the data in the upper 10–40 m are closely aligned with the ratio predicted from melting ice into seawater (dashed line) on the SA–Θ diagram (Supplementary Fig. 7c)30,31. The salinities in the immediate vicinity of the ice cliff (black line, Supplementary Fig. 7b) are at or above the salinities measured in open water 250 m away32, but the temperatures are consistently lower in the top 40 m of the water column (black line, Supplementary Fig. 7a). Whereas ice melt is also demonstrated by the melt cusps in the ice cliff, the lack of a salinity gradient suggests no substantial discharge of freshwater at the grounding line. We could not find any indication (runnels, suspended matter)9 suggesting subglacial discharge along the 90 m of grounding line we inspected.

Seafloor

To assess how the decadal waxing and waning of the calving front affects the seafloor, we carried out a 230 m ROV transect normal to the grounding zone. We found a heavily scoured seafloor with half-buried boulders and clasts on the coarse-sediment surface. The slope of the seafloor (2.5%) was identical to the seaward slope under the ice sheet, suggesting a glacially levelled seafloor. Erosional planing of the seafloor is supported by observation and modelling. Deep subparallel scours running in a NWW direction along the ROV transect (Figs. 1e and 4d) mark previous advances of the ice terminus. FEA confirms an ice terminus advancing with insignificant lift or bending, consistent with a flat seafloor planed off by the advancing ice front (Supplementary Fig. 9). In order to determine origin and transport paths of the clasts encountered on the seafloor in the grounding zone, we analysed their shape after Powers33. The predominantly subrounded shape of the clasts (Supplementary Table 1) suggests that the clasts are derived from a basal zone of shearing and crushing34,35. A supraglacial origin can be ruled out by the lack of angular clasts and by the absence of nunataks or valley sides in the study region (Fig. 1). Subbottom acoustic profiling data showed strong surface reflectors, low penetration and no subbottom reflectors (Supplementary Fig. 6), confirming the visual impression of a glacially compacted till which is typical for shelf diamicton in the area36. At and near the calving front, sedentary fauna were rare: a large ascidian (Molgula sp.) was found between clasts under the calving front (Fig. 4b), occasional stalked ascidians and sponges (Homaxinella balfourensis) were found perched between clasts, polychaete tubes and bryozoans were scattered on the sides (but not: tops) of the clasts, covering less than 5% of the available surface (Supplementary Movie 1). All of the above pioneer species are fast-growing early colonizers of recent scour marks (stage 0)37,38. Mobile fauna included fish (adult Pagothenia borchgrevinki, occasional channichthyids), ophiuroids, and crinoids. At some 50 m distance from the calving front, the first patches of post-scour growth appeared (stage 1)37,38, featuring loose stands of H. balfourensis and bryozoans, bordering abruptly with barrens caused by iceberg scour (Fig. 4c). At the end of the transect, the ROV transited into the next post-scour successional stage (light green area, Fig. 1e, stage 2)37,38, featuring the appearance of the first gorgonians (Thouarella spp.), the first lollipop sponges (Stylocordyla chupachups), denser stands of H. balfourensis and epizooic holothurians on the upper parts of the gorgonians and rocks (Fig. 4d). The appearance of stage 2, which also harboured a denser fish fauna, corresponds to the maximum extent of ice at the end of 2015 (white line, Fig. 1e). We propose that this line is less frequently exceeded by the advancing calving front, so that it allows for more time of settlement by benthic fauna.

Fig. 4: Grounding zone biology.
figure 4

a Algal tufts rim the scalloped melt cusps on the ice cliff (20 m depth), many of which harbour juvenile fish (Pagothenia borchgrevinki, inset). b Sessile fauna is scarce (stage 0, Fig. 1e) in the grounding zone; only a large acidian (Molgula sp.) is visible in the background behind the ridge. c Early recolonization after scouring (stage 1, Fig. 1e) involves fast-growing demosponges (Homaxinella balfourensis). d Later stage of recolonization showing higher benthic cover (stage 2, Fig. 1e) with gorgonians (bottle-brushes), contrasting a scour mark devoid of benthos in the upper right of the panel (stage 0). Most of the organisms, including the feather-star (foreground) and the epizoic holothurians (white, background), are all suspension-feeding organisms that take advantage of the phytodetritus produced at the calving front.

Full size image

Ice cliff and water column biota

A surprising new finding, to the best of our knowledge, is the abundance of algal tufts lining the ridges separating the scalloped melt cusps of the meteoric ice (Fig. 4a), particularly in the upper marine part of the ice cliff (Fig. 5a). The ice itself showed no trace of pigmentation, suggesting that drifting phytoplankton (not sympagic algae) seeded the growth of algal tufts on the submarine ice cliff face. Given the dominance of chain-forming diatoms in Weddell Sea phytoplankton blooms39, we propose that chain-forming diatoms drifting with the currents along the ice front get caught up in the open pores of the elevated ridges of the melting ice, where they proliferate under the relatively more favourable light, flow and nutrient environment. Particularly iron, a trace element limiting diatom growth in the Antarctic40, is known to be released from melting meteoric ice41 encouraging diatom "superblooms” near the calving front39,42. These conditions may have favoured the proliferation of algal tufts in our study. Chlorophyll a concentrations in the water column show that a summer bloom was underway (Fig. 5b) with peak values (>1 mg m−3) at the thermo- and halocline at 20 m (Supplementary Fig. 3), corresponding to the highest levels that can be sustained in summer in open waters of the Weddell Sea43. The phytoplankton maximum coincides with the maximum of the algal tufts (Fig. 5a) and contributes to the maximum in oxygen concentration (Supplementary Fig. 3) due to photosynthesis44. The lower margin of the algal tufts at 90 m (Fig. 5a) marks the compensation depth44, where algal growth equals respiration, while phytoplankton concentrations remain high beyond the compensation depth down to the seabed, showing that the critical depth for the phytoplankton45 exceeded 148 m at the calving front. Because phytoplankton were abundant beyond the compensation depth, it shows also that the algal tufts are due to biological proliferation, not physical accumulation. The greenish tinge on the seafloor (Supplementary Movie 1) suggests that sinking phytodetritus from the ice cliff and/or water column accumulated in the grounding zone. Juvenile fish (Pagothenia borchgrevinki) were observed in the melt cusps of the meteoric ice (Fig. 4a, inset), supporting earlier ice shelf observations46. Whereas these carnivores are probably not consuming the algae, they are likely to take advantage of invertebrate prey47 associated with the tufts.

Fig. 5: Calving front primary producers.
figure 5

a Algal tufts abound in the upper marine part of the ice cliff (Supplementary Data 1). Their disappearance beyond 90 m marks the compensation depth. b High levels of chlorophyll a throughout the water column indicate a phytoplankton bloom with a critical depth reaching down to the seabed. Dots represent the 5 m binned means, error bars the standard deviations.

Full size image

Ice sheet—ocean and carbon pump

Coastal polynyas open up regularly around the Antarctic Ice Sheet, supporting one of the highest primary production rates in the Southern Ocean48, fuelled by glacial inputs of limiting iron41. The export of this biomass by sinking and downwelling in the coastal Southern Ocean is considered a global hotspot of carbon sequestration49. The flux of organic matter correlates well with the abundance of benthic suspension feeders50,51, while deposition and burial of food particles appears to be inversely related to their species richness51,52,53. Iceberg keel scouring reduces the biomass of benthic consumers54 and supports carbon deposition and burial51,52,53. A given seafloor location on the Antarctic continental shelf is disturbed by icebergs, on average, every 340 yr55,56. Scouring is much higher at our study site (once every 5 or 10 yr) leading to an extreme paucity of benthic consumers by Weddell Sea standards38, but also low relative to Mackay Glacier seafloor community in the Ross Sea, the only other Antarctic grounding zone study available9,57,58. We therefore postulate that a reduced mineralization of organic matter in combination with a high flux of phytodetritus from phytoplankton and ice cliff algae enhance organic carbon export and burial in the grounding zone49,53. As tidewater ice cliffs fringe 38% of the Antarctic coastline5, our findings have potential importance for carbon sequestration.

Implications for glaciology and biology

Our ROV dive to the tidewater ice cliff grounding zone of Coats Land in the Weddell Sea revealed a basal ice layer of exceptional transparency, an impoverished benthic fauna affected by scouring of the seafloor, and a rich flora on the calving front and in the water column, likely fuelled by glacial inputs of iron (Fig. 6). We show that the basal ice was formed by slow centuries-long freeze-on to an ice sheet lifted from its bed by liquid subglacial meltwater, most likely in the marine portion of the ice sheet (Figs. 3c and 6), which could be due to a meltwater head replacing denser seawater29. Traces of basal debris found in the meteoric ice above the clear ice layer support the hypothesis that the meteoric ice must have been in direct contact with the ice-sheet bed, before being wedged apart by basal freeze-on. Calving of icebergs occurs on average every 5–10 yr. The advancing ice front leads to heavy scouring of the seafloor, preventing the build-up of benthic biomass. Melt-derived nutrients and a favourable light environment support high growth rates of the phytoplankton and the ice cliff algae. Phytodetritus from both sources accumulates near the grounding zone in the absence of benthic consumers, increasing the availability of organic carbon for export and burial. By contributing to the control of the amount of the greenhouse gas CO2, the biological pump in grounding zones may play an important part in the global carbon cycle and in regulating climate49.

Fig. 6: Main findings of the Coats Land grounding zone study.
figure 6

Basal meltwater contributes to basal freeze-on in the marine portion of the ice sheet, where the ice is buoyed up, loses friction with the ice bed and speeds up. Continuous accretion of basal ice over 400 yr (6.5 km) contribute to the transparent facies of 400 mm at the calving front (blue layer at ice base). Basal debris picked up by the meteoric ice in the terrestrial part of the ice sheet melts out at the calving front. Melting releases dust-borne iron (Fe, green arrow) that fuels the growth of algae on the ice front and in the water column. Downwelling of High Salinity Shelf Water (HSSW) associated with sea-ice formation and sinking phytodetritus (black arrows), along with low mineralization by an impoverished benthos lead to a high export of organic matter. Debris, algae, and basal-ice layer not drawn to scale.

Full size image

Methods

Equipment

The study was conducted with a ROV (model V8Sii, Ocean Modules, Sweden) equipped with a 4k resolution camera (25 fps; 16 Mpx still option) 1Cam Mk6 (SubC Imaging, Canada). Environmental data were measured with a ROV-mounted 19plusV2 CTD (Seabird Electronics, USA). Polarstern’s onboard USBL-system (GAPS, iXblue, France) provided underwater positioning.

Determination of freeboard height

Freeboard height was derived from ROV video footage. The ROV was hovering over Polarstern’s working deck perfectly balanced (pitch 0∘) 5.6(±0.2) m above sea level, prior to deployment. Hence, distance between image centre and water surface was equal to ROV’s elevation. Freeboard of the ice front was approximated according to this reference (Supplementary Fig. 4).

Two-dimensional scaling

Reference lasers marked a distance of 10 cm vertically and horizontally. In cases where the lasers were not well reflected, i.e. on the ice’s surface, an altimeter was used to measure acoustically the distance from camera to the observed object. Length and areal scales were calibrated on images where lasers are clearly visible and no obstacle blocked the acoustic measurements.

$$w(x)=1.508x+0.192,\ ({R}^{2}=0.878)$$
(1)

Image width (w) was determined as a function of altimeter distance (x, in metres). Image height h was calculated as

$$h(x)=\frac{w(x)}{a}$$
(2)

where a = 16/9 represents the aspect ratio.

Tuft algae cover

Relative cover of algae attached to the ice front was derived from rgb (red green blue) standardized video images. The video footage was converted into a frame sequence (one frame per second, total 1158 images) at 4k resolution (3840 by 2160 px) using FFmpeg 3.4.8. by Fabrice Bellard. The changing illumination, from predominantly natural light near the surface to almost exclusively artificial light (LED of the ROV) at depth, required colour normalization of the images. This was done by substracting the overall average rgb value from the stack from the rgb value of the respective image. In order to reduce horizontal variations caused by spotlight illumination, towards the left and right border of each frame, this method was applied columnwise to the pixel matrix. Colour values were restricted to 8 bit integers with a lower and upper cut-off at 0 and 255. To differentiate algae from underlying ice, rgb images were converted into 8 bit hsv (hue saturation value) integers. Hue values less than 132 were considered as algae; hence, relative cover is the number of pixels for hue less than 132 divided by the number of image pixels. All calculations and conversions were made with scilab 6.0.2 and the IPCV 4.1.2 (Image Processing and Computer Vision) toolbox.

Three-dimensional reconstruction

Video footage was used for stereophotogrammetry. FFmpeg was used to convert the video files into 25 frames per second at 4k resolution (3840 × 2160). Four metres of grounding zone were reconstructed from 57 frames in Metashape v1.6.2(64 bit) from Agisoft (Supplementary file "GLineMeshImg.zip”). Frames were aligned sequentially with high accuracy, a key point limit of 1.5 M, and 50 k tie points. A dense cloud was built in medium quality and mild depth filtering. The mesh was reconstructed from the dense cloud with high face count setting. The resulting three-dimensional model was scaled to conform with the distance of 10 cm given by reference lasers. Local measurements could be taken on the scale-corrected model without distortions of images perspectives (Fig. 2b).

Ice-sheet modelling

Reverse flow lines

Rignot et al.24,25 and Mouginot et al.23 provide comprehensive flow-velocity data of the Antarctic Ice Sheet. Available north and east velocity fields are given in [m yr−1] on a 450 × 450 m grid. Values between grid points were linearly interpolated. Flow lines reflect the path ice travels along the velocity field. Flow downstream follows the velocity field forward in time, velocity vector \(\overrightarrow{u}\) and location \(\overrightarrow{p}\) of a ice portion are known. It is possible to predict where the ice will be after a given time step Δt. A reverse flow line goes back in time and looks for a location with its velocity that leads, in a given time, to the current position \({\overrightarrow{p}}_{m}={\overrightarrow{p}}_{m-1}+\overrightarrow{u}m-1{{\Delta }}t\) (m: time step index). Since previous location and corresponding velocity are unknown, Newton’s method was used to approximate the former location of an ice portion in an iterative loop (Eq. (3)). To do this for each year back in time, we need two interlaced loops: an outer loop (index m) which takes us back in time, year after year, and an inner loop which approaches the position within each time step for n iterations, until the residual 10−6 m yr−1 is reached. Exit condition for the outer loop was set to ice flow less than half a metre per year (\({\overrightarrow{u}}_{{\overrightarrow{p}}_{m-1}}<0.5\) m yr−1).

$${\overrightarrow{p}}_{m-1}^{\langle n+1\rangle }={\overrightarrow{p}}_{m}-\int \overrightarrow{u}{(t)}_{{\overrightarrow{p}}_{m-1}^{\langle n\rangle }}\ {\mathrm{d}}t$$
(3)

FE analysis of ice sheet flexure

Numerical FEA was used to determine the degree of ice-sheet bending caused by ice depressed below neutral buoyancy. Ice thickness was taken from the IBCSO bathymetric model59 along a cross section at the ROV site parallel to the ice flow. Water depth was derived from the IBCSO bathymetric bed model59 and adapted for a high-water and low-water spring tide level. Buoyancy of ice below sea level and weight of ice above sea level were calculated as a function of ice thickness H derived from ice densities presented by Orheim20 (Eq. (4)). Seawater density was taken from CTD data (Supplementary Fig. 3 and Supplementary Data 2) assuming a mixed water column ρwater = 1028 kg m−3. Difference of ice weight and replaced water is the effective load deflecting the ice (see Supplementary Figs. 8b and 9c). Load was applied in 50 m integrated intervals. Geometry of the ice sheet was built in FreeCAD version 0.19, meshed with Netgen, and solved by Calculix. Mesher and Solver are implemented in the FEA module of FreeCAD. Tetrahedra elements were generated using user defined settings of two segments per edge with a growth factor of 0.3. Differential equations were solved using the linear static method of Calculix, assuming the following values for Young’s modulus and Poisson’s ratio, respectively: (E = 9 GPa, ν = 0.3; ref. 60).

Ice density ρice was expressed as a function of ice thickness H derived from data given by Orheim20:

$${\rho }_{\mathrm{{ice}}}=527.062{H}^{0.090}\,({R}^{2}=0.976)$$
(4)

Ice thickness and water depths were determined as linearly regressed function along the ice cross section x. Origin of x was chosen at the ice front. Relation of ice thickness H (Eq. (5)), water depth Dh at high-water spring tide (Eq. (6)), and water depth Dl at low-water spring tide (Eq. (6)) was regressed over the last 1000 m of the ice sheet terminus.

$$H=-0.070x+172.620\,({R}^{2}=0.999)$$
(5)
$$\begin{array}{lll}{D}_{\mathrm{{h}}}&=&0.025x+149.710\,({R}^{2}=1.000)\\ {D}_{\mathrm{l}}&=&0.025x+146.710\,({R}^{2}=1.000)\end{array}$$
(6)

Ice load Fh, in [N], for high-water spring tide and Fl, in [N], for low-water spring tide are obtained by subtracting seawater weight from ice weight (g = 9.81 m s−2):

$$\begin{array}{lll}{F}_{\mathrm{h}}&=&(-H{\rho }_{\mathrm{{ice}}}+{D}_{\mathrm{h}}\ {\rho }_{\mathrm{{water}}})\ g\\ {F}_{\mathrm{l}}&=&(-H{\rho }_{\mathrm{{ice}}}+{D}_{{\mathrm{l}}}\ {\rho }_{{\mathrm{{water}}}})\ g\end{array}$$
(7)

Replacing ice density (Eq. (4)), ice thickness (Eq. (5)), and water depth (Eq. (6)), ice load is given as a function of its location x on the ice sheet where g = 9.81 m s−2:

$$\begin{array}{lll}{F}_{\mathrm{h}}&=&848.54x+83390.41\\ {F}_{\mathrm{l}}&=&889.64x+62178.79\end{array}$$
(8)

Forces for the FEA were integrated over 50 m sections of the ice sheet model and applied as face loads (Supplementary Figs. 8b and 9c).

Analytical beam validation of FEA

Analytical validation of the numerical approach was simplified as a beam.

$$w=\frac{F}{E\ I}\left(\frac{1}{2}x\ {l}^{2}-\frac{1}{6}{l}^{3}\right)$$
(9)

Deflection w [m] is a function of applied force F [N] and its location x [m], Young’s modulus E [N m−2], second moment of area I = H3/12 [m4] with beam’s height H = 174 m and the beam length l = 150 m.

The expression for applied force is based on Eq. (8) with the coefficients m = 848.54 and b = − 41013.17. Coefficient b was adapted to move the beam’s origin (x = 0) to the limit of deflection at −150 m. The beam therefore extends from x = 0 to x = 150 m. Total moment Mtot is

$${M}_{\mathrm{{tot}}}=\mathop{\int }\limits_{0}^{150}m{x}^{2}+bx\ {\mathrm{d}}x$$
(10)

Assuming a very rigid beam, the integral is zero where negative and positive moments cancel each other out.

$$0=\mathop{\int }\limits_{0}^{{x}_{{M}_{0}}}\frac{1}{3}m{x}^{3}+\frac{1}{2}b{x}^{2}\ {\mathrm{d}}x$$
(11)
$$\to {x}_{{M}_{0}}=-\frac{3b}{2m}$$
(12)

The total moment consequently takes effect on the region between \({x}_{{M}_{0}}\) and 150 m. The total force F of the moment is then,

$$F=\mathop{\int }\limits_{{x}_{{M}_{0}}}^{150}F\ {\mathrm{d}}x$$
(13)

Location x of the effective force F is then (Supplementary Fig. 10)

$$x=\frac{{M}_{\mathrm{{tot}}}}{F}$$
(14)

Material properties are given above. Coordinate centre is point F (the limit of flexure) in Supplementary Fig. 8a and x = 150 m represents the calving front.

Basal friction

A general friction law that brings basal shear stress (τ) and effective normal stress (N) in relation to the ice flow velocity (u) is given by28

$$\tau =C\ N\ {u}^{1/m}$$
(15)

Considering an ice column of 1 m2, the effective shear stress τ equals friction force R. Assuming velocity u constant at a given location, the sum of all forces at this point is zero; thus, downhill-slope force D is equal to friction force R. When τ = R and R = D, with \(D=\sin \alpha \ {F}_{g}\) (Fg: weight of ice), \(\tau =\sin \alpha \ {F}_{g}\). Neglecting basal-water pressure, normal force applied on the slope is \(N=\cos \alpha {F}_{g}\). Eq. (15) is then

$$\sin \alpha \ {F}_{g}=C\ \cos \alpha \ {F}_{g}\ {u}^{1/m}$$
(16)

Assuming ice velocity has a linear effect (m = 1), ice is incompressible, mass flux is constant, we can solve Eq. (16) for C to obtain the friction coefficient, where \(\sin\! /\!\!\cos =\tan\):

$$C=\frac{\tan (\alpha)}{u}$$
(17)

As the ice velocity is effected by thinning, we modified the original Eq. (15)28 by replacing velocity u with the ice flux (flux = uH). By introducing velocity and flux into the general friction law, friction coefficient C was replaced by the friction factor f with the unit [s m−2].

$$f=\frac{\tan (\alpha)}{u\ H}$$
(18)

Ice front extrapolation

The shape of the 2015 ice front was digitized from satellite image TDX1-SAR © DLR, 31 December 2015 using QGIS. The basis for motion interpolation of the ice front was given by the ice flow vector field from Rignot et al. and Mouginot et al.23,24,25 (Fig. 1c). Flow components of the 2015 ice front were determined by the radial basis function (rbf) and linear interpolation from the scientific python (scipy) module. Every point of the 2015 ice front was extrapolated 25.5 months (31 Dec 15 to 18 Feb 18) into the future (light blue line in Fig. 1d). We found implausible data at the boundary. In order to avoid potential contamination and bias from boundary effects, we removed all boundary data.

Clast shape distribution

We analysed the shape of the clasts on 22 randomly selected images (n = 1026) using Powers’ semi-quantitative roundness chart (Supplementary Table 1)33. Observed roundness was compared to published "basal debris” and "rockfall” roundness distributions35.