Abstract
The Himalayan megathrust accommodates most of the relative convergence between the Indian and Eurasian plates, producing cycles of blind and surface-breaking ruptures. Elucidating the mechanics of down-dip segmentation of the seismogenic zone is key to better determine seismic hazards in the region. However, the geometry of the Himalayan megathrust and its impact on seismicity remains controversial. Here, we develop seismic cycle simulations tuned to the seismo-geodetic data of the 2015 Mw 7.8 Gorkha, Nepal earthquake to better constrain the megathrust geometry and its role on the demarcation of partial ruptures. We show that a ramp in the middle of the seismogenic zone is required to explain the termination of the coseismic rupture and the source mechanism of up-dip aftershocks consistently. Alternative models with a wide décollement can only explain the mainshock. Fault structural complexities likely play an important role in modulating the seismic cycle, in particular, the distribution of rupture sizes. Fault bends are capable of both obstructing rupture propagation as well as behave as a source of seismicity and rupture initiation.
Similar content being viewed by others
Introduction
At subduction zones and continental collisional margins, the convergence between tectonic plates is accommodated by shortening along megathrusts characterised by extensive seismogenic zones that produce some of Earth’s largest earthquakes. Megathrusts oftentimes undergo seismic super-cycles, alternating frequent moderate-size events that break the seismogenic zone in a piece-wise fashion with occasional giant earthquakes that break the entire seismogenic width1,2,3. Understanding what determines the spatial extent of seismic ruptures is important to produce realistic bounds on seismic hazards, as larger earthquakes produce greater levels of shaking hazard over wider areas with different frequency contents. In particular, events that rupture to the surface, for example, the 2005 Mw 7.6 Kashmir earthquake4, exhibit greater hazards to life and property compared to blind ruptures like the 2015 Mw 7.8 Gorkha earthquake that do not reach the surface. However, the underlying mechanics of full and partial ruptures of the seismogenic zone is poorly constrained. The development of seismic super-cycles may be controlled by several factors, such as particular frictional properties5,6, geometric complexity7, off-fault deformation in the hanging wall8, and residual stress from past earthquakes9. The remaining challenge is to assess the relative contribution of these factors at specific plate boundaries10,11.
Most of the relative convergence between the Indian and Eurasian plates is currently accommodated along the Himalayan megathrust, which follows the surface-emergent Main Frontal Thrust (MFT) that soles into a gently dipping décollement called the Main Himalayan Thrust (MHT). The seismic cycle at the MHT embodies both along-strike and down-dip segmentation12, with surface-breaking ruptures, like the 1934 Nepal-Bihar event13,14, that unzip the entire seismogenic width, but also blind ruptures, like the 1833 Kathmandu event15,16, that break only a small section of the megathrust. The 2015 Mw 7.8 Gorkha earthquake represents a partial rupture17,18,19,20,21, but the factors responsible for the rupture termination in the middle of the seismogenic zone are still controversial22. Some argue for the predominant role of morphological gradients23,24,25 while others invoke a frictional control26.
Fault bends along the MHT control many aspects of the Himalayan orogeny at geological time scales. For example, the ramp-décollement structure extending below central Nepal is linked to the Gorkha-Pokhara Anticlinorium27 and is responsible for the high Himalayan topography28. Along-strike morphological gradients may constitute important boundaries for interseismic strain accumulation in Nepal29, but the impact of fault bends on down-dip segmentation of the MHT is lesser known, in part because the detailed structural layout of the MHT is controversial. The MHT has been described as a ramp-flat-ramp structure27,30, a duplex system31, or with an additional ramp in the middle of the seismogenic zone23. Since structural complexity may play a significant role in megathrust behaviour, it is paramount that we reduce uncertainties in fault geometry.
We will show that partial ruptures of the seismogenic zone similar to the 2015 Gorkha earthquake can be obtained either on a wide frictionally unstable décollement or on one with additional fault bends, as long as the characteristic size for earthquake nucleation is much smaller than the seismogenic zone width. However, a sequence with a mainshock followed by shallow dipping aftershocks consistent with observations can only be obtained with a middle ramp. To support these claims, we present numerical simulations of the seismic cycle in Nepal that explain the slip distribution and surface deformation associated with the 2015 Gorkha earthquake using two end-member fault geometry models with and without a middle ramp. The simulations reveal the respective roles of fault bends and stress residuals from antecedent seismicity on down-dip segmentation and the spatial distribution of aftershocks on the Kathmandu section of the Himalayan megathrust.
Results
Seismic cycle modelling of the Gorkha earthquake
We investigate the various controls on seismicity using quasi-dynamic numerical models of the seismic cycle based on a physics-based rate- and state-dependent friction law32,33 with the boundary integral method (see “Methods”). We consider two-dimensional models along a representative cross-section perpendicular to the plate boundary that crosses the Gorkha-Pokhara Anticlinorium in the middle of the Gorkha coseismic rupture (Fig. 1). The distribution of frictional properties and the detailed geometry of the megathrust are poorly known. Therefore, we consider end-member scenarios that allow us to study the impact of fault bends on the seismic cycle. We base the analysis on megathrust geometry models that embody different assumptions about fault complexity. Model E27 is based on the Gorkha coseismic surface displacements in conjunction with other geological and geophysical data and describes the MHT with a large-scale ramp-flat-ramp geometry. Model H23 assimilates regional geological constraints in a balanced cross-section and features a ramp in the middle of the seismogenic zone. Both fault geometry models have a shallow fault bend where the MFT soles into the MHT and a mid-crustal ramp that approximately coincides with the bottom of the seismogenic zone (Supplementary Fig. 1).
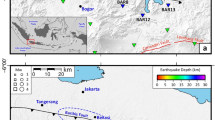
a Distribution of coseismic slip7 in the source region of 2015 Mw 7.8 Gorkha, Nepal earthquake (background colours). GNSS measurements are represented by circles for vertical displacement and arrows for horizontal displacements. Near-field GNSS station names are highlighted in yellow and the far-field stations in grey. The black dots represent the aftershock sequence recorded by the Nepal Array Measuring Aftershock Seismicity Trailing Earthquake (NAMASTE) network31. The focal mechanisms are for the immediate aftershock sequence43. b Sub-surface geological cross-section along profile A-A' constrained using surface geology23. c Geological cross-section constrained by coseismic geodetic data27. The velocity-weakening regions are indicated in red and velocity-strengthening regions in black. The focal mechanisms (coloured by the focal depth and scaled to magnitude) are superimposed on the cross-section. These cross-sections show the major thrust faults in the region including the surface-emergent MFT (Main Frontal Thrust), Main Boundary thrust (MBT), and Main Central Thrust (MCT).
The spatial distribution of the frictional parameters controls many aspects of fault behaviour34,35,36. As the spatial variations of frictional properties on the MHT are poorly constrained, we consider simple cases with piece-wise homogeneous frictional properties in the seismogenic zone and the aseismic region underneath. In this context, the style of fault dynamics can be described and predicted predominantly by two non-dimensional parameters33, i.e., the ratio of the seismogenic width with a characteristic nucleation size37 and the ratio of frictional parameters that control the static and dynamic stress drops during seismic ruptures38 (Eqs. (6) and (7) in “Methods”). Here, the characteristic nucleation size results from a dimensional analysis of the governing equation and represents an intrinsic length scale of the mechanical system. It is uniquely defined for the entire rupture sequence up to a constant multiplier. The actual nucleation size of simulated events may vary throughout the cycle due to geometric complexity and variable pre-stress at the time of rupture initiation. Numerical simulations with different physical parameters leading to the same non-dimensional parameters exhibit similar dynamics33. For example, cycles of partial and full ruptures can be obtained on planar fault segments without structural complexity as long as the characteristic size for earthquake nucleation is much smaller than the seismogenic width32,37,39,40,41. Following these theoretical insights, we explore a space of constitutive parameters that produce a wide range of associated non-dimensional parameters for each of the geometry models. We simulate the seismic cycle for a period of 10,000 years for the models discussed in this section, and for a period of 45,000 years for the two models described in the next section with a background loading rate of 20 mm per year. We discard the first 5000 years to mitigate the effect of initial conditions.
First, we explore the ratio of the seismogenic width with a critical nucleation size (Supplementary Table 1). Self-emergent partial ruptures can be obtained if this ratio is >20 for model E and >6 for model H (Supplementary Fig. 2). Additional fault bends in the middle of the seismogenic zone are responsible for fault segmentation to occur at lower ratios in model H. However, the presence of a middle ramp is not a sufficient condition for partial ruptures and specific frictional properties in the presence of fault bends must be considered to explain the MHT behaviour. Next, we explore the parameters that control the static and dynamic stress drops (Supplementary Table 2, Supplementary Fig. 3). Cycles associated with a large ratio of seismogenic width to nucleation size and a large ratio of static to dynamic stress drops contain ruptures that start as crack-like and transition to pulse-like towards the end (Supplementary Fig. 4). The pulse-like ruptures happen without additional coseismic weakening processes and are specifically a consequence of the high ratio between the static and dynamic stress drops in our quasi-dynamic simulations (see “Methods”). Models with lower ratios do not exhibit this feature, illustrating the strong frictional controls on the details of a seismic rupture. Fault bends in both geometry models attract persistent seismicity under these conditions (Supplementary Fig. 3). For example, giant ruptures sometimes initiate where the MFT soles into the décollement with model E and many ruptures initiate around the middle ramp in model H under some conditions. Up-dip aftershocks are often associated with fault bends while down-dip aftershocks are mostly associated with the transition zone where the fault behaviour changes from velocity-weakening to velocity-strengthening. The transition zone marks the base of the seismogenic zone, but also the top of a large mid-crustal ramp in the Himalayan region, so the variations of friction and geometry are combined at this location.
Among the numerical simulations that produce cycles of full and partial ruptures of the MHT, we retain those that best explain the geodetic measurements associated with the Gorkha earthquake (Fig. 1), in particular, the Global Navigation Satellite System (GNSS) and Synthetic Aperture Radar interferometry (InSAR)17,19 data. Even though the GNSS network offers limited resolution for fault imaging42, four near-field stations show clear coseismic deformation. The large swath of Advanced Land Observing Satellite (ALOS) line-of-sight displacements constrain coseismic fault slip7,27. With both geometry models, the main features of the coseismic geodetic data and inferred slip distributions can be explained well. Some discrepancies between the geodetic data and our forward models could be reduced by adapting the position of the mid-crustal ramp or other adjustments, but the two-dimensional approximation will presumably remain a limiting factor. Even with these constraints, the choices of non-dimensional parameters that can explain the mainshock slip distribution and fault slip within the larger context of super-cycles with partial and full ruptures for both model E and model H is non-unique. Therefore, we narrow our search to simulations that consistently explain both the mainshock and the early aftershocks relocated using advanced broadband waveform modelling techniques43.
Our exploration of a wide range of models shows that no aftershock up-dip of a coseismic rupture similar to that of the Gorkha sequence can be obtained on a flat décollement using model E. We cannot exclude that shallow aftershocks would occur because of down-dip variations of frictional properties, but we cannot justify the presence of frictional contrasts above the coseismic rupture unless they are accompanied by morphological gradients. In contrast, shallow aftershocks can be obtained in the presence of a middle ramp, as in model H, for a particular range of frictional parameters that lead to large ratios of static to dynamic stress drops. We therefore focus the remaining discussion on simulation results based on specific frictional parameters (Table 1) that are similar for model E and model H, i.e., with a ratio of seismogenic width to characteristic nucleation size of 60 and a ratio of parameters controlling static and dynamic stress drops of 0.9 (Supplementary Fig. 3d, i). This simulation explains the mainshock and shallow aftershock sequence consistently on model H but only the mainshock with model E. This allows us to investigate the specific differences introduced by morphological gradients within simulations that can explain the cycle of full and partial ruptures of the MHT and the deformation associated with the Gorkha earthquake.
Impact of geometry on seismic super-cycle
We start by describing our simulations of seismic super-cycles without a fault bend in the middle of the seismogenic zone. We define a super-cycle as the period that separates two consecutive through-going ruptures and encompasses one or several partial ruptures. Our preferred model using fault geometry E (Table 1) produces surface displacements that show a similar signature to the GNSS and InSAR geodetic data of the Gorkha earthquake along the profile B-B’ (Fig. 2). The recurrence times of giant ruptures (e.g., events E17 and E21) that break the entire seismogenic width range between 1300 and 1700 years (Fig. 3a). All the intervening partial ruptures (events E15, E19, and E23) are of similar size and extent, but event E23 matches the Gorkha earthquake data more closely (Fig. 2).
a, b The two tracks of Advanced Land Observing Satellite (ALOS) line-of-sight displacements that recorded the coseismic displacements. c, d Simulated surface displacements using model E27 and model H23 compared with ALOS2-157 and ALOS2-048 InSAR scenes. e–g Simulated horizontal (north and east components) and vertical displacements indicated using black solid (model H) and dashed (model E) profiles compared against GNSS horizontal and vertical data. The blue data points correspond to near-field stations indicated by yellow labels in Fig. 1 and red data points correspond to far-field stations indicated by grey labels. h Simulated fault slip using our numerical method indicated in black solid (model H) and dashed (model E) lines. Fault slip estimated by inverting geodetic data with geometry H (orange solid) and geometry E (orange dashed) lines. The error bars indicate an uncertainty of 5% added to the data.
a Spatio-temporal evolution of slip on the Himalayan megathrust using geometry model E27. b Similar simulations using geometry model H23. Earthquakes of different sizes are differentiated using colours; red indicates giant surface-breaking ruptures, purple represents partial ruptures of varying sizes, blue represents Gorkha-like events, and black represents aftershocks. Stars indicate the hypocenter locations. The initial and final slip velocities for seismic events are 0.1 and 0.001 m/s respectively.
The seismogenic zone is locked during the interseismic period and remains so following the partial ruptures. However, partial coupling and interseismic creep are predominant at the base of the MFT (Supplementary Fig. 3), as is often found at fault bends8,10,11. The transition zone between velocity-strengthening and velocity-weakening friction is characterised by high stresses (Fig. 4b). Previous ruptures leave behind notable stress residuals that explain subsequent down-dip rupture segmentation due to non-uniform pre-stress along the fault at the time of rupture initiation. All the ruptures initiate at depths between 12 and 15 km because of the presence of the transition zone and the thrust ramp at this depth, which are two separate causes for rapid inter-seismic stress accumulation (Figs. 3 and 4). Model E showcases aftershocks E18 and E22 following the through-going events E17 and E21, respectively. These aftershocks occur near the transition zone where afterslip immediately below rapidly decays in the months and years that follow through-going ruptures. However, no aftershocks follow the Gorkha-like event, whether up-dip or down-dip.
Slip accumulated on the fault plotted against the down-dip distance using geometry E (a) and geometry H (c). The colour indicates the fault slip rate, with red indicating seismic slip and blue represents interseismic creep. The black contours are cumulative coseismic slip values plotted every 5 s. The white contours are cumulative aseismic slip values plotted every 50 years. The large slip deficit in the shallow regions of the fault is recovered during through-going ruptures. The stars represent hypocenter locations. b, d Shear stress accumulation on the fault; red regions indicate areas of high-stress accumulation and blue indicates areas of low stress. Previous ruptures and geometric complexities cause stress concentrations where earthquakes often nucleate. Hypocenter locations are represented by stars, yellow stars represent Gorkha-like events.
We now compare these results with our seismic cycle simulation that includes fault bends in the middle of the seismogenic zone. The presence of the middle ramp impacts several inter-connected aspects of the seismic cycle, such as rupture size and extent, and recurrence patterns. Model H produces more partial ruptures that break different segments of the MHT with varying sizes. Among these, events H43 and H65 closely match the coseismic signature of the Gorkha earthquake (Fig. 2). Eventually, the fault completely fails in a single through-going rupture with recurrence times varying between 900 and 2000 years (Fig. 3), i.e., almost thrice the variability found in model E. (Fig. 3). Super-cycles are also more aperiodic, containing Gorkha-like ruptures (e.g., events H43 and H65), but also larger events (e.g., H50 and H57), with a wider variability in the number of partial ruptures.
High-stress concentrations at the fault bend attract persistent seismicity at the middle ramp (Fig. 4c and d), including ramp-spanning isolated ruptures (e.g., events H55 and H59) and aftershocks (e.g., events H44 and H66). The middle ramp is also capable of terminating partial ruptures (e.g., event H43, H65), thereby acting as a geometric barrier. However, partial ruptures may propagate up-dip through the ramp, creating events of larger size and extent than the Gorkha earthquake (e.g., events H50 and H57). Whether or not ruptures pass the ramp in our simulations is controlled by the spatial distribution of pre-stress, which depends on the history of the previous seismicity.
The complexity of the rupture sequence can be qualified by the distribution of rupture sizes (Supplementary Fig. 5). Chaotic seismic sequences are expected to follow a power-law statistical distribution, an example of which in nature is the Gutenberg-Richter distribution. The super-cycles with model H exhibit a power-law distribution of rupture size spanning four orders of magnitude, possibly truncated for small-magnitude events due to numerical limitations that impose a lower bound on rupture size. In contrast, simulations with model E produce events with only three orders of magnitude with a more uniform distribution of rupture sizes.
Within the assumptions of the model, fault bends represent zones of rapid stress accumulation in the interseismic period, making these regions prone to earthquake nucleation. As a result, all rupture initiations in our models are in close proximity to a bend. Fault bends therefore play an important role during all stages of the earthquake cycle by attracting seismicity and altering the background stress level.
Aftershocks at fault bends
The hypocenters and focal mechanisms of several relocated aftershocks of the 2015 Gorkha earthquake for the first 12-h window following the mainshock43 indicate significant deviations from a planar megathrust geometry (Fig. 5). Our simulations with model H explain some of the frictional and geometric controls of the up-dip aftershocks of the Gorkha seismic sequence.
a Geological cross-section along profile A-A' that describes the MHT geometry using model H23. b The 2015 Gorkha event and the seven early aftershocks during the 12-h time window relocated using advanced waveform techniques43. We monitor the slip velocity at various observation points on the fault surface. The middle ramp consists of three observation points: Points A and C represent the position of the kink formed at the two fault bends of the middle ramp and B is located at its centre. Points D and E are on the décollement that ruptured during the 2015 event. Point E experiences the coseismic slip of the simulated partial event H65 while D represents the termination point that is completely locked. c The evolution of peak slip velocity representing the maximum slip speed attained anywhere in the model showing the Gorkha mainshock and the subsequent updip aftershock that happened after 14 h. d, e The evolution of slip velocity is plotted with the colours indicating the position of the observation points.
Events H44 and H66 represent small-magnitude seismic events rupturing the top of the middle ramp in the early postseismic phase of the Gorkha-like events H43 and H65, respectively. For example, the up-dip aftershock H66 happens ~14 h following the mainshock at the shallow fault bend joining the upper décollement and middle ramp (Fig. 5). Triggering of aftershocks at the boundary of coseismic ruptures can be caused by rapid coseismic stress changes, but this type of event does not occur with model E. As fault bends are associated with rapid interseismic stress accumulation, they constitute prime regions for aftershock triggering because the stress level is already elevated at the start of the mainshock. In fact, in other circumstances, the same regions become the nucleation point of large earthquakes in our simulations.
The focal mechanisms of the up-dip aftershocks following the Gorkha earthquake may be explained by the fault bends at this location, confirming the ~30∘ dip and the small width of a few kilometres of the middle ramp23,43. The spatio-temporal evolution of the mainshock-aftershock sequence closely matches our simulations with model H. However, the numerical model only explains a single aftershock, presumably due to the computational constraints, e.g., the two-dimensional approximation or the assumption of piece-wise planar fault geometry, that limit the size of events and the geometric complexity that can be resolved numerically.
Discussion
The devastating Mw 7.8 Gorkha, Nepal earthquake resulted in about 9,000 fatalities and injured million others17. Although the quake took place in a previously known seismic gap44,45, the seismic rupture only relaxed the lower half of the locked MHT region, raising questions about the timing, location, and size of impending earthquakes. As the shallow section of the fault remains locked with no evidence of widespread shallow afterslip46,47, we contemplate why the rupture stopped in the middle of the seismogenic zone. It is unclear whether the next event will unzip the remaining locked section, repeat the 2015 scenario, or break the entire megathrust in a single giant rupture. Our numerical simulations provide new insights into these fundamental questions.
The partial rupture of the seismic gap can be understood as the natural behaviour of a chaotic seismic cycle characterised by non-periodic sequences of full and partial ruptures that naturally emerge—with or without a middle ramp—because of the particularly small characteristic nucleation size relative to the seismogenic width, compatible with prior assessments26. The partial rupture of the lower segment of the MHT followed by full locking of the upper section therefore provides strong constraints on the frictional parameters of the megathrust. The MHT is capable of seismic ruptures from the deep ramp to the MFT following partial ruptures similar to the 2015 event and the physical properties that govern the frictional behaviour on the fault must combine to a ratio of seismogenic width to characteristic nucleation size of at least 60, according to our simulations. However, additional consideration of the Gorkha aftershock sequence indicates that these particular frictional properties are also accompanied by non-planar fault geometry in the middle of the seismogenic zone.
Gorkha-like ruptures followed by up-dip aftershocks are systematically followed by giant ruptures with a delay ranging from about 250 to 300 years, based on our preferred model with geometry H. Small ruptures breaking only the upper section of the MHT are therefore unlikely, based on the assumptions of the model. However, more imminent seismic hazard in Kathmandu may originate from seismic ruptures that break different sections of the Himalayan megathrust, initiating outside the Kathmandu Klippe7. Different scenarios of future seismicity are also possible due to the many remaining unknown mechanical properties of the plate boundary, including deformation of the upper plate by faulting and folding8,48, more complex frictional behaviour of the megathrust49, and interactions with other segments of the Himalayan megathrust50.
The study illustrates the complex footprint of fault bends and ramps on megathrust seismic cycles. Fault bends are often simply portrayed as geometric barriers that can abruptly terminate rupture propagation51, but this characterisation is incomplete when multiple seismic cycles are considered52. In addition, the impact of fault geometry is multi-faceted and cannot be deconvolved from the frictional control (Supplementary Figs. 2 and 3). Fault bends in the seismogenic zone are always associated with accruing stress during the interseismic period in our simulations. This stress can be manifested by creep, for example at the bottom of the MFT, by the propagation of large earthquakes across a ramp, by the arrest of ruptures at the middle ramp, by the enhancement of aftershock activity at the ramp, or by promoting larger ruptures that propagate across the deep décollement and slightly beyond the ramp. In addition, the background stress may be sufficiently elevated across the domain to facilitate through-going ruptures that break the entire seismogenic zone.
Fault ramps incite more complexity than isolated velocity-strengthening barriers5,53, which only imply a binary cycle of ruptures that either do or do not break the obstacle. The complexity of stress interactions due to the presence of morphological gradients54 on the megathrust translates to a wider range of rupture sizes and recurrence patterns manifested by a statistical distribution of earthquake sizes that approaches a power-law and a strongly aperiodic earthquake recurrence pattern. Power-law statistics of earthquake size distribution may also be obtained on a planar fault under specific physical properties leading to a ratio of seismogenic zone width to characteristic nucleation size greater than about 40037. Under these conditions, however, the ruptures are systematically starting from the bottom of the seismogenic zone, extending up-dip to varying distances. Our study shows that with non-planar faults, the power-law distribution of earthquake size can be approached for a wider range of frictional parameters than for a planar fault, also producing more widely distributed nucleation points. Variability in hypocenter location may also arise from a damage zone surrounding the plate interface55, which constitutes another kind of structural complexity.
Several models describe the Himalayan megathrust geometry, but the exact geometric features and their role in Himalayan tectonics remain controversial. Our work illustrates the impact of fault bends on seismic cycles and their importance to consistently explain the coseismic and postseismic behaviour of the Kathmandu section of the Himalayan megathrust. Our simulations reveal that seismicity at the MHT can be explained by the complex dynamics of frictional sliding with morphological gradients. The frictional properties allow seismic super-cycles of full and partial ruptures, but the rapid inter-seismic stress accumulation at geometric gradients modulates the earthquake size and recurrence patterns. Our results help better constrain the geometry of the MHT and the impact of fault bends on the seismic cycle. Incorporation of high-resolution models of fault geometry56,57 into rupture dynamics models may be key to better predict future seismicity at subduction and collision margins.
Methods
Exploring the frictional regime with rate- and state-dependent friction
Constitutive framework
We use the rate- and state-dependent friction framework, first introduced by Dieterich, Ruina, and Rice58,59,60, supported by extensive experimental data, to model fault dynamics. Seismic cycle simulations using this framework is capable of explaining a gamut of rupture modes and styles observed in nature, which includes fault slip occurring at all stages of a seismic cycle like slow earthquakes, slow-slip events, and quasi-static aseismic processes. We follow the physics-based formulation of Barbot32, whereby the fault strength depends on the area of contacts that bear the normal and shear loads. The real area of contact per unit fault area is given by
where μ0 is the coefficient of static friction, \(\overline{\sigma }\) is the effective normal stress, χ is the indentation hardness, V0 is a reference velocity, ψ is a state variable associated with contact aging, L is the characteristic weakening distance, and b ≪ 1 is a power exponent. The constitutive law for the sliding velocity is given by
where a ≪ 1 is a power exponent, Q is an activation energy, R is the universal gas constant, and T is the absolute temperature. We obtain the constitutive equations for rate- and state-dependent friction by combining (1) and (2) as
The state variable captures the evolution of the real area of contact with sliding history and follows the evolution law
where the first and second terms on the right-hand side correspond to healing and weakening of the fault surface, respectively. In this study, we ignore changes of temperature induced by shear heating or other reactions and limit ourselves to isothermal conditions with T = T0. The model is more adequate for seismic cycle simulations than previous formulations59 because it avoids issues with vanishing velocities. We also ignore the changes in normal stress along the fault even though changes in normal stress at fault bends can make the contact frictionless or in unbounded compression after only a few seismic cycles, making the numerical simulation intractable. In reality, these stresses are relaxed by folding and other visco-elasto-plastic off-fault processes, but these are challenging to model because experimental data on low-temperature plastic deformation mechanisms are not available. In our simulations, we assume that the stress perturbations at fault bends are effectively counteracted by other processes that relieve the bends of these perturbations instantaneously, maintaining the effective normal stress constant.
Governing equations
We simulate fault slip and rupture dynamics assuming isothermal conditions in a quasi-dynamic set-up. Our model does not include the wave-mediated stress transfers and we employ the Runge-Kutta solver with adaptive time steps and four/fifth-order accuracy to simulate earthquake cycles numerically. We track the changes in shear traction due to fault slip using the integral method
where K is the traction kernel or Green’s functions tensor that describes the fault stress interactions, VL is the loading rate on the fault due to the far-field tectonic loading, V denotes the instantaneous velocity vector, and Vs is the shear wave velocity. The traction kernel in Eq. (5) describes the distribution of stress in the surrounding medium due to a point double-couple source. Radiation damping that is used to approximate the inertial effects due to wave-mediated stress transfers is denoted by the last term on the right-hand side of Eq. (5). We numerically solve the kinematics, stress interactions, velocity, and constitutive behaviour using the boundary integral method, which was partially benchmarked against other methods61.
Controls on fault dynamics from dimensional analysis
Simulations with rate- and state-dependent friction often display complexity depending on the distribution of physical properties41,62. Different physical parameters control various different aspects of the seismic cycle, for example, stress drop, recurrence times, and whether the rupture is slow or fast. Dimensional analysis of the physical parameters that control fault dynamics and rupture styles is useful to reduce the vast parameter space involved and identify the combinations of parameters that control rupture dynamics and rupture style.
We use the two non-dimensional parameters that exhibit the most variability in nature32 to explore the frictional regime that controls rupture styles. The Dieterich-Ruina-Rice number Ru is defined for a fault system with a single velocity-weakening asperity as
where G is the rigidity, and W is the size of the velocity-weakening region, i.e., the width of the seismogenic zone. The Ru number represents a ratio of the seismogenic zone size to a characteristic rupture nucleation dimension. Stable fault slip in velocity-weakening regions are associated with Ru < 1, owing to its large nucleation size compared to the fault dimension. The value of Ru increases for increasing weakening behaviour with unstable slip represented by Ru ≫ 1 values. Physical properties of the velocity-weakening region that fall in increasing values of Ru exhibit cycles of characteristic and periodic ruptures, transitioning to more chaotic sequences33,37. For example, higher values of Ru give rise to chaotic cycles with full ruptures followed by partial ruptures of varying sizes.
The second non-dimensional number considered is
which describes the ratio of frictional properties that control the static and dynamic stress drops. The ratio of these fundamental source properties control the style of rupture and the relative fraction of the rupture energy consumed in fracture. Large Rb values favour ruptures with strong-weakening behaviour with proportionally limited fracture energy. Low Rb values represent conditions close to velocity neutral representative of the transition zone between velocity-weakening and velocity-strengthening friction.
The Ru-Rb phase space can fill up the spectrum of fault behaviour ranging from simple and periodic to deterministic chaos. Large Ru values result in complex seismic cycles with full and partial ruptures compared to low values of Ru that result in slow-slip and slow earthquakes. Although it is difficult to constrain these values in natural settings, an exploration of this phase space, helps us to understand rupture dynamics and behaviour. Also, complex fault geometry and shear stress variations due to fault non-planarity can affect rupture styles in more complicated ways than observed for planar faults8. We design a careful study that takes into account both fault geometry and the frictional regime in the Ru−Rb phase space.
Data availability
Seismic data, geodetic data, and data sets generated in the current study can be found at the public repository with free access at https://zenodo.org/record/4679513.
Code availability
The software code and data are publicly available at https://zenodo.org/record/4679513.
References
Satake, K. Geological and historical evidence of irregular recurrent earthquakes in Japan. Phil. Trans. R. Soc. A 373, 20140375 (2015).
Philibosian, B. et al. Earthquake supercycles on the mentawai segment of the sunda megathrust in the seventeenth century and earlier. J. Geophys. Res. 122, 642–676 (2017).
Philibosian, B. & Meltzner, A. J. Segmentation and supercycles: a catalog of earthquake rupture patterns from the sumatran sunda megathrust and other well-studied faults worldwide. Quaternary Sci. Rev. 241, 106390 (2020).
Avouac, J. P., Ayoub, F., Leprince, S., Konca, O. & Helmberger, D. V. The 2005, mw 7.6 kashmir earthquake: sub-pixel correlation of aster images and seismic waveforms analysis. Earth Planetary Sci. Lett. 249, 514–528 (2006).
Kaneko, Y., Avouac, J. P. & Lapusta, N. Towards inferring earthquake patterns from geodetic observations of interseismic coupling. Nat. Geosci. 3, 363–369 (2010).
Noda, H. & Lapusta, N. Stable creeping fault segments can become destructive as a result of dynamic weakening. Nature 493, 518–521 (2013).
Qiu, Q. et al. The mechanism of partial rupture of a locked megathrust: the role of fault morphology. Geology 44, 875–878 (2016).
Sathiakumar, S., Barbot, S. & Hubbard, J. Earthquake cycles in fault-bend folds. J. Geophys. Res. 125, e2019JB018557 (2020).
Herrendörfer, R., Van Dinther, Y., Gerya, T. & Dalguer, L. A. Earthquake supercycle in subduction zones controlled by the width of the seismogenic zone. Nat. Geosci. 8, 471–474 (2015).
Shi, Q. et al. Structural control and system-level behavior of the seismic cycle at the Nankai trough. Earth Planets Space 72, 1–31 (2020).
Barbot, S. Frictional and structural controls of seismic super-cycles at the Japan trench. Earth Planets Space 72 (2020).
Pandey, M., Tandukar, R., Avouac, J., Lave, J. & Massot, J. Interseismic strain accumulation on the Himalayan crustal ramp (Nepal). Geophys. Res. Lett. 22, 751–754 (1995).
Chen, W. P. & Molnar, P. Seismic moments of major earthquakes and the average rate of slip in central asia. J. Geophys. Res. 82, 2945–2969 (1977).
Sapkota, S. et al. Primary surface ruptures of the great Himalayan earthquakes in 1934 and 1255. Nat. Geosci. 6, 71–76 (2013).
Bilham, R. Location and magnitude of the 1833 Nepal earthquake and its relation to the rupture zones of contiguous great Himalayan earthquakes. Current Sci. 69, 101–128 (1995).
Bilham, R. et al. Earthquakes in India and the Himalaya: tectonics, geodesy and history. Annals Geophys. (2004).
Avouac, J.P., Meng, L., Wei, S., Wang, T. & Ampuero, J.P. Lower edge of locked Main Himalayan Thrust unzipped by the 2015 Gorkha earthquake. Nat. Geosci. (2015).
Galetzka, J. et al. Slip pulse and resonance of the Kathmandu basin during the 2015 Gorkha earthquake, Nepal. Science 349, 1091–1095 (2015).
Lindsey, E.O. et al. Line-of-sight displacement from ALOS-2 interferometry: Mw 7.8 Gorkha Earthquake and Mw 7.3 aftershock. Geophys. Res. Lett. (2015).
Wang, K. & Fialko, Y. Slip model of the 2015 Mw 7.8 Gorkha (Nepal) earthquake from inversions of ALOS-2 and GPS data. Geophys. Res. Lett. (2015).
Grandin, R. et al. Rupture process of the Mw= 7.9 2015 Gorkha earthquake (Nepal): insights into Himalayan megathrust segmentation. Geophys. Res. Lett. 42, 8373–8382 (2015).
Ghoshal, S. et al. Constraining central Himalayan (Nepal) fault geometry through integrated thermochronology and thermokinematic modeling. Tectonicse2020TC006399 (2020).
Hubbard, J. et al. Structural segmentation controlled the 2015 Mw 7.8 Gorkha earthquake rupture in Nepal. Geology 44, 639–642 (2016).
Mugnier, J. L. et al. Segmentation of the Himalayan megathrust around the Gorkha earthquake (25 April 2015) in Nepal. J. Asian Earth Sci. 141, 236–252 (2017).
Dal Zilio, L., van Dinther, Y., Gerya, T. & Avouac, J. P. Bimodal seismicity in the Himalaya controlled by fault friction and geometry. Nat. Commun. 10, 48 (2019).
Michel, S., Avouac, J. P., Lapusta, N. & Jiang, J. Pulse-like partial ruptures and high-frequency radiation at creeping-locked transition during megathrust earthquakes. Geophys. Res. Lett. 44, 8345–8351 (2017).
Elliott, J. et al. Himalayan megathrust geometry and relation to topography revealed by the gorkha earthquake. Nat. Geosci. 9, 174 (2016).
Avouac, J. P. Mountain building, erosion, and the seismic cycle in the Nepal Himalaya. Adv. Geophys. 46, 1–80 (2003).
Dal Zilio, L., Jolivet, R. & van Dinther, Y. Segmentation of the Main Himalayan Thrust illuminated by Bayesian inference of interseismic coupling. Geophys. Res. Lett. 47, e2019GL086424 (2020).
Duputel, Z. et al. The 2015 Gorkha earthquake: a large event illuminating the Main Himalayan Thrust fault. Geophys. Res. Lett. 43, 2517–2525 (2016).
Mendoza, M. et al. Duplex in the Main Himalayan Thrust illuminated by aftershocks of the 2015 Mw 7.8 Gorkha earthquake. Nat. Geosci. 1-5 (2019).
Barbot, S. Modulation of fault strength during the seismic cycle by grain-size evolution around contact junctions. Tectonophysics 765, 129–145 (2019).
Barbot, S. Slow-slip, slow earthquakes, period-two cycles, full and partial ruptures, and deterministic chaos in a single asperity fault. Tectonophysics 768, 228171 (2019).
Dublanchet, P., Bernard, P. & Favreau, P. Interactions and triggering in a 3-d rate-and-state asperity model. J. Geophys. Res. 118, 2225–2245 (2013).
Ray, S. & Viesca, R. C. Earthquake nucleation on faults with heterogeneous frictional properties, normal stress. J. Geophys. Res. 122, 8214–8240 (2017).
Ong, S. Q. M., Barbot, S. & Hubbard, J. Physics-based scenario of earthquake cycles on the ventura thrust system, california: the effect of variable friction and fault geometry. Pure Appl. Geophys. 176, 3993–4007 (2019).
Cattania, C. Complex earthquake sequences on simple faults. Geophys. Res. Lett. 46, 10384–10393 (2019).
Gabriel, A. A., Ampuero, J. P., Dalguer, L. A. & Mai, P. M. The transition of dynamic rupture styles in elastic media under velocity-weakening friction. J. Geophys. Res. 117 (2012).
Kato, N. Repeating slip events at a circular asperity: Numerical simulation with a rate-and state-dependent friction law. Bull. Earthq. Res. Inst. Univ. Tokyo 78, 151–166 (2003).
Lapusta, N. & Rice, J. R. Nucleation and early seismic propagation of small and large events in a crustal earthquake model. J. Geophys. Res. 108 (2003).
Wu, Y. & Chen, X. The scale-dependent slip pattern for a uniform fault model obeying the rate-and state-dependent friction law. J. Geophys. Res. 119, 4890–4906 (2014).
Sathiakumar, S., Barbot, S. D. & Agram, P. Extending resolution of fault slip with geodetic networks through optimal network design. J. Geophys. Res. 122, 10–538 (2017).
Wang, X., Wei, S. & Wu, W. Double-ramp on the Main Himalayan Thrust revealed by broadband waveform modeling of the 2015 Gorkha earthquake sequence. Earth Planet. Sci. Lett. 473, 83–93 (2017).
Ader, T. et al. Convergence rate across the Nepal Himalaya and interseismic coupling on the Main Himalayan Thrust: Implications for seismic hazard. J. Geophys. Res. 117, 16 (2012).
Stevens, V. & Avouac, J. Interseismic coupling on the main Himalayan thrust. Geophys. Res. Lett. 42, 5828–5837 (2015).
Mencin, D. et al. Himalayan strain reservoir inferred from limited afterslip following the Gorkha earthquake. Nat. Geosci. 9, 533–537 (2016).
Zhao, B. et al. Dominant controls of downdip afterslip and viscous relaxation on the postseismic displacements following the mw7. 9 gorkha, nepal, earthquake. J. Geophys. Res. 122, 8376–8401 (2017).
Whipple, K. X., Shirzaei, M., Hodges, K. V. & Arrowsmith, J. R. Active shortening within the Himalayan orogenic wedge implied by the 2015 Gorkha earthquake. Nat. Geosci. 9, 711 (2016).
Wang, L. & Barbot, S. Excitation of san andreas tremors by thermal instabilities below the seismogenic zone. Sci. Adv. 6, eabb2057 (2020).
Li, L., Yao, D., Meng, X., Peng, Z. & Wang, B. Increasing seismicity in Southern Tibet following the 2015 Mw 7.8 Gorkha, Nepal earthquake. Tectonophysics 714, 62–70 (2017).
King, G. & Nábělek, J. Role of fault bends in the initiation and termination of earthquake rupture. Science 228, 984–987 (1985).
Duan, B. & Oglesby, D. D. Nonuniform prestress from prior earthquakes and the effect on dynamics of branched fault systems. J. Geophys. Res. 112 (2007).
Kato, N. Earthquake cycles in a model of interacting fault patches: Complex behavior at transition from seismic to aseismic slip. Bull. Seism. Soc. Am. 106, 1772–1787 (2016).
Romanet, P., Sato, D. S. & Ando, R. Curvature, a mechanical link between the geometrical complexities of a fault: application to bends, kinks and rough faults. Geophys. J. Int. 223, 211–232 (2020).
Thakur, P., Huang, Y. & Kaneko, Y. Effects of low-velocity fault damage zones on long-term earthquake behaviors on mature strike-slip faults. J. Geophys. Res.e2020JB019587 (2020).
Kyriakopoulos, C., Newman, A., Thomas, A., Moore-Driskell, M. & Farmer, G. A new seismically constrained subduction interface model for Central America. J. Geophys. Res. 120, 5535–5548 (2015).
Handy, M. R. et al. Coupled crust-mantle response to slab tearing, bending, and rollback along the Dinaride-Hellenide orogen. Tectonics 38, 2803–2828 (2019).
Dieterich, J. H. Modeling of rock friction 1. experimental results and constitutive equations. J. Geophys. Res. 84, 2161–2168 (1979).
Ruina, A. Slip instability and state variable friction laws. J. Geophys. Res. 88, 10,359–10,370 (1983).
Rice, J. R. & Ruina, A. L. Stability of steady frictional slipping. J. Appl. Mech. 50, 343–349 (1983).
Erickson, B. A. et al. The community code verification exercise for simulating sequences of earthquakes and aseismic slip (SEAS). Seismol. Res. Lett. 91, 874–890 (2020).
Cattania, C. & Segall, P. Crack models of repeating earthquakes predict observed moment-recurrence scaling. J. Geophys. Res. (2018).
Acknowledgements
We thank the reviewers for their constructive feedback that helped improve the quality of the manuscript. We thank Xin Wang and Shengji Wei for technical help with seismological data. The study benefited from funding from the National Science Foundation, under award number EAR-1848192.
Author information
Authors and Affiliations
Contributions
S.S. and S.B. designed the study, S.S. conducted the study, and S.S. and S.B. wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Primary handling editor: Joseph Aslin
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sathiakumar, S., Barbot, S. The stop-start control of seismicity by fault bends along the Main Himalayan Thrust. Commun Earth Environ 2, 87 (2021). https://doi.org/10.1038/s43247-021-00153-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-021-00153-3
This article is cited by
-
Complex seismic image of the Main Himalayan Thrust in Garhwal and implication to earthquake hazard
Journal of Earth System Science (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.