Abstract
Determining the injection of glacial meltwater into polar oceans is crucial for quantifying the climate system response to ice sheet mass loss. However, meltwater is poorly observed and its pathways poorly known, especially in winter. Here we present winter meltwater distribution near Pine Island Glacier using data collected by tagged seals, revealing a highly variable meltwater distribution with two meltwater-rich layers in the upper 250 m and at around 450 m, connected by scattered meltwater-rich columns. We show that the hydrographic signature of meltwater is clearest in winter, when its presence can be unambiguously mapped. We argue that the buoyant meltwater provides near-surface heat that helps to maintain polynyas close to ice shelves. The meltwater feedback onto polynyas and air-sea heat fluxes demonstrates that although the processes determining the distribution of meltwater are small-scale, they are important to represent in Earth system models.
Similar content being viewed by others
Introduction
Floating ice shelves buttress the Antarctic Ice Sheet and decelerate the flow of its grounded ice. However, many ice shelves around Antarctica are thinning rapidly due primarily to basal melting1. The strongest melt has been reported in West Antarctic ice shelves such as the Pine Island Ice Shelf (PIIS) and Thwaites Ice Shelf2,3 where the deep (below about 450 m) intrusion of warm modified Circumpolar Deep Water (mCDW) transports heat southward via bathymetric troughs crossing the continental shelf4. The warm mCDW (about 3 °C above freezing) then enters the ice-shelf cavity (i.e. ocean beneath the ice shelf), circulates beneath the ice shelf providing heat for basal melting, and forms a relatively fresh meltwater-rich water mass that is colder than mCDW but warmer than the surrounding Winter Water (WW)4,5,6.
The fate and impact of the meltwater-rich water depends greatly on the depth at which it achieves neutral buoyancy and leaves the region flowing along density surfaces. If the relatively fresh meltwater-rich water rises, it could offset the brine rejected by sea ice formation and reduce occurrences of deep convection and bottom-water formation7,8. The relatively warm meltwater-rich water may also melt the sea ice in front of the ice shelf9,10,11. The resulting polynya would allow air-sea heat exchange and feedback onto ice-shelf basal melt by influencing the upper-ocean heat content1,8,12. The outflow of meltwater may boost the overturning circulation resulting in an enhanced heat flux into the ice cavity13,14,15,16. The meltwater-rich water is also a key supply of iron for continental shelf seas17. Therefore, although the volume of meltwater produced is small in comparison with the volumes of Antarctic shelf seas, it is believed to exert a disproportionate influence on regional and circumpolar circulation and climate.
PIIS is one of the most rapidly melting ice shelves2,3. Although meltwater has been identified in front of PIIS4,5,6,15,18,19,20, its spatial pattern is complex and poorly observed and understood. Meltwater is usually detected by its signature in hydrographic (i.e. temperature and salinity) observations. Nonetheless, as solar warming in the near-surface layer (upper 200 m) can be mistaken for the signal of relatively warm meltwater exiting the ice-shelf cavity, the apparent near-surface meltwater-rich layer deduced from austral summer hydrographic observations is usually thought to be an artefact of solar warming and is therefore neglected5,6,18,19. Thus, to date, the primary scientific focus in front of warm-cavity ice shelves has been on the deep meltwater layer with a maximum concentration at around 200–400 m5,15,18,19. However, in austral winter, when there can be no effect of solar radiation on the calculation of meltwater, the vertical meltwater distribution has hitherto been completely unknown due to the lack of available observations. The cyclonic Pine Island Bay (PIB) gyre is well defined from the sea surface to about 700-m depth in front of PIIS in both observational data4,21 and model outputs22, but the sparse observations have not yet clearly revealed the influence of the PIB gyre on the meltwater distribution. Introducing new datasets and approaches in this region is therefore important for ocean, cryosphere and climate research.
In this study we turn to newly available Antarctic winter observations (July–September 2014) to determine the distribution of near-surface meltwater exiting from beneath PIIS in winter. In winter, heat loss to the atmosphere and wind mixing lead to a mixed layer of cold WW with no summertime warm water remaining near the sea surface. The basal meltwater is much warmer (up to about 1 °C above freezing) than other upper-ocean water masses which have temperatures near the freezing point (about −1.9 °C) in winter. In this way we unambiguously distinguish ice-shelf basal meltwater from the ambient water masses. Here we present a set of 625 novel wintertime full-depth profiles of salinity and temperature collected by sensors attached onto three seals (see Methods), yielding four sections across PIB (Fig. 1). A meltwater signal is apparent in all sections in both winter (Figs. 2b, 2c, 3c, 4c, 5b, 6b) and summer (Figs. 3d, 4d). Our winter observations reveal clear signals of meltwater both at depth and near surface, connected by distinct meltwater-rich columns, while much of the WW layer remains meltwater-poor. This spatial heterogeneity is in contrast to the relatively high and horizontally-uniform upper-ocean meltwater content indicated by summer ship-based hydrography and previously-unpublished near-surface noble gas measurements. We argue that in winter, compared with the cold and dense ambient water, the meltwater-rich water has sufficient buoyancy to rise to near surface without undergoing intense lateral mixing. The winter processes revealed by our study are likely important for bringing nutrients to the near-surface layer prior to the spring bloom, and for bringing heat to the surface to prevent sea ice from forming and thus maintaining the polynyas in front of the ice shelves.
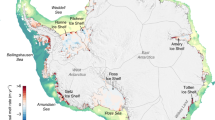
Positions of the seal-tag hydrographic profiles collected in winter (July–September) 2014 are indicated by solid dots and diamonds coloured by the conservative temperature, Θ, above freezing at 2 dbar (upper colour scale in red and blue). Positions of ship-based hydrographic profiles collected by conductivity-temperature-depth sensor in February 2014 are indicated by green diamonds aligned perpendicular and along to PIIS. Positions of profiles collected by vertical-microstructure profiler in February 2014 are indicate by the thick black line along PIIS. Ship-based conductivity-temperature-depth sensor profiles overlay seal-tag profiles, vertical-microstructure-profiler profiles are at the bottom. Thick grey arrows show the schematic of PIB gyre21. Rectangles enclose the profiles (diamonds) used for sections used in Figs. 3, 4, 5, 6. Bathymetry from RTOPO52 is shaded with grey colour scale on the left-hand side and ice photography (MODIS image from the 11 February, 2014) is shaded in blue with coastline in black. Inset map shows the location of southeastern Amundsen Sea.
a The observed values (thin lines and dots) and the depth-mean values (thick lines) passed through a 10-m moving-average filter of meltwater content in Section 1 (pink rectangle in Fig. 1), calculated from hydrographic data collected by seals in winter (blue), noble gas tracers in summer (black), ship-based hydrographic data collected by conductivity-temperature-depth sensor in summer (red) and vertical-microstructure profiler in summer (grey). Supplementary Fig. 1a,1b show the same plot as a, but for potential temperature and absolute salinity. b The conservative temperature—absolute salinity (\({\Theta} - S_{\mathrm{A}}\)) diagram of wintertime hydrographic data. The background shading indicates the meltwater content. The grey dots represent all data collected by seals in our study region (Fig. 1) in winter 2014. Thick lines overlaying the grey dots denote the depth-mean profiles in different sections (pink, green, blue and orange for Sections 1–4 in rectangles Fig. 1). WW and mCDW end-points (see Methods) are marked by dots near “WW” and “mCDW” texts. Isopycnals are indicated by solid black lines with labels. c same as b, but for the summertime ship-based hydrographic data collected by conductivity-temperature-depth sensor and vertical-microstructure profiler.
a Conservative temperature (Θ) above freezing (red–blue colour scale) and potential-density isopycnals (in \({\mathrm{kg}}\;{\mathrm{m}}^{ - 3}\)) contours from Section 1 (pink rectangle in Fig. 1) collected by seals in austral winter (Jul–Sep) 2014, with positions of profiles marked as triangles at the top of the panel. b Same as a, but for data from hydrographic profiles collected by ship-based vertical-microstructure profiler in February 2014. c, d same as a and b, but coloured by meltwater content (blue colour scale). Summertime meltwater signal in water layers above 27.42 isopycnal is partly associated with solar warming so is masked5,6,18,19 in d. Meltwater content calculated from noble gas tracers are indicated by dots overlaying the meltwater content calculated by ship-based hydrographic data in d. Supplementary Fig. 2a, 2b show the same plots as a and b, but coloured by absolute salinity.
a Conservative temperature (Θ) above freezing (red–blue colour scale) and potential-density isopycnals (in \({\mathrm{kg}}\;{\mathrm{m}}^{ - 3}\)) contours from Section 2 (green rectangle in Fig. 1) collected by seal in winter 2014, with positions of profiles marked as triangles at the top of the panel. b Same as a, but for data from ship-based hydrographic profiles collected by conductivity-temperature-depth sensor in February 2014. c, d same as a and b, but coloured by meltwater content (blue colour scale). Summertime meltwater signal in water layers above 27.42 isopycnal is partly associated with solar warming5,6,18,19 so is masked in d. Meltwater contents calculated from noble gas tracers are indicated by dots overlaying the meltwater content calculated by ship-based hydrographic data in d. Supplementary Fig. 3a, 3b show the same plots as a and b, but coloured by absolute salinity.
a Conservative temperature (Θ) above freezing (red–blue colour scale) and potential-density isopycnals (in \({\mathrm{kg}}\;{\mathrm{m}}^{ - 3}\)) contours from Section 3 (blue rectangle in Fig. 1) collected by seals in winter 2014, with positions of the profiles marked as triangles at the top of the panel. b Same as a, but coloured by meltwater content (blue colour scale). Supplementary Fig. 4a, 4b show the same plots as a and b, but coloured by absolute salinity.
a Conservative temperature (Θ) above freezing (red–blue colour scale) and potential-density isopycnals (in\({\mathrm{kg}}\;{\mathrm{m}}^{ - 3}\)) contours from Section 4 (orange rectangle in Fig. 1) collected by seals in winter 2014, with positions of the profiles marked as triangles at the top of the panel. b Same as a, but coloured by meltwater content (blue colour scale). Supplementary Fig. 5a, 5b show the same plots as a and b, but coloured by absolute salinity.
Results
Meltwater distribution in summer
Meltwater content values calculated from ship-based hydrographic and noble gas data are fairly consistent below about 150 m but significantly different above 150 m (Fig. 2a), where higher values from hydrographic data might be partly an artefact related to solar warming5,6,18,19. Noble gas tracers are considered a more reliable indicator of meltwater as no known processes other than glacial ice melting can generate the noble gas signal23,24,25. Although noble gas can be lost to the atmosphere, which can slightly decrease the value of the calculated meltwater content, this uncertainty is small compared with the uncertainties caused by air-sea interaction on the hydrographic tracers26,27. We therefore mask the meltwater content located above the \(27.42\) isopycnal (approximately the upper 200 m) that is calculated from hydrographic data in summer in Figs. 3d, 4d. In the following text, for the meltwater content in the masked region (Figs. 3d, 4d), we only discuss results calculated from noble gas data.
The hydrographic data reveal a strongly stratified water column above the \(27.55\) isopycnal (at about 450 m in summer, Figs. 3b, 4b). This stratification results from summertime solar warming, sea ice meltwater and surface runoff. The meltwater-rich water exported from ice cavity with density greater than the 27.55 \({\mathrm{kg}}\;{\mathrm{m}}^{ - 3}\) stays below the \(27.55\) isopycnal while the rest keeps ascending until it reaches neutral buoyancy. Summertime hydrographic and noble gas data in front of PIIS (dots and lines in black and red, Fig. 2a) reveal the meltwater content to gradually increase from about 500 m to about 100 m.
The summertime meltwater content above 27.55 isopycnal is always greater than 5 \({\mathrm{g}}\;{\mathrm{kg}}^{ - 1}\), which makes the horizontal variability of meltwater content relatively small in summer (Figs. 2a, 2c, 3d, 4d). Note that there is no indication of meltwater-poor layers nor columns above 400 m in summer from either the noble gas or hydrographic data in front of PIIS (Figs. 2a, 2c, 3d, 4d).
We identify a clear isopycnal dome centred at about 32 km from PIIS (Fig. 4b) that may be associated with the cyclonic PIB gyre21. The meltwater content is highest in front of PIIS and decreases with distance from PIIS until the centre of the PIB gyre, where it reaches its minimum value (Fig. 4d). The meltwater content then increases with distance from the gyre centre to the northwestern edge of the PIB gyre along Section 2 (Fig. 4d). This suggests that the PIB gyre is transporting meltwater from PIIS cyclonically to the outer PIB.
Unambiguous meltwater signal in winter
In austral winter, the consistently negative air-sea heat flux leads to a cold WW layer occupying the upper 400 m (Figs. 3a, 4a, 5a, 6a). However, Fig. 1 reveals a striking near-surface warm signature in front of PIIS spreading from the northeastern end of PIIS toward the southwest and along the coast toward Thwaites Ice Shelf, probably following the cyclonic PIB gyre. This water is about 0.6 °C above freezing, suggesting the existence of a heat source, which can only be the warm meltwater rising from the ice-shelf cavity that forms a warm near-surface meltwater-rich layer. Unlike summertime temperature measurements, which need noble gas data to confirm a near-surface meltwater content5,6,18,19, wintertime temperature data themselves are robust enough to allow us to unambiguously identify the presence of meltwater from the cold ambient water. Seal-tag profiles to the east of Thwaites Ice Shelf and in front of Dotson Ice Shelf, further west in the Amundsen Sea, also show a similar surface warming feature (Supplementary Fig. 6). We propose that this near-surface warming induced by the rising meltwater is a common but previously unidentified feature for warm-cavity ice shelves.
Close to PIIS (within about 5 km), unlike the relatively spatially uniform summertime meltwater distribution (Figs. 2a, 3d, 4d), the wintertime meltwater distribution is highly heterogeneous both horizontally and vertically (Figs. 2a, 3c, 4c, 5b, 6b). A near-surface meltwater-rich layer spreading above the cold WW (between the surface and the 27.45 isopycnal at about 250 m) and a deep meltwater-rich layer at around 450 m spreading below WW (near the 27.55 isopycnal) in front of PIIS, are clearly identified in all sections in winter (Figs. 3c, 4c, 5b, 6b). There are meltwater-rich columns connecting the deep and near-surface meltwater-rich layers through the WW layer, while a large proportion of the WW remains meltwater-poor (Figs. 2a, 2b, 3c, 4c, 5b, 6b). The meltwater-rich columns may be produced by sub-ice channels, which have been observed along the underside of the ice shelf9,10,11,28. These channels can potentially focus the glacial meltwater outflow as an inverted stream of buoyant freshwater that is trapped beneath the ice shelf until it exits the cavity in the form of plumes9,10,11,28.
To characterise the meltwater spreading away from PIIS in winter, we examine three sections that start from PIIS (Figs. 4c, 5b, 6b). Section 2 starts at the southwestern end of PIIS and extends across the whole PIB gyre toward the northwest (green rectangle in Fig. 1). The isopycnal doming associated with the PIB gyre is about 25 km further northwest in winter than summer in 2014 (Figs. 4c, 4d). Similar to the meltwater distribution pattern in summer (Fig. 4d), the meltwater distribution pattern in winter along Section 2 is concentrated near the ice-shelf front and the northwestern edge of the PIB gyre, and decreases towards the gyre centre (Fig. 4c). Section 3 also starts from the southwestern end of the ice-shelf front, but extends to the west downstream in the PIB gyre (blue rectangle in Fig.1). In Section 3, we detect a meltwater distribution pattern very similar to Section 1 (Fig. 3c), characterised by the two-layer structure and scattered meltwater-rich columns (Fig. 5b). The similarity of the meltwater distribution between Sections 1 and 3 suggests that large amounts of meltwater are transported westwards, which may impede the meltwater flowing toward the gyre centre and therefore cause the meltwater-poor gyre centre identified in Section 2 (Fig. 4c). Section 4 starts at the northeastern end of PIIS calving front and extends to the northwest against the direction of rotation of the PIB gyre (orange rectangle in Fig.1). The near-surface meltwater from PIIS is apparent up to about 23 km along Section 4 (extends against the PIB gyre circulation, Fig. 6b), about 35 km along Section 2 (almost across the PIB gyre centre, Fig. 4c) and at least 70 km along Section 3 (extends along the PIB gyre circulation, Fig. 5b). These differences may further imply that the PIB gyre plays an important role in the distributions of meltwater and its associated heat, and probably also nutrients such as iron, in PIB.
Unlike the summertime strongly stratified upper ocean, surface cooling and wind stirring lead to a homogeneous mixed layer above the 27.55 isopycnal in winter in regions where the meltwater and the heat it carries are absent (Figs. 3a, 4a, 5a, 6a). Therefore, the water above mCDW is denser in winter than in summer, which may allow meltwater-rich water to be comparably more buoyant and rise to a shallower depth in winter than in summer.
Discussion
The near-surface meltwater-rich layer appears to spread less far from PIIS than the deep meltwater-rich layer in Sections 2 and 4 in winter (Figs. 4c, 6b). Wintertime surface air-sea-ice interaction processes could be partially responsible for this apparent rapid loss of near-surface meltwater content. As soon as the meltwater exits the cavity and reaches the surface (and prior to the measurements being recorded by seals), some of the meltwater-related warm signal is likely to be quickly eroded by the strong surface cooling and likewise, the meltwater-related fresh signal may be obscured by brine rejected during sea ice formation7. Thus, the actual heat and freshwater supply from the meltwater could be larger than implied by our surface temperature and salinity measurements. Figure 2b reveals that both an increase of salinity and a decrease of temperature can lower the value of calculated meltwater content. Typical wintertime heat29 and salt fluxes30,31 induced by air-sea-ice interactions in front of PIIS might cause a decrease in meltwater content on the order of 2 \({\mathrm{g}}\;{\mathrm{kg}}^{ - 1}\;{\mathrm{day}}^{ - 1}\) (about 20% of the averaged wintertime near-surface meltwater content, see Methods).
Although the meltwater content calculated by wintertime hydrographic data may be decreased by surface processes, we suggest that it provides a reliable lower bound of the meltwater content rising to near surface in winter, because the observed meltwater signal near surface cannot be an artefact caused by solar warming, but only generated by meltwater itself. Noble gas measurements during both winter and summer would be necessary to accurately determine the extent of meltwater spreading20,32 but would be challenging to obtain in a region covered in sea ice for 10 months each year.
As mentioned above, there are meltwater-poor columns and two meltwater-rich layers in winter but not in summer (Figs. 3c, 3d, 4c, 4d, 5b, 6b). We hypothesise that the seasonal meltwater distributions found in the WW layer are caused by the seasonal stratification (Fig. 7). Previous research suggests that, in summer, when solar warming, sea ice melting and surface runoff stratify the WW layer (Figs. 3b, 4b), the rising meltwater can tilt isopycnals and trigger a centrifugal instability and related intense lateral mixing15. In contrast, in winter when surface cooling and wind mixing generate a homogeneous WW layer (Figs. 3a, 4a, 5a, 6a), we propose that rising meltwater can penetrate through WW via the meltwater-rich columns without undergoing intense lateral mixing (Fig. 7a). Therefore, in summer, the rising meltwater mixes intensely with the ambient water and spreads throughout the WW layer (Figs. 3d, 4d), whereas in winter, it spreads through meltwater-rich columns in the WW layer and leaves the rest of the WW layer meltwater-poor (Figs. 3c, 4c, 5b, 6b). Consequently, the spatial and temporal inhomogeneities of meltwater distribution are reduced in summer but strongly maintained in winter.
a Wintertime meltwater either spreads along pycnocline or rises through uniform water layers without undergoing intense lateral mixing. Wintertime meltwater rising to near surface melts sea ice and forms polynyas. b Summertime meltwater spreads along pycnocline as well. However, in contrast to wintertime meltwater, summertime rising meltwater penetrating through stratified water mixes with ambient water intensively and spreads widely.
Near the outflow region of the Totten Ice Shelf, a warm-cavity ice shelf in East Antarctica, an unstratified upper ocean, similar to the WW layer in front of PIIS in winter, was observed when sea ice blocks solar warming in summer33. Just as we identify in front of PIIS in winter, the meltwater distribution near Totten Ice Shelf is variable33, which may suggest that the mixing between the meltwater-rich water and the ambient water is also weak in the unstratified near-surface layer near the Totten Ice Shelf. This supports our hypothesis that upper-ocean stratification strongly influences the upward motion of basal meltwater from warm-cavity ice shelves.
The two layers of meltwater-rich water in winter suggest that different mechanisms create and/or control them. The melt rate of PIIS can vary by more than one order of magnitude within a month34 and might form meltwater-rich water with different buoyancies35. As the wintertime upper ocean dominated by WW is uniform, meltwater-rich water with density greater than WW (about \(1027.56\;{\mathrm{kg}}\;{\mathrm{m}}^{ - 3}\)) remains in the pycnocline below the WW layer while the remaining less dense meltwater-rich water can rise. Process model results show that meltwater-rich water with a buoyancy of \(2 \times 10^{ - 3}\;{\mathrm{m}}\;{\mathrm{s}}^{ - 2}\), equivalent to a density of about \(1027.36\;{\mathrm{kg}}\;{\mathrm{m}}^{ - 3}\), will be trapped in stratified water and cannot surface15. Therefore, the pycnocline at the mCDW-WW interface year-round may trap part of the rising meltwater and contribute to the deep meltwater-rich layer, while the meltwater-rich water with a density less than \(1027.36\;{\mathrm{kg}}\;{\mathrm{m}}^{ - 3}\) is likely to surface.
The seasonal meltwater distribution may vary interannually due to a range of processes. For example, in high-melting years, meltwater tends to be more buoyant and more likely to rise across isopycnals and reach a shallower depth15,36. In addition, interannual variability of the temperature and volume of mCDW might change the meltwater distribution by changing the melt rate and the pycnocline depth, where the deep meltwater-rich layer is located. The presence of sea ice blocking solar radiation could also alter the summertime meltwater distribution by weakening the solar-warming-related stratification of the upper ocean, as occurs near Totten Ice Shelf7. The spatially uniform meltwater distribution therefore may not be apparent in summer every year. However, due to the persistently negative net heat flux and strong wind stirring in winter, the wintertime upper-ocean stratification tends to be consistently weak. Thus, the highly variable meltwater distribution and weak lateral mixing of the rising meltwater seen in winter 2014 are likely to be representative of winter in other years.
We acknowledge several caveats to these results. First, we only have one year of seal-tag data in front of PIIS. One year is not enough to capture the long-term mean wintertime meltwater distribution nor its interannual variability in response to the large-scale forcing from, for example, El Niño–Southern Oscillation and the Southern Annular Mode, which may affect the meltwater distribution as the ocean state in front of PIIS is changed37,38. More data in winter are required. Second, the value of calculated meltwater content is sensitive to the choice of end-points (see Methods). Meltwater-poor profiles were identified in front of PIIS in summer 2009 and 19945. However, a meltwater calculation using the 2009 and 1994 data with the same end-points as our study cannot reproduce the same summertime meltwater-poor feature. The values of end-points of 2014 summertime WW are determined based on the WW formed in the previous winter (i.e. 2013 winter). WW properties are likely to vary interannually, but we assume here that the WW has been fully replenished in 2014.
If rising meltwater penetrates through the WW layer with less intense mixing, it can rise to near surface nearly unmodified. Wintertime meltwater is significantly more concentrated near surface than at depth, which may maintain more iron in the euphotic zone (i.e. upper 200 m) to boost productivity in the following spring17. The heat transported by the meltwater can increase the temperature of the near-surface layer up to about 1 °C above freezing (Fig. 1). Previous studies have pointed out that the residual meltwater near surface could maintain polynyas9,10,11. We therefore argue that the heat from meltwater that we observe is likely to prevent sea ice formation, allow melting of sea ice and thus increase the spatial extent of local polynyas in front of ice shelves. The strong offshore wind near the ice-shelf front may also transport warm near-surface water further away from PIIS and expand the meltwater-influenced region. The enlarged polynyas can then lead to enhanced air-sea fluxes and have further impacts on iceberg calving7,10,39 and ice-shelf melting7,12. The rising of meltwater might even reinforce the water mass exchanges and local ventilation near the ice shelf, as well as the reported overturning circulation14,15,16 to bring more warm water into the ice cavity to melt the ice shelf16. Because meltwater is critical to local ventilation13,14,15,16 and sea ice conditions7,9,10, representation of meltwater in climate models as uniform layers at specific depths without seasonality could lead to significant biases in the representation of ocean circulation, ocean-ice-shelf interaction, and surface heat exchanges.
Methods
Ship-based datasets
We used conductivity-temperature-depth (CTD) profiles, vertical-microstructure profiler (VMP-2000) temperature and salinity yoyo profiles, and noble gas measurements obtained during expedition JR294/29539, which took place on the RRS James Clark Ross under the Ocean2ice project of the UK’s Ice Sheet Stability programme (iSTAR, http://www.istar.ac.uk). The CTD was a Sea-Bird SBE 911 with two sensor pairs of conductivity and temperature. Temperature was calibrated using a Sea-Bird SBE 35 deep thermometer while salinity was calibrated using a Guildline Autosal salinometer. CTD data were averaged into 2-dbar pressure bins. We follow the Thermodynamic Equations of Seawater-10 standard40 for all hydrographic data. Full details of ship-based measurements can be found in the JR294/295 cruise report at https://www.bodc.ac.uk/resources/inventories/cruise_inventory/reports/jr294.pdf.
Nine CTD stations were occupied along PIIS calving front (see diamonds in the pink rectangle in Fig. 1, the median and mean distances from PIIS to the locations of CTD stations were both 0.5 km) on 11 February 2014 and seven additional CTD stations were occupied perpendicular to PIIS towards to northwest from 9 to 20 February 2014.
Fifty-eight VMP profiles of temperature and salinity were obtained along PIIS calving front (thick black line in the pink rectangle in Fig. 1, the median and mean distances from PIIS to the locations of VMP stations were about 1 and 1.5 km, respectively) deployed on 12 and 13 February 2014. Salinity data collected from VMP were calibrated against the calibrated salinity data from CTD. VMP data were averaged into 0.25-dbar pressure bins.
Seventy-one noble gas samples were collected at the CTD stations along PIIS calving front in copper tubes and sealed by crimping at both ends41. Noble gas samples were analysed in the Isotope Geochemistry Facility at Woods Hole Oceanographic Institution. Dissolved gas extracted from the water is captured into aluminosilicate glass bulbs that are maintained at a liquid nitrogen bath at \(- 196\;^\circ {\mathrm{C}}\). Then the bulbs are attached to a dual mass spectrometric system and analysed for He, Ne, Ar, Kr and Xe27. The noble gas are isolated on two cryogenic traps and selectively warmed to sequentially release each gas into the Hiden Quadrupole Mass Spectrometer for measurement by peak height manometry42. The reproducibility from \(N = 6\) duplicate samples for noble gas is between 0.1 and 1.8% and the analytical precision for noble gas is about 0.5–1%27. Noble gas are reported in micromoles per kilogram. We only use neon, argon, krypton and xenon in this study as the helium content can be influenced by mantle sources43.
Seal-tag hydrographic dataset
Seven southern elephant seals (Mirounga leonina) and seven Weddell seals (Leptonychotes weddellii) were captured and tagged with CTD-Satellite Relayed Data Loggers44 during the same cruise under the same project (iSTAR) around the Amundsen Sea in February 2014. Three tagged seals occupied Pine Island Bay while the tags kept measuring and transmitting data during winter. For our study, we defined four seal-tag CTD sections: Section 1 is oriented along the PIIS calving front (pink rectangle in Fig. 1), Section 2 extends from the southeastern end of the ice-shelf front towards the northwest (green rectangle in Fig. 1), Section 3 extends from the southeastern end of the PIIS calving front towards the west along the coast downstream with the PIB gyre circulation (blue rectangle in Fig. 1), and Section 4 extends from the northeastern end of the PIIS calving front towards the northwest upstream opposing the PIB gyre circulation (orange rectangle in Fig. 1). All measurements included in these four sections were collected by the same female southern elephant seal (# EF838). The median and mean distances from PIIS to the locations of seal-tag CTD measurements are about 1.5 and 2 km, respectively.
We bin-average the seal-tag profiles along each section using a horizontal bin size of 200 m. Most bins contain only one profile (Section 1 has 41 bins, including 6 bins that contain two profiles and the 35 bins that contain one profile; Section 2 has 12 bins, including 1 bin that contains two profiles and 11 bins that contain one profile; Section 3 has 30 bins, including 2 bins that contain two profiles and 28 bins that contain one profile; Section 3 has 30 bins, including 3 bins that contain three profiles, 4 bins that contain two profiles and 23 bins that contain one profile). All profiles used to produce transect plots are collected between 1 July 2014 and 10 September 2014 (Supplementary Fig. 7), when there is no solar radiation and when sufficient cooling, combined with wind mixing, leads to a consistent mixed layer of cold WW with no summer stratification and warm near-surface water remaining. The sampling biases of temperature measurements and related meltwater content are negligible, compared to the meltwater-induced variability.
The seals’ tags sample the temperature, salinity and pressure every 2 s then apply a 5-second median filter on the time series44. To reduce data transmission time, tags only select 18 depths to be transmitted to the Argos satellite system44,45. Each CTD profile was programmed to include measurements at 2 dbar, the depth maximum, the temperature minimum and the deep (over 100 dbar) temperature maximum to ensure data from near surface, centre of WW and CDW are included in the dataset. In addition to these four measurements, the other 14 measurements were chosen at equally spaced depths between the sea surface and the maximum depth. Tags measure only when seals ascend from their dives as seals tend to ascend nearly vertically. Only the deepest cast in every 4 h is transmitted44,46,47. We accessed fully-quality-controlled linearly interpolated data from Marine Mammals Exploring the Oceans Pole to Pole48,49 (http://www.meop.net/; MEOP). We further remove two data points with abnormally high salinity values collected on 8 August 2014. Estimated accuracy is \(\pm\!0.03\;^\circ {\mathrm{C}}\) for temperature and \(\pm\!0.05\) \({\mathrm{g}}\;{\mathrm{kg}}^{ - 1}\) for salinity. Full details can be found at http://www.meop.net/meop-portal/ctd-data.html.
Calculation of meltwater content from hydrographic data
We use the composite-tracer method50 for meltwater fraction calculation. The water masses used in this calculation are mCDW, WW and glacial meltwater. Tracers are conservative temperature (Θ) and absolute salinity (\(S_{\mathrm{A}}\)) for all hydrographic data and are assumed to be conservative. In temperature-salinity space (Figs. 2b, 2c), two lines connect the core characteristics of mCDW, WW and glacial meltwater: the mCDW-WW mixing line, where the mixture of mCDW and WW lies and mCDW-meltwater mixing line (i.e. Gade line51), where the mixture of mCDW and meltwater lies. The mixture of CDW, WW and meltwater lies between these two lines. The fractions of water masses at a data point are then determined by the distance that the point lies from the lines, derived from CTD measurements:
where \(\varphi _{{\mathrm{meltwater}}}\) is the meltwater fraction and Θ and \(S_{\mathrm{A}}\) with subscripts are the observed values or the characteristic properties (i.e. end-points) of water masses.
We chose the end-points following previously published research. The values of WW end-points (−1.86 °C of \({\Theta}_{{\mathrm{WW}}}\) and 34.32 \({\mathrm{g}}\;{\mathrm{kg}}^{ - 1}\)of \(S_{{\mathrm{A}}_{{\mathrm{WW}}}}\)) were derived by Biddle et al. (“pure WW” of Biddle et al., 201920) and do not vary seasonally. When we define the end-points for the meltwater, we consider it as an ice cube rather than a water parcel—as the meltwater comes from the interaction between the mCDW and the ice shelf. The \({\Theta}_{{\mathrm{meltwater}}}\) is calculated from the heat required to bring the far-field ice temperature (between −20 and −15 °C) to the melting temperature and the latent heat of fusion51. The end-points for the meltwater used in this study are therefore \(- 90.8^\circ {\mathrm{C}}\) for \({\Theta}_{{\mathrm{meltwater}}}\) and \(0\;{\mathrm{g}}\;{\mathrm{kg}}^{ - 1}\) for \(S_{{\mathrm{A}}_{{\mathrm{meltwater}}}}\) and do not vary seasonally19. The values of mCDW end-points (1.15 °C of \({\Theta}_{{\mathrm{mCDW}}}\) and 34.87\({\mathrm{g}}\;{\mathrm{kg}}^{ - 1}\)of \(S_{{\mathrm{A}}_{{\mathrm{mCDW}}}}\)) come from hydrographic data collected in PIB in summer19. Our seal-tag data from PIB reveal the \({\Theta}_{{\mathrm{mCDW}}}\) to be about \(0.03\;^\circ {\mathrm{C}}\) higher in summer (\(1.15\;^\circ {\mathrm{C}}\)) than in winter (\(1.12\;^\circ {\mathrm{C}}\)) while \(S_{{\mathrm{A}}_{{\mathrm{mCDW}}}}\) is almost unchanged seasonally (Supplementary Fig. 8). To estimate the uncertainty induced by the seasonal change in the mCDW endpoint, we re-calculated the meltwater content in our four wintertime sections using the wintertime endpoint. The meltwater content calculated with the wintertime endpoint values is slightly higher than the value calculated with summertime endpoint values (mean and median values increase, respectively, of 5.1% and 2.2% for Sections 1, 4.8% and 5.2% for Sections 2, 2.7% and 1.5% for Section 3, and 3.7% and 1.7% for Section 4) but the pattern of meltwater distribution remains the same. The comparison between the calculations using summertime and wintertime end-points is shown in Supplementary Figs. 9–12.
To estimate the uncertainty induced by the limited accuracy of the seal-tag hydrographic data, we run a Monte Carlo simulation on a set of 200 randomly generated hydrographic measurements. We perturb each simulated measurement 5000 times with normally distributed perturbations varying up to the largest uncertainty of seal-tag data (\(\pm\!0.03\;^\circ {\mathrm{C}}\) for temperature and \(\pm\!0.05\) \({\mathrm{g}}\;{\mathrm{kg}}^{ - 1}\)for salinity, Supplementary Fig. 13). We find these uncertainties in seal-tag hydrographic data can cause an uncertainty of \(\pm 2.87\;{\mathrm{g}}\;{\mathrm{kg}}^{ - 1}\) in the calculated meltwater content (Supplementary Fig. 14), which is about 30% of the averaged wintertime near-surface meltwater content. Nonetheless, we have confidence in the spatial distribution of hydrographic features in our study because all profiles we used in our four seal-tag sections were collected by a single Elephant Seal.
These uncertainty estimates suggest some sensitivity of the absolute values of meltwater content to the accuracy of chosen end-points and observational measurements. However, we do not expect a qualitative change to the pattern of meltwater content.
Quantifying the effect of wintertime surface cooling on derived meltwater values
In front of PIIS, the net heat flux calculated from ERA5 reanalysis data29 from 2014 winter (July–September) is on the order of \(3 \times 10^7\;{\mathrm{J}}\;{\mathrm{m}}^{ - 2}{\mathrm{day}}^{ - 1}\) and the 10-year climatology (2004–2013) net salt flux in winter produced by Tamura et al., 201131 is on the order of \(1\;{\mathrm{kg}}\;{\mathrm{m}}^{ - 2}{\mathrm{day}}^{ - 1}\). Note that, the datasets of surface fluxes we use here may contain substantial uncertainties in front of PIIS. If we assume that the surface cooling and brine rejection can only affect the mixed layer and the mixed-layer depth is 400 m, the heat and salt fluxes can cause a temperature decrease on the order of \(0.02\;^\circ {\mathrm{C}}\;{\mathrm{day}}^{ - 1}\) and a salinity increase on the order of \(3 \times 10^{ - 3}\;{\mathrm{g}}\;{\mathrm{kg}}^{ - 1}{\mathrm{day}}^{ - 1}\), which would be approximately equivalent to an apparent \(2\;{\mathrm{g}}\;{\mathrm{kg}}^{ - 1}{\mathrm{day}}^{ - 1}\) decrease (equivalent to about 20% of the averaged wintertime near-surface meltwater content) in derived meltwater in front of PIIS.
Calculation of meltwater content from noble gas datasets
The water masses used in this calculation are mCDW, air equilibrated water (AEW) and glacial meltwater. AEW is directly affected by the atmosphere and represents surface saturation values of the NG24. The end-points used for mCDW, AEW and meltwater chosen following previous research are: \(8.12 \times 10^{ - 3}\), \(8.43 \times 10^{ - 3}\)and \(91.6 \times 10^{ - 3}\;\mu {\mathrm{mol}}\;{\mathrm{kg}}^{ - 1}\) for \({\mathrm{Ne}}\); \(16.42\), \(17.52\) and \(44.46\;\mu {\mathrm{mol}}\;{\mathrm{kg}}^{ - 1}\) for \({\mathrm{Ar}}\); \(4.01 \times 10^{ - 3}\), \(4.43 \times 10^{ - 3}\) and \(5.84 \times 10^{ - 3}\;\mu {\mathrm{mol}}\;{\mathrm{kg}}^{ - 1}\) for Kr; \(0.604 \times 10^{ - 3}\), \(0.660 \times 10^{ - 3}\) and \(0.414 \times 10^{ - 3}\mu {\mathrm{mol}}\;{\mathrm{kg}}^{ - 1}\) for \({\mathrm{Xe}}\).
As the number of NG-tracer constraints plus mass conservation are more than the number of water masses to be identified in this calculation, we use Optimum Multiparameter Analysis to calculate the water mass fractions19,24. This calculation uses a least-squares regression with a nonnegativity constraint for our overdetermined equation:
where the \(\varphi _{{\mathrm{water}}\;{\mathrm{masses}}}\) is the fractions of water mases and names of noble gas with subscripts are the observed values or the characteristic properties of water masses. The reliability of meltwater content calculated from noble gas data is estimated by Biddle et al. 201920 to be \(\pm 0.5\;{\mathrm{g}}\;{\mathrm{kg}}^{ - 1}\).
Data availability
Bedrock topography is from RTOPO (2019) available at https://doi.pangaea.de/10.1594/PANGAEA.905295. Ice photography is a MODIS image (11/Feb, 2014) from the National Snow and Ice Data Center (NSIDC), available at https://nsidc.org/data/iceshelves_images/index_modis.html. Seal-tag data are available at http://www.meop.net/ and the British Oceanographic Data Centre (www.bodc.ac.uk/data/documents/cruise/8529/). Ship-based CTD and VMP data are available at the British Oceanographic Data Centre (www.bodc.ac.uk/data/documents/cruise/8529/). Noble gas data are available from the IEDA Earthchem Library at https://ecl.earthchem.org/view.php?id=1152. Salt flux data are available at http://www.lowtem.hokudai.ac.jp/wwwod/polar-seaflux/ and reanalysis data for heat fluxes calculation are available at https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-land?tab=form.
References
Pritchard, H. et al. Antarctic ice-sheet loss driven by basal melting of ice shelves. Nature 484, 502–505 (2012).
Paolo, F. S., Fricker, H. A. & Padman, L. Volume loss from Antarctic ice shelves is accelerating. Science 348, 327–331 (2015).
Rignot, E. et al. Four decades of Antarctic Ice Sheet mass balance from 1979–2017. Proc. Natl Acad. Sci. USA 116, 1095–1103 (2019).
Heywood, K. J. et al. Between the devil and the deep blue sea: the role of the Amundsen Sea continental shelf in exchanges between ocean and ice shelves. Oceanography 29, 118–129 (2016).
Jacobs, S. S., Jenkins, A., Giulivi, C. F. & Dutrieux, P. Stronger ocean circulation and increased melting under Pine Island Glacier ice shelf. Nat. Geosci. 48, 519 (2011).
Jenkins, A. et al. West Antarctic Ice Sheet retreat in the Amundsen Sea driven by decadal oceanic variability. Nat. Geosci. 11, 733–738 (2018).
Silvano, A. et al. Freshening by glacial meltwater enhances melting of ice shelves and reduces formation of Antarctic Bottom Water. Sci. Adv. 4, eaap9467 (2018).
Mackie, S., Smith, I. J., Ridley, J. K., Stevens, D. P. & Langhorne, P. J. Climate response to increasing Antarctic iceberg and ice shelf melt. J. Clim. 33, 8917–8938 (2020).
Bindschadler, R., Vaughan, D. G. & Vornberger, P. Variability of basal melt beneath the Pine Island Glacier ice shelf, West Antarctica. J. Glaciol. 57, 581–595 (2011).
Mankoff, K. D., Jacobs, S. S., Tulaczyk, S. M. & Stammerjohn, S. E. The role of Pine Island Glacier ice shelf basal channels in deep-water upwelling, polynyas and ocean circulation in Pine Island Bay, Antarctica. Ann. Glaciol. 53, 123–128 (2012).
Le, Brocq et al. Evidence from ice shelves for channelized meltwater flow beneath the Antarctic Ice Sheet. Nat. Geosci. 6, 945–948 (2013).
Fogwill, C. J., Phipps, S. J., Turney, C. S. M. & Golledge, N. R. Sensitivity of the Southern Ocean to enhanced regional Antarctic ice sheet meltwater input. Earth’s Future 3, 317–329 (2015).
Nakayama, Y., Timmermann, R., Rodehacke, C. B., Schröder, M. & Hellmer, H. H. Modeling the spreading of glacial meltwater from the Amundsen and Bellingshausen Seas. Geophys. Res. Lett. 41, 7942–7949 (2014).
Jourdain, N. C. et al. Ocean circulation and sea‐ice thinning induced by melting ice shelves in the Amundsen Sea. J. Geophys. Res. Oceans 122, 2550–2573 (2017).
Naveira Garabato, A. C. et al. Vigorous lateral export of the meltwater outflow from beneath an Antarctic ice shelf. Nature 542, 219–222 (2017).
Webber, B. G., Heywood, K. J., Stevens, D. P. & Assmann, K. M. The impact of overturning and horizontal circulation in Pine Island Trough on ice shelf melt in the eastern Amundsen Sea. J. Phys. Oceanogr. 49, 63–83 (2019).
St‐Laurent, P. et al. Modeling the seasonal cycle of iron and carbon fluxes in the Amundsen Sea Polynya, Antarctica. J. Geophys. Res. Oceans 124, 1544–1565 (2019).
Nakayama, Y., Schröder, M. & Hellmer, H. H. From circumpolar deep water to the glacial meltwater plume on the eastern Amundsen Shelf. Deep Sea Res. Part I 77, 50–62 (2013).
Biddle, L. C., Heywood, K. J., Kaiser, J. & Jenkins, A. Glacial meltwater identification in the Amundsen Sea. J. Phys. Oceanogr. 47, 933–954 (2017).
Biddle, L. C., Loose, B. & Heywood, K. J. Upper ocean distribution of glacial meltwater in the Amundsen Sea, Antarctica. J. Geophys. Res. Oceans 124, 6854–6870 (2019).
Thurnherr, A. M., Jacobs, S. S., Dutrieux, P. & Giulivi, C. F. Export and circulation of ice cavity water in Pine Island Bay. West Antarctica. J. Geophys. Res. 119, 1754–1764 (2014).
Schodlok, M. P., Menemenlis, D., Rignot, E. & Studinger, M. Sensitivity of the ice-shelf/ocean system to the sub-ice-shelf cavity shape measured by NASA IceBridge in Pine Island Glacier, West Antarctica. Ann. Glaciol. 53, 156–162 (2012).
Hohmann, R., Schlosser, P., Jacobs, S., Ludin, A. & Weppernig, R. Excess helium and neon in the southeast Pacific: Tracers for glacial meltwater. J. Geophys. Res. Oceans 107, 19–1 (2002).
Loose, B. & Jenkins, W. J. The five stable noble gases are sensitive unambiguous tracers of glacial meltwater. Geophys. Res. Lett. 41, 2835–2841 (2014).
Beaird, N., Straneo, F. & Jenkins, W. Spreading of Greenland meltwaters in the ocean revealed by noble gases. Geophys. Res. Lett. 42, 7705–7713 (2015).
Loose, B., Schlosser, P., Smethie, W. M. & Jacobs, S. An optimized estimate of glacial melt from the Ross Ice Shelf using noble gases, stable isotopes, and CFC transient tracers. J. Geophys. Res. Oceans 114, C8 (2009).
Stanley, R. H., Jenkins, W. J., Lott, D. E. III. & Doney, S. C. Noble gas constraints on air‐sea gas exchange and bubble fluxes. J. Geophys. Res. Oceans 114, C11 (2009).
Payne, A. J. et al. Numerical modeling of ocean‐ice interactions under Pine Island Bay’s ice shelf. J. Geophys. Res. Oceans 112, C10 (2007).
Copernicus Climate Change Service, Fifth generation of ECMWF atmospheric reanalyses of the global climate (ERA5). Copernicus Climate Change Service Climate Data Store https://cds.climate.copernicus.eu/cdsapp#!/home, (2017)
Tamura, T., Ohshima, K. I. & Nihashi, S. Mapping of sea ice production for Antarctic coastal polynyas. Geophys. Res. Lett. 35, 7 (2008).
Tamura, T., Ohshima, K. I., Nihashi, S. & Hasumi, H. Estimation of surface heat/salt fluxes associated with sea ice growth/melt in the Southern Ocean. Sci. Online Lett. Atmos 7, 17–20 (2011).
Kim, I. et al. The distribution of glacial meltwater in the Amundsen Sea, Antarctica, revealed by dissolved helium and neon. J. Geophys. Res. Oceans 121, 1654–1666 (2016).
Silvano, A., Rintoul, S. R., Peña‐Molino, B. & Williams, G. D. Distribution of water masses and meltwater on the continental shelf near the Totten and Moscow University ice shelves. J. Geophys. Res. Oceans 122, 2050–2068 (2017).
Davis, P. E. et al. Variability in basal melting beneath Pine Island Ice Shelf on weekly to monthly timescales. J. Geophys. Res. Oceans 123, 8655–8669 (2018).
Kimura, S. et al. Ocean mixing beneath Pine Island Glacier ice shelf. West Antarctica. J. Geophys. Res. Oceans 121, 8496–8510 (2016).
Kimura, S. et al. Oceanographic controls on the variability of ice‐shelf basal melting and circulation of glacial meltwater in the Amundsen Sea Embayment. Antarctica. J. Geophys. Res. Oceans 122, 10131–10155 (2017).
Nakayama, Y., Menemenlis, D., Zhang, H., Schodlok, M. & Rignot, E. Origin of circumpolar deep water intruding onto the Amundsen and Bellingshausen Sea continental shelves. Nat. Commun. 9, 1–9 (2018).
Dutrieux, P. et al. M. Strong sensitivity of Pine Island ice-shelf melting to climatic variability. Science 343, 174–178 (2014).
Heywood, K. J. et al. Ocean processes at the Antarctic continental slope. Philos. Trans. R. Soc. 372, 2019–20130047 (2014).
McDougall, T. J. & Barker, P. M. Getting started with TEOS-10 and the Gibbs Seawater (GSW) oceanographic toolbox. SCOR/IAPSO WG 127, 1–28 (2011).
Loose, B. et al. Estimating the recharge properties of the deep ocean using noble gases and helium isotopes. J. Geophys. Res. Oceans 121, 5959–5979 (2016).
Lott, D. E. Improvements in noble gas separation methodology: a nude cryogenic trap. Geochem. Geophys. Geosyst. 2, 2001GC000202 (2001).
Loose, B. et al. Evidence of an active volcanic heat source beneath the Pine Island Glacier. Nat. Commun. 9, 1–9 (2018).
Boehme, L. et al. Animal-borne CTD-Satellite Relay Data Loggers for real-time oceanographic data collection. Ocean Sci. 5, 685–695 (2009).
Photopoulou, T., Fedak, M. A., Matthiopoulos, J., McConnell, B. & Lovell, P. The generalized data management and collection protocol for conductivity-temperature-depth satellite relay data loggers. Animal Biotelem. 3, 21 (2015).
Fedak, M., Lovell, P., McConnell, B. & Hunter, C. Overcoming the constraints of long range radio telemetry from animals: getting more useful data from smaller packages. Integr. Comp. Biol. 42, 3–10 (2002).
Fedak, M. Marine animals as platforms for oceanographic sampling: a “win/win” situation for biology and operational oceanography. Mem. Natl Inst. Polar Res. 58, 133–147 (2004).
Roquet, F. et al. Estimates of the Southern Ocean general circulation improved by animal‐borne instruments. Geophys. Res. Lett. 40, 6176–6180 (2013).
Roquet, F. et al. A Southern Indian Ocean database of hydrographic profiles obtained with instrumented elephant seals. Sci. Data 1, 140028 (2014).
Jenkins, A. The impact of melting ice on ocean waters. J. Phys. Oceanogr. 29, 2370–2381 (1999).
Gade, H. G. Melting of ice in sea water: a primitive model with application to the Antarctic ice shelf and icebergs. J. Phys. Oceanogr. 9, 189–198 (1979).
Schaffer, J. & Timmermann, R. An update to Greenland and Antarctic ice sheet topography, cavity geometry, and global bathymetry (RTopo-2.0.4). PANGAEA https://doi.org/10.1594/PANGAEA.905295 (2019).
Acknowledgements
We thank the scientists, technicians and crew of the RSS James Clark Ross on the iSTAR cruise, especially those who helped with hydrographic measurements, for their hard work during the cruise to make the data collection possible. We thank Michael A. Fedak (Sea Mammal Research Unit, University of St Andrews) for help with seal tagging and Helen Mallett for quality control of seal-tag data after the iSTAR cruise. We thank Anna Wåhlin (University of Gothenburg), Alessandro Silvano (University of Southampton) and Shenjie Zhou (British Antarctic Survey) for helpful discussion. This work is funded by the UK Natural Environment Research Council under the iSTAR Programme through grants NE/J005703/1 (K.J.H., D.P.S., B.G.M.W.); European Research Council (under H2020-EU.1.1.) under research grant COMPASS (Climate-relevant Ocean Measurements and Processes on the Antarctic continental Shelf and Slope, grant agreement ID: 741120, K.J.H., Y.Z.); National Science Foundation Division of Polar Programs and Natural Environment Research Council under the research grant TARSAN (Thwaites-Amundsen Regional Survey and Network, NSF PLR 1738992 and NE/S006419/1, K.J.H.). Y.Z. is supported by China Scholarship Council and University of East Anglia. L.C.B. is supported by a Wallenberg Academy Fellowship (WAF 2015.0186) and Swedish Research Council grant (VR2019-04400) of S. Swart.
Author information
Authors and Affiliations
Contributions
Y.Z. performed the data analysis and wrote the manuscript with help from K.J.H., B.G.M.W., D.P.S., L.C.B., L.B. and B.L. K.J.H. led the JR294/295 cruise and L.C.B. joined it. L.B. helped with quality control of seal-tag data. L.C.B. and B.L. helped with the analysis and quality control of noble gas data. All authors discussed the results and contributed to the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Primary handling editor: Heike Langenberg
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zheng, Y., Heywood, K.J., Webber, B.G.M. et al. Winter seal-based observations reveal glacial meltwater surfacing in the southeastern Amundsen Sea. Commun Earth Environ 2, 40 (2021). https://doi.org/10.1038/s43247-021-00111-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-021-00111-z
This article is cited by
-
Ice shelf basal channel shape determines channelized ice-ocean interactions
Nature Communications (2024)
-
On-shelf circulation of warm water toward the Totten Ice Shelf in East Antarctica
Nature Communications (2023)
-
Suppressed basal melting in the eastern Thwaites Glacier grounding zone
Nature (2023)
-
Ocean variability beneath Thwaites Eastern Ice Shelf driven by the Pine Island Bay Gyre strength
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.