Abstract
The attribution of climate change allows for the evaluation of the contribution of human drivers to observed warming. At the global and hemispheric scales, many physical and observation-based methods have shown a dominant anthropogenic signal, in contrast, regional attribution of climate change relies on physically based numerical climate models. Here we show, using state-of-the-art statistical tests, the existence of a common nonlinear trend in observed regional air surface temperatures largely imparted by anthropogenic forcing. All regions, continents and countries considered have experienced warming during the past century due to increasing anthropogenic radiative forcing. The results show that we now experience mean temperatures that would have been considered extreme values during the mid-20th century. The adaptation window has been getting shorter and is projected to markedly decrease in the next few decades. Our findings provide independent empirical evidence about the anthropogenic influence on the observed warming trend in different regions of the world.
Similar content being viewed by others
Introduction
The attribution of the observed warming to natural and anthropogenic drivers is fundamental for the study of climate change1,2,3,4,5. Estimates of the contribution of natural and anthropogenic forcing to the observed changes in regional temperatures provide relevant information for policymakers to propose portfolios of mitigation and adaptation strategies6,7. These can also create more accurate perceptions of the risks of climate change and support pertinent climate policies. The Paris Agreement illustrates the international consensus about the anthropogenic contribution to warming and the need to curb greenhouse gas emissions6. However, in some political circles, (e.g., in the US), there seems to be an increasing skepticism that could hamper the success of international agreements8. This is important since even short delays in the participation of key countries in the Paris Agreement could render the climate targets unattainable9. Such a situation would require the adoption of prompter and stronger adaptation and risk reduction strategies. The current global health crisis10,11 and the expected economic downturn could significantly reduce international efforts to mitigate climate change.
A clear human fingerprint on global and hemispheric warming has been corroborated by a variety of physical and statistical methods, sometimes based on conflicting assumptions and approaches12,13,14,15,16,17. In contrast, regional attribution studies of long-term trends have been largely based on climate models1,18,19, which depend on the models’ performance to reproduce the observed climate and, despite their improvements, are less reliable at this scale5,20. Furthermore, model performance evaluation, and thus attribution results, may imply circular reasoning21. Observation-based attribution studies do not depend on climate models’ performance, tuning or calibration and can provide independent evidence (see “Methods”).
The attribution of regional changes in climate can influence the perception and participation in risk management efforts due to a sense of information sufficiency and responsibility22,23,24. The time of emergence (ToE)25 is a property of the climate system and provides an estimate of the date when the projected anthropogenic climate signal would exceed some measure of long-term natural variability. The ToE has also been used to estimate risk measures in ecological systems26 as well as the benefits of mitigation policy for reducing climate risk27. It can further be extended to represent a risk in the socio-environmental realm as a property of the interaction of the climate and human systems. For this, a more relevant metric for decision-makers consists in determining when the climate signal becomes larger than the variability societies have experienced in the recent past and what they are presently prepared for. Current thermal comfort standards, infrastructure, services, productive, and recreational activities, energy consumption, disease distribution, among many others are more a function of observed rather than of long-term climate natural variability28,29,30,31. We define this metric as the social time of emergence (SToE) and it consists of the signal to noise ratio of the climate response to changes in radiative forcing relative to a measure of the observed natural variability to which a society is able to adapt (“Methods”). A related metric is defined as the Time to Adapt (TtA) which expresses the expected number of years to reach a novel climate.
Based on recent statistical methods, we analyze annual mean surface air temperature from a variety of sources to evaluate the anthropogenic contribution to the observed warming trends. The analysis is performed for three different spatial scales: latitude belts, continent, and country levels. A set of 13 countries was selected based on a combination of spatial extension, their aggregate emissions and fossil fuels reserves, and relevance for international climate policy negotiations. Detection of climate change based on analyzing observed trends is not addressed here, instead, we focus on inferring the underlying warming trends produced by global aggregates of external forcing12,32,33. Natural variability and external forcing factors with marked influence on regional scales modulate the underlying warming trends imparted by the globally aggregated radiative forcing34,35 and can make observed and inferred warming trends differ in magnitudes and features such as breaks and their associated break dates32,33. We apply statistical methods to test the existence of common trends in nonstationary variables36,37,38. The tests allow us to evaluate the influence of anthropogenic forcing on the observed warming and whether the trend imparted by anthropogenic greenhouse gas forcing is present, accounting for factors such as the regional effects of forcings and natural variability that may have altered some relevant features (e.g., breaks in trend) of temperature series12.
Results
Common trends, the observed contributions of external forcing, and the evaluation of SToE and TtA
Cotrending tests36,37,38 were applied to sets of variables that include the radiative forcing of well-mixed greenhouse gases (WMGHG), the sum of all natural and anthropogenic radiative forcing (TRF), and the regional temperatures of interest (see “Methods”). This allows us to investigate the attribution of the observed warming in regional annual temperatures to anthropogenic influence. The selection of variables allows us to test for a common trend in WMGHG, TRF, and regional temperature. Finding a common trend implies that WMGHG, which has an anthropogenic origin, imparts the secular movement in TRF and regional temperatures, allowing other factors such as low-frequency natural variability and the regional effects of external forcing to have an important modulating influence.
For every region, continent and country analyzed there is strong evidence of a common trend between forcing variables and annual mean temperatures due to anthropogenic forcing (Supplementary Tables S1–S18). Across tests and datasets, the existence of cotrending is seldomly rejected and in all cases at least two out of the three tests support the conclusion of a common trend (Supplementary Table S19). These results strongly suggest a warming trend attributed to anthropogenic forcing at all spatial scales: latitude belts, continent, and country levels. The warming has been widespread and followed a common secular movement, modulated by the effects of regional climate variability, and the regional effects of forcings. These conclusions are robust to the use of different radiative forcing, temperature datasets, and cotrending tests (Supplementary Tables S1–S19).
The existence of a common long-term trend allows the use of ordinary least squares regression to estimate the transient climate response (TCR) for each temperature series, which measures the response of regional temperatures to changes in external radiative forcing (Supplementary Tables S20–S22). This is in accordance with the established linear relationship between radiative forcing and perturbative temperature changes, including regional temperatures with the exception of areas in which strong regional effects of external forcing occur1,39,40. At the most aggregated level, only the TCR of the extratropical region in the northern hemisphere (24°N–90°N) is statistically larger (±2SE) than those of the southern hemisphere and the tropics. The results for finer latitude belts reveal that, in general, only the values for the high latitudes in the northern hemisphere are statistically larger than those for other latitude belts (Supplementary Fig. S1). This is consistent with the results from climate models, in which the high latitudes warm faster than the rest of the world due to the arctic amplification phenomenon41,42. At the continental and country levels, the TCR tends to be larger at higher latitudes (Supplementary Figs. S2 and S3). With the BEST dataset, Asia and North America have the largest TCR values (0.79 and 0.76 °C per W m−2, respectively) followed by Europe, Africa, and South America (0.70, 0.63, 0.62 °C per W m−2, respectively). The lowest value is for Oceania (0.52 °C per W m−2), probably because of the ocean influence. These estimates are not statistically different from each other except for Asia and Oceania: for Asia, the TCR value is larger than those of Africa, South America, and Oceania; for Oceania, it is smaller than those of North America and Asia. Canada and Russia show the largest TCR of all countries, regardless of the temperature dataset used.
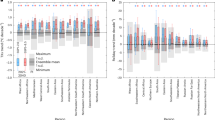
Estimates of the contributions of total and specific radiative forcing components to the secular trend at the country level can help decision-makers and the society to have a clearer picture of the magnitude of climate change and its causes. Using the estimated values of TCR, these contributions to the warming trends can be approximated (Fig. 1). To estimate the increase in temperature due to changes in both natural and anthropogenic radiative forcing, the TCR values are multiplied by TRF, while the TCR values are multiplied by WMGHG and solar forcing (SOLAR) to approximate the changes in temperatures due to these specific components of anthropogenic and natural forcings, respectively. Note that the estimates based on WMGHG and SOLAR do not represent the full response to changes in anthropogenic and natural forcings. The increase in anthropogenic radiative forcing due to WMGHG with respect to 1880 has produced significant warming in all selected countries, while non-WMGHG forcing had a modulating effect. By the year 2011, TRF contributed to an average increase of about 1 °C, with warming near 1.2–1.3 °C in France, Germany, and China and up to 1.6 °C and 1.7 °C in Canada and Russia (Fig. 1a and Supplementary Fig. S4a). Without the modulating effect of other forcing factors (Fig. 1b and Supplementary Fig. S4b), WMGHG would have led to a warming of at least 1.5 °C in most countries and more than 2.8 °C in Canada and Russia. Solar forcing alone would have produced slight warming of about 0.1–0.2 °C (Fig. 1c and Supplementary Fig. S4c). However, these warming estimates do not provide a clear perspective about how extreme these changes are. The SToE and TtA metrics offer a simple and easy way to quantify the relative magnitude of the changes and how fast they are occurring.
Panel a shows the response of regional temperature trends to changes in TRF. The response of regional temperature trends to changes in WMGHG is shown in panel b. Panel c shows the response of temperature trends to changes in SOLAR. Estimates of radiative forcing for 2011 are from Hansen’s dataset (see “Methods”). Units are °C.
The SToE was calculated for four reference years: 1880 and 1960, using the historical TRF43; 2010 and 2020 using the projections of TRF from the Representative Concentration Pathways (RCP) RCP8.5, RCP4.5, and RCP2.6 scenarios44. For each case, the warming signal was obtained as \(\Delta {\it{T}}_{{\it{ref,i,t}}} = {\it{TCR}}_{\it{i}} * ( {{\it{TRF}}_{\it{t}} - {\it{TRF}}_{{\it{ref}}}} )\), where i and t denote region and time, respectively, and ref is the reference year (“Methods”). The estimates of the temperature variability experienced by societies (σi) are the standard deviation of the residuals when regressing temperatures on TRF. The social time of emergence is defined as \({\mathrm{SToE}}({\mathrm{B}})_{{\it{i,ref}}} = min\left[ {year * {\it{I}}\left( {\frac{{\Delta {\it{T}}_{{\it{ref,i,t}}}}}{{B\sigma _i}} \ge 1} \right)} \right]\), where B is a constant; I(·) is the indicator function and year is the calendar date (“Methods”). Note that for trend stationary variables such as temperatures12,45, a warming signal (ΔT) equal to Bσi implies that the whole distribution of temperatures has shifted toward higher temperature values, not only the mean value. For example, if changes in temperatures are normally distributed and B = 2, the reference climate as experienced by the affected population at date SToE2 would have a very small overlap. The new mean temperature societies would experience at date SToE2 corresponds to the 97.5th percentile of the previous temperature distribution. For a SToE based on three standard deviations (SToE3), there would be no discernable overlap between the reference climate and the SToE.
The results show that most groups (whether by countries, continents, and latitude belts) are already experiencing annual mean temperatures that would have been considered extreme values with respect to the temperature distributions at the end of the 19th century or even during the second part of the 20th century. For the reference year 1880, the SToE2 dates are similar for all groups (Tables 1–3 and Supplementary Tables S23–S25), with estimated values in the late 1970s. When considering 1960 as the reference year, the SToE2 values increase slightly to the late 1980s. Such small variations when changing the reference year indicate that the climate is warming at an accelerated pace. The general spatial patterns of SToE2 values are similar to those of ToE reported in the literature25,46,47. The warming signal emerges from natural variability sooner in the tropics than in high latitudes where SToE occurs decades later. We also find that mid-latitude regions in the southern hemisphere may also experience novel climate conditions sooner than other latitudes. These regions are commonly identified as particularly vulnerable and with low financial and adaptation capacities46. The uncertainty in the estimates of StoE and TtA was evaluated using a bootstrap procedure (see “Methods”; Supplementary Tables S33–S35). The confidence intervals show the uncertainty in SToE to be highly skewed towards higher values and, in agreement with previous studies based on climate models’ simulations, the uncertainty is larger for higher latitudes than for near-tropical regions48.
The TtA metric (\({\it{TtA}}_{{\it{B,i,ref}}} = S{\it{ToE}}\left( {\it{B}} \right)_{{\it{i,ref}}} \;- \;{\it{year}}_{{\it{ref}}}\)) measures the transition time to reach a novel climate, i.e., the time available to adapt to a new climate. Taking 1880 as the reference year, TtA2,1880 is close to 100 years for most latitude belts and continents (Tables 1 and 2 and Supplementary Tables S23–S25), and for some countries it can be as large as 130 years (Table 3 and Supplementary Table S24). The TtA value decreased rapidly during the 20th century. By the mid-20th century (circa 1960), for most latitude belts, transitioning to a new climate (TtA2,1960) took only about 2–3 decades and at the continental level about 3 to 4 decades, with few exceptions such as Europe and North America, where this threshold is reached a decade later. The SToE2 dates and TtA are slightly more heterogeneous at the country level but follow a similar pattern (Table 3 and Supplementary Table S25). The time to adapt was more than halved in the mid-20th century, with TtA2,1960 values ranging from 30 to 60 years; e.g., the TtA2,1960 value is 57 years for the UK and Germany, while it is as low as 28 years for China and Brazil.
To illustrate the pace of change in climate and the reduction in the time societies may have to adapt given the change in climate, three RCP scenarios were used to project TtA and StoE using 2020 as the reference year (Tables 1–3 and Supplementary Tables S26–S32). These were selected to represent different levels of international mitigation policy: RCP8.5 represents a high warming scenario with no mitigation actions, while RCP4.5 and RCP2.6 can be viewed as approximations to the strict compliance of the Nationally Determined Contributions (NDC) commitments and the goals of the Paris Agreement49, respectively. Under the RCP8.5, the time available to adapt during this century becomes markedly shorter. The TtA values with respect to 2020 are about 12 years for Asia, Africa, and South America and 20 years for Europe and North America (Table 2 and Supplementary Tables S28–S29). At the country level, the TtA2,2020 values are around 20 years, with countries such as China and Brazil having values as low as 13 years (Table 3). Hence, in general, it would take about 10–20 years to experience mean temperatures that would be considered extreme by today’s standards. It is also notable that the confidence intervals for TtA and SToE2 become increasingly narrower for higher warming trajectories (Supplementary Tables S33–S35). This illustrates the magnitude of the adaptation challenges that societies would experience under high warming and no climate policy scenario. Moreover, the TtA values get smaller through the 20th century as the reference period is updated, making it unlikely that adaptation processes could keep up with the pace of change in climate conditions. Achieving strict compliance of the NDC would provide about 10–15 years more for most countries to adapt, although, for countries like Germany and the UK, the TtA2,2020 values could be about 25 years (Table 3). In contrast, under an emission scenario consistent with the goal of the Paris Agreement, the pressure to adapt would be much lower as the future and current climate would remain similar to that of 2020 during this century and the SToE22020 would take values beyond the present century (Table 3 and Supplementary Tables S31–S32).
Conclusions
We provided an observation-based regional attribution study that shows the existence of a dominant warming trend of anthropogenic origin in annual mean temperature series at different spatial scales, including continent and country level. The attribution results are robust to different temperatures, forcing datasets, cotrending tests, and assumptions about the time-series properties of the various series. The results show that a common nonlinear trend imparted by anthropogenic forcing (WMGHG) is present in all temperature series and that other forcing factors as a whole and natural variability have modulated it. Warming is widespread among the different regions with external forcing contributing to an increase of about 1 °C in 2011 across the world relative to 1880. Solar forcing had a slight warming effect of about 0.1° to 0.2 °C, while WMGHG forcing alone had a warming effect up to almost 3 °C in high latitudes of the northern hemisphere. The results are consistent with estimates of regional warming produced by climate models and with attribution studies based on models’ simulations1,42,50, providing an independent confirmation.
The concept of time of emergence was modified to make it more informative for decision-makers. It is based on the natural temperature variability over the observed period, which is better able to reflect what societies are prepared for, than long-term natural variability used in the standard construction of the ToE metric. Our study uses the attribution results to compute all the necessary ingredients to obtain SToE and TtA, which are interrelated metrics that express: (1) the date when the climate signal would exceed a threshold of B times the standard deviation of experienced natural temperature variability; and (2) the number of years left to reach this new climate. The results show that the time to adapt to a novel climate has been rapidly decreasing since the late 19th century. While TtA had values near 100 years at the beginning of the 20th century, by the mid-20th century it decreased to about 3 or 4 decades. Then, in only 3 or 4 decades most parts of the world have experienced mean temperature values that would have been considered extreme realizations from the right tail of temperature distributions with respect to the 1960s. Projections for this century indicate that taking 2020 as the reference year, most parts of the world would experience in about 10–20 years a novel climate that would now be considered extreme if warming is not controlled by relevant climate policies. Moreover, TtA is projected to rapidly decrease during this century. These results have important implications about the time available to adapt and whether successful adaptation is feasible. The estimates based on the RCP4.5 scenario suggest that an intermediate international mitigation effort could help by providing about 10–15 additional years for adaptation. Under an emissions scenario consistent with the Paris Agreement, most countries, continents, and regions would not experience temperature conditions much different than current ones.
Methods
Statistical methods for detection and attribution of climate change
The use of time-series methods in detection and attribution studies has a long history in climate change literature12,33,45,51,52,53. While these methods offer the advantages of not depending on the accuracy and performance of complex climate models, attribution is not possible without invoking a physical model that may be implicit in the statistical framework used and without assessing its physical consistency1. As described below, our attribution analysis is grounded on a zero-dimensional energy balance model and on the well-established result of stationary spatial patterns found in different generations of complex global atmosphere-ocean general circulation models54,55,56. Another challenge of attribution studies based on statistical techniques has been the correct identification of the time-series properties of climate and forcing variables. One of the main problems for obtaining empirical evidence about the influence of anthropogenic forcing using observed temperature records was the lack of adequate statistical tests to relate trending variables. While this was apparently solved with the introduction of cointegration techniques51,52, they impose important restrictions about the type of data-generating processes for temperature and forcing time series57. The analysis of the time-series properties of these variables using modern econometric tests indicates that cointegration techniques may find spurious relationships which generated a debate12,58,59,60. Here, we use an encompassing strategy based on a selection of cotrending tests that (1) makes results robust to the possible misidentification of the integration order and; (2) implies the existence of common breaks between the group of time series when a cotrending relationship is found. This is of importance because it provides strong evidence of causality in the relationships as recently argued61.
Zero-dimensional energy balance model and analyzing the influence of aggregate anthropogenic forcing at regional scales
The cotrending tests used here to analyze the influence of anthropogenic forcing are interpreted in terms of zero-dimensional energy balance model12,62,63 and the assumption of stationarity in the spatial patterns of change frequently used in the literature54,55,56.
The foundations of time-series models to analyze the relationships between radiative forcing and temperature series have been established in previous publications62,63. The time-series models used in our study can be represented by
where Tt is global temperature, Ft is a measure of the change in radiative forcing, α and γ are the intercept and slope parameters, respectively, and εt is a stochastic noise process that represents high to low-frequency natural variability12. The structural model supporting this statistical model can be described by a simple two-compartment climate model12,62,64,65. It consists of an upper compartment (U) which represents mainly the atmosphere and the upper ocean, and a lower compartment (L) associated with the deep ocean. These components are thermally coupled and can be described by the following equations62:
where CU and CL represent the heat capacity of the upper and lower compartments, respectively, and ΔTU and ΔTL are the changes in temperature in the respective compartments. F is the external forcing, and λ and β are the climate response and heat exchange coefficients. The heat capacity is much larger in the lower than in the upper compartment. The time constant of the response of the upper compartment is ~4–9 years, while for the lower compartment this value ranges from 400 to 580 years62,64. The analysis in this paper relates to the transient climate response (TCR) which characterizes how the upper compartment responds to sustained increases in the external radiative forcing. The TCR is defined by \({\it{S}}_{{\it{tr}}} = \left( {\kappa + \lambda } \right)^{ - 1}\) were κ is the heat uptake coefficient of the climate system. This coefficient relates the time-dependent changes in surface temperature and external forcing via ΔT(t) = StrF(t) and it is represented as γ in Eq. (1)12. The response of surface temperatures to external radiative forcing is dominated in the observed period by the short time constant of the upper compartment and the TCR. This provides a physical explanation of why temperatures and external forcing share a common nonlinear trend and common features such as co-breaks. By construction and following the physical model described above, the selection of variables used for two of the three cotrending tests36,38 (TRF, WMGHG, and temperature) implies evaluating causality and the importance of anthropogenic greenhouse gas forcing. The simplest radiative forcing series included in the cotrending tests is WMGHG and if its nonlinear trend is common to TRF and temperature series, this indicates that it is the dominant driver of the secular movement in TRF and temperatures. Moreover, co-breaking is a necessary condition for cotrending in one of the tests used and the existence of common breaks provides strong evidence for causality61. The third cotrending test used was developed specifically to test for a linear stable relationship between temperature and TRF and complements the other cotrending results37.
The analysis of simulations from different generations of global coupled ocean–atmosphere general circulation models have shown strong support for stationary spatial patterns of change in variables such as surface temperature54. This result has been used for a variety of purposes such as producing scaling patterns or climate scenarios56,66, time of emergence25, and regional TCR estimates based on aggregate quantities55. The regional estimates of TCR can be estimated regressing regional temperatures on external forcing series:
where β = φγ is the regional TCR, γ is the global TCR from Eq. (1), c is the intercept, Ft is a measure of TRF, and Tt,r is surface temperature in region r. It is important to note that if regional forcing (such as aerosols) significantly distorts the underlying global forcing trend, instead of only modulating it, there would be no cotrending between WMGHG, TRF, and regional temperature. Our results show that at the spatial scales and regions chosen for the analysis, regional forcing factors have not altered the secular movement imparted by global radiative forcing enough to preclude finding a common nonlinear trend between WMGHG and/or TRF and regional temperatures. Finding a cotrending relationship between TRF and regional temperatures helps to identify physically meaningful TCR, SToE, and TtA estimates. It also provides a rationale consistent with climate physics to use TRF to decompose regional temperature series into their trend and noise components, the latter including both natural oscillations and the modulation effects produced by regional external forcing.
Carrion-i-Silvestre and Kim cotrending and cointegration tests
Carrion-i-Silvestre and Kim37 proposed joint tests of cotrending and cointegration, which were developed specifically for a linear stable relationship between temperature and TRF. These tests are quasi-likelihood ratio tests in a bivariate system of temperature and TRF. Under the null hypothesis, TRF and temperature are linearly related; under the alternative, they are not. These tests aim at offering valid inferences regardless of the true type of the trends in the data. TRF is allowed, but not assumed, to have a stochastic trend in addition to an obvious trend due to the well-mixed greenhouse gas forcing. Temperature is also allowed, though not assumed, to have any of a stochastic trend, a broken linear trend, a trend due to the well-mixed-greenhouse-gases forcing. We use the \(\hat S_2\) test, which tests for an exact linear relationship. It is constructed as follows. Suppose that y, x, and m are observed vectors of temperature, total radiative forcing, and well-mixed greenhouse-gases series: y = (y1, …, yT)′, x = (x1, …, xT)′, and m = (m1, …, mT)′. In addition, define regressors such as 1T = (1, …, 1)′, Dx = [1T, m], \(\tau = (1, \cdots ,{\mathrm{T}})^{\prime}\), \({\mathrm{B}}\left( {\left[ {{\mathrm{T}}\pi } \right]} \right) = (0, \cdots ,0,1,2, \cdots ,{\mathrm{T}} - [{\mathrm{T}}\pi ])^{\prime}\) with \(\pi \in (0,1)\). The \(\hat S_2\) statistic combines \(\hat S_2^ +\) and \(\hat S_2^ -\) via \(\hat S_2 = \hat S_2^ + \cdot 1(\hat \alpha _s = 1) + \hat S_2^ - \cdot \left( {1 - 1\left( {\hat \alpha _s = 1} \right)} \right)\), where 1(·) is an indicator function; \(\hat \alpha _s = \hat \alpha\), if \(\left| {\hat \alpha - 1} \right| \,> \, 1.96{\mathrm{T}}^{ - 1/2}\), and 1, otherwise; and \(\hat \alpha\) is a consistent estimator for the sum of autoregressive coefficients of \(\hat x_0 = x\)-\(D_x(D_x^\prime D_x)^{ - 1}D_xx\). The \(\hat S_2^ +\) statistic is computed as follows. Let \(\hat \beta\) and \(\hat \delta _y\) be the ordinary least squares estimate from a regression of y on x and Dx and let \(\hat \delta _x\) be the ordinary least squares estimate from a regression of x on Dx. Obtain \({\hat{\mathrm{u}}} = [y - x\hat \beta - D_x\hat \delta _y,{\hat{u}}_x]\) and \({\hat{u}}_x = {{\Psi }}_0^{ - 1/2}(x - D_x\hat \delta _x)\) with \({{\Psi }}_0^{1/2}\) being a lower triangular matrix of ones. Then, estimate the long-run variance of \({\hat{\mathrm{u}}}_{\mathrm{t}}\), the transpose of the tth row of \(\hat u\) by \({\hat{{\Sigma }}} = T^{ - 1}\mathop {\sum } {\hat{u}}_t{\hat{u}}_t^\prime\), \({\hat{{\Gamma }}} = \sum _j \kappa \left( {\frac{j}{{b_T}}} \right)R(j)\), \({\it{R}}({\it{j}}) = {\it{T}}^{ - 1}\mathop {\sum } {\hat{u}}_{\it{t}}{\hat{u}}_{{\it{t}} + {\it{j}}}^\prime\), and \({\hat{{\Omega }}} = {\hat{{\Sigma }}} + {\hat{{\Gamma }}} + {\hat{{\Gamma }}}^{\prime}\), where κ(·) is a kernel function and bT is a bandwidth. Partition \({\hat{{\Omega }}} = \left( {\begin{array}{*{20}{c}} {\hat \omega _{yy}} & {\hat \omega _{xy}} \\ {\hat \omega _{yx}} & {\hat \omega _{xx}} \end{array}} \right)\), \({\hat{{\Sigma }}} = \left( {\begin{array}{*{20}{c}} {\hat \sigma _{yy}} & {\hat \sigma _{xy}} \\ {\hat \sigma _{yx}} & {\hat \sigma _{xx}} \end{array}} \right)\), and \({\hat{{\Gamma }}} = \left( {\begin{array}{*{20}{c}} {\hat \gamma _{yy}} & {\hat \gamma _{xy}} \\ {\hat \gamma _{yx}} & {\hat \gamma _{xx}} \end{array}} \right)\). Then, \(\hat \omega _{yy|x} = \kappa ^\prime \hat \Omega \kappa\), \(\hat \gamma _{{\it{yy|x}}} = \kappa ^\prime \hat \Gamma \kappa\), and \({\hat{{\Lambda }}}_x = (\hat \sigma _{xy} + \hat \gamma _{xy},\hat \sigma _{xy} + \hat \sigma _{xx})\) with \(\kappa = (1, - \hat \omega _{xy}/\hat \omega _{xx})^{\prime}\). Define \(l_{T}^{+} ( \theta {\mathrm{|}}Z) = - \frac{1}{2}\log \frac{{|Z^{\prime} {\Psi}_{\theta} ^{ - 1}Z|}}{{|Z^{\prime} Z|}} - \frac{1}{{2\hat \omega _{yy|x}}}y_\theta ^{ + \prime }( {\Psi}_\theta ^{ - 1} - {\Psi}_\theta ^{ - 1}Z(Z^{\prime} {\Psi}_\theta ^{ - 1}Z)^{ - 1} Z^{\prime} {\Psi}_\theta ^{ - 1} )y_{\theta}^{+}\) for a given θ and Z where \(y_\theta ^ + = y - \theta \hat u_x\hat \omega _{xx}^{ - 1}\hat \omega _{xy} - \hat u{\hat{{\Sigma }}}^{ - 1}{\hat{{\Lambda }}}_x^\prime \hat \beta\) and \({{\Psi }}_\theta ^{1/2}\) is a lower triangular matrix with ones on the diagonal and 1 − θ off the diagonal. Then, \({\hat {S}}_2^ + = - 2\left[ {{\mathrm{l}}_{\mathrm{T}}^ + \left( {1{\mathrm{|Z}}_2^ + } \right) - \mathop {{\max }}\nolimits_{\pi \in \left[ {.15 ,.85} \right]} {\mathrm{l}}_{\mathrm{T}}^ + \left( {\bar \theta {\mathrm{|Z}}_\pi ^ + } \right)} \right] - 2{\bar {\lambda}} {\hat {\omega }}_{yy|x}^{ - 1}{\hat {\gamma }}_{yy|x}\) where \({\mathrm{Z}}_2^ + = [x^ + ,1_T]\), \({\mathrm{Z}}_\pi ^ + = [{\mathrm{x}}^ + ,D_x,\tau ,{\mathrm{B}}([{\mathrm{T}}\pi ])]\), \({\mathrm{x}}^ + = {\it{x}} - \hat u\hat \Sigma ^{ - 1}\hat \Lambda _{\it{x}}^\prime\), \(\bar \theta = 1 - \bar \lambda /T\), and \(\bar \lambda = 13.5\). On the other hand, the \(\hat S_2^ -\) statistic is computed as follows. \({\hat {S}}_2^ - = - 2\left[ {{\mathrm{l}}_{\mathrm{T}}^ - \left( {1{\mathrm{|Z}}_2} \right) - \mathop {{\max }}\nolimits_{\pi \in \left[ {.15 ,.85} \right]} {\mathrm{l}}_{\mathrm{T}}^ - \left( {\bar \theta {\mathrm{|Z}}_\pi } \right)} \right] - 2\bar \lambda \hat \omega _{yy}^{ - 1}\,\hat \gamma _{yy}\), where \({\mathrm{l}}_T^ - \left( {\theta {\mathrm{|}}Z} \right) = - \frac{1}{2}\log \frac{{|Z^\prime {{\Psi }}_\theta ^{ - 1}Z|}}{{|Z^\prime Z|}} - \frac{1}{{2\hat \omega _{yy}}}y^{\prime}\left( {{{\Psi }}_\theta ^{ - 1} - {{\Psi }}_\theta ^{ - 1}Z(Z^\prime {{\Psi }}_\theta ^{ - 1}Z)^{ - 1}Z^{\prime}{{\Psi }}_\theta ^{ - 1}} \right)y\) and \(\hat \omega _{yy}\) and \(\hat \gamma _{yy}\) are obtained from \({\hat{\mathrm{u}}} = [y - x\hat \beta - D_x\hat \delta _y,x - D_x\hat \delta _x]\).
Bierens nonparametric nonlinear cotrending test
The advantage of the test proposed by Bierens36 is that the nonlinear trend does not have to be parameterized, it can be modeled as zt = g(t) + μt where \(g\left( t \right) = \beta _0 + \beta _1t + f\left( t \right)\); zt is a k-variate time series, μt is a k-variate zero-mean stationary process and f(t) is a deterministic k-variate general nonlinear trend function that allow for structural changes. Nonlinear cotrending occurs when there exists a non-zero vector θ such that θ′f(t) = 0 where a’b is the inner product of two vectors a and b. Hence, the null hypothesis of this test is that the multivariate time series zt is nonlinear cotrended, and one or more linear combinations of the time series are stationary around a constant or a linear trend. This test is a cointegration test in the case when it is applied to series that contain unit roots. The nonparametric test for nonlinear cotrending is based on the generalized eigenvalues of the matrices M1 and M2 defined by \(M_1 = T^{ - 1}\mathop {\sum}\nolimits_{t = 1}^T {\hat F\left( {t/T} \right)\hat F\left( {t/T} \right)^\prime }\), where \(\hat F\left( x \right) = T^{ - 1}\mathop {\sum}\nolimits_{t = 1}^{\left[ {Tx} \right]} {( {z_t - \hat \beta _0 - \hat \beta _1t} )}\) if \(x \in \left[ {T^{ - 1},1} \right]\) and \(\hat F\left( x \right) = 0\) if \(x \in \left[ {0,} \right.\left. {T^{ - 1}} \right)\), with \(\hat \beta _0\) and \(\hat \beta _1\) being the estimates of the vectors of intercepts and slope parameters in a regression of zt on a constant and a time trend. M2 is defined as \({M}_{2} = {T}^{ - 1}\sum_{t = m}^{T} [ {m}^{-1}\sum_{j = 0}^{m - 1} ({z}_{{t} - {j}} - \hat{\beta} _{0} - \hat{\beta} _{1} ( {t} - {j} ) ) ][{m}^{ - 1}\sum_{j = 0}^{m - 1} ( {z}_{t} - {j} - {\hat{\beta}}_{0} - {\hat{\beta}}_{1}( t - j ) )]^{\prime}\), where m = Ta with T the number of observations and α = 0.5. Solving \(\left| {M_1 - \lambda M_2} \right| = 0\) and denoting the solution of the largest rth eigenvalue by \(\hat \lambda _r\), the test statistic is \(T^{1 - \alpha }\hat \lambda _r\). The null hypothesis is that there are r cotrending vectors against the alternative of r − 1 cotrending vectors. The test has a non-standard distribution and the critical values are tabulated in Bierens36. The existence of r cotrending vectors in r + 1 series indicates the presence of r linear combinations of the series that are stationary around a linear trend and that these series share a single common nonlinear deterministic trend. Such a result indicates a strong secular co-movement in the r + 1 series.
Guo and Shintani consistent cotrending rank selection when both stochastic and nonlinear deterministic trends are present
Guo and Shintani38,67 propose a model-free consistent cotrending rank selection procedure when both stochastic and nonlinear deterministic trends are present in a multivariate system. Their procedure defines two cotrending ranks: r1, which is the total number of linearly independent vectors in an m-variables system that can eliminate both stochastic and deterministic trends at the same time; and r2, which is the total number of linearly independent vectors that can eliminate the deterministic trend, regardless of whether they eliminate the stochastic trend at the same time. r2 is called the weak cotrending rank and m − r2 is the total number of common deterministic trends. These cotrending ranks can be estimated in paired or joint ways, but for large enough samples (T = 100) the two methods yield similar results. The proposed cotrending rank selection procedure allows for a wide variety of nonlinear trends, including breaks in the trend function and smooth transitions. In the case of breaks in the trend function, no common deterministic trends will be reported by this procedure if either: (1) there is no co-breaking (i.e., the breaks in the trend functions of the variables in the system are not common) or; (2) not all of the piece-wise trend slope coefficients are proportional between the trend functions. For cotrending to hold, co-breaking is a necessary, but not sufficient, condition. Here we report only the weak cotrending rank r2 as the literature has shown temperature and radiative forcing series to be better represented as trend stationary processes with breaks in their trend function3,39,43. Let Zt denote an m-variate process for t = 1, …, T. Let \(\hat \lambda _1 \ge \hat \lambda _2 \ge \cdots \ge \hat \lambda _m\) denote the eigenvalues of \(S_{11}^{ - 1}{\mathrm{S}}_{00}\) where \({\mathrm{S}}_{11} = T^{ - 1}\mathop {\sum }\nolimits_{t = 1}^T z_tz_t^{\prime}\) and \({\mathrm{S}}_{00} = T^{ - 1}\mathop {\sum }\nolimits_{t = 2}^T (z_t - z_{t - 1})(z_t - z_{t - 1})^{\prime}\). The paired procedure selects r1 and r2 independently by minimizing each of \({\mathrm{VN}}_1\left( {r_1} \right) = - \mathop {\sum }\nolimits_{i = 1}^{r_1} \hat \lambda _i + {\mathrm{f}}\left( {{\mathrm{r}}_1} \right){\mathrm{C}}_{\mathrm{T}}/T\) and \({\mathrm{VN}}_2\left( {r_2} \right) = - \mathop {\sum }\nolimits_{i = 1}^{r_2} \hat \lambda _i + {\mathrm{f}}\left( {{\mathrm{r}}_2} \right){\mathrm{C}}_{\mathrm{T}}^{\prime}/T^2\). The joint procedure selects both r1 and r2 by minimizing \({\mathrm{VN}}\left( {r_1,r_2} \right) = - T^a\mathop {\sum}\nolimits_{i = 1}^{r_1} {\hat \lambda _i - \mathop {\sum}\nolimits_{i = r_1 + 1}^{r_2} {\hat \lambda _i + {\mathrm{f}}\left( {{\mathrm{r}}_1} \right){\mathrm{C}}_{\mathrm{T}}/T + {\mathrm{f}}\left( {{\mathrm{r}}_2} \right){\mathrm{C}}_{\mathrm{T}}^\prime /T^2} }\) with 0 < a < 1. CT = In(T), 2 In (In(T)), and 2 for the Bayesian information criterion (BIC), Hannan–Quinn criterion (HQ), and Akaike information criterion (AIC), respectively. f(s) is an increasing function in s. The BIC was used for the results presented here.
Regression-based method to estimate the TCR and natural variability around the warming trend
The results from cotrending tests and of the procedure to estimate the cotrending rank indicate that temperature series from all spatial scales considered share a single common trend which is imparted by TRF and dominated by WMGHG. Deviations from such a trend are consistent with a second-order stationary process and thus natural variability is deemed to remain stable during the sample period. Both the estimation of TCR and the natural variability around the trend use the results of the cotrending tests. First, we use ordinary least square to estimate the regression Tt = α + βTRFt + εt, in which β represents the TCR. The residuals εt represent the variations around the warming trend produced by natural variability and other factors such as regional/local forcing. We use εt to produce estimates of the natural variability around the warming trend (σ) required to calculate SToE and TtA. Given the time-series properties of εt, σ is assumed to be invariant during the observational period and thus we use the full sample to estimate the value of σ to provide a measure of the variations in temperature for which societies are assumed to be prepared for and able to cope with.
ToE and the procedure to compute SToE and TtA
ToE has been commonly used in the climate change literature to estimate when the warming signal will become larger than the background climate variability25. ToE helps to put into context how extreme warming projections are with respect to climate variability and thus seek to identify regions where risk could be higher and faced sooner. Examples of the application of this concept are found in ecology26, climate policy, and reducing the risk of climate extremes27. Its application covers diverse spatial and temporal scales as well as climate variables25,46,47,68. These studies typically involve using simulations from complex physical models to approximate the climate signal and a measure of long-term climate variability.
The social time of emergence SToE is evaluated using the estimates of TCR and σ via the following steps: (1) obtain estimates of the warming trend for a given reference period; (2) estimate the warming trend via \(\Delta {\it{T}}_{{\it{ref,i,t}}} = {\it{TCR}}_{\it{i}} * ( {TRF_t - TRF_{ref}} )\) where i and t denote region and time, respectively, and ref represents the reference year. Subtracting the constant TRFref from TRFt implies that at the reference year ΔTref,i,t is equal to zero; (3) the social time of emergence is calculated as \({\it{SToE}}({\it{B}})_{{\it{i,ref}}} = {\it{min}}\left[ {year*I\left( {\frac{{\Delta T_{ref,i,t}}}{{B\sigma _i}} \ge 1} \right)} \right]\), where B is a constant; I(·) is the indicator function; year is the calendar year and σi the standard deviation of the residuals obtained from regressing temperatures of region i on TRF. The time to adapt metric TtA is obtained by subtracting the reference year from the estimated SToE value, i.e., \(TtA_{B,i,ref} = SToE\left( B \right)_{i,ref}\; -\; year_{ref}\).
Bootstrap procedure for constructing SToE and TtA confidence intervals
The bootstrap procedure we employ consists of two steps: (i) we estimate the regression, \({\mathrm{T}}_{\mathrm{t}} = \alpha + \beta F_t + {\it{\epsilon }}_t\) to obtain \({{\hat \epsilon }}_t = {\mathrm{T}}_{\mathrm{t}} - \hat \alpha - \hat \beta F_t\). Then, we fit an auto-regression of order 2 on \(\hat \epsilon _t\), which is \({{\hat \epsilon }}_t = c_0 + c_1{{\hat \epsilon }}_{t - 1} + c_2{{\hat \epsilon }}_{t - 2} + \eta _t\). Since the ordinary least squares estimator used for an auto-regression is subject to bias, we correct it by a bootstrap procedure. That is, we subtract from the ordinary least squares estimate of (c0, c1, c2) the bias computed as the difference between the average of bootstrap estimates and the original estimate. If the bias adjusted estimates imply a nonstationary autoregressive process, then we reduce the magnitude of bias adjustment until the implied autoregressive process becomes stationary; (ii) Using the bias-corrected estimate of (c0, c1, c2), we re-construct bootstrap samples of \(\hat \epsilon _t\) and combine them with \(\hat \alpha + \hat \beta F_t\) to generate bootstrap samples of Tt. For each bootstrap sample of Tt, we compute and store SToE and TtA measures. The confidence intervals reported in Supplementary Tables S33–S35 are percentiles of the bootstrap distributions of SToE and TtA.
Data description and sources
The annual mean near-surface temperature anomalies for zonal means (latitude belts) were obtained from the GISTEMP dataset69 of the Goddard Institute for Space Studies of NASA (https://data.giss.nasa.gov/gistemp/), the HadCRUT4 dataset70 version HadCRUT.4.6.0.0 from the Met Office https://www.metoffice.gov.uk/hadobs/hadcrut4/ and the Climate Explorer website (https://climexp.knmi.nl/select.cgi?hadcrut4); the corrected and filled-in HadCRUT4 dataset (version 2; referred to here as HadCRUT4k) of Cowtan and Way71, see https://www-users.york.ac.uk/~kdc3/papers/coverage2013/series.html; https://climexp.knmi.nl/select.cgi?had4sst4_krig_v2).
The continent-level annual mean near-surface temperature anomalies were obtained from the Berkeley Earth Surface Temperatures (BEST; http://berkeleyearth.org/) and; the NOAA GlobalTemp dataset (https://www.ncdc.noaa.gov/cag/global/time-series). The country-level annual mean surface temperature anomalies were obtained from the Berkeley Earth Surface Temperatures (BEST; http://berkeleyearth.org/) and the CRU TS v. 4.0372 and the derived CY v. 4.03 dataset (https://crudata.uea.ac.uk/cru/data/hrg/).
We use two radiative forcing datasets from the Goddard Institute for Space Studies of NASA (https://data.giss.nasa.gov/modelforce/). The main one used is that of Hansen43 and for sensitivity analyses we also consider the Miller dataset73. The aggregated radiative forcing variables used are the well-mixed greenhouse gases (WMGHGs; carbon dioxide (CO2), methane (NH4), nitrous oxide (N2O), and CFCs), and the total radiative forcing (TRF), which includes WMGHG plus ozone (O3), stratospheric water vapor, solar irradiance, land-use change, snow albedo, black carbon, reflective tropospheric aerosols, and the indirect effect of aerosols.
We use simulations from climate models included in the Atlas subset of the CMIP5 ensemble50 to compare our regional TCR estimates with those that can be inferred from current climate projections. The Atlas subset includes a single realization per model in the CMIP5 ensemble. We use the historical simulations and those produced under the RCP4.5 scenario. The complete list of models is given in Table 1 of the Annex of the Working Group I AR5 report50. The models with simulations for the RCP4.5 scenario are HadGEM2-CC, HadGEM2-ES, inmcm4, IPSL-CM5A-LR, IPSL-CM5A-MR, IPSL-CM5B-LR, MIROC5, MIROC-ESM, MIROC-ESM-CHEM, MPI-ESM-LR, MPI-ESM-MR, MPI-ESM-P, MRI-CGCM3, NorESM1-M, NorESM1-ME. For each simulation, we calculated a 20-year average centered around 2011 (the year for which estimates in Fig. 1 are reported) and obtained the TRF value for 2011 from the RCP emission scenario database (http://www.pik-potsdam.de/~mmalte/rcps/index.htm)44. TCR is calculated as \({\it{TCR}} = \frac{{\Delta \bar T_{2011}}}{{{\it{TRF}}_{2011}}}\). Supplementary Tables S20 to S22 provide the TCR estimates (ensemble mean and 95% confidence intervals) for each region based on the IPCC’s Atlas subset. The results show that the estimates of TCR based on the Atlas subset of the CMIP5 and those presented here are similar for all regions. Moreover, in all cases, our estimates fall within the confidence intervals of the models’ projections.
Data availability
No datasets were generated during this study. All data used in this study are publicly available from the sources cited in “Methods” and at https://doi.org/10.6084/m9.figshare.13380779.v1.
References
Bindoff, N. L. et al. Detection and attribution of climate change: From global to regional. in Climate Change 2013: The physical science basis. Contribution of working group i to the fifth assessment report of the intergovernmental panel on climate change (eds Stocker, T. F. et al.) 867–952 (Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2013).
Rogelj, J. et al. Paris agreement climate proposals need a boost to keep warming well below 2°C. Nature 534, 631–639 (2016).
Trenberth, K. E., Fasullo, J. T. & Shepherd, T. G. Attribution of climate extreme events. Nat. Clim. Chang. 5, 725–730 (2015).
Rosenzweig, C. & Neofotis, P. Detection and attribution of anthropogenic climate change impacts. Wiley Interdiscip. Rev. Clim. Chang 4, 121–150 (2013).
Wallace, J. M., Deser, C., Smoliak, B. V. & Phillips, A. S. Attribution of climate change in the presence of internal variability. World Scientific Series on Asia-Pacific Weather and Climate 6, 1–29 (2016).
Schleussner, C. F. et al. Science and policy characteristics of the Paris Agreement temperature goal. Nat. Clim. Chang. 6, 827–835 (2016).
Millar, R. J. et al. Emission budgets and pathways consistent with limiting warming to 1.5°C. Nat. Geosci. 10, 741–747 (2017).
Tollefson, J. It’s official: Trump begins process to exit Paris climate agreement. Nature https://doi.org/10.1038/d41586-019-03230-y (2019).
Sanderson, B. M. & Knutti, R. Delays in US mitigation could rule out Paris targets. Nat. Clim. Change 7, 92–94 (2017).
Yang, P. & Wang, X. COVID-19: a new challenge for human beings. Cell. Mol. Immunol. 17, 555–557 (2020).
Berkley, S. COVID-19 needs a Manhattan Project. Science 367, 1407 (2020).
Estrada, F., Perron, P. & Martínez-López, B. Statistically derived contributions of diverse human influences to twentieth-century temperature changes. Nat. Geosci. 6, 1050–1055 (2013).
Hasselmann, K. Multi-pattern fingerprint method for detection and attribution of climate change. Clim. Dyn. 13, 601–611 (1997).
Stern, D. I. & Kaufmann, R. K. Detecting a global warming signal in hemispheric temperature series: a structural time series analysis. Clim. Change 47, 411–438 (2000).
Allen, M. R. & Tett, S. F. B. Checking for model consistency in optimal fingerprinting. Clim. Dyn. 15, 419–434 (1999).
Allen, M. R. & Stott, P. A. Estimating signal amplitudes in optimal fingerprinting, part I: theory. Clim. Dyn. 21, 477–491 (2003).
Hasselmann, K. Optimal fingerprints for the detection of time-dependent climate change. J. Clim. 6, 1957–1971 (1993).
Stott, P. A. et al. Detection and attribution of climate change: a regional perspective. Wiley Interdiscip. Rev. Clim. Chang 1, 192–211 (2010).
Hegerl, G. & Zwiers, F. Use of models in detection and attribution of climate change. Wiley Interdisciplinary Rev.: Clim. Change 2, 570–591 (2011).
Flato, G. et al. Evaluation of climate models. in Climate Change 2013 the Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (eds Stocker, T. F. et al.) Vol. 9781107057, 741–866 (Cambridge University Press, 2013).
Curry, J. A. & Webster, P. J. Climate science and the uncertainty monster. Bull. Am. Meteorol. Soc. 92, 1667–1682 (2011).
Yang, Z. J., Seo, M., Rickard, L. N. & Harrison, T. M. Information sufficiency and attribution of responsibility: predicting support for climate change policy and pro-environmental behavior. J. Risk Res. 18, 727–746 (2015).
Tversky, A. & Kahneman, D. Judgment under uncertainty: heuristics and biases. Science 185, 1124–1131 (1974).
Chang, J. J., Kim, S. H., Shim, J. C. & Ma, D. H. Who is responsible for climate change? Attribution of responsibility, news media, and South Koreans’ perceived risk of climate change. Mass Commun. Soc 19, 566–584 (2016).
Hawkins, E. & Sutton, R. Time of emergence of climate signals. Geophys. Res. Lett. 39, L01702 (2012).
La Sorte, F. A., Fink, D. & Johnston, A. Time of emergence of novel climates for North American migratory bird populations. Ecography https://doi.org/10.1111/ecog.04408 (2019).
Ciavarella, A., Stott, P. & Lowe, J. Early benefits of mitigation in risk of regional climate extremes. Nat. Clim. Change 7, 326–330 (2017).
Estrada, F., Tol, R. S. J. & Botzen, W. J. W. Extending integrated assessment models′ damage functions to include adaptation and dynamic sensitivity. Environ. Model. Softw. 121, 104504 (2019).
Watts, N. et al. The 2019 report of The Lancet Countdown on health and climate change: ensuring that the health of a child born today is not defined by a changing climate. The Lancet 394, 1836–1878 (2019).
Dell, M., Jones, B. F. & Olken, B. A. What do we learn from the weather? The new climate–economy literature. J. Econ. Lit. 52, 740–798 (2014).
Ray, D. K., Gerber, J. S., Macdonald, G. K. & West, P. C. Climate variation explains a third of global crop yield variability. Nat. Commun. 6, 5989 (2015).
Kim, D., Oka, T., Estrada, F. & Perron, P. Inference related to common breaks in a multivariate system with joined segmented trends with applications to global and hemispheric temperatures. J. Econom. 214, 130–152 (2020).
Estrada, F. & Perron, P. Extracting and analyzing the warming trend in global and hemispheric temperatures. J. Time Ser. Anal. 38, 711–732 (2017).
Wu, Z., Huang, N. E., Wallace, J. M., Smoliak, B. V. & Chen, X. On the time-varying trend in global-mean surface temperature. Clim. Dyn. 37, 759–773 (2011).
Swanson, K. L., Sugihara, G. & Tsonis, A. A. Long-term natural variability and 20th century climate change. Proc. Natl Acad. Sci. USA 106, 16120–16123 (2009).
Bierens, H. J. Nonparametric nonlinear cotrending analysis, with an application to interest and inflation in the united states. J. Bus. Econ. Stat. 18, 323–337 (2000).
Carrion-i-Silvestre, J. L. & Kim, D. Statistical tests of a simple energy balance equation in a synthetic model of cotrending and cointegration. J. Econom. 1–17. https://doi.org/10.1016/j.jeconom.2011.06.018 (2019).
Guo, Z. & Shintani, M. Consistent co‐trending rank selection when both stochastic and non‐linear deterministic trends are present. Econom. J. 16, 473–484 (2013).
Frame, D. J., Stone, D. A., Stott, P. A. & Allen, M. R. Alternatives to stabilization scenarios. Geophys. Res. Lett. 33, L14707 (2006).
King, A. D. et al. On the linearity of local and regional temperature changes from 1.5 °C to 2 °C of global warming. J. Clim. 31, 7495–7514 (2018).
Dai, A., Luo, D., Song, M. & Liu, J. Arctic amplification is caused by sea-ice loss under increasing CO2. Nat. Commun. 10, 121 (2019).
Jones, G. S., Stott, P. A. & Christidis, N. Attribution of observed historical near-surface temperature variations to anthropogenic and natural causes using CMIP5 simulations. J. Geophys. Res. Atmos. 118, 4001–4024 (2013).
Hansen, J., Sato, M., Kharecha, P. & von Schuckmann, K. Earth’s energy imbalance and implications. Atmos. Chem. Phys. 11, 13421–13449 (2011).
Meinshausen, M. et al. The RCP greenhouse gas concentrations and their extensions from 1765 to 2300. Clim. Change 109, 213–241 (2011).
Estrada, F. & Perron, P. Detection and attribution of climate change through econometric methods. Boletín la Soc. Matemática Mex. 20, 107–136 (2014).
Mahlstein, I., Knutti, R., Solomon, S. & Portmann, R. W. Early onset of significant local warming in low latitude countries. Environ. Res. Lett. 6, 034009 (2011).
Mahlstein, I., Hegerl, G. & Solomon, S. Emerging local warming signals in observational data. Geophys. Res. Lett. 39, L21711 (2012).
Hawkins, E. et al. Uncertainties in the timing of unprecedented climates. Nature 511, 183–187 (2014).
Vandyck, T. et al. Air quality co-benefits for human health and agriculture counterbalance costs to meet Paris agreement pledges. Nat. Commun. 9, 1–11 (2018).
Stocker, T. F. et al. Climate change 2013 the physical science basis: Working Group I contribution to the fifth assessment report of the intergovernmental panel on climate change. in Climate Change 2013 the Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. (eds Stocker, T. F. et al.) Vol. 9781107057, 1311–1394 (Cambridge University Press, 2013).
Tol, R. S. J. & de Vos, A. F. Greenhouse statistics-time series analysis. Theor. Appl. Climatol. 48, 63–74 (1993).
Kaufmann, R. K. & Stern, D. I. Evidence for human influence on climate from hemispheric temperature relations. Nature 388, 39–44 (1997).
Pretis, F., Mann, M. L. & Kaufmann, R. K. Testing competing models of the temperature hiatus: assessing the effects of conditioning variables and temporal uncertainties through sample-wide break detection. Clim. Change 131, 705–718 (2015).
Tebaldi, C. & Arblaster, J. M. Pattern scaling: Its strengths and limitations, and an update on the latest model simulations. Clim. Change 122, 459–471 (2014).
Leduc, M., Damon Matthews, H. & De Elía, R. Regional estimates of the transient climate response to cumulative CO2 emissions. Nat. Clim. Chang. 6, 474–478 (2016).
Santer, B. D., Wigley, T. M. L., Schlesinger, M. E. & Mitchell, J. F. B. Developing climate scenarios from equilibrium GCM results. Report/Max-Planck-Institut für Meteorol. 47, 1–29 (1990).
Gay-Garcia, C., Estrada, F. & Sánchez, A. Global and hemispheric temperatures revisited. Clim. Change 94, 333–349 (2009).
Estrada, F., Gay, C. & Sánchez, A. A reply to ‘does temperature contain a stochastic trend? Evaluating conflicting statistical results’ by R. K. Kaufmann et al. Clim. Change 101, 407–414 (2010).
Estrada, F., Perron, P., Gay-García, C. & Martínez-López, B. A time-series analysis of the 20th century climate simulations produced for the IPCC’s fourth assessment report. PLoS ONE 8, e60017 (2013).
Kaufmann, R. K., Kauppi, H., Mann, M. L. & Stock, J. H. Does temperature contain a stochastic trend: Linking statistical results to physical mechanisms. Clim. Change 118, 729–743 (2013).
Estrada, F. & Perron, P. Causality from long-lived radiative forcings to the climate trend. Ann. N. Y. Acad. Sci 1436, 195–205 (2019).
Schwartz, S. E. Determination of earth’s transient and equilibrium climate sensitivities from observations over the twentieth century: strong dependence on assumed forcing. Surv. Geophys. 33, 745–777 (2012).
Gregory, J. M. & Forster, P. M. Transient climate response estimated from radiative forcing and observed temperature change. J. Geophys. Res. Atmos. 113, D23105 (2008).
Held, I. M. et al. Probing the fast and slow components of global warming by returning abruptly to preindustrial forcing. J. Clim. 23, 2418–2427 (2010).
Gregory, J. M. Vertical heat transports in the ocean and their effect on time-dependent climate change. Clim. Dyn. 16, 501–515 (2000).
Lynch, C., Hartin, C., Bond-Lamberty, B. & Kravitz, B. An open-access CMIP5 pattern library for temperature and precipitation: description and methodology. Earth Syst. Sci. Data 9, 281–292 (2017).
Guo, Z. & Shintani, M. Consistent cotrending rank selection when both stochastic and nonlinear deterministic trends are present. http://www.fas.nus.edu.sg/ecs/events/seminar/seminar-papers/05Apr11.pdf (2011).
Ho, C. K., Hawkins, E., Shaffrey, L. & Underwood, F. M. Statistical decadal predictions for sea surface temperatures: a benchmark for dynamical GCM predictions. Clim. Dyn. 41, 917–935 (2013).
GISTEMP Team. GISS Surface temperature analysis (GISTEMP). NASA Goddard Institute for Space Studies https://doi.org/10.1029/2010RG000345 (2019).
Morice, C. P., Kennedy, J. J., Rayner, N. A. & Jones, P. D. Quantifying uncertainties in global and regional temperature change using an ensemble of observational estimates: the HadCRUT4 data set. J. Geophys. Res. Atmos. 117, D8 (2012).
Cowtan, K. & Way, R. G. Coverage bias in the HadCRUT4 temperature series and its impact on recent temperature trends. Q. J. R. Meteorol. Soc. 140, 1935–1944 (2014).
Harris, I., Osborn, T. J., Jones, P. & Lister, D. Version 4 of the CRU TS monthly high-resolution gridded multivariate climate dataset. Sci. Data 7, 1–18 (2020).
Miller, R. L. et al. CMIP5 historical simulations (1850-2012) with GISS ModelE2. J. Adv. Model. Earth Syst. 6, 441–477 (2014).
Author information
Authors and Affiliations
Contributions
F.E., P.P., and D.K. contributed equally to the conceptual design and to the writing of the paper; F.E., D.K., and P.P. analyzed the data. All authors discussed the results and commented on the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Primary handling editor: Joe Aslin.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Estrada, F., Kim, D. & Perron, P. Anthropogenic influence in observed regional warming trends and the implied social time of emergence. Commun Earth Environ 2, 31 (2021). https://doi.org/10.1038/s43247-021-00102-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-021-00102-0
This article is cited by
-
Anthropogenic influence on extremes and risk hotspots
Scientific Reports (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.