Introduction

Earthquake ground motion results from a sudden release of elastic energy, accumulated over decades to millennia, in the shape of a slip distribution along a fault. Surface ground motion transmits forces to structures and thus, predicting the ground motion is the basis of earthquake risk assessment. Strong motion records are typically used by the earthquake engineering community to design key structures like power plants, bridges or dams, and to analyze the response of existing buildings for a potential future earthquake. One major issue is that near-fault strong motion recordings are still too scarce to fully understand the physics involved in the highly variable ground motion within a few kilometers from the rupture plane (e.g., ref. 1,2). Consequently, ground motion prediction models are not calibrated for near-field motion and are accurate only at fault-plane distances greater than ~10 km (ref. 3). Numerical ground motion simulation techniques, including physical description of the fault rupture process, have then become popular to investigate near-source characteristics of ground motion (e.g., ref. 4).

On November 11, 2019, a Mw 4.9 earthquake occurred in the south east of France (referred to as the Le Teil event, Fig. 1a) close to the city of Montélimar within the lower Rhône river valley, a moderate seismicity area. This industrial region hosts several operating nuclear power plants. The unexpected level of damage for this magnitude (epicentral intensity VIII, ref. 5) attests an intense ground shaking. Unfortunately strong motion was not recorded by accelerometers near the fault, in the damage area. The earthquake causative fault, which was not considered as active, is part of the Cévennes fault system (ref. 6,7). Seismological, geodetical and field observations indicate a reverse-fault mechanism, a rupture area of about 4 km by 1.5 km, a hypocenter at about 1 km and surface rupture evidences (ref. 7,8). Such a shallow location is exceptional. Moderate-sized earthquakes overwhelmingly occur at seismogenic depths larger than ~5 km in stable continental regions (ref. 9). The shallow location may be related to quarry extraction directly above the rupture area (ref. 10,11,12). In a few cases, small to moderate-sized anthropogenic earthquakes with reverse-faulting style are reported in the immediate proximity of quarries (e.g., ref. 13,14,15,16). Superficial hypocenter depth is reported as a common feature for anthropogenic seismicity (e.g., ref. 17,18).

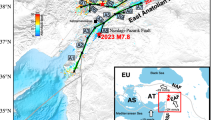
Fig. 1: Methodology to compute ground acceleration.
figure 1

a Map of the Le Teil area. The colored rectangle shows one realization of rupture model (chosen within the 2000 generated models), with final slip indicated by the color scale (max = 40 cm in red), and white contour lines indicating the rupture front every 0.5 s. The rupture plane reaches the surface and dips 58° toward the southeast. The star denotes the hypocenter. Modeling of funeral slab motion is performed at cemetery C1, including a large majority of the observations (Table S3, Fig. S7). We observed only a few (<5) displaced slabs at C2 and C3, while all slabs remained stable at C4 and C5. The orange polygon is the area where displaced rocks are observed. b Flow chart describing the strategy to compute near-fault ground acceleration.

Full size image

Near-field seismological observations of moderate-sized superficial events (depth <3 km) are inexistent in France and only a very few are reported worldwide. The European strong motion database (ref. 3) contains only eight recordings (over 23,014) of superficial events recorded <5 km from the rupture plane, all of them being from earthquakes with local magnitude lower than 4.5. Two cases of superficial events with Mw~5 and causing exceptional ground motions (i.e., with Peak Ground Acceleration—PGA—exceeding 5 m/s2) were reported in California (ref. 19) and in Nevada (ref. 20).

In the absence of near-fault strong motion recording for the Le Teil earthquake we conduct numerical predictions of the ground acceleration (Fig. 1b). First we perform a source analysis and generate a suite of rupture models, describing the space-time distribution of slip across the fault. The rupture models are calibrated based on the Interferometric SAR slip model proposed by (ref. 8). Next we characterize the 1D structure of the earth crust using seismic noise recorded at temporary seismological stations installed after the earthquake in the fault vicinity (ref. 8). Finally we obtain a set of ground acceleration time histories on a dense array of virtual stations, centered on the fault. Furthermore, we collect in-situ observations providing independent estimates of the ground acceleration, such as displacements of funeral slabs in cemeteries and displaced rocks above the fault. Both numerical analysis and in-situ measurements of displaced objects converge toward exceptional ground acceleration, exceeding gravity in the immediate fault vicinity. Our study provides new insights on seismic hazard due to superficial seismicity in stable continental regions.

Results

Source analysis and rupture modeling

Defining proper rupture models is a crucial point because near-fault surface ground motion is sensitive to the details of the fault slip history. Theoretical and numerical studies indeed show that near-fault ground acceleration is primarily controlled by local processes on the fault, occurring near the recording site, including local stress drop, strong spatial variations of the rupture velocity (in particular when the rupture front hits the fault edges) and local fault slip acceleration (e.g., refs. 21,22,23). We use a kinematic representation of the rupture process. Six properties must then be defined, namely the rupture size, the final slip distribution, the rupture duration, the position of the rupture initiation, the rupture velocity and the local slip velocity. As shown hereafter, most of them are constrained by observations, except the slip velocity that needs to be calibrated based on past earthquake studies.

Thanks to the shallow rupture, the co-seismic displacement field could be mapped by Interferometric SAR and inverted to provide a final slip distribution (ref. 8), that we use to constrain the low frequency slip features (Methods). Slip shows a reverse-fault mechanism and is characterized by two main slip patches localized between 0 and ~1 km depth on a roughly 4 km*1.5 km fault plane dipping 58 °SE, resulting in a magnitude Mw = 4.9. Analysis of the farfield seismological recordings gives the same magnitude (moment tensor inversion, ref. 7), indicating that the slip obtained from InSAR is primarily seismic.

In order to constrain the rupture duration, we use seismograms recorded by the real-time broadband and accelerometric permanent stations of the French seismologic and geodetic network (RESIF) (59 stations with source-site distances from 27 to 290 km, Fig. S1a). We employ a spectral approach and perform a Bayesian estimation of the corner frequency (Methods, Fig. S1b). The later is related to the rupture duration given a source model. Our analysis yields rupture duration of 2.0 s (confidence interval at 68%, 68% CI: 1.4–3.4 s). The Brune (1970) stress drop24 we obtain is 1.0 MPa (68% CI: 0.2–3.4 MPa). This value is close to the average of worldwide reported stress drops (e.g., refs. 25,26,27). Furthermore, the azimuthal distribution of the apparent rupture duration (i.e., “seen” from any station) is classically used to track the main rupture direction (e.g., refs. 28,29,30). The corner frequency shows weak azimuthal dependence, revealing a bilateral rupture, i.e., initiation about midway between the SW and NE rupture terminations (Methods, Fig. S2). This is consistent with the analysis by (ref. 11) and with the hypocenter location available at the time, based on inversion of farfield seismological data and placing the hypocenter at the fault center at 1 km depth with spatial uncertainty of 1 km (ref. 7). The rupture may have started slightly southwestward as suggested by coherency analysis of high-frequency waveforms at two neighboring farfield stations (ref. 31). Knowing the position of the rupture initiation, the rupture duration and the rupture dimension, we infer an average rupture velocity of ~1.8 km/s. Considering the 1D velocity model developed in this study (section Velocity model), it is between 50% and 90% of the shear-wave velocity (VS), as reported for most large earthquakes (e.g., refs. 32,33).

Furthermore, it is necessary to define how local slip evolves with time (slip velocity function). We use a function in which slip starts with a short acceleration phase and then slowly decelerates until the final slip is reached (ref. 34), as shown by laboratory experiments and dynamic rupture simulations (e.g., refs. 34,35). We impose constant slip duration of 0.3 s (68% CI: 0.2–0.4 s) as proposed by36 for a Mw4.9 event. The average slip velocity over the fault is then 0.5 m/s, as commonly reported from near-fault seismological data (e.g., refs. 32,37) and observations during fault scarp formation (e.g., refs. 38,39). The peak slip velocity locally reaches 4 m/s (Fig. S3a, ref. 40). The duration of the slip acceleration phase is poorly constrained, but we checked that the ground acceleration time series presented hereafter are not sensitive to this parameter in the considered frequency range (<5 Hz).

In order to account for source heterogeneity involved in the high-frequency seismic energy (e.g., ref. 41), we introduce small-scale variability of the rupture parameters by considering self similar spatial distributions. Self-similarity of slip distribution is supported by observations of slip images obtained from geodetic or seismological data and topography analysis of exhumed faults (ref. 42). Finally, we obtain 2000 rupture models representing the uncertainties in the above-defined rupture parameters, described by probability density functions (Methods, Fig. S3).

Velocity model

We derive a 1D velocity model of the earth crust based on three-component beamforming method (ref. 43) using the seismic noise recorded at temporary post-seismic stations installed in the fault vicinity (Fig. 1a) and the Conditional Neighborhood Inversion Algorithm (ref. 44) (Methods, Fig. S5). The shear-wave ground velocity profile (Fig. 2) exhibits materials with increasing stiffness from the surface to 1.2 km depth overlaying less competent deposits. This peculiar ground velocity profile with the presence at depth of softer material is consistent with the geological settings of the area (ref. 45) and deep boreholes in the region (geological logs BSS002ARWX, BSS002ASXR, BSS002ASEZ available at http://infoterre.brgm.fr) that show, from surface to depth, alternating layers of marls and limestone from the lower Cretaceous, a more competent thick Jurassic limestone layer, and thick claystones from lower to upper Jurassic age that overlay a Triassic bedrock. At the vicinity of the fault zone, the geological cross-section proposed by (ref. 7) reports a 0.7 km thick Barremian limestone layer overlaying a 1.7 km thick formation composed of marls and limestones from Hauterivian and Valanginian age, resting on Tithonian formation. Outcropping Hauterivian and Valanginian formations (Fig. 2) indicate that the Valanginian formation is particularly rich in soft marls compared to Hauterivian formation, consistently with observations in the deep regional boreholes and in the Vonvocian basin (ref. 46). The 1D velocity model is thus consistent with geological information leading to the following interpretation: 0.6 km thick Barremian limestones with Vs ~2 km/s and 0.6 km thick Hauterivian marls and limestones with Vs ~3.6 km/s overlaying Valanginian marls with Vs ranging from ~1.2 km/s to 2.3 km/s. The velocity contrast at about 2.2 km depth would correspond to the Tithonian formation. The rupture is confined between the surface and the soft Valanginian marl layer, which probably acted as a barrier to the rupture propagation. It likely initiated in the stiff Hauterivian formations, expected to be more brittle, which is consistent with the hypocenter position at 1 km depth inferred from farfield seismological data (ref. 7).

Fig. 2: Velocity model.
figure 2

(Left panel) Shear-wave velocity profile (black line indicates the best misfit profile, gray lines indicate the ensemble of inverted VS profiles that explain dispersion data within their uncertainty bound) overlaying the geological cross-section modified from (ref. 7) (licensed under CC BY 4.0.). (Right panel) Pictures of the outcropping Hauterivian and Valanginian marls and limetsones.

Full size image

Numerical prediction of ground acceleration

In order to simulate ground acceleration, the seismic energy radiated by each rupture model is propagated in the inferred best misfit velocity model toward the array of near-fault virtual stations. The array is composed of 234 stations with interstation distance of 500 m and is centered on the fault (Fig. 3). Then we compute the impulse response of the medium and following the Representation theorem (ref. 47), we convolve the medium response with the slip velocity and obtain 2000 ground motion time series up to 5 Hz for each station (Methods).

Fig. 3: Numerical prediction of ground acceleration.
figure 3

Top: simulated median values of the Peak Ground Acceleration (PGA) between 0 and 5 Hz on the array of virtual stations. The inter-stations distance is 500 m. Bottom: PGA variability, computed over 2000 realizations of rupture models, expressed in terms of the standard deviation of the log10 values. The dashed rectangle represents the surface rupture projection. The thick black polygon line is the area where displaced rocks are observed.

Full size image

The results indicate intense ground shaking above the fault rupture projection, primarily vertical, with horizontal PGA up to 7.5 m/s2 (68% CI: 3.0–19 m/s2) and vertical PGA exceeding gravity (13 m/s2, 68% CI: 5.8–29 m/s2) above the main slip area (Figs. 1a and 3). The decay of ground acceleration with distance to rupture is however very fast. In addition, directivity effects are known to cause ground motion amplification at a given site as the rupture propagates toward the site and when the direction of slip points toward the site (e.g., refs. 48,49). For a reverse-fault mechanism with a dip angle of ~60°, such effects are assumed to be very weak along the fault strike direction—as observed in our simulations—and maximized along the up-dip direction. Nevertheless, the weak amount of slip above the nucleation area for the Le Teil event (Fig. S3a) results in the absence of up-dip directivity effects and consequently, ground accelerations are lower toward NW.

It is known that PGA for small earthquakes can be strong without causing damage, because it may be controlled by energetic frequencies that are much higher than the typical resonance frequencies of civil structures (>20 Hz). However, our simulations result also in large values of the Peak Ground Velocity (PGV) for frequencies below 5 Hz (exceeding locally 1 m/s, Fig. S4). Moreover, the ratio PGA/PGV, which equals about 2π multiplied by the dominant frequency, has values ranging between 10 and 15 s−1, implying a dominant frequency around 2 Hz and hence accelerations prone to damage structures (ref. 3), in agreement with the observed Intensity of VIII in the fault vicinity.

Near-field observations of displaced objects

In order to obtain independent estimations of the ground acceleration, we collected in-situ observations of displaced rigid objects, either natural or man-made, that fulfill the following criteria: (1) there is evidence that displacement is due to the earthquake; (2) the objects loosely lie on the ground; (3) their structure is simple enough so that their displacement can be related to ground acceleration using simple mechanical concepts. We compiled a database of displaced rocks and a database of funeral slabs displacements.

After the Le Teil event, we observed, in specific places, that tens of stones and rocks, which are numerous in this back country of smooth hills and scattered limestone outcrops, had been displaced and sometimes freshly fractured and broken (Fig. 4, Methods, Table S2, Fig. S6). Freshness of cuts and fractures and the consistency of several tens of observations indicate that some of these rocks were tossed into the air during the earthquake, with breakage occurring at the time of impact, implying that vertical acceleration exceeded gravity (e.g., refs. 50,51). All the evidences for upthrown and displaced rocks are located in the vicinity of the SW part of the surface fault trace (Fig. 1a and S6), an area that remarkably coincides with the area where simulated vertical PGA exceeds gravity (Fig. 3).

Fig. 4: Displaced rocks.
figure 4

Examples of observed displaced rocks as upthrown stones, freshly fractured and broken at the impact on ground, imply a vertical acceleration exceeding gravity during the Le Teil event. a–d Broken stones, apparently flung laterally. For c and d, the bottom figures show the reconstruction from fragments. The detailed observations and site locations for all displaced rocks are available in Fig. S6 and Table S2. All the observed site locations, which cluster close to the SW branch of the surface rupture, are reported as a polygon on Figs. 1 and 3, for comparison with the simulated seismic slip and ground acceleration.

Full size image

In addition, tens of funeral slabs were displaced in a cemetery (C1) located about 200 m from the northern rupture termination (Fig. 5a, Methods, Table S3, Fig. S7). The cemetery is located within an area of Intensity VIII on the EMS-98 scale (ref. 52). This translates into a horizontal PGA of 2.8 m/s2 (68% CI: 1.5–6 m/s2) from empirical relationships (ref. 53), which coincides with the median horizontal PGA value we simulated at this place (2.8 m/s2, 68% CI: 0.5–7.9 m/s2). In order to obtain independent estimations of the ground acceleration, we model the slab motion by conducting numerical simulations based on a Coulomb friction model. The method uses the suite of 2000 three-component ground motion time series modeled in cemetery C1 as input and provides the slab displacement time series in the EW-NS plane (Methods, Fig. 5b). The slabs can move with respect to ground if:

$$\frac{{\sqrt {a_{EW}^2(t) + a_{NS}^2(t)} }}{\mu } - a_Z\left( t \right) > g$$
(1)

where aEW, aNS and aZ represent ground acceleration in the NS, EW and vertical directions, respectively, μ is the static friction coefficient and g is gravity. 65% of the simulated ground motion time series verify Eq. 1, and hence can induce a slab displacement. The slab motion is illustrated in Fig. 5b for one realization of ground acceleration that well represents the field observations. Equation 1 is verified soon after the S wave arrival, resulting in a ground displacement toward the south. This S-wave pulse induces a force on the slab in the opposite direction (north), but the headstone blocks the slab motion. From the simulations, the slab starts sliding with the arrival of a stopping phase (pulse of high-frequency ground motion) generated by the rupture arrest at the northern fault termination. This stopping phase is associated with an abrupt change of ground displacement polarity and a force rotating toward the south, coinciding with the final southward slab displacement. A global analysis (Fig. 5c) shows that a horizontal PGA of 3 m/s2 generates slab motion of 0.8 cm (68% CI: 0.3–1.2 cm), while we observed in cemetery C1 a median displacement of 4.5 cm (68% CI: 2–7 cm). Such a displacement corresponds to a simulated horizontal PGA of 4.8 m/s2 (68% CI: 4.3–5.4 m/s2). This indicates that the numerical ground motion simulations probably provide a lower bound of the ground acceleration that actually happened at the cemetery C1. Indeed, local site amplification effects are not considered in this study. Finally the median simulated PGA values at cemeteries C2–C5 are in the range 1.5–2 m/s2, consistent with the quasi absence of observed displaced slab.

Fig. 5: Displaced funeral slabs.
figure 5

a Illustration of the typical funeral slab layout in cemetery C1 (see Figs. 1 and 3 for C1 location). The slabs back onto N70°-oriented headstones. Most of the slabs lying on the SE side were displaced during the ground shaking, while slabs lying on the other side experienced smaller displacements or did not move (Table S3, Fig. S7). Note that some of the slabs collapsed, as shown on the bottom-right inset figure. b Example of ground motion acceleration time history (top) and resulting modeled slab displacement using a friction coefficient of 0.2 (bottom) (Methods). The color scale on the bottom figure points to the different time steps as defined on the ground motion time histories, for a better visualization of the time evolution of the slab displacement. The color scale defines the time window during which Eq. 1 is verified, that is when the inertial force is sufficient to induce sliding of the slab. The arrows on the bottom figure indicate the direction and amplitude of forces transmitted to the slab at different time steps. The ground displacement (light gray) and slab displacement (dark gray) diverge at the arrival of the stopping phase generated by the rupture arrest, about 200 meters from the cemetery. The relative slab displacement is shown in purple, indicating a final displacement of 6 cm in the direction N168°. c 2D-probability density function of simulated PGA (geometrical mean of horizontal components) and modeled relative final slab displacement, obtained from 2000 realizations of rupture models. The median final relative slab displacement measured on field (4.5 cm) yields a median PGA value of 4.8 m/s2 (CI 68% 4.3–5.4 m/s2) in the cemetery during the Le Teil earthquake.

Full size image

Conclusion

The 2019 Mw4.9 Le Teil earthquake occurred in a stable continental region at unusually shallow depth (~1 km). Such superficial events are rare and thus their rupture characteristics are very poorly documented. The level of ground motion that they can produce is basically unknown. We demonstrated that the average rupture properties (stress drop, rupture- and slip- velocity) are consistent with the ones commonly observed for large deeper earthquakes. We also showed that the unusually shallow rupture with generation of energetic seismic waves up to the ground surface resulted in an exceptional and destructive level of ground acceleration exceeding gravity on some localized patches in the immediate fault vicinity, as evidenced by the consistency between the numerical predictions and the body of in-situ observations. Then, our simulation results point on a fast decay of motion amplitude with fault distance for the first few kilometers. Inside the near-source area, the simulated ground motion shows a high level of heterogeneity that is fully related to the rupture characteristics along the fault plane (distribution of slip and rupture velocity, position of hypocenter).

Our results dramatically change the perception of the impacts of superficial moderate earthquakes on local hazard assessment. The scarcity of observations of Le Teil-event type implies that they are not represented in regulatory assessments of seismic hazard based on empirical ground motion models (e.g., ref. 54). Earthquake recurrence models and ground motion models that would be accurate for such superficial, possibly triggered events are not available. This raises the question of how prepared the society can be to deal with this low probability high impact- type of event. This is particularly critical in areas where long term safety of nuclear plants is involved. The Le Teil earthquake occurred in the vicinity of active nuclear power plants located within the Rhône river valley, 12 km north- and 20 km south- ward, respectively. The earthquake causative fault, which was not considered as active, is part of the Cévennes fault system, this later extending eastward across the Rhône valley a couple of kilometers from the northern nuclear power plant (ref. 6,7). Our analysis points on the key role of the 1.2 km thick superficial stiff rock matrix on the unusually strong ground shaking we quantify for such an earthquake size. Such geological units being common for this region (ref. 45), future geological and geophysical analyses should characterize the extent and thickness of the geological units and the seismogenic potential of the local faults, so as to constrain the probability of a superficial earthquake (either tectonic or anthropogenic) in the immediate vicinity of the power plants.

Methods

Spectral analysis of seismological data

For each station of the RESIF network used in our analysis (Fig. S1a), we compute the seismic moment M0 and the corner frequency fc. Due to the unusually weak number of aftershocks, we could unfortunately not find adequate small earthquake recordings to represent the details of the wave propagation in the earth crust. We then use a simplified spectral approach (e.g., ref. 55). We select the P wave (time window of 12 s starting from the P arrival, ref. 56) and compute the RMS of the 3-components Fourier displacement amplitude spectra. According to24, the level of the low frequency plateau Ω0 is:

$${\Omega}_0 = \frac{{2M_0U_{\phi \vartheta }}}{{4\pi \rho c^3R}}$$
(2)

where Uϕθ is the average radiation pattern (0.52 for P wave), c is the P wave velocity, ρ is density and R is the hypocentral distance. For each station, we then normalized the displacement spectrum by 2Uϕθ/(4πρc3R) so that the low frequency plateau provides the seismic moment. Finally, we stack all the spectra and model the resulting average spectrum as (refs. 56,57):

$${\Omega}(f) = \frac{{e^{ - \pi ft/Q}}}{{\left[ {1 + \left( {\frac{f}{{f_c}}} \right)^{\gamma n}} \right]^{1/\gamma }}}$$
(3)

where t is the travel time of the considered wave and Q is the quality factor of the considered wave.

We then perform a Bayesian estimation of the model parameters fc, M0 and Q (Supplementary Methods), yielding median values Mw = 4.85 (68% CI: 4.65–5.05) and fc = 0.44 Hz (68% CI: 0.26–0.66 Hz) (Fig. S1b). The joint posterior probability density functions Pfc,m0(fc,m0) and PQ,fc(Q,fc) indicate that the fc uncertainty mainly arises from a strong tradeoff between Q and fc (Fig. S1c). Following58, we obtain that the rupture duration for P-waves is between 0.84 fc and fc assuming a symmetric circular crack rupture model and a rupture velocity VR between 50% and 90% of the S-wave velocity VS (consistent with the inferred average VR of ~1.8 km/s and our velocity model), i.e., an average duration of 2.0 s (68% CI: 1.4–3.4 s).

We next compute the corner frequency for various classes of source-station azimuths, and compare the azimuthal variations with the theoretical predictions for a simple horizontal line source (Fig. S2). For a unilateral rupture:

$$f_{cU}\left( \theta \right) = \frac{1}{{T(1 - \alpha \sin (i)\cos (\theta ))}}$$
(4)

where T is the rupture duration, α is the ratio VR/VS, i is the take off angle and θ is the source-station azimuth. For a bilateral rupture,

$$f_{cB}\left( \theta \right) = \min \left[ {f_{cB}\left( \theta \right),\;f_{cB}\left( { - \theta } \right)} \right]$$
(5)

Despite the uncertainty on fc(θ) and considering various values of i and VR, the results indicate a bilateral rupture (Fig. S2).

Kinematic rupture modeling

We generate a suite of 2000 rupture models with the code developed by59. The rupture area is represented by a rectangle with fixed length L and width W of 4.2 km and 1.4 km, respectively. The distributions of slip and rupture time are self similar (k−2 decay in the wavenumber domain), and the local slip duration (rise time) is constant over the fault plane. The rupture duration follows a lognormal distribution with median of 2 s and standard deviation of 0.15 (in log10 units) (Fig. S3d). The along-strike position of the rupture initiation follows a normal distribution with median 0.5*L and standard deviation 0.1*L, while the along-dip position is uniformly distributed between 0.5 and 1 km depth. The values of the local slip duration are uniformly distributed between 0.15 and 0.45 s. The method ensures that source functions are compatible with a “ω−2” model24 (Fig. S3d). For a specific application to Le Teil earthquake, we bring the following modifications to the code: (1) the self similar slip distributions, which have random phases, are low pass filtered below a wavenumber of 1.5 e−3 m−1 and replaced with the InSAR slip, high pass filtered above the same wavenumber; (2) the slip velocity function is defined according to (ref. 34); (3) the rupture time perturbations are replaced by rupture velocity perturbations. The rupture time is then directly computed from the rupture velocity distribution, using the algorithm of60. This change does not modify the spectral properties of the source functions, but allows setting the maximum rupture velocity to the shear-wave velocity (the prevailing rupture mode is III, which excludes supershear ruptures, e.g., ref. 61). Figure S3a shows examples of generated rupture models.

Velocity structure and near-fault wave propagation

A representative 1D velocity model was derived from the analysis of 6 days of continuous seismic ambient noise recorded synchronously by 19 temporary seismological stations deployed after the Le Teil earthquake (Fig. 1a, Table S1). Rayleigh and Love wave dispersion curves and signed ellipticity of Rayleigh waves were measured with the 0.1–4 Hz frequency range using a three-component beamforming method (ref. 43) implemented in the open-source Geopsy software (ref. 62) (Fig. S5a-c). Dispersion estimates above 1 Hz are controlled by ambient noise recorded by seismic stations located within 3 km from the epicenter location. Dispersion estimates have been inverted by using the Conditional Neighboorhood Algorithm (ref. 44). The best misfit inverted ground velocity profile (Fig. S5d) exhibits a 0.6 km thick layer (Vs ~2 km/s) and a very competent 0.6 km thick layer (VS~3.6 km/s) overlaying a ~1 km thick layer of softer materials. Note that the resolution of the very shallow earth structure (up to 300 m depth) is poor, so that we do not model potential surface rock alteration that may enhance ground acceleration above 5 Hz. Note also that the Triassic bedrock depth is not resolved by the inversion.

The impulse response of the inferred 1D velocity structure (Green’s functions) is next computed for each couple of fault point and virtual station of the dense array using the discrete wave number technique of 63 (AXITRA computer package, ref. 64). The array is composed of 234 stations with inter-stations distance of 500 m. A distance between the fault points of 60 m ensures stability of the computed ground motion up to 5 Hz.

Displaced rock analysis

After the Le Teil Mw 4.9 event, displaced rocks were observed during field surveys on several locations. The fieldwork began 1 month after the earthquake, with several visits within 2 months. A detail description of the observations is provided in Supplementary Information (Supplementary text, Table S2, Figs. S6.1–S6.8). All the observations support the density of upthrown rocks and the location of displaced rocks overlap with the above-gravity peak values of numerical predictions of ground motions (Fig. 3). It supports strong ground motion to be of the order of the gravity during Le Teil earthquake. References on previous worldwide observations of displaced rocks for larger earthquakes are also provided in Supplementary References.

Observations of funeral slab displacement

We inspected five cemeteries located in the fault vicinity (Fig. 1a). The structure of French tombs is generally simple, composed of a vault covered by a rectangular granite slab backing onto a headstone (Fig. 5a). We observed that the slabs, which were relying loosely without joints, were displaced during the earthquake. We compile a database of 48 slab displacements from cemetery C1 containing a large majority of the observations and located about 200 m from the northern fault rupture termination (Table S3, Fig. S7). We reported only a few sparse observations with smaller displacements in cemeteries C2 and C3, while no displacement was seen in cemeteries C4 and C5. 75% of the observations in C1 corresponds with slabs backing onto N70°-oriented headstones. Interestingly, within this group of slabs, 80% of the reported displacements are for the slabs backing onto the SE side of the headstones, with an average of 4.5 cm (68% CI: 2–7 cm), against 2.5 cm for the remaining 20% (Figs. S7, 5a).

Modeling of funeral slab displacement

We conduct numerical simulations to model the observed funeral slab displacements. We exclude from our analysis slab observations associated with rotation and focus on slabs backing onto N70-oriented headstones. Since the fundamental frequency of the slab is >100 Hz (considering a granite slab with dimension 200 × 100 × 8 cm), we modeled it as a mass particle with three degrees of freedom. The particle, subjected to gravitational force, is in frictional contact with the EW-NS plane, which is animated by the three-dimensional seismic ground motion. The friction law we used is the standard Coulomb friction model without tangential force regularization. From Newton’s second law, we obtain the differential equation of motion of the undamped particle:

$$m\left( {\sqrt {a^2_{EW}\left( t \right) + a^2_{NS}\left( t \right)} } \right) = F_T\left( t \right)$$
(6)

Either \(|F_T(t)| < \mu .m(g + a_Z\left( t \right))\) if the slab sticks to the EW-NS plane, or \(\overrightarrow {F_T} \left( t \right) = - \mu .m\left( {g + a_Z\left( t \right)} \right)\frac{{\vec v}}{{||\vec v||}}\) if the slab moves with a relative velocity v(t) to the plane. FT is the Coulomb friction force, μ is the static friction coefficient, g is the constant acceleration gravity, m is the slab mass and aEW, aNS and aZ are ground accelerations in the EW, NS and vertical directions, respectively. During the motion, a perfectly inelastic collision is imposed on the slab, which does not penetrate the headstone (wall azimuth on Fig. 5 and S8, and defined below as azimuth ranges). A forward incremental Lagrange multiplier method compatible with explicit time integration operators (ref. 65) is used to solve the particle motion. Convergence is achieved for a time step <10−3 s.

We conduct two sets of simulations with two ranges of inhibited azimuth displacement: for set 1 and 2, the slab movement is blocked in the [N-110 – N70] and [N70 – N250] azimuth ranges, respectively. For each set, we consider values of the friction coefficient μ of 0.2, 0.4 and 0.6 (reported values for granite range between 0.2 and 0.4, ref. 66). First, for μ = 0.2, the simulated slab movement is smaller when the azimuth displacement is blocked in the [N-110 – N70] direction (set 1 gives values on average 30% smaller than set 2), as observed on field (Fig. S7). This observation is not reproduced using μ = 0.4 or μ = 0.6 (Fig. S8b). In addition, the values of μ = 0.4 and μ = 0.6 underestimate the displacements observed on field in the SE direction (Fig. S8a). For μ = 0.4 and μ = 0.6, the median observed displacement (4.5 cm) corresponds to simulated median horizontal PGA values of 9.0 and 12 m/s2, respectively, which are not consistent with an Intensity of VIII (ref. 55). For μ = 0.2, a displacement of 4.5 cm corresponds to a simulated median horizontal PGA of 4.8 m/s2. Accordingly the 0.2 value of friction coefficient μ best approximates the observations. Small variations of μ may explain part of the variability of the field observations.