Abstract
Internal solitary waves are ubiquitous in coastal regions and marginal seas of the world’s oceans. As the waves shoal shoreward, they lose the energy obtained from ocean tides through globally significant turbulent mixing and dissipation and consequently pump nutrient-rich water to nourish coastal ecosystem. Here we present fine-scale, direct measurements of shoaling internal solitary waves in the South China Sea, which allow for an examination of the physical processes triggering the intensive turbulent mixing in their interior. These are convective breaking in the wave core and the collapse of Kelvin–Helmholtz billows in the wave rear and lower periphery of the core, often occurring simultaneously. The former takes place when the particle velocity exceeds the wave’s propagating velocity. The latter is caused by the instability induced by the strong velocity shear overcoming the stratification. The instabilities generate turbulence levels four orders of magnitude larger than that in the open ocean.
Similar content being viewed by others
Introduction
Internal solitary waves (ISWs) are ubiquitous in coastal regions and marginal seas of the world’s oceans1. They are mostly evolved from the nonlinear steepening of internal tides generated when tidal currents flow over abrupt topography, e.g., shelf breaks or submarine ridges. After generation, ISWs are able to persist for a few days traveling hundreds of kilometers until they shoal into shallow water. During the shoaling stage, ISWs can fission into multiple waves, reverse their polarity, and break2,3,4,5,6, all of which induce strong and rapid turbulent dissipation and mixing. It is recognized the turbulence driven by internal tides results in mixed water masses, which subsequently flow into the vast ocean interior7 and dissipate a significant amount of energy in the world’s oceans8. Since ISWs play a role in mediating tidal energy into smaller-scale turbulence, a better understanding of the physics of energy dissipation and mixing throughout ISW evolving from generation to shoaling may contribute to better parameterization of mixing and understanding of the energy budget in global ocean models and climate models. In ocean environment, energetic currents and turbulence associated with ISWs can re-suspend sediments9,10,11,12,13, alter acoustic transmission14,15,16, damage offshore engineering structures17, and influence the ecosystems in the nearshore18,19,20.
The most vigorous internal solitary waves in the world’s oceans have been observed in the South China Sea (SCS)4,21,22,23, where their horizontal and vertical velocities are larger than 2 and 0.5 m s−1, respectively, and their amplitude can reach 100–200 m24,25,26,27. Internal tides generated over the ridges in Luzon Strait are the source of ISWs in the SCS27,28,29 (Fig. 1a). As the internal tides propagate westward across the SCS deep basin, they evolve into more bore-like structures30,31 via nonlinear steepening, and are further amplified by the shoaling continental slope. These processes create strong packets of ISWs above the Dongsha plateau (the area between 200 m and 500 m isobaths in Fig. 1a). Strong turbulent dissipation has been observed to be ~O(10−6–10−4) W kg−1 when the ISWs shoal25,32, motivating a search for the mechanism by which the energetic ISWs transfer their energy to turbulence. In the present context, ISWs dissipate their energy through turbulence as a result of wave instabilities as the ISWs shoal. Shoaling of an ISW over a steep slope larger than 0.0333 (bottom slope angle 1.7°) generally leads to intense wave break (overturning), deformation processes, fission and production of multiple elevation waves (transformation) that propagate up the slope4,5,34, while the instabilities are unclear or absent due to the rapid and intense wave evolution. When an ISW shoals over a relatively gentle slope (bottom slope angle <1.7°), it is found the instabilities occur in the waves’ interior or in the bottom boundary layer11,35,36. The former includes shear instabilities driven by enhanced vertical shear of horizontal currents3,37,38,39,40,41,42 and convective instabilities in the wave core occurring when the particle velocity exceeds the wave velocity6,33,43,44,45,46,47. A detailed review can be found in ref. 48. However, clear signatures of shear and convective instabilities within the ISWs have rarely been observed in the ocean due to their intermittence and rapid evolution.
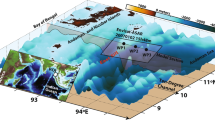
a Bathymetry and surface signatures of ISW, pointed out by the red arrows, from Moderate Resolution Imaging Spectroradiometer (MODIS) image snapshot at 02:55 A.M. 18 April, 2003, b MODIS image snapshot at 02:45 A.M. 18 May, 2019 inside the red dashed box in a, c cross-section of bathymetry along the yellow line in b, and d time series of vertical velocity averaged from 150 to 250 m (black curve) at A1, maximum particle velocity within the ISW (red dots) at A1, and propagation speeds of ISWs (blue dots). The horizontal blue, red and green lines in c are the ship tracks for the first, second and third shipboard surveys, respectively. The positions of thermistor chain (T1) and ADCP mooring (A1) were 252 m apart, as denoted by the red and black dots, respectively, in b and by the red and dashed black vertical lines, respectively, in c. The 15 ISW packets observed during May 15–23, 2019 are numbered and labeled in d. “RW” and “DW” in b denote the reflected waves and diffracted waves, respectively. The gray shade area in d represents the 95% confidence interval.
Nevertheless, field observations using a combination of echo sounding and conductivity–temperature–depth (CTD) profiling on the Oregon Shelf37 and on the Dongsha Plateau in the SCS3 revealed trains of ISWs with clear manifestation of shear instabilities that were the primary source of turbulence. Subsequently, a series of numerical experiments40,41,42,45 and laboratory experiments38,39,49 was conducted based on the observations of ref. 37 and ref. 3 to address the generation mechanism and criteria of occurrence for these instability waves. References 6 and 47 presented observations of a shoaling ISW of depression in the SCS as it underwent the formation of a recirculating trapped core as a result of convective breaking.
Those previous observations were mostly recognized by echo sounder images and hydrographic data with limited resolution and subsequently supplemented by laboratory experiments and numerical simulations. Here, we present observational evidence of Kelvin–Helmholtz (KH) instability and convective overturn and their resultant turbulence within the ISWs using multiple platform measurements (see “Methods”) including a fast-sampling moored thermistor chain (T1) with a vertical resolution of 4–5 m spanning 26–270 m depth, moored acoustic Doppler current profiler (ADCP) (A1), shipboard echo sounder, and shipboard turbulence profiler collected off just east of the Dongsha Atoll in the SCS (Fig. 1b, c). The sampling intervals for the thermistors and ADCP were 10 s and 6 s, respectively, capable of capturing the instabilities within the ISW. A series of 15 ISW packets was measured. All of the leading waves in these packets had maximum particle velocity larger than propagation speed, indicative of convective breaking and the formation of trapped cores. Both the convective overturning and Kelvin–Helmholtz billows were observed and their resultant turbulent mixing was quantified. The observations are used to compare with the previous observations, to examine the results of previous laboratory experiments and numerical simulations, and to assess the competition between shear and stratification, which govern the formation of instabilities and turbulent mixing.
Results
Observed wave properties
In spite of the commonly observed diffracted and reflected waves (Fig. 1b), the present study focuses on the incoming ISWs east of the Dongsha Atoll, where they shoal onto the shallow water near the atoll (Fig. 1b, c). The cross-section of bathymetry along 20°42′N east of the atoll (yellow line in Fig. 1b) presents a shallowing continental slope from 117°30′E (870 m) to 116°57′E (100 m) (Fig. 1c), with a mean slope of 0.013 (bottom slope angle 0.74°). The bottom slope around our mooring site at 300 m is 0.025 (bottom slope angle 1.43°). As previously mentioned, the slope angle (<1.7°) may favor the occurrences of the instabilities in the waves’ interior and/or in the bottom boundary layer (BBL). Unfortunately, these observations of temperature and velocity commenced above the BBL were not observed, and consequently were not discussed further. The leading wave of a wave packet, typically the largest and having a vertical velocity of 0.3–0.5 m s−1, was an indicator of the ISW packets in the 9-day moored observations (black curve in Fig. 1d). ISW packets arrived at our moorings primarily at a semidiurnal period, i.e., twice per day. In total, 15 ISW packets, numbered from 1 to 15 in Fig. 1d, were measured by the thermistor chain and ADCP. Propagation speeds (C) of those measured ISWs ranged from 1.0 to 1.5 m s−1 (blue dots), and had a mean value of 1.3 m s−1 (see “Methods” for the estimate of C). The maximum value of C was 2.1 m s−1 during the passage of ISW #10. Maximum particle velocity within the ISW (Umax) is shown as the red dots in Fig. 1d. It is found all of the observed ISWs reached the limit of convective breaking6, Umax > C. The average Umax was 1.7 m s−1, 30% larger than mean propagating speed.
Time-depth contours of the 15 observed leading ISWs are illustrated in Fig. 2 and Supplementary Fig. S1. As a whole, the 18 °C isotherm (magenta curve) is consistent with a typical mode-1 depression waveform and it effectively divides the ISW into a calm region below it and a very dynamical region above it where the isotherms undulate. The maximum vertical displacement ηmax estimated from the depression of the 18 °C isotherm ranged from 76 m (ISW #2) to 125 m (ISW #11) with a mean value of 103 m (black curve in Supplementary Fig. S2a). The horizontal wavelength measured at half of the wave amplitude, i.e., the half-amplitude full width λη/2, ranged from 0.53 km (ISW #1) to 1.16 km (ISW #10) with a mean value of 0.79 km (blue curve in Supplementary Fig. S2a). Except for ISW #1, the observed ISWs have an asymmetric waveform characterized by a gently sloping front edge and steepening at the trailing edge. This is because the wave trough slows down with respect to the upper layer currents as the waves shoal34,42. It is a subtle effect in these plots indicating that the waves are just starting to feel the bottom at the 300 m isobath.
Isothermal contour plots of a ISW #4, b ISW #7, c ISW #8, and d ISW #11 measured by mooring T1. The black contour line interval in a–d is 0.5 °C. The cyan contour lines in b range from 26.7 °C to 27.3 °C with an interval of 0.1 °C. The magenta contour line is the 18 °C isotherm. The red dots in a are the locations of the temperature sensors. The time axis is relative to the arrival time of the ISWs (see “Methods” for details). The undulation of the upper boundary of the contoured region is because the thermistor chain was bent over by the wave-induced current drag.
KH instabilities and breaking of the waveform
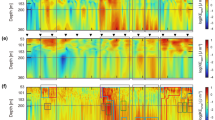
All of the ISWs measured by the thermistor chain revealed different degrees of breaking and undulation along the depressed waveform (Fig. 2 and Supplementary Fig. S1). The breaking pattern of ISWs can be seen mostly at the trailing edge and immediately above the isotherms where the stratification is strong, forming the breaking tail of the ISWs (for example, ISWs #4, #7, #8 and #11 in Figs. 2 and 3). A detailed example of breaking can be found in ISW #4 (Fig. 2a). A train of roll-up thermal patterns on the wave trough with a vertical scale of ~15 m is visible. Clearly, the roll-up thermal patterns are KH billows50,51,52,53. Following this train, a breaking of waveform encompassing a chaotic thermal patch and numerous overturns occurs in the wave’s trailing edge. Note the collapse is not constrained to the leading wave but can extend downstream and affect the following waves. A similar breaking structure can be seen in ISWs #7, #8, and #11 (Fig. 2). However, the features of KH billows near their wave trough are less organized than those observed in ISW #4, presumably because the billows were in an early stage of development or/and their resulting billow size was smaller than our measuring resolution. Comparing our observations with previous observations37 and numerical simulations42, the waveform breaking in the trailing edge could be related to the growth and ultimate collapse of the KH billows, mostly in the wave rear. As the propagating speed of the billows is less than the ISW’s propagating speed, the age of the billows in a train increases toward the trailing edge of the waves. The other 11 ISWs shown in Supplementary Fig. S1 depict less apparent breaking in the trailing edge. ISW #6 shows a sequence of KH billows-like structure with a vertical scale of ~10 m in the trough. The largest KH billows appear in ISW #14. A train of four KH billows occupies the ISWs from ahead of the wave trough to the wave trough.
Contours of S2 (first column), N2 (second column) and S2/N2 (third column) for ISW #4 (first row), ISW #7 (second row), ISW #8 (third row) and ISW #11 (forth row). The black contour lines are the isotherms from 12 to 29 °C with an interval of 0.5 °C. The magenta contour line is the 18 °C isotherm. The yellow and cyan curves are the contours of Ri = 0.25 and Ri = 0.1, respectively. The time axis is relative to the arrival time of the ISWs (see “Methods” for details).
On the whole, the above features are in qualitative agreement with previous field observations based on the echo sounder images (Fig. 5 in ref. 37, Fig. 9 in ref. 3), laboratory experiments (Fig. 10 in ref. 49, Fig. 4 in ref. 38, Fig. 3 in ref. 39), and numerical simulations (Fig. 4 in ref. 40, Fig. 7 in ref. 41, Fig. 13 in ref. 42, Fig. 13 in ref. 45). Having also direct observations of density and velocity at high resolution allows further quantification of the wave breaking process.
a, b UVMP microstructure profiling superimposed on a simultaneous echo sounder image and zonal velocity for the first survey of ISW #11. c Echo sounder image for the second survey. d, e UVMP microstructure profiling with the background of simultaneous echo sounder image and zonal velocity for the third survey. Black contour lines in b and e are the isotachs ranging from −1.6 m s−1 to 1.6 m s−1 with an interval of 0.2 m s−1. A positive zonal velocity is to the east. Thick black contour lines and magenta contour lines in b and e are the 0 m s−1 isotach and −0.4 m s−1 isotach, respectively. The wave shown in a–c (first survey) propagates to the left. The wave shown in d–e propagates to the right.
The occurrence of the KH instability depends on the competition between shear characterized by S2 (Methods) and stratification characterized by N2 (Methods), which tend to destabilize and stabilize the fluid layer, respectively, forming the critical Richardson number Ri = N2/S2. The canonical criterion for the instability of a parallel stratified shear flow is54,55 Ri < 0.25, which is not a sufficient condition for instability within the ISW. Instead, laboratory experiments and numerical simulations39,40,41,42,49 have suggested the conditions under which the shear instabilities within the ISW occur (curved stratified shear flow) include (1) Ri < 0.1 and (2) Lx/λη/2 > 0.86, where Lx is the length scale of the unstable region in which Ri < 0.25 and λη/2 is the half-amplitude full width (half width) of ISW. The conditions (1) and (2) allow the instabilities to have sufficient time to grow and eventually form KH billows. For ISWs #4, #7, #8, and #11 (Fig. 3), the shear squared S2 is found to be mostly stronger along the lower periphery of the wave core and occasionally extended to the wave core. The stronger stratification characterized by N2 is located predominantly below the periphery of the wave core. As a result, the region satisfying Ri < 0.25 (yellow contour line) are predominantly along the lower periphery of the wave core and slightly above the layer of strong stratification (second row in Fig. 3). The similar distribution of Ri in the waves can be found in the other ISW events (Supplementary Fig. S3). Only ISWs #1, #2, and #5 have the minimum Ri value larger than 0.1, as indicated by cyan contour lines in Fig. 3 and Supplementary Fig. S3 and as summarized in Supplementary Fig. S2b. Similarly, the value of Lx/λη/2 is smaller than 0.86 (red dashed line Supplementary Fig. S2c) for only ISWs #1, #2, #3, and #5. If a lenient criterion of Lx/λη/2 = 0.8 (blue dashed line; ref. 42) is taken, the conclusion is the same. Indeed, ISWs #1, #2, #3, and #5 have relatively smooth waveform in comparison with the other ISWs, suggesting the absence of KH instability.
Convective breaking
Unlike shear instability, the convective instability grows primarily within the wave core48,56,57, where the stratification is very weak. Previous observations6,47 and numerical simulations33,46,56,57 have indicated the convective breaking limit of ISWs was reached as they shoaled. During the upslope propagation of an initial wave at which Umax < C, the wave propagation speed decreased successively whereas the particle velocity remained a constant value, and ultimately met the breaking regime Umax > C. In summary, four stages of wave evolution were recognized according to those previous studies: (1) an asymmetric waveform characterized by a gentle sloping front edge and steepening at the rear edge as the shoaling waves adjust to the new depth, (2) formation of overturning (heavy-over-light fluid) evolved from the asymmetric waveform, (3) plunging of the heavier fluid into the wave core from the steepening rear edge, and (4) trapped core formed as an enclosed isopycnal region containing heavier fluid. Here, as indicated in Fig. 1d, all of the observed ISWs reach the condition of convective breaking Umax > C. Except for ISW #1, our observed ISWs have a waveform similar to the feature of Stage 1, i.e., the gentle front edge and steepening trailing edge in response to the shoaling. Distinct features of convective instability resembling to Stages 2 and 3 are seen in ISWs #1, #7, and #13. ISWs #1 (Supplementary Fig. S1a) and #13 (Supplementary Fig. S1g) show cold-water plunging from the rear edge of wave core as highlighted by the isotherms of 25–29 °C with an interval of 0.1 °C (cyan contour lines). The ISW #7 (Fig. 2b) show a convective roll-like pair, pointing to an event of colder water injection into the wave core as well, which is referred to Stage 3 and is highly coincident with previous numerical simulations (Fig. 7c in ref. 56, and Fig. 7c in ref. 33). The ISW #11, which is the largest amplitude wave (125 m), reveals a fully developed convective instability within its core (Fig. 2d). It shows warm water near the surface plunging down to ~100 m in the front part of the wave and then rolling up near the trough, while a region of well-mixed water develops at the rear, resembling a large convective overturning (Stage 4). The observed scene is consistent with simulated fully developed convective instability (Fig. 7d in ref. 56 and Fig. 7d in ref. 33). In ISW #11, the region containing vertically well-mixed water at the rear may be the “trapped core” as described in previous studies, but the core structure is relatively unclear, which may be smeared by the KH instabilities as some billow-like structures can be seen in the rear edge of the wave. The presence of billows in the rear of the ISW #11 can be seen in the echo sounder image as shown in Fig. 4a, c. Otherwise, N2 computed from the VMP casts prior to the arrival time of ISW #11 showed a very strong stratification (>1 ☓ 10−3 s−2) in the upper 30 m (Supplementary Fig. S4). The result supports the previous argument that upper layer must be inhomogeneous for the occurrences of convective instability58,59.
The interplay between the convective and shear instabilities
All the observed ISWs reached the condition of convective breaking Umax > C, but only four of them revealed the remarkable features of convective overturning in the wave core. The intermittence of the convective overturing can be the cause. To speculate further, the waveform breaking in the trailing edge as a result of the collapse of KH billows may hinder the process of the plunging of cold-water and consequent formation of trapped core by stirring the interface between cold and warm water. Hence, the shear instability could potentially suppress the occurrences of convective instability. This point of view hasn’t been noticed in the previous studies and needs to be further demonstrated. By contrast, it is well known that the convective instability could enhance the occurrences of shear instability37,38,45. Mixing induced by the convective overturning in the wave core (or upper water column) enhances isopycnal compression, which strengthen the stratification (N2) and shear (S2) simultaneously between the core and the pycnocline. However, the strengthening of S2 is an order larger than N2 in response to the decrease of dz due to isopycnal compression (see “Methods” for the calculation of S2 and N2), in favor of the occurrences of shear instability. Our observations mostly support the above argument as the enhanced S2 is generally found to be stronger along the lower periphery of the wave core and stronger N2 is located predominantly below the periphery of the wave core (Fig. 3). The prevailing region where Ri < 0.25 is primarily between the core and the thermocline, which support the findings in ref. 37,38,45. Taken together, these results suggest a scenario of the occurrences of wave instabilities. As an ISW shoal onto the continental slope, convective instability occurred as the wave rear steepened and the trough decelerated in response to the shallower depth. Formation of the convective overturning compressed the isopycnal between the core and the thermocline within the ISW, where the occurrences of KH instability was enhanced. As these previous numerical simulations and water tank experiments have suggested the occurrences of KH instability do not require the presence of shoaling topography39,40,41,42, our observations suggest that the shoaling topography may enhance the KH instability and subsequent turbulence by focusing both the shear and the stratification at the bottom of the wave.
Wave evolution and turbulence
The largest wave ISW #11 was tracked and measured three times until it reached the Dongsha Atoll (Methods). The echo sounder images taken in the first two surveys (Fig. 4a, c) show similar features with those taken by the moored thermistor chain (Fig. 2d), i.e., the plunging tongue in the wave front and the KH billow train (tilted S-shaped band60) adjacent to the wave trough. The strong echo as a result of flow instability is primarily in the region of strong westward current as enclosed by the −0.4 m s−1 isotach (magenta curve in Fig. 4b, e). The 0 m s−1 isotach (thick black curve) well characterizes the depressed waveform. Within the ISW, the maximum current speed of 1.6 m s−1 is larger than its wave speed 1.35 m s−1, which favors the onset of convective instability. Before the arrival of the ISW (Fig. 4a), the turbulence kinetic energy (TKE) dissipation ε was O(10−9–10−7) W kg−1, which are commonly observed values in the open ocean. Cast 4 sliced through the range of the plunging tongue and KH billow train, revealing \(\bar \varepsilon\) = 2 × 10−7 W kg−1 and \(\bar \varepsilon\) = 4.5 × 10−6 W kg−1, respectively, in their nearby regions. Cast 5 captures a greater range of the plunging tongue (40–110 m), where \(\bar \varepsilon\) = 2.2 × 10−6 W kg−1, while \(\bar \varepsilon\) = 3 × 10−5 W kg−1 in the KH billows (127–137 m). Casts 6 and 7 were taken within the well-mixed rear as a result of the combination of waveform collapse and convective instability (Figs. 4a and 2d). The well-mixed rear has a mean ε of 2.3 × 10−5 W kg−1 and has a maximum value of 1.7 × 10−4 W kg−1 adjacent to the strong echo band. During the third survey (Methods), the ISW was shoaling up an abrupt slope, where the bottom rapidly rose ~100 m (Fig. 4d). The waveform depicted by the echogram is drastically distorted due to the shoaling. In contrast, the westward zonal current structure retained its similarity with the measured zonal velocity from the previous survey as shown by the −0.4 m s−1 isotach (magenta curves in Fig. 4b, e), but the maximum zonal current velocity decreased to 0.8 m s−1. The eastward zonal currents in the lower layer appear to be squeezed between the westward velocity above and the rising bottom (Fig. 4e), forming a jet-like layer. Measurements taken in the front part of the wave revealed a higher value of 1 × 10−6 W kg−1 around 160 m in cast 5. Within the wave rear, which strongly interacts with the sloping bottom, distinct KH billows with an amplitude of 20–30 m were seen ~20 m above the bottom. The strong turbulence of ε ~ 10−5–10−4 W kg−1 is predominant within the KH billows and their upper region, where the convective breaking may be dominant. The strongest ε is 1.4 × 10−3 W kg−1 as shown in Cast 8.
Discussion
Shoaling internal solitary waves can transport and mix cold and nutrient-rich water beneath the thermocline into shallow water and coastal regions18,61,62. The mechanism has been found to change water properties, influence the metabolism of benthic communities, and shape the resilience of coastal ecosystems such as coral reefs19,20,63. The Dongsha Atoll, a Taiwanese National Park and the largest aggregation of coral reef in the northern SCS, is located in the prevailing path of the large ISWs analyzed here. In order to understand the influence of ISWs on biological functioning or potential resilience of reefs, we need to quantify mixing and understand the physical processes leading to turbulence within shoaling internal waves and the transport of sub-thermocline waters to these shallow ecosystems. Distributions of the eddy diffusivity64 Kρ = 0.2ε N−2 before and during the passage of ISW #11 are shown in Fig. 5. The criterion for the occurrences of shear instability45,46 S2/N2 = 4 clearly distinguishes the distributions of Κρ as a function of S2/N2 as is shown in Fig. 5a (black line). About 82% of the measurements fall in the stable state (S2/N2 < 4) with a wide range of Κρ from 10−6 to 100 m2 s−1. Only 18% of our measurements reach the instability condition S2/N2 > 4, but the value of Kρ is generally elevated. It seems that the Miles and Howard’s criterion remains applicable. The criterion of the shear instability applicable to ISW instability S2/N2 > 10 (red dashed line) derived from numerical simulation38 further concentrates Kρ on a range of high values 10−2 to 100 m2 s−1 as highlighted by the gray shading. The gray shading band (Kρ ~ 10−2–100 m2 s−1) also includes a region of S2/N2 < 4, suggesting the absence of shear instability, which is expected to be related to the convective breaking primarily occurring in the wave core where the shear and stratification (Fig. 5a) are weak and the westward currents are strong (Fig. 5b). The mean value of Κρ (10−1 m2 s−1) in the shaded band is close to previous measurements within an ISW6,37,47 and four orders larger than the common value found in the open ocean7 (10−5 m2 s−1) away from topography and in the absence of ISWs. Finally, the estimated maximal Kρ here is 3–4 orders of magnitude higher than the maximum value possible in the K-Profile Parameterization scheme65 commonly used in numerical ocean models.
Methods
Mooring instrument observations
To investigate the small-scale processes as ISWs shoal, two moorings A1 and T1 were deployed ~10 km east of Dongsha Atoll (as denoted by the red and black dots, respectively, in Fig. 1b), as part of a joint field observation conducted by investigators from Taiwan and the U. S. A1 was located 252 m northeast of T1. The T1-A1 line has an angle of 30o to the east. At A1, a 75-kHz acoustic Doppler current profiler (ADCP) was mounted on the bottom at 321 m depth (dashed vertical line in Fig. 1c). The ADCP resolved currents in segments spanning about 40–300 m in 8-m bins. The sampling interval was 6 s. Mooring T1 was equipped with 58 thermistors and deployed at a 323 m water depth (red vertical line in Fig. 1c). The thermistors were attached to the mooring line distributed with a vertical resolution of 4–5 m spanning 26–270 m (red dots in Fig. 2a and Supplementary Fig. S2a). The rapid sampling rate of 0.1 Hz permitted detailed observations of the thermal structure of internal solitary waves, having a typical time scale of 10–20 min and amplitude of 100–150 m. Here, only the overlap period of the two moorings is considered. Two moorings were simultaneously operational during the period 14 May–22 May 2019, which encompassed the arrivals of a set of 15 ISW packets generated surrounding a spring tide (Fig. 1d). The accuracy of the temperature sensors is 0.002 °C. The measuring error of ADCP current velocity is 0.076 m s−1, which is lowered to 0.024 m s−1 if the 1-min average is taken (for the calculation of shear).
Mooring data integration during ISW events
The ADCP (A1) and thermistor (T1) mooring are 252 m apart, leading to the time lag of observed ISWs between the two datasets. It is essential to combine the two datasets for further analysis. Depending on the ISW propagation speed, the arrivals of ISW at A1 often lead those at T1 1–3 min. The zonal velocity averaged from 150–250 m (Um) and temperature averaged from 150 to 250 m (θm) were used to defined the arrival time of the 15 ISW events at A1 and T1, respectively. The arrival time of an ISW at A1 (tA) was obtained as the mean time of the two points in time at the half maximal amplitude of Um. Likewise, the arrival time of ISW at T1 (tT) was obtained as the mean time of the two points in time at the half maximal amplitude of θm. Hereafter, the time frame of an ISW event at A1 and T1 was relative to (centered at) tA and tT (Fig. 2 and Supplementary Fig. S2), respectively, so that the two datasets are comparable by assuming the ISW did not significantly evolve from A1 to T1.
Shipboard observations
The shipboard surveys were performed in the cruise during 18–23 May 2019 onboard the Taiwan’s Research Vessel (R/V) Ocean Researcher III (OR3). Our observations were primarily taken along 20°42′N, (yellow line in Fig. 1b) perpendicular to the prevailing ISW propagation direction (Fig. 1a), using the combination of shipboard 75 kHz ADCP, 120-kHz echo sounder, and tow-yo turbulence profiler. The ADCP was sampled using 8-m vertical bins and 1-min ensembles averaged over ∼20 pings. The echo sounder sampled at 0.5 Hz with a vertical resolution of 10−2 m. The tow-yo turbulence profiler used was the Vertical Microstructure Profiler‐250 (VMP-250) manufactured by Rockland Scientific International Inc. (RSI). The VMP-250 was slack tethered by a thin spectra line spooled from a Teledyne Oceanscience Underway CTD (UCTD) winch for vertically profiling turbulence. The system combining the VMP-250 and UCTD winch has been termed the Underway Vertical Microstructure Profiler (UVMP)66. Sensors on the VMP-250 include two shear probes and one fast response thermistor (FP07) to respectively sample microscale velocity shear and temperature gradient at 512 Hz. Here, we only focus on the microscale shear measurements and their resultant estimates of dissipation rate of turbulent kinetic energy. The dissipation rate is defined as \({\it{\epsilon }} = 7.5\upsilon \overline {u_z^2}\), where υ is the molecular viscosity and \(\overline {u_z^2}\) is mean square microscale velocity shear. ODAS software provided by RSI was used to estimate the TKE dissipation rate. Additionally, a Conductivity–Temperature (CT) sensor is mounted on the nose of UVMP to simultaneously sample conductivity and temperature at 16 Hz.
Estimate of wave speed
As mooring A1 was at 252 m northeast of mooring T1, the arrivals of ISW at A1 often lead those at T1 by 1–3 min, which allows computation of the wave speed estimates. As well, wave speed and direction of the leading ISW are estimated by the current measurements at A1 using the iteration method67. The distortion of the waveform in velocities as a result of the beam spreading effect of ADCP measurements was also corrected. Propagation speeds estimated using the iterative method (Ci) and the arrival time between A1 and T1 (Ca) were consistent, mostly within 1–1.5 m s−1. Both the mean Ci and Ca of the 15 measured ISWs are 1.3 m s−1. The mean values of Ci and Ca are in agreement with previous observations68, giving an ISW propagation speed of 1.05 m s−1 at water depths of 200–300 m north of our mooring sites. Hereafter, the wave speed C, the average of Ci and Ca, is used for the following analyses (blue dots in Fig. 1d).
Calculation of velocity shear and buoyancy frequency
Both the current velocity and temperature data were interpolated to a 4-m by 10-second grid. The velocity shear squared is computed as \(S^2 = (\frac{{\partial u}}{{\partial z}})^2 + (\frac{{\partial v}}{{\partial z}})^2\), where u and v are 1-min averaged zonal and meridional velocity (to reduce the velocity error to 0.024 m s−1), respectively. The buoyancy frequency squared is computed as \(N^2 = - \frac{g}{{\rho _0}}\frac{{\partial \rho }}{{\partial z}}\), where ρ is the density and ρ0 (1025 kg m−3) is a reference density, and g (9.81 m s−2) is the gravitational acceleration. ρ is computed from the equation of state by substituting 1-min averaged temperature and a constant value of salinity (34.5 psu).
Wave chasing
ISW #11 was tracked and measured three times before it reached Dongsha Atoll. In the beginning, the ship waited at 20°42′N, 117°1.59′E (350-m water depth and 2.89 km east of T1) for the arrival of the ISW from the east (Fig. 1c). When the wave arrived, the ship drifted westward with the surface currents induced by the ISW but kept essential steerage so that the ship heading was to the east, to allow the tow-yo UVMP operation on the back deck. About 40 min later, the ISW passed through the ship since the wave speed (>1 m s−1) was slightly higher than the drifting speed of ship (0.4–1 m s−1). After the ISW’s passage, the ship immediately turned around and caught up with the ISW at full speed (~10 knots) for the second survey (without UVMP). The ship tracks in which the ISW was detected underwater in the first and second surveys were shown as horizontal blue and red lines in Fig. 1c. For the first two surveys, we define a wave coordinate xw(t) moving with the ISW (Fig. 4a–c), that is xw(t) = xs(t) − Ct, where xs is the ship displacement and C is the wave speed. Ship displacement xs is determined by GPS. It is noted T1 mooring is nearly centered at the track of the second survey. Therefore, wave speed of 0.92 m s−1 (C of ISW #11 in Fig. 1d) was applied for the wave coordinate transformation. The wave speed during the first survey is unknown but is inferred as 1.35 m s−1 here, so that the horizontal scale of ISW in the two surveys is nearly consistent (~1.4 km as denoted by two vertical dashed lines in Fig. 4a–c). The mean wave speed of ISW #11 estimated using the travel time between the location of the first encounter (western end of the blue line in Fig. 1c) and T1 is 1.22 m s−1, a value between 0.92 and 1.35 m s−1 in support of our inference. Having transited westward across the ISW #11 for the second survey, we stopped ahead of the wave for the third survey and allowed it to pass the ship to perform the drifting tow-yo UCTD profiling as was done during the first survey. The ship was drifting upslope (westward), advected by the ISW-induced surface current during the passage of the ISW. We did not try to apply the wave coordinate transformation to the third survey because the wave speed here changed rapidly. Seven turbulence profiles, numbered from 1 to 7 in Fig. 4a, were taken before the arrival of the ISW (casts 1–3) and during its passage (casts 4–7) during the first survey. Eleven turbulence profiles were obtained, numbered from 1 to 11 in Fig. 4d, during the third survey.
Data availability
We produced Fig. 1a, b using the reflectance (true color) data distributed by NASA Land Processes Distributed Active Archive Center (LP DAAC). The reflectance data can be downloaded from https://oceancolor.gsfc.nasa.gov. Bathymetry data (Fig. 1a) can be downloaded from https://www.ngdc.noaa.gov/mgg/global/etopo2.html. Data drawn from ship-based and moored measurements used to produce the figures presented in this article can be obtained from Zenodo repository69 (https://doi.org/10.5281/zenodo.4289412).
Code availability
ODAS software (MATLAB code) used to estimate the TKE dissipation rate is available from RSI upon request. The code for ADCP data processing can be freely obtained at https://www.eoas.ubc.ca/~rich/#RDADCP. Custom codes used for analyses in this article can be obtained upon reasonable request to the corresponding author.
References
Jackson, C. R., da Silva, J. C. B. & Jeans, G. The generation of nonlinear internal waves. Oceanography. 25, 108–123 (2012).
Klymak, J. M. & Moum, J. N. Internal solitary waves of elevation advancing on a shoaling shelf. Geophys. Res. Lett. 30, 2045 (2003).
Orr, M. H. & Mignerey, P. C. Nonlinear internal waves in the South China Sea: observation of the conversion of depression internal waves to elevation internal waves. J. Geophys. Res. 108, 3064 (2003).
Ramp, S. R. et al. Internal solitons in the northeastern South China Sea part I: Sources and deep water propagation. IEEE J. Oceanic Eng. 29, 1157–1181 (2004).
Shroyer, E., Moum, J. & Nash, J. Observations of polarity reversal in shoaling nonlinear internal waves. J. Phys. Oceanogr. 39, 691–701 (2009).
Lien, R.-C. et al. Trapped core formation within a shoaling nonlinear internal wave. J. Phys. Oceanogr. 42, 511–525 (2012).
Munk, W. H. & Wunsch, K. Abyssal recipes. II: energetics of tidal and wind mixing. Deep-Sea Res. 45, 1977–2010 (1998).
Egbert, G. D. & Ray, R. D. Significant dissipation of tidal energy in the deep ocean inferred from satellite altimeter data. Nature 405, 775–778 (2000).
Bogucki, D., Dickey, T. & Redekopp, L. Sediment resuspension and mixing by resonantly generated internal solitary waves. J. Phys. Oceanogr. 27, 1181–1196 (1997).
Hosegood, P., Bonnin, J. & van Haren, H. Solibore-induced sediment resuspension in the Faeroe-Shetland Channel. Geophys. Res. Lett. 31, L09301 (2004).
Bogucki, D. J., Redekopp, L. G. & Barth, J. Internal solitary waves in the coastal mixing and optics 1996 experiment: multimodal structure and resuspension. J. Geophys. Res. 110, C02024 (2005).
Butman, B., Alexander, P. S., Scotti, A., Beardsley, R. C. & Anderson, S. P. Large internal waves in Massachusetts Bay transport sediments offshore. Cont. Shelf Res. 26, 2029–2049 (2006).
Reeder, D., Ma, B. & Yang, Y. J. Very large subaqueous sand dunes on the upper continental slope in the South China Sea generated by episodic, shoaling deep-water internal solitary waves. Mar. Geol. 279, 12–18 (2011).
Reeder, D. B., Duda, T. F. & Ma, B. In Ocean 2008—MTS/IEEE Kobe Techno-Ocean. Vol. 1–3, 65–172 (IEEE, 2008)..
Kuperman, W. A. & Lynch, J. F. Shallow water acoustics. Phys. Today 57-1010, 55–61 (2004).
Chiu, L. Y. S. et al. Enhanced nonlinear acoustic mode coupling resulting from an internal solitary wave approaching a shelf break. J. Acoust. Soc. Am. 133, 1306–1319 (2013).
Osborne, A. R. & Burch, T. L. Internal Solitons in the Andaman Sea. Science 208-4443, 451–460 (1980).
Wang, Y. H., Dai, C. F. & Chen, Y. Y. Physical and ecological processes of internal waves on an isolated reef ecosystem in the South China Sea. Geophys. Res. Lett. 34, 1–5 (2007).
DeCarlo, T. M. et al. Community production modulates coral reef pH and the sensitivity of ecosystem calcification to ocean acidification. J. Geophys. Res. Oceans 122, 745–761 (2017).
Reid, E. C. et al. Internal waves influence the thermal and nutrient environment on a shallow coral reef. Limnol. Oceanogr. 11162, 1–17 (2019).
Duda, T. F. et al. Internal tide and nonlinear internal wave behavior at the continental slope in the Northern South China Sea. IEEE J. Ocean. Eng. 20, 1105–1130 (2004).
Yang, Y. J. et al. Solitons northeast of Tung-Sha Island during the ASIAEX pilot studies. IEEE J. Oceanic Eng. 29, 1182–1199 (2004).
Alford, M. H. et al. The formation and fate of internal waves in the South China Sea. Nature. 521, 65–69 (2015).
Lien, R.-C., Tang, T. Y., Chang, M.-H. & D’Asaro, E. A. Energy of nonlinear internal waves in the South China Sea. Geophys. Res. Lett. 32, L05615 (2005).
Chang, M.-H., Lien, R.-C., Tang, T. Y., D’Asaro, E. A. & Yang, Y. J. Energy flux of nonlinear internal waves in northern South China Sea. Geophys. Res. Lett. 33, L03607 (2006).
Chang, M.-H., Lien, R.-C., Tang, T. Y., Yang, Y. J. & Wang, J. A composite view of surface signatures and interior properties of nonlinear internal waves: Observations and applications. J. Atmos. Oceanic Technol. 25, 1218–1227 (2008).
Alford, M. H. et al. Speed and evolution of nonlinear internal waves transiting the South China Sea. J. Phys. Oceanogr. 40, 1338–1355 (2010).
Niwa, Y. & Hibiya, T. Three‐dimensional numerical simulation of M2 internal tides in the East China Sea. J. Geophys. Res. 109, C04027 (2004).
Jan, S., Lien, R.-C. & Ting, C.-H. Numerical study of baroclinic tides in Luzon Strait. J. Oceanogr. 64, 789–802 (2008).
Davis, K. A. et al. Fate of internal waves on a shallow shelf. J. Geophys. Res. Oceans 125, e2019JC015377 (2020).
Zhao, Z., Klemas, V., Zheng, Q. & Yan, X.-H. Remote sensing evidence for baroclinic tide origin of internal solitary waves in the northeastern South China Sea. Geophys. Res. Lett. 31, L06302 (2004).
St. Laurent, L. Turbulent dissipation on the margins of the South China Sea. Geophys. Res. Lett. 35, L23615 (2008).
Rivera-Rosario, G., Diamessis, P. J., Lien, R., Lamb, K. G. & Thomsen, G. N. Formation of recirculating cores in convectively breaking internal solitary waves of depression shoaling over gentle slopes in the South China Sea. J. Phys. Oceanogr. 50, 1137–1157 (2020).
Vlasenko, V. & Hutter, K. Numerical experiments on the breaking of solitary internal wavesover a slope–shelf topography. J. Phys. Oceanogr. 32, 1779–1793 (2002).
Stastna, M. & Lamb, K. G. Vortex shedding and sediment resuspension associated with the interaction of an internal solitary wave and the bottom boundary layer. Geophys. Res. Lett. 29, 1512 (2002).
Carr, M., Davies, P. A. & Shivaram, P. Experimental evidence of internal solitary wave‐induced global instability in shallow water benthic boundary layers. Phys. Fluids 20, 066603 (2008).
Moum, J. N., Farmer, D. M., Smyth, W. D., Armi, L. & Vagle, S. Structure and generation of turbulence at interfaces strained by internal solitary waves propagating shoreward over the continental shelf. J. Phys. Oceanogr. 33, 2093–2112 (2003).
Carr, M., Fructus, D., Grue, J., Jensen, A. & Davies, P. A. Convectively induced shear instability in large amplitude internal solitary waves. Phys. Fluids 20, 126601 (2008).
Fructus, D., Carr, M., Grue, J., Jensen, A. & Davies, P. A. Shear-induced breaking of large internal solitary waves. J. Fluid Mech. 620, 1–29 (2009).
Barad, M. F. & Fringer, O. B. Simulations of shear instabilities in interfacial gravity waves. J. Fluid Mech. 644, 61–95 (2010).
Carr, M., King, S. E. & Dritschel, D. G. Numerical simulation of shear-induced instabilities in internal solitary waves. J. Fluid Mech. 683, 263–288 (2011).
Lamb, K. G. & Farmer, D. Instabilities in an internal solitary-like wave on the oregon shelf. J. Phys. Oceanogr. 41, 67–87 (2011).
Fructus, D. & Grue, J. Fully nonlinear solitary waves in a layered stratified fluid. J. Fluid Mech. 505, 323–347 (2004).
Helfrich, K. R. & White, B. L. A model for large-amplitude internal solitary waves with trapped core. Nonlinear Process. Geophys. 17, 303–318 (2010).
Carr, M., King, S. E. & Dritschel, D. G. Instability in internal solitary waves with trapped cores. Phys. Fluids 24, 016601 (2012).
He, Y., Lamb, K. & Lien, R.-C. Internal solitary waves with subsurface cores. J. Fluid Mech. 873, 1–17 (2019).
Lien, R.-C., Henyey, F., Ma, B. & Yang, Y. J. Large-amplitude internal solitary waves observed in the northern South China Sea: properties and energetic. J. Phys. Oceanogr 44, 1095–1115 (2014).
Lamb, K. G., Lien, R.-C. & Diamessis, P. J. In Encyclopedia of Ocean Sciences. 3rd edn. Vol. 3, 533–541 (Elsevier, 2019).
Troy, C. D. & Koseff, J. R. The instability and breaking of long internal waves. J. Fluid Mech. 543, 107–136 (2005).
Smyth, W. D., Moum, J. N. & Caldwell, D. R. The efficiency of mixing in turbulent patches: inferences from direct simulations and microstructure observations. J. Phys. Oceanogr. 31, 1969–1992 (2001).
van Haren, H. & Gostiaux, L. A deep ocean Kelvin-Helmholtz billow train. Geophys. Res. Lett. 37, L03605 (2010).
van Haren, H., Gostiaux, L., Morozov, E. & Tarakanov, R. Extremely long Kelvin-Helmholtz billow trains in the Romanche Fracture Zone. Geophys. Res. Lett. 41, 8445–8451 (2014).
Smyth, W. D. & Moum, J. N. Ocean mixing by Kelvin-Helmholtz instability. Oceanography. 25, 140–149 (2012).
Miles, J. W. On the stability of heterogeneous shear flows. J. Fluid Mech. 10, 496–508 (1961).
Howard, L. N. Note on a paper by J. W. Miles. J. Fluid Mech. 10, 509–512 (1961).
Lamb, K. G. A numerical investigation of solitary internal waves with trapped cores formed via shoaling. J. Fluid Mech. 451, 109–144 (2002).
Lamb, K. G. Shoaling solitary internal waves: on a criterion for the formation of waves with trapped cores. J. Fluid Mech. 478, 81–100 (2003).
Grue, J., Jensen, A., Rusas, P. & Sveen, J. Breaking and broadening of internal solitary waves. J. Fluid Mech. 413, 181–218 (2000).
Grue, J., Jensen, A., Rusas, P. & Sveen, J. Properties of large-amplitude internal waves. J. Fluid Mech. 380, 257–278 (1999).
Chang, M. ‐H., Jheng, S. Y. & Lien, R. ‐C. Trains of large Kelvin‐Helmholtz billows observed in the Kuroshio above a seamount. Geophys. Res. Lett. 43, 8654–8661 (2016).
Leichter, J. J., Wing, S. R., Miller, S. L. & Denny, M. W. Pulsed delivery of subthermocline water to conch reef (Florida Keys) by internal tidal bores. Limnol. Oceanogr. 41, 1490–1501 (1996).
Davis, K. A. & Monismith, S. G. The modification of bottom boundary layer turbulence and mixing by internal waves shoaling on a barrier reef. J. Phys. Oceanogr. 41, 2223–2241 (2011).
Wyatt, A. S. J. et al. Heat accumulation on coral reefs mitigated by internal waves. Nat. Geosci. 13, 28–34 (2020).
Osborn, T. R. Estimates of the local rate of vertical diffusion from dissipation measurements. J. Phys. Oceanogr. 10, 83–89 (1980).
Large, W. G., McWilliams, J. C. & Doney, S. C. Oceanic vertical mixing: a review and a model with a nonlocal boundary layer parameterization. Rev. Geophys. 32, 363–403 (1994).
Nagai, T. et al. First evidence of coherent bands of strong turbulent layers associated with high‐wavenumber internal‐wave shear in the upstream Kuroshio. Sci. Rep. 7, 14555 (2017).
Chang, M.-H., Lien, R.-C., Yang, Y.-J. & Tang, T.-Y. Nonlinear internal wave properties estimated with moored ADCP measurements. J. Atmos. Oceanic Technol. 28, 802–815 (2011).
Fu, K. H., Wang, Y. H., St Laurent, L., Simmons, H. & Wang, D. P. Shoaling of large-amplitude nonlinear internal waves at Dongsha Atoll in the northern South China Sea. Cont. Shelf Res. 37, 1–7 (2012).
Chang, M.-H. Instabilities and turbulence observed within large internal solitary waves. Zenodo https://doi.org/10.5281/zenodo.4289412 (2020).
Acknowledgements
We thank the crew and officers of the R/Vs Ocean Researcher 1 and 3 for supporting our experiments. We also thanks Wen-Hwa Her, Sin-Ya Jheng, Wei-Ting Hung, Chih-Ting Lee, Meng-Chiao Hsieh, and Chia-Ying Hsieh for mooring preparation and operation. Bee Wang prepared the UVMP system. Hsiang‐Chih Hsieh and Meng-Chiao Hsieh assisted with UVMP operations. Comments from Kevin Lamb and two anonymous reviewers improved the preliminary manuscript markedly. M.H.C., Y.J.Y., and S.J. were supported by the MOST grants 107-2611-M-002-015, 107-2611-M-002-016, and 107-2611-M-002-017, respectively. Y.H.C. was supported by the CWB of Taiwan through Grant 1092037 C. K.A.D. was supported by NSF-OCE 1753317. S.R.R. was supported by the U.S. Office of Naval Research under grant N00014-19-1-2686. Source of satellite data used in Fig. 1a, b: NASA Goddard Space Flight Center, MODIS Characterization Support Team, MODIS Adaptive Processing System; (2017): Terra/MODIS Level 1A Scans of raw radiances in counts, NASA LAADS DAAC. https://doi.org/10.5067/MODIS/MOD01.061. Accessed on 2020/12/14.
Author information
Authors and Affiliations
Contributions
M.-H.C., Y.J.Y., S.J., S.R.R., D.B.R., and K.A.D. designed the field experiment. Y.J.Y., S.R.R., D.B.R., and H.-J.S. performed the field observations. Y.-H.C. and W.-T.H. helped the preparations of the moorings and UVMP profiling. H.-J.S. and R.-S.T. technically supported the VMP profiling. D.S.K. provided the model prediction needed for the field work. M.-H.C. and Y.-H.C. analyzed the data and performed relevant figures. M.-H.C. provided the fundamental idea for interpreting the data and wrote the initial draft. All authors contributed to the data interpretation and writing of the final version of the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Primary handling editor: Heike Langenberg.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chang, MH., Cheng, YH., Yang, Y.J. et al. Direct measurements reveal instabilities and turbulence within large amplitude internal solitary waves beneath the ocean. Commun Earth Environ 2, 15 (2021). https://doi.org/10.1038/s43247-020-00083-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-020-00083-6
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.