Abstract
Physical laws governing friction on shallow faults in the Earth and spatial heterogeneity of parameters are critical to our understanding of earthquake physics and the assessment of earthquake hazards. Here we use a laboratory-derived fault-friction law and high-quality strong-motion seismic recordings of the 2020 Elazığ earthquake, Turkey, to reveal the complex rupture dynamics. We discover an initial Mw 5.8 rupture stage and explain how cascading behavior of the event, involving at least three episodes, each of M > 6, caused it to evolve into a large earthquake, contrarily to other M5+ events on this part of the East Anatolian Fault. Although the dynamic stress transfer during the rupture did not overcome the strength of the uppermost ~5 kilometers, surface ruptures during future earthquakes cannot be ruled out. We foresee that future, routine dynamic inversions will improve understanding of earthquake rupture parameters, an essential component of modern, physics-based earthquake hazard assessment.
Similar content being viewed by others
Introduction
While kinematic modeling of earthquakes for their space-time slip history on faults has become almost routine task nowadays1,2, applications of the fault friction-laws in dynamic source inversions are rare and challenging3,4,5. Dynamic inversions, involving causative stresses and strengths have the potential to surmount standard kinematic approaches that are considered to provide strongly non-unique results6,7. Instead, dynamic inversion can obtain a better-constrained picture of the rupture evolution, because rupture dynamics strongly couple the complete rupture history in terms of the energy release, and the mechanical fault features along the propagating rupture front via the employed friction law. Although the feasibility of dynamic rupture inversions was demonstrated in the 1990’s5,8,9, there are just a handful of real-data discoveries in coseismic dynamics, with none yet from the East Anatolian Fault Zone (EAFZ).
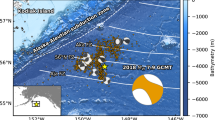
The EAFZ is a major intra-continental left-lateral strike-slip structure between the Arabia plate and the Anatolian Block of the Eurasia plate, slipping at ~1 cm/y10,11,12,13,14. Despite being known as the birthplace of significant historical events15, the first earthquake illuminating rupture details of the EAFZ occurred just recently16,17, on January 24, 2020 (Mw 6.8, Global Centroid Moment Tensor, GCMT), see Fig. 1. The Elazığ earthquake killed 41 people and heavily damaged over 700 buildings18. Coseismic surface faulting has not been observed.
a The bottom-right inset shows a broader region with the North Anatolian Fault Zone and East Anatolian Fault Zone (NAFZ, EAFZ). The GCMT focal mechanism is shown with gray beachball. Three major subevents of multiple-point source inversion of broadband and strong motion records, MPS-BB-SM, are plotted with circles sized with their seismic moment and colored with their rupture time. The multiplicity of the subevents (and their nodal lines) reflects the uncertainty revealed by jackknifing. The three best-fitting subevents, shown with black-white beachballs, are labeled by their moment magnitudes. Green and blue stars refer to epicenters H and H’ calculated from the first (weak) and the secondary (strong) P and P’ onsets, respectively, delimiting the source nucleation. Relocated aftershocks are color-coded relative to their occurrence time. Positions of the Ms ~ 7 historical earthquakes are shown schematically. b Velocity records filtered between 0.05–2.5 Hz for strong-motion stations 4401 and 2302 (plotted in panel a), rotated into the fault-parallel and fault-normal system. Real data (black) are compared with synthetics (red) calculated using the dynamic model of Fig. 2 (see also Supplementary Fig. S12). The waveforms illustrate the ground motion complexity, including directivity effect. The zoomed initial parts of the waveforms demonstrate the P and P’ onsets due to H and H’, respectively (for other stations see Supplementary Fig. S12).
The EAFZ is considered an immature fault zone, 2–5 Ma old, with 22–33 km offset19,20. Despite its historical seismicity and geomorphological evidence, some studies12,19 claim that the seismic quiescence of the EAFZ during the last ~100 years suggests the EAFZ is locked, accumulating elastic strain energy. Contrarily, recent studies employing InSAR, GPS and creepmeter data report creep within a zone from surface to the seismogenic depth, along the segments to the north-east of Lake Hazar21,22,23. Yet, many open questions about the creep segmentation (location, rate, origin, etc.) need to be addressed in more detail24.
Here, based on seismic data of the Turkish networks, and using innovative methodology, we decipher stress and frictional parameters of the Elazığ earthquake fault rupture in a detail allowing new tectonic and mechanical interpretations. In particular, we explain why the recent earthquake did not produce surface faulting, and we show that moderate earthquakes of the inter-seismic period are undeveloped rudiments of potentially large events.
Results
Bayesian dynamic model of the fault rupture
For our recently developed Bayesian dynamic source inversion25, we assume a planar fault of 75 × 20 km based on the preceding Multiple-point source modeling (see Methods and Fig. 1), adjusted to conform to the aftershocks. The fault plane reaches the surface. The spontaneous rupture is governed by linear slip-weakening friction26 (Fig. 2a) with spatially variable left-lateral prestress and frictional parameters. We model strong-motion records at stations shown in Fig. 2c, d. The frequency range considered is 0.05–0.30 Hz in the case of the closest stations (2301, 2302, 2308, 4401, 4404), and 0.05–0.15 Hz elsewhere.
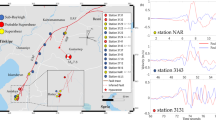
a Sketch illustrating the slip-weakening friction law26 and the physical meaning of the dynamic parameters (see text for details). b Slip-rate snapshots of the MAP source model showing the rupture evolution (also available as Supplementary Movie 1). The two asterisks denote hypocenters H and H’. c Comparison between the observed (black) and synthetic (red) displacement waveforms at stations shown by triangles in the inset of panel d. d Slip distribution in a map view (color-coded). The rectangle is a surface projection of the fault considered in the inversion, the top edge plotted in bold, and dots are aftershocks. The left inset shows stations used in the inversion (triangles) and those used for posterior check by the forward prediction (inverted triangles) in Supplementary Fig. S1. The bottom-right inset is the moment rate function of the rupture model.
Fig. 2c shows the waveform fit for our estimated maximum a posteriori (MAP) source model with variance reduction of 70%. Some of the stations were deliberately omitted in the inversion and serve as an independent check of the predictive power of the dynamic model (Supplementary Fig. S1). The main kinematic and dynamic parameters are displayed in Fig. 3. The seismic moment is 1.7 × 1019 Nm (Mw 6.8), the average stress drop is 12 MPa, and the mean slip is 1.5 m. Despite the considerable uncertainty of the dynamic parameters (see Supplementary Figs. S2–S5), the key characteristics of the rupture remain stable. In particular, the rupture starts from a patch at the located hypocenter H. It initially propagates up-dip and towards the north-east (Fig. 2b), creating ~5 s long minor episode in the moment rate release (Fig. 2d). The rupture reaches its final extent towards the north-east close to H’, which we located as a secondary hypocenter based on strong P’ phases identified in the seismograms (see Methods and Fig. 1). The rupture then turns to south-west and produces the first major moment release for another ~5 s. After minor weakening, the rupture continues unilaterally towards the south-west between 10 and 15 s after the origin time and releases about 4 meters of slip at the strongest asperity with the local stress drop of 40 MPa. After almost ceasing, the rupture reactivates in the third major episode breaching bilaterally a smaller asperity of similar stress drop within the last ~5 s. The rupture velocity varies significantly, having a relatively small mean value of ~2 km/s. We point out that none of the accepted rupture scenarios reaches the surface, in agreement with the fact that there was no co-seismic surface rupture observed.
a–h Black and blue contours outline the slip and nucleation patch, respectively. Blue asterisks denote the H and H’ hypocenters. Substantial spatial variability of the parameters can be seen. Note that only the parameters within the ruptured area are to be interpreted because the outer parameters are unconstrained, as the rupture did not reach them.
The three main episodes revealed here entirely agree with the three-point-source models (Fig. 1 and Methods) and the SCARDEC time function27. The slip distribution and mean rupture speed agree with smooth images inferred from geodetic inversions16,17. As we show in Supplementary Fig. S6, although the episodic character is not very visible in the rather smooth slip distribution, it is clearly expressed in the slip rate functions, exhibiting multiple peaks due to the partial reactivation after each major stress drop episode. The ceasing of the rupture is dynamically due to the relatively large values of Dc and strength excess (difference between strength and prestress) along the fault, resulting in locally large fracture energy expended in the rupture process.
The main rupture parameters28 are the slip-weighted mean stress drop 12.0 ± 0.7 MPa, mean Dc 1.04 ± 0.07 m, total fracture energy 3.3 ± 0.4 × 1015 J, and radiated energy 0.5 ± 0.1 × 1015 J, suggesting that relative to other shallow earthquakes the radiation efficiency of ~0.1–0.2 is low28. The mean fracture energy, also known as breakdown work density, is 10 ± 1 MJm−2. The latter value is in agreement with inferences for past earthquakes29.
The birth and growth of the rupture
The earthquake records reveal two P onsets (Fig. 1), weak and strong, and the source of the latter (H’) was located on the fault about 10 km to the north-east from the hypocenter (H). The inferred model explains this preparatory part as weak nucleation lasting 4–5 s, including a fast-slow-fast transition of the rupture from H to H’ (Fig. 3). We performed a simple experiment where we reduced the initial stress in the top 12 km by 10% (corresponding to an increase of the strength excess) to simulate earlier state of the fault. We obtained an Mw 5.8 earthquake, which failed to develop into a larger event (Supplementary Fig. S7). During 1964–2020, seven events of such size occurred at the investigated fault segment, despite being considered a seismic gap resisting significant rupture in-between the strong earthquakes of the last 150 years30, see Supplementary Fig. S8. These seven events ranged from Mw 5.1 to 5.7 and included an Mw 5.3 of the 4th April 2019, situated almost at the epicenter of the 2020 event. This suggests that these previous events failed to rupture large fault segments, analogously to the above simple experiment with the reduced initial stress, perhaps because they occurred too early when the segment was not yet ready to go31,32. Contrarily, by January 2020, the whole segment was ready to fail and the initial Mw 5.8 nucleation event spontaneously evolved to the Mw 6.8 rupture. Therefore, the final magnitude of the 2020 earthquake was not determined at the time of its nucleation. Although it may not necessarily be a typical behavior, these findings might contribute to the explanation of the wide scatter in empirical correlations between the observed P-wave onsets and the earthquake magnitude33,34,35,36, or perhaps even indicate a lack of any causal relation. This represents an important contribution to early warning systems.
The area of the dominant slip in our model is characterized by a paucity of aftershocks (Fig. 3 and Supplementary S2). Most of the aftershocks appeared below the major slip, mainly in the nucleation area, and at the north-east and south-west edges of the slipped area. The spatial distribution of aftershocks is in good agreement with the Coulomb stress change37 calculated from the inverted slip model (Supplementary Fig. S9). The rupture seems to have stopped by reaching other distinct segments of the EAFZ, namely restraining bend near the Yarpuzlu city to the south-west and releasing bend near Lake Hazar to the north-east.
The largest slip (4 m) was released at the patch with the largest initial stress (and thus the largest stress drop) of 40 MPa, see Fig. 3. The patch is also associated with large Dc and strength, resulting in locally 5-times larger fracture energy than average. The rupture speed reaches supershear values of ~4 km/s when approaching the asperity, and then the rupture slows down to propagate over the asperity at subshear speed (2–3 km/s). This asperity is mainly responsible for strong directivity pulses at stations in the south-west direction (e.g., 4401 in Fig. 1b). After breaking this strong asperity, the rupture experienced a subsequent short inhibition due to lower prestress and large fracture energy. This can also be understood as a proxy of some (unmodeled) geometrical fault complexity38,39,40,41, perhaps related to the bending of the Euphrates River (Fig. 2d). The rupture then proceeded into another area of a 20-MPa stress drop. This time the entered area had small fracture energy, which resumed the rupture. In most of the accepted models, the crack propagated over this patch bilaterally and possibly at supershear speed locally, but always with strong radiation expressed by the later pulses in the seismograms (Fig. 2c).
Shallow slip deficit and implications for East Anatolian Fault
No surface rupture was created by the Elazığ earthquake. Fig. 3 suggests that the stress transfer from the rupture did not overcome the strength at the subsurface ~5-km fault strip, and thus the earthquake failed to reach the surface. One of the explanations of the subsurface slip deficit is the creep in Paleozoic-Mesozoic metamorphic rocks, Mesozoic serpentinite-rich ophiolites, and volcanoclastics with moderate to very low strength, characterizing the EAFZ42,43. This would resemble vertical segmentation of the fault hosting the 2011 Mw 7.1 Van, Turkey, earthquake, at 10-20 km depths, suggested to explain the lack of a shallower rupture44. This slip deficit was later at least partially ameliorated by 1.5 years of postseismic deformation45. In our case, a persistent creep seems to be contraindicated by the weak and rapidly decaying afterslip observed from the InSAR measurements16. A counteracting of the slip deficit by inelastic off-fault deformation during the event46,47 seems also unlikely because field observations48 and dynamic rupture simulations with fault zone plasticity49 suggest that this effect is limited to much shallower depths (< 0.1–1 km). Although a significant slip deficit can be a general property of immature faults50, we propose that the energy release rate of a future earthquake may, at shallow depths, surpass the abundant fracture energy or switch to brittle rheology51. This way, future earthquake will eventually reach the surface, conciliating the shallow slip deficit. Examples of such surface-breaking ruptures on faults considered immature are the recent earthquake at Ridgecrest, California, Mw 7.1, 201952, Norcia, Central Italy, Mw 6.5, 201653, and Fandoqa, southeast Iran, Mw 6.6, 199854.
Discussion
Our Bayesian dynamic source inversion revealed information imprinted in the near-fault strong motion seismograms, suggesting the following picture of the Elazığ earthquake and its broader role in the fault evolution. The event occurred on the Pütürge segment of the EAFZ, situated between strong earthquakes that happened 100–150 years ago, and, since that time, the segment remained with no Mw 6+ occurrence. The fault is loaded by aseismic slip at the base of the brittle (velocity-weakening) part of the fault at ~15–20 km depth, which produces earthquakes sporadically reaching magnitude Mw above 5. Most of these Mw ~5+ events occurred too early and thus failed to rupture the whole Pütürge segment. In 2020, relatively weak nucleation at ~15 km depth corresponding in terms of its duration and size to an Mw5.8, succeeded to advance further. After initial up-dip and north-east propagation, the rupture stopped at the Lake Hazar releasing bend and triggered off-fault aftershocks, suggesting a distributed fault network. The rupture then continued mostly unilaterally towards the south-west. It ruptured a very strong asperity of 40 MPa at a moderate speed, that was then inhibited by locally large fracture energy. The rupture resumed and broke another 20-MPa asperity at high speed due to relatively low fracture energy, prolonging the rupture duration and increasing the earthquake seismic moment. This episodic, partially bilateral rupture propagation resulted in a relatively small mean rupture velocity (~2 km/s). Up to 90% of the total available energy was expended in the fracture process, while just 10% was radiated by seismic waves, which might be a signature of the fault zone immaturity. The earthquake failed to propagate through a 5-km subsurface fault strip and did not rupture the Earth’s surface. The slip deficit and weak afterslip suggest that the shallow portions of the fault remain primarily locked and could release its accumulated strain in a future earthquake.
Methods
Mainshock relocation
We manually picked the first weak (yet identifiable) P-onset from 10 strong-motion (SM) and 8 broadband (BB) records at epicentral distances <110 km (Supplementary Table S1). During picking we estimated the inaccuracy for each station independently (P-picks: 0.03-0.6 s, S-picks: 0.2–1.7 s). The S-picks were uncertain due to emergent onset of S waves from complex preceding wavegroups. We located hypocenter H by the NonLinLoc probabilistic method55 considering only P-picks with their uncertainty as a data error. To assess the error due to structural effects, we repeated location in several velocity models. The effect was significant mainly upon the source depth. As detailed in the next paragraph (and Supplementary Fig. S10), we prefer location in model VM156 (Supplementary Fig. S11a). While the epicenter is well constrained at 38.360°N, 39.091°E, with +/−2 km uncertainty in the NNW-SSE direction (Fig. 1 and Supplementary S11), the depth remained poorly constrained between 10 and 20 km. The S-minus-P travel time difference of 3.9 s at the nearest SM station (code 2308) points to the hypocenter depth of 12–14 km and origin time 17:55:10.8 (UTC).
Note that we identified large time residuals for certain SM stations (not shown in Supplementary Table S1), obviously due to GPS time error, and hence we excluded them from the relocation. Later, in the waveform modeling, two important SM stations with the large residuals were used after forward-shifting their records by the residuals (6.6 and 4.6 s at 2301 and 2302, respectively).
Recordings at many stations exhibit a second (strong) P’ onset with small amplitudes between P and P’ (Fig. 1 and Supplementary S12). We picked P’ (Supplementary Table S1) and located respective hypocenter H’ at 38.439 °N 39.188°E, 0-10 km depth, and ~4.5 s after the origin time (see Fig. 1 and Supplementary S11).
Relocation of the sequence
We located the whole Elazığ sequence using manual picks adopted from the DDA Catalog of AFAD, the HYPOINVERSE code57, and velocity model VM1. Using other models of the region, VM258, VM359, and VM460, spurious concentrations of hypocenters occurred at certain depths (Supplementary Fig. S10). Such artifacts are quite common: For events situated closely above a sharp velocity discontinuity, observed first arrivals are interpreted by the location code as head waves; travel times are then weakly sensitive to actual depth differences, and hence hypocenters collapse to a narrow depth range. Therefore, for all modeling in this paper, we use solely VM1. Relocation with the HypoDD code61 efficiently focused the hypocenters, clearly revealing three aftershock clusters (Fig. 1 and Supplementary S13). The central cluster (no. 1 in Supplementary Fig. S13), near the mainshock hypocenter, is quite tight. The north-east (no. 2) and south-west (no. 3) clusters reveal a fault dip of 70–80° to the north-west, with a lower dip angle of the third cluster.
Multiple-point source (MPS) model
The GCMT solution of the mainshock with strike/dip/rake (°) = 246/67/-9, representing a point-source model at low frequencies and large distances, corresponds to a left-lateral strike-slip motion, consistent with the local strike of EAFZ. We improved the space-time characterization of the source by employing 12 non-clipped near-regional BB stations and 7 local SM stations (Supplementary Fig. S14), and jointly inverted them for an MPS-BB-SM model in the complementary frequency ranges of 0.01–0.05 and 0.05–0.10 Hz, respectively. Using iterative deconvolution of the established ISOLA software62,63,64,65,66,67 we calculated full and deviatoric moment tensors (MTs). Still, the double-couple (DC) part of those models was low, DC < 50%, due to the multiplicity of subevents. Therefore, we adopted a DC-constrained MPS modeling (DC = 100%). The multiple point sources were grid-searched at several fixed depths, 5–15 km, with just a weak preference of 10 km, hereafter assumed as a source depth in the MPS modeling. Preliminary tests have revealed that the subevent positions are better resolved along the EAFZ strike than across. Therefore, a linear grid of trial sources (azimuth 246°) is a justified approximation. Our preferred model consists of three subevents, providing the total magnitude Mw = 6.7 and fitting waveforms with global variance reduction (VR) of 0.77 (Fig. 1 and Supplementary S14). One or two (largest) subevents would produce only Mw 6.5, VR 0.34, and Mw 6.6, VR 0.59, respectively. The improvement by considering two or three subevents is significant, see Supplementary Fig. S15. Additional subevents are smaller and have unstable properties, and do not improve the fit considerably.
Although the DC-constrained MTs of the three subevents were free in the inversion, their focal mechanisms are remarkably similar. Scalar moments and the subevent timing are only weakly varying with various perturbations of the model setup, for example, with the depth and azimuth of the grid, frequency range, used stations, etc. Fig. 1 shows the 3-point MPS-BB-SM model accompanied by a jackknife test (repeatedly removing one station). The MPS models are independent of the assumed hypocenter position. Nevertheless, the source process starts between H and H’ with a subevent of Mw 6.4 at ~8 s after origin time. Then the process continues with a major subevent of Mw 6.5 at ~12 s, located towards the south-west, near the GCMT centroid. The process ends at ~17 s with a third subevent of Mw 6.3, further displaced to the south-west. The focal mechanism of the latest subevent appears to have a gentler fault dip (in agreement with aftershocks) and a thrust-faulting component. We note that the first-motion polarities of phase P support the left-lateral strike-slip faulting mechanism of initial nucleation, which is too weak to be captured by the earliest subevent of our model.
Back-projection
We also back-project the normalized high frequency (HF, 2–8 Hz) S-waveforms from the strong-motion recordings following the previously developed methods68,69. The result (in Supplementary Fig. S16) shows that ~5 s after the origin time, S-wave HF energy appears close to H’. Similarly to the paper16, the HF sources then migrate towards the south-west along the fault strike, concentrating at similar locations as the three MPS subevents (Fig. 1).
Dynamic source inversion
We apply Bayesian dynamic source inversion25. The method has been validated via synthetic tests, inversion of the 2016 Amatrice, Central Italy earthquake70, and via modeling of rupture scenarios to reconcile the stress drop ambiguity71. We assume a planar fault of 75 × 20 km based on the previous Multiple-point source modeling with strike 246°, dip 80° and rake 0°, adjusted by a 2 km northward shift of hypocenter (i.e., within its inaccuracy) to conform to the aftershocks. The assumed fault plane reaches the surface. We calculate waveforms following the representation theorem, i.e., by convolving Green’s functions calculated in velocity model VM1 with slip rates calculated by very efficient 3D finite-difference (FD) dynamic rupture simulator FD3D_TSN72.
The spontaneous rupture is governed by the linear slip-weakening friction26 (Fig. 2a) with spatially variable left-lateral prestress τ0 and frictional parameters. The latter include characteristic slip-weakening distance Dc and strength τs = µsσn, where µs is the static coefficient of friction, and σn is the normal stress assumed to increase linearly with depth (Supplementary Table S2). Dynamic friction coefficient µd is considered constant. Since the Elazığ earthquake did not rupture the surface, the total value of stress is unimportant, and the rupture is controlled by (i) initial stress τi, i.e., the difference between prestress τ0 and dynamic stress τd = µdσn, and (ii) friction drop Δµ = µs − µd from the static to dynamic friction. The parameters are bilinearly interpolated from 31 × 9 regularly distributed control points to the FD grid. At the control points, the parameter values are sought using Monte Carlo Markov Chain (MCMC) approach, assuming Gaussian data errors with a constant standard deviation of the observed displacements (0.05 m) and prior uniform parameter distribution in broad ranges (Supplementary Table S2). Rupture nucleation (a process in the area with negative strength excess over the initial stress) is permitted only within a 5-km radius from the located hypocenter.
The MCMC exploration has been initiated from a relatively smooth kinematic model obtained by the recently developed parametric inversion method73. The initial model had a negative VR, so it is not shown here. Significant improvement of the MCMC performance was achieved by adding a constraint on the seismic moment, formally introduced as a prior Gaussian with the mean 1.8 × 1019 Nm (Mw 6.8) and standard deviation 0.3 × 1019 Nm. We also added a constraint on the maximum overstress in the nucleation patch (2 MPa) to limit the effect of the nucleation on the subsequent rupture propagation.
The calculations ran on an in-house farm of 10 GPUs, where a single rupture simulation took less than 1 min. With the total number of the simulations exceeding one million, the computing time was ~3 weeks. Supplementary Figs. S2–S5 demonstrates the estimated uncertainty as captured by 2800 accepted models within 2% of the estimated maximum of the posterior probability density function.
Data availability
Data were downloaded from Disaster and Emergency Management Authority Presidential of Earthquake Department (AFAD; https://tdvms.afad.gov.tr/list-station/457758/39.063/38.3593, last accessed November 2020). Manual picks of the sequence were downloaded from the DDA Catalog of AFAD (https://deprem.afad.gov.tr/depremdetay?eventID=457758, last accessed November 2020). Topography was taken from SRTM 1 Arc-Second Global (https://doi.org/10.5066/F7PR7TFT), and faults from ref. 30.
Code availability
ISOLA software is available at http://geo.mff.cuni.cz/~jz/for_ISOLAnews/. Code for dynamic rupture simulation FD3D_TSN is available at https://github.com/JanPremus/fd3d_TSN, being wrapped in inversion code FD3D_TSN_PT available at https://github.com/fgallovic/fd3d_tsn_pt. Figures were plotted using GMT5 (Wessel et al., 2013).
References
Ide, S. 4.07 Slip Inversion. In Earthquake Seismology, Treatise on Geophysics, Vol. 4 (ed. Kanamori, H.) 193–224 (Elsevier, 2007).
Hayes, G. P. The finite, kinematic rupture properties of great-sized earthquakes since 1990. Earth Planet. Sci. Lett. 468, 94–100 (2017).
Ma, S., Custódio, S., Archuleta, R. J. & Liu, P. Dynamic modeling of the 2004 Mw 6.0 Parkfield, California, earthquake. J. Geophys. Res. Solid Earth 113, 1–16 (2008).
Ruiz, S. et al. Nucleation phase and dynamic inversion of the Mw 6.9 Valparaíso 2017 earthquake in Central Chile. Geophys. Res. Lett. 44, 10,290–10,297 (2017).
Peyrat, S. & Olsen, K. B. Nonlinear dynamic rupture inversion of the 2000 Western Tottori, Japan, earthquake. Geophys. Res. Lett. 31, L05604 (2004).
Mai, P. M. et al. The Earthquake‐Source Inversion Validation (SIV) project. Seismol. Res. Lett. 87, 690–708 (2016).
Gallovič, F. & Ampuero, J. P. A new strategy to compare inverted rupture models exploiting the eigenstructure of the inverse problem. Seismol. Res. Lett. 86, 1679–1689 (2015).
Guatteri, M. & Spudich, P. What can strong-motion data tell us about slip-weakening fault-friction laws? Bull. Seism. Soc. Am 90, 98–116 (2000).
Guatteri, M., Spudich, P. & Beroza, G. C. Inferring rate and state friction parameters from a rupture model of the 1995 Hyogo‐ken Nanbu (Kobe) Japan earthquake. J. Geophys. Res. 106, 26511–26521 (2001).
Barka, A. A. & Kadinsky-Cade, K. Strike-slip fault geometry in Turkey and its influence on earthquake activity. Tectonics 7, 663–684 (1988).
Barka, A. & Reilinger, R. Active tectonics of the Eastern Mediterranean region: deduced from GPS, neotectonic and seismicity data. Ann. di Geofis XL, 587–610 (1997).
Cetin, H., Güneyli, H. & Mayer, L. Paleoseismology of the Palu-Lake Hazar segment of the East Anatolian Fault Zone, Turkey. Tectonophysics 374, 163–197 (2003).
Reilinger, R. et al. GPS constraints on continental deformation in the Africa-Arabia-Eurasia continental collision zone and implications for the dynamics of plate interactions. J. Geophys. Res. Solid Earth 111, 1–26 (2006).
Taymaz, T., Yilmaz, Y. & Dilek, Y. The geodynamics of the Aegean and Anatolia: Introduction. Geol. Soc. Spec. Publ. 291, 1–16 (2007).
Ambraseys, N. N. & Jackson, J. A. Faulting associated with historical and recent earthquakes in the Eastern Mediterranean region. Geophys. J. Int. 133, 390–406 (1998).
Pousse-Beltran, L. et al. The 2020 Mw 6.8 Elazig (Turkey) earthquake reveals rupture behavior of the East Anatolian Fault. Geophys. Res. Lett. 47, e2020GL088136 (2020).
Melgar, D. et al. Rupture Kinematics of January 24, 2020 Mw 6.7 Doğanyol-Sivrice, Turkey Earthquake on the East Anatolian Fault Zone Imaged by Space Geodesy. Earth Planet. Sci. Lett. 1–20 (2020).
Lekkas, E., Carydis, P. & Mavroulis, S. The January 24, 2020 Mw 6.8 Elazığ (Turkey) Earthquake. (Newsletter of Environmental, Disaster and Crises Management Strategies, 2020).
Dewey, J. F., Hempton, M. R., Kidd, W. S. F., Saroglu, F. & Şengör, A. M. C. Shortening of continental lithosphere: the neotectonics of Eastern Anatolia - a young collision zone. Geol. Soc. London Spec. Publ. 19, 1–36 (1986).
Şaroğlu, F., Emre, Ö. & I., K. The East Anatolian fault zone of Turkey. Ann. Tectonicae 6, 99–125 (1992).
Senturk, S. et al. Surface Creep Along the East Anatolian Fault (Turkey) revealed by InSAR Time Series: Implications for Seismic Hazard and Mechanism of Creep. In American Geophysical Union, Fall Meeting Abstracts G21A-G21006 (2015).
Cetin, S. et al. Investigation of the Creep Along the Hazar–Palu Section of the East Anatolian Fault (Turkey) Using InSAR and GPS Observations. In EGU General Assembly, Geophysical Research Abstracts, Vol. 18, EGU20163938 (2016)..
Ergintav, S. et al. Aseismic slip and surface creep on the Hazar-Palu Section of the East Anatolian Fault, Turkey. In American Geophysical Union, Fall Meeting Abstracts 8, December 01, 201 (2017)..
Hubert-Ferrari, A. et al. A 3800 yr paleoseismic record (Lake Hazar sediments, eastern Turkey): Implications for the East Anatolian Fault seismic cycle. Earth Planet. Sci. Lett. 538, 116152 (2020).
Gallovič, F., Valentová, Ľ., Ampuero, J. P. & Gabriel, A. A. Bayesian dynamic finite‐fault inversion: 1. method and synthetic test. J. Geophys. Res. Solid Earth 124, 6949–6969 (2019).
Ida, Y. Cohesive force across the tip of a longitudinal-shear crack and Griffith’s specific surface energy. J. Geophys. Res. 77, 3796–3805 (1972).
Vallée, M. & Douet, V. A new database of source time functions (STFs) extracted from the SCARDEC method. Phys. Earth Planet. Inter. 257, 149–157 (2016).
Kanamori, H. & Brodsky, E. The physics of earthquakes. Rep. Prog. Phys 67, 1429–1496 (2004).
Viesca, R. C. & Garagash, D. I. Ubiquitous weakening of faults due to thermal pressurization. Nat. Geosci. 8, 875–879 (2015).
Duman, T. Y. & Emre, Öm The east anatolian fault: geometry, segmentation and jog characteristics. Geol. Soc. Spec. Publ. 372, 495–529 (2013).
Barbot, S., Lapusta, N. & Avouac, J. Under the hood of the earthquake. Science 336, 707–710 (2012).
Kostka, F. & Gallovič, F. Static Coulomb stress load on a three-dimensional rate-and-state fault: possible explanation of the anomalous delay of the 2004 Parkfield earthquake. J. Geophys. Res. Solid Earth 121, 3517–3533 (2016).
Zollo, A., Amoroso, O., Lancieri, M., Wu, Y. M. & Kanamori, H. A threshold-based earthquake early warning using dense accelerometer networks. Geophys. J. Int. 183, 963–974 (2010).
Meier, M. A., Heaton, T. & Clinton, J. Evidence for universal earthquake rupture initiation behavior. Geophys. Res. Lett. 43, 7991–7996 (2016).
Melgar, D. & Hayes, G. P. Characterizing large earthquakes before rupture is complete. Sci. Adv. 5, 1–8 (2019).
Olson, E. L. & Allen, R. M. The deterministic nature of earthquake rupture. Nature 438, 212–215 (2005).
Toda, S., Stein, R. S., Sevilgen, V. & Lin, J. Coulomb 3.3 Graphic-Rich Deformation and Stress-Change Software for Earthquake, Tectonic, and Volcano Research and Teaching–User Guide. (2011).
Wang, H., Liu, M., Duan, B. & Cao, J. Rupture propagation along stepovers of strike-slip faults: effects of initial stress and fault geometry. Bullet. Seismol. Soc. Am. 1–14 (2020).
Ulrich, T., Gabriel, A. A., Ampuero, J. P. & Xu, W. Dynamic viability of the 2016 Mw 7.8 Kaikōura earthquake cascade on weak crustal faults. Nat. Commun. 10, 1–16 (2019).
Harris, R. A. & Day, S. M. Dynamics of fault interaction: parallel strike-slip faults. J. Geophys. Res. Solid Earth 98, 4461–4472 (1993).
Lozos, J. C., Oglesby, D. D., Brune, J. N. & Olsen, K. B. Small intermediate fault segments can either aid or hinder rupture propagation at stepovers. Geophys. Res. Lett. 39, 5–8 (2012).
Hempton, M. R. Structure and deformation history of the Bitlis suture near Lake Hazar, southeastern Turkey. Geol. Soc. Am. Bull. 96, 233–243 (1985).
Khalifa, A., Çakir, Z., Owen, L. A. & Kaya, Ş. Morphotectonic analysis of the East Anatolian Fault. Turkey. Turkish J. Earth Sci. 27, 110–126 (2018).
Elliott, J. R., Copley, A. C., Holley, R., Scharer, K. & Parsons, B. The 2011 Mw 7.1 Van (Eastern Turkey) earthquake. J. Geophys. Res. Solid Earth 118, 1619–1637 (2013).
Dogan, U. et al. Postseismic deformation following the Mw 7.2, 23 October 2011 Van earthquake (Turkey): Evidence for aseismic fault reactivation. Geophys. Res. Lett. 41, 2334–2341 (2014).
Fialko, Y., Sandwell, D., Simons, M. & Rosen, P. Three-dimensional deformation caused by the Bam, Iran, earthquake and the origin of shallow slip deficit. Nature 435, 295–299 (2005).
Kaneko, Y. & Fialko, Y. Shallow slip deficit due to large strike-slip earthquakes in dynamic rupture simulations with elasto-plastic off-fault response. Geophys. J. Int. 186, 1389–1403 (2011).
Brooks, B. A. et al. Buried shallow fault slip from the South Napa earthquake revealed by near-field geodesy. Sci. Adv. 3, 1–12 (2017).
Roten, D., Olsen, K. B. & Day, S. M. Off-fault deformations and shallow slip deficit from dynamic rupture simulations with fault zone plasticity. Geophys. Res. Lett. 44, 7733–7742 (2017).
Li, Y., Bürgmann, R. & Zhao, B. Evidence of fault immaturity from shallow slip deficit and lack of postseismic deformation of the 2017 Mw 6.5 Jiuzhaigou earthquake. Bull. Seismol. Soc. Am. 110, 154–165 (2020).
van den Ende, M. P. A., Chen, J., Niemeijer, A. R. & Ampuero, J. P. Rheological transitions facilitate fault‐spanning ruptures on seismically active and creeping faults. J. Geophys. Res. 125, e2019JB019328 (2020).
Goldberg, D. E. et al. Complex rupture of an immature fault zone: a simultaneous kinematic model of the 2019 ridgecrest, CA earthquakes. Geophys. Res. Lett. 47, e2019GL086382 (2020).
Pizzi, A., Di Domenica, A., Gallovič, F., Luzi, L. & Puglia, R. Fault segmentation as constraint to the occurrence of the main shocks of the 2016 central Italy seismic sequence. Tectonics 36, 2370–2387 (2017).
Berberian, M. et al. The 1998 March 14 Fandoqa earthquake (Mw 6.6.) in Kerman province, Southeast Iran: Re-rupture of the 1981 Sirch earthquake fault, triggering of slip on adjacent thrusts and the active tectonics of the Gowk fault zone. Geophys. J. Int. 146, 371–398 (2001).
Lomax, A., Zollo, A., Capuano, P. & Virieux, J. Precise, absolute earthquake location under Somma-Vesuvius volcano using a new three-dimensional velocity model. Geophys. J. Int. 146, 313–331 (2001).
Acarel, D., Cambaz, M. D., Turhan, F., Mutlu, A. K. & Polat, R. Seismotectonics of Malatya fault. Eastern Turkey. Open Geosci. 11, 1098–1111 (2019).
Klein, F. W. User’s Guide to HYPOINVERSE-2000: A Fortran Program to Solve for Earthquake Locations and Magnitudes. (2002).
Maden, N. One-dimensional thermal modeling of the eastern pontides orogenic belt (NE Turkey). Pure Appl. Geophys. 169, 235–248 (2012).
Gallovič, F. et al. Fault process and broadband ground-motion simulations of the 23 October 2011 Van (Eastern Turkey) earthquake. Bull. Seismol. Soc. Am. 103, 3164–3178 (2013).
Pasyanos, M. E., Walter, W. R., Flanagan, M. P., Goldstein, P. & Bhattacharyya, J. Building and testing an a priori geophysical model for Western Eurasia and North Africa. Pure Appl. Geophys. 161, 235–281 (2004).
Waldhauser, F. & Ellsworth, W. L. A Double-difference Earthquake location algorithm: Method and application to the Northern Hayward Fault, California. Bullet. Seismol. Soc. Am. 90, 1353–1368 (2000).
Zahradník, J. & Sokos, E. The Mw 7.1 Van, Eastern Turkey, earthquake 2011: two-point source modelling by iterative deconvolution and non-negative least squares. Geophys. J. Int. 196, 522–538 (2014).
Zahradník, J. & Sokos, E. ISOLA code for multiple-point source modeling –review. in Moment Tensor Solutions - A Useful Tool for Seismotectonics, 1–28 (Springer Natural Hazards, 2018).
Sokos, E., Evangelidis, C., Serpetsidaki, A. & Plicka, V. Earthquake: dominant strike-slip faulting near subducting slab. Seism. Res. Lett. 91, 721–732 (2020).
Zahradník, J. et al. A recent deep earthquake doublet in light of long-term evolution of Nazca subduction. Sci. Rep. 7, 1–11 (2017).
Sokos, E. et al. Asperity break after 12 years: The M w 6.4 2015 Lefkada (Greece) earthquake. Geophys. Res. Lett. 43, 6137–6145 (2016).
Sokos, E. et al. Rupture process of the 2014 Cephalonia, Greece, earthquake doublet (Mw6) as inferred from regional and local seismic data. Tectonophysics 656, 131–141 (2015).
Kao, H. & Shan, S. J. The source-scanning algorithm: mapping the distribution of seismic sources in time and space. Geophys. J. Int 157, 589–594 (2004).
Evangelidis, C. P. & Kao, H. High-frequency source imaging of the 2011 October 23 Van (Eastern Turkey) earthquake by backprojection of strong motion waveforms. Geophys. J. Int. 196, 1060–1072 (2013).
Gallovič, F., Valentová, Ampuero, J. P. & Gabriel, A. A. Bayesian dynamic finite-fault inversion: 2. application to the 2016 Mw 6.2 Amatrice, Italy, Earthquake. J. Geophys. Res. Solid Earth 124, 6970–6988 (2019).
Gallovič, F. & Valentová Earthquake stress drops from dynamic rupture simulations constrained by observed ground motions. Geophys. Res. Lett. 47, e2019GL085880 (2020).
Premus, J., Gallovič, F., Hanyk, L. & Gabriel, A.-A. FD3D_TSN: Fast and simple code for dynamic rupture simulations with GPU acceleration. Seismol. Res. Lett. 91, 2881–2889 (2020).
Halló, M. & Gallovič, F. Bayesian self-adapting fault slip inversion with Green’s functions uncertainty and application on the 2016 Mw 7.1 Kumamoto earthquake. J. Geophys. Res. Solid Earth 1–32 (2020).
Acknowledgements
F.G. and J.Z. acknowledge financial support through the bilateral project of the Czech Science Foundation (18‐06716J) and DFG (GA 2465/2‐1). E.S., Ch.E. and I.F. acknowledge funding from the HELPOS Project “Hellenic Plate Observing System” (MIS 5002697).
Author information
Authors and Affiliations
Contributions
F.G. conducted the dynamic inversion and finite fault modeling, J.Z. performed the point source inversions, V.P. located the mainshock, E.S. relocated aftershocks, Ch.E. and I.F. applied the back-projection method, F.T. provided expertize on the East Anatolian Fault. All authors contributed to writing the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Primary handling editor: Joe Aslin.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gallovič, F., Zahradník, J., Plicka, V. et al. Complex rupture dynamics on an immature fault during the 2020 Mw 6.8 Elazığ earthquake, Turkey. Commun Earth Environ 1, 40 (2020). https://doi.org/10.1038/s43247-020-00038-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-020-00038-x
This article is cited by
-
Complex evolution of the 2016 Kaikoura earthquake revealed by teleseismic body waves
Progress in Earth and Planetary Science (2023)
-
Long-period directivity pulses of strong ground motion during the 2023 Mw7.8 Kahramanmaraş earthquake
Communications Earth & Environment (2023)
-
An Mw 7.8 Earthquake on 6 February 2023 on the East Anatolian Fault, Turkey
Journal of the Geological Society of India (2023)
-
Co-seismic stress changes and triggering mechanism of earthquake-induced landslides: a case of 2005 Kashmir earthquake
Arabian Journal of Geosciences (2021)
-
The 24 January 2020 (Mw 6.8) Sivrice (Elazig, Turkey) earthquake: a first look at spatiotemporal distribution and triggering of aftershocks
Arabian Journal of Geosciences (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.