Introduction

Laser additive manufacturing (LAM) is a powerful and versatile technique for the fabrication, layer-by-layer, of complex 3D components from metallic alloy wires/powders directly from a digital design. LAM has advantages over traditional manufacturing processes to create unconventional geometries and high-value applications such as aerospace, power generation, and biomedical industries. LAM involves a rapidly moving laser to melt the feedstock, which fuses into a solid mass. The laser-matter interaction happens at the scale of a millisecond, and the rate of solidification is a few orders of magnitude higher than conventional processes1. This facilitates columnar grain growth and hot tears or cracks, which degrades the mechanical performance of the final products.

Hot cracking is especially problematic for higher-strength aluminum alloys2,3,4. The susceptibility to hot-cracking is particularly high for 6xxx series high-strength aluminum alloys5,6 because of their large solidification range, particularly near the end of solidification due to the small amounts of eutectic, and their relatively high shrinkage during solidification and thermal expansion coefficient7. For alloy 6061, in the Laser powder bed fusion process, Roberts et al.8 showed that hot cracks spread across all conditions using the standard linear scan strategy. However, there has been substantial research focused on alleviating cracking in aluminum alloys. One approach is through the modification of alloy composition. Another approach is the modification of the thermal field.

The most common reason for the minor elements added to the alloy is to refine the grain size through the addition of grain refiners, which are well-known to reduce hot tearing9. Grain refining additions have included the traditional Ti–B and Ti–C systems10,11,12,13,14,15 or through the use of pro-peritectic phases, such as with the addition of Zr or Ti16,17. Sc acts in a similar way to Zr or Ti at hypereutectic additions9,15. Oxides and nitrides have also been used18. Interestingly, nano-particles have been found to be very effective19,20, which is not the case in cast alloys. The modifications to the solidification path have also been used to improve the not tear susceptibility through the addition of elements to increase the final eutectic volume and improve feeding, although the intermetallics also seem to have a role in coalescing the microstructure also benefiting hot tearing14,21,22.

Modifying the thermal field through modification of the processing conditions is another approach since many defects form due to the solidification shrinkage, which leads to a build-up of thermal/residual stress, which can be alleviated by crack propagation. This is exacerbated by the high solidification rates in AM. The fundamental idea is to minimize the thermal gradient associated with LAM to suppress the cracking, which has the additional benefit of reducing the susceptibility to epitaxial grain growth. Successful approaches have included pre-heating the build plate2,23, running a preheat scan, and an interlayer pause in laser direct energy deposition18. Using higher energy densities can also reduce cracking24,25,26,27. Although effective in reducing cracking and residual stresses, prolonged times at high temperatures can cause microstructure coarsening, reducing the mechanical properties.

Another approach is to modify the laser energy application, e.g., Wu et al.28 introduced high-frequency laser oscillation as an alternative approach. By distributing laser energy over a wider area, laser oscillation effectively changed the thermal gradients, thus the solidification rates and the thermal stresses. This shows an alternative to modifying the thermal field using laser scanning strategies. In welding, pulsed lasers have been reported29,30,31 to inhibit the propagation of cracks by designing ramp-down pulse shaping but also reducing crack sensitivity by appropriately increasing the average laser power and pulse frequency. These changes effectively reduce the solidification rate, thermal gradient, and solidification stresses.

Modification of the beam profile has not been widely applied to LAM as yet, although successfully implemented in welding32, hence it provides a possible better solution for a much higher thermal gradient and solidification rate. It is important to capture the solidification behavior during the process and provide an in-depth understanding to instruct the process design. Furthermore, compared to complex laser oscillation manipulation, this approach is more straightforward to implement and sets the foundation for further thermal field modification. If proven to be effective, the ground truth gained can be utilized in modeling and applied to more complicated setups, including laser oscillation. Here, synchrotron in situ X-ray imaging, with high resolution and frame rate, has been applied in this study to capture key physics involved, especially the correlation between cracking and solidification pathways. Ghasemi-Tabasi et al.33 directly observed the crack formation in the laser powder bed fusion process and concluded that in CM247LC, cracks form as a result of local melting of solute-enriched grain boundaries. However, the limitation of time (10,000 images s−1) resolution in their study prevented the resolution of the solidification/cracking pathway. Taking advantage of the highly intense and (partial) coherence X-rays of beamline ID19 at the European Synchrotron ESRF, we managed to achieve 100,000 images s−1 framerate and 4 μm pixel size and, for the first time to our best knowledge, recorded the solidification pathway, a key observation, to decipher the effect of pulsed laser ramp down, indicated by hot cracking susceptibility in LAM.

In this paper, we utilized synchrotron X-ray fast imaging to capture the cracking behavior of AA6061 in two different ramp-down pulse shapes and compared it with AlSi10Mg, a less crack-susceptible alloy system. For the first time to our best knowledge, the detailed timing of the solidification features has been recorded for each laser pulse and compared with the pulse shapes. Crack initiation and propagation are also recorded to examine its correlation with porosity and further investigated by post-build microstructural analysis. The observations are correlated with the prediction of a modified Rappaz–Drezet–Gremaud hot tearing model to further the understanding of the phenomenon observed.

Results and discussion

In situ X-ray imaging of the cracking events

Figure 1 shows the radiography results captured at 100,000 images s−1 during the experiment. Figure 1a shows the experiment setup and an example image captured. When the laser turns on, a melt pool is formed beneath the laser. The liquid–solid boundary of the melt pool is marked with a white dotted line. The substrate traverses toward the left side of the Field of View in the figure. The laser-blazed area forms a melt track behind the laser after the molten material solidifies. Porosity is observed forming in the melt pool and eventually consolidating in the melt track. These pores are likely hydrogen pores formed due to the moisture in the environment as the chamber is not sealed, although shielding gas is supplied.

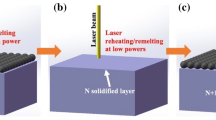
Fig. 1: In situ X-ray imaging results of the solidification behavior of Aluminum alloys during laser processing.
figure 1

a Schematic of the experimental setup includes an X-ray image captured during the laser processing. b Two pulse shapes were used in the experiment, rectangular and ramp-down, respectively. c AA6061 solidification behavior under pulsed laser with rectangular pulse shape. d AA6061 solidification behavior under pulsed laser with 10 ms ramp down pulse shape. e AlSi10Mg solidification behavior under pulsed laser with rectangular pulse shape. Scale bar = 250 μm.

Full size image

Two laser pulse shapes, rectangular and ramp-down, were used in the experiment to observe and compare the solidification behavior of two aluminum alloys, AA6061 and AlSi10Mg, respectively. For the rectangular pulse shape, the laser turns on for 10 ms at 1.4 kW. For the ramp-down pulse shape, the laser reduces the power linearly from 1.4 kW to zero within 10 ms after it turns on for 5 ms. The two pulse shapes maintain the same energy input. The pulse cycle is 40 ms to keep a 70% overlap of the melt pool to form a continuous melt track, and a full cycle of solidification behavior can be observed within each pulse to evaluate the solidification cracking.

Figure 1c and Supplementary Video 1 show the behavior of AA6061 under a rectangular pulse shape. A melt pool immediately formed after the laser was turned on. At t = 0 ms, before the laser was turned off in one pulse cycle, the melt pool reached maximum geometry. The solid-liquid boundary gradually moved toward the central surface of the melt pool, and an example image is shown in Fig. 1c at t = 1.83 ms, we measured the instant speed of the movements, and this part of the information can be found in Section “Modeling”. At t = 3.09 ms, the solid–liquid interface disappeared in the center, only leaving behind a dip created by the laser blazing. 3.51 ms later, we observed cracks started to propagate from just below the maximum melt pool boundary. We also tracked the speed of the crack propagation, and it is 22.78 μm ms−1. Figure 1d and Supplementary Video 2 show the solidification behavior of AA6061 with a ramp-down of the laser pulse. Similar to Fig. 1c, the solid–liquid interface of the melt pool gradually moved toward the center of the melt pool but at a much slower speed. The instantaneous speed is also measured. At t = 9.78 ms, the solid-liquid interface disappeared in the center, 6.69 ms slower than the rectangular pulse shape. 1.86 ms after, crack propagation was observed initiated in the middle of the melt pool region with a propagation speed of 41 μm ms−1. The cracks seem to be smaller in the extended region compared to the ones from a rectangular pulse shape. Crack tip lengths are measured to be an average of 4 μm for a rectangular pulse shape, whereas, for a ramped-down pulse shape, the average crack tip length is measured to be 3 μm. This is due to a much larger melt pool region. Similar results are observed in tomography results in the next section.

The same experiments were carried out on AlSi10Mg alloy. We did not observe any cracks form in the radiographs from either laser pulse shape. Figure 1e shows the radiographs from the rectangular pulse shape as an example. The melt pool geometry is observed to be longer and deeper compared to the melt pool in Fig. 1b, c, and it indicates a better laser energy absorptivity. Although the laser turned off immediately at t = 0 ms, it took 9.2 ms for the molten liquid to consolidate, and the longer solidification time allowed the material to release the stresses from the large thermal gradient introduced by the laser. This also indicates that extending the solidification time/thermal field can reduce hot cracks. However, excessive porosity is observed in the radiographs compared to AA6061 alloy. Although not the focus of our study, we hypothesize that the different pore behaviors are linked with the differences in the solidification front. The metallographic results confirm that the AlSi10Mg alloys have a more planar solidification front, which pushes the pores along in the melt pool during LAM1. This phenomenon can result in more obvious pores in the laser-processed region.

X-ray tomography characterization of the cracks

Figure 2 shows the crack network corresponding to Fig. 1c, d acquired through high-resolution Synchrotron X-ray tomography. The network is the segmented 3D reconstruction of the gaps between solid materials. Figure 2a corresponds to AA6061 processed by a pulsed laser with a rectangular pulse shape, as shown in Fig. 1c. We can see that the cracks distribute along the center of the laser track and extend in a tree-branch shape on both sides from the top view in Fig. 2a3 and cross-sectional view in Fig. 2b2. The cross-section view shows that the crack network extends to the boundary of the melt pool area and follows the heat transfer direction. Figure 2a1 shows the 3D crack network morphology. We can see that the cracks extend continuously in 3D and form connected crack faces. The depth of the cracks from the substrate surface to the crack tip is about 300 μm, and the volume of the cracks in the detected region is 0.0020 mm3. Although we did not identify porosity at the crack tip, we noticed that pores are linked by the crack network. Compared to the rectangular pulse shape, a 10 ms ramp down significantly improved the cracking susceptibility of the material. A much smaller crack network is observed in Fig. 2b. The crack network shares a similar shape, but the angles of the crack with respect to the laser traverse direction are larger, as shown in Fig. 2b. This is possibly due to the slower speed of the solid–liquid line during the solidification process. The cracks also have much fewer network branches, and the connectivity of the network is lower, as shown in Fig. 2b1. This observation corresponds well with the radiographs. Although the longest cracks are also found initiated from the bottom of the melt pool with a length of about 400 μm, the majority of the cracks are initiated in the center area of the melt pool. The volume of the cracks in the detected region is 0.0010 mm3. Fewer pores are observed in Fig. 2b, and interestingly, they are also agglomerated along the crack network. We also processed the tomography scan of AlSi10Mg from a rectangular pulse-shaped laser (Supplementary Fig. 1). No cracks are observed from the scan, which shows the superior cracking resistance of this material even at the fastest cooling rate. However, excessive porosity is observed from the 3D reconstruction. The porosity is observed to have a wide size distribution, and a proportion of the pores are not spherical, especially toward the surface of the track.

Fig. 2: X-ray tomography results of the AA6061 alloys after laser processing showing 3D crack network.
figure 2

a1 3D Crack network formed after being treated with a pulsed laser with a rectangular pulse shape, shown in 3D, a2 cross-section view of the crack network perpendicular to the laser direction; a3 cross-section view of the crack network along the laser direction. b1 3D Crack network formed after being treated with a pulsed laser with a ramp-down pulse shape, shown in 3D, b2 cross-section view of the crack network perpendicular to the laser direction; b3 cross-section view of the crack network along the laser direction.

Full size image

Metallurgy results

BSE images of the melt pool reveal that no cracks were observed in the AlSi10Mg sample (Fig. 3a), however, prominent cracks can be seen at the melt pool bottom boundaries for the AA6061 sample (Fig. 3b, c). This is consistent with the in situ observations in Fig. 2. The cracks were found to be predominately intergranular and propagated across the melt pool boundaries under both laser conditions in Fig. 3b1 and c1. This correlates well with the cracking analysis in Fig. 3. The microstructure also indicates that the cracks were initiated from the heat-affected zone where low-melting-temperature eutectic containing Mg2Si and AlFeSi phases at grain boundaries were partially melted by the laser. When solidification begins, this partially melted region makes it more challenging for the liquid to feed shrinkage and prevent cracking. Therefore, cracks occur and extend along the grain boundaries from the heat-affected zone to the center of the melt pool, which is in good agreement with the observations in Fig. 1c, d. Here, we believe that it is important to highlight the similarities between liquation cracking and hot tearing. Both are initiated in regions where there are low melting point reactions. The shrinkage from these reactions makes it difficult to feed through the mushy zone from the liquid pool due to the tortuous solid network. The difference between the mechanisms is that liquation cracking occurs from the re-melting of a previously solid material, whilst hot tearing occurs in a material that is cooled continuously. This means that the solidification path controls hot tearing, whilst with liquation cracking it is the state of the microstructure which may also be affected by homogenization or heat treatment methodology. Hence it is very difficult to separate the effects of hot tearing and liquation cracking as the fundamental reason for the cracking is similar.

Fig. 3: BSE images showing the melt pool cross-section.
figure 3

Of a AlSi10Mg alloy under pulsed laser with rectangular pulse shape, b AA6061 alloy under pulsed laser with rectangular pulse shape and c AA6061 alloy under pulsed laser with a ramp down pulse shape; b1, c1 are the enlarged regions showing cracks at the melt pool boundaries in (b) and (c), respectively; d–f are the EBSD maps showing the melt pool grain morphology of (a–c), respectively. The fitted ellipse aspect ratio of grains in the melt pools of (e) and (f) are plotted in (g) and (h), respectively.

Full size image

Additionally, the grain morphology in the melt pools shows directional growth towards the center of the melt pool, which is parallel to the thermal gradient and anti-parallel to the heat extraction, as shown in Fig. 3d–f. Based on the time calculation of the solid–liquid interface disappearance, the solidification rate of the rectangular pulsed laser is 1.5 times higher than that of the ramp-down pulsed laser. This resulted in the difference in grain aspect ratio in the melt pool, where grains are more elongated under the faster solidification rate, as shown in Fig. 3g, h.

Modeling

The present understanding of solidification cracking implicates a strong dependence on the form of the solid fraction vs. temperature curve34,35. This stems from the observation that a relatively long solidification interval, particularly near the end of solidification, tends to indicate a higher cracking likelihood due to a prolonged period in the sensitive mushy state. Figure 4 shows the solid fraction curves of AA6061 and AlSi10Mg computed by Scheil-Gulliver simulation with the compositions described in Table 2. The period an alloy spends in this fragile state lies between the coherence point, where strain can be transferred across the mush, taken at the fS = 0.4, and coalescence point, where the fraction solid is vanishing, taken around fS = 0.98, and their corresponding temperatures can be extracted from Fig. 4. The difference in the cracking susceptibility of the two alloys can then be explained, in part, by the difference in the form of these curves. The region between the coherence and coalescence points is considered the fragile mushy state, which has a high susceptibility to cracking if the system remains in this state for a prolonged period. For a given cooling rate, due to a larger temperature range in the mushy state, AA6061 is more prone to cracking than AlSi10Mg. This finding conforms with our radiographical observation that, using the same pulse shape, AlSi10Mg appears to not have any cracks. The fS(T) curve for AA6061 is used in the cracking calculation section below to compare the predicted cracking parameters between the two beam envelope conditions. The finer grain size in Al10SiMg is likely to also contribute to the lower hot tearing susceptibility.

Fig. 4: The solid fraction vs temperature computed by Scheil–Gullliver simulation.
figure 4

For a AA6061 and b AlSi10Mg. The temperature interval over which AlSi10Mg solidifies is significantly condensed compared to AA6061. AA6061 is more susceptible to cracking due to longer time spent in the crack-susceptible mushy-state, between Tco and Tca.

Full size image

In order to understand the response of the cracking susceptibility to the modulation of the laser pulse shape, we analyzed the cracking susceptibility of the material under the two laser pulse shapes with the mod-RDG model and indicated with a hot cracking indicator (HCS, Fig. 5e, k). We extract the solidification velocity from the high-speed photography and choose a mush length that depends on the distance of the candidate crack location at the edge of the maximum extent of the molten pool, up to the present solid front location, using the phase contrast of the molten and solid materials, as described in Section “Modeling”. We use the measured average grain sizes of the remelted track cross sections at dg from Fig. 3. Seven candidate locations along the bottom of the pool are considered, and the path length is extracted, as shown in Fig. 5. The temperature of the solid front is assumed to be the coherence temperature, Tco, and the candidate location along the bottom of the pool is fixed at the coalescence temperature, Tca. We assume a linear approximation of the temperature gradient along this distance.

Fig. 5: Processing of synchrotron data for input into cracking indicator, beam power modulation strategy.
figure 5

Rectangular (orange data in panels (a–f)); and ramp down (blue data in panels (g–l)). Cracking location marker style is preserved across the panels. Panels a and g solidification front progress from candidate crack locations (gray symbols at the root of each track) up to the top of the pool at the end of solidification; b, h solidification velocity (ν) vs.t; c, i average velocity \(\bar{\nu }\) against angle of the candidate solidification track (θ) from vertical; d, j critical strain rate, εc, computed by mod-RDG for the candidate locations vs. length, r of the track, the decrease with track length demonstrates the increased likelihood of crack formation as the pool solidifies; e, k hot cracking indicator, HCS, vs.t, reflecting the inference of the previous plots. f, l MIN(εc) vs. θ showing the change in cracking likelihood along the bottom of the melt track. A negative value indicates that compression must be applied to offset the propagation of the crack.

Full size image

The average solidification velocity for two laser pulse shapes lies in the range of 0.2–0.8 ms−1. The measured velocity across all considered candidate locations begins at lower values as the phase transition conditions are established and then proceeds to higher average values as the pool solidifies (Fig. 5b, h). The average velocities are slightly higher in the rectangular pulse shape condition (Fig. 5b) compared to the ramp-down condition (Fig. 5h). The average velocities for both laser pulse shapes show a slight increase at the front of the pool, which is slightly more pronounced in the rectangular pulse shape. All candidate locations appear to show a decrease in the critical strain rate with solidification progress (Fig. 5d, j). Several factors contribute to this behavior. The assumed temperature gradient is defined between the cracking candidate location and the tracked solid front and, therefore, reduces in magnitude as solidification progresses. This, in turn, increases the length of the mushy zone, leading to a reduction in the critical strain rate (Fig. 5d, j), due to its appearance in the denominator of both terms in Eq. (1), and representing the increased length of the tortuous path. The remaining viscous intergranular liquid must traverse to offset the pressure drop at the root of the path36,37. The magnitude of these distributions shows the differences between the two laser pulse shapes, where the critical strain rate in the track with the rectangular pulse shape dips to negative values (due to the logarithmic axes, the negative values are represented as the data dropping off the lower end of the plot: Figure 5d. This negative value indicates that the sample would need local compression to compensate for the pressure drop in the crack candidate location and is, therefore, very likely to crack since solidification shrinkage tends to exert a local tensile strain. This negative value can be predicted by the model in two scenarios: the metallostatic pressure being eclipsed by the surface tension factor, i.e., \({p}_{m} \, \lesssim \, 4\gamma /{d}_{g}(1-{f}_{ca}^{1/3})\) or where the solidification velocity is large with respect to the mush length in the third term of Eq. (1). In the present case, both of these conditions are active, given the velocity is large, the mush length is small, and the small pool depth does not facilitate a sufficiently large pressure force to offset the drop at the crack candidate locations. Differences in the cracking susceptibility of the different regions of the molten pool roughly track the variation in the distribution of velocities, where the highest observed velocities of the solid front correlate with the largest depressions in the critical strain rate (Fig. 5f, l). The variation in magnitude of the minimum εc (Fig. 5f, l) with position along the pool boundary shows that a slight decrease in solid front velocity is enough to effect a significant increase in the critical strain rate. This is consistent with the expectation that modulating the beam envelope to reduce the solidification velocity may confer a reduction in the cracking susceptibility. Compared with the total volume of cracks in the analyzed samples, the difference in cracking susceptibility computed by this method is consistent with the observed difference in the total volume of cracks.

Conclusion

A ramp-down pulsed laser shape significantly reduced the hot cracking volume of alloy AA6061 by approximately 50% compared with a laser with a rectangular pulse shape. Synchrotron X-ray in situ fast imaging, captured at 100,000 images s−1, showed that the ramped-down shape reduced the solidification rate, and the thermal gradient calculated from the images was also reduced. The use of a modified RDG model was used to show that these variations in solidification conditions and the more equiaxed grain structure lead to a lower predicted strain rate in the mushy zone and, consequently, a lower hot crack susceptibility for the ramped-down pulse. Alloy Al10SiMg was also investigated but did not show any cracking due to its much smaller solidification range, particularly towards the end of solidification and refined grain structure. The results demonstrate that modifying thermal conditions provides a pathway to crack elimination in LAM and the model established in our study sets the foundation for further complex laser manipulation in modifying the printability in LAM.

Method

Materials and manufacturing

Commercially forged AA6061 plate and laser-powder bed fusion (L-PBF) manufactured AlSi10Mg alloy were used in this study. The in situ radiography experiments were performed using a laser processing replicator developed by TU Ilmenau (Germany). The device is optimized for usage at synchrotron beamlines by adding two glassy carbon windows (at the back and front), allowing the incoming X-ray beam to interact with the laser-matter interaction area. The geometry of the substrate is 2 × 3 × 150 mm3. The schematic of the set-up is shown in Fig. 1a. A more detailed description of the device can be found in38.

An IPG Photonics YLR-450/4500-QCW fiber laser equipped with an IPG Photonics D30-R processing head was selected for the experiment. The laser parameters of the study are listed in Table 1. The focal diameter was determined via Primes FocusMonitor and D86 beam width measurement method. Two different pulse shapes were chosen to adjust the solidification rate while keeping the pulse energy constant. First, a pulse duration of 10 ms was used at the peak power of 1400 W. Second, a pulse duration of 5 ms at the peak power followed by a linear ramp down to zero was used to decelerate the solidification rate. Both pulse shapes are shown in Fig. 1b. Argon was supplied as shielding gas at a flow rate of 6 l per min (nozzle length: 60 mm, diameter: 3 mm).

Table 1 Parameters of laser setup
Full size table

In situ synchrotron-based high-speed X-ray imaging

Insitu studies by means of high-speed radiography were carried out at the 150 m-long beamline ID19 of the European Synchrotron (ESRF). In order to reach a sufficiently high photon flux density for the desired image acquisition rate, the beamline operated in a white configuration: the emitted photons of an undulator source (type: u32, gap 11.8 mm) were filtered by diamond (0.8 mm) and aluminum (2.8 mm) attenuators only. The resulting broad polychromatic spectrum has a mean photon energy of approximately 30 keV. The high-speed imaging acquisition was realized by an indirect detector consisting of a CMOS-based camera by Photron (Japan), type: SAZ (1024 × 1024 pixels), which is lens-coupled to a 250 μm-thick LuAG: Ce single-crystal scintillator using a 5 × (0.14NA) lens (Mitutoyo, Japan)39. The effective pixel size (nominal) is 4 μm, the full field of view 4 × 4 mm2. The detector was positioned 4.5 m downstream of the sample in order to benefit from propagation-based phase contrast in polychromatic illumination40. In order to reach a frame rate of 100,000 images s−1 the emitted radiation was further collimated by adding 10 so-called compound-refractive lenses (CRLs) in the X-ray optical beam path, approximately 35 m downstream of the source. At the desired frame rate, the SAZ needs to operate with a region-of-interest of the sensor of 512 × 328 pixels (2 mm × 1.2 mm field of view).

Synchrotron-based X-ray microtomography

Samples were imaged by means of synchrotron-based microtomography at beamline ID19 as well. In order to reach high sensitivity while maintaining short acquisition times, the beamline was operated in a pink beam configuration: the radiation emitted by a so-called single-harmonic undulator (type: u13, gap 15 mm, 26.1 keV photon energy) was only filtered by a diamond window (0.8 mm). At a distance of 150 m from the source, this ensures a homogeneous wavefront: excellent properties for the use of propagation-based phase contrast. An indirect system was used as the detector, consisting of a 10 μm-thin Eu-doped GGG single-crystal scintillator deposited on a 150 μm-thin substrate, which is lens coupled with a 10× objective (0.3NA) to an sCMOS-based camera (pco.edge, type: 5.5, PCO AG, Germany)39 with a final voxel dimension of 0.6 × 0.6 × 0.6 μm. Structures in the images are enhanced by propagation-based phase contrast, the required drift space between the sample and detector is set to 25 mm41.

Scanning electron microscope imaging

The laser re-melted samples were sectioned perpendicularly to their laser travel direction to reveal the microstructure of the cross-section of the melt pool. The Backscattered electrons (BSE) images and Electron backscatter diffraction (EBSD) maps were performed using a JEOL 7200F Scanning electron microscope with 20 kV accelerating voltage. The EBSD maps were collected with a step size of 0.75 μm. A fitted ellipse aspect ratio was used to represent the grain morphology in the melt pool using the Aztec Crystal software.

Analysis of the solidification rate

High-speed imaging of the molten pool was analyzed to extract the solidification velocity by image processing. The molten pool is a diminishing approximately hemispherical cap. The solidification velocity was extracted by image division between frames with a stride of 30 frames (Δt = 30/FPS = 300 μs). Seven approximately equidistant locations along the solid–liquid boundary near the initiation of solidification were chosen for front-tracking analysis. Successive points in each frame were chosen by projecting the approximate interface normal to the next solid front location. Given the projection of the ellipsoidal cap onto a flat plane, the assumed location of the tracked front is the corresponding furthest point from the centroid (the purple line in Fig. 5).

Assessment of crack initiation by modeling

The cracking susceptibility of each alloy is assessed through the computation of a modified Rappaz-Drezet-Gremaud (mod-RDG) solidification cracking model36,37,42. The mod-RDG model computes the critical strain rate above which a crack is likely to form. This critical strain rate quantifies the amount of strain the delicate mush can tolerate before resulting in a crack. The mod-RDG model assumes that the formation of a crack is driven by the ability of the liquid to be forced into the vanishing intergranular region to offset the pressure drop at the coalescence point due to solidification shrinkage36,37. This strain rate is formulated as,

$${\varepsilon }_{c}=\frac{{\rho }_{c}}{180(1+\beta )B\mu {L}^{2}}\left({p}_{m}-\frac{4\gamma }{{d}_{g}(1-\root 3 \of {{f}_{ca}})}\right)-\frac{{\nu }_{{T}_{co}}\beta A}{(1+\beta )BL},$$
(1)

where β = ρL/ρS − 1, is the solidification shrinkage factor, μ the average viscosity of the mush, γ the liquid–vapor (void) interface energy, pm = patm + ρLgh is the metallostatic pressure at liquid depth (height above) h, dg the grain size, \({\nu }_{{T}_{co}}\) the isotherm velocity at the coherence temperature, and L the length of the mush, defined by the region between the coherence point, (fco, Tco), where strain can be transferred across the mush and the coalescence point, (fca, Tca), at the end of solidification. The terms A, B, and F are integrals of the solid fraction vs temperature curve, defined by,

$$A={(\Delta T)}^{-1}\int\nolimits_{{T}_{co}}^{{T}_{ca}}\frac{{f}_{S}{(T)}^{2}}{{(1-{f}_{S}(T))}^{2}}dt,$$
(2)
$$B={(\Delta T)}^{-1}\int\nolimits_{{T}_{co}}^{{T}_{ca}}\frac{{f}_{S}{(T)}^{2}F}{{(1-{f}_{S}(T))}^{3}}dt,$$
(3)
$$F={(\Delta T)}^{-1}\int\nolimits_{{T}_{co}}^{{T}_{ca}}{f}_{S}(T)dt,$$
(4)
$$\Delta T={T}_{ca}-{T}_{co}$$
(5)

The numerator in the leading term of Eq. (1), ρc, is a critical length that either takes the value of the grain size or the secondary dendrite arm spacing (SDAS) depending on whether the morphology of the grain is dendritic, where ρc = λ2, or globular ρc = dg. We smoothly vary this value according to a logistic function to ensure a smooth variation between the description of the morphology of the grains, as either of dendritic where dg > > λ2, or globular where λ ≳ dg. The characteristic length, ρc is computed by Eq. (6),

$${\rho }_{c}=\left| {d}_{g}+\frac{{\lambda }_{2}-{d}_{g}}{1+\exp \left(-4\left(\frac{{d}_{g}}{{\lambda }_{2}}-3\right)\right)}\right| .$$
(6)

Using Eq. (1) we can compare the relative cracking likelihood of each track by computing a “Hot-Cracking Susceptibility”, HCS, from the critical strain rate, by

$${{{{{\rm{HCS}}}}}}={\left\vert {\varepsilon }_{c}\right\vert }^{-1}$$
(7)

Estimating parameters for the modified Rappaz–Drezet–Gremaud model

To facilitate the calculation of the mod-RDG model, model variable values are obtained from the radiographic observation and ex-situ analysis. The coalescence temperature isotherm velocity, \({\nu }_{{T}_{ca}}\), is assumed to follow the solid front velocity obtained from the radiographic measurements discussed above, extracted per frame. The height, h, of the mush above the crack initiation site is measured as the vertical distance above the candidate cracking site. We observe that cracks appear to form as the leading edge of the solidification front vanishes at the top of the frame, as presented in Fig. 1, and therefore assume that the whole molten pool can be considered in a mushy state. The grain size is obtained from the EBSD analysis in Fig. 3, and an average SDAS, λ2, is extracted from BSE images of the remelted region.

For each alloy, fS(T) is computed by Scheil-Gulliver calculation of the solidification pathway using JMatPro 13.2 (Sente Software)43,44 with the 2022 Al database using the composition vector as input. The composition of the alloys is presented in Table 2. The value of the coherence solid fraction is set at fco = fS(Tco) = 0.4. The coalescence solid fraction is assumed to be fca = fS(Tca) = 0.98, consistent with most preceding literature34,36,42,45. The corresponding temperatures, Tco and Tca, are determined by interrogation of the alloy’s fS(T) curve. Along with fS(T), the solidification calculation also gives material parameters of surface tension γ, viscosity μ, and the shrinkage factor, β, where densities are taken for the liquid at ρL(fS(T) = 0) and solid at ρL(fS(T) = 0).

Table 2 Composition of the alloys used in solidification calculations. Values by weight % chosen from the center of the specification band for each element
Full size table

The velocity of the solid front is extracted from the X-ray data, taking the progress of the front between frames, normal to the interface, such that

$$\nu \, \approx \, \Delta r(t)/\Delta {t}_{{{{{\rm{frame}}}}}},$$
(8)

where (Δr)2 = (Δx)2 + (Δy)2 and Δx = x(tn+1) − x(tn). νfront is computed in the plane of the image and, therefore, corresponds to a plane in the molten pool whose cross-product resolves to the beam transmission vector (Fig. 1). Δt is the inverse of the frame rate (10 μs). The temperature gradient, used to compute the mush length by,

$$L=\frac{{T}_{co}-{T}_{ca}}{\nabla T},$$
(9)

is computed by assuming that the cracking candidate location remains at the coalescence point, Tca(fca), over the course of solidification. This assumption is only transiently valid, with the highest accuracy as the solid front reaches its final moments of solidification.