Abstract
Transition metal dichalcogenides exhibit many fascinating properties including superconductivity, magnetic orders, and charge density wave. The combination of these features with a non-trivial band topology opens the possibility of additional exotic states such as Majorana fermions and quantum anomalous Hall effect. Here, we report on photon-energy and polarization dependent spin-resolved angle-resolved photoemission spectroscopy experiments on single crystal 1T-VSe2, revealing an unexpected band inversion and emergent Dirac nodal arc with spin-momentum locking. Density functional theory calculations suggest a surface lattice strain could be the driving mechanism for the topologically nontrivial electronic structure of 1T-VSe2.
Similar content being viewed by others
Introduction
Two-dimensional (2D)-layered transition metal dichalcogenides (TMDCs) are highly promising candidates for applications in electronics, spintronics, and optoelectronic1,2. This has led to extensive studies of their electronic structure to foster bottom-up engineering of physical properties. In this regard, the large number of transition metals and chalcogens provide ample opportunities to synthesize various compounds hosting superconductivity, Mott insulator, topological insulators, ferromagnetism, and charge density wave states (CDW)3,4,5,6.
Among TMDCs, considerable attention has been given to 1T-VSe2 due to the claims of a 3D-CDW phase in bulk specimens below 110 K7, and a related multi-CDW phase appearing in monolayers over a wide range of temperatures8,9,10 as well as various anomalies in transport and magnetic measurements11,12,13. In particular, the surface electronic structure of 1T-VSe2 has been the subject of many studies reporting an overall good agreement between experimental data and ab initio calculations7,8,9,10. The main features of the electronic structure are a flower-like, V-3d derived Fermi surface and highly dispersive Se-4p derived bands that nearly touch the Fermi level at the Brillouin zone center. The major focus of the previous investigations has been on the CDW phase limiting the studies to only certain parts of the electronic structure. On the other hand, various approaches can be applied in photoemission to reveal additional details and uncover exotic states14,15,16.
Here, we investigate the surface electronic structure of 1T-VSe2 by utilizing a polarization-dependent approach to angle-resolved photoemission spectroscopy (ARPES). A topological band inversion, in which the usual ordering of the conduction and valence bands with different parities is inverted, is experimentally identified between the conduction band bottom (CBB) and the valence band top (VBT) at \(\bar{M}\)-point. It manifests as a sharp switch of the spectral intensity with light polarization, from linear vertical (LV) to linear horizontal (LH). This is due to the different character (orientation in space) of the orbitals forming the conduction band (CB) and valence band (VB) as revealed in orbital-projected band structure calculation. In this regard, the use of linear light polarization becomes an effective way to gain experimental access to band inversion. The corresponding Dirac cone is analyzed with circularly polarized light directly yielding the full electronic state with bulk bands and the Dirac point located inside the inverted gap. The presence of topological surface states (TSSs) is further confirmed by the observation of strong in-plane spin polarization and helical spin-momentum locking in spin-resolved ARPES data. Furthermore, the Dirac point forms a nodal arc connecting \(\bar{M}\), and \(\bar{{M}_{1}}\)-points through \(\bar{\Gamma }\)-point. Through density functional theory (DFT) calculations, a lattice strain near the surface is a possible mechanism driving the topological phase transition. The emergent Dirac nodal arc in 1T-VSe2 has not been observed or predicted before. These observations are crucial - yet missing - elements in the surface electronic structure of 1T-VSe2 that can be fertile for future studies and understanding of the transport anomalies in this material.
Results
Calculated band structure of VSe2
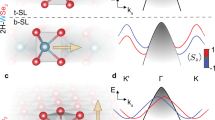
1T-VSe2 is a layered material formed by stacking Se – V – Se monolayers as shown in Fig. 1a. The corresponding 3D hexagonal Brillouin zone is shown in Fig. 1b. The band structure of stoichiometric 1T-VSe2 is known to be topologically trivial7,8,9,10. Keeping this in mind, DFT calculations are used to identify the atomic and orbital characters of the electronic states and explore possible band inversion experimentally. The band structure of 1T-VSe2 in the normal state, neglecting the spin-orbit coupling (SOC) effects is shown in Fig. 1c. The bands near the Fermi level are mostly comprised of V 3d or Se 4p orbitals. We project the bands onto these orbitals and analyze the irreducible band representations (Irreps) at high symmetry points. Specifically, detailed analysis at the L and M-points for the normal state of 1T-VSe2 shows that the CB (\({\Gamma }_{1}^{+}\)) is dominated by V d (about 40% \({d}_{{z}^{2}}\) and 40% dxz and dyz combined) and Se pz bonding states, while the VB (\({\Gamma }_{1}^{-}\)) is composed of Se px/py antibonding states (Fig. 1c and Supplementary Figs. 1 and 2). The latter form multiple, highly dispersive, hole bands extending from several eV to just below the Fermi level on approaching the Γ(A)-points. The V 3d-derived bands are much less dispersive and located in the vicinity of the Fermi level. In agreement with earlier reports7,8,9,10 and based on above data, band inversion is not observed at the L-point. However, the bulk band gap in TMDCs may not be captured accurately in DFT13 while the calculated band structure reveals an important aspect of the orbital character, i. e. that the CB (V \({d}_{{z}^{2}}\), dxz/dyz and Se pz) and VB (Se px/py) have perpendicular orbital orientations in space. Since the spectral weight in the photoemission process depends on the transition matrix elements given by \(\left\langle f | {{{{{\bf{E}}}}}} \cdot {{{{{\bf{r}}}}}}| i\right\rangle\), where E, f, and i are the light electric field, final, and initial states of the photoexcited electrons, respectively, a non-vanishing intensity is obtained if the initial state has the same orientation in space with E ∙ r17,18. Therefore, in the case of 1T-VSe2, a possible band inversion could be detected in ARPES by monitoring the spectral intensity switching between CBB and VBT under the tunable linear polarized lights. Furthermore, if there is a band inversion, a TSSs will form a Dirac point inside the inverted bulk band gap. Therefore, circularly polarized lights will be required to construct the complete Dirac cone electronic state with TSSs and bulk bands.
ARPES band structure characterization
To pursue the above assumption, APRES spectra taken with different light polarizations are presented in Fig. 2. Various aspects of the surface electronic structure of 1T-VSe2 single crystal emerge from the analysis of these data. Figure 2a displays the Fermi surface taken with 92.5 eV LH polarized light. Fermi surface is a flower-like with a pronounced 3-fold symmetry. Experimental electronic structures along the \(\bar{{K}_{1}}-\bar{M}-\bar{K}\) direction taken with LV (panel b) and LH (panel c) polarized lights show interesting behaviors. With LV light, the V 3d-derived CB appears to be truncated: only the top part is visible with two branches crossing the Fermi level at opposite momenta while the bottom tip at the \(\bar{M}\)-point is fully suppressed. This shows that the lower part of the CB has a different orbital orientation in space than the upper part16. On the other side, the tip of the CB is clearly visible in the spectra with LH light (label CBB in Fig. 2c). Essentially the opposite behavior is observed for the Se-derived VB: the VBT is well resolved with LV light (Fig. 2b) and vanishes with LH light (Fig. 2c). These spectral features are consistent with a band inversion at the \(\bar{M}\)-point. Furthermore, a pair of linearly dispersing, crossing bands, strongly reminiscent of TSSs, appear inside the inverted bulk gap (dashed orange lines in panel c). A complete band structure is schematically illustrated in Fig. 2d and such spectral characteristics are unique to topological electronic structures19,20. Thereby, linear polarized lights, in this case, can be used to probe the band inversion, experimentally since out-of-plane (V \({d}_{{z}^{2}}\), dxz/dyz and Se pz) and in-plane (Se px/py) atomic orbitals form the CB and VB, respectively.
a VSe2 Fermi surface taken with 92.5 eV LV polarized light. The hexagon represents the 2D- Brillouin zone. b, c ARPES spectra along the \(\bar{{K}_{1}}-\bar{M}-\bar{K}\) line in LV and LH geometry, respectively. Dashed orange lines in c represent the TSSs. d Color-coded representation of the band inversion between VBT and CBB (see the main text for detail). e, f ARPES spectra taken with CR and CL light polarization. g Sum of the spectra presented in e and f. h Same as g but for the \(\bar{K}-\bar{{M}_{1}}-\bar{{K}_{1}}\) direction. Dashed black lines in b, c and e–h are the EDCs taken along the \(\bar{M}\)(\(\bar{{M}_{1}}\))-point. Dashed red lines are the same multiplied by a factor of five for clarity. In addition to the band crossing, the VB marked with red horizontal line is observed as a spectral bump in the EDCs. i Schematic representation of the complete Dirac cone electronic structure. j–n Photon energy dependence of the Dirac cone electronic structure. The Dirac point (DP) is shown with horizontal arrows in ARPES spectra.
To construct the complete Dirac cone with helical spin-orbit texture, we perform ARPES experiments with circularly polarized lights. Figure 2e shows the surface electronic structure of 1T-VSe2 taken with the circular right (CR) polarization. Bulk CBB at 0.74 eV and VBT at 1.26 eV binding energy are now simultaneously resolved with only one of the branches of in-gap surface states (see left-pointing arrow in Fig. 2e). A similar band structure is also obtained with circular left (CL) polarized light except that the opposite branch of in-gap surface states is now resolved (see right-pointing arrow in Fig. 2f). The sum of the CL and CR spectra is given in Fig. 2g which composes the complete surface electronic structure at \(\bar{M}\)-point. In this data, a clear Dirac cone located inside the bulk band gap with a Dirac point is fully resolved. In analogy with the 3D-topological insulators21,22,23, right, and left-handed bands seen with CR and CL polarized lights can be confidently attributed to the spin-orbit helicity of the Dirac surface states having opposite spins at opposite crystal momentum. A similar observation in the circularly polarized light geometry is also obtained for the \(\bar{{M}_{1}}\)-point given in Fig. 2h. A schematic representation of these findings is summarized in Fig. 2i. Furthermore, the 2D-nature of the Dirac cone is confirmed by photon energy-dependent ARPES experiments as presented in Fig. 2j–n in which the Dirac point is located at fixed binding energy, irrespective of the excitation energy. Thereby, the main characteristic features of a topological electronic structure are constructed through polarization dependent ARPES experiments. The ARPES maps along with energy distribution curves (EDCs) and momentum distribution curves (MDCs) are also presented in Supplementary Fig. 3 to further support our findings. A pair of crossing bands spanning the bulk band gap can be clearly seen in the data. Furthermore, these observations also indirectly reveal that the ferromagnetic order on the surface region of the sample is absent. Otherwise, an energy gap is expected at the Dirac point due to the broken time reversal symmetry. Furthermore, similar ARPES data showing the band inversion and TSSs is also obtained at 150 K above structural transition temperature (Supplementary Fig. 4). This indicates that the topologically non-trivial band structure is independent from the lattice distortion. Furthermore, a Dirac cone electronic structure has also been reported in Ti doped VTe224. In this material, however, TSSs are found to be the more sensitive to structural transition. This could be due to the more dramatic change in the overall electronic structure of VTe2 originating from 1T″ lattice distortion.
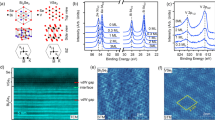
Figure 2b, c experimentally reveals the band inversion and Fig. 2e–h show the linearly dispersive surface states with a band crossing located inside the bulk band gap. These observations feature a Dirac cone electronic structure. In addition to these characteristics, another solid experimental evidence for TSSs would be revealing the helical spin texture. This ensures electrons to have spins in opposite directions for opposite k-momenta and consequently the absence of the backscattering of the Dirac electrons21,22,23. This is established through a spin-resolved ARPES experiment presented in Fig. 3. Spin-resolved ARPES spectra are shown in Fig. 3a, b for spin orientations, parallel and anti-parallel to the \(\bar{\Gamma }-\bar{M}\) direction, respectively. A clear spectral intensity switching, particularly in the bottom cone, is evident. Spin-integrated photoemission intensity is also presented in Fig. 3c. Energy and momentum dependent in-plane spin polarization for the band structure along the \(\bar{{K}_{1}}-\bar{M}-\bar{K}\) direction is shown in Fig. 3d in a color scale where red (blue) represents direction of the polarization parallel (anti-parallel) to the \(\bar{\Gamma }-\bar{M}\) direction. The Dirac cone exhibits a spin-momentum locking, i.e., a polarization reversal between the left and right sides and across the binding energy of the Dirac point. These can be better seen in Fig. 3e, f where spin polarization is plotted as a function of the binding energy and momentum for the left/right and upper/lower part of the Dirac cone, respectively. The spin polarization of the upper part of the cone is weaker compared to the bottom one. This is possibly due to the more dominant effect of the bulk bands. As also expected, there is a nodal line at the binding energy of the Dirac point where spin polarization goes to zero. Furthermore, a similar helical spin texture in the VB of VSe2 has been reported in a recent study25. However, in the same work, a bulk band gap is reported in contrast to the gapless band structure at the \(\bar{M}(\bar{{M}_{1}})\)-point observed in our work. This difference likely arises from the energy-momentum resolution, beam spot size and the sample quality used in the present work.
a, b In-plane spin-spectra for parallel and anti-parallel orientation to the \(\bar{\varGamma }-\bar{M}\) direction, respectively. c Spin-integrated photoemission intensity. d Spin-polarization ([(a)-(b)]/(c)/0.25 where 0.25 is the Sherman function). Color scale in d represents the sign and value of the in-plane spin-polarization as red (blue) meaning parallel (anti-parallel) to the \(\bar{\varGamma }-\bar{M}\). e Energy-dependent spin polarization along the vertical red and blue dashed lines in d. f Spin-resolved MDCs obtained along the horizontal green and cyan dashed lines in d. Vertical lines with caps in e, f represent the error bars. Data is collected with 45 eV photon energy at 20 K with LH polarized light.
To reveal the Dirac nodal arc, a series of constant energy cuts and ARPES maps taken along the ky momentum direction is presented in Fig. 4. The ellipsoidal pockets at the Fermi level transform into line-like dispersions at the Dirac point (Fig. 4a). This represents the Dirac nodal arc laying along \(\bar{M}-\bar{\Gamma }\) direction. 1D-Dirac nodal arc can be further traced in 2D-ARPES maps taken parallel to the \(\bar{{K}_{1}}-\bar{M}-\bar{K}\) direction at different ky momentum while moving towards the \(\bar{\Gamma }\)-point. The binding energy of the Dirac point does not exhibit a prominent change up to ky = 0.7 Å−1 and then starts moving towards lower binding energy approaching the \(\bar{\Gamma }\)-point. Simultaneously, the surface states and bulk bands decouple and can be distinguished as marked with dashed orange and red curves in Fig. 4b. This yields the realization that surface states flatten while the Dirac point moves towards lower binding energy and Brillouin zone center. This can be also seen in the ARPES map along the \(\bar{M}-\bar{\Gamma }-\bar{{M}_{1}}\) direction (Fig. 4c). Highly, dispersive bulk bands (red dashed line) cross the Fermi level at k|| = ±0.4 Å−1 while the surface states (orange dashed line) exhibit a flat feature in the vicinity of the Fermi level. This forms a line-like dispersion at the Fermi surface connecting ellipsoidal pockets to the \(\bar{\Gamma }\)-point as shown with a red arrow in Fig. 4a.
a Constant energy maps at the indicated binding energies. The portion of the Fermi surface around the \(\bar{\Gamma }\)-point is recolored to highlight the flat dispersion marked with a red arrow. The 2D- Brillouin zone together with the high symmetry points is also shown. b Binding energy versus kx cuts as a function of ky. The position of the DP is indicated with an arrow on each spectrum. c Binding energy versus k|| along the \(\bar{M}-\bar{\Gamma }-\bar{{M}_{1}}\) direction. Yellow and red dashed curves highlight portions of the surface state and bulk bands, respectively. The spectra are measured with 115 eV LH polarized light. The Dirac point (DP) is shown with horizontal arrows in ARPES spectra.
Tuning the topological properties of 1T-VSe2
In contrast to the computed band structure of an ideal crystal structure of VSe2, the experimental data strongly support the presence of topological states in this material. This could be related to structural properties, such as strain26,27,28,29 or ordered Se vacancies as proposed for PtSe2 and MoS230. Since 1T-VSe2 is a 2D van der Waals material, lattice relaxations near the surface could be a potential mechanism behind the band inversion. Hence, we consider models of strained VSe2 and find that the band gap at the L-point is sensitive to strain. Although, high-resolution x-ray diffraction (XRD) experiment measures bulk lattice parameters of a = 3.354 Å and c = 6.133 Å (Supplementary Fig. 5), consistent with the literature31, strain can still be effective on the sample surface due to the mechanical cleaving. As discussed in Supplementary Notes 1 and shown in Supplementary Table 1, the bulk band gap at the L-point shrinks under either in-plane compression or out-of-plane tension. The gap seen in the normal state (Fig. 5a) fully closes under a strain of ~1% in both directions. Even larger strain eventually leads to band inversion (Fig. 5b). This is due to the compression in the x-y plane which shortens the Se-Se bond and strengthens the in-plane px/y−px/y hybridization. The combined in-plane compression and out-of-plane tension decrease the angle (θ) between the V-Se bond and the y axis, thus strengthening the coupling between V dxz/yz and Se pz orbitals and lowering the energy of the bonding states (Supplementary Fig. 2). The effect is more significant on the dyz−pz hybridization because its hopping integral is proportional to cos(θ). As a result, the even parity state \({\Gamma }_{1}^{+}\) (V d dominated) moves below the odd parity state \({\Gamma }_{1}^{-}\) (Se \({p}_{x}/{p}_{y}\) dominated) at the L-point and causes band crossing along the A-L line, which implies a topological phase transition.
DFT electronic band structures of VSe2 projected onto V 3d and Se 4p orbitals. a unstrained without SOC. b strained (2% in-plane compression and 1.5% out-of-plane tension) without SOC. c strained (same as b) with SOC. d Trivial surface electronic structure of unstrained VSe2. e Topologically protected Dirac surface states of VSe2 under 2% of in-plane compression and 1.5% out-of-plane tension. Color bar indicates the calculated spectral intensity: black for vacuum; red for bulk states; yellow for surface states.
When SOC is included in the band structure of strained VSe2, a gap is opened at the band crossing near the L-point, as shown in Fig. 5c. The point group irreps of \({\Gamma }_{1}^{+/-}\) turn into double group irreps \({\Gamma }_{3}^{+/-}\oplus {\Gamma }_{4}^{+/-}\). If we consider a gap indicated by the red dashed line, the Z2 invariant can be defined. The inversion parity analysis at time-reversal-invariant momenta (TRIM: Γ, M, L, and A) reveals a trivial Z2 invariant, \(\left({\nu }_{0};{\nu }_{1}{\nu }_{2}{\nu }_{3}\right)=(0;000)\), in the unstrained structure, but a non-trivial one, (1;001), in the strained structure consistent with a strong topological insulator (Supplementary Tables 2 and 3). It suggests the emergence of TSSs at \(\bar{M}\) of the 2D Brillouin zone in the strained VSe2. To confirm the TSSs we construct Maximally localized Wannier functions (MLWFs) of V 3d and Se 4p orbitals and build an effective tight-binding Hamiltonian. In contrast to the trivial states in the unstrained VSe2 (Fig. 5d), there is a Dirac crossing in the surface state (bright yellow) connecting bulk bands (red) at the \(\bar{M}\)-point in the strained VSe2 as shown in Fig. 5e, which is consistent with the ARPES measurement. Although this approximation induces a topological phase transition, a full nodal arc along the \(\bar{\Gamma }-\bar{M}\) is missing. Instead, a partial Dirac nodal arc is observed on the computed band structure, which is dictated by the fact that a strong topological insulator cannot have topologically protected full Dirac nodal lines32. However, if the system has in-plane time reversal symmetry, a strong topological insulator can still form a partial Dirac nodal arc connecting the point where the bulk band gap closes, as demonstrated in the Liu-Qi-Zhang model32. Indeed, from our the DFT calculation, we observe a partial Dirac nodal arc surface states along the \(\bar{\Gamma }-\bar{M}\) line protected by the time reversal symmetry and the Γ-M-L-A mirror plane symmetry, which ends at the bulk band crossing (Supplementary Fig. 6). The exact location of the bulk band crossing point is sensitive to multiple factors, such as defects, strain, and interlayer coupling, which may not be fully accounted for by our DFT model. These factors could explain the remaining discrepancy between experiment and theory on the length of the Dirac nodal arc.
Conclusion
In summary, we presented a systematic band structure study showing the existence of an unexpected Dirac nodal arc in the surface electronic structure of 1T-VSe2. Our photoemission experiments reveal a non-trivial nature of the band structure in 1T-VSe2 characterized by band inversion supporting a spin-momentum locked topological surface state. Although this does not exclude other possible mechanisms, DFT calculations demonstrate that a band inversion at the L-point can be driven by a lattice strain. Such states are predicted to be protected by a special symmetry, called in-plane time reversal symmetry32,33,34. This could be satisfied by the combination of mirror and time reversal symmetries based on ref. 29. From this point of view, 1T-VSe2 is a stacking of 2D quantum spin Hall insulators, suggesting it as graphene like material34. This might open possibilities to observe quantum anomalies and build novel devices functioning at higher temperatures since the bulk band gap is larger in 1T-VSe2. The transport properties are also expected to be dominated by the topological states since the Dirac point is in the vicinity of the Fermi level in the Brillouin zone center. Therefore, 1T-VSe2 is a unique quantum material exhibiting a topologically non-trivial electronic structure which could prove ideal for future device applications.
Methods
Sample
Single crystal 1T-VSe2 samples were obtained from 2dsemiconductors company (part number: BLK-VSe2).
Angle-resolved photoemission spectroscopy
ARPES experiments were performed at the ESM beamline of NSLS-II (21ID-1) and the APE-LE beamline of Elettra using DA30 Scienta electron spectrometers at 20 K. The samples were cleaved in situ. The base pressure in the photoemission chambers was 1 × 10−11 Torr. The energy resolution was better than 12 meV and the beam spot size was approximately 5 µm2 for 21-ID-1 and (150 × 50 µm2 for APE-LE). The synchrotron radiation incidence angle was 55° and the analyzer slit was along the \(\bar{{K}_{1}}-\bar{M}-\bar{K}\) direction during polarization dependent and spin-resolved ARPES experiment. LV polarized light is parallel to the sample surface and analyzer slit while LH polarized light is on the incident plane.
Band structure calculations
The band structures of unstrained and strained VSe2 are calculated with DFT under the generalized gradient approximation for the exchange-correlation potential using the Perdew–Burke-Ernzerhof (PBE)35 parameterization, as implemented in the plane-wave pseudopotential package, Quantum ESPRESSO36,37. The full relativistic norm conserving pseudopotentials from Pseudo Dojo38,39 are used in the calculation. The experimental lattice parameters of a = b = 3.355 Å and c = 6.134 Å are used to build the hexagonal unit cell of the unstained 1T-VSe2 structure. We also study multiple strained structures, and the main results are reported for the structure with a = b = 3.288 Å (2% compression), while allowing the unit cell to relax in the out-of-plane direction. This results in c = 6.227 Å (1.5% tension). The planewave cutoff of 80 and 320 Ry are used for wavefunction and charge density. The Brillouin zone is sampled by a 15 × 15 × 15 k point mesh. MLWFs40,41,42,43 are constructed with the Wannier90 package41 and used to build tight-bind models of the semi-infinite slab. The Green’s function of the surface states of the semi-infinite slab is calculated using the iterative method implemented in Wannier Tools44.
X-ray diffraction
XRD experiment was carried out on the ISR beamline, 4-ID, with a wavelength of 1.079 Å. A Dectris 1 M area detector was used with a Huber six circle diffractometer to obtain detailed reciprocal space maps of the crystal.
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
References
Mak, K. F. & Shan, J. Photonics and optoelectronics of 2D semiconductor transition metal dichalcogenides. Nat. Rev. Mater. 2, 17033 (2017).
Manzeli, S., Ovchinnikov, D., Pasquier, D., Yazyev, O. V. & Kis, A. 2D transition metal dichalcogenides. Nat. Rev. Mater. 2, 17033 (2017).
Hsu, Y.-T., Vaezi, A., Fischer, M. H. & Kim, E.-A. Topological superconductivity in monolayer transition metal dichalcogenides. Nat. Commun. 8, 14985 (2017).
Luxa, J. et al. Origin of exotic ferromagnetic behavior in exfoliated layered transition metal dichalcogenides MoS2 and WS2. Nanoscale 8, 1960 (2016).
Ritschel, T. et al. Orbital textures and charge density waves in transition metal dichalcogenides. Nat. Phys. 11, 328–331 (2015).
Shi, W. et al. Superconductivity series in transition metal dichalcogenides by ionic gating. Sci. Rep. 5, 12534 (2015).
Strocov, V. N. et al. Three-dimensional electron realm in VSe2 by soft-X-ray photoelectron spectroscopy: origin of charge-density waves. Phys. Rev. Lett. 109, 086401 (2012).
Duvjir, G. et al. Emergence of a metal-insulator transition and high-temperature charge-density waves in VSe2 at the monolayer limit. Nano Lett 18, 5432–5438 (2018).
Wong, P. K. J. et al. Evidence of spin frustration in a vanadium diselenide monolayer magnet. Adv. Mater. 31, 1901185 (2019).
Chen, P. et al. Unique gap structure and symmetry of the charge density wave in single-layer VSe2. Phys. Rev. Lett. 121, 196402 (2018).
Barua, S., Hatnean, M. C., Lees, M. R. & Balakrishnan, G. Signatures of the Kondo effect in VSe2. Sci. Rep. 7, 10964 (2017).
Yu, W. et al. Chemically exfoliated VSe2 monolayers with room-temperature ferromagnetism. Adv. Mater. 31, 1903779 (2019).
Fuh, H. R. et al. New type single-layer magnetic semiconductor in transition-metal dichalcogenides VX2 (X = S, Se, and Te). Sci. Rep. 6, 32625 (2016).
Damascelli, A., Hussain, Z. & Shen, Z. X. Angle-resolved photoemission studies of the cuprate superconductors. Rev. Mod. Phys. 75, 473–540 (2003).
Kevan, S. D. (ed.) Angle-Resolved Photoemission: Theory and Current Applications (Elsevier, 1992).
Moser, S. An experimentalist’s guide to the matrix element in angle resolved photoemission. J. Electron Spectrosc. 214, 29–52 (2017).
Hüfner, S. Photoelectron Spectroscopy: Principles and Applications (Springer, 2003).
Eberhardt, W. & Himpsel, F. J. Dipole selection rules for optical transitions in the fcc and bcc lattices. Phys. Rev. B 21, 5572–5576 (1980).
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Moore, J. E. The birth of topological insulators. Nature 464, 194–198 (2010).
Park, S. R. et al. Chiral orbital-angular momentum in the surface states of Bi2Se3. Phys. Rev. Lett. 108, 046805 (2012).
Scholz, M. R. et al. Reversal of the circular dichroism in angle-resolved photoemission from Bi2Te3. Phys. Rev. Lett. 110, 216801 (2013).
Xu, C.-Z. et al. Photoemission circular dichroism and spin polarization of the topological surface states in ultrathin Bi2Te3 films. Phys. Rev. Lett. 115, 016801 (2015).
Mitsuishi, M. et al. Switching of band inversion and topological surface states by charge density wave. Nat. Commun. 11, 2466 (2020).
Jiang, Q. et al. Independent spin polarized valence electronic states in VSe2 from charge density wave transition. J. Electron Spectros. Relat. Phenomena 238, 146868 (2020).
Chege, S., Ning’i, P., Sifuna, J. & Amolo, G. O. Origin of band inversion in topological Bi2Se3. AIP Adv. 10, 095018 (2020).
Young, S. M. et al. Theoretical investigation of the evolution of the topological phase of Bi2Se3 under mechanical strain. Phys. Rev. B 84, 085106 (2011).
Zhu, Z. Y., Cheng, Y. C. & Schwingenschlogl, U. Band inversion mechanism in topological insulators: a guideline for materials design. Phys. Rev. B 85, 235401 (2012).
Zhao, M., Zhang, X. & Li, L. Strain-driven band inversion and topological aspects in antimonene. Sci. Rep. 5, 16108 (2015).
Crasto de Lima, F. & Fazzio, A. At the verge of topology: vacancy-driven quantum spin Hall in trivial insulators. Nano Lett. 21, 9398 (2021).
Carmalt, C. J., Parkin, I. P. & Peters, E. S. Atmospheric pressure chemical vapour deposition of WS2 thin films on glass. Polyhedron 22, 1499–4505 (2003).
Lau, A., Ortix, C. & van den Brink, J. One-dimensional Dirac electrons on the surface of weak topological insulators. Phys. Rev. B 91, 085106 (2015).
Dai, J. et al. Experimental observation and spin texture of Dirac node arcs in tetradymite topological metals. Phys. Rev. Lett. 126, 196407 (2021).
Hosen, M. M. et al. Distinct multiple fermionic states in a single topological metal. Nat. Commun. 9, 3002 (2018).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Giannozzi, P. et al. Advanced capabilities for materials modelling with quantum ESPRESSO. J. Phys. Condens. Matter 29, 465901 (2017).
Giannozzi, P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502 (2009).
van Setten, M. et al. The pseudodojo: training and grading a 85 element optimized norm-conserving pseudopotential table. Comput. Phys. Commun. 226, 39–54 (2018).
Hamann, D. R. Optimized norm-conserving Vanderbilt pseudopotentials. Phys. Rev. B 88, 085117 (2013).
Marzari, N., Mostofi, A. A., Yates, J. R., Souza, I. & Vanderbilt, D. Maximally localized Wannier functions: theory and applications. Rev. Mod. Phys. 84, 1419–1475 (2012).
Marzari, N. & Vanderbilt, D. Maximally localized generalized wannier functions for composite energy bands. Phys. Rev. B 56, 12847–12865 (1997).
Souza, I., Marzari, N. & Vanderbilt, D. Maximally localized wannier functions for entangled energy bands. Phys. Rev. B 65, 035109 (2001).
Mostofi, A. A. et al. wannier90: a tool for obtaining maximally-localised Wannier functions. Comput. Phys. Commun. 178, 685–699 (2008).
Wu, Q., Zhang, S., Song, H.-F., Troyer, M. & Soluyanov, A. A. WannierTools: an open-source software package for novel topological materials. Comput. Phys. Commun. 224, 405–416 (2018).
Acknowledgements
This research used 21-ID and 4-ID beamlines of the National Synchrotron light source II, a US Department of energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Brookhaven National Laboratory under Contract number DE-SC0012704. This work also used the theory and computation resources of the Center for Functional Nanomaterials, which is a U.S. DOE Office of Science User Facility at the Brookhaven National Laboratory under Contract number DE-SC0012704. P.M.S., A.V.M., and P.M. acknowledge the project EUROFEL-ROADMAP ESFRI of the Italian Ministry of Education, University, and Research. The work has been partly performed in the framework of the nanoscience foundry and fine analysis (NFFA-MUR Italy Progetti Internazionali) facility.
Author information
Authors and Affiliations
Contributions
T.Y. conceived and guided the research. T.Y. and E.V. performed the photoemission experiments at 21-ID-1 beamline. P.M.S., A.V.M., P.M., F.M., I.V., and J.F. performed the spin-resolved ARPES experiments at APE-LE beamline. D.L. and X.J. performed theoretical calculations. T.Y. and E.V. wrote the manuscript with contributions from all the authors. K.E.L. performed the XRD experiments. All authors contributed to the scientific discussion of the results.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Materials thanks the anonymous reviewers for their contribution to the peer review of this work. Primary Handling Editors: Toru Hirahara and Aldo Isidori. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yilmaz, T., Jiang, X., Lu, D. et al. Dirac nodal arc in 1T-VSe2. Commun Mater 4, 47 (2023). https://doi.org/10.1038/s43246-023-00376-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-023-00376-1