Abstract
Growth of ice crystals is ubiquitous around us, but we still do not know what is occurring at the forefront of crystallization. In general, the interfacial structure is inseparably involved in the microscopic ordering during crystal growth. However, despite its importance in nature and technology, the intrinsic role of the interfacial structure in the melt growth of ice remains to be elucidated. Here, using extensive molecular dynamics simulations, we comprehensively explore how supercooled water molecules are incorporated into the ice basal face. Structural and dynamic characterizations of the ice-water interface demonstrate that the ice basal face is sharp at the molecular level and its growth proceeds layer-by-layer through two-dimensional nucleation without any intermediate structures. We further quantify the crossover from layerwise to adhesive growth, called kinetic roughening, with the height difference correlation and the normal growth rate analysis. Moreover, we identify the presence of an ultra-low density water layer in contact with the structural interface, which assists two-dimensional nucleation at a small amount of supercooling without involving any triggers, such as dislocations.
Similar content being viewed by others
Introduction
Growth of ice crystals from supercooled liquid water (the melt growth of ice) exhibits anisotropic kinetics depending on the nature of the exposed ice surface, in which the basal face is known to grow much slower than the prism and secondary prism faces1,2,3. In general, such anisotropy is a source of the so-called crystal habit, which also results in, for example, the rich variety of snow crystals grown from water vapor in the atmosphere. In the melt growth of ice, the underlying anisotropy in molecular attachment and its link to the interfacial structure has been of great interest in fundamental sciences4,5, as well as various applications in sub-zero environments, e.g., the recognition of different ice surfaces by anti-freeze proteins and the resulting molecular insights for cryopreservation6,7,8. However, despite intensive studies due to its broad significance, the microscopic mechanism resulting in the anisotropic growth kinetics remains elusive. To elucidate its origin, a fundamental understanding beyond the linear growth picture is highly required.
One plausible explanation of this anisotropy is that the ice basal face is faceted and grows in a layer-by-layer manner. It is well-known that, for faceted interfaces (e.g., the ice basal face), incorporation of atoms and molecules into crystal lattices only takes place at kinks of step edges, which makes their growth rate slower than that for rough interfaces (e.g., the ice prism face), allowing the incorporation to take place anywhere. However, direct access to the microscopic growth kinetics by experiments is extremely difficult as the growth proceeds through an interface between two condensed phases. For example, modern probe-based techniques, such as atomic force microscopy (AFM), are invasive and suffer from the presence of the surrounding melt in addition to the rapidly growing interface. Using an advanced optical scope with ultrahigh height resolutions (a subnanometer level), Murata et al. recently succeeded in making in-situ observations of growing interfaces during ice melt growth in a non-invasive manner. They clarified the self-organization of elementary steps (step-bunching instability) in the vicinal basal face, which suggests the presence of the faceted basal face even in supercooled water9. However, the lateral (xy) resolution of their microscopy remains at the submicrometer level due to the diffraction limit of light, as with conventional optical microscopy. Thus, molecular-level understanding of the melt growth of ice remains a persistent challenge even for state-of-the-art experiments.
Computational approaches are a promising candidate to overcome such experimental difficulties, allowing us to directly follow the melt growth of ice on the molecular scale. Molecular dynamics (MD) simulations have obtained evidence of layer-by-layer growth on the basal face, using different water models2,4,10,11,12,13. These studies have clarified the sharp growing interface exposed to liquid water and its stepwise structural ordering. However, the identification of “smooth (or sharp)” in the conventional studies basically relied on the abrupt structural change in the direction perpendicular to the ice-water interface. Moreover, the possible heterogeneity in the lateral direction has not been taken into account, while its importance is recently being recognized in the premelting of ice occurring at ice-vapor interfaces near the melting point14,15,16,17. Thus, even accepting the fact that the ice basal face is smooth, it is yet to be fully understood what structural and dynamic features of the interface, not only in the perpendicular but also in the lateral directions, determine the ice growth kinetics.
One may consider that the ice melt growth is rather simple and its behavior is easy to expect numerically contrary to the vapor growth of ice, exhibiting complex interplay with the premelting layer near the melting point3,16,18. For simple melt growth, there also remain several fundamental questions of, for example, whether thermal fluctuations alone can increase a two-dimensional (2D) ice embryo up to its critical size in accordance with the classical nucleation pathway, or whether there is an alternative non-classical route19,20, such as a metastable crystal as conjectured in Ostwald’s step rule or a precursor structure wetting crystal surface.
Furthermore, in general, the layerwise nucleation growth is expected to be followed by barrier-less adhesive growth at deeper supercooling, where the nucleation barrier reaches the same level as the thermal energy. This spinodal-like crossover is known as kinetic roughening, which leads to a rough interface even below the temperature of the thermal roughening transition. However, to the best of our knowledge, there are no reports demonstrating the crossover of the growth mode on the ice basal face.
To address these issues, we perform extensive MD simulations for the melt growth of ice on the basal plane. Our primary focus on the molecular rearrangement at ice-water interfaces benefits from the fast dissipation of latent heat by a thermostat. In the absence of screw dislocations resulting in spiral growth, we highlight how the ice melt growth proceeds without any preliminary structural triggers. Our numerical approach offers insights into the molecular mechanism of the melt growth of ice through detailed structural and dynamic characterizations of ice-water interfaces, which have not been experimentally accessible so far.
Results
Time evolution
MD simulations for ice crystallization on the basal face are carried out in the orthorhombic box consisting of ice, liquid water and vacuum phases (Fig. 1a), while varying the degree of supercooling (ΔT ≡ Tm − T). Although layers of cubic (Ic) and hexagonal (Ih) ice stack seamlessly on the pre-existing ice substrate at ΔT > 0 K, ending up as a stacking-disordered ice21, the exposed ice Ic and Ih faces possess identical molecular arrangements, namely chair form hexagonal rings (Supplementary Fig. 1). A water molecule is classified into ice-like or liquid-like according to the average bond order parameter (\({\bar{q}}_{6}\))22,23. Visualization by \({\bar{q}}_{6}\) in Fig. 1a displays a clear segregation between ice (reddish) and liquid water (bluish) domains.
a Simulation cell containing ice, liquid water, and vacuum phases, in which the bottom ice layer is restrained. Molecules are colored according to \(\bar{{q}_{6}}\). Time evolution of b the average potential energy per molecule U and c the number of ice-like molecules Nice in typical trajectories at ΔT = 0.1, 0.5, 1.1, and 4.3 K.
Figure 1b, c show the time evolution of the average potential energy per molecule (U) and the total number of ice-like molecules (Nice) at three different ΔTs. At ΔT = 0.1 and 0.5 K, step-wise changes in both U and Nice are clearly identified. Note that the decrease in U and the corresponding increase in Nice indicate the progress of ice crystallization. Conversely, during the period when both U and Nice remain constant, the system is trapped in a local free energy minimum, in which ice crystallization does not proceed, but small 2D ice nuclei repeatedly form and disappear (see Supplementary Movies 1, 2, and 3 for ΔT = 0.1 K). An abrupt change in U and Nice means that a 2D ice nucleus reaches the critical size and spreads in the lateral direction. As a consequence, Nice rises by 3520 molecules in average (\({\bar{N}}_{{{{{{{{\rm{L}}}}}}}}}\)), which corresponds to one ice layer of the basal face in this study. These results undoubtedly demonstrate that crystallization on the ice basal face proceeds via a single-layer nucleation at small supercoolings.
The mode of melt growth varies with the magnitude of supercooling. First, the induction time for a nucleation (the length of plateaus in U and Nice) is shortened with an increase ΔT, as seen from ΔT = 0.1 K to 0.5 K. At ΔT = 1.1 K, multiple 2D nucleations occur on the ice face. Although short induction times are sometimes seen, one-layer by one-layer growth is not obvious. Further supercooling then eliminates the induction time, and both U and Nice show a rapid evolution as seen at ΔT = 4.3 K. The increase in ΔT, thus the enhancement of the driving force for crystallization, lowers the free energy barrier to form a critical nucleus, which drives simultaneous multiple nucleations. Independent 2D nuclei consisting of ice Ih and ice Ic sometimes form in the same layer, and their competition and the fusion into either one delays the total growth of ice12. However, U and Nice gradually develop even during that competition, dissimilar to the steady state situation during the induction time at lower supercoolings. Thus, at deeper supercoolings, the melt growth proceeds uninterruptedly, which mode is referred to as adhesive growth.
Interfacial characterization of ice basal face
The crossover from nucleation growth to adhesive growth results in a rough growth front, called kinetic roughening. We first visualize the interface before and after undergoing the kinetic roughening. Figure 2a, b display the topographic views of ice-like molecules at the equilibrium ice-water interface (ΔT = 0.0 K). We find that the outermost ice layer, colored in sky blue, involves many 2D islands (green) and holes (blue) owing to the thermal fluctuations. The islands can function as ice embryos for nucleation, whereas the holes arise from the incomplete hexagonal hydrogen-bond network (Fig. 2c). In Movie 4, sequential conformational changes at ΔT = 0.0 K demonstrate that the surface structure is dynamically changing on the scale of hundreds ps. Here, it is worth noting that, at lower ΔTs, the height difference at two distant locations are mostly suppressed within the bilayer, regardless of the existence of islands and holes. In contrast, the surface geometry becomes remarkably complicated after the kinetic roughening at higher ΔTs. Figure 2d, e show the presence of some independent large islands (orange) and further small islands (red) on those islands at ΔT = 4.3 K (also see Supplementary Movie 5).
Typical ice-water interfaces obtained at a–c ΔT = 0.0 K and d, e 4.3 K. a, d Side views, from above, and b, e top views of the ice layers with a color gradient. c Hydrogen-bond networks describing the sky blue outermost layer in panels (a and b), in which non-6-member rings are filled by sky blue. f Probability Pclst to find a cluster consisting of n liquid-like molecules (hole) within the outermost ice layer and that for n ice-like molecules (island) on the outermost ice layer, both at ΔT = 0.0 K. Solid lines are linear fittings to ln(Pclst) at \(\sqrt{n}\, > \,5\). g Height difference correlation G plotted as a function of the separation rxy on the ice-water interface at ΔT = 0.0 and 4.3 K. The error bars represent the standard deviations calculated from three different trajectories (each 100 ns).
Here, we deal with the equilibrium ice-water interface phenomenologically. At ΔT = 0, the free energy to create a 2D island (hole) of linear size ϕ is βϕ for a step free energy β, because the chemical potentials of liquid water and ice are identical. Thus, the probability Pclst to find a 2D island (hole) with ϕ is in proportion to \(\exp (-\beta \phi /{k}_{{{{{{{{\rm{B}}}}}}}}}T)\) with kB being the Boltzmann constant. If 2D islands (holes) are assumed to be round in shape, ϕ is replaced by \(2\sqrt{\pi {A}_{{{{{{{{\rm{0}}}}}}}}}n}\) using the average area occupied one molecule A0 (0.085 nm2) in the lateral direction and the 2D cluster size n of ice-like (liquid-like) molecules. Figure 2f plots ln(Pclst) for both islands and holes as a function of \(\sqrt{n}\). Their slopes, corresponding to β, are found to vary with n and eventually become constant at n > 25, indicating the growth of smaller islands (holes) requires a higher cost in free energy. The linear fittings at n > 25 provide an estimate of β as 2.0 ± 0.1 × 10−12 J m−1. We note that the β obtained at the ice-water interface agrees well with the experimental (3.4 × 10−12 J m−1 at − 0. 5 ∘C and 0.8 × 10−12 J m−1 at − 2 ∘C)24,25 and computational ( ~ 10−12 J m−1 at 0 to –10 ∘C)16 estimations at the ice-vapor (quasi-liquid) interface.
We now prove the onset of the kinetic roughening more quantitatively. It is well-established that the surface roughness is best characterized by the height difference correlation G at two separated points via an equation of
where h is the height at rxy ≡ (x, y) on the lateral plane (hereafter ∣rxy∣ = r). Note that G diverges logarithmically as \(({k}_{{{{{{{{\rm{B}}}}}}}}}T/\pi \tilde{\alpha })\ln (r/a)\) for rough surfaces (\(\tilde{\alpha }\) being a stiffness), whereas G remains finite at r → ∞ for faceted surfaces. Figure 2g shows that, at ΔT = 0.0 K, G remains constant (G ~ 0.08 nm2) for a large distance, due to the strong height-height correlation. This clearly indicates that, at lower ΔTs, the thermal fluctuation excites no more than single or bilayer islands as seen in Fig. 2a, b (ΔT = 0.0 K), so that the basal face is faceted within one molecule thick.
Furthermore, the G analysis allows us to estimate β independently because β couples to the correlation length of G in the in-plane direction, ξxy, via the relation of β = (4/π)a2γ/ξxy, where a is the step height and γ is the solid/liquid interfacial tension, respectively16. For ΔT = 0.0 K, ξxy is found to reach almost 2 nm (Fig. 2g). Employing a = 0.36 nm and γ = 3.45 × 10−2 J m−2 (ref. 26), we consequently obtain β = 3 × 10−12 J m−1. One finds that this value is found to be close to that obtained by the Pclst analysis (see above).
In contrast, at ΔT = 4.3 K, G diverges logarithmically with \(\tilde{\alpha }\) of 1.7 × 10−2 J m−2 (Fig. 2g), which agrees well with the experimental value (3.3 × 10−2 J m−2)27. The divergence means that the surface heights at different positions fluctuate with a correlation length beyond the system size in the in-plane direction (ideally, an infinite correlation length). The different propensities in G at the two temperatures prove that the kinetic roughening actually takes place at deeper supercooling.
We also check carefully the size dependence on G by further employing MD simulations for two other system sizes having 1/4 smaller (8.4 × 8.9 nm2) and 9/4 larger (25.3 × 26.6 nm2) xy planes than the current system (16.9 × 17.7 nm2). All the systems show the divergence of G at higher ΔTs, but the magnitude of roughness is less prominent with decreasing the system size due to the suppression by the periodic boundary condition (Supplementary Fig. 2). Thus, the resulting stiffness decreases with increasing the system size. For the 1/4 system, we find that the surface geometries before and after the kinetic roughening are indistinguishable by their structures. More specifically, at one half the xy plane size, G shows 0.07 nm2 at ΔT = 0.2 K, while that is 0.12 nm2 even at a much higher ΔT of 9.5 K (Supplementary Fig. 2). In contrast to the suppression of the fluctuation in the height direction, the correlation length in the xy direction reaches ξxy ~ 2 nm even for the faceted surface (see Fig. 2g and the discussion above). This means that small systems with comparable correlation lengths mimic rough interfaces. These results suggest that a sufficiently large system size is required for robust identification of interfacial roughness, which is the main reason why past studies did not find kinetic roughening on the ice basal face in addition to a lack of G analysis.
We further examine if the growing rough interface is characterized by the Kardar-Parisi-Zhang (KPZ) equation28,29. Supplementary Fig. 3 shows the time evolution of G in the early transient process from the initial faceted to a rough interface for the current and 9/4 larger size systems described above. The results indicate that it is inconclusive at this stage whether the G for the current system shows logarithmic divergence or the power law scaling, while that for the larger system is likely to follow the latter, whose exponent is close in value to that of the KPZ scaling30 (the details are described in Supplementary Note 1). Although further studies are required to elucidate the link between the KPZ equation and the kinetic roughening in this system, the divergence of G in either case evidently shows the onset of kinetic roughening.
Structural changes at the ice-water interface
We next examine the change in molecular arrangements in the vicinity of a stable ice-water interface, at which new 2D nuclei are ready to grow. We pick as an example the period between 10 and 60 ns in the freezing trajectory at ΔT = 0.1 K in Fig. 1b, c, during which the five-layered ice structure persists. The black line in Fig. 3a shows the continuous density profile perpendicular to the basal face. According to this density profile, reflecting the layered structure, the system is divided into several slabs with a width of 0.36 nm and the slabs are named as L1, L2, ⋯ from the bottom of the ice (see the labels on the top of Fig. 3a). We find that the density wave propagates over a range of several layers in the liquid side31,32. This means that the density change across the interface is rather diffuse, which is also supported by the slab-average density profile (the pink bars in Fig. 3a).
a Density of water molecules shown in a continuous manner (black, left) and in a slab-averaged manner (pink, right). The slabs with a width of 0.36 nm are numbered from the left as L1, L6, and L12 are shown on the top. b Fraction of ice-like molecules. The inset shows \(\bar{{q}_{6}}\) distributions at L4, L5, L6, and L12 slabs. The black dashed line indicates the threshold of 0.31 for the identification between ice-like and liquid-like molecules. c Number of 5-, 6-, and 7-member rings. d Time evolution of the number of ice-like molecules within the slabs from L4 to L8. e Self-diffusion coefficient D in the lateral and normal directions, computed from the short duration of 10 ps. f Relaxation time of the auto-correlation function cl of staying within a slab. The inset shows the cl curves for L3, L4, L5, L6, and L12. The data, except for panel d, is computed from the period between 10 and 60 ns of the trajectory at ΔT = 0.1 K in Fig. 1a, b.
In contrast, the order parameters quantifying local molecular arrangements clearly define the ice-water interface. Figure 3b plots the change in the fraction of ice-like molecules against the number of the slab, demonstrating that the fraction of ice-like molecules rapidly drops between L5 and L6. In the inset of Fig. 3b, we further see that the probability of \({\bar{q}}_{6}\) within a slab shows the abrupt change between L5 and L6. Moreover, the similarity of distribution between L6 and L12 indicates that the local molecular arrangements in L6 effectively resemble bulk liquid. In Fig. 3c, we focus on the topology of the hydrogen-bond network, more specifically, the change in the number of 5-, 6- and 7-member rings with the number of the slab. We find that the change in the number of the rings shares the same trend as that in the fraction of ice-like molecules (Fig. 3b). Namely, the number of 6-member rings, the elements of perfect ice structure, drops between L5 and L6, while the numbers of 5- and 7-member rings, reflecting hydrogen-bond networks slightly hindered than purely tetrahedral structures, rise at the same location. Consequently, we can conclude that the local order in the Cartesian and topological spaces obviously defines a sharp ice-water interface in the normal direction, which is consistent with the result of the height difference correlation function. (see Eq. (3) and Fig. 2g).
Those results obviously indicate a decoupling between structural and density ordering. For the melt growth, the importance of the diffuse nature of density at the interface has been strongly recognized so far in that the diffuse interface, associated with density fluctuations, helps the continuous ordering needed to make the crystal, which facilitates its growth drastically33. However, this decoupling suggests that density ordering is just a shadow, induced by the genuine structural interface acting as a base. Contrary to the conventional thought, at least for the ice basal face, the density ordering is not a direct player in the crystal growth, but it is coupled to the growth through dynamic slowing down of water molecules near the interface as described in the next section.
Figure 3b, c further predict that the outermost ice layer (L5) is not fully covered with ice fragments due to the presence of holes (the coverage ~80%, see also Fig. 2c), while the second ice layer (L4) from liquid is intact. On the other hand, the L6 slab includes a small portion of ice-like molecules and 6-member rings (~10%, see Fig. 3b) due to the iterated formation of 2D nuclei. Interestingly, following the time evolution of the number of ice-like molecules in each slab (see 62 and 75 ns in Fig. 3d and Supplementary Movies 1, 2, and 3), we see that the complete paving of the second ice layer, the formation of the outermost ice layer, and the emergence of ice-like molecules on the outermost ice layer occur simultaneously. It is worth noting that the ice crystallization proceeds simultaneously over the three layers, although the single layering mode is responsible for the growth itself.
Dynamical changes at the ice-water interface
We also focus on the characteristics in dynamics, using the same trajectory. One may guess that molecules within the outermost ice layer (L5) rarely move because the layer is almost frozen in structure (80% by ice-like molecules and 90% by 6-member rings). However, contrary to this intuition, those water molecules are found to be not frozen in their dynamics.
The diffusivity of water molecules within 10 ps is evaluated by the self-diffusion coefficients in the lateral (Dxy) and normal (Dz) direction. In Fig. 3e, we see that water molecules are immobile in L1 to L4, but they start to diffuse in L5, then their diffusivity is magnified with distance from the ice-water interface. The perturbation of the diffusivity is found to span a range of several layers, which shares this as a common feature with the density profile. Furthermore, in the vicinity of the ice-water interface, we see the decoupling between Dxy and Dz, indicating that the diffusion in the lateral direction is greater than in the normal direction. This is because the layered density distribution of liquid water in parallel to the ice face restricts transportation in the normal direction. Here we note that the recovery to the bulk value of the self-diffusion coefficient and the disappearance of the decoupling are finally accomplished at L12.
Despite the presence of the dynamic slowing down near the interface, its degree is more moderate than that experimentally determined by Murata et al24,34, which revealed that QLLs have an approximately 200 times higher viscosity34 (and 90 times larger relaxation time24) than bulk water. The large mismatch between the numerical and the experimental result may come from several assumptions and approximations employed in these experimental works. Thanks to the direct assessment from molecular dynamics itself, our numerical value is supposed to be rather reliable. To ensure the validity of the value obtained, experimental approaches, allowing us to access the molecular dynamics at ice-water interface more directly, are highly required in future.
The probability of surviving in the same slab after a certain time t is evaluated via the time-dependent autocorrelation function cl(t) for the l-th slab. The inset of Fig. 3f shows that c12(t) immediately decays to zero because liquid molecules readily transport between neighbor slabs. In contrast, a significantly slow decay is observed for c3(t) and c4(t), because water molecules on the ice-lattice rarely move to neighbor slabs. Remarkably, the decay of c5(t) resembles that for liquid (c12(t)) rather than the frozen dynamics in ice (c3(t) and c4(t)). In Fig. 3f, the relaxation time, where cl(t) = 1/e, shows a crucial gap between L4 and L5, dissimilar to that between L5 and L6 for the structural parameters in Fig. 3b, c. Water molecules in L4 are less mobile, so that the fast decay in L5 results from the frequent exchange of molecules between L5 and L6 slabs. The pronounced mobility in the outermost ice layer (L5) is also manifested from the fragile surface geometry, which drastically transforms within hundreds ps as observed in Supplementary Movie 4. Thus, the outermost ice layer at the stable ice-water interface preserves a certain amount of ice fragments, but water molecules composing the ice fragments are frequently exchanged with neighboring liquid-like water molecules.
Such a dynamic nature of the interface is closely linked to the growth kinetics. In particular, for faceted crystals, including this system at ΔT < 2 K, the kinetics is limited by Dxy of the nearest neighbor layer of the structural interface (L6), where nucleation growth of a new layer is ready to occur. We find that Dxy at L6 is reduced to one half of the bulk value (at L12). Here, note that Dxy couples not only to the prefactor of the nucleation rate but also to the kinetic coefficient of the growth rate, each of which is proportional to Dxy/a2 and Dxy/a, respectively. In contrast, the dynamics in the normal direction, characterized by Dz and cl(t), is likely to be involved in the diffusion of latent heat, generated by the nucleation growth of new ice layers. The latent heat diffusion is the main rate-limiting process in the real melt growth system near the melting point. Thus, we remark on the significance of Dz and cl(t) in addition to Dxy, although our numerical simulations can ignore the effect of latent heat diffusion.
Growth rate
The normal growth rate Vn is one of the key quantities reflecting the underlying growth mechanism. Because of the simplicity of observations, Vns for melt growth of ice crystals have been intensively measured for a long time27. Moreover, recent numerical simulations35,36 have allowed covering Vn in a wide range of ΔT, which is not experimentally accessible. Here, we specifically focus on the relationship between the ΔT dependence of Vn and the crossover from nucleation growth to adhesive growth. Note that the normal growth rate is described as
where a (=0.36 nm) is the height of one ice layer. Note that \({\bar{N}}_{{{{{{{{\rm{L}}}}}}}}}=\) 3520 in this system as described above. The slope ΔNice/Δt is obtained from a linear fitting to the time (t) evolution of Nice. Figure 4a shows that a non-linear evolution of Vn with \(\mathop{\lim }\limits_{{{\Delta }}T\to 0}{V}_{{{{{{{{\rm{n}}}}}}}}}/{{\Delta }}T=0\) asymptotically transforms to a linear one at ΔT > 2 K.
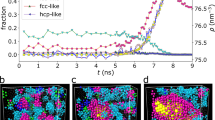
a Growth rate Vn in the normal direction as a function of ΔT. The blue line is the fitting by Eq. (6) to 0.0 K < ΔT < 2.4 K and the black line is a linear fitting to 2.0 K < ΔT < 4.4 K. One may notice that there is a significant gap in Vn between the experimental value42 and that obtained by our simulation. The experimental growth rate is approximately 10,000 times smaller than our numerical value. However, this gap is rather natural because the mW model employed in this study exhibits a larger kinetic prefactor in crystal growth (see the Model section) and the effect of latent heat diffusion, which increases the local temperature near the interface, is ignored in our simulation. The error bars represent the standard deviations calculated from three different freezing trajectories. b Committer probability Pc (green, left) and the largest cluster size n (black, right) of ice-like molecules in the L6 slab in a part of the freezing trajectory at ΔT = 0.1 K. c, d Snapshots of the critical 2D nucleus (Pc = 0.5) within the L6 slab (yellow), obtained at 62.0 and 62.3 ns.
The black line in Fig. 4a clearly demonstrates that Vn at higher ΔTs follows the Wilson-Frenkel formula (Vn ∝ ΔT)37, where liquid water molecules immediately incorporate into location on a rough ice surface. However, a close look at the local structures on the molecular scale reveals that the ice face is not fully roughened but partial facets still persist, as seen in Fig. 2d, e.
The non-linear change in Vn at lower ΔTs is described within the formalism of the classical 2D nucleation theory37. We here consider the direct ice nucleation from liquid water, because of the absence of any intermediate structures at the birthplace. The form of Vn under the multi-nucleation growth is expressed by
where K is a part of the kinetic prefactor and ρice is the density of ice. Here, the chemical potential Δμ of liquid with respect to ice is safely approximated by ΔHmΔT/Tm, where ΔHm is the enthalpy of melting38. The blue line in Fig. 4a indicates that Eq. (5) well represents the ΔT dependence of Vn. Using the bulk quantities, ρice = 0.978 g cm−3 and ΔHm = 5.27 kJ mol−1 at 0.1 MPa39, the fitting curve estimates a β of 1.8 × 10−12 J m−1, the value of which is very close to the estimate from the probability of holes and islands (2.0 ± 0.1 × 10−12 J m−1, see the above subsection “Interfacial characterization of ice basal face”).
The 2D critical nucleus size is given by
This equation produces an nc of 250 at ΔT = 2.0 K, when the obtained β = 2.0 × 10−12 J m−1, the above bulk ρice and ΔHm are employed. This prediction looks reasonable at this temperature. In turn, at ΔT = 0.1 K, where the single nucleation growth occurs, nc is given as 1 × 105. The estimated nc is approximately 30 times larger than the number of molecules composing one layer (3520), implying that, even with the virtue of the periodic boundary conditions, new ice layers are unlikely to form. However, our MD simulations surely demonstrate the melt growth of the basal face even at ΔT = 0.1 K (Fig. 1b). This discrepancy implies that some of the parameters in Eq. (6) are inconsistent with reality.
The actual critical 2D nuclei are sampled via the committer analysis40,41, which detects the progress of 2D crystallization by measuring the probability that a random MD shot from a nucleus seeded from the freezing trajectory crystallizes before returning to the liquid basin. The committer probability is exactly one-half for the critical nucleus, as a critical nucleus is equally likely to melt or to grow. Figure 4b shows the time evolution of the largest cluster size in the L6 slab in a part of the freezing trajectory at ΔT = 0.1 K and the committer probability Pc for each configuration. The ice nucleus is found to attain its critical size at 62.0 ns and 62.3 ns, where the largest cluster consists of 530 and 748 water molecules, respectively. At 62.0 ns, there are relatively large second and third-largest clusters, as seen in Fig. 4c, which possibly merge into the largest cluster. In contrast, Fig. 4d shows that most ice-like molecules compose one largest cluster at 62.3 ns. Thus, when the growth of a single nucleus is considered, the critical nucleus size nc is estimated as 750 water molecules. Thus, again we emphasize that Eq. (6) with bulk quantities significantly overestimates nc.
What facilitates the critical nucleation in very weakly supercooled liquid? We find that the density averaged over each slab shows a valley-like profile at the ice-water interface (see the pink boxes in Fig. 3a). More specifically, the slab-averaged density at L6, 0.971 g cm−3, is lower than that of either of bulk ice or bulk liquid. Thus, the melt growth takes place within the ultra-low density liquid water, rather than in bulk liquid water. Here, with bulk liquid water at this density assumed, a negative pressure of –125 MPa must be applied and the potential energy slightly increases by 0.15 kJ mol−1. According to the Clapeyron equation with simulation data39, the melting curve in the (T, p) diagram has a negative slope of –45 MPa K−1 at 0.1 MPa. Thus, a ΔT of 0.1 K at 0.1 MPa rises to 2.9 K at –125 MPa. These refined ΔHm and ΔT values yield an estimate of 120 for nc, which underestimates the actual size (nc = 750) but is much closer than the estimation using bulk properties (nc = 1 × 105). Using the inverse argument, the nc of 750 is equivalent to a ΔT = 1.2 K from Eq. (6). Therefore, although there remains room to consider how our observations are implemented into Eq. (6), the existence of ultra-low density liquid water at the ice-water interface and the resulting enhancement of the effective supercooling are likely arguments to rationalize why the nucleation growth of ice can be accomplished even at a very small supercooling.
In general, for a small Δμ (here, a minuscule supercooling), growth through the 2D nucleation is difficult to achieve stochastically because the free energy barrier for nucleation is unreachable by thermal fluctuations. Instead, spiral growth, initiated by a screw dislocation, is the stable growth mode even at the limit of Δμ → 0, because an outcropping step always exists on the screw dislocation. Our finding proposes an alternative mechanism of crystal growth at a shallow supercooling, without explicit triggers42.
Discussion
Many studies of crystallization of water, colloids, and metals have revealed that relatively ordered or less-mobile liquid molecules serve as precursors for nuclei43,44,45,46,47. Also, for the growth process, a rough and thick preordered interface helps the rapid or barrier-less growth, because the preordered structures require a very small rearrangement to reach the final crystal structures48,49. In contrast, such an intermediate state is not observed even within the birthplace (L6) for ice in our study. More specifically, regarding the quantities for ice fragments (Fig. 3b, c) and the residence time (Fig. 3f), except the trace for ice embryos, water molecules in L6 closely resemble bulk liquid. Note that the anomaly of the diffusivity (Fig. 3e) near the interface doe not have a structural origin but arises from the dynamic coupling to the density fluctuations, induced by the genuine interface. Accordingly, the observed distinct ice-water interface can be responsible for the slow growth rate of the basal face than other ice faces.
The question that remains unanswered here is why the distinct faceted interface persists on the basal face, even when reaching the melting point. In other words, why does the basal face have no thermal roughening transition at any temperature below the melting point, unlike the rough prism face? Note that the prism face is known to have the thermal roughening transition at 253–263 K and 100–180 MPa near the ice-water equilibrium point (ΔT = 0.1 K)50. Theoretically, the roughening transition temperature is described as \({T}_{{{{{{{{\rm{R}}}}}}}}}=2{a}^{2}\tilde{\alpha }/\pi {k}_{{{{{{{{\rm{B}}}}}}}}}\)37,51. Importantly, TR is also directly coupled to the interfacial width (or the fluctuation width) lw through the relation of \({l}_{{{{{{{{\rm{w}}}}}}}}} \sim \sqrt{{k}_{{{{{{{{\rm{B}}}}}}}}}T/\tilde{\alpha }}\)51. Recently, Mukherjee and Bagchi numerically demonstrated that the entropic gain (in particular, the rotational entropy) plays a key role in the formation of the sharp ice-water interface32, which is a promising answer to the above question.
This perspective offers further interesting insight into the significant gap in the interfacial nature between the basal and the prism face. Because of the presence of the thermal roughening transition, the interfacial width of the prism face is expected to be wider than that of the basal face. This presumption is supported by a numerical simulation by Nada and Furukawa4, revealing that the prism face is rather diffusive (large lw) and its growth proceeds through collective incorporation, although this is mainly focused in the direction perpendicular to the interface. Along the lines of the present analysis for the basal face, to elucidate detailed structure and dynamics of the prism face and its link to the growth mode are an interesting issue to be addressed in future.
We confirm that the melting temperature and the density profile perpendicular to the solid-liquid interface change little even when we reduce the harmonic constant for position restraints by half (Supplementary Fig. 4). These results indicate that the application of position restraints negligibly influences on the stability of ice and the surface structure. Moreover, we verify that the key findings for the mW model are also true for the TIP4P/Ice water model52; namely, the variation of the growth mode from a layer-by-layer manner to a rapid evolution, a sharp solid-liquid interface, and the depletion of water density just above the ice face (Supplementary Fig. 5).
Conclusions
In summary, we have provided a comprehensive molecular picture of how the melt growth of the ice basal face proceeds with varying the degree of supercooling. This study quantified the onset of kinetic roughening for the ice basal face, that is the crossover from layerwise growth to adhesive growth, and characterized the molecular mechanism behind each growth mode. We also revealed the structural and dynamical basis of the ice basal face-water interface and its intrinsic link to the growth kinetics. Moreover, we identified the presence of ultra-low density water at the ice-water interface and its role to facilitate the melt growth at a miniscule supercooling along the classical nucleation pathway, which takes place at the sharp ice-water interface without the aid of pre-ordered structures.
Finally, we expect there to be a link between the melt growth of silicon and ice crystals, both of which preferentially adopt tetrahedrally coordinated structures. It is acknowledged that, at ambient pressure, silicon crystals, having the diamond-cubic structure, exhibit both faceted ({111}) and rough interfaces (e.g., {100} and {110}) in their melt53 and growth anisotropy between their interfaces54. The faceted {111} face shows the lowest growth rate. Furthermore, the layer-by-layer growth driven by elementary step flow has been confirmed for the {111} face by MD simulations of Stillinger-Weber silicon55 and in situ transmission electron microscopy56. Thus, our approach on ice crystals can be applied to investigate the melt growth, interfacial structure and dynamics of silicon crystals.
Furthermore, the microscopic understanding of ice growth closely pertains to the unique function of antifreeze proteins (AFPs). Hyperactive AFPs that exhibit a high performance on thermal hysteresis can bind to the basal face, unlike moderately active AFPs8. Aside from the direct ice-AFP interaction, although the affinity to ice from the AFP side, such as pre-ordering and long-range dynamics of hydration shell, has been studied57,58,59, the attraction from the ice side has not been paid attention. Hydration shells around the ice binding sites (IBSs) are known to have a lower density than that around non-IBSs60. The large hydrophobic IBS of hyperactive AFP preferentially orients toward the air at a water-air interface61. In that sense, our results suggest that the depletion of liquid density at the ice basal face, ranging over 0.7 nm (see L6 and L7 in Fig. 3c), is likely to allow water to mediate the attraction of the IBS of hyperactive AFPs at a distance.
We hope that the ultra-low density water seen in our simulations might be detectable, for example using sum frequency generation spectroscopy. Finally, our findings offer microscopic insights into the melt growth mechanism shared among faceted crystals and the functions of AFPs, all of which are significant in industrial, material, and medical applications.
Methods
Model
Water is represented by the coarse-grained mW model39. This specific water model excellently reproduces the experimental thermodynamic properties that play a crucial role in crystallization; such as densities of ice and liquid water, the melting point39, the difference in the chemical potential between ice and water, the enthalpy (latent heat) and entropy of melting62, and the ice-water interfacial free energy26,38. Although the mW model exhibits a larger kinetic prefactor in crystal growth due to the lack of explicit hydrogen bonds35,38, it in turn allows brute-force simulations of nucleation 41,44,63,64.
MD simulations
MD simulations are carried out using the LAMMPS package65. The equations of motion are integrated using the velocity-Verlet algorithm with a timestep of 5 fs. All MD simulations are conducted using the canonical ensemble with periodic boundary conditions applied to all directions. Temperature is controlled by the Nos\(\acute{{{{{{{{\rm{e}}}}}}}}}\)-Hoover thermostat66,67 with a dumping constant of 1 ps. The cut-off distance for intermolecular interactions is 0.432 nm.
Systems
As the primary system, the orthogonal simulation cell (approximately 16.9 × 17.7 × 14.5 nm3) consists of three blocks of ice, liquid water and vacuum, in which the ice basal face is exposed. The number of water molecules N is 106080. We first build four layers of hexagonal ice with the density of 0.978 g cm−3 (ref. 39) by GenIce68 and pour liquid water onto one side of the ice block. An equilibration MD run for 10 ns is performed at 300 K while restraining the four ice layers by applying a harmonic potential to each particle. The harmonic constant (k) is 48,240 kJ mol−1 nm−2. Then, three independent freezing trajectories of 100 ns are generated at each temperature by giving different momenta to the equilibrated configuration, while the position restraint is applied only to molecules in the bottom layer with k = 965 kJ mol−1 nm−2. Crystallization near the liquid-vapor interface ( < ~ 3.0 nm) is not used for analyses. To examine the size dependence, we also conduct MD simulations of ice crystallization in two other systems (N = 26,520 and 238,680), which have 1/4 smaller and 9/4 larger lateral areas.
Although a melting temperature Tm of 274.6 K was proposed for the mW model39, we independently compute Tm of 275.3 K for our primary system through the direct coexistence method69, because Tm slightly depends on the type of exposed ice surface and MD conditions2.
As the secondary system, 4096 molecules are enclosed into a cubic box in order to compute the potential energy and pressure of bulk liquid water at different densities. The temperature is 275.3 K. At each density, a 20 ns MD simulation is performed and the last 10 ns is used for analyses.
Ice-like and liquid-like molecules
The average bond order parameter22,23 \({\bar{q}}_{6}\) is used to measure the local spatial arrangement of water molecules. We identify water molecules with \({\bar{q}}_{6} > \) 0.310 as ice-like, otherwise liquid-like. The threshold of \({\bar{q}}_{6}\ge 0.310\) is slightly looser than that for bulk ice (\({\bar{q}}_{6}\ge 0.358\))70. Two water molecules are considered to be bonded neighbors and belong to same cluster if their separation is less than 0.35 nm and 1.5 × 0.35 nm, respectively. If an ice-like molecule belongs to the largest cluster consisting of the ice-like molecules and binds to at least one liquid-like molecule, the molecule is defined to be located at the ice-water interface.
Self-diffusion coefficient
Slab-averaged self-diffusion coefficients in the normal (Dz) and the lateral (Dxy) directions to the ice-water interface are evaluated via
where 〈Δr2〉 is the mean square displacement; d = 2 and Δr2 = Δx2 + Δy2 for Dxy; d = 1 and Δr = Δz for Dz. The duration t is 10 ps and the Δr is calculated for the water molecules which are initially present in their respective slabs.
Time-dependent autocorrelation function
The duration that a molecule stays in the same slab is evaluated via the time-dependent autocorrelation function;
where ηl(t) is a binary function defined as ηl(t) = 1 if the molecule is in the l-th slab at time t, otherwise ηl(t) = 0. 〈 ⋯ 〉 is the average over all the molecules in the system. The time at cl = 1/e is defined as the relaxation time.
Committer analysis
We apply the committer analysis to statistically measure the progress of 2D nucleation40,41. Thirty independent MD runs of 2 ns each are shot from the conformations taken along a nucleation trajectory. Then, we determine the probability of freezing using the threshold of 600 molecules.
Data availability
The authors declare that the data supporting the findings of this study are available within the paper and its supplementary information files.
Code availability
For questions or clarifications about the code, please contact the authors at kenji_mochizuki@zju.edu.cn.
References
Furukawa, Y. & Shimada, W. Three-dimensional pattern formation during growth of ice dendrites—its relation to universal law of dendritic growth. J. Cryst. Growth 128, 234–239 (1993).
Rozmanov, D. & Kusalik, P. G. Anisotropy in the crystal growth of hexagonal ice, i(h). J. Chem. Phys. 137, 094702 (2012).
Libbrecht, K. G. Physical dynamics of ice crystal growth. Annu. Rev. Mater. Res. 47, 271–295 (2017).
Nada, H. & Furukawa, Y. Anisotropy in molecular-scaled growth kinetics at ice water interfaces. J. Phys. Chem. B 101, 61636163 (1997).
Benet, J., Llombart, P., Sanz, E. & MacDowell, L. G. Premelting-Induced smoothening of the ice-vapor interface. Phys. Rev. Lett. 117, 096101 (2016).
Voets, I. K. From ice-binding proteins to bio-inspired antifreeze materials. Soft Matter 13, 4808–4823 (2017).
Mochizuki, K. & Molinero, V. Antifreeze glycoproteins bind reversibly to ice via hydrophobic groups. J. Am. Chem. Soc. 140, 4803–4811 (2018).
Bar Dolev, M., Braslavsky, I. & Davies, P. L. Ice-Binding proteins and their function. Annu. Rev. Biochem. 85, 515–542 (2016).
Murata, K.-I. et al. Step-bunching instability of growing interfaces between ice and supercooled water. Proc. Natl. Acad. Sci. USA 119, e2115955119 (2022).
Nada, H. & Furukawa, Y. Anisotropy in growth kinetics at interfaces between proton-disordered hexagonal ice and water: A molecular dynamics study using the six-site model of H2O. J. Cryst. Growth 283, 242–256 (2005).
Nada, H. & Furukawa, Y. Anisotropic growth kinetics of ice crystals from water studied by molecular dynamics simulation. J. Cryst. Growth 169, 587–597 (1996).
Choi, S., Jang, E. & Kim, J. S. In-layer stacking competition during ice growth. J. Chem. Phys. 140, 014701 (2014).
Carignano, M. A., Shepson, P. B. & Szleifer, I. Molecular dynamics simulations of ice growth from supercooled water. Mol. Phys. 103, 2957–2967 (2005).
Pickering, I., Paleico, M., Sirkin, Y. A. P., Scherlis, D. A. & Factorovich, M. H. Grand canonical investigation of the quasi liquid layer of ice: is it liquid? J. Phys. Chem. B 122, 4880–4890 (2018).
Qiu, Y. & Molinero, V. Why is it so difficult to identify the onset of ice premelting? J. Phys. Chem. Lett. 9, 5179–5182 (2018).
Llombart, P., Noya, E. G. & Mac Dowell, L. G. Surface phase transitions and crystal habits of ice in the atmosphere. Sci. Adv. 6, eaay9322 (2020).
Cui, S., Chen, H. & Zhao, Z. Premelting layer during ice growth: role of clusters. Phys. Chem. Chem. Phys. 24, 15330–15339 (2022).
Kuroda, T. & Lacmann, R. Optical study of roughening transition on ice ih (10\(\bar{1}\)0) planes under pressure. J. Cryst. Growth 56, 189–205 (1982).
Mochizuki, K., Himoto, K. & Matsumoto, M. Diversity of transition pathways in the course of crystallization into ice vii. Phys. Chem. Chem. Phys. 31, 16419–16425 (2014).
Lee, J., Yang, J., Kwon, S. G. & Hyeon, T. Nonclassical nucleation and growth of inorganic nanoparticles. Nat. Rev. Mater. 1, 1–16 (2016).
Carignano, M. A. Formation of stacking faults during ice growth on hexagonal and cubic substrates. J. Phys. Chem. C 111, 501–504 (2007).
Lechner, W. & Dellago, C. Accurate determination of crystal structures based on averaged local bond order parameters. J. Chem. Phys. 129, 114707 (2008).
Reinhardt, A., Doye, J. P. K., Noya, E. G. & Vega, C. Local order parameters for use in driving homogeneous ice nucleation with all-atom models of water. J. Chem. Phys. 137, 194504 (2012).
Murata, K.-I., Nagashima, K. & Sazaki, G. How do ice crystals grow inside quasiliquid layers? Phys. Rev. Lett. 122, 026102 (2019).
Libbrecht, K. G. & Rickerby, M. E. Measurements of surface attachment kinetics for faceted ice crystal growth. J. Cryst. Growth 377, 1–8 (2013).
Espinosa, J. R., Vega, C. & Sanz, E. Ice–Water interfacial free energy for the TIP4P, TIP4P/2005, TIP4P/Ice, and mw models as obtained from the mold integration technique. J. Phys. Chem. C 120, 8068–8075 (2016).
Hobbs, P. V. Ice Physics (Oxford University Press, 1974).
Kardar, M., Parisi, G. & Zhang, Y.-C. Dynamic scaling of growing interfaces. Phys. Rev. Lett. 56, 889–892 (1986).
Pimpinelli, A. & Villain, J. Physics of Crystal Growth (Cambridge University Press, Cambridge, 1998).
Pagnani, A. & Parisi, G. Numerical estimate of the kardar-parisi-zhang universality class in (2+1) dimensions. Phys. Rev. E 92, 010101 (2015).
Karim, O. A. & Haymet, A. D. J. The ice/water interface: a molecular dynamics simulation study. J. Chem. Phys. 89, 6889–6896 (1988).
Mukherjee, S. & Bagchi, B. Entropic origin of the attenuated width of the Ice–Water interface. J. Phys. Chem. C 124, 7334–7340 (2020).
Mikheev, L. & Chernov, A. Mobility of a diffuse simple crystal-melt interface. J. Cryst. Growth 112, 591–596 (1991).
Murata, K.-I., Asakawa, H., Nagashima, K., Furukawa, Y. & Sazaki, G. In situ determination of surface tension-to-shear viscosity ratio for quasiliquid layers on ice crystal surfaces. Phys. Rev. Lett. 115, 256103 (2015).
Espinosa, J. R., Navarro, C., Sanz, E., Valeriani, C. & Vega, C. On the time required to freeze water. J. Chem. Phys. 145, 211922 (2016).
Montero de Hijes, P., Espinosa, J. R., Vega, C. & Sanz, E. Ice growth rate: Temperature dependence and effect of heat dissipation. J. Chem. Phys. 151, 044509 (2019).
Saito, Y. Statistical Physics of Crystal Growth (WORLD SCIENTIFIC, 1996). https://www.worldscientific.com/doi/abs/10.1142/3261. https://www.worldscientific.com/doi/pdf/10.1142/3261.
Espinosa, J. R., Sanz, E., Valeriani, C. & Vega, C. Homogeneous ice nucleation evaluated for several water models. J. Chem. Phys. 141, 18C529 (2014).
Molinero, V. & Moore, E. B. Water modeled as an intermediate element between carbon and silicon. J. Phys. Chem. B 113, 4008–4016 (2009).
Bolhuis, P. G., Chandler, D., Dellago, C. & Geissler, P. L. Transition path sampling: throwing ropes over rough mountain passes, in the dark. Annu. Rev. Phys. Chem. 53, 291–318 (2002).
Fitzner, M., Sosso, G. C., Cox, S. J. & Michaelides, A. The many faces of heterogeneous ice nucleation: Interplay between surface morphology and hydrophobicity. J. Am. Chem. Soc. 137, 13658–13669 (2015).
Yokoyama, E. et al. Measurements of growth rates of an ice crystal from supercooled heavy water under microgravity conditions: Basal face growth rate and tip velocity of a dendrite. J. Phys. Chem. B 115, 8739–8745 (2011).
Matsumoto, M., Saito, S. S. & Ohmine, I. Molecular dynamics simulation of the ice nucleation and growth process leading to water freezing. Nature 416, 409–413 (2002).
Moore, E. B. & Molinero, V. Structural transformation in supercooled water controls the crystallization rate of ice. Nature 479, 506–508 (2011).
Fitzner, M., Sosso, G. C., Cox, S. J. & Michaelides, A. Ice is born in low-mobility regions of supercooled liquid water. Proc. Natl. Acad. Sci. USA 116, 2009–2014 (2019).
Kawasaki, T. & Tanaka, H. Formation of a crystal nucleus from liquid. Proc. Natl. Acad. Sci. USA 107, 14036–14041 (2010).
Tan, P., Xu, N. & Xu, L. Visualizing kinetic pathways of homogeneous nucleation in colloidal crystallization. Nat. Phys. 10, 73–79 (2013).
Gao, Q. et al. Fast crystal growth at ultra-low temperatures. Nat. Mater. 20, 1431–1439 (2021).
Sun, G., Xu, J. & Harrowell, P. The mechanism of the ultrafast crystal growth of pure metals from their melts. Nat. Mater. 17, 881–886 (2018).
Maruyama, M., Kishimoto, Y. & Sawada, T. Optical study of roughening transition on ice ih (10\(\bar{1}\)0) planes under pressure. J. Cryst. Growth 172, 521–527 (1997).
Nozières, P. Shape and Gowth of Crystals, book section 1, 1–154 (Cambridge University Press, 1992).
Abascal, J. L. F., Sanz, E., García Fernández, R. & Vega, C. A potential model for the study of ices and amorphous water: TIP4P/Ice. J. Chem. Phys. 122, 234511 (2005).
Fujiwara, K., Chuang, L.-C. & Maeda, K. Dynamics at crystal/melt interface during solidification of multicrystalline silicon. High Temp. Mater. Processes 41, 31–47 (2022).
Cullis, A., Chew, N., Webber, H. & Smith, D. J. Orientation dependence of high speed silicon crystal growth from the melt. J. Cryst. Growth 68, 624–638 (1984).
Buta, D., Asta, M. & Hoyt, J. J. Kinetic coefficient of steps at the si(111) crystal-melt interface from molecular dynamics simulations. J. Chem. Phys. 127, 074703 (2007).
Nishizawa, H., Hori, F. & Oshima, R. In-situ hrtem observation of the melting-crystallization process of silicon. J. Cryst. Growth 236, 51–58 (2002).
Meister, K. et al. Long-range protein-water dynamics in hyperactive insect antifreeze proteins. Proc. Natl. Acad. Sci. USA 110, 1617–1622 (2013).
Ebbinghaus, S. et al. Antifreeze glycoprotein activity correlates with long-range protein-water dynamics. J. Am. Chem. Soc. 132, 12210–12211 (2010).
Hudait, A. et al. Preordering of water is not needed for ice recognition by hyperactive antifreeze proteins. Proc. Natl. Acad. Sci. USA 115, 8266–8271 (2018).
Biswas, A. D., Barone, V. & Daidone, I. High water density at Non-Ice-Binding surfaces contributes to the hyperactivity of antifreeze proteins. J. Phys. Chem. Lett. 12, 8777–8783 (2021).
Meister, K. et al. Investigation of the Ice-Binding site of an insect antifreeze protein using Sum-Frequency generation spectroscopy. J. Phys. Chem. Lett. 6, 1162–1167 (2015).
Jacobson, L. C., Hujo, W. & Molinero, V. Thermodynamic stability and growth of guest-free clathrate hydrates: a low-density crystal phase of water. J. Phys. Chem. B 113, 10298–10307 (2009).
Mochizuki, K., Qiu, Y. & Molinero, V. Promotion of homogeneous ice nucleation by soluble molecules. J. Am. Chem. Soc. 139, 17003–17006 (2017).
Lupi, L. et al. Role of stacking disorder in ice nucleation. Nature 551, 218–222 (2017).
Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comp. Phys. 117, 1–19 (1995).
Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 81, 511–519 (1984).
Hoover, W. G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 31, 1695–1697 (1985).
Matsumoto, M., Yagasaki, T. & Tanaka, H. GenIce: Hydrogen-Disordered ice generator. J. Comput. Chem. 39, 61–64 (2018).
García Fernández, R., Abascal, J. L. F. & Vega, C. The melting point of ice ih for common water models calculated from direct coexistence of the solid-liquid interface. J. Chem. Phys. 124, 144506 (2006).
Sanz, E. et al. Homogeneous ice nucleation at moderate supercooling from molecular simulation. J. Am. Chem. Soc. 135, 15008–15017 (2013).
Acknowledgements
This work was supported by the Startup Foundation for Hundred-Talent Program of Zhejiang University and by National Natural Science Foundation of China (Grant Nos. 22250610195 and 22273083). Murata also acknowledges JSPS KAKENHI Grant Numbers JP21H01824 from the Japan Society of the Promotion of Science (JSPS).
Author information
Authors and Affiliations
Contributions
X.Z. performed MD simulations. K. Mochizuki analyzed the data. K. Mochizuki and K. Murata designed the research and wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Materials thanks Luis MacDowell and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary handling editor: Aldo Isidori. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mochizuki, K., Murata, Ki. & Zhang, X. Microscopic ordering of supercooled water on the ice basal face. Commun Mater 4, 33 (2023). https://doi.org/10.1038/s43246-023-00359-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-023-00359-2
This article is cited by
-
In-layer inhomogeneity of molecular dynamics in quasi-liquid layers of ice
Communications Chemistry (2024)
-
Fast crystal growth of ice VII owing to the decoupling of translational and rotational ordering
Communications Physics (2023)