Abstract
Some oxide nanostructures have recently been shown to host quantum well (QW) states that are promising for quantum device applications by designing the wave function of their strongly correlated electrons. However, it is unclear why QW states only appear in certain oxides, limiting the possibilities of wave-function engineering. Here, we demonstrate that the electron mean free path λ is one of the essential conditions to form standing waves of strongly correlated electrons in oxide nanostructures. We have investigated the QW states formed in SrTi1–xVxO3 (STVO) ultrathin films using in situ angle-resolved photoemission spectroscopy. The controllability of λ in STVO while maintaining an atomically flat surface and chemically abrupt interface enables us to examine the evolution of QW states with varying λ. A detailed analysis reveals that the intensity of the QW states is almost linearly correlated to λ and may disappear at the Ioffe–Regel criterion, corresponding to the nearest neighbor inter-vanadium distance in STVO. Our findings provide design guidelines for creating and controlling novel quantum phenomena in oxide nanostructures.
Similar content being viewed by others
Introduction
Quantum confinement of strongly correlated electrons in oxide artificial structures has provided an opportunity to better understand the fundamental low-dimensional phenomena of strongly correlated electron systems and attracted considerable interest for its potential technological application in future oxide electronics1. Dimensionality reduction changes the complex interaction among the spin, charge, and orbital degrees of freedom of the correlated electrons, yielding unusual quantum phenomena2,3,4,5. Recently, quantum-well (QW) states have been clearly observed using angle-resolved photoemission spectroscopy (ARPES) for some QW structures of correlated conductive oxides such as SrVO36,7,8,9,10 and IrO211, as well as for two-dimensional electron gas states in oxide semiconductors such as SrTiO312,13,14,15,16, KTaO317,18, and anatase TiO219,20,21. Such use of quantum confinement to form low-dimensional electronic states provides a foundation for studying the behavior of strongly correlated electrons under reduced dimensions, and for controlling the extraordinary physical properties of strongly correlated oxides by designing the wave function of their strongly correlated electrons9.
However, quantized states have not been observed in all conductive correlated oxides. For example, quantized states did not appear in QW structures (ultrathin films) of LaNiO322,23,24,25, La1–xSrxMnO326, SrRuO327,28, and SrIrO329,30,31, even though they appear in band-structure calculations where they show a subband splitting that should be readily resolved in the experiment32. Thus, it is essential to determine the conditions that result in realizing the QW states in strongly correlated oxides. Since the QW states are caused by the standing waves of electrons confined in space by a potential well, which are characterized by the quantum number n, that is, the number of half-wavelengths that span the well, the appearance of QW states may closely be related to the mean free path λ of the electrons, as well as the reflectivity of the electrons at the potential walls (surface and interface). Assuming high reflectivity at the surface and interface, the formation of the standing waves may strongly depend on the relationship between λ and the width of QW structure (layer thickness) L; when λ is comparable to L, the standing waves (QW states) are formed25.
Recent ARPES studies on LaNiO3 ultrathin films demonstrated the formation of two-dimensional electronic states (i.e., no kz dependence of the band dispersions was observed) and the occurrence of the dimensional crossover-driven metal-insulator transition at a critical film thickness of a few monolayers (MLs)22,23,24,25. However, although these behaviors at the lower dimension are similar to the case of SrVO38, no QW states exist in the LaNiO3 ultrathin films. Cappelli et al. reported that λ was steeply reduced with decreasing L from 5 ML and argued that the reduction of λ explains the puzzling absence of QW states reported in all previous ARPES experiments on LaNiO3 ultrathin films25. However, a similar reduction of λ has also been observed in SrVO3 where the formation of QW states is clearly observed8, implying that the absence of QW states in LaNiO3 originates from other factors, such as the possible roughness and disorder at the surface and interface. Thus, to clarify the condition for forming QW states in conductive oxides, further research is required. In particular, systematic control of λ, while maintaining the reflectivity at the potential wall and L, is necessary to resolve the issue.
In this study, we selected SrTi1–xVxO3 (STVO) ultrathin films epitaxially grown on Nb-doped SrTiO3 (Nb:STO) to investigate the relationship between λ and the appearance of quantization states. Our previous work has demonstrated that λ can be linearly controlled by varying x in STVO33. Furthermore, STVO in film form can be fabricated with an atomically flat and well-ordered surface34,35,36 and a chemically abrupt STVO/Nb:STO interface37,38, each of which is a precondition for quantum confinement (see Supplementary Note 1). By adopting the STVO QW structures, we examined the relationship between QW formation and λ, while the fundamental structural factors remain fixed. We performed in situ ARPES measurements of QW states formed at STVO ultrathin films. With the reduction of x (λ), the second quantization states (n = 2) become weaker and eventually almost vanish at x = 0.6, whereas the first quantization states (n = 1) with a bulk-like character remain to the end. The detailed analysis reveals the close relationship between λ and the intensity of quantization states, demonstrating that λ plays one of the essential roles in forming quantization states in correlated conductive oxides.
Results
QW states in λ-controlled STVO QW structures
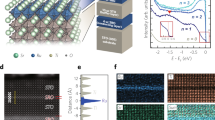
Figure 1 shows the ARPES intensity map for STVO ultrathin films for x = 0.6–1.0 taken along the Γ–X direction along with the momentum distribution curve (MDC) at the Fermi level (EF) and the energy distribution curve (EDC) at the Γ point. The thickness of STVO ultrathin films (width of QW structures) is 6 ML. According to the band-structure calculations39,40, the band structures of SrVO3 (STVO with x = 1.0) along the Γ–X direction consist of three bands: two degenerate parabolic dispersions derived from the dxy and dzx states and a nearly nondispersive dyz state. In the QW structure, only dyz and dzx states are subject to quantization owing to the orbital-selective quantization reflecting the anisotropic orbital nature of V 3d t2g states6,7. Here, the ARPES images consist of only the dzx bands of V 3d t2g states in the present experimental geometry (see Supplementary Fig. 2), owing to the dipole selection rules for the light polarizations and each orbital symmetry with respect to the mirror plane41. Since the extraction of only the dzx-derived subbands is optimal for quantitative analysis of QW formation, we utilized this polarization geometry throughout the present study.
The MDCs at EF with an energy window of ±25 meV are shown in the respective ARPES images (top panel), while EDCs at the Γ point [along the center line (kx = 0)] are on the right-hand side of each image. The intensity of n = 1 and n = 2 is reversed on the left- and right-hand sides with respect to the centerline owing to pronounced matrix-element effects. The red and orange arrows in the EDCs indicate the n = 1 and n = 2 quantization energies (bottom energies of subbands), respectively. In the MDCs, the fitting results for n = 1, n = 2, and total are overlaid by red, orange, and blue curves, respectively (see Supplementary Fig. 6). It should be noted that the ARPES images consist of only the dzx bands of V 3d t2g states in the present experimental geometry (see Supplementary Note 2) owing to the dipole selection rules for the light polarizations and each orbital symmetry with respect to the mirror plane41.
As can be seen in Fig. 1, clear parabolic subband dispersions are observed for SrVO3. The subbands in SrVO3 correspond to n = 1 (490 meV) and 2 (230 meV) from the bottom. It should be noted that the spectral intensity of each quantized band significantly depends on photon energy hν6,7, although the subband dispersions themselves remain unchanged owing to the low-dimensional character of the quantized states (see Supplementary Figs. 3 and 4). Since the intensity of n = 2 is maximum at hν = 82 eV (see Supplementary Fig. 3), the ARPES data acquired at hν = 82 eV are used in the detailed analysis discussed as follows. As x decreases, the bottom energy of subbands approaches EF, reflecting the hole doping associated with the chemical substitution of V (d1) with Ti (d0), and the Fermi momentum kF consequently decreases. Each quantization state gradually shifts by approximately 50 meV per x = 0.1 from x = 1.0 to 0.6, although the parabolic subband dispersion itself remains almost unchanged. The rigid-band-like behavior of V 3d states in the QW structures is consistent with that of STVO thick films33, demonstrating that the fundamental electronic structure of STVO QW structures is described by the framework of the rigid-band model as in the case of STVO thick films.
In contrast to the rigid-bandlike behavior in the subband dispersion, the relative intensity of n = 2 to n = 1 states significantly weakens with decreasing x, and n = 2 states seem to almost disappear at x = 0.6, although the n = 1 states are still visible in the ARPES images. The steep suppression in the n = 2 states relative to n = 1 is highlighted in Fig. 2, where the ARPES spectra at the Γ point are plotted aligned at the peak position of n = 1 (see also Supplementary Fig. 5). Meanwhile, in the MDC at EF shown in the top panels of Fig. 1, the peak width significantly increases with reducing x. Since the MDC width (Δk) corresponds to 1/λ42, the broadening of the MDC peak indicates that the λ value decreases with decreasing x (see Supplementary Figs. 6 and 7), as in the case of STVO films33. These results suggest that the observed suppression in the n = 2 states may originate from the reduction of λ.
a ARPES spectra at the Γ point for STVO QWs. The data are the same as the EDCs shown in Fig. 1, but are plotted aligned at the peak position of n = 1. b Line-shape analysis of the EDCs for STVO QW states. The EDCs have been fitted to a combination of two Voigt functions corresponding to n = 1 (red hatched) and n = 2 (orange hatched) with a smooth background (dashed line), multiplied by the Fermi-Dirac function.
Relationship between QW states and λ
In order to see the spectral behavior in further detail, we extract the QW states of n = 2 and n = 1 from the EDCs at the Γ point, as shown in Fig. 2b. Each EDC is fitted by the combination of Voigt functions corresponding to the respective subbands with a smooth background, multiplied by the Fermi-Dirac function. For the background, we used a function roughly representing a momentum-independent background that was determined by integrating the EDCs outside the Fermi surface (see Supplementary Figs. 8–10). Such backgrounds may result from angle-integrated spectral weight due to imperfections of the film surface and the broad tail of intensity of the V-3d incoherent states located in the energy range of 1.0–1.5 eV8,22. It should be noted that since there is no reliable regression function for ARPES spectra, Voigt functions were used for the EDC fitting, but the Gaussian width was restricted to be above the experimental energy resolution of 25 meV. It can be observed from Fig. 2b that the line shape of the EDCs is well reproduced by the present curve fitting, suggesting the essential validity of the present curve fitting.
Subsequently, to address the relationship between the spectral intensity suppression and the reduction of λ, we plot in Fig. 3 the relative intensity (area under the curve) of n = 2 to n = 1 as a function of λ for n = 1 (λn=1) and n = 2 (λn=2) that are estimated from the MDCs at EF (see Fig. 1 and Supplementary Figs. 6 and 7). Here, we explain why the relative intensity of n = 2 to n = 1 can be used as an indicator for the suppression of QW states (standing waves). In the n = 1 state, the half-wavelength of an envelope function spans the well. The resultant n = 1 wave function is expected to mimic a bulk-like wave function (no standing wave), where a uniform traveling wave exists at the Γ point (k = 0). In this situation, the spectral intensity of n = 1 is nearly indistinguishable from that of the bulk-like electronic state (the electronic state due to the traveling wave). In fact, the n = 1 subband in the STVO QW structure is nearly identical to the band dispersion of bulk (see Supplementary Figs. 11 and 12). This is consistent with the previous report that the observed band structures for LaNiO3 ultrathin films, where no quantized states are observed, are in good agreement with those of bulk22,23,24,25. Since the intensity of “n = 1” observed in the ARPES spectra, i.e., the sum of the QW intensity due to the envelope function and the intensity due to the traveling wave, must remain constant regardless of the quantized state formation, the relative intensity of n = 2 to “n = 1” is a good indicator for evaluating the rate of formation of the quantized levels. Furthermore, the bulk-like behavior of n = 1 states suggests that it is reasonable to consider λn=1 as λ in “bulk” STVO.
The relative intensity (area under the curve) of n = 2 to n = 1 states is plotted as a function of λn=1 (red-filled circles) and λn=2 (orange-filled circles). The values of λ are estimated from the respective MDCs at EF. The Ioffe–Regel criterion (λIFmin = a) for STVO is indicated by a dotted line. The results of a line fit for the data are shown by dashed lines. The plot indicates a proportional relationship between the QW intensity and λ, and the disappearance of QW intensity around λIFmin. The error bars reflect the uncertainties in the curve fitting.
It can be observed from Fig. 3 that the relative intensity of n = 2 to n = 1 is proportional to λ, clearly demonstrating a proportional relationship between the formation of QW states and λ. In Fig. 3, the Ioffe–Regel (IR) criterion (λIFmin)43,44 for STVO that corresponds to the interatomic spacing a of STVO (λIFmin = 3.82 – 3.91 Å) is overlaid. The line fit for the data (dashed line) suggests that the QW states may vanish around the λIFmin, implying that the condition of QW-state formation is responsible for the IR criterion (λ > a). These results indicate that λ plays a decisive role in the formation of QW states.
Discussion
The physical meaning of λIFmin is that λ is equal to a (the nearest neighbor V–V distance in STVO in the present case)43,44. Thus, for λ > λIFmin, coherent quasiparticle conductivity is preserved, and the system exhibits metallic conductivity, whereas it shows insulating (bad metallic) behavior for λ < λIFmin, even in the existence of density of states at EF. In fact, STVO undergoes a composition-driven MIT at a critical composition of x = 0.4–0.6, where λ becomes smaller than λIFmin owing to the reduction in λ induced by the strong disorder due to the chemical substitution of V ions with Ti ions33. Furthermore, the intensity of the quasiparticle peaks in the ARPES spectra of STVO decreases significantly with decreasing λ. Such spectral behavior was also observed for the present STVO QW structures (see Supplementary Fig. 10). Since the coherent quasiparticles cannot survive at λ < λIFmin 43,44, the formation of QW states (standing waves) should disappear. In other words, the QW states reflect the coherent phenomena of conduction electrons. Thus, it is reasonable that the intensity of the QW states disappears at λIFmin as a result of the depletion of coherent quasiparticle states.
Finally, we briefly discuss the origin of the puzzling absence of QW states reported in all previous ARPES experiments on LaNiO3 ultrathin films22,23,24,25, although QW states appear in band structure calculations32. LaNiO3 with a = 3.84 Å is a paramagnetic metal similar to SrVO345 and exhibits better electrical conductivity at low temperatures than SrVO322,25,33. Indeed, λ of LaNiO3 ultrathin films (QW structures) ranges from 20 to 35 Å in the thickness range of 4–7 ML25, which is larger than that of the STVO 6-ML QW (λn=1 = 5.1–18.5 Å and λn=2 = 3.5–9.1 Å for x = 0.6–1.0). If λ is the only condition for the formation of a quantized state, quantization should also occur at LaNiO3 (Supplementary Discussion). Although the origin of the absence of QW states in LaNiO3 is not clear at the moment, one of the most likely scenarios for the lack of QW states in LaNiO3 is the low reflectivity at the surface and interface.
Another condition for the formation of standing waves is high reflectivity at the surface and interface. To satisfy this condition, a steep and uniform potential barrier must be formed at the surface and interface. In bulk perovskite nickelates, it is well known that their physical properties are very sensitive to the Ni-O-Ni bond angle and that the reduction of the bond angle causes the transition from metal to insulator45. A recent scanning transmission electron microscopic study on LaNiO3/LaAlO3 revealed that the bond angle was significantly modulated in the interface and surface regions owing to compressive strain (–1.3%) and relaxation from lattice mismatch, respectively32. The existence of such transient layers at the boundaries compromises the sharpness of the potential wall and consequently hinders the formation of quantization states because of a decrease in reflectivity. In addition, roughness and disorder at the surface and interface induce the inhomogeneities in reflectance at the boundaries. The resultant spatial randomness in the phase shift of wave reflection may be responsible for the suppression of standing wave formation (see Supplementary Fig. 13). Furthermore, the difference in the local electronic states due to the inhomogeneities may also hinder the formation of standing waves.
In sharp contrast to the nickelate case, the physical properties of SrVO3 are not very sensitive to changes in bond angle and structural modulation46. The metallic states in SrVO3 are robust to the change in the V-O-V bond angle; SrVO3 with Ca substitution (Ca1–xSrxVO3) remains metallic in the entire x range, in which the V-O-V bond angle is changed from 180° to 160°46. Furthermore, the lattice mismatch between SrVO3 and SrTiO3 is tensile (+1.6%), leading to no change in the bond angle in SrVO3 (180°) and resultant much less randomness at the interface. In fact, the previous ARPES on SrTiO3/SrVO3/SrTiO3 QW structures revealed that nearly ideal quantum confinement is achieved at the interface with SrTiO3 by analyzing the phase shifts38. Although complex interactions of strongly correlated electrons at the surfaces and interfaces47,48,49,50,51 must be considered, these facts suggest that the reflectivity of electrons at surfaces and interfaces is crucial for the presence or absence of quantization of strongly correlated electrons in QW structures. To clarify the issue, further systematic investigation is required. In particular, the influence of potential-barrier degradation on the QW states should be examined. In addition, it should be kept in mind that the effects of other parameters, such as electron density, cannot be ruled out in the present study. In order to clarify the quantization conditions of strongly correlated electrons, theoretical calculations incorporating such effects, as well as the complex interactions of strongly correlated electrons, are desired. Such calculations are certainly necessary to understand the puzzling absence of QW states in some oxides, but this issue remains to be resolved.
Conclusion
In summary, we have performed in situ ARPES on STVO QW structures epitaxially grown on the lattice-matched SrTiO3 substrates. Using the linear controllability of λ in STVO films while maintaining an atomically flat surface and a chemically abrupt interface, we investigated the change of QW states as a function of λ. The detailed analysis reveals the close relationship between λ and the formation of standing waves in STVO QW, demonstrating that λ plays one of the essential roles in forming quantization states in correlated conductive oxides. The findings of this study are expected to contribute to the understanding of the puzzling phenomena occurring in the QW structure of strongly correlated oxides and the quest for novel quantum phenomena by designing the wave function of their strongly correlated electrons.
Methods
Laser molecular-beam epitaxy
Digitally controlled STVO ultrathin films (QW structures) were grown on the atomically flat (001) surfaces of TiO2-terminated Nb:STO substrates in a laser molecular-beam epitaxy chamber connected to an ARPES system at BL-2A MUSASHI of the Photon Factory (PF)9,52. During the growth, the thickness was precisely and digitally controlled on the atomic scale by monitoring the intensity oscillation of reflective high-energy electron diffraction spots. The growth condition details are described in earlier reports6,7,8,9,33,37,38, and the characterizations of the grown films are provided in Supplementary Note 1. It should be noted that the characterization results for the STVO films were essentially identical to those reported in a previous study33.
In situ angle-resolved photoemission spectroscopy
After growth, the QW structures were transferred to the ARPES chamber under an ultrahigh vacuum of 10−10 Torr to avoid the degradation of the sample surfaces on exposure to air. The ARPES experiments were conducted in situ under an ultrahigh vacuum of 10−11 Torr at a temperature of 20 K using horizontal linear polarization of the incident light (see Supplementary Fig. 2). The energy and angular resolutions were set to approximately 25 meV and 0.3°, respectively. The EF of the samples was calibrated by measuring a gold foil that was electrically connected to the samples. Details of the ARPES measurement setups are described in a previous study9. The surface structure and cleanliness of the STVO QW structures were examined by low-energy electron diffraction and core-level photoemission measurements immediately before the ARPES measurements. We have carefully characterized the thickness of the STVO layers, and the chemical abruptness of the STVO/STO interfaces, by analyzing the relative intensities of the relevant core levels. Because it is known that SrTiO3 and SrVO3 host oxygen vacancies upon irradiation with light and exhibit signature spectral features near EF12,13,14,15,16,53, we paid special attention to the possibility of spectral changes induced by light irradiation. Owing to the relatively large spot size (200 μm × 500 μm) of the synchrotron light at PF, there were no detectable spectral differences before and after 70 min of synchrotron-light irradiation (Supplementary Fig. 14). Nonetheless, we changed the location of the light spot within each sample every 60 min during the spectroscopic measurements to avoid possible irradiation-induced effects.
Data availability
All data supporting the key findings of this study are available within the article and its Supplementary Information. All raw data generated during the current study are available from the corresponding author on reasonable request.
Code availability
All the codes to analyze the experimental data in this study are available from the corresponding author upon reasonable request.
References
Hwang, H. Y. et al. Emergent phenomena at oxide interfaces. Nat. Mater. 11, 103–113 (2012).
Takagi, H. & Hwang, H. Y. An emergent change of phase for electronics. Science 327, 1601–1602 (2010).
Mannhart, J. & Schlom, D. G. Oxide interfaces—an opportunity for electronics. Science 327, 1607–1611 (2010).
Tokura, Y., Kawasaki, M. & Nagaosa, N. Emergent functions of quantum materials. Nat. Phys. 13, 1056–1068 (2017).
Imada, M., Fujimori, A. & Tokura, Y. Metal-insulator transitions. Rev. Mod. Phys. 70, 1039–1263 (1998).
Yoshimatsu, K. et al. Metallic quantum well states in artificial structures of strongly correlated oxide. Science 333, 319–322 (2011).
Kobayashi, M. et al. Origin of the anomalous mass renormalization in metallic quantum well states of strongly correlated oxide SrVO3. Phys. Rev. Lett. 115, 076801 (2015).
Kobayashi, M. et al. Emergence of quantum critical behavior in metallic quantum-well states of strongly correlated oxides. Sci. Rep. 7, 16621 (2017).
Yukawa, R. et al. Resonant tunneling driven metal-insulator transition in double quantum-well structures of strongly correlated oxide. Nat. Commun. 12, 7070 (2021).
Gabel, J. et al. Toward functionalized ultrathin oxide films: the impact of surface apical oxygen. Adv. Electron. Mater. 8, 2101006 (2022).
Kawasaki, J. K. et al. Engineering carrier effective masses in ultrathin quantum wells of IrO2. Phys. Rev. Lett. 121, 176802 (2018).
Santander-Syro, A. F. et al. Two-dimensional electron gas with universal subbands at the surface of SrTiO3. Nature 469, 189–193 (2011).
Meevasana, W. et al. Creation and control of a two-dimensional electron liquid at the bare SrTiO3 surface. Nat. Mater. 10, 114–118 (2011).
King, P. D. C. et al. Quasiparticle dynamics and spin–orbital texture of the SrTiO3 two-dimensional electron gas. Nat. Commun. 5, 3414 (2014).
Plumb, N. C. et al. Mixed dimensionality of confined conducting electrons in the surface region of SrTiO3. Phys. Rev. Lett. 113, 086801 (2014).
Wang, Z. et al. Tailoring the nature and strength of electron–phonon interactions in the SrTiO3(001) 2D electron liquid. Nat. Mater. 15, 835–839 (2016).
King, P. D. C. et al. Subband structure of a two-dimensional electron gas formed at the polar surface of the strong spin-orbit perovskite KTaO3. Phys. Rev. Lett. 108, 117602 (2012).
Santander-Syro, A. F. et al. Orbital symmetry reconstruction and strong mass renormalization in the two-dimensional electron gas at the surface of KTaO3. Phys. Rev. B 86, 121107 (2012).
Moser, S. et al. Tunable polaronic conduction in anatase TiO2. Phys. Rev. Lett. 110, 196403 (2013).
Rödel, T. C. et al. Engineering two-dimensional electron gases at the (001) and (101) surfaces of TiO2 anatase using light. Phys. Rev. B 92, 041106 (2015).
Wang, Z. et al. Atomically precise lateral modulation of a two-dimensional electron liquid in anatase TiO2 thin films. Nano Lett. 17, 2561–2567 (2017).
King, P. D. C. et al. Atomic-scale control of competing electronic phases in ultrathin LaNiO3. Nat. Nanotechnol. 9, 443–447 (2014).
Yoo, H. K. et al. Latent instabilities in metallic LaNiO3 films by strain control of Fermi-surface topology. Sci. Rep. 5, 8746 (2015).
Yoo, H. K. et al. Thickness-dependent electronic structure in ultrathin LaNiO3 films under tensile strain. Phys. Rev. B 93, 035141 (2016).
Cappelli, E. et al. A laser-ARPES study of LaNiO3 thin films grown by sputter deposition. APL Mater. 8, 051102 (2020).
Tebano, A. et al. Preferential occupation of interface bands in La2/3Sr1/3MnO3 films as seen via angle-resolved photoemission. Phys. Rev. B 82, 214407 (2010).
Sohn, B. et al. Observation of metallic electronic structure in a single-atomic-layer oxide. Nat. Commun. 12, 6171 (2021).
Sohn, B. et al. Sign-tunable anomalous Hall effect induced by two-dimensional symmetry-protected nodal structures in ferromagnetic perovskite thin films. Nat. Mater. 20, 1643–1649 (2021).
Nie, Y. F. et al. Interplay of spin-orbit interactions, dimensionality, and octahedral rotations in semimetallic SrIrO3. Phys. Rev. Lett. 114, 016401 (2015).
Schütz, P. et al. Dimensionality-driven metal-insulator transition in spin-orbit-coupled SrIrO3. Phys. Rev. Lett. 119, 256404 (2017).
Kong, S. et al. Isostructural metal-insulator transition driven by dimensional-crossover in SrIrO3 heterostructures. Phys. Rev. Mater. 6, 034404 (2022).
Fowlie, J. et al. Conductivity and local structure of LaNiO3 thin films. Adv. Mater. 29, 1605197 (2017).
Kanda, T. et al. Electronic structure of SrTi1-xVxO3 films studied by in situ photoemission spectroscopy: screening for a transparent electrode material. Phys. Rev. B 104, 115121 (2021).
Okada, Y. et al. Quasiparticle interference on cubic perovskite oxide surfaces. Phys. Rev. Lett. 119, 086801 (2017).
Oka, H., Okada, Y., Hitosugi, T. & Fukumura, T. Two distinct surface terminations of SrVO3 (001) ultrathin films as an influential factor on metallicity. Appl. Phys. Lett. 113, 171601 (2018).
Oka, H. et al. Width-induced metal–insulator transition in SrVO3 lateral nanowires spontaneously formed on the ultrathin film. Appl. Phys. Lett. 117, 051603 (2020).
Yoshimatsu, K. et al. Dimensional-crossover-driven metal-insulator transition in SrVO3 ultrathin films. Phys. Rev. Lett. 104, 147601 (2010).
Yoshimatsu, K. et al. Determination of the surface and interface phase shifts in metallic quantum well structures of perovskite oxides. Phys. Rev. B 88, 115308 (2013).
Pavarini, E., Yamasaki, A., Nuss, J. & Andersen, O. K. How chemistry controls electron localization in 3d1 perovskites: a Wannier-function study. New J. Phys. 7, 188–188 (2005).
Zhong, Z., Zhang, Q. & Held, K. Quantum confinement in perovskite oxide heterostructures: tight binding instead of a nearly free electron picture. Phys. Rev. B 88, 125401 (2013).
Hüfner, S. Photoelectron Spectroscopy (Springer Science & Business Media, 1995).
Valla, T. et al. Evidence for quantum critical behavior in the optimally doped cuprate Bi2Sr2CaCu2O8+δ. Science 285, 2110–2113 (1999).
Gurvitch, M. Ioffe-Regel criterion and resistivity of metals. Phys. Rev. B 24, 7404–7407 (1981).
Hussey, N. E., Takenaka, K. & Takagi, H. Universality of the Mott–Ioffe–Regel limit in metals. Philos. Mag. 84, 2847–2864 (2004).
Torrance, J. B., Lacorre, P., Nazzal, A. I., Ansaldo, E. J. & Niedermayer, C. H. Systematic study of insulator-metal transitions in perovskites RNiO3 (R=Pr, Nd, Sm, Eu) due to closing of charge-transfer gap. Phys. Rev. B 45, 8209–8212 (1992).
Inoue, I. H., Goto, O., Makino, H., Hussey, N. E. & Ishikawa, M. Bandwidth control in a perovskite-type 3d1-correlated metal Ca1-xSrxVO3. I. Evolution of the electronic properties and effective mass. Phys. Rev. B 58, 4372–4383 (1998).
Okamoto, S. Anomalous mass enhancement in strongly correlated quantum wells. Phys. Rev. B 84, 201305 (2011).
Zhong, Z. et al. Electronics with correlated oxides: SrVO3/SrTiO3 as a mott transistor. Phys. Rev. Lett. 114, 246401 (2015).
Zhong, Z. & Hansmann, P. Band alignment and charge transfer in complex oxide interfaces. Phys. Rev. X 7, 011023 (2017).
James, A. D. N., Aichhorn, M. & Laverock, J. Quantum confinement induced metal-insulator transition in strongly correlated quantum wells of SrVO3 superlattices. Phys. Rev. Res. 3, 023149 (2021).
Domínguez, C. et al. Length scales of interfacial coupling between metal and insulator phases in oxides. Nat. Mater. 19, 1182–1187 (2020).
Horiba, K. et al. A high-resolution synchrotron-radiation angle-resolved photoemission spectrometer with in situ oxide thin film growth capability. Rev. Sci. Instrum. 74, 3406–3412 (2003).
Backes, S. et al. Hubbard band versus oxygen vacancy states in the correlated electron metal SrVO3. Phys. Rev. B 94, 241110 (2016).
Acknowledgements
The authors are very grateful to H. Suzuki and T. Komeda for their helpful discussions and acknowledge X. Cheng and T. T. Kim for their support during the experiments at KEK-PF. The authors also thank R. Yukawa for sharing his program for analyzing ARPES data, with us and for his assistance with the data analysis. This work was financially supported by a Grant-in-Aid for Scientific Research (Nos. 16H02115, 16KK0107, 20KK0117, 22H01947, and 22H01948) from the Japan Society for the Promotion of Science (JSPS), CREST (JPMJCR18T1) from the Japan Science and Technology Agency (JST), and the MEXT Element Strategy Initiative to Form Core Research Center (JPMXP0112101001). N.H. acknowledges the financial support from the Chemistry Personnel Cultivation Program of the Japan Chemical Industry Association. T.K. acknowledges the financial support from the Division for Interdisciplinary Advanced Research and Education at Tohoku University. The work performed at KEK-PF was approved by the Program Advisory Committee (proposals 2022T001 and 2021S2-002) at the Institute of Materials Structure Science, KEK.
Author information
Authors and Affiliations
Contributions
The samples were grown and characterized by T.K., D.S., A.W., and R.H. ARPES measurements were performed by T.K., D.S., A.W., R.H., Y.M., and N.H.; M.K. shared the infrastructure at PF and assisted with the measurements. T.K. and H.K. analyzed the ARPES data. T.K., D.S., K.Y., and H.K. contributed to the interpretation. T.K. and H.K. wrote the paper with input and discussion from all the co-authors. H.K. devised the project and was responsible for its overall planning and direction. All authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Materials thanks the anonymous reviewers for their contribution to the peer review of this work. Primary Handling Editor: Aldo Isidori. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kanda, T., Shiga, D., Wada, A. et al. Quantization condition of strongly correlated electrons in oxide nanostructures. Commun Mater 4, 27 (2023). https://doi.org/10.1038/s43246-023-00354-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-023-00354-7