Abstract
A grand challenge of materials science is predicting synthesis pathways for novel compounds. Data-driven approaches have made significant progress in predicting a compound’s synthesizability; however, some recent attempts ignore phase stability information. Here, we combine thermodynamic stability calculated using density functional theory with composition-based features to train a machine learning model that predicts a material’s synthesizability. Our model predicts the synthesizability of ternary 1:1:1 compositions in the half-Heusler structure, achieving a cross-validated precision of 0.82 and recall of 0.82. Our model shows improvement in predicting non-half-Heuslers compared to a previous study’s model, and identifies 121 synthesizable candidates out of 4141 unreported ternary compositions. More notably, 39 stable compositions are predicted unsynthesizable while 62 unstable compositions are predicted synthesizable; these findings otherwise cannot be made using density functional theory stability alone. This study presents a new approach for accurately predicting synthesizability, and identifies new half-Heuslers for experimental synthesis.
Similar content being viewed by others
Introduction
The search for novel compounds with exotic properties has long been a major initiative of materials science research. This search has traditionally been difficult due to hypothetical materials having a virtually infinite design space1,2,3, where stoichiometric, compositional, and structural degrees of freedom must be considered. Once a material’s stoichiometry is determined, such as AB2C for full-Heuslers or ABC3 for perovskites, the compositional degrees of freedom involve all the ways a set of elements can be permuted in a stoichiometry (e.g., Co2MnSi or SrTiO3). The final degree of freedom, for a given stoichiometry and composition, involves the theoretically endless number of crystal structures that a composition can be arranged in. Traditional approaches for experimentally exploring hypothetical materials have often involved substituting elements in reported compounds with chemically similar ones or tweaking well-known synthesis procedures4,5,6,7. And while these approaches have worked reliably, they are limited in finding innovative materials in completely unexplored composition and structural spaces. Empirically derived rules and trends take researchers a step further, enabling studies to branch out further from existing work, such as electron counting for Zintl compounds8 or the Hume-Rothery Rules9 for solid solution formation. However, rules and trends are seldom widely generalizable and often require extensive and thorough experimental studies to develop. Thus, there is a substantial need for devising faster methods to predict experimental synthesizability. Owing to exponential advances in technology over the recent decades, computational techniques have become increasingly popular and successful in revolutionizing materials discovery1,2.
Density functional theory (DFT) calculations can provide a material’s zero-kelvin energetic stability10,11,12 and are commonly used as a first approach for predicting experimental synthesizability. By calculating the DFT energy of a compound and its competing phases within a compositional system, the formation energies of the compound and the entire convex hull can be determined. At a given composition, the formation energy of the convex hull is the lowest linear combination of energies from competing phases. We define the difference between the formation energy of a given compound and that of the convex hull as the energy above the convex hull, denoted Ehull, which describes the compound’s zero-kelvin thermodynamic stability (lower Ehull values indicate greater stability). In this work, we label materials with Ehull = 0 eV/atom as DFT-stable, and DFT-unstable if otherwise; we continue our discussion using the terms “stable” and “unstable” interchangeably with “DFT-stable” and “DFT-unstable”. Many studies have used DFT stability as a condition of experimental synthesizability to screen candidate materials for synthesis. For instance, Gautier et al.13 determined DFT stabilities for 18-electron ABC compounds and found 54 out of 400 unreported compounds to be stable, of which they experimentally synthesized 15 and confirmed all to be in their predicted structures. Most of Gautier et al.’s predicted compounds were half-Heuslers and they find that compounds with Ehull < –0.13 eV/atom can be synthesized in their predicted single-phase. Zhu et al.14 used a similar approach to search for thermoelectric materials; among thousands of candidates, they identified several promising candidates that are stable which they subsequently synthesized.
Yet, zero-kelvin DFT stability does not perfectly describe experimental synthesizability, that is, not all stable compounds have been synthesized and not all unstable compounds are necessarily unsynthesizable. This is due to other important factors affecting experimental synthesizability such as synthesis temperature, pressure, and method that cannot be easily explained by DFT stability. Diamond and its allotrope graphite are well-known materials which demonstrate the importance of processing techniques when synthesizing one form of carbon over the other. Both allotropes have been successfully synthesized at different pressures and temperatures, despite diamond being less stable than the ground-state structure graphite. When analyzing the Inorganic Crystal Structure Database (ICSD)15, we find that roughly half of experimentally reported compounds are stable while the other half are metastable (unstable, yet experimentally synthesizable) with a median Ehull of 22 meV/atom as calculated through the Open Quantum Materials Database (OQMD)10. Furthermore, some experimentally reported compounds have hypothetical structures that are relatively more stable, yet these have never been synthesized. Thus, while experimentally reported materials tend to be stable or have lower metastability (i.e. lower Ehull), DFT stability does not provide a full explanation of experimental synthesizability.
Further studies have attempted to elucidate the relationship between DFT energetics and synthesizability for metastable materials. Sun et al.16 calculated DFT stabilities for ICSD-reported compounds to investigate the degree of metastability for synthesizable materials. They separately analyze Ehull distributions for binaries, ternaries, quaternaries, and 5+ element compounds, finding that experimentally reported compounds generally (1) are more abundant at lower metastability, and (2) have lower ranges of metastability as the number of elements they are comprised of increases. While these findings suggest that low metastability means greater chances of synthesizability, Sun et al. also find many polymorphs that are relatively stable and unreported (and thus assumed unsynthesizable). Therefore, low Ehull appears to be an important, yet insufficient condition for synthesizability, meaning there are factors beyond zero-kelvin thermodynamics that affect and further complicate synthesizability predictions. Aykol et al.17 extend Sun et al.’s work by quantifying the Ehull limit of metastable compounds. Aykol et al. first used the ICSD to identify 41 compounds for which they calculated DFT stability. Then, they calculated the stabilities of various polymorphs for all 41 compounds and calculated the stability of the amorphous state of each reported compound. For all 41 compounds, the metastability of the reported compound was always lower than that of the corresponding amorphous phase. This suggests that polymorphs with Ehull greater than that of the amorphous phase, termed the “amorphous limit”, are unsynthesizable, though the converse is not necessarily true. That is, all polymorphs above the amorphous limit are unsynthesizeable, but not all polymorphs under the amorphous limit are synthesizable. While Aykol et al.’s findings provide a way to accurately identify materials that are unsynthesizable, the task of calculating many amorphous limits is prohibitively costly, and the problem of accurately predicting the synthesizability of all polymorphs under the amorphous limit remains a challenge.
We present a matrix in Fig. 1 to help visualize the relationship between DFT stability and synthesizability by defining four categories for classifying compounds. Category I and II contain compounds that respectively are stable or unstable in their reported and hence synthesizable structures, while category III and IV contain unreported and hence unsynthesizable compounds that respectively are stable or unstable. The assumption that a compound is unsynthesizable if unreported depends on whether any compound with the same composition has been studied and reported. Because compounds of a given composition can be unreported if never studied, in which case being unreported may not reasonably indicate unsynthesizablility, the matrix in Fig. 1 does not apply to unstudied compositions. Compounds with compositions that have been studied can be categorized into one of these four categories, so it is important to consider all categories together when predicting synthesizability. Some previous studies only consider subsets of this matrix at a time, such as Sun et al.’s16 and Aykol et al.’s17 works investigating ICSD-reported metastable materials (category II and IV). In another work by Aykol18, the network properties of ICSD-reported stable materials as connected by tie-lines in the OQMD are used to model synthesizability. This work captures both scientific and nonscientific factors that influence synthesizability, but only considers stable compounds reported in the ICSD (category I).
A matrix for categorizing materials that have been attempted for synthesis based on their synthesizability and stability. Category I materials are stable and synthesizable; category II materials are unstable, yet synthesizable; category III materials are stable, yet unsynthesizable; category IV materials are unstable and unsynthesizable. Categories labeled “correlated'' include materials whose stability directly describes their synthesizability. That is, materials are expected to be synthesizable if stable and are expected to be unsynthesizable if unstable.
We consider stable compounds that are synthesizable (category I) and unstable compounds that are unsynthesizable (category IV) as “correlated” (since DFT stability and synthesizability are correlated), while unstable compounds that are reported and stable compounds that are not reported are labeled “uncorrelated”. There are multiple ways of rationalizing uncorrelated materials, where finite-temperature thermodynamics like entropy may cause compounds stable at zero kelvin to become unstable at higher synthesis temperatures (category III). This explanation for uncorrelated materials has been observed in cases where materials of half-Heusler-like chemistry are synthesized in non-half-Heusler structures19,20 despite being stable at zero kelvin in the half-Heusler structure, and studies on other materials have pointed to vibrational entropy as the cause of such phenomena21,22. Likewise, entropy may also stabilize compounds that are unstable at zero kelvin leading to materials in category II. Explanations for uncorrelated compounds may also lie beyond thermodynamics where kinetic barriers may allow or prevent the formation of certain materials16,23,24. Experimental mischaracterization or DFT-related errors may also explain why some materials are category II or III, though we believe this applies to only a minority of reported materials. Regardless of the reason, there are cases where DFT stability does not perfectly describe a material’s synthesizability, thus there is strong interest in developing new methods for predicting experimental synthesizability.
Onex such method involves using machine learning (ML), which has emerged as a powerful tool in the materials science community and enabled researchers to devise highly accurate models that describe increasingly complex trends25,26,27,28. Models have already been developed for a diverse range of applications, from predicting material properties29,30,31,32, to DFT energetics32,33, and even force fields for molecular dynamics34. ML models have also been used to predict experimental synthesizability. To find favorable conditions for growing MoS2, Tang et al.35 trained a model on hundreds of synthesis conditions reported to lead to successful or unsuccessful synthesis. They optimized synthesis conditions and identified the most influential synthesis parameters by analyzing feature importances. In another study proposing a general framework that can be hypothetically applied to any material, Kim et al.36 leveraged the vast trove of scholarly articles published online to identify favorable synthesis conditions. By combining natural language processing techniques with ML algorithms, they extracted thousands of properties and synthesis conditions across half a million articles to identify trends that are difficult to find manually. They illustrated their approach by focusing on titania nanotubes, for which they identified new synthesis heuristics involving various parameters like calcination temperature, calcination time, solvent concentration, and precursors.
ML synthesizability models are more feasible to construct than ever, owing to publicly available databases such the OQMD, Materials Project11, AFLOW, ICSD, and many others. Jang et al.37 used the Materials Project database to train a neural network that accurately predicts a material’s synthesizability given its composition and crystal structure. They represent materials by their structural features and are able to identify thousands of synthesizable, yet unreported materials in the OQMD and Materials Project. Using the ICSD, Davariashtiyani et al.38 built a model that similarly also predicts a material’s synthesizability given composition and structure. ML models more focused on specific materials classes have also been reported for various materials such as full-Heuslers39, Chevrel phase chalcogenides40, perovskites41,42,43, and polyelemental nanoparticles44; by focusing on specific material classes or compositions, these models sacrifice generalizability for improved accuracy. In this work, we focus on half-Heusler materials, for which two previous studies have developed ML synthesizability models.
Our paper begins by examining these two reported ML models by Gzyl et al.45 and Legrain et al.46 that predict half-Heusler synthesizability. These models do not use DFT stability when making predictions, and suggest a surprising number of highly metastable candidates to be synthesizable. While metastable materials certainly exist, previous works suggest there is to some degree, a positive correlation between synthesizability and DFT stability13,14,16,17. That is, we expect most synthesizable materials to be stable. Thus, we hypothesize that combining DFT stability with composition-based features may enable a more accurate ML synthesizability model. While some studies have used DFT stability to find new synthesizable materials whereas others use ML with non-DFT features to do the same, no single model has integrated the two approaches. So in this paper, we use DFT stability with composition-based features to build an ML model that predicts the synthesizability of an ABC composition in the half-Heusler structure. Our model reproduces an expected correlation between DFT stability and synthesizability, yet it also can identify metastable half-Heuslers and stable half-Heuslers that are unsynthesizable (compositions where a non-half-Heusler structure is metastable). We show prediction improvements for several half-Heuslers predicted by Gzyl et al.45, and our model achieves a precision of 0.82 and recall of 0.82. We conclude by applying our model on several thousand ABC compositions unreported in literature and identify promising candidates for further experimental study.
Results and discussion
Previous half-heusler synthesizability models
Numerous studies have directly used DFT stability as a screening criteria for discovering new synthesizable half-Heuslers and other Heuslers. Anand et al.47 calculated Ehull to evaluate DFT stability while Vikram et al.48 used Ef (formation energy) to assess DFT stability for identifying synthesizable half-Heuslers. Jia et al.49 more recently used a criteria of Ehull < 100 meV/atom for synthesizability in addition to other clustering techniques to to identify new half-Heuslers candidates. Other works have found magnetic Heuslers50, low thermal conductivity Heuslers51, and others with various novel properties2,52,53,54,55,56. In all of these studies, new half-Heuslers were discovered, however, it is unclear whether all stable half-Heuslers were actually synthesizable and if all unstable half-Heuslers were unsynthesizable.
Thus, our study begins by focusing on ML-based half-Heusler synthesizability models by Gzyl et al.45 and Legrain et al.46, which do not use DFT stability to directly filter candidates for synthesis. Legrain et al. used a random forest algorithm with a training dataset comprised of ABC compositions flagged as reported in the ICSD within the AFLOW12 database. Each ABC composition is labeled as (1) half-Heusler if reported as such, generating one positive (i.e. half-Heusler) example, and (2) non-half-Heusler if reported as non-half-Heusler along with its five other compositional permutations (BAC, BCA, CAB, CBA, ACB), generating 6 negative (i.e. non-half-Heusler) examples. This process yields 164 half-Heusler examples and 11022 non-half-Heusler examples for the training dataset. Each example is represented by composition-based features such as electronegativity, difference in atomic radius, covariance of element column numbers, and many others; the feature vectors are order-specific with respect to compositional permutations to account for elemental site preferences (e.g. the feature vector for BAC is not equivalent to that of CAB). Before discussing this model’s performance, we first clarify several terms that are used throughout this paper to evaluate model performance.
For a synthesizability models, a true positive (TP) prediction is a synthesizable material predicted as synthesizable, and a false positive (FP) prediction is an unsynthesizable material predicted as synthesizable. True negative (TN) predictions are unsynthesizable materials predicted as unsynthesizable, and false negative (FN) predictions are synthesizable materials predicted as unsynthesizable. With these definitions, we introduce two accuracy metrics that are useful for evaluating synthesizability models:
Precision: % of compounds predicted synthesizable that are known to be synthesizable \(\left( \frac{{{{{{{{\rm{TP}}}}}}}}}{{{{{{{{\rm{TP+FP}}}}}}}}}\right)\)
Recall: % of compounds known to be synthesizable that are predicted synthesizable \(\left (\frac{{{{{{{{\rm{TP}}}}}}}}}{{{{{{{{\rm{FN+TP}}}}}}}}}\right)\)
Low precision models will recommend candidates that are seldom synthesizable, while low recall models will incorrectly rule out many candidates that are truly synthesizable. Thus, ML models should maximize both precision and recall, though this is a difficult task since the two metrics tend to be anti-correlated. Legrain et al.’s model obtains a precision of 0.91, and a recall of 0.51. The second model, by Gzyl et al., uses an ensemble of six different ML algorithms to produce an aggregated synthesizability prediction. The model is trained on a dataset of 180 half-Heusler (minority class) examples and 2638 non-half-Heusler (majority class) examples found in Pearson’s Crystal Data; in order to balance the dataset, additional minority class data points are generated from the existing 180 half-Heusler datapoints using the synthetic minority oversampling technique. The model features are also constructed solely from composition-based properties, such as atomic number, ionic radius, melting point, and many others. Various arithmetic operations are applied to these properties to generate model features, and their model attains a precision of 0.77 and a recall of 0.88.
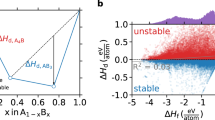
These two synthesizability models reported by Gzyl et al. and Legrain et al. are especially useful for guiding materials discovery given their narrowed focus on one particular material class (i.e. half-Heuslers). Confining a model to one material class generally improves accuracy while remaining generalizable to compositions within the material class’ compositional design space. However, these two models do not directly account for DFT stability, which we expect to correlate to some degree with synthesizability. Using the OQMD, we obtain DFT stabilities for the half-Heuslers that Gzyl et al. and Legrain et al. predict to be highly synthesizable and plot the stabilities against each models’ predicted synthesizabilities in Fig. 2. We observe in Gzyl et al.’s predictions a cluster of highly synthesizable (>0.90) compositions with Ehull values up to 500 meV/atom. This is unexpected since only two experimentally reported half-Heuslers from the ICSD and Springer Materials (SM)57 have Ehull > 400 meV/atom. Furthermore, metastable half-Heuslers only make up around 28% of experimentally reported half-Heuslers from the ICSD and Springer Materials, and less than half of these have Ehull > 73 meV/atom. Gzyl et al.’s model also seems to predict synthesizabilities that have no correlation with stability, which is unexpected. Legrain et al.’s predictions more closely follow an expected inverse relationship between synthesizability and Ehull, though a large majority of Legrain et al.’s synthesizable predictions are still surprisingly far above the convex hull.
Comparisons of Ehull from the OQMD and synthesizability for synthesizable half-Heuslers as determined by (a) Gzyl et al.’s45 and (b) Legrain et al.’s46 models. Both models are not informed of DFT stability and predict many unstable half-Heuslers to be synthesizable. The dashed red line depicts the median Ehull (73 meV/atom) of all unstable half-Heuslers experimentally reported in the ICSD as calculated in the OQMD.
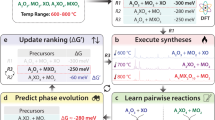
Without any knowledge of DFT stability, these synthesizability models by Gzyl et al. and Legrain et al. predict many highly unstable half-Heuslers to be synthesizable. We hypothesize that a combination of half-Heusler DFT stabilities with composition-based features can enable an improved half-Heusler synthesizability model that makes predictions more aligned with our expectations from DFT stability. We test our hypothesis using a ML prediction process summarized in the flowchart from Fig. 3. First, we gather experimental data for ABC compositions reported as half-Heusler and non-half-Heusler as found in the ICSD, Springer Materials, and ASM International’s Alloy Phase Diagram Database (ASM)58. Next, we represent each composition with its DFT stability in the half-Heusler structure in addition to various composition-based features. The data is used to then predict a synthesizability score between 0 and 1, which is compared against empirically derived cutoffs to determine whether an ABC composition is synthesizable as a half-Heusler.
First, we calculate DFT stabilities for experimentally reported ABC compositions from the ICSD, Springer Materials, and ASM in the half-Heusler structure. The calculated stabilities are then used with composition-based features produced through Magpie to train the machine learning model. Final synthesizability labels are made based on how predicted synthesizabilities compare against empirically derived cutoffs.
When classifying experimentally reported ABC compositions in our training set into the four categories in Fig. 1, we find that DFT stability does not perfectly describe half-Heusler synthesizability. A composition is considered “synthesizable” if reported as half-Heusler and “unsynthesizable” if reported in another crystal structure. We find 71% (Category \(\frac{{{{{{{{\rm{I}}}}}}}}}{{{{{{{{\rm{I+II}}}}}}}}}\)) of reported half-Heuslers to be stable in the half-Heusler structure and 72% (Category \(\frac{{{{{{{{\rm{I}}}}}}}}}{{{{{{{{\rm{I+III}}}}}}}}}\)) of ABC compositions that are stable in the half-Heusler structure to be reported as half-Heusler. Evidently, properties beyond DFT stability must be accounted for to more accurately predict synthesizability.
While there are helpful rules for predicting half-Heusler synthesizability, they are insufficient alone for evaluating all possible ABC compositions that can form a half-Heusler. The well-known 18 electron rule is one such rule, which has aided the discovery of several half-Heuslers13,47,59,60; this rule borrows from Zintl compounds the observation that valence electron count strongly correlates with structure and bonding8. While fairly accurate, this rule’s generalizability is questionable since many non-18-electron half-Heuslers have also been reported in literature. Other works have tried to link defects and elemental site preferences with half-Heusler synthesizability47,61, though the findings do not fully apply to all half-Heuslers in the ABC compositional design space. Thus, we use ML coupled with DFT to learn the complex rules that determine an ABC composition’s synthesizability in the half-Heusler structure. With thousands of ABC compositions still unreported in literature, even modest accuracy gains over current predictive methods may reveal many new promising half-Heuslers.
DFT stability as a benchmark synthesizability model
Because our ML model is expected to show improvement over using DFT stability alone for predicting synthesizability, we first evaluate the performance of a synthesizability model informed only by a compound’s DFT stability as a benchmark. We report in Fig. 4 the precisions and recalls as a function of an Ehull cutoff for the benchmark model applied to our training set; materials with half-Heusler stabilities higher than a given cutoff are considered unsynthesizable in the half-Heusler structure and are synthesizable if otherwise. We find precision to monotonically decrease as the Ehull cutoff increases for metastable materials since experimentally reported materials tend to have low Ehull values. When the Ehull cutoff is 73 meV/atom, the model predicts half of all experimentally known unstable half-Heuslers as synthesizable (recall = 0.5), and only about 15% of such predictions are correct (precision = 0.15). Accuracies for stable half-Heuslers are not plotted in Fig. 4, since recall equals 1 and precision is just the y-intercept of the solid precision line (precision = 0.72). While this benchmark model has moderate accuracy, we show next that our ML-driven approach coupled with DFT stability can make improved synthesizability predictions.
Accuracies for the benchmark half-Heusler synthesizability model applied to the ABC compositions in our training set, based solely off a composition’s Ehull in the half-Heusler structure. A composition with Ehull ≤ a cutoff is considered synthesizable as a half-Heusler, and is unsynthesizable otherwise. Dashed lines depict accuracies for only metastable (Ehull > 0 meV/atom) compositions, for which this model performs especially poorly. Because precisions for only stable compositions always equal 0.72 and their respective recalls always equal 1, their curves are not drawn here.
Machine learning model accuracy
We evaluate our ML model by using leave-one-out cross-validation to determine the synthesizability of all compositions used to train the model. Our model undersamples 600 data points among category IV compositions in order to reduce the training set class imbalance; the remaining compositions excluded from the training sets during the under-sampling process are also predicted on during cross-validation. This cross validation procedure is repeated for 10 trials, with new batches of 600 under-sampled data points per trial, and synthesizability values are averaged across all trials. Compositions with predictions above a synthesizability cutoff are determined as synthesizable in the half-Heusler structure. We finalize a cutoff of 0.50 for stable compositions and 0.75 for unstable compositions, which provide sufficiently accurate predictions (see Supplementary Note 1 for more details). At these cutoffs, the model has a precision of 0.95 and a recall of 0.90 among stable compositions, for which the DFT stability benchmark model with a precision of 0.72 and recall of 1. More notably, the overall precision for unstable compositions is 0.92 while the recall is 0.43. The precision is 0.12 for the benchmark model at the same recall of 0.43. Thus, with almost eight times the precision at the same recall, our ML model provides a significant accuracy boost for predicting synthesizable half-Heuslers among unstable candidates. Even among stable compositions, our ML model provides a sizable boost in precision (from 0.72 to 0.95) with only a slight penalty in recall (from 1 to 0.90).
In Fig. 5, we report our model’s precision and recall as a function of the synthesizability cutoff. Our model predicts the synthesizability of stable half-Heuslers more accurately than unstable half-Heuslers, and recall monotonically decreases while precision increases as the synthesizability cutoff is increased. The precision is 0.82 and recall is 0.82 for a synthesizability cutoff of 0.5, which Gzyl et al. and Legrain et al. use in their models. While our model has comparable precisions and recalls with those of models from Gzyl et al. and Legrain et al., we refrain from closely comparing accuracies due to nonidentical datasets used to evaluate each model. We also find our model, when trained only on single-phase compounds, poorly generalizes to the ABC compositions known to phase separate (visualized in Supplementary Fig. 2). This suggests that synthesizability models trained only on single-phase compounds, like in Gzyl et al.’s and Legrain et al.’s models, may erroneously predict unknown materials that phase separate as synthesizable.
Precisions and recalls for our synthesizability model as a function of a synthesizability cutoff. Dashed lines depict accuracies for either (a) stable compounds or (b) unstable compounds. Compositions with synthesizabilities lower than a given cutoff are labeled non-half-Heusler, and are half-Heusler otherwise. Accuracies are determined through leave-one-out cross-validation, where dashed lines depict the accuracies among stable or unstable compositions. When the cutoff equals 0, precisions can be interpreted as the chance of selecting a half-Heusler through random guessing.
Feature discussion
We now examine the most important model features that determine synthesizability as listed in Table 1, where we find DFT stability to be the most important feature. We plot stability against synthesizability in Fig. 6 and observe that maximum Ehull values (\({E}_{{{{{{{{\rm{hull}}}}}}}}}^{\max }\)) tend to decrease for increasingly synthesizable materials; this is in line with our intuition that low Ehull is a necessary, though insufficient condition of synthesizability. We quantify this inverse relationship between \({E}_{{{{{{{{\rm{hull}}}}}}}}}^{\max }\) and synthesizability by finding \({E}_{{{{{{{{\rm{hull}}}}}}}}}^{\max }\) among compounds of synthesizabilities within steps of 0.05, and calculating the spearman rank correlation between \({E}_{{{{{{{{\rm{hull}}}}}}}}}^{\max }\) and synthesizability. The spearman rank correlation describes the monotonic correlation between two sets of values, where a correlation of -1 indicates a perfectly inverse correlation (i.e. as one set of values increases, the corresponding set of other values always decreases). We find \({E}_{{{{{{{{\rm{hull}}}}}}}}}^{\max }\) to have a spearman rank correlation of –0.902 with synthesizability, indicating a strong inverse correlation. By definition, the energy above the convex hull is non-negative, so the inverse trend is interrupted at Ehull = 0. Thus, we try replacing Ehull with decomposition energy, the formation energy difference between the half-Heusler and its decomposition products (non-ABC stoichiometry compounds that make the convex hull), which can be negative. We observe the inverse trend between synthesizability and Ehull continues below Ehull = 0 (visualized in Supplementary Fig. 3), confirming our intuition that synthesizable compounds tend to be more stable. The inverse correlation between the maximum decomposition energies versus synthesizability is also very strong, with a spearman rank correlation of -0.908. We note that replacing Ehull with decomposition energy does not improve model performance, so we continue using Ehull as a model feature. Furthermore, we emphasize that because the model does not solely rely on Ehull to make predictions, it can identify known metastable half-Heuslers with high synthesizability and identify known non-half-Heusler compositions that are stable in the half-Heusler structure with low synthesizability. These category II and III compounds are of particular interest since their synthesizability cannot be modeled with DFT stability alone. The fourth most important feature, Mendeleev number, is an intuitive feature since it orders elements by chemical similarity62. Other top features such as covalent radii and electron counts are also intuitively important, though our model cannot provide specific and interpretable rules that relate these features with synthesizability. This limitation is a widely-acknowledged weakness of using ML, since the decision criteria a model uses to generate predictions is often complex and difficult to interpret.
Energies above the convex hull for predictions made by our model on training data compounds using leave-one-out cross-validation. Data points are colored according to their true experimental labels, as either half-Heusler, another structure, or phase-separating. We observe an inverse trend between synthesizability and \({E}_{{{{{{{{\rm{hull}}}}}}}}}^{\max }\), which agrees with the intuition that compounds that are more stable are more likely to be synthesizable.
Validation on previously reported compounds
Next, we validate our model against experimental data reported in literature on ABC compounds that are not used to train our ML model. We begin by comparing our model against Gzyl et al.’s45 for seven new compounds they predict as half-Heusler, of which six are reported to be synthesized as half-Heusler. We first simulate X-Ray Diffraction (XRD) patterns to identify the six reported half-Heuslers, which is non-trivial since there are many possible ordered and disordered atomic arrangements for Heusler-type structures that correspond to visually similar diffraction patterns; we formally define these arrangements in Supplementary Note 2. We find that while most reported peak positions match those of our simulated patterns for the half-Heusler structures that Gzyl et al. report, the relative peak intensities do not match, suggesting that none of the reported half-Heuslers are actually ordered ideal-stoichiometry (ABC) half-Heuslers. Thus, our next step was to identify other Heusler-type structures that better match the reported XRD patterns. We simulated XRD patterns for non-stoichiometric and disordered half-Heuslers and identified patterns with peak positions and intensities that more closely match those reported. The simulated patterns can be found in Supplementary Figs. 4 and 5, and more details on the identified disordered structures is in Supplementary Table 2.
We conclude that while both our model and Gzyl et al.’s model are accurate, our model shows improvement in correctly identifying non-half-Heusler compositions; we summarize our comparison in Table 2. The only composition Gzyl et al. finds to be non-half-Heusler is MnRhPb, which they report is a mixture of binary phases despite the composition having the highest predicted synthesizability of 0.935 from their model; meanwhile, we correctly predict a much lower synthesizability of 0.401. The observed XRD patterns for MnPdIn and MnNiSn most closely match the simulated patterns for the full-Heuslers MnPd2In and MnNi2Sn, respectively. This is intuitive since the full-Heuslers are stable as determined by DFT calculations and have been reported63,64, whereas the half-Heusler counterparts MnPdIn and MnNiSn are unstable; for these two compositions, our model predicts low synthesizabilities. We note that because secondary phases are reported for all observed ABC compositions, non-ABC stoichiometry compounds like full-Heuslers may be observed. MnPdSn and MnRhSn have synthesizabilities near the cutoff we set at 0.75, and most resemble disordered half-Heusler structures. For disordered compounds, we generate their special quasirandom structure65, the small-unit-cell periodic representation of a disordered structure, using the Alloy Theoretic Automated Toolkit66 and calculate their energies above the convex hull using DFT. The observed disordered phase for MnRhSn is more stable than its respective ordered half-Heusler counterpart, which may help explain why the ordered half-Heusler structure is not observed, while the disordered phase for MnPdSn is only slightly less stable than its ordered half-Heusler structure. While the disordered structures for VRhSn and MnRuSb are noticeably less stable than their ordered half-Heusler structures, there are also many unidentifiable peaks in both compounds’ XRD patterns, leading us to have lower confidence in the disordered phases we identify. Nevertheless, we are confident VRhSn and MnRuSb are not ordered half-Heuslers as originally claimed. For each composition in Table 2, we also list the compounds that make up each convex hull in Supplementary Table 3. Gzyl et al. also attempt to synthesize seven additional compositions they predict to have low probabilities of forming half-Heuslers. For all seven compositions, they do not observe half-Heusler structures, and all seven are predicted by our model to have synthesizabilities close to 0. While both models appear to be accurate and are in agreement when predicting compositions expected to form half-Heusler, our model offers improved predictive accuracy for compositions expected to not form half-Heusler.
The next dataset we use to validate our model includes compositions experimentally reported in multiple structures as found during training set construction; these compositions are labeled “multiple prototype” and are omitted from our model’s final training data set. We are interested in whether our ML model can maintain high prediction accuracy despite being uninformed of synthesis conditions and techniques, which we hypothesize are particularly influential for determining half-Heusler synthesizability among these “multiple prototype” compositions. We consider a “multiple prototype” composition as half-Heusler if any of its reported structures is half-Heusler; with these compositions, our model achieves a precision of 0.82 and a recall of 0.62, which are slightly lower than the leave-one-out cross-validation accuracies when predicting on training data compositions. Where the positive labels are half-Heuslers, our model predicts 18 true positives, 4 false positives, 11 false negatives, and 405 true negatives. To rule out the possibility of compositions being erroneously marked as “multiple prototype” due to database entry errors, we manually verify published papers corresponding to each entry for the non true negative compositions. Only a few compositions are erroneously labeled as “multiple prototype”, so we conclude most compositions are truly polymorphic. The decreased accuracy we observe for “multiple prototype” compositions suggests our model may be missing important features like synthesis conditions, which play an important role in determining a specific polymorph’s synthesizability. Accounting for synthesis conditions is outside the scope of this paper due to the difficulties acquiring the requisite data, so we continue while acknowledging this limitation as an area for improvement.
In another paper focused on a broader set of ABC ternary materials, Gautier et al.13 use DFT stability alone to determine synthesizability. They try to synthesize 28 materials, all of which but one are not in our training set; of these 28 materials attempted for synthesis, 12 are half-Heusler, 5 are MgSrSi-type (Pnma), and 11 are phase separating. Our model applied on these 28 compounds predicts 9 compositions as synthesizable half-Heuslers, of which all are reported to be half-Heuslers by Gautier et al. This means our model achieves a precision of 1 and a recall of 0.75 (9/12) for predicting synthesizable half-Heuslers, which further validates our model’s predictive accuracy. The 28 compounds and their predicted synthesizabilities can be found in Supplementary Table 4.
Predicting new half-heuslers
We conclude our paper by applying our model on unreported ABC compositions to find new synthesizable half-Heuslers. ABC compositions are generated by combinatorially combining the set of A, B, and C elements found across all half-Heuslers in our training set. After removing compositions already in the training set, we calculate DFT stabilities for 4141 compositions in the half-Heusler structure, which we predict synthesizabilities for with our ML model. The predicted synthesizabilities for these compositions are plotted with the respective DFT stabilities in Fig. 7. Most compositions are unsynthesizable, which can be rationalized by the facts that (1) 90% (n = 3745) of all compositions are quite unstable with Ehull > 100 meV/atom, of which only 44 are predicted synthesizable, and (2) synthesizable half-Heuslers have elemental site preferences, so combinatorially generated compositions should generally be unfavorable and thus unsynthesizable. We also find that while only 2% (n = 98) of all compositions are stable, where over half (n = 59) of these are considered synthesizable. As expected, there is an inverse trend between synthesizability and Ehull similar to what we observe from training data predictions. Of the synthesizable compounds identified by our model, 38 have nonzero band gaps ranging from 0.21 eV to 1.73 eV and may be suitable for thermoelectric and photovoltaic applications, though more precise band structure and electronic property calculations should be performed first. These calculations are beyond the scope of our work which focuses solely on experimental synthesizability, and will be completed in a follow up study.
Predicted half-Heusler synthesizabilities with calculated Ehull values for (a) 4141 ABC compositions that are unreported in the ICSD, Springer Materials, and ASM, and (b) the subset that is synthesizable. Compositions are generated by combinatorially combining sets of A, B, and C elements found in reported half-Heuslers. Compositions are considered synthesizable when predicted synthesizabilities > 0.5 if stable and > 0.75 if unstable. As expected from the combinatorial composition generation, a majority are predicted unsynthesizable.
While our predictions have not been experimentally verified, the DFT stabilities for synthesizable half-Heuslers are within expected values observed in previously reported materials. In total, 121 compositions are predicted synthesizable by our model, with 59 being stable and 62 being unstable. We list the most synthesizable candidates in Table 3, and the full list of synthesizable half-Heuslers can be found in Supplementary Table 5.
Conclusion
Here, we present a ML model that predicts whether an ABC composition can be synthesized as a half-Heusler. We first establish that DFT stability is an important, yet insufficient, property to consider when predicting synthesizability, which some reported models do not do. Thus, we combine DFT stability with composition-based features to represent materials in our synthesizability ML model, which is trained on experimentally reported half-Heuslers, non-half-Heuslers, and compositions observed to phase separate. Our model attains significantly improved accuracy over using DFT stability alone as a synthesizability criteria, with a precision of 0.82 and recall of 0.82; most notably, our model achieves almost eight times the precision over using DFT stability as a synthesizability predictor for unstable half-Heuslers. When validated against the experimental results from Gzyl et al., our model correctly identifies more compounds to be unsynthesizable, and when applied to the 28 ABC compounds synthesized by Gautier et al., our model predicts 9 of the 12 known half-Heuslers to be half-Heusler, with all 9 predictions being correct. Further validation carried out on polymorphic (“multiple prototype”) compositions result in reduced accuracies, which we suspect is due to our model not accounting for synthesis conditions. When applied on combinatorially enumerated ABC compositions, our model predicts 121 of 4141 unreported compositions to be synthesizable, with many possessing favorable band gaps for thermoelectric and photovoltaic applications. With regards to experimental synthesizability, the most interesting predictions are the 39 stable compositions predicted unsynthesizable and 62 unstable compositions predicted synthesizable; these predictions provide examples of compounds whose synthesizability may not be described by DFT stability alone, which can be further studied to elucidate the relationship between thermodynamic stability and synthesizability. While this work focuses on half-Heusler materials, we emphasize our DFT-informed ML approach for predicting synthesizability is applicable to any class of materials. With computational resources becoming increasingly available, this ML-driven framework can enable more accurate synthesizability models for more efficient materials discovery.
Methods
Half-Heuslers are encompass a large compositional design space and are widely studied for their thermoelectric8,61,67,68, ferromagnetic69,70,71, and spintronic56,72,73 applications. half-Heuslers are cubic (\(F\bar{4}3m\)) ternary compounds with ABC compositions, where A is typically an early transition metal or rare earth element, B is a late transition metal, and C is a main group element from the right half of the periodic Table61. The half-Heusler structure has occupied Wyckoff positions 4a (0, 0, 0), 4b (\(\frac{1}{2}\), \(\frac{1}{2}\), \(\frac{1}{2}\)), and 4c (\(\frac{1}{4}\), \(\frac{1}{4}\), \(\frac{1}{4}\)), where the 4c atom is cubically coordinated by the 4a and 4b elements, while the 4a and 4b atoms are octahedrally coordinated by each other. This leads to three distinct half-Heusler prototype configurations for a given ABC composition, where the experimentally observed (and usually most energetically stable) configuration involves the A element in the 4a site, B element in the 4c site, and C element in the 4b site.
Machine learning training data curation
Our ML model’s training dataset comprises three kinds of compositions: those experimentally reported (i) as half-Heusler, (ii) as another prototype/structure (still with ABC stoichiometry), and (iii) to phase separate into decomposition products (i.e. compounds with non-ABC stoichiometry). These compositions are sourced from three databases: the ICSD, Springer Materials, and ASM International’s Alloy Phase Diagram Database. Data from the ICSD and Springer Materials are used to identify half-Heuslers and compositions found in other prototypes. Compositions queried in the ICSD and Springer Materials often return multiple entries, so all entries of duplicate structures are first removed. If multiple unique entries remain, the composition is marked as “multiple prototype” (438 total). Likewise, those with only one unique reported structure remaining are marked “single prototype”. We hypothesize the compositions reported in multiple structures have half-Heusler synthesizabilities that strongly depend on synthesis conditions and techniques, which are not considered by our model. Thus, our finalized training set excludes these compositions. We then calculate the DFT stability for training set compositions, which involves three configurations of the half-Heusler structure, and report the most stable of the three as the half-Heusler stability for a given composition. The final training set has 149 half-Heuslers (positive/synthesizable examples) and 1906 compounds of other prototypes (negative/unsynthesizable examples). We note that while the “unsynthesizability” of an ABC composition in the half-Heusler structure cannot be definitively proven, we assume that an ABC composition found in a non-half-Heusler structure is unlikely to also be synthesizable as a half-Heusler. Of the “multiple prototype” compositions that we find, only 3% of compositions involve the half-Heusler structure and another non-half-Heusler structure, suggesting our “unsynthesizability” criteria is reasonable.
Next, we obtain from ASM the ABC compositions expected to phase separate into non-ABC decomposition products. Including these phase-separating compositions is important for generalizing predictions to all unreported ABC compositions since attempts to synthesize materials can also result in multi-phase separation. However, because phase separation is often considered as the failure to synthesize a material, this “negative” data is seldom reported among works focusing on synthesizing ABC compounds; the difficulty of accessing these “dark reactions” has been discussed and studied as a barrier to producing accurate synthesizability ML models74. In our work, we identify phase separating compositions by querying ternary phase diagrams from ASM and searching for the presence of a single phase at the ABC composition. If a single phase at the ABC composition does not exist, the composition is labeled “phase separating”, but only if the composition is within a study’s attempted composition range (a single phase may be absent from the phase diagram simply because it was not attempted in a study). This search method yields 335 ABC compositions which phase separate, bringing the total number of negative examples to 2241. Categorizing all compositions into the matrix in Fig. 1, we find 106 in category I (reported half-Heusler and stable), 43 in category II (reported half-Heusler and unstable), 41 in category III (reported non-half-Heusler and stable), and 2200 in category IV (reported non-half-Heusler and unstable).
Machine learning model parameters and features
Our ML model is constructed using the Scikit-learn python package, and uses a random forest classifier to predict synthesizability values defined as the fraction of trees (100 trees) that classify a composition as half-Heusler. The model represents materials using a combination of features generated by Magpie75, a software package that applies statistical operators like mean, minimum, maximum, and standard deviation on composition-based properties such as atomic radius, mendeleev number, melting point, and many others. The featurizer is applied to the whole ABC composition, as well as on each element individually, with elements ordered by increasing electropositivity. The latter is done to help inform the model of elemental site preferences. The difference between the features of the cubically-coordinated element and the means of the octahedrally-coordinated element features are also used to represent materials, further informing the model of elemental site preferences. And most importantly, we add the energy above the convex hull for the half-Heusler structure calculated through the OQMD as a feature, where the most stable of the three prototype configurations for the half-Heusler structure is used. The complete list of features and their importances can be found in Supplementary Data 1.
Data availability
Data for reproducing major parts of this work are posted in the Github repository: https://github.com/andrewlee1030/machine_learned_synthesizability_from_DFT.
Code availability
Code for reproducing major parts of this work are posted in the Github repository: https://github.com/andrewlee1030/machine_learned_synthesizability_from_DFT.
References
Marzari, N., Ferretti, A. & Wolverton, C. Electronic-structure methods for materials design. Nat. Mater. 20, 736–749 (2021).
Curtarolo, S. et al. The high-throughput highway to computational materials design. Nat. Mater. 12, 191–201 (2013).
Oganov, A. R., Pickard, C. J., Zhu, Q. & Needs, R. J. Structure prediction drives materials discovery. Nat. Rev. Mater. 4, 331–348 (2019).
Koinuma, H. & Takeuchi, I. Combinatorial solid-state chemistry of inorganic materials. Nat. Mater. 3, 429–438 (2004).
van Dover, R. B., Schneemeyer, L. F. & Fleming, R. M. Discovery of a useful thin-film dielectric using a composition-spread approach. Nature 392, 162–164 (1998).
van Dover, R. & Schneemeyer, L. Deposition of uniform zr-sn-ti-o films by on-axis reactive sputtering. IEEE Electron Device Lett. 19, 329–331 (1998).
Chang, H., Takeuchi, I. & Xiang, X. D. A low-loss composition region identified from a thin-film composition spread of (ba1-x-ysrxcay)tio3. Appl. Phys. Lett. 74, 1165–1167 (1999).
Zeier, W. G. et al. Engineering half-Heusler thermoelectric materials using Zintl chemistry. Nat. Rev. Mater. 1, 16032 (2016).
Hume-Rothery, W., Mabbott, G. W. & Evans, K. M. C. The freezing points, melting points, and solid solubility limits of the alloys of silver, and copper with the elements of the b sub-groups. Philos. Trans. R. Soc. Lond. A. Math. Phys. Sci. 233, 1–97 (1934).
Saal, J. E., Kirklin, S., Aykol, M., Meredig, B. & Wolverton, C. Materials design and discovery with high-throughput density functional theory: The open quantum materials database (oqmd). JOM 65, 1501–1509 (2013).
Jain, A. et al. The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 1, 011002 (2013).
Curtarolo, S. et al. Aflowlib.org: A distributed materials properties repository from high-throughput ab initio calculations. Comput. Mater. Sci. 58, 227–235 (2012).
Gautier, R. et al. Prediction and accelerated laboratory discovery of previously unknown 18-electron ABX compounds. Nat. Chem. 7, 308–316 (2015).
Zhu, H. et al. Computational and experimental investigation of tmagte2 and xyz2 compounds, a new group of thermoelectric materials identified by first-principles high-throughput screening. J. Mater. Chem. C 3, 10554–10565 (2015).
Bergerhoff, G., Brown, I. & Allen, F. et al. Crystallographic databases. Int. Union Crystallogr. Chester 360, 77–95 (1987).
Sun, W. et al. The thermodynamic scale of inorganic crystalline metastability. Sci. Adv. 2, e1600225 (2016).
Aykol, M., Dwaraknath, S. S., Sun, W. & Persson, K. A. Thermodynamic limit for synthesis of metastable inorganic materials. Sci. Adv. 4, 1–8 (2018).
Aykol, M. et al. Network analysis of synthesizable materials discovery. Nat. Commun. 10, 1–7 (2019).
Kleinke, H. & Franzen, H. F. Crystal structures, bonding and electronic structures of MM’As, a series of new ternary arsenides (M = Zr, Hf; M’ = Fe, Co, Ni). Zeitschrift fur Anorganische und Allgemeine Chemie 624, 51–56 (1998).
Koga, K. Original papers. Heterocycles 66, 7 (2005).
Wolverton, C. & Ozoliņš, V. Entropically favored ordering: The metallurgy of al2Cu revisited. Phys. Rev. Lett. 86, 5518–5521 (2001).
Guo, S., Anand, S., Zhang, Y. & Snyder, G. J. Vibrational Entropy Stabilizes Distorted Half-Heusler Structures. Chemistry of Materialsacs.chemmater.0c01404 (2020). https://doi.org/10.1021/acs.chemmater.0c01404.
Whitelam, S. & Jack, R. L. The statistical mechanics of dynamic pathways to self-assembly. Ann. Rev. Phys. Chem. 66, 143–163 (2015).
Tappan, B. A. & Brutchey, R. L. Polymorphic metastability in colloidal semiconductor nanocrystals. ChemNanoMat 6, 1567–1588 (2020).
Schmidt, J., Marques, M. R. G., Botti, S. & Marques, M. A. L. Recent advances and applications of machine learning in solid-state materials science. npj Comput. Mater. 5, 83 (2019).
Jain, A., Hautier, G., Ong, S. P. & Persson, K. New opportunities for materials informatics: Resources and data mining techniques for uncovering hidden relationships. J. Mater. Res. 31, 977–994 (2016).
Kim, C., Pilania, G. & Ramprasad, R. From organized high-throughput data to phenomenological theory using machine learning: The example of dielectric breakdown. Chem. Mater. 28, 1304–1311 (2016).
Balachandran, P. V., Theiler, J., Rondinelli, J. M. & Lookman, T. Materials prediction via classification learning. Sci. Rep. 5, 13285 (2015).
Chen, C., Zuo, Y., Ye, W., Li, X. & Ong, S. P. Learning properties of ordered and disordered materials from multi-fidelity data. Nat. Comput. Sci. 1, 46–53 (2021).
Ward, L., Agrawal, A., Choudhary, A. & Wolverton, C. A general-purpose machine learning framework for predicting properties of inorganic materials. npj Comput. Mater. 2, 16028 (2016).
Ward, L. et al. A machine learning approach for engineering bulk metallic glass alloys. Acta Materialia 159, 102–111 (2018).
Stanley, J. C., Mayr, F. & Gagliardi, A. Machine learning stability and bandgaps of lead-free perovskites for photovoltaics. Adv. Theory Simul. 3, 1–6 (2020).
Meredig, B. et al. Combinatorial screening for new materials in unconstrained composition space with machine learning. Phys. Rev. B 89, 094104 (2014).
Park, C. W. et al. Accurate and scalable graph neural network force field and molecular dynamics with direct force architecture. npj Comput. Mater. 7 https://doi.org/10.1038/s41524-021-00543-3 (2021).
Tang, B. et al. Machine learning-guided synthesis of advanced inorganic materials. Mater. Today 41, 72–80 (2020).
Kim, E. et al. Materials synthesis insights from scientific literature via text extraction and machine learning. Chem. Mater. 29, 9436–9444 (2017).
Jang, J., Gu, G. H., Noh, J., Kim, J. & Jung, Y. Structure-based synthesizability prediction of crystals using partially supervised learning. J. Am. Chem. Soc. 142, 18836–18843 (2020).
Davariashtiyani, A. & Kadkhodaei, S. Predicting synthesizability of crystalline materials via deep learning. Commun Mater. 2, 115 (2021).
Oliynyk, A. O. et al. High-throughput machine-learning-driven synthesis of full-heusler compounds. Chem. Mater. 28, 7324–7331 (2016).
Singstock, N. R. et al. Machine learning guided synthesis of multinary chevrel phase chalcogenides. J. Am. Chem. Soc. 143, 9113–9122 (2021).
Balachandran, P. V. et al. Predictions of new ABo3 perovskite compounds by combining machine learning and density functional theory. Phys. Rev. Mater. 2, 043802 (2018).
Pilania, G., Balachandran, P. V., Kim, C. & Lookman, T. Finding new perovskite halides via machine learning. Front. Mater. 3, 19 (2016).
Tao, Q., Xu, P., Li, M. & Lu, W. Machine learning for perovskite materials design and discovery. npj Comput. Mater. 7, 23 (2021).
Wahl, C. B. et al. Machine learning–accelerated design and synthesis of polyelemental heterostructures. Sci. Adv. 7, eabj5505 (2021).
Gzyl, A. S., Oliynyk, A. O. & Mar, A. Half-heusler structures with full-heusler counterparts: Machine-learning predictions and experimental validation. Crystal Growth Design 20, 6469–6477 (2020).
Legrain, F., Carrete, J., van Roekeghem, A., Madsen, G. K. & Mingo, N. Materials screening for the discovery of new half-heuslers: Machine learning versus ab initio methods. J. Phys. Chem. B 122, 625–632 (2018).
Anand, S. et al. A valence balanced rule for discovery of 18-electron half-Heuslers with defects. Energy Environ. Sci. 11, 1480–1488 (2018).
Vikram, Sahni, B., Barman, C. K. & Alam, A. Accelerated discovery of new 8-electron half-heusler compounds as promising energy and topological quantum materials. J. Phys. Chem. C 123, 7074–7080 (2019).
Jia, X. et al. Unsupervised machine learning for discovery of promising half-heusler thermoelectric materials. npj Comput. Mater. 8, 34 (2022).
Sanvito, S. et al. Accelerated discovery of new magnets in the heusler alloy family. Sci. Adv. 3, e1602241 (2017).
Carrete, J., Li, W., Mingo, N., Wang, S. & Curtarolo, S. Finding unprecedentedly low-thermal-conductivity half-heusler semiconductors via high-throughput materials modeling. Phys. Rev. X 4, 011019 (2014).
He, J. et al. Ultralow thermal conductivity in full heusler semiconductors. Phys. Rev. Lett. 117, 046602 (2016).
Kocevski, V. & Wolverton, C. Designing high-efficiency nanostructured two-phase heusler thermoelectrics. Chem. Mater. 29, 9386–9398 (2017).
Kim, K. et al. Machine-learning-accelerated high-throughput materials screening: Discovery of novel quaternary heusler compounds. Phys. Rev. Mater. 2, 123801 (2018).
He, J., Naghavi, S. S., Hegde, V. I., Amsler, M. & Wolverton, C. Designing and discovering a new family of semiconducting quaternary heusler compounds based on the 18-electron rule. Chem. Mater. 30, 4978–4985 (2018).
Ma, J. et al. Computational investigation of half-Heusler compounds for spintronics applications. Phys. Rev. B 95, 1–25 (2017).
Madelung, O., Rössler, U. & Schulz, M. Springer materials—the landolt-börnstein database. see http://www.springermaterials.com (2010).
Villars, P., Okamoto, H. & Cenzual, K. Asm alloy phase diagrams database. ASM International, Materials Park, OH, USA (2006).
Liu, Z. et al. Design of high-performance disordered half-heusler thermoelectric materials using 18-electron rule. Adv. Funct. Mater. 29, 1–10 (2019).
Zeier, W. G. et al. Using the 18-electron rule to understand the nominal 19-electron half-heusler NbCoSb with Nb vacancies. Chem. Mater. 29, 1210–1217 (2017).
Graf, T., Felser, C. & Parkin, S. S. Simple rules for the understanding of Heusler compounds. Progr Solid State Chem. 39, 1–50 (2011).
Villars, P., Cenzual, K., Daams, J., Chen, Y. & Iwata, S. Data-driven atomic environment prediction for binaries using the Mendeleev number: Part 1. Composition AB. J. Alloys Compounds 367, 167–175 (2004).
Xu, X. et al. Magnetic properties of Mn 2 PdSn and Mn 2 PdIn. J. Magnetism Magnetic Mater. 401, 618–624 (2016).
Li, X.-Z., Zhang, W.-Y., Valloppilly, S. & Sellmyer, D. J. New Heusler compounds in Ni-Mn-In and Ni-Mn-Sn alloys. Sci. Rep. 9, 7762 (2019).
Zunger, A., Wei, S.-H., Ferreira, L. G. & Bernard, J. E. Special quasirandom structures. Phys. Rev. Lett. 65, 353–356 (1990).
van de Walle, A., Asta, M. D. & Ceder, G. The alloy theoretic automated toolkit: a user guide. Calphad 26, 539–553 (2002).
Zhu, H. et al. Discovery of TaFeSb-based half-Heuslers with high thermoelectric performance. Nat. Commun. 10, 1–8 (2019).
Mi, J. L. et al. Elaborating the crystal structures of MgAgSb thermoelectric compound: polymorphs and atomic disorders. Chem. Mater. 29, 6378–6388 (2017).
Chibueze, T. C., Ekuma, C. E., Raji, A. T., Rai, D. P. & Okoye, C. M. I. Ferromagnetic half-metallicity in half-Heusler AuMnSn : Te Alloy Ferromagnetic half-metallicity in half-Heusler AuMnSn : Te Alloy (2020).
Galanakis, I., Dederichs, P. H. & Papanikolaou, N. Origin and properties of the gap in the half-ferromagnetic Heusler alloys. Phys. Rev. B - Condensed Matter Mater. Phys. 66, 1–10 (2002).
Sanyal, B. et al. Ferromagnetism in Mn doped half-Heusler NiTiSn: Theory and experiment. Appl. Phys. Lett. 89, 1–4 (2006).
Elphick, K. et al. Heusler alloys for spintronic devices: review on recent development and future perspectives. Sci. Technol. Adv. Mater. 22, 235–271 (2021).
Casper, F., Graf, T., Chadov, S., Balke, B. & Felser, C. Half-Heusler compounds: Novel materials for energy and spintronic applications. Semiconductor Sci. Technol. 27, 063001 (2012).
Raccuglia, P. et al. Machine-learning-assisted materials discovery using failed experiments. Nature 533, 73–76 (2016).
Ward, L., Agrawal, A., Choudhary, A. & Wolverton, C. A general-purpose machine learning framework for predicting properties of inorganic materials. npj Comput. Mater. 2, 16028 (2016).
Acknowledgements
This work was supported by the Department of Energy, Energy Efficiency and Renewable Energy program, agreement 34933 at SLAC National Accelerator Laboratory, under contract DE-AC02-76SF00515.
Author information
Authors and Affiliations
Contributions
A.L. carried out this study and prepared the manuscript under close guidance of C.W. and A.M.. S.S. and A.M. carried out the analysis for and wrote the discussion of the XRD comparison with literature. J.S., L.W., and C.B. contributed key ideas and assisted in the manuscript preparation. A.P. and C.W. supported and supervised this work.
Corresponding author
Ethics declarations
Competing interests
C.W. declares a financial interest in Citrine Informatics. All other authors declare no competing interests.
Peer review
Peer review information
Communications Materials thanks the anonymous reviewers for their contribution to the peer review of this work. Primary Handling Editors: Milica Todorović and Aldo Isidori. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lee, A., Sarker, S., Saal, J.E. et al. Machine learned synthesizability predictions aided by density functional theory. Commun Mater 3, 73 (2022). https://doi.org/10.1038/s43246-022-00295-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-022-00295-7
This article is cited by
-
Knowledge-integrated machine learning for materials: lessons from gameplaying and robotics
Nature Reviews Materials (2023)
-
Accelerating the prediction of stable materials with machine learning
Nature Computational Science (2023)