Abstract
Light and flexible thermoelectric generators working around room temperature and within a small temperature range are much desirable for numerous applications of wearable microelectronics, internet of things, and waste heat recovery. Herein, we report a high performance flexible thermoelectric generator made of polymeric thermoelectric composites and heat sink fabrics. The thermoelectric composites comprise n- and p-type Bi2Te3 particles and poly(3,4-ethylenedioxythiophene) polystyrene sulfonate, exhibiting a synergic effect that results in Seebeck coefficients higher than those of the constituent alloys and conductive polymer. The flexible and light thermoelectric generator produces an output power of 9.0 mW, a specific output power of 2.3 mW/g, and an areal power density of 6.5 W/m2 at ΔT = 45 K. By using the heat sink fabrics to maintain a large and uniform distribution of temperature difference across the generator, a three-fold increment of the output power is obtained.
Similar content being viewed by others
Introduction
Harvesting low-grade thermal energy from three-dimensional complex shaped objects or human body requires a generator device with low rigidities of bending, in-plane shear, and tensile deformation so that intimate close contacts and efficient heat transfer can be achieved between the generator and heat source. Therefore, light and flexible thermoelectric generators (FTEGs) working at room- or low-temperature are much desirable for applications of wearable microelectronics, IoT, active microclimate controlling systems, and waste heat utilization1,2,3,4,5,6.
An output power in the order of mini-watts from an FTEG, operating within a temperature difference of ~50 K, is required for driving common wearable microelectronic and IoT devices working at near room temperature. The FTEG output performance depends on its functional and structural materials, device structural design, and fabrication process. At present, heavy and rigid semi-conductor functional and structural materials have been used to fabricate most thermoelectric generators that require annealing at high temperature, at which most polymers or fibers cannot survive5. In addition, the application of liquid-state ionic gelation is limited owing to their super low electrical conductivity, noncontinuous discharge, and inflexible encapsulation. New high-performance flexible thermoelectric (TE) materials must be developed so that they can be adopted in divers FTEGs fabrication. Inorganic-polymer composites may offer an alternative strategy to replace the rigid, heavy, and sometimes toxic semiconductor TE materials. Since polymers are lighter and more flexible with endowed environmental friendliness. Cooperating various nanostructured inorganic thermoelectric particles or nano films into polymers can obtain both high TE performance with the required flexibility and light-weight. The flexible TE precursor materials may take a solution form, containing inorganic semiconductors, organic binders, or conducting polymers. They can be printed, painted, or drop casted, followed by drying or curing processes at an elevated temperature, in order to form solid TE materials or structures5. However, a great challenge is that FTEGs made from such precursors may inevitably have non-conducting binder residuals between the semiconducting particles that reduce the electric conductivity and bring down the TE performance of the composites. It is necessary to strike a balance between the flexibility and performance of FTEGs.
There are several major types of FTEGs categorized by their device structures, that is, sandwich, thin-film, and fabric-structured FTEGs. An increasing number of thin-film structured FTEGs has been reported, where physical/chemical deposition, photolithography, patterning, and ink printing have been used5. Although thin-film structured FTEGs demonstrated have a output power in a range of nW~µW7,8. It is still believed that one of the favorable techniques for the flexible device fabrication because of material saving, one-shot synthesis, structural flexibility, and low-temperature operation. The sandwich-structured FTEGs have better performance. Cho’s group has developed several lightweight watch-like Bi2Te3-based FTEGs via screen printing9. However, high temperature annealing is usually needed for such FTEGs. The functional materials are semi-conductive alloys, rigid but have high TE performance. Son’s group reported p- and n-type Bi2Te3 inorganic paints, geometrically compatible to curve surface10,11. The fabric type FTEGs are newcomers, yet they show some promises in flexibility but fail to offer high performance. The impacts of FTEG device structure on their output performance have remained elusive. For instance, so far very few studies have paid attention to the heat sink effect on FTEGs, although improved performance is known for a rigid generator with heat sink.
The progress of FTEGs has been hindered by lack of suitable TE materials, poor understanding of structural design of the flexible devices and their fabrication process. Therefore, in this paper, we will address the following critical issues. At first, we design and synthesize new printable flexible TE materials via the route of composite precursor with inorganic semi-conductor particles of n- and p-type Bi2Te3 alloys and conductive polymer PEDOT:PSS. We investigate the annealing processes of the composites and determine the optimized operating conditions for the flexible device assembly. We discover significant synergistic effects on the Seebeck coefficients of both n- and p-type composites that render the composites higher coefficient values than the individual constituent pure alloys and polymer. The resultant sandwich-structured FTEG shows an output power of 9.0 mW, specific output power of 2.3 mW/g and areal power density of 6.5 W/m2 at ΔT = 45 K, illustrating its promising application in low-grade thermal energy harvesting devices requiring a driving power of several mWs. The marked three-fold improvement of output power of FTEG with heat-sink fabrics are revealed. Discussions on the further improvements for the FTEGs are offered considering the derived theoretical upper limit of the output power. This work will stimulate more research interests in pursuing easy-encapsulating flexible TE materials and their large feasible scope of applications in wearable electronics, IoT, low-heat waste thermal energy harvesting.
Results and discussion
Sandwich structured FTEGs
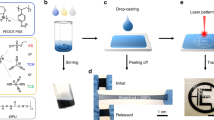
Figure 1a, b illustrates the sandwich device structures and photographs of as-made wearable FTEGs by using the flexible substrates and relatively rigid composites. The sandwich structured FTEG includes two flexible polyimide (PI) thin-film circuit boards with electrodes and connecting tracks, and the chips made from the TE composites consisting of n- and p-type Bi2Te3 alloys and conductive polymer PEDOT:PSS, sandwiched between the PI films, and connected electrically with the electrodes. The p- and n-type composite chips with ZT of 0.4 and 0.5 were connected serially in a π-pair fashion. Compared with the works of BixTey-based composites previously reported in the literatures, both the present n- and p- TE composites show superior properties12,13,14,15,16,17,18,19 (Fig. 1c). To reveal the effects of heat sinks on the device performance, copper fabrics and thermally conductive glue were employed. The fabrication steps of the FTEG are described in the section of “Methods”. The photos of wearable FTEGs of 35 × 40 mm2 in area are shown with and without the heat sinker fabrics (Fig. 1b). Comprising the whole segments, the FTEG still keeps thin (~2 mm) and light (0.38 g/cm2) compared to conventional rigid TEGs with bulky top and bottom ceramic layers.
a Schematic illustration of FTEG, comprising n- and p-TE composite chip pairs connected by flexible polyimide circuit boards as well as copper fabrics as the heat sink. b Photograph of the fabricated FTEG device made from p-/n-composites with (top) and without(middle) the fabric heat sink. (Scale bar: 10 mm). c Performance benchmark of this work against other BixTey-based composites reported in the literatures. The gray background denotes the p-type composites, pink background means the n-type composites. d Output voltage, e output power, f power density and power per mass of the composites FTEGs with/ without the heat-sink copper fabric. Simulated temperature distributions of FETGs without (g)/with (h) the heat-sink fabrics. Calculated relationships between the output power and thermal conductance of one unit under various fixed temperature differences, i and j correspond to the device with and without the heat sink, respectively.
The FTEG were made from n- and p-Bi2Te3 /PEDOT:PSS composites, which were prepared by following the processed in section “Methods” and Supplementary Fig. 1a, b. In the n/p-type composite, several constituent components are present: n-Bi2Te3 (Bi2Te2.68Se0.32) and p-Bi2Te3 (Bi0.52 Sb1.48Te3) alloy particles, PEDOT:PSS, with dimethyl sulfoxide (DMSO), ethanol, α-terpineol and isopropanol added as binding materials for fabricating composite precursor as the flexible materials. The resultant composite precursors acted as a printing paste ink, followed by solidification and annealing at specific temperatures. The major challenge for our strategy is to adjust the rheological property of the ink to guarantee the uniformity of extrusion structure. The high stability of the materials is required to avoid pinhead clogging which might arise from particle sedimentation. Isopropanol and α-terpineol are used to adjust the paste viscosity. Also, we believe the PEDOT:PSS serves as the Sulfur doping agent and conducting connection, regulating the electrical behavior of the composite. The Seebeck coefficient of both n-/p-Bi2Te3 ink-based samples without PEDOT:PSS are inferior than the corresponding samples with PEDOT:PSS. For the electrical conductivity, the results are also slightly lower than that of the composite samples (see Supplementary Fig. 2).
Figure 1d depicts the measured open-circuit voltage as a function of the temperature difference cross the composite FTEG devices with and without copper fabric heat sink. The curves are almost linear. The voltage is 381 mV for the FTEG with fabric heat sink at ΔT = 45 K. It doubles that for FTEG without fabric heat sink at the same temperature difference. When the internal resistance is matching the external load, the measured output power curve of FTEG with heat sink tripled that of the FTEG without the sink fabrics. The heat sink fabric made of fine copper filaments has an outstanding flexibility and thermal conductivity. When ∆T = 45 K, the 32-pair FTEG device of 3.5 × 4.0 cm2, equipped with the fabric heat sink, produces an output power of 9.0 mW (Fig. 1e). This output is comparable to that of a previously reported shape-conformable TEG employing all inorganic Bi2Te3 inks10,11. The FTEG is of lightweight and the specific output power is approximately 2.25 mW/g. The areal output power density is up to 0.64 mW/cm2 or 6.4 W/m2 (Fig. 1f). More importantly, for wearable applications, the temperature difference between human body and environment is small, normally around 15 K if indoor conditions are applied. The single FTEG produces 1.5 mW at 15 K, at an areal power density of 1.07 W/m2. It has competitiveness as compared with other energy harvesting approaches, as the areal output power density of this FTEG is more than twice of the 500 mW/m2 produced by the best triboelectric generator reported so far20.
Numeric calculations based on the measured performance of materials, as described in Supplementary Table 1, yield the theoretical upper limit of the output power of 25.9 mW for an ideal 32-pair FTEG unit made from the identical TE composite and device structure without contact resistance. The output power of the realized device is only 34.7% of the theoretical upper limit thus indicating the large space for improving the device structure and fabrication process in the future.
To deeply understand the influence of the heat sink fabric on the performance of FTEG device, analytical and numerical treatments were applied. The related calculation parameters are presented in the method section. Figure 1g illustrates the simulated large temperature variations of FTEGs without the fabric heat sink, while with the heat sink fabric, the temperature variation on each TE leg is neglectable (Fig. 1h). Taking a closer observation on the surface of the PI substrate, this flexible substrate is not smooth as shown in Supplementary Fig. 3. There will be air gaps between the FTEG and heat source. This effect will induce the temperature variation. The soft and conformable thermal conductive adhesive tape also fills up the airgap between the FTEG and hot or cold surface of the experimental setup.
The calculated results shown in Fig. 1i, j further reveal the relationship between output power and thermal conductance for one unit under distinct temperature difference with or without heat sink fabric, respectively. When the temperature difference is 42 K, for the device with and without heat sink, the output power is 7.4 and 2.8 mW, respectively (Fig. 1e). Correspondingly, the calculated output powers of one pair unit are 0.463 and 0.175 mW, respectively. Some segments of the simulated lines are crossed with the line of 0.463 and 0.175 mW. This means that the numerical results are close to the experimental results under certain temperature difference and thermal conductance. The detailed information is listed in Supplementary Tables 2 and 3. The results reveal that if the thermal conductance at each interface is a constant, the average of temperature difference on TE legs should be in the range of 37–42 K for the device with heat sink; in the range of 23–27 K for the device without heat sink. Therefore, the application of heat sink in the way of enhancing the average temperature difference on TE legs is very effective to achieve the potential of a FTEG device.
Keeping the same thermal conditions of the experimental set-up for about 60 min, the temperature gradient between the both sides of devices will reduce gradually (Fig. 2a–c). This reduction in composite FTEG with heat sink is from 45 to 34 K, smaller than that (44–31 K) of the one without heat sink (Fig. 2a). The output voltage and power reduce with time too (Fig. 2b, c). The copper fabric as the heat sink reduces the thermal resistance while the micro-void in composite can increase the thermal resistance of the device. To illustrate the mechanical performance of the large FTEG (4*3.5 cm, 32 pairs), we measured the resistance variation of the device under bending with radius up to ~15 mm, that is, the index of resistance change (ΔR) to the initial resistance (R0). As shown in the Fig. 2d, the electrical resistance of the FTEG increases slightly with the bending curvature of 15 cm−1, the resulted ΔR/R of the device is less than 40%. Moreover, the FTEG exhibits excellent fatigue resistance as it can be repeatedly bent for 100 cycles, and its resistance recovers after being released (Fig. 2e). For the TE performance, the as-made FTEG with 32 pairs is bent and attached on the tube (curvature radius of ~15 mm) containing warm water with around 305 K and generates an output current-voltage of 88 mV. In general, the variance of the output current-voltage and output power at a applied of ~10 K can be neglected even after 100 bending cycles along the same direction (Fig. 2f). These results show that our highly integration possess a certain extent bendability with a high stable power output, which allows the large-area compliant TEGs to be applied on the human body for energy harvesting. As shown in the Fig. 2g, the FTEG was attached on the arm, here, we assume the thermal contact resistance as zero, thus, the arm skin temperature can be simply regarded as the hot side (Th). For another, the cold side is exposed to the atmosphere, and the room temperature can be considered as Tc. Thus, the temperature gradient through the FTEG is ΔT = Th – Tc. The as-made FTEG with 32 pairs attached on the arm generates an output voltage of about 88 mV with a ΔT of ~8 K (FLIR image). Such an FTEG is enough to drive the sub-microwatt or microwatt electronics for instance memory device or biology sensors. In general, this FTEG indicates the promising potential to working on the human body as the self-powered wearable electronics.
a Measured temperature differences of FTEGs as time lapses. b, c Measured output voltage and power of composite FTEGs plotted against time, when the temperature difference is fixed by the testing device. d Electrical resistance of the FTEG with the bending radius. (inset images: the lateral view of the compliant FTEG under bending radius). e The stability of electrical resistance of the bent FTEG during and after 100 bending cycles with ~15 mm bending radius. f Experimentally measured output voltage and power of 32-pairs FTEG after different bending cycles. g Demonstration for measuring the VOC of FTEG (32 pairs) worn on arm at room temperature. (Scale bar: 40 mm), FLIR image: Temperature distribution between arm and surface of FTEG. h Experimental demonstration for observing the response of FTEG attached on beaker filled with hot water. (Scale bar: 40 mm, see Supplementary Movie 1). i Front view and side view of temperature distributions of the FTEG attached on the outside of a beaker containing hot water. (Scale bar: 40 mm). j Time-resolved Voc of FTEG attached on beaker when adding hot water and going through a natural cooling process. (Scale bar: 40 mm). k An FTEG drives an LED fabric skirt via demo board. (See Supplementary Movie 2). l Time-resolved Voc of FTEG when light on the LEDs.
Figure 2h, i illustrates that an as-made FTEG with 8 pairs is bent and attached on the curved surface of a beaker containing hot water and generates an output voltage of 45 mV. Significantly, owing to the heat sink fabric and inner low thermal conducting TE chips, the device can keep the temperature difference for powering for a while after adding the hot water and going through the natural cooling process. The drop of the output voltage of this device is shown as a function of time (Fig. 2j). The retention rate of the output voltage of this device is 60.7% after 37 s with the hot-water natural cooling, while the reported apparatus without heat sink design remained only 16.7% within 20 s21. Thus, in this system, the thermal-electric conversion shows more efficiency and long-term. Such an FTEG can drive an illuminating fabric with arrays of LEDs in seconds, when applying a temperature difference to the FTEG by the lab-made experimental set-up (Fig. 2k, l).
Here, we further compared the major TE properties of our composites and the output power of FTEGs made from the TE composites, and other BixTey-based FTEGs reported previously in the literature, as illustrated by Supplementary Table 4. It is very encouraging that the present n-type composite has the highest near-room-temperature Seebeck coefficient, superior to all other n-type BixTey alloys and their corresponding BixTey/PEDOT:PSS materials. The present p-type composite also exhibits a high Seebeck coefficient, slightly higher than its constitutive alloy and much higher than other reported works. Due to the low electrical conductivity of the composites, the power factors for the n- and p-type composites have much space to improve, as compared with their constituent alloys. The output power of the composite FETG is better or comparable to most reported previously9,10,11,12,21,22,23,24,25,26,27,28. The present composite FTEG has an improvement space of one order of magnitude before reaching it theoretical limit of the output power for the composite FTEGs. The optimization of device structure and reduction of contact resistance can further improve the output power of the composite FTEGs.
We also used the same TE composite precursor ink paste to print on thin films of elastomer polydimethylsiloxane by a substrate transfer process, followed by thermal annealing treatment of 423 K. The PDMS FTEG shows a great foldability and durability in repeated bending test, as illustrated in Supplementary Fig. 4. The electrical resistance of the FTEG increases slightly with the bending curvature (from 0 to 2.5 cm−1). The FTEG exhibits excellent fatigue resistance as it can be repeatedly bent for 100,000 cycles, and its resistance recovers after being released. Mechanically, the FTEG also reverts to its original state when being released. These results show that the FTEG can be crimped and worked on the curved body as TE power sources. However, the thin-film-structured FTEG exhibits four orders of power less than the sandwich-structured FTEGs made of composite (Supplementary Fig. 5). We believe that the lack of densification process and lower annealing temperature of the printed FTEGs contribute to the impaired compactness of TE composite and its TE performance.
TE properties of n-type Bi2Te3/PEDOTP:PSS composites
As shown in Supplementary Fig. 6, the size of n-Bi2Te3 particles used in these FTEGs fabrications are varied with the average size of ~5 µm. According to the X-ray diffraction (XRD), the peaks allocations of n-Bi2Te3 in the composites are in accordance with Bi2Te3, PDF #08-0027, accompanied by spikes of amorphous matrix, PEDOT:PSS (Supplementary Fig. 7a). On the basis of thermal stability test (Supplementary Fig. 7b), the n-composites go through a few stages with the thermal increment. In the first stage, the weight loss up to 473 K is attributed to the vaporization of organic solvents. In other word, the n-Bi2Te3 and PEDOT:PSS coexist in the composite29. Then in the second stage, the de-composition of PSS starts from 538 K and ends at 593 K with a weight loss of 25 wt%. When the materials comes to the third stage, the decomposition of PEDOT begins with 623 K and ends at 873 K with a weight loss of 10 wt%29. Combined with the X-ray photoelectron spectroscopy analysis, the samples under 623 K annealing or above, both liner structure of PEDOT and part of carbonization co-existed (Supplementary Fig. 8 and Note 1). The annealing process has an effect on not only the structure and composition of the composites but also the TE properties. The treatment temperatures were selected according to the stages, as 423, 593, 623, and 673 K, respectively.
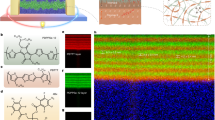
The morphology and thermoeletric properties of n-Bi2Te3 alloy and n-Bi2Te3/PEDOT:PSS composite, annealed at the selected temperatures, measuring from RT to 423 K, are evaluated. Figure 3a–d demonstrates the top-view SEM images of n-composite samples annealed at various temperatures. The n-composite particles tend to merge with the increasing temperature treatments (from 423 to 623 K). The particles distribute randomly without any apparent aligned structure. The presence of PEDOT:PSS plays an significant role in this phenomenon. When temperature increases up to 623 K, the PEDOT:PSS connects the particles. However, when the temperature further rises (673 K), the degradation and vaporization of polymers dominate thus some pores are visible inside the composite.
a–d Top-view SEM images of n-Bi2Te3/PEDOT:PSS composites annealed at 423, 593, 623, and 673 K, respectively. e Curves of electrical conductivity vs. temperature of n-Bi2Te3/PEDOT:PSS, and PEDOT:PSS, respectively. f Room-temperature electrical conductivity of annealed n-Bi2Te3/PEDOT:PSS composites as a function of weight. g Seebeck coefficients of n-Bi2Te3/PEDOT:PSS samples and PEDOT:PSS. h Hall mobility, and i carrier concentration of n-Bi2Te3/PEDOT:PSS samples, j thermal conductivity, k Power factor, l figure of merit of n-Bi2Te3/PEDOT:PSS composites and PEDOT:PSS.
The electrical conductivity (σ) of the composite samples enhances with the annealing treatment. Yet, the σ of PEDOT:PSS is low at 6.96 × 102 S m−1 and does not change much from the 298 to 423 K. The pure n-Bi2Te3 alloy samples always exhibit higher σ when comparing with the composites (Fig. 3e and Supplementary Fig. 9a). It appears the room-temperature electrical conductivity of the composites reaches a peak between 593 and 623 K, then declines with the increasing annealing temperature30,31. The conducting performance of n-composites is dominated by the intrinsic property of the n-Bi2Te3 and PEDOT:PSS matrix, and also influenced by the polymer-filler interactions. For the DMSO doped n-composite sample, the PEDOT chains covert from a coil shape to an entangled linear structure (Supplementary Fig. 10 and Note 2). This conformational change has a positive effect on electrical conductivity since the linear structure reduces the energy barrier of the PEDOT chains, promoting the carrier shifting through the p-conjugated PEDOT skeletons32.
The room-temperature σ of the n-composite is plotted against the weight residual under annealing in Fig. 3f, illustrating the four stages of n-composites transformation. We can use the percolation-like theory to interpret this phenomenon33,34. In the first stage, the composite contains n-Bi2Te3 particles, PEDOT:PSS and few organic insulated binders (n-composite −423 K), demonstrating the lowest σ of 2.23 × 102 S m−1. Then the conductivity is enhanced with the annealing temperature up to 593 K (Second stage), the σ of sample increases to 90.09 × 102 S m−1. The room temperature σ of the annealed composite peaks between 623 and 673 K, being about 94.89 × 102 S m−1 and 55.97 × 102 Sm−1, respectively. From the first to the third stage, with the increasing annealing temperature, the insulating PSS degrades first. The degradation and re-orientation of the PEDOT:PSS may affect the electrical conductivity, and the PEDOT acts as the bridges to couple the Bi2Te3 particles, forming the crisscross circulation network between the particles, which facilitates the charge transport. More pores appear because of the Se sublimation (Supplementary Table 5) and degradation of PEDOT:PSS. The electrical performance are blunted since the pores inside impeded grain growth instead. Eventually, when the percolation threshold is achieved, in this regards, adding more fillers could not promote the electron shifting further.
The Seebeck coefficient of n-composites are much greatly improved with annealing in a nonmonotonic manner. The room-temperature Seebeck coefficients of annealed n-composites can be listed in a descending order, 673, 423, 623, and 593 K. Most interestingly, there is a surprisingly large synergy of the n-alloy and PEDOT:PSS. With the same annealing temperature, the Seebeck coefficient of each composite is higher than that of its corresponding pure n-Bi2Te3 counterpart. A coefficient value of −218.0 μVK−1 at room temperature is obtained from the composites annealed at 673 K, much higher than −98.0 μVK−1 of its pure alloy (Supplementary Fig. 9b), higher than those reported previously in other TE composite works (Supplementary Table 6). Previously, adding p-type PEDOT:PSS into the n-type inorganics did not yield a high n-type performance18. This surprisingly great enhancement may be attributed to that the effect of Sulfur (S) in PEDOT:PSS, which acts as the substitutional impurity, promoting the Seebeck coefficient of the whole material system35. As shown in XPS spectrum (Supplementary Fig. 11), apart from the band of S 2s positioned at 228.4 eV from PEDOT:PSS, a S 2s sub-band of 232.2 eV that was produced by the thioligated pnictogen and chalcogen is detected. In the composite, the S from PEDOT:PSS diffuses into the rigid Bi2Te3 alloy particles, enabled by the annealing treatment. This S doping is similar to the Se, playing a crucial part in Seebeck coefficient enhancement. In addition to guiding the connection of composite annealing at a selected temperature, PEDOT:PSS here also serves as the Sulfur doping agent, regulating the electrical behavior of the composite.
Figure 3h presents the mobility (μH) of annealed TE samples as a function of temperature, with all the samples displaying a declining trend. At the lowest annealing temperature of 423 K, the carrier mobility in the composite is the lowest among all the composite samples. The pores in TE materials may influence the charge carrier transport because of the potential perturbation near the pore sites36,37. The Matthiessen’s rule in Eq. (1) describes the total scattering contributions by different carrier scattering mechanisms, due to those by impurity, grain boundary, pores, and the bulk acoustic phonons, respectively38.
Assuming no any other impurities in the n-Bi2Te3 alloys, μboundary and μpore should be the main reasons to affect the overall mobility. The boundary and porosity effects on mobility become weaker for larger grains as suggested by Lee et al.18. For the n-composite, the mobility is lower than those for the alloys (Supplementary Fig. 9c). The possible reason is that more phonons in the composite than in the alloys, and thus increases carrier scattering, which tends to reduce mobility. The relationship between the mobility and annealing temperature is more complicated in the composites. Annealing at the range from 423 to 623 K, the mobility of composite is enhanced gradually, after that it is reduced at 673 K. The mobility increment is ascribed to the connection of PEDOT and Bi2Te3, activating the conducting access through the interfaces. However, when the temperature raising to the 673 K, with thermal degradation of PEDOT, the mobility reduces owing to the high porosity. Consequently, the relatively high number density of pores can result in the low electrical conductivity of 673 K—annealed composite sample.
The composites present relatively low concentration contrast to the pure n-Bi2Te3,(Fig. 3i) which attributing to the high Seebeck coefficient. For the n-type Bi2Te3 (Bi2Te2.68Se0.32) samples with 423 K-, 593 K- annealing, the values are relatively low (1.45 × 1018–1 × 1019 cm−3) compared to typical bulk Bi2Te3-based materials, which is answerable for the comparatively poor electrical conducting performance of 623 K-, 673 K- annealed samples, as well as other related bulk materials (Supplementary Fig. 9d). This is because the lower the annealing temperature, the higher the Se content in the semiconductors which will lead to the reduced carrier density. When doping with the Se in the Bi2Te3 system, Se will occupies the Te vacancies and make up two free electrons forming the SeTe anti-defects, that is, \({{{{{\rm{Se}}}}}}+{V}_{{{{{{\rm{Te}}}}}}}+2{e}^{-}={{{{{{\rm{Se}}}}}}}_{{{{{{\rm{Te}}}}}}}\), which will decreases the carrier density in the whole system39. The results for the 423 K-, 593 K- annealing samples are in tune with the similar Bi2Te2.7Se0.3 material40. For the intense heating preparing (623 K-, 673 K- n-Bi2Te3), the corresponding performance of the materials are higher than the 423 K-, 593 K- annealed samples. One possible reason is accounting to the vaporization of Selenium (Se). Se is much easier to evaporate during the annealing process because of low energy of evaporation and thus it leaves Se vacancies and free electrons, which may contribute to higher electrical conductivity30. This can be indicated in the following Eq. (2):30,31
The decreased Se vacancies and increased anti-defects make the carrier concentration converges to about 1 × 1020 cm−3, thus improve the electrical conductivity. Traditionally, PEDOT:PSS is a p-type material and even using an n-type inorganic material like Bi2Te3 could not yield composite materials with high n-type performance18. This is a main reason for the low carrier density of all the n-type composites. However, taking advantage of the high flexibility of PEDOT:PSS chains, noting that the PEDOT:PSS can potentially be de-doped by Bi2Te3 through electron transfer show the potential for inverting the nature of the majority charge carrier (from holes to electrons) in PEDOT:PSS, in principle, obtain n-type hybrids with promising TE properties.
Figure 3j in the present composite system, the highest thermal conductivity of composite is 0.53 Wm−1K−1, annealed at 623 K owing to its compact structure. The low thermal conductivity of 423 K, 593 K annealed composite samples is because of the presence of thermally insulating PEDOT:PSS. For the low thermal conductivity of the 673 K annealed sample, the pores act as the thermal blockers instead. On the other hand, the limited phonon mean free path in this composite system can effectively reduce its phonon thermal conductivity41. Thermal conductivity is also influenced by scattering induced by the morphology. By adding scattering centers, or by thermal degradation of PEDOT:PSS, or by inducing micro-rough surface due to annealing, the thermal conductivity can be effectively reduced when compared with the pure alloys (Supplementary Fig. 9e).
Figure 3k, l displays the power factor and ZT curves as a function of temperature. The power factor for n-type composite varies from 9 to 306 μWm−1 K−2 less than that of the alloys annealed at the same temperature. The maximum power factor of the n-composite is 306 μWm−1 K−2, obtained from the sample annealed at 623 K. Although the Seebeck coefficient of the optimized composite shows unexpected two times higher than the alloy at room temperature, its electrical conductivity is almost one order of magnitude inferior to the alloy. The combined effects are reflected on the difference of power factor between the composite and alloy (Supplementary Fig. 9f). At room temperature, the composite has a ZT of 0.26 close to that of the alloy annealed at 673 K (Supplementary Fig. 9g). Normally, one may expect that the power factor and ZT of the composites are always lower than those of the constituent alloy, as it is reasonable to assume that a homogeneous composite composed of disparate ingredients working separately cannot have a higher power factor or ZT than that of any single component. However, this work indicates the very possibility for a composite to achieve a comparable ZT value of the constituent alloy while exhibiting high flexibility via careful engineering of the composite material electric and TE properties.
TE properties of p-type Bi2Te3/PEDOTP:PSS composites
In this p-composite precursor, the average size of p-Bi2Te3 particles is roughly 20 µm (Supplementary Fig. 12), bigger than the n-type alloy. The small granular particles can fill into the interspace of the large ones, generating a compact packing. The structures of p-Bi2Te3, PEDOT:PSS, and their composites are revealed by XRD, Raman spectra, Fourier Transform Infrared Spectroscopy (FTIR), as shown in Supplementary Fig. 13. According to the results in TGA analysis (see Supplementary Fig. 14), the range of annealing temperatures for the p-type samples was similar to the n-type ones. As shown in (Fig. 4a–d), the schistose particles appear in the 593 K-annealed sample then grow up with further raising temperature, some of the polyhedral particles reach a size of about 20 μm. Moreover, samples annealed at 623 and 673 K have a higher density than the 423 and 593 K annealed samples (see Supplementary Fig. 15). The variation in density and ordered structures will affect the TE properties accordingly. In addition to the morphology, the constituent composition of p- Bi2Te3 alloy varies with the annealing temperature. These two effects will have impact on the electrical conductivity of the composites as well.
a–d Top-view SEM images of p-Bi2Te3/PEDOT:PSS samples annealed at 423, 593, 623, and 673 K, respectively. e Measured temperature-dependent electrical conductivity of p-Bi2Te3/PEDOT:PSS and PEDOT:PSS, respectively. f Measured room temperature electrical conductivity of p-Bi2Te3/PEDOT:PSS with the weight variance under annealing, respectively. Measured temperature-dependent. g Seebeck coefficient of p-Bi2Te3/PEDOT:PSS samples and PEDOT:PSS, respectively. Temperature-dependent h Hall mobility, and i carrier concentration of p-Bi2Te3/PEDOT:PSS samples j thermal conductivity, k power factor, l figure of merit of p-Bi2Te3/PEDOT:PSS and PEDOT:PSS, respectively.
The temperature-dependent electrical conductivity of p-composites and PEDOT:PSS, are displayed in Fig. 4e, respectively. For the p-composites, the higher annealing temperature treatments result in higher electrical conductivity. The corresponding merits near room temperature is enhanced from 0.70 × 102 to 66.8 × 102 S m−1, with the annealing temperature from 423 to 673 K. Interestingly, the effect on the pure Bi2Te3 alloys is not the same, the optimal peformance of temperature is 623 K (see Supplementary Fig. 16a). This tendency of the p-composites is related to the weight variance due to the annealing treatments, as shown by TGA data. Figure 4f illustrates room-temperature conductivity of the annealed p-composites with various anealing treatments. In the first stage, the p-composite presents the lowest σ of 0.70 × 102 S m−1. When the annealing temperature reaches 593 K, the low-boiling-point organic binders evaporate and the PSS decomposites, a weight loss of 1.5% occurs. Furthermore, more compact microstructure can be found in the samples annealed at 623 and 673 K. Their room-temperature electrical conductivities are increased to 56.8 × 102 Sm−1, and 66.8 × 102 S m−1, respectively. The solid composite is formed with p-Bi2Te3 particles in an electrically conductive PEDOT matrix, when annealed at 673 K. The initially small particles of p-Bi2Te3 grow up and occupy the interspace between the bulky particles, enhancing the system packing density, thus increasing the conductivity. When the annealing temperature increases at or above 673 K, the electrically conductive PEDOT degrades a lot thus p-Bi2Te3 particles form their own connected network in the composite. The electrical conductivity is enhanced with grain growth as well as structure densification. Furthermore, the presence of PEDOT:PSS reduces the oxidization of the Bi2Te3 in the composites, as shown by XPS spectra (see Supplementary Fig. 17), displaying the interaction between p-Bi2Te3 and PEDOT:PSS. As a whole, different from the n-type composites, the evidences demonstrate the positive effects of the gradually increasing annealing treatment on electrical conductivity of the p-composites.
The temperature-Seebeck coefficient curves are displayed in Fig. 4g. The raising annealing temperature drastically enhances the room-temperature Seebeck coefficient of the p-composites from 168.9 to 273.3 μV K−1, that of the alloy from 198.0 to 270.0 μV K−1, respectively (Fig. 14b). In the measurement range, the Seebeck coefficients of the composites reach the same level as those of the pure Bi2Te3 alloys, when annealed at 593 K or above. Both the composites and Bi2Te3 show a similar monotonic declination from 296 to 423 K. The annealing effect in Bi2Te3 alloys is similar to but smaller than that in the composites. Both exhibit considerably high Seebeck coefficients when benchmarking with other contemporary works (see Supplementary Tables 7 and 8).
Figure 4h presents the Hall mobility of annealed TE samples. The Hall mobility is reduced with increasing temperature while the carrier concentration shows the opposite tendency (Fig. 4i). The mobility values of the composites and alloys are increased with the annealing treatments (Fig. 14c). However, the μH value for the 623 K-annealed samples decreases in composites with PEDOT:PSS. The possible reason is that more phonons in the p-composite than in the Bi2Te3 alloys, thus more carrier scattering, which tends to reduce their mobility. The access of the electrical network is owing to the interaction between p-Bi2Te3 and the conjugated thiophene chains in PEDOT:PSS. The carrier mobility of the Bi2Te3 is increased from 26.7 up to 146.28 cm2 V−1s−1 at room temperature by the annealing treatment. High temperature annealing caused a reduction in grain boundary and scattering center, which provide a long effective mean free path of carriers, attributing to the mobility enhancement42,43. The carrier concentrations of the p-Bi2Te3 (Bi0.52 Sb1.48Te3) samples with varied thermal treatments are relatively lower those of typical bulk Bi2Te3 alloys (see Supplementary Fig. 16d), leading to the comparatively poor electrical conductivity. Here the major charge carriers are holes, generated by BiTe and SbTe antisite defects44. The evaporation energy of Bi, Sb and Te are 104.80, 77.14, and 52.55 kJ mol−1, respectively, demonstrating that Te tends to vaporize more easily than Bi and Sb during a high thermal process45. Since the carrier concentration in (Bi2Te3)x(Sb2Te3)1−x decreases with increasing Bi2Te3 content, for the p-Bi2Te3 samples, reducing the annealing temperature will lead to the lower antistructure defects of BiTe and SbTe owing to the large difference in electronegativity among Bi, Sb and Te. The relatively mild thermal treatments in this work confine the carrier concentration to the 3 × 1018 cm−3 which are relatively lower compared with 1 × 1019–3 × 1019 cm−3 of typical bulk Bi2Te3-based materials.
For the p-type composites, owing to intrinsic comparatively small carrier concentrations of the p-Bi2Te3 samples (3 × 1018–3 × 1019 cm−3) and PEDOT:PSS, it is reasonable to assume that the resulting composites possess the relatively less carriers. When the annealing treatment enhances up to 623 and 673 K, parts of thermal decomposition of PEDOT and carbonization does not induce extra carriers further.
The annealing treatments lead to increased thermal conductivity of all samples, as illustrated in Fig. 4j. The lowest thermal conductivity is 0.28 Wm−1K−1 (annealed at 423 K), owing to the thermally insulating PEDOT:PSS polymer of ~0.27 Wm−1K−1, filling gaps and spreading well on the interface between the particle and matrix. The composites have lower values of thermal conductivity in all the cases compared with the p-Bi2Te3 alloy samples (see Supplementary Fig. 16e). In the 623 K- and 673 K-annealed composite samples, the pores act as the thermal blockers instead of PEDOT:PSS as a result of thermal degradation of PSS then PEDOT. The limited phonon mean free path in the composite can effectively reduce its thermal conductivity according to Boltz-mann equation46. Thermal conductivity is also influenced by the morphology via scattering mechanism. By adding scattering centers, or by heat-induced degradation of PEDOT:PSS, or by inducing micro-rough surface due to annealing, the thermal conductivity will be further reduced47.
The power factor and Figure of merit (ZT) are plotted in Fig. 4k–l, respectively. The maximum power factor of the p-composite is 473.5 μWm−1K−2, obtained from the sample annealed at 673 K. The room-temperature ZT value of the composite increases from 0.002 to almost 0.4. These promising ZT values of the composite samples originate in high values of Seebeck coefficient, electrical conductivity, and ultra-low values of thermal conductivity. Although the power factor and ZT of the composites are always lower than those of the pure p-Bi2Te3 alloys (see Supplementary Fig. 16f, g). The highest room temperature power factor and ZT of the composite samples are comparable to those of the bulk p-Bi2Te3 alloy samples annealed at the low temperature.
Conclusion
A sandwich-structured FTEG with heat sink fabric has been designed and fabricated by employing high-performance TE composites, producing an output power of 9.0 mW, specific output power of 2.3 mWg−1 and an areal power density of 0.65 mWcm−2 with a temperature difference of 45 K. The employment of the heat sink fabrics has yielded three-fold increment in the output power of the generator. More significant result is the high output power at a relatively small temperature difference, say, between human body and office environment around 15 K. The solid and stationary sandwich-structured FTEG has an areal output power density of 1.07 Wm−2 at 15 K. This value is comparable to the output of an indoor solar cell and more than twice of the highest power value from a flexible triboelectric generator reported so far. It is promising to drive microelectronic devices for indoor wearable and IoT applications.
Secondly, flexible n-type and p-type Bi2Te3/PEDOT:PSS TE composites have been designed, fabricated and characterized for making the generators. The effect of annealing and optimized annealing processing conditions have been determined experimentally. The composites display the highest values for both the Seebeck coefficient and power factor among all BixTey polymer composites previously reported in the literature. The optimized TE composite displays a surprisingly high room-temperature Seebeck coefficient of −218.0 μV K−1 (n-type), much higher than its constituent bulk alloy and polymer matrix; 273.3 μV K−1 (p-type) slightly higher than the bulk constitutive alloy. The synergic phenomena in the TE composites are attributed to the interactions between the doped Bi2Te3 alloy particles and PEDOT:PSS polymer during the annealing process.
The present sandwich-structured FTEG only produces 34.7% of the theoretical output power from the ideal device made from identical materials and structure. Hence, there is a large scope for further improvement of their performance. Therefore, this study illustrates the current limitations, sets the theoretical upper limits for output power of FTEGs, and charts up a roadmap for achieving the theoretical upper output limits. We believe that this work will stimulate more investigations, eventually leading to the successful applications of FTEGs as an alternative power source for wearable microelectronic devices.
Methods
Materials
Bi2Te2.68Se0.32, Bi0.52 Sb1.48Te3 (99.99%, Kaiyada materials, China), poly(3,4-ethylenedioxythiophene) polystyrene sulfonate (5.0 wt. %, conductive screen printable ink, Sigma Aldrich), dimethyl sulfoxide (99.9% %, VWR Chemicals), ethanol (99.8%, VWR Chemicals), α-terpineol (96%, Alfa Aesar), isopropanol (AR, UNI-CHEM), neutral silicone (100%, Ele-wintex), tetrahydrofuran (99.9%, VWR Chemicals), Silver paste DGP80 TESM8020 (75%, Sigma Aldrich), were purchased commercially and used without any further treatment.
Preparation of Bi2Te3/PEDOT:PSS Hybrid Ink Paste
The TE ink was prepared based on a well-dispersed mixture of Bi2Te3 and PEDOT:PSS, with addition of DMSO, isopropanol and α-terpineol. During the mixing process Bi2Te3 particles and PEDOT:PSS were immersed into organic solvent, forming a homogeneous paste. The ink paste consists of 3 g Bi2Te3, 0.4 g DMSO, 2.0 g PEDOT:PSS, 0.43 g isopropanol, and 0.46 g α-terpineol. The mixing paste was stirred for 12 h to maintain the specific viscosity used for the printing approach. The viscosity of the paste was measured by DV-E Viscometer, Brookfield.
Sample preparation for characterization and tests of TE properties
All the Bi2Te3, Bi2Te3/PEDOT:PSS samples were pressed as the pellets. Then the pellet samples were annealed at 423, 593, 623, and 673 K using the tube furnace under argon atmosphere for 3 h before the measurements.
Structural characterization
The morphology of TE materials was characterized by scanning electron microscopy (Tescan VEGA3). Raman spectra measurements were carried out on a Raman spectrometer (BaySpec’s Nomadic™ Raman microscope 3-in-1, λexc = 532 nm), FT-IR spectra of TE materials were recorded on Perkin Elmer Spectrum 100 FT-IR and FT-IR Spectrometers. The crystalline structure of TE materials was obtained from Rigaku Smart Lab with Cu Kα radiation (λ = 1.5406 Å). Thermal stability analysis of TE materials was conducted on thermogravimetric analyzer (METTLER TOLEDO Thermal Analysis, STARe system) in an atmosphere of nitrogen. X-ray photoelectron spectrometry (XPS) analysis was measured by Physical Electronics 5600 multi-technique system, using monochromatic Al-alpha source.
Evaluation of performance
The thermal stability of the samples was tested by Thermo-gravimetric analysis (TGA), under a nitrogen atmosphere created by fluxing 50 ml/min of N2 from 323 to 1200 K at the heating rate of 10 K/min. Seebeck coefficient and electrical conductivity of the TE films were obtained by SBA 458 Nemesis® measurement Setup (NETZSCH Group, German). Three measurements were done for each sample and the average value was quoted. The thermal conductivity was measured by laser flash apparatus (LFA 457 MicroFlash®, NETZSCH Group, German). Hall effect of TE samples were tested by pressure-assisted molybdenum contacts with 1T magnet, employing the van der Pauw technique.
Fabrication of Sandwich-structured FTEGs
Both p-Bi2Te3/PEDOT:PSS and n-Bi2Te3/PEDOT:PSS films were dried at 623 K under argon condition for about 3 h. Afterwards, the films became powders. Then, the sample powders were under hot pressing process to obtain the TE pillars. In this process, the powder was filled into the graphite die, then placed in a hot-press system. The p-Bi2Te3/PEDOT:PSS sample were hot pressed at 673 K under a pressure of 1.2 GPa for 1 h in argon. The n-Bi2Te3/PEDOT:PSS sample were hot pressed at 623 K under a pressure of 1.2 GPa for 1 h in argon. Subsequently, the chamber was filled with Ar and the sample was heated with a rate of 10 K/min to different temperatures, and then was cooled down in the system to room temperature. The final products were ready for chips engineering.
Then, the hot-pressed p- and n-composite pillars were cut into small chips with a square cross section of 2 mm × 2 mm and 2 mm in height. Then, the TE chips were arrayed into a 4 × 8 matrix with 2 mm interspace between adjoining chips. The array of 32 π-chip pairs was attached to a flexible PI circuit board with Cu electrodes and tracks by using an Ag epoxy adhesives, followed up with heating at about 573 K for 10 min. The repetitive operation was reused for the bottom layer assembly. The π-chip pairs were connected in series. The Cu electrodes and tracks on the PI circuit board were made by etching process before for the electric connection. After that, a double-sided thermal conductive adhesive tape was attached on the outside of PI circuit board and followed by adhesion of a copper wire fabric.
Evaluation method of FTEG performance
For the performance evaluation, lab-made TE measurement system was used to evaluate the TE performance of the FTEGs. In this system, the voltmeter and temperature detector are used for output voltage and temperature difference recording. A lab-made system that includes a Keithley 2700 multimeter, Whatlent TEC temperature Control offers heat/cold source. A temperature control system including a pump and cooling water tank is used to cooling down the whole system. The output voltages were measured by Keithley 2700 and temperature difference of the module was tested by Anbat AT4516 simultaneously. A external load resistance is selected to match the internal device resistance to obtain the maximum power. The top/bottom surface of the FTEG is in direct contact with the hot/cold side in the experimental set-up.
For the FTEG demonstration, the whole system were assembled with FTEG module, LED fabric, heat/cold sink, and reusable connectors. The demo setup can show us the potential of FTEG, roughly predict how much energy generated from the device can be fully applied. The switched output voltage was promoted by a DC–DC step-up converter, optimized for harvesting and managing energy. Simply locate the FTEG on heat/cold sink, then offer the temperature difference on the top and bottom surface of the FTEG, and watch the decorative LED light up in seconds.
Simulation
According to the experimental results, for one pair of TE legs, the matched external resistance is \(0.3125\,\Omega\). The internal resistance of one pair of TE legs can be given by
where \(\sigma\) is the electrical conductivity; \(L\) is the length of TE leg, which is 2 mm; \(A\) is the cross-sectional area of TE leg, which is (2 mm2); the subscript \(i\) represents the p- or n-type TE legs. Thus, \({R}_{{{{{{\rm{TE}}}}}}} \, < \, {R}_{{{{{{\rm{ex}}}}}}}\), which means that the existence of electrical contact resistance (ECR) at the interface between the TE leg and electrode. Suppose the ECR on each interface is same. For one pair of p- and n-type TE legs, there are four interfaces between TE legs and electrodes. Therefore, the ECR at each interface is
Correspondingly, the electrical conductance is
The simulation was conducted by a commercial software, COMSOL Multiphysics®. The geometrical and material parameters come from the former experimental results48. There are some assumptions: (1) only conductive heat transfer; (2) isotropic material properties; (3) electrical conductance at the interface between TE legs and electrodes is \(5.4\times {10}^{6}\,{{{{{\rm{S}}}}}}/{{{{{{\rm{m}}}}}}}^{2}\); (4) thermal contact resistance (TCR) is same at each interface between TE legs and electrodes. One unit of the deivce is composed of 2 pairs of p- and n-type TE legs. Thermal contact resistance (\({\theta }_{c}\)) is given by
where \({h}_{{{{{{\rm{tc}}}}}}}\) is the thermal conductance (W/m2·K), which is in the range of 2 × 103–1 × 105 W/m2·K49. The ideal case is no thermal contact resistance, that is, \({h}_{{{{{{\rm{tc}}}}}}}=\infty {{{{{\rm{W}}}}}}/{{{{{{\rm{m}}}}}}}^{2}\cdot {{{{{\rm{K}}}}}}\).
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Wan, Q. P., Teh, Y. K., Gao, Y. & Mok, P. K. T. Analysis and design of a TE energy harvesting system with reconfigurable array of thermoelectric generators for IoT applications. IEEE Trans. Circuits Syst. I-Regular Papers 64, 2346–2358 (2017).
Wan, Q. P. & Mok, P. K. T. A 14-nA, highly efficient triple-output thermoelectric energy harvesting system based on a reconfigurable TEG Array. IEEE J. Solid-State Circuits 54, 1720–1732 (2019).
Lin, S. P., Zeng, W., Zhang, L. S. & Tao, X. M. Flexible film-based thermoelectric generators. MRS Adv. 4, 1691–1697 (2019).
Zeng, W. et al. Defect-engineered reduced graphene oxide sheets with high electric conductivity and controlled thermal conductivity for soft and flexible wearable thermoelectric generators. Nano Energy 54, 163–174 (2018).
Zhang, L. S. et al. Fiber-based thermoelectric generators: Materials, device structures, fabrication, characterization, and applications. Adv. Energy Mater. 8, 1700524 (2018).
Tao, X. M. Study of fiber-based wearable energy systems. Accounts Chem. Res. 52, 307–315 (2019).
Karthikeyan, V. et al. Wearable and flexible thin film thermoelectric module for multi-scale energy harvesting. J. Power Sources 455, 227983 (2020).
Burton, M. R. et al. Thin film tin selenide (SnSe) thermoelectric generators exhibiting ultralow thermal conductivity. Adv. Mater. 30, 1801357 (2018).
Kim, S. J., We, J. H. & Cho, B. J. A wearable thermoelectric generator fabricated on a glass fabric. Energy Environ. Sci. 7, 1959–1965 (2014).
Park, S. H. et al. High-performance shape-engineerable thermoelectric painting. Nat. Commun. 7, 13403 (2016).
Kim, F. et al. 3D printing of shape-conformable thermoelectric materials using all-inorganic Bi2Te3-based inks. Nat. Energy 3, 301–309 (2018).
Wang, W. et al. A high packing density micro-thermoelectric power generator based on film thermoelectric materials fabricated by electrodeposition technology. Surface Coat. Technol. 231, 583–589 (2013).
Du, Y., Cai, K. F., Chen, S., Cizek, P. & Lin, T. Facile preparation and thermoelectric properties of Bi2Te3 based alloy nanosheet/PEDOT:PSS composite films. ACS Appl. Mater. Interfaces 6, 5735–5743 (2014).
Goo, G. et al. Proton-irradiation effects on the thermoelectric properties of flexible Bi2Te3/PEDOT:PSS composite films. Adv. Electron. Mater. 5, 1800786 (2019).
Shin, S. M., Roh, J. W., Kim, H. S. & Chen, R. K. Role of surfactant on thermoelectric behaviors of organic-inorganic composites. J. Appl. Phys. 123, 205106 (2018).
Sahu, A. et al. Bottom-up design of de novo thermoelectric hybrid materials using chalcogenide resurfacing. J. Mater. Chem. A 5, 3346–3357 (2017).
Abd Rahman, A. A., Umar, A. A. & Othman, M. H. U. Effect of bismuth telluride concentration on the thermoelectric properties of PEDOT:PSS-glycerol organic films. Physica E-Low-Dimensional Syst. Nanostruct. 66, 293–298 (2015).
Zhang, B., Sun, J., Katz, H. E., Fang, F. & Opila, R. L. Promising thermoelectric properties of commercial PEDOT:PSS materials and their Bi2Te3 powder composites. ACS Appl. Mater. Interfaces 2, 3170–3178 (2010).
We, J. H., Kim, S. J. & Cho, B. J. Hybrid composite of screen-printed inorganic thermoelectric film and organic conducting polymer for flexible thermoelectric power generator. Energy 73, 506–512 (2014).
Yu Song, J. M. et al. Wireless battery-free wearable sweat sensor powered by human motion. Sci. Adv. 6, eaay9842 (2020).
Lee, B. et al. High-performance compliant thermoelectric generators with magnetically self-assembled soft heat conductors for self-powered wearable electronics. Nat. Commun. 11, 5948 (2020).
Kashiwagi, M., Koshi, T. & Iwase, E. High performance flexible thermoelectric device included rigid material. IEEE, 2019 IEEE 32nd International Conference on Micro Electro Mechanical Systems (Mems) 1010–1012 (Institute of Electrical & Electronics Engineers, 2019).
Ren, W. et al. High-performance wearable thermoelectric generator with self-healing, recycling, and Lego-like reconfiguring capabilities. Sci. Adv. 7, eabe0586 (2021).
Peng, J. et al. 3D extruded composite thermoelectric threads for flexible energy harvesting. Nat. Commun. 10, 5590 (2019).
Shi, Y. G., Wang, Y. C., Mei, D. Q. & Chen, Z. C. Wearable thermoelectric generator with copper foam as the heat sink for body heat harvesting. IEEE Access 6, 43602–43611 (2018).
Lee, G. et al. Flexible heatsink based on a phase-change material for a wearable thermoelectric generator. Energy 179, 12–18 (2019).
Park, H. et al. Mat-like flexible thermoelectric system based on rigid inorganic bulk materials. J. Phys. D-Appl. Phys. 50, 494006 (2017).
Hong, S. et al. Wearable thermoelectrics for personalized thermoregulation. Sci. Adv. 5, eaaw0536 (2019).
Sakunpongpitiporn, P., Phasuksom, K., Paradee, N. & Sirivat, A. Facile synthesis of highly conductive PEDOT:PSS via surfactant templates. RSC Adv. 9, 6363–6378 (2019).
Liu, R. et al. Enhanced thermoelectric performance of Te-doped Bi2Se3-xTex bulks by self-propagating high-temperature synthesis. Crystals 7, 257 (2017).
Pan, Y., Wei, T. R., Wu, C. F. & Li, J. F. Electrical and thermal transport properties of spark plasma sintered n-type Bi2Te3-xSex alloys: the combined effect of point defect and Se content. J. Mater. Chem. C 3, 10583–10589 (2015).
Kumar, S. R. S., Kurra, N. & Alshareef, H. N. Enhanced high temperature thermoelectric response of sulphuric acid treated conducting polymer thin films. J. Mater. Chem. C 4, 215–221 (2016).
Lu, N. D., Li, L. & Liu, M. A review of carrier thermoelectric-transport theory in organic semiconductors. Phys. Chem. Chem. Phys. 18, 19503–19525 (2016).
Smith, J. et al. Solution-processed organic transistors based on semiconducting blends. J. Mater. Chem. 20, 2562–2574 (2010).
Mehta, R. J. et al. A new class of doped nanobulk high-figure-of-merit thermoelectrics by scalable bottom-up assembly. Nat. Mater. 11, 233–240 (2012).
Garland, J. C. & Tanner, D. B. Electrical Transport and Optical Properties in Inhomogeneous Media (Amer Inst of Physics, 1977).
Lee, H. et al. Effects of nanoscale porosity on thermoelectric properties of SiGe. J. Appl. Phys. 107, 094308 (2010).
Ashcroft, N. W. & David, M. N. Solid State Physics (Holt, Rinehart and Winston, 1976).
Fang, H. Y. et al. Thermoelectric properties of solution-synthesized n-type Bi2Te3 nanocomposites modulated by Se: An experimental and theoretical study. Nano Res. 9, 117–127 (2016).
Ma, S. F. et al. High-pressure synthesis and excellent thermoelectric performance of Ni/BiTeSe magnetic nanocomposites. J. Mater. Chem. A 8, 4816–4826 (2020).
Chen, H. Y. et al. Thermal conductivity of polymer-based composites: Fundamentals and applications. Prog. Polym. Sci. 59, 41–85 (2016).
Wei, Q. S., Mukaida, M., Naitoh, Y. & Ishida, T. Morphological change and mobility enhancement in PEDOT:PSS by adding co-solvents. Adv. Mater. 25, 2831–2836 (2013).
Lin, V. J., Zeng, J. J. & Tsai, C. L. Enhancement of the carrier mobility of poly(3,4-ethylenedioxythiophene) doped with poly(4-styrenesulfonate) by incorporating reduced graphene oxide. Appl. Phys. Lett. 101, 053305 (2012).
Pei, Y. Z. et al. Convergence of electronic bands for high performance bulk thermoelectrics. Nature 473, 66–69 (2011).
Hu, L. P., Zhu, T. J., Liu, X. H. & Zhao, X. B. Point defect engineering of high-performance bismuth-telluride-based thermoelectric materials. Adv. Funct. Mater. 24, 5211–5218 (2014).
Katz, H. E. & Poehler, T. O. Innovative Thermoelectric Materials: Polymer, Nanostructure and Composite Thermoelectrics xv, 276 (Imperial College Press Distributed by World Scientific Publishing Co. Pte Ltd., 2016).
Zhou, X. Y. et al. Routes for high-performance thermoelectric materials. Mater. Today 21, 974–988 (2018).
Zhang, L.S., Yang, B., Lin, S. P., Hua, T. & Tao, X. M. Predicting performance of fiber thermoelectric generator arrays in wearable electronic applications. Nano Energy 76, 105117 (2020).
Ouyang, Z. L. & Li, D .W. Modelling of segmented high-performance thermoelectric generators with effects of thermal radiation, electrical and thermal contact resistances. Sci. Rep. 6, 24123 (2016).
Acknowledgements
The work has been partially supported by Research Grants Council, Hong Kong (Grant. No.15201419E, 15200917E, and 15204715E) and Hong Kong Polytechnic University (Grant No. AAB3 and 847A). S.P.L. thanks Hong Kong Polytechnic University for a postgraduate scholarship. Technic supports were received from Dr. Wan Qiping, Dr. Jian Song, Dr. Yingqiao Yang, Ms. Ching Lee, Mr. Zhiming Geng, Mr. Linqi Pan.
Author information
Authors and Affiliations
Contributions
L.S.P. designed, conducted experiments, and drafted the paper. Z.L.S. did the theoretical and simulation analysis of FTEG performance. Z.W., L.J., S.D.L., and Y.B. contributed to the discussions and results analysis. D.X.J. designed and fabricated the wearable LED fabric. L.S. provided the flexible circuit. XJT fabricated the flexible electrodes. H.B.L. contributed to mechanistic analysis and provided XPS measurement equipment. K.K.L. provided TE measurement devices and discussed the results. X.M.T. initiated the research, obtained the funding, supervised the work, analyzed the results, and revised the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Materials thanks Yuan Deng and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editors: Yanzhong Pei and Aldo Isidori.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lin, S., Zhang, L., Zeng, W. et al. Flexible thermoelectric generator with high Seebeck coefficients made from polymer composites and heat-sink fabrics. Commun Mater 3, 44 (2022). https://doi.org/10.1038/s43246-022-00263-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-022-00263-1
This article is cited by
-
Investigation of Seebeck coefficient in organic materials under a magnetic field
Indian Journal of Physics (2024)
-
Flexible thermoelectric generator fabricated by screen printing method from suspensions based on Bi2Te2.8Se0.2 and Bi0.5Sb1.5Te3
Journal of Central South University (2023)
-
Functional Materials and Innovative Strategies for Wearable Thermal Management Applications
Nano-Micro Letters (2023)