Challenges in identifying chiral spin textures via the topological Hall effect

Abstract

Chiral spin textures such as skyrmions are of interest to the field of spintronics for their potential use in future computing devices. Hall effect measurements are a simple and powerful method to probe the electronic and magnetic properties of materials. The topological Hall effect, which appears as anomalies in Hall resistance versus magnetic field measurements compared to magnetic measurements, has frequently been used to establish the occurrence of chiral spin textures. However, in addition to experimental issues, intrinsic electronic mechanisms combined with inhomogeneity in materials and at interfaces can lead to an inhomogeneous anomalous Hall effect which could be mistaken for a topological Hall signal. This review covers recent research using Hall effect measurements to probe chiral spin textures, focusing on SrRuO₃ as a model system. The ambiguity between Hall effects due to topological sources has led to disagreement in the interpretation of experimental results and casts doubts on the effectiveness of these techniques for investigating chiral spin textures.

Introduction

Topologically non-trivial spin textures have attracted significant research interest due to their potential application in next-generation logic and memory devices. The most well-known of these spin textures is the magnetic skyrmion, but a plethora of other topologically non-trivial spin textures have been discovered or proposed¹. The topological protection means the spin textures cannot be unwound without forming a discontinuity, providing them with high stability even at small sizes. Skyrmions can be created, manipulated and read without externally applied fields using low current densities. These properties may allow for improvements in devices such as domain-wall racetrack memory^2,3,4, and there have been proposals for skyrmion-based logic gates⁵, transistor-like devices⁶ and neuromorphic devices^7,8.

Chiral spin textures like skyrmions are typically stabilised by a competition between the Dzyaloshinskii–Moriya interaction⁹ (DMI) (or anti-symmetric exchange coupling), normal (symmetric) exchange coupling, magnetic anisotropy and an externally applied magnetic field. The DMI arises from a combination of spin–orbit coupling and broken inversion symmetry, which can be due to a non-centrosymmetric crystal structure or the presence of an interface. Skyrmions are often investigated using Hall effects since the magnetic chirality generates a so-called ‘topological Hall effect’ (THE) in addition to the anomalous Hall effect (AHE) and ordinary Hall effect (OHE)¹⁰. A Hall effect due to spin chirality was first reported in manganites^11,12 and frustrated ferromagnets¹³, then later due to skyrmions in bulk crystals¹⁴.

There have been many recent reports of skyrmions in thin-film heterostructures from THE measurements, including metallic films and structures^15,16,17,18, oxide semiconductors¹⁹, ferromagnetic insulators^20,21 and metallic oxides^{22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37}. In these studies, a non-monotonic Hall effect (after subtracting a linear OHE) or discrepancy between magnetic hysteresis and Hall hysteresis loops is used as evidence of a THE. However, recent experimental evidence has shown that inhomogeneities in the magnetic and electronic structure of films creating an inhomogeneous AHE lead to very similar Hall signals. For example, this has been shown as a result of thickness variations, either within heterostructures³⁸ or in single films^39,40, modification from surfaces or interfaces^41,42, defects⁴³, strain relaxation⁴⁴, or other spatial variations of magnetic properties⁴⁵. The difficulty in separating the different contributions to the Hall effect makes the unambiguous confirmation of a THE challenging, and so it is important to be aware of the limitations of this experimental technique.

Other articles have covered details about the physics of skyrmions and recent advances in skyrmion electronics^{1,46,47,48,49,50,51,52,53}, Berry phase physics^54,55, the different contributions to the AHE^56,57 and the THE¹⁰. In this review, we focus on the experimental application of Hall measurements combined with real-space imaging to investigate chiral spin textures such as skyrmions. Firstly, we describe the different contributions to the Hall effect in thin-film ferromagnets. We review the investigation of skyrmions in a number of material systems by various experimental techniques and look at the application of the THE in these systems. We then review studies into Hall effect anomalies using SrRuO₃ thin films as a prototypical system, first through the THE interpretation, then the inhomogeneous AHE interpretation, and we link these interpretations to other material systems. We then critically discuss the misconceptions and limitations in both of these interpretations. Finally, we propose possible further experiments that could clarify these issues.

Hall effects

In the Hall effect, a transverse electric field (E_x) is generated under an applied longitudinal current density (J_y). Using conventional tensor notation E_x = ρ_xyJ_y, where ρ_xy is the Hall resistivity. The Hall resistivity is the off-diagonal element of the resistivity tensor, ρ_ij, which is the inverse of the conductivity tensor, σ_ij. The Hall resistivity is related to Hall conductivity by ${\rho }_{xy}=\frac{-{\sigma }_{xy}}{{\sigma }_{xx}^{2}+{\sigma }_{xy}^{2}}$, and for small Hall angles (σ_xy ≪ σ_xx) this can be approximated as ${\rho }_{xy}=\frac{-{\sigma }_{xy}}{{\sigma }_{xx}^{2}}$.

Here we focus on the Hall effect in ferromagnetic materials with three main contributions to the measured Hall resistivity, illustrated in Fig. 1a: the OHE due to the Lorentz force; the AHE caused by broken time-reversal symmetry, spin–orbit coupling and intrinsic Berry curvature in momentum space (which can also be non-vanishing in anti-ferromagnets^58,59); and the THE which commonly refers to Berry curvature effects arising from chiral spin textures including skyrmions. For small Hall angles, the sum of individual contributions gives the total Hall resistivity: ${\rho }_{xy}^{{{{{{{{\rm{Total}}}}}}}}}={\rho }_{xy}^{{{{{{{{\rm{OHE}}}}}}}}}+{\rho }_{xy}^{{{{{{{{\rm{AHE}}}}}}}}}+{\rho }_{xy}^{{{{{{{{\rm{THE}}}}}}}}}$. For inhomogeneous samples with multiple AHE channels, such as the examples shown in Fig. 1c, the individual Hall resistivities can also be linearly summed with a weighting that depends on the geometry and longitudinal resistivity of the materials, assuming that the Hall angles are small and magnetoresistance is negligible. Hall effect anomalies are ambiguous and could result from an AHE + THE or from multiple AHEs, as shown in Fig. 1b.

Fig. 1: The interpretation of Hall effects.

a The Hall resistivity in a ferromagnet is a sum of three main components: an OHE due to the Lorentz force on charged carriers, an AHE due to spin–orbit coupling in the ferromagnet, and a THE due to chiral spin textures. b How different non-monotonic Hall signals could be interpreted as either a multiple AHEs, or by a sum of an AHE and THE. c Multiple AHEs result from an inhomogeneous electronic structure in thin films, for example caused by thickness variations, defects or electronic and structural reconstruction from interfaces. d A THE is a result of spin chirality, for example from skyrmionic phases, chiral domain walls or chiral fluctuations illustrated by a triad of spins subtending a solid angle Ω.

Ordinary Hall effect

The OHE is the lateral deflection of charge carriers in a conductor due to an applied magnetic field, caused by the Lorentz force. Considering a thin film with the normal in the z-direction, to the first approximation the OHE is linear in field:

$${\rho }_{xy}^{{{{{{{{\rm{OHE}}}}}}}}}={R}_{0}{\mu }_{0}{H}_{z},$$

(1)

where R₀ = −1/nq is the ordinary Hall coefficient, n is the number density of charge carries and q their charge, μ₀ is vacuum permeability and H_z is the applied magnetic field in the z-direction.

In ferromagnets other Hall effects can dominate the Hall resistivity at low fields, so the OHE is usually extracted as a high field linear component of the data. However, this assumes that only one type of charge carrier contributes to the OHE, and if more than one band is considered then the OHE can have significant deviations away from linearity. This is important, for example, when the mobility and carrier density of electrons and holes are similar in a material, and a two-band OHE has been used to explain non-linear and non-monotonic Hall effects^60,61.

Anomalous Hall effect

The AHE is found in ferromagnetic and anti-ferromagnetic materials as a Hall resistivity, which can occur in the absence of an applied magnetic field. In ferromagnetic materials, this follows the empirical relation:

$${\rho }_{xy}^{{{{{{{{\rm{AHE}}}}}}}}}={R}_{s}{M}_{z},$$

(2)

where R_s is the anomalous Hall coefficient, and M_z is the z-component of the magnetisation.

This is not simply caused by the Lorentz force from the demagnetising field, but rather is due to broken time-reversal symmetry and spin–orbit coupling within the material. A full theoretical understanding of the AHE has been entangled in decades of controversy and confusion due to the difficulty in separating different contributions to the AHE experimentally, as well as the topological concepts needed to accurately describe some contributions not being available until recently. It is now understood that the total anomalous Hall resistivity is a combination of three mechanisms: the intrinsic contribution, skew-scattering and side-jump. Skew-scattering and side-jump are extrinsic scattering mechanisms. Skew-scattering is significant at low temperatures in clean systems, roughly defined as a residual longitudinal resistivity ρ_xx0 < 10⁻⁴ Ω cm⁵⁷. Side-jump has the same longitudinal resistivity dependence as the intrinsic mechanism, so is difficult to separate unambiguously.

Recently, the intrinsic mechanism has been reinterpreted in terms of topological concepts as a Berry phase in momentum-space^62,63. The Berry-phase is the phase change of a wavefunction after experiencing a cyclic change in external parameters, similar to the Aharonov-Bohm effect⁵⁵. In crystals, this leads to the ‘Berry curvature’, a local property of the band structure in k-space which creates an emergent magnetic field and modifies the motion of electrons. The intrinsic component of anomalous Hall resistivity is found by integrating the Berry curvature over all occupied states in k-space. For more detailed reviews of the different mechanisms of the AHE, see refs. ^56,64,65.

Topological Hall effect

As opposed to the intrinsic AHE, which depends on the Berry curvature in k-space, the THE is related to Berry-phase accumulation in real space¹⁰ due to chiral spin textures. If an electron is in a slowly changing exchange field in a ferromagnet, in the adiabatic limit (or strong-coupling limit) its spin will follow the direction of the magnetisation. If the magnetisation varies in a closed loop, the electron has experienced a cycle in parameter space and thus acquires a geometric phase. In this case, the phase is proportional to the solid angle subtended by the exchange field. This additional phase creates an additional emergent magnetic field experienced by the electrons and thus can contribute to the Hall effect.

As illustrated in Fig. 1d, spin chirality can take the form of static spin structures such as compact skyrmions or chiral bubble domains in a multi-domain ferromagnet, sometimes referred to as skyrmion bubbles. Chirality could also result from magnetic frustration or thermally activated spin chirality fluctuations^{11,12,30,66,67}.

Typically spin chirality is stabilised over a limited field range, so the THE appears as a peak in the Hall effect versus field. The size of this peak is commonly approximated as:

$${\rho }_{xy}^{{{{{{{{\rm{THE}}}}}}}}}=P{R}_{0}{B}_{{{{{{{{\rm{eff}}}}}}}}}=P{R}_{0}{n}_{{{{{{{{\rm{sk}}}}}}}}}{{{\Phi }}}_{0},$$

(3)

where P is the transport spin polarisation of the ferromagnet, R₀ is the effective charge density to the THE, usually taken as the ordinary Hall coefficient¹⁸, and B_eff is the effective magnetic flux density generated by the skyrmions⁶⁸. This effective magnetic flux density is defined as B_eff = n_skΦ₀, where n_sk is the skyrmion density and Φ₀ is the magnetic flux quantum.

Is the topological Hall effect really topological?

One possible source of confusion is the naming of the ‘topological’ Hall effect. In most definitions, the THE is a result of an effective magnetic flux generated by electrons passing through a chiral spin texture, or equivalently it is a Hall effect resulting from a real-space Berry curvature. This definition does not require that spin texture is topologically non-trivial. The experimental signature of the THE from a chiral spin texture is a peak or dip in the Hall effect that vanishes in the high-field limit; however, this also cannot determine whether the spin texture is topologically nontrivial or not.

Chiral spin textures that are not characterised by integer topological charge can still contribute a Hall effect due to Berry phase. This is the case in chiral spin fluctuations above T_C^30,66 and in frustrated ferromagnets⁶⁹. These effects were originally referred to as an ‘AHE’ but are now sometimes referred to as a ‘THE’. Since the signature of a THE does not necessarily require a topologically non-trivial spin texture, it may be more appropriate to use a more general term such as ‘spin chirality Hall effect’. However, to remain consistent with prior literature, we will continue to use the term ‘topological Hall effect’ in this review.

On the other hand, the intrinsic AHE is due to Berry curvature in k-space and thus it naturally includes topological aspects of the band structure, so could be viewed as ‘topological’. It has also been shown that in kagome ferromagnets the AHE can be understood as an effective ‘THE’ due to spin-orbit coupling after a coordinate transformation⁶⁹.

From a phenomenological point of view, the intrinsic and topological Hall effects can both be viewed as a Berry curvature in real or momentum space⁷⁰. Ultimately, the convention usually followed is that the intrinsic AHE is the Hall effect due to a Berry curvature commensurate with the crystal lattice giving a macroscopically uniform emergent effective field⁷¹. We usually say this is a Berry curvature ‘in k-space’ as this is how it is most easily represented. The THE is due to chiral spin textures which are not necessarily commensurate with the lattice and give spatially non-uniform emergent fields⁷¹. One could call this a Berry curvature ‘in real space. Drawing the line here may seem arbitrary, since the intrinsic AHE and THE are more closely related than, for example, the intrinsic AHE and skew-scattering. However, the distinction is useful from an experimental point of view as it follows what is often separable in practice.

Corrections to the topological Hall effect

Finally, it is worth noting some additional caveats to the THE. Equation (3) is an approximation and assumes strong exchange coupling and adiabatic transport of electrons so that the electron spin follows the local magnetisation of the material. If the exchange coupling is weak then the non-adiabatic THE contribution can become significant⁷².

There are also other contributions to the Hall effect in the presence of spin chirality. At the next level of approximation, the effect of spin-orbit coupling is included in the electron propagation, then additional contributions to the Hall effect are expected to appear^70,73. This can be interpreted as a modification to the Berry phase interpretation⁷⁰, or as a separate so-called ‘Chiral Hall effect’ proposed by Lux et al.⁷³.

Skyrmions in thin-film heterostructures

Skyrmions were discovered in single crystals of MnSi by neutron diffraction¹⁴ in a narrow range of magnetic field near the helical transition temperature, and shortly after more stable two-dimensional (2D) skyrmion lattices were observed in ion-milled thin films of Fe_0.5Co_0.5Si⁷⁴, FeGe⁷⁵, MnSi⁷⁶ and Co₂OSeO₃⁷⁷ using Lorentz force transmission electron microscopy.

Thin-film heterostructures grown by vapour deposition processes are more practical for hosting stable skyrmions in devices, and many other techniques have been used to probe skyrmions in thin films; for example Heinze et al.⁷⁸ and Romming et al.⁷⁹ used spin-polarised scanning tunnelling microscopy (SP-STM) to probe skyrmions in single atom thick Ir(111) layers. Chen et al.⁸⁰ used spin-polarised low-energy electron microscopy to measure the magnetisation vector in Fe/Ni films, and Boulle et al.⁸¹ photo-emission electron microscopy combined with X-ray magnetic circular dichroism to measure the chirality of skyrmions in Pt/Co/MgO heterostructures. Skyrmions are now routinely observed in thin-film structures through a variety of techniques and can be created, manipulated and detected in a fairly controlled manner⁴⁶.

The Hall effect resulting from real-space spin chirality was first discussed in relation to colossal magnetoresistance manganites^11,12,67,82 as well as pyrochlore ferromagnets¹³ and non-coplanar anti-ferromagnets⁸³. This was not due to skyrmions, but rather a spin chirality at the microscopic level was proposed due to thermally excited chiral fluctuations or magnetic frustration.

A THE caused by skyrmions was first reported in bulk samples of single-crystal MnSi^68,84 and polycrystalline MnGe⁸⁵. However, there are often difficulties correlating a THE to skyrmions measured by real-space imaging. A THE was found in the frustrated ferromagnet Fe₃GeTe₂⁸⁶ and then later skyrmions were observed by Lorentz transmission electron microscopy (LTEM)⁸⁷ but with the magnetic field applied along a different crystallographic direction. One study showed both THE and LTEM imaging of skyrmions in NdMn₂Ge₂, and the two methods gave different temperature and field stability ranges⁸⁸. Another found an anti-skyrmion crystal in Heusler alloy by LTEM⁸⁹, but a corresponding THE was observed only at lower temperatures⁹⁰. In addition to composition and material quality, the stability of different skyrmion phases is strongly dependent on sample dimensions. The requirement to mill samples into thin lamellae for transmission electron microscopy (TEM) makes it very challenging to correlate these measurements with Hall effects. There are very few TEM holders that can both cryo-cool and electrically bias, but this is an emerging area of research and there are possibilities for correlating these measurements more precisely in the future. For example, there have recently been observations of individual skyrmion motion due to applied current pulses in a TEM⁹¹.

The detection of a THE in thin films remains controversial primarily due to the disagreement between the THE and real-space imaging. There have been recent reports of a THE in Ir/Fe/Co/Pt heterostructures¹⁵, but several studies later used Hall measurements in conjunction with real-space skyrmion imaging and found that the change in Hall signal in similar structures is too large to be solely due to the THE^16,17,18. The discrepancy has been attributed to a change in the AHE from skyrmions changing the net magnetisation value¹⁶, though when accounting for this AHE change an additional size-independent component of the skyrmion Hall contribution has been found which also does not match the expected THE value¹⁷. This calls into question the assumptions used in Eq. (3), for example Raju et al.¹⁸ question whether the ordinary Hall coefficient R₀ can be used as the effective charge density contributing to the THE, and whether the adiabatic approximation can be used in thin films where spin-flip scattering is significant, among other possibilities.

As well as metallic heterostructures such as Co/Pt^15,16,17,18 there have also been reports of THEs in a wide range of thin films, for example intermetallics FeGe^92,93, MnGa⁹⁴, MnSi⁹⁵, Mn₂CoAl⁹⁶, Heusler compounds such as Mn₂RhSn⁹⁷, topological insulator heterostructures^98,99, and a plethora of oxide thin-film systems, such as EuO¹⁹, the ferromagnetic insulator heterostructure Tm₃Fe₅O₁₂/Pt^20,21, and perovskites La_0.7Sr_0.3MnO₃/SrIrO₃¹⁰⁰, La_0.7Sr_0.3MnO₃/SrRuO₃^101,102,103 and SrRuO₃/SrIrO₃²² among others. Recently, a giant THE orders of magnitude larger than those seen in other single-crystal and thin-film systems has been observed in Ce-doped calcium manganite³⁷.

Many studies do not use real-space imaging of skyrmions with techniques such as magnetic force microscopy (MFM) or LTEM, but rather rely on the observation of a non-monotonic Hall signal or discrepancy between magnetic and Hall hysteresis loops as evidence of chirality. When real-space imaging is used, the results can be complex to interpret and frequently the number of bubble-like features counted in imaging is often lower than the number of skyrmions expected based on the Hall effect and theory predictions. The practice of attributing Hall effect anomalies to chiral spin textures has been called into question³⁸ since the topological Hall signals could be interpreted as multiple AHEs resulting from different kinds of inhomogeneity. This ambiguity between different interpretations of the same Hall data will be the focus of the following sections using SrRuO₃ as a model system.

An overview of SrRuO₃

SrRuO₃ is a metallic, ferromagnetic, moderately correlated perovskite oxide which is a prototypical system for exploring thin-film magnetism in oxides due to its interesting properties and the ease of near-perfect epitaxial growth on SrTiO₃(001) by a variety of physical vapour deposition methods¹⁰⁴. It is chemically and physically stable, electrically conducting without doping, and easily incorporated into epitaxial heterostructures thanks to close lattice matching to many other popular perovskites¹⁰⁴. In bulk crystals SrRuO₃ has an orthorhombic structure consisting of distorted perovskite cells¹⁰⁵. Due to the differences in Sr-O and Ru-O bond length, the RuO₆ octahedra are rotated, leading to displacements of O and Sr, and this leads to many of the exotic properties of SrRuO₃. For convenience this slightly distorted structure is often approximated as a pseudo-cubic perovskite unit cell (UC) with a = 3.93 Å. This convention will be used throughout this review.

Magnetic properties

SrRuO₃ has a Curie temperature (T_C) of 160 K, and a low temperature magnetisation of about 1.4 μ_B Ru⁻¹. In thin films, these values are slightly suppressed, and there is a strong uniaxial magnetocrystalline anisotropy with the easy axis at a small angle from the normal to the film. Below the T_C, the easy axis rotates from ≈45° to ≈30° from the normal in a 100 nm-thick film on SrTiO₃(001)¹⁰⁶. Below a thickness of 10 UC, the T_C drops significantly until ferromagnetism disappears between 2 and 3 UC¹⁰⁷. The exact cause of the thickness limit for magnetism is not well understood, but may be caused by an anti-ferromagnetic layer forming at the substrate interface¹⁰⁷. The magnetism (and metallicity) can be enhanced with a SrTiO₃ capping layer, and in this case SrRuO₃ can show signals of ferromagnetism down to a single UC layer¹⁰⁸. The magnetocrystalline anisotropy also depends on the film thickness; at low temperature the easy axis rotates from ≈30° to ≈14° as thickness decreases to the ultra-thin limit, likely due to the increasing contribution of surface anisotropy^107,109.

The anomalous Hall effect

The AHE in SrRuO₃ shows unconventional behaviour. It is strongly dependent on (and can change sign as a function of) various parameters such as magnetisation¹¹⁰, temperature¹¹¹, strain¹¹², film thickness⁴⁰, doping¹¹³ and more. SrRuO₃ is expected to host a large number of Weyl nodes near the Fermi level which contribute to the AHE via the intrinsic Berry curvature mechanism^{110,114,115,116}, and the dependence of the AHE on these various parameters is ultimately due to the sensitivity of intrinsic Berry curvature on the electronic structure of the material. The intrinsic AHE in SrRuO₃ has been shown theoretically to be sensitive to Fermi-level position and spin-splitting¹¹⁰, strain¹¹² and crystal symmetry breaking¹¹⁷. We reiterate that although this contribution to the AHE is due to topological features in k-space, under the current naming scheme it is distinct from a ‘topological Hall effect’.

There have been reports that the Berry curvature mechanism alone cannot describe the AHE in SrRuO₃ and that the temperature dependence is well described by a combination of the intrinsic Berry curvature mechanism and the extrinsic side-jump mechanism^118,119. In most real films the extrinsic skew-scattering mechanism would not be expected to be significant since SrRuO₃ does not usually have a sufficiently low residual resistivity⁵⁷.

Weyl points are only defined in three dimensions, but in the 2D limit the AHE of SrRuO₃ still shows a similar non-monotonic dependence with sign changes as a function of external parameters. In the 2D limit, the source of Berry curvature can be related to topological charges^41,120 or to nodal lines and other types of band crossings¹²¹. The sign change of the AHE with temperature for SrRuO₃ in the 2D limit can be captured by evaluating the Berry curvature of the electronic structure, which is also modified by different interfaces⁴¹. Experimentally, AHE sign changes have also been observed as the film thickness is reduced towards the 2D limit^{22,24,26,29,31,39,40,122,123}.

The topological Hall effect in SrRuO₃

First detection of skyrmions in SrRuO₃

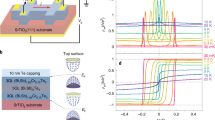
A THE was first reported in SrRuO₃/SrIrO₃ heterostructures by Matsuno et al.²². SrRuO₃ films were grown on SrTiO₃ with a 2 UC SrIrO₃ capping layer. A DMI originates from the interface with the SrIrO₃, which breaks inversion symmetry and provides strong Rashba spin-orbit coupling, similar to how interfacing with metallic Ir is used to give a DMI in Co/Pt structures^15,16,17,18. When the SrRuO₃ was 4 or 5 UC, additional peaks were seen in the Hall effect near the coercive field, as shown in Fig. 2a. The OHE is removed by a high field linear fit, and to separate the AHE and THE, the AHE is assumed to be proportional to the magnetisation, M. The magnetisation versus magnetic field loop [M(H)] is measured using the magneto-optical Kerr effect (MOKE). It is assumed that at high field the THE is zero and the Hall signal is entirely due to the saturated AHE, so the MOKE loop is scaled to match saturation values to give the AHE component. The THE is then determined by subtracting the scaled MOKE data from the Hall data. This technique is used frequently throughout the literature to separate the AHE and the THE. Equation (3) is then used to estimate a skyrmion spacing (${n}_{{{\mathrm{sk}}}}^{-1/2}$) of approximately 10 to 20 nm, assuming adiabatic transport. At the same time, Pang et al.²³ showed additional Hall peaks in SrRuO₃/SrIrO₃ superlattices with 4 nm-thick SrRuO₃, with a similar explanation of the THE due to a chiral spin textures, though the topological peak was smaller. Unusual peaks were detected in the Hall effect of SrRuO₃ before this, but not commented on¹²⁴ or attributed to an intermixing of ordinary and anomalous Hall effects¹²⁵.

Fig. 2: Evidence of a THE in SrRuO₃.

a Skyrmions in SrRuO₃ capped with SrIrO₃. The THE (green) is found from subtracting a scaled MOKE measurement (orange) assumed to be proportional to the AHE, from overall Hall data (blue). b Gate-voltage-dependent THE. The THE is found using the same method as in a. The gate voltage switches the sign of the AHE and changes the THE size. c, d Field-angle dependence of the THE in uncapped SrRuO₃. c Hall resistance of a single layer of SrRuO₃ with the field applied at an angle θ from the normal. Vertical offset added for clarity. d Phase diagram from the data from c, showing the stability of skyrmion phase with respect to an in-plane field. The inset shows the definition of θ, H_⊥ and H_∥. e, f Ferroelectrically tunable skyrmions. e SrRuO₃ capped with ferroelectric BaTiO₃. Atomic shifts for upward and downward ferroelectric polarisation as measured in TEM. The marker and error bar give the average and standard deviation for the atomic shifts in each monolayer. The absolute shift ∣δ_A−B∣ is larger in the SrRuO₃ for the upward polarisation. f Effect of ferroelectric polarisation on Hall effect. From left to right the area fraction polarised upwards is reduced. The Hall effect shows a larger THE peak for more upward poling while the AHE contribution is mostly unchanged. a adapted with permission from ref. ²². ⓒ The Authors, some rights reserved; exclusive licensee AAAS. Distributed under CC BY-NC 4.0. Reprinted with permission from AAAS. b adapted from ref. ²⁴ under CC BY 4.0. c, d adapted from ref. ²⁵ under CC BY 4.0. e, f adapted from ref. ²⁶ by permission from Springer Nature: Nature Materials ⓒ 2018.

Skyrmion manipulation with electric field

The report of interface stabilised skyrmions in SrRuO₃ prompted a flurry of research into skyrmions in SrRuO₃-based heterostructures. A primary motivation is to be able to manipulate skyrmions for use in devices, so many studies investigate the THE dependence on gate voltages. Ohuchi et al.²⁴ observed a THE in a variety of SrRuO₃/SrIrO₃ structures, but not in the uncapped SrRuO₃ film. Applying a gate voltage appeared to affect the Hall effect in the samples—the AHE could switch sign, and the THE peak changed size (Fig. 2b). It is argued that because the normal (longitudinal) transport properties do not change significantly under the gate voltage, the change in the THE peak is due to a change in the number of skyrmions, and not due to changes in carrier concentrations, mobility or spin polarisation. It is proposed that the gate voltage varies the DMI by changing the band structure and varying the spin–orbit coupling strength at the interface, which in turn tunes the skyrmion size.

There have been a number of other reports of gating effects in thin films. Qin et al.²⁷ measured a THE with the same method of subtracting an M(H) loop from Hall data in 3, 4, 5 and 6 nm-thick single SrRuO₃ layers (a larger thickness range than observed by other groups). Liquid-ion gating was used to bias the films, finding a similar result to Ohuchi et al.²⁴, but here without the SrIrO₃ layer and using a much lower voltage. Likewise, Gu et al.²⁹ found Hall peaks from 8 to 5 UC-thick films and observed a back-gating dependence similar to Ohuchi et al.²⁴.

Li et al.³⁶ found Hall peaks in much thicker SrRuO₃ films by inserting protons into the film with ion liquid gating. Both 30 and 70 nm-thick films show a topological peak only when a voltage is applied and the film is protonated. When a voltage is applied, protons are inhomogeneously inserted into the film, with the maximum at the surface and a decay length around 10 nm, and in this state the topological Hall peak appears. It is reasoned that the compositional gradient of protons enhances the DMI and reduces the magnetisation, which enables the stabilisation of a chiral spin texture.

Skyrmions in uncapped SrRuO₃

While some studies show no THE in uncapped SrRuO₃^24,26, others have reported the opposite^25,27,29,32. Sohn et al.²⁵ reported skyrmions in 4 and 5 UC-thick films of SrRuO₃ without any capping layer. Clear peaks were observed in the Hall effect, an example of which is shown in Fig. 2c. The distortion and rotation of oxygen octahedra were measured by surface X-ray scattering, and a corresponding DMI strength of 2.1 meV was estimated from density functional theory (DFT) calculations, which is thought to stabilise a chiral spin texture and provide a THE. Additionally, it is shown that the Hall peak has a remarkable stability to in-plane field, remaining up to 6.5 T, as shown in Fig. 2c, d. A similar robustness to in-plane field has been attributed to the complex magnetic anisotropy of SrRuO₃³². This kind of robustness to in-plane field is unusual for skyrmions, for example in EuO the THE disappears when tilting the magnetic field to 10°¹⁹. Tilting the magnetic field in-plane has been used as a method to separate the topological Hall contribution, for example in Mn_1−xFe_xSi thin films¹²⁶.

Skyrmion manipulation with ferroelectrics

Wang et al.²⁶ reported skyrmions in SrRuO₃ capped with ferroelectric BaTiO₃. Peaks in the Hall effect were observed for films 6 UC-thick and below, and were enhanced by the BaTiO₃ capping. The polarisation of the BaTiO₃ layer can be switched by a biased conducting atomic force microscope tip. The polarisation of the ferroelectric causes lattice distortions in the SrRuO₃, breaking inversion symmetry. The distortion is stronger for the upward polarisation as measured in TEM, shown in Fig. 2e. This enhanced symmetry breaking increases the DMI and so may be expected to increase the THE strength. The effect of BaTiO₃ poling on the Hall effect is shown in Fig. 2f. This change in the peak size is evidence of a change in the number of skyrmions due to the ferroelectric poling. MFM imaging is used to quantify the skyrmion density using pixel-by-pixel subtraction of images at different fields to count the number of additional skyrmions created at each field step, however the numbers are a factor of 5 smaller than from those calculated from the THE. It is suggested that this is due to the THE calculation assuming adiabatic transport of electrons, whereas there could be a significant non-adiabatic THE contribution.

The inhomogeneous anomalous Hall effect in SrRuO₃

Many studies find the THE by assuming that the AHE is proportional to the magnetisation of the film, but in inhomogeneous systems this assumption is not necessarily valid. If films contain regions with different anomalous Hall coefficients with different magnetic field dependencies, then Hall effect anomalies can appear as illustrated in Fig. 1b. Among other possibilities, this inhomogeneity could be due to structural modifications at the interface, film thickness variations, or from defects in the film, illustrated in Fig. 1c.

Artificial inhomogeneity in heterostructures

Gerber³⁸ has explained how the ‘topological peaks’ and non-monotonic Hall effects in general could arise from multiple AHEs in heterogeneous ferromagnetic systems, demonstrated by Co/Pt stacks of differing thicknesses, and highlighted SrRuO₃ among many other systems where this effect could apply. Several groups showed this more directly for the case of SrRuO₃ by growing heterostructures consisting of SrRuO₃ separated by spacer layers of SrIrO₃¹²⁷ or SrTiO₃¹²⁸. Similar ‘artificial’ topological-like Hall effects have been demonstrated in topological insulator heterostructures¹²⁹.

Defects

The first doubts about the claims of a THE in SrRuO₃ appeared in mid-2018 by Kan and Shimakawa⁴³. Here, Hall peaks were found in 3–5 nm-thick SrRuO₃ films on (110)-oriented GdScO₃ substrates, and the peak size increases as film thickness decreases. It was suspected that Ru deficiencies caused local variations to the magnetisation and Berry curvature in the film, and these inhomogeneities caused the peak shape to appear. In addition to the films grown with a 30% excess Ru target, a 3 nm-thick film was grown with a 40% excess Ru target and the Hall peaks disappeared. It was therefore proposed that the Ru deficiencies caused the anomalous peak, and not chiral spin textures.

Kan et al.¹³⁰ later built upon their original paper⁴³. By measuring minor Hall loops, they showed the behaviour of two separately switching magnetic regions, and also could reproduce the hump behaviour by assuming an inhomogeneity in the temperature at which the AHE changed sign. In a further study, it was shown that there were sweep-rate dependent shifts in the coercive field and peak in the Hall effect¹³¹. The zero-crossing and peak showed the same activation energy, while the magnitude of the peak remained constant. These observations imply the switch and the peak in Hall effect are governed by the same magnetisation reversal process, consistent with the inhomogeneous AHE interpretation. However magnetisation dynamics are complex and whether domain walls are chiral or not, they will still depend on conventional domain nucleation and expansion to an extent.

A similar defect-induced magnetic inhomogeneity was investigated by Kim et al.¹³², who grew 25–30 nm-thick SrRuO₃ films on (LaAlO₃)_0.3-(SrAl_0.5Ta_0.5O₃)_0.7 (LSAT) (001) substrates. The Ru-deficiency was varied by changing target material and deposition temperature and monitored with Raman spectroscopy and through the residual resistance ratio. Hall peaks were found in a limited temperature range near the AHE sign change temperature, the peak size and temperature window increased as the Ru deficiency concentration increased until disappearing when the AHE no longer changed sign as a function of T. The films in this study are an order of magnitude thicker than most others reporting Hall peaks so thickness variation or interface effects should be less significant. The Hall peaks are correlated with a broadening of T_C and H_c so are attributed to the creation of inhomogeneous magnetism related to the Ru deficiency. However, it is worth noting most other films in literature are epitaxially grown on SrTiO₃ substrates. Growing on LSAT gives larger epitaxial strains in the film and generally produces films with more partial strain relaxation¹³³, which may contribute to a structural inhomogeneity in this case.

Malsch et al.¹³⁴ used MFM to show inhomogeneous switching behaviour in 4 UC SrRuO₃ films with and without SrIrO₃/SrZrO₃ capping layers. Hall peaks were observed in the capped sample in a small temperature range, but could not be correlated to bubble-like features or the length of domain walls found in MFM. The MFM showed a range of coercive fields in both capped and uncapped samples. Regions that switched together could span both over many terrace steps and within a single step in regions of uniform thickness. This suggests that a mechanism other than thickness variation, for example stoichiometry variations, is affecting the band structure and the magnetic properties.

Interface modification

After the alternative explanation by Kan et al.¹³⁰, other groups suggested different origins for the inhomogeneity. Groenendijk et al.⁴¹ argued that the peaks arose due to the asymmetric interfaces in the films. Here, symmetric structures are grown where SrRuO₃ films are interfaced on both sides with either SrTiO₃ or SrIrO₃. These structures showed no peaks but had different sign AHEs at low temperatures as shown in Fig. 3a, showing that interface modification could significantly affect the Berry curvature of the SrRuO₃. In the asymmetric structure where SrRuO₃ is interfaced with SrTiO₃ and SrIrO₃ on each side, Hall effect peaks were observed, however in contrast to many previous studies this was over a smaller temperature range of 40–60 K as shown in Fig. 3b. The peaks were explained by a superposition of a positive and negative AHE with different coercive fields from the SrRuO₃/SrIrO₃ interface and SrRuO₃/SrTiO₃ interface, respectively, as shown in Fig. 3b–d. Minor Hall-loop measurements supported this interpretation, and a theoretical calculation of Berry curvature modified by the different interfaces showed how for intermediate magnetisation values the anomalous Hall conductivities could be opposite signs at the two interfaces.

Fig. 3: Evidence of AHE inhomogeneity giving peaks in the Hall effect.

a–d Interface modification of AHE in heterostructures of SrRuO₃ (SRO), SrIrO₃ (SIO) and SrTiO₃ (STO). a Saturated anomalous Hall resistance versus temperature. The symmetric STO/SRO/STO structure starts positive at high temperature, then becomes negative at lower temperatures. The SIO/SRO/SIO structure is positive for the whole temperature range. The asymmetric structure starts positive and switches to negative. Near the sign reversal temperature, peaks appear in the Hall effect, marked by the dark grey area. b Close up of the saturated anomalous Hall signal in the asymmetric structure from a. In the range 35–57 K, peaks appear in the Hall effect that can be separated into the contributions from two Hall channels resulting from the STO and SIO interfaces. The spontaneous anomalous Hall resistance of the individual channels is indicated in green and purple. The inset is a schematic of the heterostructure showing the origin of the two channels. c Peaks in the Hall effect near the total sign reversal temperature, fit to two AHEs. Vertical offset added for clarity. d Components of the fit, attributed to the two channels: SRO modified by the STO (green) and SIO (purple). Vertical offset added for clarity. e In a different structure, thickness inhomogeneity can give rise to a peak in Hall effect. The top graphics illustrate how non-integer thicknesses are composed of at least two regions with one UC thickness difference. The AHE is positive at 4 UC and negative at 5 UC. At intermediate thicknesses, the Hall signal is modelled as a linear combination of the 4 and 5 UC loops shown by the dotted line. The data match reasonably well with this simple model. a–d adapted from ref. ⁴¹ under CC BY 4.0. e adapted with permission from ref. ⁴⁰, ⓒ 2020 American Chemical Society.

The fact the Hall peaks in this system only arose over a small temperature range meant that this explanation was disregarded in other works where Hall peaks were measured over the whole temperature range³⁶. The interface modification can explain the Hall peaks in the present system, and there are other cases where peaks appear in a small temperature window near an AHE sign change in asymmetric structures²⁷. However there are also many cases where peaks are observed in other systems over much larger temperature ranges, and in particular it is not clear why similar structures of SrTiO₃/SrRuO₃/SrIrO₃ with similar thicknesses do not show the same temperature dependence²⁴.

A THE has been reported in the compensated ferrimagnet CoTb interfaced with different materials¹³⁵, where inhomogeneities in the AHE from thickness variation were ruled out due to the disappearance of the peak structure in the symmetrically interfaced film. However, these results would still be consistent with the peak structure forming due to interface modification of the AHE as demonstrated in SrRuO₃⁴¹.

Hall anomalies occurring in symmetric structures have also been attributed to interface modification of the AHE due to the difference in bulk versus interface properties. For example in Pr_0.7Ca_0.3MnO₃/SrRuO₃ superlattices, it has been suggested that the structural modification from interfaces may create orthorhombic and tetragonal regions at the interface and core of the SrRuO₃ layers, respectively, with different magnetic properties and AHE signs creating Hall anomalies¹²². Furthermore, in the study of the magnetically doped topological insulator V-doped (Bi,Sb)₂Te₃, Hall anomalies were attributed to the difference in bulk and surface ferromagnetism creating an inhomogeneous AHE⁴², in contrast to the THE explanation proposed in similar structures^98,136.

Thickness variations

Shortly after the reports of skyrmions in SrRuO₃/SrIrO₃ structures^22,24, Wu and Zhang¹³⁷ wrote a comment explaining how thickness inhomogeneity and a mixture of positive-AHE 4 UC and negative-AHE 5 UC regions could lead to the observed Hall peaks in these studies. The magnetic properties of SrRuO₃ change drastically in the ultra-thin limit. In most films, when decreasing thickness from 5 to 4 UC the volume magnetisation drops, the coercive field drops and the low-temperature AHE changes from negative to positive. This AHE sign change is likely related to the intrinsic electronic structure of SrRuO₃⁴¹. If a film contains a mixture of 4 and 5 UC regions, for example due to inevitable single UC thickness variation, then the combination of two AHEs leads to the peak shape.

The same group which demonstrated ferroelectrically tunable skyrmions in SrRuO₃/BaTiO₃ later showed evidence of thickness inhomogeneity in bare SrRuO₃ films being the cause of the peak shape⁴⁰. In this study, films of SrRuO₃ were grown varying from 4 to 5 UC, where non-integer values such as 4.5 UC would necessarily contain a mixture of 4 and 5 UC regions. Here it was shown that the 4 UC and 5 UC films have different coercive fields and AHE signs, and that the intermediate thicknesses contains a mixture of the two resulting in the peak shape (Fig. 3e). Complementary M(H) loops showed a two-step switching consistent with the two switches in the Hall effect, in addition AFM and MFM data showed stripe domains resulting from the thickness variations. A similar study showed two Curie temperatures and two coercive fields which matched between magnetometry and Hall measurements consistent with the two-channel AHE model, and MFM measurements indicated that thickness variations from step-flow growth were responsible³⁹.

This mechanism could be responsible for the THE reported in Mn₂CoAl, which showed an AHE that changed sign from negative at 1.32 nm to positive 2.31 nm, with Hall peaks appearing in the intermediate-thickness films. These films also showed minor-loop behaviour attributed to the nucleation and annihilation of skyrmions, which could also be explained by the superposition of magnetic regions with different coercive fields and AHE signs supported by the thickness-dependent AHE measurements.

Strain relaxation

Most studies so far have considered very thin films on substrates with a close lattice matching. It has been shown that Hall anomalies can also occur in thicker SrRuO₃ films (15–60 nm) grown on substrates with a larger lattice mismatch⁴⁴. While thinner films were coherently strained and showed uniform magnetic switching, thicker films showed partial relaxation and multiple regions with different magnetic properties, which coincided with the appearance of peaks in the Hall effect. In such thick films the DMI from interfaces, effects of interface modification and thickness variations are likely to be negligible.

Problems with topological interpretation

Subtracting two measurements

Frequently in literature, the AHE is found by scaling an M(H) loop to the saturation of an R_xy(H) loop, then the difference in the two loops is taken as the THE. This technique relies on both the assumption that the AHE is proportional to the magnetisation of the film, and that the two measurements are directly comparable. There are several possible issues with comparing measurements:

• Films are often patterned into Hall bars after magnetometry measurements, changing the region sampled by the measurement. Furthermore, most magnetisation measurements are volumetric (e.g. vibrating sample magnetometry) or surface sensitive (e.g. magneto-optical Kerr effect), whereas transport measurements are particularly sensitive to interfaces and domain walls, and are dependent on the current distribution.

• Volume magnetometry measurements usually need to be corrected for non-hysteretic paramagnetic, diamagnetic, or ferromagnetic substrate components¹³⁸. It has been argued that a non-hysteretic correction would not affect qualitative conclusions from a THE measurement⁹⁷, but this is not necessarily true. Taking two identical hysteresis loops, adding a non-hysteretic error to one, scaling the two loops to match saturation and subtracting one from the other will result in a hysteretic difference.

• The sample properties can change between measurements. For example, SrRuO₃ is generally considered extremely stable, but this may not be valid in the 2D limit. It has been shown that the properties of ultra-thin SrRuO₃ can change from water leaching¹³⁹, changes in oxygen vacancies¹⁴⁰ and can change over time when exposed to air^39,123.

• Measurements also need to have the same magnetic-field calibration and field angle. The field sweep-rate used can also change the reported coercive field value and width¹³¹.

THE temperature dependence

Some groups have argued against the inhomogeneity by interface modification proposed by Groenendijk et al.⁴¹ because in that case the peaks only appeared over a small temperature range near the AHE sign change. For example, Li et al.³⁶ disregard this explanation since the Hall peak “persists through the whole temperature region below T_C, which could not be explained by the trivial mixed AHE model”³⁶. However, the mixed AHE model can explain peaks persisting through the whole temperature range if there is a sufficient change in the ρ_xy(T) behaviour of the two channels. An illustration of how the small and large temperature window for peaks could arise is shown in Fig. 4a, b, respectively. A large temperature window for a mixed-AHE has been reported several times^{39,40,130,141}. The small temperature window found in Groenendijk et al.⁴¹ is a result of the two AHE channels only having slightly different ρ_xy(T) dependences.

Fig. 4: Problems with interpreting Hall and magnetisation data.

a, b Hall peaks existing down to zero temperature has been used as an argument against the two-channel model; however, it is still consistent. a Spontaneous AHE, R_xy,s, versus temperature, T. The grey dashed line indicates zero. If there are two anomalous Hall channels with slightly different T dependence, there is a region near the sign-change temperature where peaks appear. Example Hall resistance, R_xy, versus magnetic field, μ₀H, loops are shown below at the indicated temperatures. b If the two channels have a larger difference in T dependence, then peaks can appear down to 0 temperature. c, d A lack of steps in magnetisation has been used as an argument against the two-channel model, but is still consistent. In these examples the anomalous Hall coefficient (scaling between magnetisation and Hall signal) are equal in the two channels, in reality they will be different, which can exacerbate this problem. c An example of how Hall peaks can appear and a step would be observable in the magnetic moment, m. d An example of Hall peaks where the two transitions overlap and a step in magnetisation is not observable.

It is often reasoned that because the THE peak is always positive and independent of the sign of the AHE this shows they have different origins^{22,24,27,29,36}. However, this can be explained by the multiple AHE model. This would mean that the coercive field is lower for the positive AHE and higher for the negative AHE, and the apparent overall sign change occurs when the two contributions have equal magnitude. Furthermore, there have been observations in certain samples of a ‘THE-like’ peak that does change sign as a function of temperature, either artificially created from two separated layers¹²⁷, or from films with an inhomogeneous defect concentration^33,36, in which defect pinning could lead to the unusual coercive field-temperature dependence.

No steps in magnetisation

If the peak is the result of two magnetic regions with different coercive fields, then there should be a step in the M(H) loop, but in many cases this is not observed. This argument is made by Sohn et al.³¹ to rule out an inhomogeneous AHE. In addition Wang et al.⁴⁰ measured steps in M(H) for their films with intentional thickness inhomogeneity, but did not observe a step for heterostructures with SrRuO₃ and BaTiO₃²⁶, which was explained by skyrmions. No steps in M(H) were found in a number of other studies^22,27,29,36. On the other hand, M(H) steps were observed in some studies but were either weak, not commented on or not easily linked to the AHE switches^24,33, or interpreted differently^23,32. This is complicated by the fact that in some cases a step is seen near zero field²⁸, but this may be caused by substrate ferromagnetism^39,138.

The problem with this argument is that often one expects small steps in magnetisation below the measurement resolution, or the coercive fields of the different magnetic regions overlap, masking the step shape. This is illustrated in Fig. 4c, d. In Fig. 4c, it is shown how two Hall channels can add to create the peak shape in the overall Hall effect, and if (for simplicity) both of these Hall channels have an equal and opposite anomalous Hall coefficient, then steps should be clearly visible in the magnetisation. However, Fig. 4d shows how two slightly more overlapping Hall channels can create a similar clear peak shape in the Hall effect, but give a single observable switch in magnetisation. This is exacerbated by the fact that the anomalous Hall coefficients will be different in the two channels, and the films used have very small magnetic moments. In cases where steps are visible in magnetisation, it is only at very low temperature, unlike the corresponding Hall peaks which are easily observable up to much higher temperatures³⁹. This means that observing a single switch in magnetisation is not sufficient to rule out a multiple-channel AHE.

Measuring magnetisation as a function of temperature can be a more sensitive complementary measurement for magnetic inhomogeneity. In field-cooled-warming or zero-field-cooling measurements the paramagnetic contribution remains small, and multiple steps or peaks (respectively) appear in M(T) if there are multiple magnetic regions with different T_Cs. These two T_Cs have been observed^39,142, and without clear separate transitions, the broadness of T_C has been correlated to Hall peaks by fitting M(T) to a power law with Gaussian T_C distribution¹³².

Bubbles are observed in magnetic force microscopy

MFM is a commonly used technique for imaging skyrmions in real space as a supplementary measurement to the THE. Several studies have reported skyrmions in SrRuO₃ using MFM^22,26,28. However, a difficulty arises in thin films since isolated skyrmions are often expected rather than a regular skyrmion lattice. Since MFM cannot measure in-plane magnetisation so cannot measure chirality, then the only indication of a skyrmion is observing a bubble shape in MFM.

This approach has been used effectively in studies on metallic systems¹⁸, but the data can be misleading. For example, usually in MFM a background subtraction is required in order to remove static magnetisation variation. However, background subtractions can give different results depending on how the subtraction is performed, for example Matsuno et al.²² found different MFM images for a given field depending on how the background subtraction is performed due to a field-dependent shift in the images.

Another method is to perform pixel-by-pixel subtraction between two images very close in field value, to detect how the magnetisation changes through a certain field range²⁶. However, it is difficult to discern between bubbles from skyrmions and bubble-like artifacts—if a ribbon-shaped domain extends then a bubble will appear in subtraction, or if the sample moves between measurements in the multi-domain state then bubble artifacts can appear. It also worth noting that ribbons and bubble domains are common in a switch of a magnetic film with an out-of-plane easy axis¹⁴³.

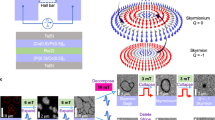
A comparison has been made by Wang et al.^26,40 between the MFM structure of BaTiO₃-capped films hosting skyrmions and bare SrRuO₃ showing thickness inhomogeneity. Here the number of bubbles that appear in subtraction images are counted and their frequency versus diameter is studied. In the film hosting skyrmions there appears to be a bimodal distribution of bubble sizes attributed to individual skyrmions and clusters (Fig. 5a–h), whereas in the film with thickness inhomogeneity there is a single peak. However, it is possible that the reason one peak appears in the film with thickness inhomogeneity is because it is a 4.5 UC film, so the ribbons of 4 and 5 UC regions are approximately equal width. If a different film thickness is used to give unequal widths of 4 and 5 UC ribbons then a bimodal distribution may appear in the bubble-size histogram, as illustrated in Fig. 5i–l. Furthermore, the shape of the bubbles is isotropic in the case of the BaTiO₃ capped film but elongated along terrace steps in the 4.5 UC film. The elongated bubbles are likely due to stripe domains switching along the terraces. However, if the bubbles result from stripes switching then the shape of the bubble depends on the change in applied field and the broadness of the coercive field. For example, MFM difference images taken through an entire magnetic switch for one of the stripes would show complete stripes, but if the difference image was taken through a fraction of the magnetic switch smaller bubble-like features would appear. It is not easy to directly compare two films with different coercive field shapes, but a comparable number of points through the transition should be made and subtractions over different field intervals could reveal anisotropy in the switching. Inhomogeneity in the capping layer could contribute to the reduction of anisotropy in switching¹³⁴. This study could be conducted with different thicknesses of SrRuO₃ film between 4 and 5 UC in order to establish whether the bimodal distribution of bubble size and lack of anisotropy is an indicator of skyrmions or can be a result of thickness inhomogeneity.

Fig. 5: MFM imaging of skyrmions.

a–e MFM images at different fields. In both saturated states (−1.00 and −3.20 T), a stripe contrast is still visible, an indication of magnetic inhomogeneity along the terrace steps. In image a, the terrace width is estimated at approximately 235 nm. f Pixel-by-pixel subtraction of image b from c. Examples of skyrmions are circled by green dashed lines, the clusters or bubbles are circled in red dashed lines. g Pixel-by-pixel subtraction at a higher field of c from d. More large clusters are visible. h Histogram of equivalent diameters for skyrmions/bubble domains in all subtraction images. This is fitted with two Gaussians with peaks near 80 and 16 nm. i–l Possible alternative for how skyrmion-like features could appear in subtraction images. i The stripe contrast results from thinner, lower M regions and thicker, larger M regions. They have widths of around 80 and 160 nm, resulting in a total step width of 240 nm, consistent with image a. j At a low field, the weaker regions start to switch. k Weaker regions continue switching, some stronger regions also switch, the new switches are shown in blue. l The subtraction image of k–l could look like a mixture of 80 nm skyrmions and 16 nm bubbles. All scale bars are 1 μm. a–h adapted from ref. ²⁶ by permission from Springer Nature: Nature Materials ⓒ 2018.

Inconsistency between topological Hall effect and real-space imaging

The skyrmion density predicted from the THE from Eq. (3) is often significantly larger than the number density of magnetic bubbles observed in MFM images. This is not just an issue in SrRuO₃^22,26 but seems to happen in most thin-film systems. For example, this discrepancy has been observed repeatedly in Co/Pt structures^16,17,18, V-doped Sb₂Te₃¹⁴⁴, Ce-doped CaMnO₃³⁷ and the half-metal manganite La_0.7Sr_0.3Mn_1−yRu_yO₃¹⁴⁵.

A reasonable possibility is that MFM resolution is too poor to measure most skyrmions. It has also been suggested that a non-adiabatic THE contribution accounts for this discrepancy^26,37. In the weak-coupling regime, the THE does not depend on spin polarisation¹⁴⁶, scales with the effective mass of electron⁷² and diverges near a Mott insulator transition in correlated materials, which has been observed in Ce-doped CaMnO₃³⁷. This may also be relevant to ultra-thin SrRuO₃, which is moderately correlated and has a metal–insulator transition in the ultra-thin limit.

Furthermore, the THE found from Eq. (3) is proportional to the polarisation of the material, P. For SrRuO₃ this is often quoted as −9.5%, from tunnelling magnetoresistance measurements¹⁴⁷. The spin polarisation of a material is given as (N_↑w_↑ − N_↓w_↓)/(N_↑w_↑ + N_↓w_↓) where N_↑↓ is the density of states of up and down spins at the Fermi level and w_↑↓ is a weighting. The value of −9.5% is from a tunnelling experiment where the relevant weights are w_↑↓ = ${\nu}_{{{\mathrm{F}}}}$_↑↓T_↑↓ where ${\nu}_{{{\mathrm{F}}}}$_↑↓ is the Fermi velocity for up and down spins, in this case in the [100] direction, and T_↑↓ are the transmission coefficients for the SrTiO₃ barrier. In band-structure calculations, it is generally agreed that the density of states of up and down spins are similar, and it is the large difference in the Fermi velocity of up and down spins that gives the negative spin polarisation^148,149. The weighting used therefore drastically affects the given spin polarisation. For ballistic and diffusive transport, the spin polarisation is weighted by ${\nu}_{{{\mathrm{F}}}}$ and ${\nu }_{{{{{{\rm{F}}}}}}}^{2}$, respectively. Weighting theoretical results for diffusive transport gives transport spin polarisation values between −42 and −92%¹⁴⁷, and Andreev reflection measurements (which cannot detect the sign of polarisation) made in the intermediate regime between ballistic and diffusive limits give a polarisation value of 50%¹⁵⁰. The relevant spin polarisation for SrRuO₃ could be much larger than the commonly used value, which would significantly decrease the density of skyrmions estimated from the THE.

Finally, there is evidence that chiral spin fluctuations can enhance the THE near the transition between isolated skyrmions and skyrmion lattices in Ir/Fe/Co/Pt heterostructures¹⁵¹. Here a power-law enhancement of the THE up to nearly 3 orders of magnitude is observed around the transition between isolated and dense skyrmions. This enhancement is attributed to fluctuations in the incipient order parameter. This is a similar effect to the chiral spin fluctuations near the Curie temperature reported in SrRuO₃, V-doped Sb₂Te₃³⁰, and Pt/anti-ferromagnet insulator heterostructures⁶⁶. As discussed previously, the Hall effect from chiral spin fluctuations could be considered not strictly ‘topological’ since it is not associated with an integer topological charge. This enhancement of the apparent THE could explain the discrepancy between Hall effects and MFM in many other interfacial systems such as SrRuO₃, V-doped Sb₂Te₃¹⁴⁴ and Ce-doped CaMnO₃³⁷.

Problems with inhomogeneity interpretation

Though it is possible to show magnetic inhomogeneity in a system, it is not straightforward to correlate this with the Hall effect. Many arguments are made for a spatially inhomogeneous AHE, but since it is not possible to measure a spatially resolved AHE one must usually infer this conclusion from fittings to an overall AHE supported by other magnetic measurements. Without a direct measurement, the results are left open to interpretation.

Skyrmions also affect the AHE and magnetisation

In contrast to the criticism that a lack of a step in M(H) does not confirm skyrmions, the presence of a step does not rule them out. In general, the presence of skyrmions will reduce the overall magnetisation of the film, reduce the overall AHE and give a THE contribution. If stabilised over a limited field range this could give a step in magnetisation as well as a peak, step or no change in the overall Hall effect depending on the relative sizes of the THE and AHE change. Evidence of magnetisation steps or changing Hall effect shapes therefore cannot rule out the existence of a THE^39,40.

No skyrmions seen in MFM

MFM is a vital tool for imaging skyrmions in real space but has a typical lateral resolution of around 10 nm, which is close to some predictions of the size of skyrmions in SrRuO₃²². It is possible that skyrmions could exist in these films and not be detected by MFM. Furthermore, studies reporting an inhomogeneous AHE still show bubble domains existing over the field region of the Hall peak^39,40. Here the anti-parallel domains are thought to result in the change in overall AHE. However, it is also possible that domain walls around extended bubbles have a net chirality due to the DMI, and thus contribute a THE. In other words, even in the absence of individual skyrmions, it is not clear whether there is a contribution from the THE from chiral domain walls in the multi-domain state¹⁵². A THE from chiral domain walls has been suggested in topological insulator heterostructures¹⁵³, and other chiral structures such as labyrinth-like patterns¹⁵⁴ have been reported.

The peak correlates with a growth parameter

Often the Hall peaks are measured as a function of a growth parameter, such as deposition time⁴⁰ or the stoichiometry of the target material⁴³, then the inhomogeneous AHE is correlated with this parameter. However, the correlation-causation problem is particularly challenging in thin-film growth as it is rarely possible to tune only one parameter. One could argue that stabilising chirality requires a sensitive balance of magnetic interactions, and changing growth parameters would disrupt this. It could also be the case that inhomogeneous magnetic textures could help stabilise chirality, as is the case in artificial skyrmions made by ion irradiation. Therefore correlating a Hall peak with a growth parameter or magnetic inhomogeneity is not sufficient to rule out a THE. Furthermore, film growth itself is often not completely reproducible: when growing multiple 5 UC films with the same growth parameters Wang et al.⁴⁰ found that some films would show Hall peaks and others would not, attributed to random variations in substrate and growth conditions giving slightly different thicknesses or growth modes.

Routes to clarify the roles of chirality and inhomogeneity

A large portion of this article has been spent reviewing and criticising Hall measurements combined with MFM imagining commonly used in the investigation of chirality, specifically in SrRuO₃ films. In the following section, we discuss different approaches and possible future experiments that could help elucidate the existence of chirality and its role in the THE in thin films.

Neutron diffraction and transmission microscopy techniques commonly associated with skyrmion detection are unlikely to be useful in the thin films in question, since a regular lattice of skyrmions is not usually expected, and to make samples electron or X-ray transparent one must mill or grow freestanding structures¹⁵⁵, which would reduce or remove the inversion symmetry breaking required for stabilising chiral spin textures. Different approaches are therefore required.

Quantifying the DMI

For a ferromagnetic film with perpendicular magnetic anisotropy, the stabilisation of skyrmions depends on the magnitude of the DMI, D, the exchange energy, J, and the uniaxial anisotropy constant K. The DMI can arise from the bulk material or from the interface, and the effective DMI from the interface decays with the thickness of the film (D_eff = D_i/t where t is thickness). It is expected that skyrmions can be stabilised if the DMI strength is larger than a critical value: ${D}_{{{{{{{{\rm{c}}}}}}}}}=\frac{4}{\pi }\sqrt{JK}$^26,47,156. J is found to be approximately 13 meV¹⁵⁷ in bulk SrRuO₃ from density functional theory (DFT), and in SrRuO₃ thin films K = (1.2 ± 0.1) J cm⁻³ which is ≈0.46 meV per Ru¹⁰⁴. These values give a critical DMI strength of the order of D_c ~ 3 meV.

There have been some theoretical calculations and some estimates of the DMI strength in SrRuO₃ heterostructures, but no experimental measurements independent of the THE. Some DMI strength estimates are found by assuming that the Hall effect peak is due to skyrmions or topological spin excitations, then finding the DMI consistent with these results. The interfacial DMI has been estimated to be D_i = 14 meV for SrRuO₃/SrIrO₃²² using a similar method as above, and D_i = 0.4 meV for SrRuO₃/SrTiO₃ found from thermally activated THE near T_C³⁰. The DMI has also been calculated using DFT under various conditions^25,26,29,41, such as using values of octahedral rumpling and distortion measured with scanning TEM²⁶ or coherent Bragg-rod analysis²⁵, with estimates varying from 0.2 to 3.6 meV depending on system and method.

These estimates are inconclusive, and to make a strong argument either way there needs to be quantification of D in ultra-thin SrRuO₃. Experimentally, one can determine the DMI strength by measuring the asymmetry in spin-wave dispersion using Brillouin light scattering^158,159 or spin-polarised electron energy loss spectroscopy¹⁶⁰. DMI measurement based on domain sizes¹⁶¹ may not be appropriate in ultrathin SrRuO₃ since the domain structure can be heavily dependent on the substrate terrace structure^40,134, although a similar technique has been used to determine a spatially dependent DMI in Ir/Co/Pt structures including the effect of thickness inhomogeneity¹⁶².

Measuring chirality with X-ray scattering

Dichroic resonant elastic X-ray scattering is a technique that allows the unambiguous determination of the magnetic structural information for ordered chiral systems through soft resonant X-ray diffraction measurements using both left and right-circularly polarised X-rays¹⁶³. This technique is powerful for measuring chiral spin structures including skyrmions and has been used by Huang et al.³⁵ to show the existence of chiral spin structures in SrRuO₃ films. A Néel-type chiral spin structure is found in the film below T_C when a magnetic field is applied. This could be a result of skyrmions or of chiral domain walls in a multi-domain state. The signal is also relatively weak and it is difficult to determine whether this spin chirality is strong enough to make a significant contribution to the Hall peak, yet it supports the existence of a Néel-type chiral spin structure.

These experiments were made on the oxygen K edge, and more direct evidence would come from similar experiments on the ruthenium L edges, though this presents further challenges such as the weak light intensity and long probing depth at this energy. Similar experiments have used linearly polarised X-rays at the Ru L₂ edge²⁵, and a similar experiment with right- and left- circularly polarised X-rays should be performed. In order to correlate these features to the Hall effect anomalies, further studies should measure the signal dependence on the magnetic field. Furthermore, more robust control measurements are needed, and systematic investigations should be made on different similar samples which do and do not show Hall effect anomalies.

Real-space chirality imaging

Magnetic force microscopy has been discussed in detail, with one of its main drawbacks being that it can only measure an out-of-plane stray field gradient, so cannot determine chirality. There are several options for non-destructive measurements with real-space resolution and sensitivity to in-plane magnetisation.

Spin-polarised low energy electron microscopy (SPLEEM) has been successfully used to image chiral domain walls in Co/Ni¹⁵². Here the full magnetisation vector in M_x, M_y and M_z can be mapped independently with a resolution of the order of 10 nm, meaning the full chiral spin structure of a thin film can be resolved¹⁵². It is not necessary to measure the entire magnetisation vector in order to establish whether domain walls are chiral. Boulle et al.⁸¹ have measured chiral domain walls using photo-emission electron microscopy combined with X-ray magnetic circular dichroism. Here magnetisation was measured along one axis with an in-plane component. When measuring across a domain wall, a signal increase or decrease indicates a domain wall rotating towards the measurement axis or away from it, and finding a bubble with opposite rotations shows that the bubble is likely chiral. This technique has a resolution of 10s of nm, so may not be sufficient for an individual skyrmions in SrRuO₃ based on early size estimates²².

Spin-polarised scanning tunnelling microscopy (SP-STM) improves on this resolution limit and can give information on chirality if the magnetisation of the tip can be canted in-plane. A THE due to skyrmions has been reported in SrRuO₃ even with large tilted applied fields^25,32. In this case, the STM tip could be magnetised at an angle to the film magnetisation, and therefore reveal the chirality by whether the signal is symmetric or asymmetric across a bubble or pair of domain walls, as shown in Fig. 6a. Alternatively, an anti-ferromagnetic tip can be used which couples weakly to applied magnetic field, therefore an out-of-plane field can be applied to the film. SP-STM has successfully been used to measure skyrmions in, for example, PdFe⁷⁹.

Fig. 6: Possible experiments to investigate chirality and its contribution to the Hall effect in SrRuO₃.

a Spin-polarised scanning tunnelling microscopy with the tip magnetised in-plane, either using an in-plane applied field or an anti-ferromagnetic tip. A THE has been reported in SrRuO₃ even with large in-plane fields. The tunnelling conductance (dI/dV) will vary across a bubble in different ways depending on whether it is chiral or non-chiral, as shown in 1D and 2D. b Hall bar on a step. Illustration of a film with some kind of inhomogeneity in the AHE, such as thickness variations in SrRuO₃ films. A nano-Hall bar could be patterned on top by, e.g., electron-beam lithography. Some of the Hall contacts could overlap two regions, while others may just be in single regions. This could determine whether the Hall anomalies are due to an inhomogeneity on the scale of the patterned Hall bar. c By patterning a sample with, for example, helium irradiation or ferroelectric poling, the anisotropy of films can be selectively altered and skyrmions can be artificially stabilised. Control measurements with no patterning and non-disc patterning should be made to establish whether the Hall peak is due to modifying the AHE or stabilisation of skyrmions. d Substrate miscut dependence. Increasing the substrate miscut angle in a film with UC thickness inhomogeneity from step-flow growth will increase the number of domain walls between the two coercive fields. If the Hall peaks are entirely due to an AHE inhomogeneity, then they should be little dependence of the peak height on substrate miscut angle. If the Hall peak is due to chiral domain walls, then there should be some additional dependence on the substrate miscut angle.

Nitrogen vacancy scanning probe microscopy is non-invasive, has an extremely high sensitivity and resolution and has been used to image the chirality of individual skyrmions¹⁶⁴. This technique is limited to operating at low magnetic fields (<1 T), so may be useful for imaging skyrmions in SrRuO₃ at high temperatures where the THE is stabilised at lower fields. Magnetic exchange force microscopy (MExFM) is another possibility¹⁶⁵. This operates on similar principles to MFM but with atomic resolution, and has been used to image nano-scale skyrmions on Fe monolayers¹⁶⁶.

There have recently been preliminary reports of SP-STM of SrRuO₃/SrIrO₃ bilayers using an anti-ferromagnetic tip and out-of-plane applied field¹⁶⁷. Here skyrmion-like features are measured, and their signal strength is independent of the thickness of SrIrO₃ capping, indicating that skyrmions are present in the insulating SrIrO₃ which is magnetised by the magnetic proximity effect¹⁶⁷. These results are the first spatially resolved magnetic measurements with an in-plane component in SrRuO₃, and give completely unexpected results. It is usually assumed that the ferromagnetic SrRuO₃ would host the skyrmions, not the SrIrO₃ layer.

Further Hall effect measurements

To show that a Hall anomaly is due to spatially inhomogeneous properties, one would ideally measure a spatially resolved AHE, but this is not easily achieved. The only feasible way to measure any spatial resolution of the AHE is to pattern a nano-Hall bar with many transverse contacts, as shown in Fig. 6b. This could give useful information if the spatial variations of the AHE occur over a relatively large scale, such as thickness inhomogeneity effects for films grown by step-flow on low-angle miscut substrates.

Another approach would be to measure a Hall effect and MOKE signal simultaneously and exploit a control parameter that allows one to tune the magnetic texture or number of skyrmions. For example, He-ion irradiation has been used to locally modify the anisotropy in patterns that stabilise skyrmions in Co/Pt films¹⁶⁸. It may also be possible to use ferroelectric poling, which could locally affect the magnetic anisotropy in SrRuO₃¹⁶⁹. An illustration of this experiment is shown in Fig. 6c. Since a THE should vary with the number of skyrmions stabilised while an inhomogeneous AHE would only vary with relative areas of the different regions, it may be possible to separate the two effects. However, careful control experiments are essential to rule out the inhomogeneous AHE, and are lacking in Co/Pt studies. Another way of controlling the magnetic texture in epitaxial films grown in step-flow growth is to vary the substrate miscut angle. Terrace edges often act as pinning sites during magnetisation reversal, and in fractional-unit-cell thickness films such as 4.5 UC SrRuO₃, varying the miscut angle will vary the number of domain walls present during magnetisation switches, while keeping the total area of the domains the same, as shown in Fig. 6d, so could provide a way to separate the Hall effects due to the domains and the domain walls.

Outlook

The understanding of chiral spin textures in thin films is an important component for designing future spintronic devices. The THE is a powerful technique for investigating chirality in thin films, and there has been a surge of interest in measuring skyrmions using this technique in a wide range of materials. However, it is now clear that the common method of subtracting a magnetisation loop from a Hall hysteresis loop to determine the THE is not a reliable technique, with many different examples in the literature where this technique would be misleading. In general, differences between magnetic and Hall hysteresis can occur due to inhomogeneity in the material or due to experimental issues. We therefore believe THE measurements in isolation should not be considered sufficient evidence for the presence of skyrmions or any other chiral spin texture.

A recurring observation in the literature is that the AHE shows sign changes as a function of some parameter such as temperature or thickness and Hall peaks appear near this sign change. In these cases, it is plausible that these peaks can be attributed to some kind of inhomogeneity that is dependent on that parameter, rather than a THE due to chirality.

The common complimentary technique of MFM can also be misleading. The Hall peak is usually correlated to the appearance of magnetic bubbles, however, Hall anomalies due to inhomogeneity in the AHE would also occur in a multi-domain state which is likely to host magnetic bubbles. There is often a poor quantitative agreement between the measured THE and MFM images in many different material systems. This discrepancy could be due to resolution limitations, the invalidity of the adiabatic assumption to calculate of the number of skyrmions, enhancement of the Hall effect by chiral fluctuations¹⁵¹ or unreliable THE determination.

In SrRuO₃, it is still not clear whether the ubiquitous peaks observed in Hall effects are caused by a THE from chirality or an inhomogeneous AHE caused by thickness variation, modification from interfaces, defects, other variations to the electronic structure or a combination of these effects. It is unlikely that one explanation can account for all the different peaks seen. It now appears less likely than originally thought that the Hall peaks can be solely attributed to a THE caused by well-defined compact skyrmions. However, this does not mean the THE can be disregarded. Even films with clear inhomogeneous magnetic properties have a multi-domain structure during the Hall peak. Domain walls in a film with strong spin-orbit coupling and broken inversion symmetry would have some net chirality and give a contribution to the THE, and the question is then whether this effect is negligibly small or significant compared to the inhomogeneous AHE.

In order to separate the AHE and THE, further Hall measurements should be made in experiments where a parameter can be used to tune the magnetic texture, and careful control measurements are extremely important to separate the different contributions to Hall anomalies. The full picture is unlikely to be resolved by Hall measurements, magnetometry and MFM imaging alone, and supplementary measurement techniques are needed. In particular, non-destructive high-resolution real-space imaging techniques that can measure a magnetisation vector with an in-plane component such as spin-polarised scanning tunnelling microscopy can give crucial insight into this problem.