Introduction

Chemical bonding lies at the heart of all-natural sciences like condensed matter physics, chemistry, and even biology. As such, the understanding of chemical bonding was a great puzzle for a long time. In the long and rich history of condensed matter physics, one cannot emphasize strongly enough the importance of the two basic concepts: dimerization1 and charge ordering2, both born in the 1930s. However, these two phenomena have been rarely found to coexist in one compound, much less in metallic systems.

Many studies in the late 1990s and early 2000s demonstrated, one example after another, how the new patterns emerge out of simple structures: hexamers in ZnCr2O43, octamers in CuIr2S44, spontaneous dimensionality reduction in Tl2Ru2O75, and the formation of trimeron in Fe3O46, to name only a few. Despite the various properties, an ever occurring theme is that these phenomena typically happen near the metal–insulator boundary, with the ordered states usually insulating. This characteristic feature is naturally captured by Mott–Hubbard physics7, and it is particularly prominent among frustrated magnets8,9,10,11. It is relatively less well-known how this rich physics plays out in metallic systems; it remains unchartered territory to date. One can imagine that this question may become more important in the newly emerging field of quantum materials that increasingly include metallic systems12.

Ru has a special place in this extensive search because of its two characteristic features: the modest spin–orbit coupling (SOC), not too small nor too large compared to the Coulomb energy and the bandwidth; another is relatively stronger importance of orbital physics7. This combination of the two has been behind the active researches on Ru oxides; for instance, superconducting Sr2RuO4 and ferromagnetic SrRuO3 are two prominent examples13,14. In comparison, there have been few studies on Na–Ru–O systems, including NaRu2O4. Using neutron diffraction, the authors of ref. 15 determined that its room-temperature structure has the space group of Pnma, the typical orthorhombic structure among oxides: to our best knowledge, it was initially reported in 197516 before being re-examined in 2006. It was reported to have a paramagnetic susceptibility down to the lowest temperature. While studying another Na compound, Na2.7Ru4O917 which was also investigated in the same ref. 15, we realized that the high-temperature phase of these Na–Ru–O systems could exhibit exciting new unreported properties and hence deserve careful studies.

In this report, we made extensive studies of both structure and physical properties of NaRu2O4 over a wide temperature range up to 600 K above which it becomes chemically unstable. We made the high-resolution XRD study above room temperature to find a surprising first-order phase transition during this study. We found that NaRu2O4 undergoes a metal–metal phase transition below 535 K with a distinct structure change, from a CaFe2O4-type structure with the orthorhombic Pnma symmetry at a higher temperature to a monoclinic structure P1121/a below Tc. By combining experimental and theoretical studies, we found that at this transition we have simultaneously a site-centered charge ordering coexisting with dimerization.

Results and discussion

Bulk properties

Electrical resistivity (ρ) measurements were carried out using a homemade system equipped with a furnace (300–685 K) and a pulsed-tube cryostat with the base temperature of 3 K. The electrical resistance was measured in a four-point geometry, where contacts were made using silver paint and 25 µm gold wire as shown in the inset of Fig. 1a. The current was applied perpendicular to the single crystal length, which is the crystallographic b-axis. As the single crystals are all in a thin needle form, we could not measure the resistivity along with the other crystallographic directions. We tested several long rod-shaped as-grown crystals and discovered the same transition (see also Supplementary Fig. 1). The resistivity data shows that a phase transition occurs in NaRu2O4 at Tc = 535 K with small hysteresis in the electrical resistivity, a sign of a weak first-order phase transition at Tc. We will extensively discuss this transition below; it is the main feature of NaRu2O4.

Fig. 1: Bulk properties.
figure 1

a The electrical resistivity data as a function of temperature is taken over single-crystal with the solid red line for the Bloch–Grüneisen model. Inset shows the single crystal used for the four-probe resistivity measurements. b Magnetic susceptibility (χ) measured at an applied magnetic field B = 0.5 T. The inset shows inverse susceptibility with the modified Curie–Weiss law (solid red line). c Temperature dependence of the specific heat Cp measured at zero fields (B = 0 T). Solid black circles are the raw data with Cp/T shown in the inset of the figure while solid red line is the corresponding Cp/T = γ + βT2 fitting.

Full size image

The resistivity ρ(T) data measured down to 3.3 K indicates metallic behavior with a room temperature resistivity of ~40 μΩ cm. To have a quantitative understanding, we analyzed the results theoretically using the Bloch–Grüneisen model. The following formula gives the expression for the temperature-dependent part of the metallic resistivity:

$$\rho\approx \left(\frac{3}{\hslash{e}^{2}{v}_{{{{{{\mathrm{F}}}}}}}^{2}}\right)\frac{{k}_{{{{{\mathrm{B}}}}}}T}{{{{{{\mathrm{Mv}}}}}}_{{{{{\mathrm{s}}}}}}^{2}}\int {\left|v(q)\right|}^{2} \left[\frac{{\left(\hslash \omega /{k}_{{\mathrm {B}}}T\right)}^{2}{q}^{3}{{{{\mathrm{d}}}}}q}{\left({{{{{\mathrm{exp}}}}}}\left(\hslash \omega /{k}_{{\mathrm {B}}}T\right)-1\right)\left(1-{{{{{\mathrm{exp}}}}} }\left(-\hslash \omega /{k}_{{\mathrm {B}}}T\right)\right)}\right],$$
(1)

where v(q) is the Fourier transform of the potential associated with one lattice site and vs is the sound velocity. When Eq. (1) was considered for the acoustic phonon contribution, it leads to the Bloch–Grüneisen function as shown below:

$${\rho }_{e-{{\mbox{ph}}}}\left(T,{\theta }_{{\mathrm {D}}}\right)=4{A}_{{{\mbox{ac}}}}{\left(T/{\theta }_{{\mathrm {D}}}\right)}^{4}\times T{\int }_{0}^{{\theta }_{{\mathrm {D}}}/T}{x}^{5}{\left({e}^{x}-1\right)}^{-1}{\left(1-{e}^{-x}\right)}^{-1}{{\mbox{d}}}x,$$
(2)

where \(x\) = ħω/kBT, θD is Debye temperature, and Aac is a proportionality constant. The total resistivity of a material can be written as

$$\rho (T)={\rho }_{0}+{\rho }_{{\mathrm {e}}-{{\mbox{ph}}}}\left(T,{\theta }_{{\mathrm {D}}}\right),$$

where \({\rho }_{0}\) is the temperature-independent residual resistivity and the second term represents the electron–phonon scattering. The Bloch–Grüneisen model is found to work well for our study, and the theoretically estimated ρ is quite consistent with the experimental data for NaRu2O4. The characteristic Debye temperature (θρ) and residual resistivity (ρ0) is found to be 452.2 K and 35.9 μΩ cm, respectively.

We also measured magnetic susceptibility and specific heat of NaRu2O4 in the accessible temperature range of 2–300 K. The susceptibility (χ) for NaRu2O4 was measured in the temperature range between 1.9 ≤ T ≤ 300 K with a 0.5 T of the external field applied perpendicular to the length of the as-grown crystal as in Fig. 1b. No magnetic ordering was observed in the measured temperature range. It is noticeable that the susceptibility is almost temperature-independent over the wide temperature range, showing a sizeable paramagnetic behavior consistent with the reported susceptibility data on the polycrystalline sample15. The low-temperature upturn is apparently due to some magnetic impurities, and it can be explained by using a modified Curie–Weiss formula as discussed in Supplementary Note 2 (see the red line in Fig. 1b). The fit yields the following values: Curie–Weiss temperature θCW = −1.8 K, observed moment μeff = 0.04 μB per Ru atoms and χ0 = 1.15 × 10−7 (cm3/Ru mol)−1, where the latter is the temperature-independent van Vleck contribution to the susceptibility. The Curie–Weiss fit gives a significantly smaller observed moment, indicating negligible localized magnetic moments in NaRu2O4, similar to the reported polycrystalline sample15.

The heat capacity was measured between 1.9 ≤ T ≤ 300 K and is displayed in Fig. 1c. The heat capacity did not show any λ-type anomaly over the entire temperature range, confirming no long-range magnetic order from 300 to 1.9 K. Low-temperature heat capacity data were analyzed using the usual formula of Cp = γT + βT3, where γ is the electronic specific-heat coefficient and β is the phonon contribution at low temperature (see the inset of Fig. 1c). The electronic contribution to the specific heat (γ) for NaRu2O4 was 3.93 mJ/mol K2, consistent with the metallic behavior.

Single-crystal XRD data and crystal structures at high and low temperatures

To understand the high-temperature phase transition seen in the resistivity data, we conducted high-resolution single-crystal diffraction experiments to obtain the most informative data. We performed the temperature-dependent SC-XRD experiment from 300 to 575 K using a single crystal diffractometer (XtaLAB P200, Rigaku) (see Fig. 2). In our room-temperature data, we observed q = (0, ½, 0) superlattice peak (satellite reflections). It is important to note that this presence of the satellite reflection cannot possibly be explained by the Pnma space group proposed in ref. 15.

Fig. 2: Room-temperature SC-XRD refinement for LT-phase: Single-crystal XRD reciprocal-lattice images and lattice parameters across the structural transition.
figure 2

a The SC-XRD refinement includes a modified structural model with a new space group (P1121/a) determined from CBED experiments. The refinement is performed by including a monoclinic merohedral twin model under twin law as (-100) (010) (00-1). The solid red and blue circles are fundamental and superlattice reflections, respectively. The inset of the figure shows the optical image of the measured crystal. b Single-crystal x-ray diffraction data measured at various temperatures below and above the phase transition (Tc = 535 K) for NaRu2O4. c The cell parameters with error bars of NaRu2O4 at different temperatures extracted from single-crystal XRD data. The vertical line corresponds to Tc.

Full size image

While searching battling for a possible true structure at room temperature, we decided to employ the convergence beam electron diffraction (CBED) as it is the most powerful technique in determining the space group and gives crucial information about the lattice’s symmetry18 (see Fig. 3). The weak superlattice reflections in the x-ray diffraction experiments already form strong evidence for broken symmetry (both translation and rotational) and lattice distortion in a crystal. In addition, the superlattice peak at q = (0, ½, 0) disappears upon heating just above Tc. We collected CBED diffraction patterns along the various [100], [130], [001], and [201] axes as shown in Fig. 3a–c at room temperature. The CBED experiment revealed P1121/a symmetry (no. 14 with setting unique axis c19) at room temperature, a subgroup of the reported Pnma symmetry. Therefore, a modified structure model under group–subgroup relation is used to solve the room temperature SC-XRD data. We used the Shelx software20 to address the twin problem in our refinement. In the twin refinement for NaRu2O4 SC-XRD data, we used a monoclinic merohedral twin model under twin law as (-100) (010) (00-1) to get better refinement parameters and statistics as well. Supplementary Note 3 provides details of monoclinic merohedral twin model under twin law. All the reflection patterns collected at 300 K could be indexed as monoclinic P1121/a symmetry with a primitive lattice of a = 9.273 (6) Å, b = 5.643 (3) Å, and c = 11.17 (7) Å.

Fig. 3: The converge beam electron diffraction (CBED) patterns at room temperature in NaRu2O4 crystal.
figure 3

The CBED patterns are taken with (a) [001], (b) [100], and (c) [130] incidences. Whole pattern symmetries of the CBED patterns are two-fold symmetry for [001] incidence, mirror symmetry perpendicular to the c-axis for [100] and [130] incidences. Dynamical extinction lines were observed at 0 0 lodd and hodd k 0 reflections at [130] incidence.

Full size image

Table 1 summarizes the SC-XRD refinement results for the low-temperature (LT) phase (300 K). All the crystallographic sites were considered to be fully occupied and were kept fixed during the refinement. We carried out the structure analysis by including the twin structure of monoclinic cells. The structural parameters were finally determined from the least-squares refinement of the single-crystal XRD data. For the single-crystal refinement, we used a total of 5021 reflections, and all the reflections were well indexed by a monoclinic a0 × 2b0 × c0 cell. We used P1121/a (no. 14) with a table setting choice: c1. No constraints were placed on the atomic positions. The comparison of calculated and observed intensity (F2) after the structural refinement at room temperature is shown in Fig. 2a.

Table 1 The single-crystal x-ray diffraction measurement of NaRu2O4 at 300 K is used for the refinement.
Full size table

As regards the high-temperature (HT) phase, our single-crystal data could not uniquely solve the structure above Tc (HT-phase) due to the sizeable diffuse scattering. Most probably, at such high temperatures, lighter Na ions located in 1D tunnels of NaRu2O4 start to move within the tunnels. In this situation, we decided to begin with positional parameters of distorted phase (Table 2, LT-phase with a0 × 2b0 × c0 P1121/a from Shelx refinement with twin), and generate undistorted positional parameters (undistorted P1121/a a0 × b0 × c0). The undistorted positional parameters of P1121/a symmetry are used to get positional parameters for orthorhombic HT-phase of Pnma symmetry under cell-symmetry and group-subgroup relation19. Expected coordinates at HT Pnma phase based on LT P1121/a structure (a0 × b0 × c0) are shown in Table 2. Excellent agreement is seen between expected positions and reported one15 (by missing superlattice reflections: a0 × b0 × c0), as shown in Table 3.

Table 2 Expected coordinates at HT Pnma phase based on LT P1121/a structure (a0 × b0 × c0) (atoms are at 4c site19).
Full size table
Table 3 Reported LT Pnma structure (a0 × b0 × c0) (atoms are at 4c site)19.
Full size table

The crystal structure of NaRu2O4 is close to that of the prototype compound CaFe2O4 with similar coordination environments. In our revised crystal structure for NaRu2O4, the most characteristic feature we found is the edge-sharing octahedra double RuO6 chain, which runs along the crystallographic b-axis. These double chains form a two-leg zigzag ladder along the crystallographic b-axis. The RuO6 octahedra are edge-sharing within each chain, tied to the neighboring chain through the corner oxygen. This leads to an interesting lattice geometry with pseudo-triangular tunnels, in which a single Na atom can be accommodated, as shown in Fig. 4a, which is also found in various CaFe2O4-type lattices21,22,23,24,25,26. Our detailed single-crystal x-ray diffraction analysis shows a transition from the HT (high-temperature) Pnma structure to the low-temperature (LT) P1121/a structure at Tc = 535 K, as shown in Fig. 4b, c: which is consistent with the results of resistivity measurements shown in Fig. 1a.

Fig. 4: High-temperature and low-temperature crystal structures.
figure 4

a The HT-phase in NaRu2O4 has an orthorhombic structure with a Pnma space group, similar to the CaFe2O4-type structure1. The octahedra and Ru atoms are represented in light brown and O atoms in red color. b The HT-phase crystal structure (Pnma) of NaRu2O4 in bc-plane. c The LT-phase crystal structure of NaRu2O4 has monoclinic symmetry P1121/a.

Full size image

According to our diffraction experiments done between 300 ≤ T ≤ 575 K, the q = (0, ½, 0) superlattice peak (satellite reflection) persist right up to 535 K as shown in Fig. 5. The line cut from the temperature-dependent reciprocal image analysis for peak q = (0, ½, 0) shows clearly the suppression of intensity as a function of temperature as in Fig. 5b, c. The q = (0, ½, 0) superlattice peak is substantially suppressed just above the first-order transition (Tc = 535 K).

Fig. 5: Single-crystal x-ray diffraction (SC-XRD).
figure 5

a Reciprocal lattice maps of the SC-XRD data for NaRu2O4 obtained at 470 and 575 K with the first-order transition at Tc = 535 K. b The line cut for various temperatures below and above the first-order phase transition as extracted from the reciprocal space analysis. c Temperature dependence of the (4 3 0) super-lattice peak.

Full size image

Charge ordering and bond valence sum (BVS)

The structure of NaRu2O4 can be visualized as the double chain of edge-sharing RuO6 octahedra running in the b-direction and forming 2-leg zigzag ladders (see Fig. 6a). The corner-sharing oxygen atoms connect these ladders, also having a zigzag pattern. In effect, there appear in this system, not one, but three different types of zigzag ladders: those in edge-sharing double chains (ladders-2 marked by red in Fig. 6b. For shortness, we will call them “red” ladders), and two types of corner-sharing zigzag ladders, marked in Fig. 6b, c by blue and green. When describing this class of materials, one often pays primary attention to the phenomena occurring in the “red” ladders (see ref. 27). But the corner-sharing ladders are sometimes found to play a more critical role in systems like hollandite K2Cr8O1628. As we will see below, these edge-sharing ladders also play a crucial role in NaRu2O4.

Fig. 6: Crystal structure of the tunnel compound NaRu2O4.
figure 6

a Top view of the low-temperature structure. b Illustration of different types of zigzag ladders: “red” ladders with edge-sharing RuO6 octahedra; “green” and “blue” ladders with corner-sharing octahedra. c The detailed structure of corner-sharing and edge-sharing ladders.

Full size image

Here it is worthwhile to think about possibility of certain effect due to off-stoichiometry. In particular, one can ask whether the observed metallic behavior is related to a sample quality issue. For instance, it is known that such stoichiometry plays an important role in determining the low-temperature properties of RuP29, whose high-quality powder samples exhibit a metal–insulator transition. On the other hand, single crystal of RuP, presumably off-stoichiometric, has a metallic ground state. For NaRu2O4, we can rule out this issue as our powder sample also shows a metallic behavior (see also Supplementary Fig. 2). Another point is that our heat capacity measurements taken on two different samples consistently show a finite gamma value at low temperature, which is consistent with the data reported in ref. 15.

An exciting picture now emerges from the detailed structural study. The HT-phase has two independent Ru sites (Ru1 and Ru2), equally spaced (2.82 Å) with the lattice constant b0 along two Ru chains. The most prominent feature of the structural changes is the appearance of strong dimerization in Ru chains (legs of zigzag ladders), leading to cell-doubling in the b-direction (see Fig. 7a). Ru–Ru distance in short Ru dimers is 2.60 Å—even shorter than the Ru–Ru distance in Ru metal (2.65 Å). It is a clear sign of direct metal–metal bonding in such dimers—which quite unexpectedly coexist with metallic conductivity. Simultaneously with the dimerization in 1D Ru chains—legs of zigzag ladders, Ru sites themselves become inequivalent, Ru(A) and Ru(B), a clear sign of a site-centered charge ordering in NaRu2O4. The coexistence of bond- and site-centered orderings is extremely rare in metallic systems, making NaRu2O4 especially interesting.

Fig. 7: Superstructure in the low-temperature phase and the results of the LSDA + U band structure calculations.
figure 7

a The unit-cell of the low-temperature phase with two dimerized Ru bonds and the valence of Ru as determined from bond valence sum (BVS) calculations. b Structure of the blue corner-sharing ladder with different valence states of Ru and different bond lengths marked. c–f Orbital-resolved DOS for four nonequivalent Ru atoms calculated within LSDA + U with U = 3.7 eV and J = 0.7 eV, assuming the charge order shown in (a). Ru orbitals are defined in local frames with the axes directed to the nearest O ions.

Full size image

Another essential feature of this superstructure is the difference of distances in the inter-chain bond length (interdimer), both in edge-sharing “red” and in corner-sharing “green” and “blue” ladders (Fig. 6b). The Ru1(A)–Ru1(A) and Ru2(A)–Ru2(A) distance in the edge-sharing ladder is 3.10 and 3.09 Å, while the Ru1(A)–Ru1(B) and Ru2(A)–Ru2(B) distance are 3.12 and 3.11 Å, respectively, with the remaining distance between dimers (Ru1(B)–Ru1(B) and Ru2(B)–Ru2(B)) being 3.16 Å (see Fig. 7a, b). From the viewpoint of the bond order, short bonds have a shape like a “letter-Z” (see Fig. 8). The same is true for two other types of ladders, edge-sharing “blue” and “green” ladders. We thus see that the dimers also form Z-type orbital clusters in corner-sharing ladders. The relative difference of interdimer bonds in these is even more prominent than in the “red” edge-sharing ladders: it is ~1.7% compared to ~0.7% in the “red” ladders. This already hints that what happens in corner-sharing ladders is probably more critical than in edge-sharing ones, as in hollandite K2Cr8O1628. According to our ab-initio calculations based on the charge valence of our choice [Ru1(A)3+, Ru1(B)4+, Ru2(B)4+, Ru2(A)3+), the nn hoppings in corner-sharing blue and green zigzags are: for blue corner-sharing bonds t = 0.40 eV, for green corner-sharing ones t = 0.29 eV, and for red edge-sharing bonds t = 0.35 eV. For other charge ordering the values are somewhat different but the blue corner-sharing bonds are always the strongest. It shows the dominance of the blue bond among all relevant bonds.

Fig. 8: Z-order in the two-leg corner- and edge-sharing RuO6 zigzag ladders.
figure 8

The sketch of self-organized Z-clusters in the low-temperature phase, formed within the edge-sharing red and corner-sharing blue ladders of NaRu2O4 lattice in the low-temperature phase.

Full size image

For the determination of the oxidation states of cations (Na and Ru), we carried out calculations by using the BVS method with an inbuilt program in Fullprof software30. The principle of BVS method in determining the valence V from different cation sites31,32 can be given by an expression V = Σi[exp(d0−di)/0.37]. Here, di is the experimental bond lengths to the surrounding ions, and d0 is a tabulated empirical value characteristic for the cation-anion pair31,32. The BVS result for NaRu2O4 was determined for the LT-phase. The charge at different Ru sites is illustrated by different colors (brown-Ru4+ and green-Ru3+) in Figs. 6 and 7. The BVSs for the eight oxygen sites were between 1.86 and 2.20. The BVSs for the four Ru cations sites for different charge configurations (we call them four different models) are shown below in Table 4. The respective reliability parameter as Global Instability Index (GII) is also listed for each BVS model for NaRu2O4.

Table 4 The four different models corresponding to four options for two dimers: counting from the left, (3+, 4+) in the upper dimer, (3+, 4+) in the lower dimer.
Full size table

To be more technical, an important question is how different Ru valence states are distributed in the low-temperature phase. Specifically, one has to know which ions, in which charge state, are connected by these shorter zigzag rungs in orbital Z clusters. For that, we used the results from the BVS analysis at each Ru, an empirical measure of its charge or its valence state33,34. In the HT-phase, all Ru are equivalent, and BVS gives the valence Ru3.5+. In contrast, Ru ions in a short dimer are indeed inequivalent in the LT-phase, with the valence estimated from BVS being 3.536 and 3.106; that is, one can think of Ru4+ and Ru3+ in each dimer. However, from our structural data alone, although collected with high-resolution single-crystal x-ray diffraction and the total number of 5021 Bragg peaks, we cannot uniquely discriminate the four possible charge ordering patterns, mainly because an x-ray experiment fundamentally suffers from the weak scattering signals of oxygen. The reliability parameters (GII) for four different charge ordering patterns are comparable to one another, about 10–11% (see Table 4). Still, a slightly better index is obtained for charge distribution with Ru4+ ions at the ends of short diagonal bonds in blue and green ladders (reliability factor 10.43% for model 3 in Table 4). In contrast, these are Ru3+ in edge-sharing red ladders. Note that different ladders are connected in the structure of NaRu2O4 so that the charges at short zigzags in neighboring ladders are opposite (see Fig. 8).

Theoretical studies

As we commented above, there is unavoidable ambiguity about our determination of the charge valence using the BVS method although we used the total number of 5021 Bragg peaks from the high-resolution single-crystal x-ray diffraction experiment. Therefore we employed ab-initio LSDA and LSDA + U calculations to clarify the charge pattern favored by the LT crystal structure. We used different Coulomb repulsion U values in the range 2.7–4.2 eV and Hund’s coupling JH = 0.7 eV as estimated from LSDA. All calculations were performed for the experimental HT and LT crystal structures. No attempts to optimize lattice geometry have been made. The effect of SOC on Ru t2g bands was relatively weak. In the following, for simplicity, we discuss the results of scalar-relativistic calculations. Our theoretical studies show that different self-consistent spin and charge-ordered solutions can be stabilized for sufficiently large U (3.7 eV). These solutions have the following common features: Ru dxy states (in local coordinates, with the axes directed from Ru to O) are strongly split into occupied bonding and unoccupied antibonding molecular orbital states (see Fig. 7c–f). Second, each dimer’s Ru ions become formally Ru3+, with its dxz, dyz orbitals being doubly occupied. Another Ru ion of the dimer, Ru4+, has one half-occupied orbital, approximated by a linear combination of dxz and dyz lying in the plane perpendicular to the b-axis. The Ru4+ ion acquires a spin moment of about 0.8 μB. The orbital-resolved density of Ru d states illustrates the charge disproportionation. With decreasing U, the hybridization becomes more robust between the unoccupied dxz, dyz orbital of Ru4+ and occupied t2g orbitals of Ru3+, a gap separating the unoccupied dxz, dyz band from the top of the valence band closes, and for U ~ 2.7 eV the charge disproportionation between Ru3+ and Ru4+ ions disappears (see Fig. 7c–f). It should be noted that this is only a rough estimate for the critical U value which may change if optimized crystal structure were used in the calculations and is in general implementation specific.

Out of the four charge ordering patterns allowed for the LT structure, three are nearly degenerate, with the energy difference being <3 meV/f.u. This finding agrees with the BVS analysis results, which give comparable reliability factors for different charge ordering. Still, the lowest total energy is found for one charge ordering pattern: for which the lowest value of GII was obtained experimentally from BVS. The final charge pattern is that the short zigzag bonds in Z-cluster in corner-sharing “blue” ladders connect Ru4+ - Ru4+ ions (see Fig. 8).

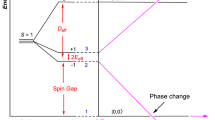
Finally, we would like to note that the structure of NaRu2O4 is composed of frustrated 2-leg zigzag ladders with a spin-singlet ground state, which makes this material quite interesting. For more details see Supplementary Figs. 4 and 5 in Supplementary Note 4. As shown in Fig. 9a, b, the orthorhombic Pnma crystal structure of NaRu2O4 has two ruthenium atoms Ru1 and Ru2. The edge-sharing bond between the two RuO6 octahedra for each dimer 1 (2.60 Å), dimer 2 (2.61 Å) and Z diagonal-bond (3.10 Å) give rise to two Ru–O–Ru bonds which are deviated from 90° for each and also all of the edge-sharing octahedral shows significant trigonal-distortion. The schematic representation shows the double chain-forming two-leg zigzag ladders (solid thick light-green, reddish-brown, and sky-blue lines) running along the crystallographic b-axis in crystal. The 2-leg zigzag ladders are connected in two different forms: the corner- (blue or green ladders) or the edge- (red ladders) sharing RuO6 octahedra. The t2g energy-level sketch with respective electron fillings is shown for a charge-ordered state, so-called Z-order (left panel) and Ru-dimer (right panel) in Fig. 9d.

Fig. 9: CaFe2O4-type tunnel structure and edge-sharing RuO6 two-leg ladders in NaRu2O4 lattice.
figure 9

a The orthorhombic Pnma crystal structure. b The bond between the two RuO6 octahedra for each dimer 1 (2.60 Å), dimer 2 (2.61 Å), and Z diagonal-bond (3.10 Å). c Schematic representation of the double chain with two-leg zigzag ladders (solid thick light-green, reddish-brown, and sky-blue lines). d The two-leg zigzag ladders in two different forms, either corner- (blue or green ladders) or edge- (red ladders), sharing RuO6 octahedra.

Full size image

Conclusions

Thus the following final picture emerges from both the experimental and theoretical studies. NaRu2O4 has very strong dimerization below Tc = 535 K (in other words, strong metal–metal bonding with the use of xy-orbitals) in one-dimensional chains forming legs of zigzag ladders (this is a bond-centered CDW). With the average valence Ru3.5+, one active electron (or one hole) remains per a dimer. And simultaneously with this dimerization (actually the orbitally driven Peierls dimerization35,36,37,38), these extra electrons order in each dimer—there appears also a site-centered charge ordering or site-centered CDW. The remaining electrons from one stronger diagonal bond between dimers in neighboring legs, creating Z-clusters (Fig. 8). The detailed form of orbitals in forming this short zigzag bond in the “blue” corner-sharing ladders is shown in Fig. 9c. But this extra bonding is not strong enough to make the system insulating, and it remains metallic below Tc due to the multi-orbital effect. These Ru–Ru dimers probably survive above Tc, forming dimer liquid as, e.g., in Li2RuO339; this dimer liquid phase in Li2RuO3 was found stable upon doping too40. This could be checked by probes like EXAFS or PDF (pair distribution function) analysis.

To put our results in a broader perspective, we would like to comment on why the dimerization and the site-centered charge ordering coexistence are favorable for metallic NaRu2O4, while it has been rarely seen in other transition metal compounds: another example is IrTe241. Most importantly, the Ru 4d bands of NaRu2O4 exhibit the delicate balance between the correlations, the Coulomb U, and the bandwidth W. Two other factors play a crucial role: orbital freedom, leading to orbitally-driven dimerization, and the mixed-valence of Ru, Ru3.5+, promoting site-centered charge ordering. These features seem to be the key to realizing charge ordering and dimer coexistence in a metallic NaRu2O4. Going further, we anticipate that our observations will prompt renewed efforts towards the hitherto scarcely investigated Mott–Hubbard physics in a metallic regime.

Methods

Sample preparations

Polycrystalline NaRu2O4 samples were synthesized by solid-state reaction of preheated RuO2 (99.999%, Aldrich) and Na2CO3 (99.999%, Aldrich) under an Ar-gas environment at 950 °C for 90 h with several intermediate grindings and pelletization. Subsequently, high-quality single crystals of NaRu2O4 were grown from this polycrystalline powder via a modified self-flux vapor transport reaction under flowing Ar-gas (ultra-pure 99.999%). Long needle-shaped high-quality single crystals (1 × 0.1 × 0.1 mm3) were obtained from the final products. The synthesized polycrystalline sample’s phase purity was checked using a Bruker D8 Discover diffractometer with a Cu-Kα source with no impurity peaks observed. Elemental analysis was subsequently done confirming the samples’ stoichiometry: we used a COXI EM-30 scanning electron microscope equipped with a Bruker QUANTAX 70 energy dispersive x-ray system.

Bulk properties

Electrical resistivity (ρ) measurements were carried out using a homemade system equipped with a furnace (300–685 K) and a pulsed-tube cryostat (down to 3 K, Oxford). The electrical resistance was measured in the four-point geometry on a static sample holder, where the contacts to the sample were made using silver paint and 25 µm gold wire. The current was applied perpendicular to the single crystal length, the crystallographic b-axis. Magnetic susceptibility χ(T) measurements were taken using an MPMS-SQUID magnetometer (Quantum Design). Heat capacity Cp(T) measurements were made using the commercial Physical Property Measurement System (PPMS, Quantum Design).

Structure analysis

The temperature-dependent single-crystal x-ray diffraction (SC-XRD) was performed from 300 to 575 K using a single crystal diffractometer (XtaLAB P200, Rigaku). The room-temperature SC-XRD data exhibit superstructures q = (0, ½, 0). The crystal structure was refined by using Fullprof suite software and the Shelx program with a modified monoclinic merohedral twin model under twin law as (-100) (010) (00-1) are presented in Supplementary Note 3. We also carried out temperature-dependent SC-XRD measurements on NaRu2O4 crystal to confirm the structural phase transition. Besides, we made a convergent beam electron diffraction (CBED) experiment, which is the most accurate in determining the correct symmetry of materials, especially regarding the loss of the inversion center. This CBED measurement allows us to determine the exact space-group of NaRu2O4. The CBED result for NaRu2O4 gives P1121/a symmetry and works well for the observed commensurate superstructures with q = (0, ½, 0).

LDA band calculations

Band structure calculations were performed for the experimentally obtained high- and low-temperature crystal structures using the LMTO method as implemented in the PY LMTO computer code42 and the Perdew–Wang43 parameterization of the exchange-correlation potential in the local spin density approximation (LSDA). To account for Coulomb repulsion within Ru d shell, we used a rotationally invariant formulation of the LSDA + U method44 with the double-counting term in the fully localized limit. An LDA calculation for the HT crystal structure gave a nonmagnetic metallic solution with partially occupied Ru1 and Ru2 t2g orbitals. The band structure’s characteristic feature is Ru t2g bands with stable quasi-one-dimensional dispersion along the b direction. These bands originate from Ru dxy orbitals and are evidence of strong direct Ru dxy–dxy hopping along the b chains. Here and in the following, Ru orbital is defined in local frames with the axes directed approximately to three nearest O ions in such a way that the local [110] direction always points along the crystallographic b-axis. The LDA band structure calculated for the LT structure is qualitatively different. Although it remains nonmagnetic and metallic, the shortening of the Ru-Ru distance within dimers leads to the splitting of Ru dxy drives bands into completely filled bonding states 2 eV below EF and unoccupied antibonding ones 1 eV above EF. The bonding dxy bands accommodate one electron per Ru while the remaining 3.5 d electrons fill bands are formed by Ru dxz, dyz states.