Abstract
Flexoelectricity is a universal property associated with dielectric materials, wherein they exhibit remanent polarization induced by strain gradient. Rare-earth iron garnets, R3Fe5O12, are ferrimagnetic insulators with useful magnetic properties. However, they are unlikely to show remanent dielectric polarization because of their centrosymmetric structure. Here, to induce flexoelectricity, we investigate various rare-earth iron-garnet thin films deposited on lattice-mismatched substrates. Atomic-resolution scanning transmission electron microscopy demonstrates the presence of 15 nm-thick strain gradients in Sm3Fe5O12 films between epitaxially strained tetragonal and relaxed cubic structures. Furthermore, negatively polarized nanodomains are imaged by scanning nonlinear dielectric microscopy. It suggests a generation of flexoelectricity, where the polarization points down toward the substrate in the out-of-plane direction. X-ray magnetic circular dichroism demonstrates hysteresis with a large coercive field originating from the strain-gradient layer. We believe that our study will pave the way for achieving dielectric polarization even in nonpolar centrosymmetric materials by strain-gradient engineering.
Similar content being viewed by others
Introduction
Garnet, a fascinating material commonly used in jewelry, has recently attracted research attraction owing to its rich spin physics and potential use in spintronics applications. Rare-earth iron garnets (RIGs) are ferrimagnetic insulators with the chemical formula R3Fe5O12 (where R is rare-earth elements)1. They are magnetically stable at room temperature because of their high Néel temperature (TN > 550 K) and large magnetization (~5 μB/f.u.). They are commercially applied as optical isolators because of their large magneto-optical effect and intensively studied as spin-wave-transport media because of their exceptionally low damping2,3,4. If remanent dielectric polarization could be introduced in RIGs at the nanoscale, simultaneous ordering of electric dipoles and spins could facilitate their application in multifunctional memory devices. However, RIGs are unlikely to show remanent dielectric polarization because they have centrosymmetric Ia3d cubic crystal structures and accommodate various cations by adjusting oxygen positions for compensation5.
To induce and/or enhance ferroelectricity, strain engineering is a possible approach6,7. The lattice structure can be modified in single-crystalline thin films by epitaxial strain originating from lattice mismatch between a film and substrate8,9. The RIG lattice constants and strain in the films could be modulated by selecting R-site ions. However, tetragonal and cubic garnet phases do not exhibit remanent polarization because they still have centrosymmetric I41/acd (tetragonal) and Ia3d (cubic) structures5. Among the 32 crystallographic point groups, only 10 could show remanent polarization; thus, homogeneous strain cannot break the centrosymmetry in RIGs. Therefore, we focused on flexoelectricity-induced remanent polarization10,11.
Flexoelectricity is a universal property of dielectric materials, thus they can exhibit a strain-gradient-induced remanent polarization. The flexoelectric polarization is expressed as PFlexoelectricity = μ∂u/∂x, where μ and ∂u/∂x represent the flexoelectric coefficient and strain gradient, respectively. Macroscopic strain gradients can be induced by bending12 or applying asymmetric compression13. Contrarily, nanoscale flexoelectricity has attracted increasing attention because the strain-gradient scale is inverse to the material dimensions. Nanoscale flexoelectricity has been reported in thin films14,15 and nanowires16. We hypothesized that the strain gradient between coherently strained and relaxed cubic phases could show flexoelectric polarization10,11,14 if the strain and film thicknesses were adjusted appropriately.
Here, we investigated various RIG thin films deposited on lattice-mismatched garnet substrates (see “Methods” for sample preparation) and confirmed that RIG films thinner than the critical thickness value exhibit a coherently strained-tetragonal phase, whereas thick RIG films show a relaxed-cubic phase (see Supplementary Note 1, Supplementary Table 1 and Supplementary Figure 1). Anomalous magnetic properties such as large coercive fields have been observed around 1% f, as shown in Supplementary Note 2, Supplementary Figures 2, 3, and Supplementary Table 2. Among various combinations of garnet films and substrates, Sm3Fe5O12 (SmIG) films deposited on Gd3Ga5O12 (GGG) substrates were investigated in detail. Their lattice mismatch f and critical thickness for dislocation formation, tc, were estimated from the bulk lattice constants as 1.17% and 60 nm, respectively (Supplementary Table 1). We fabricated numerous SmIG/GGG films with various thicknesses and investigated the structural, dielectric, and magnetic properties. The structural analysis reveals the presence of strain gradients in SmIG films between epitaxially strained tetragonal and relaxed cubic structures. In the strain gradients, simultaneous remanent dielectric polarization and magnetization are demonstrated at room temperature.
Results
Structural analysis
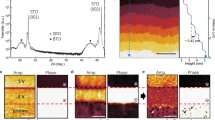
Figure 1(a) shows representative 2θ–ω X-ray diffraction (XRD) scans of the SmIG films with thicknesses t of 20, 40, 60, and 180 nm. We observed (00 l) peaks from the films and substrates but no impurity phases (Supplementary Figure 1(l)). For films with t < tc (t = 20 and 40 nm), distinct Laue oscillations indicated smooth surfaces. Contrarily, much thicker films (t ≥ tc; t = 60 and 180 nm) did not exhibit Laue oscillations, and peak separations toward strain relaxation were observed. To characterize the in-plane and out-of-plane lattice parameters, reciprocal space mapping (RSM) was performed for the asymmetric (408) plane (Fig. 1(b–e)). When t < tc (Fig. 1(b, c)), the SmIG films exhibited coherent epitaxy and tetragonal elongation perpendicular to the film surface due to epitaxial strain. As t increased to 60 nm, the strain started to relax (Fig. 1(d)) and the diffraction peak changed from tetragonal to a fully relaxed cubic phase (Fig. 1(e)).
a 2θ–ω XRD scans of SmIG films with different film thicknesses on GGG (001) substrates. b-e RSM around (408) substrate peaks for (b) 20 nm, (c) 40 nm, (d) 60 nm, and (e) 180 nm-thick SmIG films. Qx and Qy indicate reciprocal lattice vector along (100) and (001), respectively. The rlu indicates reciprocal lattice unit. The black and red arrows denote the peaks from GGG substrates and SmIG films, respectively. f, g Film thickness dependence of (f) tetragonal distortion c/a and (g) FWHM of omega scans for tetragonal and cubic phases. Closed squares and open circles represent the values for strained tetragonal and relaxed-cubic phases, respectively.
The thickness-dependent tetragonal distortion represented by c/a and full-width-at-half-maximum (FWHM) of omega (ΔωFWHM) are summarized in Fig. 1(f) and (g). The c/a values for the tetragonal and cubic phases were 1.029 ± 0.004 and 1.002 ± 0.002 (mean ± s.d.), respectively. The average lattice constant of the relaxed cubic SmIG was 12.56 Å, which is larger than the value of bulk (12.53 Å). The lattice expansion is attributed to the oxygen vacancies typically observed in films grown under low oxygen pressure (see Supplementary Note 1 and Supplementary Figure 1(m)). Therefore, the effective lattice mismatch at the SmIG/GGG interface was 1.37%, which is larger than the estimated value (1.17%). We re-calculated tc as 45 nm using the effective lattice mismatch, which agrees well with the structural, dielectric, and magnetic property measurements discussed later. The ΔωFWHM for t < tc in the tetragonal phase (0.018 ± 0.010°, mean ± s.d.) was lower than that for the tetragonal and cubic phases with t ≥ tc (0.066 ± 0.039° and 0.299 ± 0.067°, respectively), indicating the thinner films had higher crystallinity. Notably, tetragonal and cubic phases co-existed in almost all SmIG/GGG films with t > tc, which was not observed in large-mismatched (f = 2.22%) LuIG/YAG films (Supplementary Figure 1). The broad continuous diffraction signals between the tetragonal and cubic phases (Fig. 1(d, e)) suggest that the optimum lattice mismatch may form a strain gradient between coherently strained tetragonal and relaxed cubic phases.
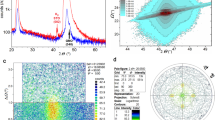
For further structural characterization and to confirm the presence of the strain gradient, we performed atomic-resolution scanning transmission electron microscopy (STEM) observation for the sufficiently thick SmIG film (t = 180 nm). Low-angle annular dark-field (LAADF) imaging (Fig. 2(a)) highlighted the strain contrast in the specimen and shows micrometer-scale lateral crystalline uniformity in the thickness range of 50 nm or less. There is a bright band along with the interface between film and substrate where strain field exists, but no dislocations are observed at the interface. Abrupt contrast change occurs at ~50 nm, indicating the existence of strain that might originate from dislocations. Figure 2(b) and (c) shows high-magnification high-angle annular dark-field (HAADF)-STEM images around the interface and inside the film (50 nm from the interface), respectively. Figure 2(b) indicates fully coherent growth at the SmIG/GGG interface. The interface was characterized by energy-dispersive X-ray spectroscopy mapping (Supplementary Figure 4).
a Micrometer-scale LAADF-STEM image. Dislocations are denoted by arrows. b Nanometer-scale HAADF-STEM image around the SmIG/GGG interface. c Nanometer-scale HAADF-STEM image around dislocations. d STEM image near the interface of SmIG film overlaid with atomic model of garnet crystal structure. The lateral and vertical lengths of the half-unit cell are defined as Δx and Δy. e Variations in Δx and Δy (mean ± s.d.) at different vertical positions quantified from Fig. 2(b). The dotted line represents the SmIG/GGG interface. f Variations in Δx and Δy (mean ± s.d.) at different vertical positions quantified from Fig. 2(c). The region surrounded by red lines in Fig. 2(c) was excluded from quantification. g Variation in tetragonal distortion c/a for vertical positions quantified from Fig. 2(c). The dotted line indicates linear fitting.
The unit structure of SmIG (depicted in Fig. 2(d)) is consistent with the atomic model of garnet. For quantitative discussion, the lateral and vertical lengths of the half-unit cell were defined as Δx and Δy, respectively, and calculated from HAADF-STEM images at different vertical positions. Near the interface (Fig. 2(b) and (e)), Δx and Δy are within the error range for the cubic GGG substrate, while Δy is elongated in the SmIG film, indicating tetragonal distortion, as expected from XRD. This structural distortion is uniform over the measured range (~15 × 15 nm). At 50 nm from the interface, dislocations could be clearly observed in the HAADF-STEM image (Fig. 2(c)). While Δy is homogeneous over the image (Fig. 2(f)), Δx gradually increases with increasing film thickness around the dislocations. This inhomogeneity is consistent with the increased ΔωFWHM for t ≥ tc in the RSM images.
The tetragonal lattice distortion, defined as c/a ( = Δy/Δx; Fig. 2(g)), indicates gradual strain relaxation while receding from the substrate. A simple linear prediction reveals that the relaxation thickness is ~15 nm, demonstrating the presence of a strain gradient of ∂u/∂x = 9 × 105 m−1. The value is much larger than that previously reported for the bulk (~0.1 m−1)17, but comparable with nanoscale strain gradients14,18,19. Notably, typical strain gradients are reported to be within a few unit cells;19 however, the strain-gradient region in our study is unexpectedly observed for a large thickness of 15 nm, which is possibly related to the comparably large lattice constant and structural flexibility of RIGs20. Furthermore, dislocations were observed inside the film and not at the interface or surfaces. According to previous studies21, such dislocations are known as stand-off dislocations, which depend on the shear moduli of SmIG and GGG.
As an order-of-magnitude approximation14,22, an internal field ES generated by the strain gradient can be expressed as ES = (e/4πε0a)(∂u/∂x), where e, ε0, and a ( ≈ 12 × 10−10 m) are the electronic charge, permittivity of free space, and lattice constant of the material, respectively. Therefore, ES and PFlexoelectricity ( = εε0ES, where ε ( ≈ 20) is the dielectric constant of RIGs) are calculated to be 1.1 MV m−1 and 0.02 μC cm−2, respectively. This polarization value is comparable with those of many multiferroics (as discussed later) and flexoelectrics10, but almost three orders of magnitude smaller than the spontaneous polarization Ps in typical displacement-type ferroelectrics like BaTiO3, PbTiO3, LiTaO3, and LiNbO3 (Ps = 26, 50, 50, and 71 μC cm−2, respectively)23,24,25,26. However, nanoscale flexoelectric remanent polarization could notably exist in essentially centrosymmetric garnet ferrites. This indicates that simultaneous ordering of spins and dipoles could exist in the garnet system.
Dielectric properties
To confirm the presence of remanent polarization owing to flexoelectricity and the distribution of the domain structure, we performed scanning nonlinear dielectric microscopy (SNDM), which is sensitive to the third rank dielectric tensor ε333 and spontaneous polarization27,28,29. Figure 3(a–e) shows SNDM images for 10-, 40-, 60-, 80-, and 120-nm-thick SmIG films in a 500 × 500 nm area. Bright spots indicating negative SNDM frequency shift and negatively polarised domains were observed only for t = 60 and 80 nm (Fig. 3(c) and (d), respectively). The maximum negative values of the SNDM signals for t = 60 and 80 nm were −1.2 and −0.5 Hz V−1, respectively. The histograms in Fig. 3(f) indicate that negative-polar domains, where the polarization points down towards substrate in the out-of-plane direction, were generated in the 60–80 nm thickness range. Background signals centered at ~0.2 Hz V−1 were observed for all samples. SNDM is surface-sensitive because the detection depth of SNDM signals is <10 nm, which is determined by the probe diameter (~25 nm) and dielectric constant of the specimen (ε ≈ 20)30. Therefore, the polarised domains exist only in films with thicknesses of around 60–80 nm, as the detection depth corresponds to the thickness region where the strain gradient is observed. The negative-polar direction is consistent with the sign of the strain gradient, as expected from STEM.
a–e SNDM images for 10-, 40-, 60-, 80-, and 120-nm-thick SmIG films in 500 × 500 nm area. Representative dielectric domains are circled by broken white lines in (c) and (d). f Histograms of SNDM signals with different film thicknesses. g–k Topographic images for 10-, 40-, 60-, 80-, and 120-nm-thick films measured in the same areas as (a–e). Solid red and broken white circles in (i) and (j) indicate the same positions as those in (c) and (d), respectively.
The maximum ε333 in the 60 nm-thick SmIG film was 0.004 aF V−1 in an order-of-magnitude estimation using an SNDM signal of ferroelectric LiTaO3 (200 Hz V−1, ε333 = 0.73 aF V−1) as a reference31. Although it is difficult to estimate the polarization from the nonlinear dielectric constant ε333, the extent of polarization is consistent with the estimation from direct observations of strain gradients by STEM. From the SNDM image in Fig. 3(c), the average diameter of polar domains and the distance between them are 27 ± 6 nm and 58 ± 21 nm (mean ± s.d.), respectively. The distance between dislocations in Fig. 2(a), is 54 ± 17 nm which matches with the distance between polar domains. Figure 3(g–k) show topographical images for 10-, 40-, 60-, 80-, and 120 nm-thick SmIG films measured in the same area as Fig. 3(a–e). The polarised domains tend to be located at convex peaks, as shown by the circles in Fig. 3(i) and (j). However, polarised domains were not observed in the 120 nm-thick film, despite its roughness being larger than that of the 60 and 80 nm-thick films. Therefore, the SNDM signals are unambiguously separate from topographical factors.
Magnetic properties
Finally, we discuss how strain-induced lattice modification and dislocations influence the magnetic properties of SmIG films. Figure 4(a) and (b) shows representative magnetic hysteresis loops measured by magnetic circular dichroism (MCD) with a photon energy of 3.26–3.40 eV (corresponding to the charge transfer from oxygen to iron excitation) for SmIG films with various thicknesses. The coercive field (Hc) values are summarised in Fig. 4(c). At t < 40 nm, rectangular hysteresis loops with Hc < 0.05 T are observed, indicating that the easy axis of magnetization is perpendicular to the film surface due to strain-induced magnetic anisotropy. However, the coercivity drastically increases at a film thickness of ~40 nm (denoted as t*) due to partial relaxation. The partially relaxed 45 nm-thick film (Fig. 4(a) inset, for the SNDM, see Supplementary Figure 5) shows the largest Hc value of 0.15 T, while that of the strained 40 nm-thick film is only 0.06 T. The large Hc in the former is attributed to crystalline defects, which act as pinning sites for magnetic domains32,33. It is difficult to accurately control the film thickness at which lattice relaxation occurs, but it seems to occur between 40 nm (t*) and 60 nm (tc) (Fig. 4(c)), which is consistent with the XRD and STEM results. As the film thickness increases further (Fig. 4(b)), the squareness of the hysteresis loops continues to decrease, indicating an increased contribution from shape anisotropy with the magnetic easy axis in the in-plane direction.
a, b Magnetic hysteresis loops of MCD with the field applied perpendicular to the film surface for (a) 10-, 40-, and 45 nm-thick and (b) 60-, 80-, and 120-nm-thick films. Partial relaxation is observed for the 45 nm-thick film as shown by RSM in the inset of (a). c Thickness dependence of coercive field Hc. tc (~60 nm) and t* (~40 nm) represent the critical thickness estimated from the bulk lattice constant and the thickness where relaxation starts as estimated from structural analysis. d Fe L3-XAS spectra. The intensities are normalized to the peak heights. The black arrow denotes the shoulder structure. e Fe L2,3-XMCD spectra. The XAS and XMCD spectra were obtained in TEY mode, except for the 20 nm-thick film, which was obtained in PFY mode. f Magnetic-field dependence of the XMCD intensity for 20-, 45-, and 110 nm-thick films at room temperature.
We elucidated the Fe ion electronic structure and depth profile of the magnetic properties by X-ray absorption spectroscopy (XAS) and X-ray magnetic circular dichroism (XMCD), respectively (see Supplementary Figure 6(a–d)). Surface-sensitive total-electron-yield (TEY) measurements for the strained t = 40 nm, partially relaxed t = 45 nm, and relaxed t = 110 nm films revealed the electronic and magnetic structures in the tetragonal, strain gradient, and cubic phases, respectively. Bulk-sensitive partial-fluorescence-yield (PFY) measurements for the 20 nm-thick film reflected the information for the tetragonal phase. Figure 4(d) shows Fe L3-XAS spectra of the SmIG films. The intensity of the shoulder structure at ~708 eV (indicated by the black arrow) depends on the film thickness. The shoulder intensity is larger for the relaxed 45 nm-thick film than that for the other films due to the different local symmetries around Fe3+ 34,35. Figure 4(e) shows the Fe L2,3-XMCD spectra. The shapes of the spectral lines are similar among the films, indicating the electronic structure contributing to the ferrimagnetic moment is approximately identical, irrespective of the thickness. Since the XMCD line shapes hardly change among the films, the Fe3+ component predominantly contributes to the magnetization. Thus, differences in the intensities reflect the net magnetization (Mtot) and different crystal fields.
Table 1 shows the spin (Mspin), orbital (Morb), and total (Mtot) magnetic moments estimated by XMCD sum rules (Supplementary Figure 6(e))36,37,38. The Mtot values for the 40- and 45 nm-thick films are 0.88- and 0.98 μB/Fe, respectively, which are consistent with the theoretical magnetization (5 μB/f.u.) of SmIG. The slightly lower Mtot for the 110 nm-thick film might be attributed to the presence of defects in the cubic phase, as this film has an inferior crystalline quality to its thinner counterparts. The non-zero values of Morb for the 40 and 45 nm-thick films indicate that the quenching of orbital moments is resolved by the reduction of the crystal symmetry from cubic to tetragonal and strain gradient. The |Morb/Mspin| values of the tetragonal and strain-gradient layers are 0.11 and 0.09, respectively, which correspond to L = 0.55 and 0.45, assuming S = 5/239. These values are unexpectedly large for the half-filled d5 Fe3+ ions.
The magnetic-field dependence of the XMCD intensity in TEY mode (Fig. 4(f)) exhibits clear hysteresis. The XMCD hysteresis of the partially relaxed 45 nm-thick film is at Hc = 0.11 T, while that of the 20 and 110 nm-thick films is at Hc = 0.02 T. Hence, Hc is much larger in the strain-gradient layer than in the tetragonal and cubic layers. Note that the Hc of the 110 nm-thick film measured by MCD is larger than that observed here (Fig. 4(c)); this larger coercive field arises from the inner strain-gradient layer, not the cubic and tetragonal layers. These findings further confirm that the strain-gradient layer functions as a pinning layer for magnetic domains. Through magnetic property measurements, we can confirm the presence of magnetisation in the tetragonal, strain gradient, and cubic SmIG films. Thus, we conclude that remanent magnetization and dielectric polarization coexist in strain-gradient SmIG films.
Discussion
Some existing materials such as multiferroics show both remanent magnetization and dielectric polarization40. BiFeO3 is the most widely studied materials with a large ferroelectric polarization (90 μC cm−2); its magnetic ordering persists well above room temperature41. Although the mechanism of its strong magnetism is still not understood, the intrinsic magnetism is weak ferromagnetism by canted spins (0.05 μB/u.c.)42. BiFeO3 is one of the very few room-temperature multiferroics; however, ferromagnetic and/or ferroelectric transitions occur at cryogenic temperatures in most multiferroics. For example, strained EuTiO3 becomes ferroelectric (10 μC cm−2) below 250 K and shows a magnetic order of 4 μB/u.c. at 4.2 K43. TbMnO3 with cycloidal spin spirals shows polarization (0.08 μC cm−2) and magnetization (0.05 μB/u.c.) below 27 K44. Another possible approach is using composite multiferroics such as ferroelectric BaTiO3/ferrimagnetic CoFe2O445 or polar LuFeO3/ferrimagnetic LuFe2O446. In comparison with the above-mentioned materials, strain-gradient SmIG films could show sufficiently large magnetization (~5 μB/f.u.) and polarization (~0.02 μC cm−2) even at room temperature in a single phase. The weak polarization is restricted because the dielectric constant of RIGs is more than an order of magnitude smaller than those of quantum paraelectric SrTiO3 and ferroelectrics. However, this design for novel multiferroics, inducing a strain gradient in magnetic materials, can be applied not only to garnet ferrites but also to other magnetic materials like spinel and perovskite, because flexoelectricity is a universal feature in dielectrics15. Furthermore, we successfully imaged self-assembled polar domains with a size of tens of nanometers that were constructed by a simple film-growth technique, which has been reported in ferroelectric nanostructures, including nanodots, nanotubes, and nanocrystals47,48,49.
Conclusion
In summary, we systematically studied strain-induced lattice distortion in epitaxially grown ferrimagnetic RIG films, where tetragonal distortion (cubic relaxation) is observed below (above) a critical thickness. Among the various RIGs, SmIG films grown on GGG substrates, where the lattice mismatch between the film and substrate was 1.17%, were investigated in detail. The SmIG films exhibited a strain-gradient structure between coherently epitaxial tetragonal and relaxed cubic phases, revealed by asymmetric XRD RSM and atomic-resolution STEM. STEM revealed an almost 15 nm-thick strain gradient around dislocations; thus, a flexoelectric polarization of 0.02 μC cm−2 is expected with an order-of-magnitude approximation. Nanoscale spatial distribution of the dielectric domains was observed by SNDM, indicating that negatively polarized dielectric nanodomains with 30 nm diameters exist in the strain-gradient layer. The magneto-optical characteristics were defined by MCD and XMCD. Ferrimagnetism and increased magnetic coercivity due to magnetic domain pinning by dislocations were observed in the strain-gradient layer. These results demonstrate that strain-gradient SmIG possesses both remanent dielectric polarization and magnetization at room temperature. Our study not only suggests the possible application of multifunctional materials with remanent magnetization and dielectric polarization but also paves the way to produce nanodomains even in centrosymmetric crystals by controlling singularity structures including dislocations.
Methods
-
1.
Materials. Rare-earth iron-garnet (RIG) films were deposited on garnet substrates of Gd3Ga5O12 (GGG) and Y3Al5O12 (YAG) (001) through pulsed-laser deposition (PLD) using an ArF excimer laser with a wavelength of 193 nm. The PLD targets were prepared through conventional solid-state reaction. R2O3 and Fe2O3 powders were mixed stoichiometrically and sintered at 1200 °C for 12 h. During the PLD process, the substrate temperature and ambient oxygen pressure were maintained at 750 °C and 0.1 Pa, respectively. The ArF excimer laser was projected onto the prepared targets at a repetition rate of 5 Hz.
-
2.
XRD. The crystalline structures of the films were analyzed using an X-ray diffraction (XRD) system with a four-cycle diffractometer (Empyrean, PANalytical). X-ray reciprocal space mapping (RSM) around the (408) plane was performed to confirm the epitaxial relationship between the thin films and substrates.
-
3.
STEM. Atomic-resolution scanning transmission electron microscopy (STEM) was performed to characterize the nanometer-scale local lattice distortion in the film. The lateral and vertical lengths of the half-unit cells defined as Δx and Δy are calculated from HAADF-STEM images using ImageJ software. The coordinates of central bright-atom columns inside the half unit cells are first extracted from HAADF-STEM images, and then the spacing along lateral (Δx) and vertical (Δy) directions are calculated from these atom coordinates. The means and standard deviations (mean ± s.d.) of Δx and Δy are calculated along with the lateral datasets, then the vertical position dependence of Δx and Δy variation is plotted.
-
4.
SNDM. Scanning nonlinear dielectric microscopy (SNDM) was used to confirm the presence of remanent polarization due to flexoelectricity and to image the nanoscale spatial distribution of the domains. The SNDM measurements were performed at room temperature.
-
5.
MCD and XMCD. The magnetic properties were measured by magnetic circular dichroism (MCD) with the magnetic field applied perpendicular to the film surface. X-ray absorption spectroscopy (XAS) and X-ray magnetic circular dichroism (XMCD) measurements were conducted at BL-16A at KEK-PF. Absorption spectra for circularly polarized X-rays were obtained by reversing the photon helicity at each photon energy and were recorded in the total-electron yield (TEY) and partial fluorescence-yield (PFY) modes. The probing depths of the TEY and PFY modes are several tens and several hundreds of nanometres, respectively. The measurements were performed under magnetic fields of 0–1.2 T applied perpendicular to the film surface. The MCD and XMCD measurements were performed at room temperature.
Data availability
The experimental data that support the finding of this study are available from the corresponding author upon reasonable request.
References
Hellwedge, K.-H., Hellwedge, A. M., Landort-Börnstein - Group III Condensed Matter Volume 12A (Part A: Garnets and Perovskites), (Springer-Verlag Berlin Heidelberg, 1978).
Kajiwara, Y. et al. Transmission of electrical signals by spin-wave interconversion in a magnetic insulator. Nature 464, 262 (2010).
Balynsky, M. et al. A magnetometer based on a spin wave interferometer. Sci. Rep. 7, 11539 (2017).
Kanazawa, N. et al. Demonstration of a robust magnonic spin wave interferometer. Sci. Rep. 6, 30268 (2016).
Baettig, P. & Oguchi, T. Why are garnets not ferroelectric? A theoretical investigation of Y3Fe5O12. Chem. Mater. 20, 7545 (2008).
Haeni, J. H. Room-temperature ferroelectricity in strained SrTiO3. Nature 430, 758 (2004).
Choi, K. J. et al. Enhancement of ferroelectricity in strained BaTiO3 thin films. Science 306, 1005 (2004).
Kubota, M. et al. Stress-induced perpendicular magnetization in epitaxial iron garnet. Thin Films, Appl. Phys. Exp. 5, 103002 (2012).
Yamahara, H., Seki, M. & Tabata, H. Epitaxial strain-induced magnetic anisotropy in Sm3Fe5O12 thin films grown by pulsed laser deposition. J. Magn. Magn. Mater. 323, 3143 (2011).
Zubko, P., Catalan, G., Alexander, A. & Tagantsev, K. Flexoelectric effect in solids. Annu. Rev. Mater. 43, 387 (2013).
Wang, B., Gu, Y., Zhang, A. & Chen, L.-Q. Flexoelectricity in solids: progress, challenges, and perspectives. Prog. Mater. Sci. 106, 100570 (2019).
Nguyen, T. D. et al. Nanoscale flexoelectricity. Adv. Mater. 25, 946 (2013).
Cross, L. E. Flexoelectric effects: charge separation in insulating solids subjected to elastic strain gradients. J. Mater. Sci. 41, 53 (2006).
Lee, D. et al. Giant flexoelectric effect in ferroelectric epitaxial thin films. Phys. Rev. Lett. 107, 057602 (2011).
Wang, H. et al. Direct observation of huge flexoelectric polarization around crack tips. Nano. Lett. 20, 88 (2020).
Liu, C., Hu, S. & Shen, S. Effect of flexoelectricity on electrostatic potential in a bent piezoelectric nanowire. Smart Mater. Struct. 21, 115024 (2012).
Zubko, P. et al. Strain-gradient-induced polarization in SrTiO3. Phys. Rev. Lett. 99, 167601 (2007).
Catalan, G. et al. Flexoelectric rotation of polarization in ferroelectric thin films. Nature Mater. 10, 963 (2011).
Gao, P. et al. Atomic-scale measurement of flexoelectric polarization at SrTiO3 dislocations. Phys. Rev. Lett. 120, 267601 (2018).
Song, Z., Zhou, D. & Liu, Q. Tolerance factor and phase stability of the garnet structure. corrigendum. Acta Cryst. C75, 1353 (2019).
Kuwabara, M., Spence, J. C. H. & Ruhle, M. On the atomic structure of the Nb/Al2O3 interface and the grown of Al2O3 particles. J. Mater. Res. 4, 972 (1989).
Gruverman, A. et al. Mechanical stress effect on imprint behavior of integrated ferroelectric capacitors. Appl. Phys. Lett. 83, 728 (2003).
Tan, P. T., Cuong, N. K., Valach, F. & Nhat, H. N. A simple method for estimating of spontaneous polarization in perovskite-like nanocrystallites. J. Phys.: Conf. Ser. 187, 012080 (2009).
Shieh, J., Yeh, J. H., Shu, Y. C. & Yen, J. H. Hysteresis behaviors of barium titanate single crystals based on the operation of multiple 90 switching systems. Mater. Sci. Eng. B 161, 50 (2009).
Haun, M. J. et al. Thermodynamic theory of PbTiO3. J. Appl. Phys. 62, 3331 (1987).
Wemple, S. H., DiDomenico, M. Jr. & Camlibel, I. Relationship between linear and quadratic electro-optic coefficients in LiNbO3, LiTaO3, and other oxygen-octahedra ferroelectrics based on direct measurement of spontaneous polarization. Appl. Phys. Lett. 12, 209 (1968).
Cho, Y., Scanning Nonlinear Dielectric Microscopy: Investigation of Ferroelectric, Dielectric, and Semiconductor Materials and Devices, Elsevier, ISBN 9780128172469 (2020).
Cho, Y., Kazuta, S. & Matsuura, K. Scanning nonlinear dielectric microscopy with nanometer resolution. Appl. Phys. Lett. 75, 2833 (1999).
Cho, Y., Kazuta, S. & Ito, H. Scanning-nonlinear-dielectric-microscopy study on periodically poled LiNbO3 for a high-performance quasi-phase matching device. Appl. Phys. Lett. 79, 2955 (2001).
Aoki, T., Hiranaga, Y. & Cho, Y. High-density ferroelectric recording using a hard disk drive-type data storage system. J. Appl. Phys. 119, 184101 (2016).
Hiranaga, Y. & Cho, Y. Measurements of Nonlinear Dielectric Constants of Pb(Zr,Ti)O3 Thin Films Using a Dynamic Measuring Method. Jap. J. Appl. Phys. 52, 09KA08 (2013).
Suzuki, Y. Epitaxial spinel ferrite thin films. Annu. Rev. Mater. Res. 31, 265 (2001).
Lu, D. et al. Strain Tuning in Complex Oxide Epitaxial Films Using an Ultrathin Strontium Aluminate Buffer Layer. Phys. Stat. Sol. PRL. 12, 1700339 (2018).
Jiménez-Villacorta, F. et al. X-ray magnetic circular dichroism study of the blocking process in nanostructured iron-iron oxide core-shell systems. Phys. Rev. B 84, 172404 (2011).
Mesilov, V. V. et al. Valence states of iron ions in nanostructured yttrium iron garnet Y3Fe5O12 studied by means of soft X-ray absorption spectroscopy. J. Elec. Spec. Relat. Phenom. 186, 598 (2012).
Thole, B. T., Cara, P., Sette, F. & van der Laan, G. X-Ray circular dichroism as a probe of orbital magnetization. Phys. Rev. Lett. 68, 1943 (1992).
Carra, P., Thole, B. T., Altarelli, M. & Wang, X. X-Ray circular dichroism and local magnetic fields. Phys. Rev. Lett. 70, 694 (1993).
Piamonteze, C., Miedema, P. & de Groot, F. M. F. Accuracy of the spin sum rule in XMCD for the transition-metal L edges from manganese to copper. Phys. Rev. B 80, 184410 (2009).
Kim, J.-Y., Koo, T. Y. & Park, J.-H. Orbital and bonding anisotropy in a half-filled GaFeO3 magnetoelectric ferrimagnet. Phys. Rev. Lett. 96, 047205 (2006).
Spaldin, N. A. & Ramesh, R. Advances in magnetoelectric multiferroics. Nature Materials 18, 203 (2019).
Wang, J. et al. Epitaxial BiFeO3 multiferroic thin film heterostructures. Science 299, 1719 (2003).
Ederer, C. & Spaldin, N. A. Influence of strain and oxygen vacancies on the magnetoelectric properties of multiferroic bismuth ferrite. Phys. Rev. B 71, 224103 (2005).
Lee, J. H. et al. A strong ferroelectric ferromagnet created by means of spin–lattice coupling. Nature 476, 114 (2011).
Kimura, T. et al. Magnetic control of ferroelectric polarization. Nature 426, 55 (2003).
Zheng, H. et al. Multiferroic nanostructures. Science 303, 661 (2004).
Mundy, J. A. et al. Atomically engineered ferroic layers yield a room temperature magnetoelectric multiferroic. Nature 537, 523 (2016).
Tan, G. et al. Observation of exotic domain structures in ferroelectric nanodot arrays fabricated via a universal nanopatterning approach. ACS Appl. Mater. Interfaces 9, 37219 (2017).
Son, J. Y. et al. Four-states multiferroic memory embodied using Mn-Doped BaTiO3 nanorods. ACS Nano. 7, 5522 (2013).
Pham, H. T. et al. Ferroelectric/dielectric double gate insulator spin-coated using barium titanate nanocrystals for an indium oxide nanocrystal-based thin-film transistor. ACS Appl. Mater. Interfaces 8, 7248 (2016).
Acknowledgements
This work was supported by Grants-in-Aid for Scientific Research, JSPS, Grant Numbers “16K21001”, “19K15022”, “18H04285”, and “19H04535”; The Murata Science Foundation; and “Nanotechnology Platform” of the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan. A part of this work was supported by Institute for AI and Beyond for the University of Tokyo. This work was partially supported by the Spintronics Research Network of Japan (Spin-RNJ).
Author information
Authors and Affiliations
Contributions
HY and HT conceived the study. HT, MS, and YI supervised the work. HY, MSS, and MA fabricated the samples. HY, BF, TT, MK, RI, and YC performed the measurements and contributed to the interpretation of the results. All authors discussed the data extensively. HY wrote the paper with the support and correction of all other authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Communications Materials thanks Federico Motti and the other, anonymous, reviewers for their contribution to the peer review of this work. Primary Handling Editors: Andreja Benčan Golob and Aldo Isidori. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yamahara, H., Feng, B., Seki, M. et al. Flexoelectric nanodomains in rare-earth iron garnet thin films under strain gradient. Commun Mater 2, 95 (2021). https://doi.org/10.1038/s43246-021-00199-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-021-00199-y
This article is cited by
-
Nonlinear flexoelectricity in extended thermodynamics
Archive of Applied Mechanics (2024)