Abstract
Cellulose-based systems are useful for many applications. However, the issue of self-organization under non-equilibrium conditions, which is ubiquitous in living matter, has scarcely been addressed in cellulose-based materials. Here, we show that quasi-2D preparations of a lyotropic cellulose-based cholesteric mesophase display travelling colourful patterns, which are generated by a chemical reaction-diffusion mechanism being simultaneous with the evaporation of solvents at the boundaries. These patterns involve spatial and temporal variation in the amplitude and sign of the helix´s pitch. We propose a simple model, based on a reaction-diffusion mechanism, which simulates the observed spatiotemporal colour behaviour.
Similar content being viewed by others
Introduction
Cellulose is a natural macromolecule that is known not only for its chirality1,2 but also for its amphiphilic character3,4. Both characteristics are imprinted by plants at the molecular level. While the chirality of the cellulosic chain is a configurational characteristic that can only be changed by breaking covalent bonds along the chain, the self-assembly of cellulose chains depends on the arrangement of hydrophilic/hydrophobic groups5. In fact, several authors mention that the hydrophilic and hydrophobic character of cellulose-based films and fibres can easily be changed6,7. Another interesting characteristic of cellulosic systems is the formation of left-handed (L), right-handed (R) or achiral self-assembled structures, at different length scales8,9,10, regardless of the cellulose chirality, which remains unchanged at the molecular level. Cellulosic liquid crystalline phases are examples of such systems, which can form chiral nematic (cholesteric) L- and R-handed structures as well as achiral nematic, lyotropic and thermotropic phases11,12,13,14. Cellulose-based lyotropic liquid crystalline phases can be obtained from cellulose and cellulose derivatives and also from cellulose nanocrystals. Cellulosic liquid crystalline cholesteric phases are characterized by Bragg-type reflections of circularly polarized light15. This characteristic is related with the sense and the pitch of the helical structure formed by pseudo nematic layers twisted along the helix axis. The existence of the twisted structure, but not the sense of its helicity, was explained by the lack of inversion symmetry of the cellulose molecules, which produces chiral intermolecular forces16. The bulk helicity was found to depend on many parameters that include the degree of substitution of non-chiral substituents, the molecular weight of the polymer, the type of solvent and temperature17,18.
The literature offers examples of systems that can present both helicities despite being formed by molecules with the same chirality. These systems show conformational changes due to the presence of an asymmetry that can arise from the existence of defect lines19, as in the case of fibres and jets produced from cellulosic liquid crystalline phases under shear, or from layers of materials having different mechanical properties20. In nature, curvature originating in bulk helicity can easily be found in tendrils of plants21, awns of Erodium22,23 and in the helicoidally stacked cellulose fibrils of Pollia condensata fruit cell walls24. All these systems have in common the intrinsic chirality of the cellulose chain and its amphiphilic character. Both should play an important role in the formation of the different conformations observed.
In some of these systems, structural colours can also be observed, as for example in Pollia condensata pixelated fruit24. Structural colour arises from the selective reflection of incident light when it interacts with micro- or nano-scale structures periodic on the length scale of the wavelength of visible light. However, it is in the animal kingdom that more research has been performed related to this type of coloration and its development. One of the many examples of structural colours is the patterns observed in the feathers of some birds25,26,27, as in the peacock, whose eyespots consist of a sequence of concentric iridescent variable coloured circles that changes in time as the animal ages27. The formation and evolution of some of these patterns were attributed to the existence of reaction-diffusion mechanisms28,29,30 initially addressed by Turing in 195231. Structural colouration is well-documented in cellulosic cholesteric structures but travelling colour patterns have not previously been investigated.
Here we present a study of the reaction-diffusion system of cellulose-based lyotropic cholesteric (hydroxypropyl)methyl cellulose (HPMC) in trifluoracetic acid (TFA). An esterification reaction, autocatalyzed by TFA, occurs between HPMC and TFA and a trifluoroacetate ester and water are produced. The system, studied as quasi-2D preparations with open boundaries allowing evaporation, demonstrates self-assembled structural colour travelling patterns at a fixed viewing angle. This open thermodynamic system has in common with living systems the development of evolving patterns. Accordingly, a reaction/diffusion simulation was performed for HPMC-TFA taking into account the material boundary conditions.
We also demonstrate that colourful oscillating R and L-handed patterns can be observed and followed in time. Solid films cast from the right and left quasi-2D preparations are investigated. Results of wettability, X-ray Photoelectron Spectroscopy (XPS), circular dichroism (CD) and scanning electron microscopy (SEM) enable us to reveal the morphology, chirality and the hydrophilic/hydrophobic character of the solid films.
Results
Lyotropic solutions in the vials
One of the routes to induce the inversion of the helix handedness, in a cellulose-based lyotropic system, is the use of reactive solvents12,32. In this study, room temperature reaction between solutions of TFA and HPMC yields iridescent colours that vary with the HPMC concentration (see Supplementary Movie 1 and Supplementary Fig. 1). The solutions in the vials yield a L-handed cholesteric phase and, if observed at a fixed angle, the colours reflected by the samples change from red to blue as the concentration of polymer increases. The wavelength of the light reflected by the samples remains stable for about 8 days and then starts to decrease. After about 26 days solutions with a higher solvent concentration became isotropic. TFA acts as an auto catalyst, in the esterification of free hydroxyl groups of HPMC (see the chemical reaction in Supplementary Fig. 2 and ref. 32).
Twisted and untwisted liquid crystalline phases in identical quasi-2D preparations
We also investigated the samples as quasi-2D thin layers (65 µm) prepared from droplets that were squeezed between two flat glass plates. This procedure allows the TFA and water to evaporate from the meniscus to the ambient air. Evaporation drives the diffusion of the two solvents from inside of the quasi-2D samples to the outside. We recall that in previous work with 1D systems (flat capillaries) similar diffusion toward the two menisci was observed32. For the same interval of time, the colours of the quasi-2D samples change significatively during the first 8 days, unlike the precursor L-handed solutions in vials. It appears that the evolution of colour in quasi-2D samples can be attributed to the non-equilibrium (open boundary) conditions imposed by evaporation and diffusion of TFA and water from the centre to the sample film edges.
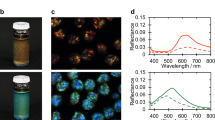
Figure 1a, b show a quasi-2D sample, 3 days after preparation of a 25% w/w solution. Bright iridescent colours (Fig. 1a) can be observed at the centre of the preparation while a fainter colouration can be seen at the outer border (Fig. 1b). Observation of the sample with circularly polarized light, in reflection mode, revealed that, at the centre, the sequence of bright colours results from reflection of the L-handed circularly polarized light (LCP), but at the periphery, the less vivid (faint) colours arise from reflection of R-handed circularly polarized light (RCP). The change from LCP to RCP reflectivity might imply some sort of reversal of helix handedness from the centre to the edge. Observations of the colours at the centre and periphery of the sample by polarizing optical microscopy (POM), in reflection mode (Fig. 1c, e), as well as the reflectance spectra, acquired for RCP and LCP channels (Fig. 1d, f) confirmed the change in helix handedness. The inversion of the helix handedness involves a continuous change of the helix wavevector q = 2π/P, where P is the helical pitch, from positive to negative values passing through zero, on the way from the centre to the periphery of the sample. POM images taken in transmitted light between crossed polarizers, indicate that the bright colours at the centre correspond to a planar texture with oily streaks (Fig. 1g). A completely different polygonal field texture (Fig. 1h) was observed for the sequence of the faint colours at the periphery. Moreover, the reflectance spectra taken at normal incidence indicate that the wavelength of the maximum selective reflection, λ0 = nP, (where n is the average index of refraction of the material and P the value of the pitch) increases from the centre to the periphery, for the L-handed cholesteric structure (seen at the centre). Conversely, it decreases for the R-handed structure observed at the periphery (values presented in Supplementary Table 1). These observations explain the observed sequence of colours, for the left cholesteric structure is in the reversed order when compared with the sequence observed for the right liquid crystalline phase. We also measured the bandwidth, Δλ, measured at half height of peaks, and given by Δλ = PΔn, where Δn is the birefringence. We find that the bandwidth Δλ is much larger for the polygonal texture observed for the right structure.
Photo of a droplet between two glass plates, prepared from a lyotropic cellulosic-based sample, 25% w/w, showing in a reflected L-handed circularly polarised (LCP) light and in b R-handed circularly polarised (RCP) light. Polarised optical microscopy (POM) images, taken in reflection mode, LCP channel (images on the left column) and RCP channel (images on the right) taken at the centre (c) and at the periphery (e) of the preparation (according to the sequence observed in a, b). Reflectance spectra at the centre (d) and at the periphery (f) of the preparation. POM images taken in transmission, between cross polarisers, planar iridescent texture with oily streaks (g At the centre of the preparation) and polygonal fields (h At the periphery of the preparation). Scale bars in a, b 2 mm, c, e 20 µm and g, h 50 µm.
It was reported in the literature that inversion of the helix handedness in cellulosic liquid crystalline systems can occur through a nematic phase in both lyotropic and in thermotropic systems12,13,14. The existence of the nematic phase was inferred from the variation of the pitch of the cholesteric phase, which tends to infinity at the approach of the inversion of the helix handedness33. While observing the quasi-2D sample, in polarized white light transmission mode, (Fig. 2a, left image) a sequence of coloured rings emanates from the centre. This confirms the existence of the L planar cholesteric structure, with the values of the pitch increasing from the centre to the outer rings. Between crossed polarizers, the most striking observation is an outer highly birefringent ring (right image). Transmission mode POM was used to investigate this outer birefringent region. The polydomain texture observed between crossed polarisers and crossed polarisers with a lambda plate (Fig. 2b, left image and right image, respectively and Supplementary Fig. 3) shows domains with fingerprints, a texture characteristic of cellulosic lyotropic solutions34. The optical axis of the cholesteric phase in these domains is aligned along the “slow axis” of the retardation plate (blue domains in Fig. 2b, on the right) and perpendicular to it (yellow domains in Fig. 2b, on the right). The values of the pitch were measured as functions of the position x inside the segment, ΔL (shown in Fig. 2a), taking into account the distance between two consecutive bright and dark bands (fingerprint texture) that corresponds to half of the helicoidal pitch (Fig. 2c). The values of the pitch were found to increase with the distance until the appearance of a bright birefringent region around x/ΔL = 0.6, with no fingerprints (Fig. 2d). Afterwards, domains with fingerprints reappear, and the values of the pitch were found to decrease, as shown in Fig. 2c. The region with no fingerprints (P→∞) located at the frontier between regions with fingerprints (Fig. 2d, e) should correspond to the nematic phase. To further investigate this phase intermediate between the cholesteric domains, a slight shear was applied to the quasi-2D samples. It is known that under shear, cholesteric phases align to a planar texture if the helical axis of the cholesteric has no particular alignment, while the nematic molecules align along the shear direction34. Figure 2f, g show the resulting textures (direction of the shear is indicated by the arrow in Fig. 2f). The sample, observed with crossed polarizers, shows a bright band between two dark regions, while, after addition of the retardation plate shows a yellow band surrounded by two lateral pink regions. In this band, the cholesteric helix is unwound by the shear flow. More precisely, the shear flow aligns the molecules of the nematic along the shear direction (white and yellow bands in Fig. 2f, g, respectively) and realigns the initial polydomain structures of the cholesterics into planar structures, with the optical axis perpendicular to the surfaces of the glass plates (black and pink regions in Fig. 2f, g, respectively, and Supplementary Fig. 4).
a Photo of a quasi-2D sample illuminated under white light between parallel (on the left) and cross polarisers (on the right). b POM pictures taken in transmission, between cross polarisers (on the left) and between crossed polarisers with a lambda plate (on the right), showing cholesteric domains with fingerprint textures, taken in region ΔL (shown in a). c Dependence of the pitch with distance (x) along ΔL (shown in a). POM pictures taken in transmission, between cross polarisers (d (left), f) and between crossed polarisers with a lambda plate (d (right), e, g), at values of x/ΔL~0.6. The sample was sheared (shear direction arrow in f) evidencing different optical axis alignment of the liquid crystalline phases, parallel and perpendicular, to the “slow axis” of the red plate (in g), for the cholesteric (Ch) and the nematic (N) phases, respectively. Scale bars in a 2 mm, in b 10 µm, in d 20 µm and in e 50 µm and f, g 100 µm.
Travelling colourful patterns in quasi-2D liquid crystalline samples
To separate the left, right and nematic (N) phases, a new sample was prepared under controlled conditions of pressure and temperature and its colour evolution was recorded (Fig. 3 and Supplementary Movie 2). The 2D samples present circular-coloured bands that change in time. For all pictures, the colours of the circular patterns at the centre are different from those that develop at the periphery. Different coloured cycles can be observed. The new coloured rings always appear at the border and shrink until the colour at the centre of the preparation vanishes.
a Example of a quasi-2D liquid crystalline sample evolution (prepared from a droplet confined between two flat glass slides) (see Supplementary Movie 2), showing the variation of the bright colours exhibited by the L cholesteric structure, time lower than 40 h, and the presence of the faint colours of the R cholesteric structure, time after 50 h. Scale bar 2 mm. b Evolution of the colours at the centre of the sample, showing the reappearance of the bright initial colours and the appearance of the faint colours, after 50 h. c Same as in b but along a line that passes through the centre of the sample with maximum length equal to dmax (shown in a). d Numerical simulations of travelling colours with square geometry (see Supplementary Movie 2) showing similar behaviour to the example shown in a. Colour map is based on the relative density of water, r, with two red-green-blue regions, matching visible light response from L and R structures, and black regions for non-visible light responses. e Evolution of the colours at the centre of the simulated square.
We propose that the appearance of the different coloured rings and their movement toward the centre can be related to the diffusion of the solvent from the centre to the periphery. This appears to be the mechanism driving the evolution of the system during the first 5 h, when the colour at the border changes from green to blue. As the solvent diffuses out of the sample, the concentration in polymer increases and the pitch of the cholesteric phase decreases. However, after 5 h another outer green ring reappears, reversing the sequence of colours. Afterwards, the green ring starts to shrink, giving rise to the formation of another outer yellow ring, which is subsequentially replaced by a red ring. Then, after 15 h, no coloured ring is visible at the periphery, and after 45 h the whole sample becomes black until another milky ring starts to appear at the border. From this point, another cycle of rings emerged with a yellow, green and blue faint colours, before the sample becomes black again. The sequence of colours observed at the centre of the quasi-2D sample is shown in Fig. 3b. When other precursor solutions were used, with different concentrations of the polymer, sequences of coloured rings were also observed. Moreover, as shown in Figs. 1 and 2, the first cycle of colours corresponds to a L-handed cholesteric while the second cycle corresponds to a R-handed one.
The observed behaviour cannot however be attributed solely to the diffusion of the solvent. The chemical reaction that can occur between the TFA and the cellulosic chain must also play a crucial role, as was identified for the 1D geometry and other cellulosic systems11,32. One of the products that results from the chemical esterification of HPMC is water. To test the effect of the water in the system, some solutions were prepared with different amounts of water and the evolution of the systems was followed. The presence of water shifts the maximum wavelength reflection of the samples to higher values (Supplementary Movie 3) and the sequence of right (R) colours (at the border) appears faster when compared with the 2D sample prepared with no water addition. To test the influence of TFA, on the right (R) and left (L) oscillations, TFA was added at the periphery of a 2D preparation that already presented an R sequence of colours at the centre, (Supplementary Fig. 5 and Supplementary Movie 4). A new sequence of L colours reappears, at the border, where the TFA was added.
To emphasize and distinguish the behaviour of the quasi-2D sample at the border and at the centre the evolution of the colours was investigated along a line passing through the centre of the sample, as shown in Fig. 3c. These results provide clear evidence of the oscillatory regime for the appearance, shrinkage and disappearance of the coloured rings. The shape of the plot line changes after the first 10 h (change of curvature), which coincides with the reappearance of a new green ring at the periphery. Then, the curvature of the line continues to change until, after about 80 h, a similar shape to the one exhibited at the beginning is recovered.
Numerical model
To better understand the mechanism driving formation of the observed travelling colour patterns, we carried out simulations of the reaction-diffusion process. We consider the reaction kinetics of four molecular species according to the chemical reaction (Supplementary Fig. 2.)
We model fast diffusion of water and slower diffusion of TFA, with a ratio Dwater/DTFA = 2, and neglect diffusion of the polymer, which is much slower relative to the time scale of the experiment. At the boundaries of the system, we model the evaporation of TFA with an exponentially decaying rate. We also model the evaporation of water, allowing its density to reach exponentially an equilibrium value determined by the ambient humidity. We visualize the spatiotemporal evolution of the system using a colour scale shown in Fig. 3d based on the relative concentration of water, r = [H2O]/([H2O] + [TFA]) which, as we conjecture, determines the local pitch P of the L- or R-handed cholesteric structure accordingly to the formula, 1/P ≈ A(r − rc) + B(r − rc)2 + C(r − rc)3, where |B| and |C| are much smaller than |A| and rc is the critical value of the relative concentration at which the handedness of the helix changes from L to R. When A is negative, the initial left handedness corresponds to a negative pitch P. The initial red colour of scale matches the initial value of r and the subsequent shift to the blue colour corresponds to a decrease of r due to the relatively fast evaporation of water from the meniscus. Subsequently, the relative concentration r in the vicinity of the meniscus increases because the evaporation of water into the humid ambient air is slowed down while the evaporation of TFA continues. The colour scale then is set to black when r becomes greater than its initial value because the corresponding L helical pitch P enters the infrared range. The sign of P changes at r = rc. When the pitch of the R-handed helix reaches the lower limit of visible region, the colour of the scale is set to red. The colour evolves then from red to blue and turns to black again when the ultraviolet (UV) range is entered. Sizes of visible and infrared regions, both L and R, are adjusted in the scale to the experimental data shown in Fig. 3b, e. The resulting spatiotemporal evolution of moving colour bands in the simulation model shows qualitative agreement with experimental observations.
Twisted right (R), left (L) and untwisted solid films nanostructures
In order to further investigate the different phases of the quasi-2D samples, solid films were cast from left (LCP films), right (RCP films) and nematic phases. The bulk properties of the films were investigated by infrared spectroscopy (Attenuated total reflection-Fourier transform infrared spectroscopy (ATR-FTIR)), X-Ray Diffraction (XRD), CD and their cross-section were observed by SEM. The ATR-FTIR spectra show that some esterification occurred for LCP as well as for RCP films (see Supplementary Fig. 6). Strong characteristic vibration bands occur at 1643, 1154, 1109 and 1055 cm−1 that can be assigned to C–O–C (asymmetrical stretching) and to cellulose glycosidic bonds35. A large band at 3445 cm−1 is attributed to the O–H stretching, while the bands between 2980 and 2824 cm−1 are due to the C–H stretching. Similar to hydroxypropyl cellulose, the band at 1452 cm−1 can be attributed to the deformation vibration of the CH2 group35 in the hydroxypropyl moiety from the cellulose derivative (HPMC), used in this work. The presence of the trifluoroacetate ester is revealed by the presence of the bands at 1785 and 1211 cm−1, which correspond to the ester C=O and to the C–O stretching vibrations, respectively35. The XRD spectra of the LCP and RCP films show small differences compared with the spectra obtained for the initial HPMC cellulose derivative (Supplementary Fig. 7). The differences are noticeable in the peaks that appear near 2θ = 9°θ and at 2θ = 20°. HPMC shows two local maxima at 2θ = 9.42° and 20.50°. Regarding the HPMC-TFA films, there is a small shift in the measured peak to 2θ = 9.16° and 21.04° for the LCP film, and to 2θ = 8.74° and 20.24° for the RCP film. These results indicate that the initial crystallinity of the HPMC sample was not much affected by the presence of the TFA.
To investigate the morphology of the films, SEM was used (Fig. 4a–c). At the cross-section nanometre scale, a layered structure formed by nanometric rods can be observed for LCP and RCP films. This is shown in Fig. 4a, c, respectively. For films obtained from the nematic phase, the cross-section of the solid films shows nanorods aligned in average along a main direction, parallel to the surfaces of the films with no positional order (Fig. 4b).
a–c Freeze-fracture SEM cross-section images of the solid films obtained from left-handed (L), when the value of the pitch tends to infinity and right-handed (R) liquid crystalline solutions, respectively. Scale bars, 200 nm. d CD spectra of solids films prepared from L and R quasi-2D liquid crystalline solutions.
Typical CD spectra are shown in Fig. 4d. Negative and positive curves were obtained for RCP and LCP solid films, respectively. These are in accordance with the helicity of the left and right precursor phases. Moreover, after removing the solvent, the values of the wavelength maxima decrease to the UV region of the electromagnetic spectrum of light, for both solid samples, compared with the precursor liquid crystalline solutions.
Hydrophilic/hydrophobic character of solid films
To better characterize the solid films and the evolution of the system from left to right structures, the surfaces of the films were characterized by XPS and wettability measurements. XPS survey spectra (Fig. 5a) for both films reveal the existence of surface C 1 s and O1s signals with binding energies of about 286 and 533 eV, respectively (similar to what is observed for HPMC film spectra, see Supplementary Fig. 8). RCP and LCP films also present small peaks ascribed to F 1 s signal at 689 eV (see Supplementary Fig. 9). The atomic (%) of C, O and F were 67.76, 31.41 and 0.83% for LCP films, while values of 65.03, 33.97 and 0.99% were observed for RCP samples (see Supplementary Table 2 and ref. 36). The oxygen to carbon ratio (O/C) is lower for LCP samples (0.42) compared with RCP (0.52) with the latter being similar to what was found for neat HPMC (0.42). The primary difference between RCP and LCP spectra lies in the region of the C 1 s spectra (Fig. 5b). Deconvolution of these core spectra shows the contribution of three component peaks. Both RCP and LCP C 1 s core spectra show a similar main peak located at 286.5 eV which can be attributed to C–O–H and C–O–C bonds (Supplementary Table 3). However, for the LCP films the peak located at 284.8 eV, assigned to C–H and C–C bonds, gives a higher contribution than the one observed for the RCP films. Moreover, the contribution of the peak at 287.9 eV, ascribed to C=O and O–C–O, increases for the RCP films compared to the same deconvoluted peak seen for the LCP films (Fig. 5b). These observations are consistent with the existence of more hydrophilic groups at the surface for the RCP than for the LCP films. The peak at 289.4 eV, associated to the O–C=O groups, is residual in both spectra. These results indicate that esterification of the hydroxyl groups of the cellulosic chain occurs and can be observed in RCP and LCP solid films.
a Wide-scan X-ray photoelectron spectra (XPS) survey spectrum of solid films prepared from left-handed (LCP) and right-handed (RCP) liquid crystalline quasi-2D solutions, the presence of TFA ester can be noticed for RCP film. b Core level C 1 s XPS spectra and the respective deconvoluted peaks for RCP and LCP samples. The contribution of the peaks from C–H, C–C (hydrophobic cellulose groups) significantly reduces from LCP to RCP samples, while the area of the peaks assigned for O–C–O, C=O (hydrophilic cellulose groups) and C–O–H and C–O–C increase for RCP sample. c Water droplet on the more hydrophilic RCP surface and in d on the less hydrophilic LCP surface.
Surface characterization of RCP and LCP films (Fig. 5c, d) via water contact angle (CA) measurement is not straightforward due to the absorbing nature of the surfaces of the RCP and HPMC films. Therefore, CA measurements give only qualitative insight into the surface properties. Nevertheless, the surface of the LCP films shows a clear tendency to be less hydrophilic (CA = 100° ± 2°; n = 10) than the surface of the RCP films (CA = 66° ± 4°; n = 10), following the trend of the results obtained by XPS. The hydrophilic trend was also observed for the HPMC films (CA = 46° ± 3°; n = 10), which is in accordance with the measurements made by other authors for HPMC films37.
Discussion
Our results demonstrate the development of travelling colourful patterns in a self-assembled lyotropic liquid crystalline system.
The interpretation of the spatiotemporal structures observed are as follows:
The lyotropic system was obtained by mixing TFA and the polymer in the vials above a critical concentration (~19%w/w). TFA autocatalyzes an esterification reaction between the acid and the hydroxyl groups of the HPMC, which produces water and ester groups substituted along the cellulosic chain. In the vials, the wavelength reflected by the iridescent solutions decreases in time and a L-handed cholesteric phase was observed, indicating that the value of the pitch P decreases, and that no inversion of the helix handedness occurs. No evaporation of TFA and water was allowed in the sealed vials and the quantity of TFA is larger compared with the amount of water present in the system (the medium is acid). The decrease of the pitch can be associated with the adjustment of the conformation of the cellulosic chain to the acidic medium. XPS and CA measurements show the presence of hydrophobic CH groups, probably bonded axially to the main chain, on the surface of solid films isolated from L samples.
The quasi-2D samples show a different behaviour. TFA and water were allowed to evaporate at the boundaries. It is known that the saturating vapour pressures of TFA and water, at 20 °C, are 1.17 and 2.34 kPa, respectively, therefore the evaporation of water to a dry air is faster than that of TFA. In general, the molecular diffusivity of liquids, D, is of the order of 10−5 cm2/s. This means that the characteristic time of diffusion of the two solvents \({\uptau} \,=\,\frac{{{{\mathrm{L}}}}^{2}}{{{{\rm{D}}}}{(2\uppi)}^{2}}\) is of the order of 1 h for L = 1 cm. This characteristic time is much smaller than the time scale of the observations of 100 h. From these data, we infer that for the quasi-2D samples, the water and the TFA should both evaporate at the boundaries (the meniscus), but water should evaporate more rapidly. However, water vapour is already present in the ambient air so that, after a certain time, the evaporation of water decays to zero. On the contrary, the evaporation of the acid continues because its vapour is absent in the ambient air. Therefore, as mentioned before, the ratio between the concentrations of water and the TFA increases in time, which results in an increase of the pitch that can be associated to the adjustment of the conformation of the cellulosic chain to the less acidic medium. The change of the chain conformation was confirmed by XPS and CA measurements. Hydrophilic sites, bonded equatorially to the cellulose chain, were found on the surface of solid films isolated from R samples.
The simulation demonstrates that evaporation of both water and TFA at the boundary, as well as the resulting concentration gradient evolution, are necessary for the formation and propagation of travelling colour waves (Fig. 3d, e). The crucial role of water evaporation was confirmed by conducting experiments in both high and low humidity environments (Supplementary Movie 3). In experiments performed at high humidity, the amplitude of the initial colour changes was much smaller than in experiments performed with lower humidity.
The cellulosic nanostructures observed, by SEM, in the cross-section of the films, suggest that the cellulosic chains in the liquid crystalline phase have the ability to self-assemble into mesostructures that can possibly be stabilized by hydrogen bonds.
Considering the characteristics of the cellulosic chain and the results obtained, we propose a simple model to interpret the formation of left and right phases. Proposed structures are shown in Fig. 6. The hydrophilic (more flexible) and hydrophobic (more rigid) groups are substituted equatorially and axially, respectively, along the cellulose main chain7. Due to the chirality of cellulose, the hydrophilic and the hydrophobic moieties are arranged asymmetrically along the chain, which results in an asymmetrical interaction with the acid, Fig. 6a, L-handed structures, and the water, Fig. 6c, R-handed structures. It is possible that a similar small imbalance might also be imposed by plants at the molecular scale.
a Left-handed helicoidal structures formed by rods (cross-section shown in the upper right corner) that expose hydrophobic groups of cellulose (red colour) and hide the hydrophilic groups (blue colour) asymmetrically from the interface, along the rods, due to the chirality of the cellulose main chain. b Nematic structure formed by symmetric rods (cross-section in the upper right corner). c Right-handed helicoidal structures formed by rods (cross-section shown in the upper right corner) that expose cellulose hydrophilic groups (blue colour) and hide the hydrophobic groups (red colour) asymmetrically along the rods.
In this work, we give evidence of the formation and motion of travelling structural coloured patterns in cellulose-based liquid crystalline materials, produced by a reaction/diffusion mechanism and the evaporation at boundaries. The beauty of the system consists not only in its travelling colourful patterns, driven by self-adjustment of the conformation of the cellulosic chain to the environment, but also in the preservation of the chirality of the precursor solutions characteristics, at a given instant, into solid films. Our results also indicate that inversion of the helix handedness, at the micro/nanoscale systems, should come from small self-conformational changes of the cellulosic chains. The oscillating inversion of the helix handedness and the formation of spatiotemporal structures opens a new field of applications, with no need of the use of sophisticated techniques; the same initial formulation is at the origin of solid matrices with distinct chiral photonic characteristics. Foreseen technological applications include the manipulation of structural colours, the preparation of templates and the design of hydrophilic/hydrophobic surfaces on demand.
Methods
Cellulose-based solutions
Cholesteric liquid crystalline solutions of HPMC (Methocel F50, Dow, 20–25 kDa average molecular weight in number) in trifluoroacetic acid (TFA, ReagentPlus, 99% purity, Sigma-Aldrich), with concentrations between 19 and 27% (w/w) were obtained by direct mixing in 1.5 mL glass vials with a needle. Following sample dissolution, the vials were sealed with a cap and allowed to homogenize at room temperature. After ~24 h at room temperature, homogenous iridescent solutions reflecting bands in the visible region were obtained.
Thin-layer samples
Thin-layer samples of liquid crystalline HPMC solutions were obtained by placing a given amount of solution between a microscope slide and a cover-glass with the aid of a needle. Thin-layer samples were stored at room temperature before further use.
2D solid films
2D films of pure HPMC and liquid crystalline solutions of HPMC in trifluoroacetic acid were produced for further analysis. Following the production of the thin-layer samples in a microscope slide/cover-glass system, the sample was allowed to relax due to the shear induced by the production method. After around 1 h, observation under the microscope indicates that the sample has relaxed (no shear bands are present) and that the sample presents only left circular polarizing reflection of light. When this is verified, the microscope slide is immersed in liquid nitrogen to freeze the sample, the cover-glass is detached using tweezers and a blade and the film is immersed in acetone to remove residual TFA and quenched to block the film structure. The obtained film is identified as LCP film. To obtain RCP films (identified as RCP film), the thin-layer sample was allowed to develop at room temperature until only the right circular polarizing light reflection is noticeable (between 1 and 2 weeks depending on the sample thickness). When the latter is verified, the film is quenched using the same method described for the LCP film samples. Both LCP and RCP films were stored between two microscope slides to avoid curling during the acetone drying process. Pure HPMC films were produced dissolving HPMC in deionized water at a concentration of 2% (w/v) and the solution was poured into PE petri dishes. Following solvent evaporation, the films were detached using tweezers and stored at room temperature until further use. Resulting LCP, RCP, pure HPMC films present average thickness of 75 ± 20, 95 ± 28, 26 ± 4 μm, respectively (average value ± standard deviation, n = 5).
Polarised optical microscopy (POM)
Images were obtained in reflection and transmission modes, by using an Olympus BX51 microscope, coupled with an Olympus DP73 CCD camera, and acquired with the Stream Basic v.1.9 Olympus software. A cold illumination source generated by a halogen lamp (KL 2500 LCD, SCHOTT) was used. The images were obtained with ×10, ×20 or ×50 objectives (Olympus, MPlanFL N) and automatically scaled by the software.
Modelling of travelling colourful patterns
A finite difference reaction-diffusion model was developed to simulate the colour behaviour observed experimentally in thin-layer samples. Quantities of four chemical species were initially set in a square grid with 50 by 50 cells with values \({P}_{1}\,=\,[{{{\rm{HPMC}}}}\,-\,{{{\rm{OH}}}}]\,=\,0.1,X\,=\,[{{{\rm{TFA}}}}]\,=\,0.64,{P}_{2}\,=\,[{{{\rm{HPMC}}}}\,-\,{{{{\rm{OCOCF}}}}}_{3}]\,=\,0.1\) and \(Y\,=\,[{{{{\rm{H}}}}}_{2}{{{\rm{O}}}}]\,=\,0.16\). We considered the chemical reaction \({P}_{1}\,+\,X\,\to {P}_{2}\,+\,Y\) with a rate constant \(\alpha \,=\,2.5\,\times\, {10}^{-3}\) and the inverse reaction has a rate constant \(\beta \,=\,1.0\,\times\, {10}^{-2}\). The concentration of P1 and P2 are assumed to be approximately constant. Then, at each time step, the concentration X and Y evolve due to the chemical reaction following the kinetic equations: \(X(t\,+\,1)\,=\,X(t)\,-\,\alpha {P}_{1}(t)X(t)\,+\,\beta {P}_{2}(t)Y(t)\) and \(Y(t\,+\,1)\,=\,Y(t)\,+\alpha {P}_{1}(t)X(t)\,-\,\beta {P}_{2}(t)Y(t)\). To model molecular diffusion, the concentration in each cell was averaged with its value and its surrounding eight neighbours using the following convolution matrix38:
where \(a\le 1/12,b=2a\) and \(c=1-6a\). For \(({P}_{1},X,{P}_{2},Y)\) a is set to \((0,1/24,0,1/12)\). We assume that X and Y species evaporate at boundaries following exponential functions, \(X=X(0){e}^{-\frac{t}{{\tau }_{X}}}\) and \(Y\,=\,{Y}_{{{{\rm{sat}}}}}\,+\,(Y(0)\,-\,{Y}_{{{{\rm{sat}}}}}){e}^{-\frac{t}{{\tau }_{Y}}}\), where τX and τY are the characteristic times of evaporation for X and Y, and Ysat is a saturation value that depends on the ambient humidity. In the simulation, we set \({\tau }_{X}\,=\,2.0\,\times\, {10}^{4}\), \({\tau }_{Y}=4.5\times {10}^{2}\) and \({Y}_{{{{\rm{sat}}}}}\,=\,0.1\). The total number of iterations was 1.1 × 104 and diffusion/evaporation step was computed before the chemical reaction step. The relative amount of water, \({{{\rm{r}}}}\,=\,[{{{\rm{H}}}}2{{{\rm{O}}}}]/([{{{\rm{H}}}}2{{{\rm{O}}}}]\,+\,[{{{\rm{TFA}}}}])\,=\,X/(X\,+\,Y)\), was matched with colours as observed experimentally. As discussed previously, the initial value of r (t = 0) corresponded to red (L structure), the minimum to blue (L structure). The black gap between visible regions from L and R structures were adjusted using experimental observations.
This first simple model provides a schematic description of the interplay between evaporation, diffusion and chemical reaction of water and TFA in the presence of HPMC. For a better fit with the experimental results, besides the change of the shape of the system (from square to circular), more realistic considerations are needed, such as the dependence of diffusivity on concentrations of species and correlation between them, and a movable boundary condition should be used (as shown in Fig. 3a). Nevertheless, this model correctly fits the travelling colours and might be used to explain other thermodynamically open systems with similar behaviour.
VIS spectroscopy
The LCP and RCP reflective wavelengths of thin-layer samples were recorder with a Sense+, Sarspec VIS spectrometer, mounted onto the microscope. Spectra were acquired by Light- Scan software, version 1.1.17. Each reflectance spectrum was normalized to the maximum registered value.
Scanning electron microscopy (SEM)
SEM images of the freeze-fracture cross-sections of the films were obtained using a Carl Zeiss Auriga crossbeam (SEM–focus-ion-beam) workstation instrument, equipped with an Oxford energy-dispersive X-ray spectrometer. In the freeze facture technique, the sample was fracture by first immersion in liquid nitrogen until frozen, then hit in order to cause fracture. Samples were mounted in aluminium stubs, coated with a thin carbon layer using a Q150T ES Quorum sputter coater. The acquisition was performed using an accelerating voltage of 3 or 5 kV with 6.5–7.2 mm as working distance.
Circular dichroism (CD)
CD experiments were performed using an Applied Photophysics ChirascanTM CD spectrometer (Surrey, UK). The scanned wavelengths ranged from 185 and 800 nm, with a bandwidth of 1 nm and a scanning rate of 200 nm/s.
X-ray photoelectron spectroscopy (XPS)
A Kratos Axis Supra equipment with a monochromatic Al Kalpha source (1486.6 eV) was used to acquire XPS spectra operated at 15 kV under a current of 10 mA. All detailed spectra were recorded at a pass energy of 160 and 10 eV, for survey and detailed scans, respectively. Electron flood gun used for charge neutralization during measurement, all peaks shifted to C 1 s at 284.8 eV. CasaXPS Version 2.3.19PR1.0 was used for data analysis. Relative sensitivity factors for quantification provided by the manufacturer.
Contact angle measurements
Static CAs were measured on the sample surfaces through the sessile drop method using an OCA20 CA measuring instrument (DataPhysics Instruments GmbH, Filderstadt, Germany). Samples were cut in a rectangular specimen with 0.5 cm × 1 cm. Water droplets of 2 μl were generated with an electronic micrometric syringe and deposited on the substrate surface according to the so-called pick-up procedure. Image acquisition, analysis and CA determination were performed using the SCA20 v.4.3.12 software (Dataphysics Instruments GmbH, Filderstadt, Germany). A total of ten droplets were dispensed, and each droplet was placed in a different region of the sample. The CA was determined after 5 s of the moment of the droplet deposition and settle. The results correspond to the average CA and are presented with the respective standard deviations.
Fourier transform infrared spectroscopy (FTIR)
FTIR spectra of the samples were recorded on a Perkin-Elmer FT-IR Spectrometer Spectrum Two (Waltham, MA, USA), equipped with an ATR cell, in the range of 4000–500 cm−1. Dried samples were applied directly on the ATR cell without further pre-treatment.
X-ray diffraction (XRD)
XRD patterns of the films were acquired with a Rigaku MiniFlex2 X-Ray diffractometer using CuKa radiation (30 kV and 15 mA) in the 5 < 2θ < 40 range with a scan speed of 0.5°/min and a sampling width of 0.02°.
Photographs and videos
Photographs and videos of the solutions in vials and of the quasi-2D preparations were obtained with a Canon EOS 550D coupled with an EF-S 60 mm Canon macro-lens under an incandescent white ring light, no polarizers were used.
Colour averaging
The most dominant colours of images were calculated by first converting the RGB (red, green and blue) colour space to HSV colour space (hue, saturation and value)39 and then clustered using the k-means method40.
Data availability
The authors declare that the data supporting the findings of this study are available within the paper and its supplementary information files.
References
Neville, A. C., Gubb, D. C. & Crawford, R. M. A new model for cellulose architecture in some plant cell walls. Protoplasma 90, 307–317 (1976).
Atalla, R. H. & Vanderhart, D. L. Native cellulose: a composite of two distinct crystalline forms. Science 223, 283–285 (1984).
Glasser, W. G. et al. About the structure of cellulose: debating the Lindman hypothesis. Cellulose 19, 589–598 (2012).
Medronho, B., Romano, A., Miguel, M. G., Stigsson, L. & Lindman, B. Rationalizing cellulose (in)solubility: reviewing basic physicochemical aspects and role of hydrophobic interactions. Cellulose 19, 581–587 (2012).
Kasai, W., Kuga, S., Magoshi, J. & Kondo, T. Compression behavior of Langmuir−Blodgett monolayers of regioselectively substituted cellulose ethers with long alkyl side chains. Langmuir 21, 2323–2329 (2005).
Fernandes, S. N. et al. Cellulose-based nanostructures for photoresponsive surfaces. Cellulose 23, 465–476 (2016).
Kondo, T. Hydrogen Bonds in Cellulose and Cellulose Derivatives. In Polysaccharides (ed. Dumitriu, S.) Ch. 3. (CRC Press, 2004). https://doi.org/10.1201/9781420030822.
Gray, D. G. Some Comments on Chiral Structures from Cellulose. in Cellulose Science and Technology (eds Rosenau, T., Potthast, A. & Hell, J.) 253–261. Ch. 11. (John Wiley & Sons, Inc., 2018). https://doi.org/10.1002/9781119217619.
Conley, K. M., Godbout, L., Whitehead, M. A. & van de Ven, T. G. M. Reversing the structural chirality of cellulosic nanomaterials. Cellulose 24, 5455–5462 (2017).
Biermann, O., Hädicke, E., Koltzenburg, S. & Müller-Plathe, F. Hydrophilicity and lipophilicity of cellulose crystal. Surfaces. Angew. Chem. Int. Ed. 40, 3822–3825 (2001).
Guo, J. X. & Gray, D. G. Chiroptical behavior of (acetyl)(ethyl)cellulose liquid-crystalline solutions in chloroform. Macromolecules 22, 2086–2090 (1989).
Ritcey, A. M., Holme, K. R. & Gray, D. G. Cholesteric properties of cellulose acetate and triacetate in trifluoroacetic acid. Macromolecules 21, 2914–2917 (1988).
Miyagi, K. & Teramoto, Y. Elucidation of the mechanism of stress-induced circular dichroic inversion of cellulosic/polymer liquid crystalline composites. Macromolecules 53, 3250–3254 (2020).
Yamagishi, T., Fukuda, T., Miyamoto, T., Ichizuka, T. & Watanabe, J. Thermotropic cellulose derivatives with flexible substituents. III. Temperature dependence of cholesteric pitches exhibiting a cholesteric sense inversion. Liq. Cryst 7, 155–161 (1990).
Fernandes, S. N., Lopes, L. F. & Godinho, M. H. Recent advances in the manipulation of circularly polarised light with cellulose nanocrystal films. Curr. Opin. Solid State Mater. Sci. 23, 63–73 (2019).
Gray, D. G. & Harkness, B. R. Chiral Nematic Mesophases of Lyotropic and Thermotropic Cellulose Derivatives. in Liquid Crystalline and Mesomorphic Polymers (eds Shibaev, V. P. & Lam, L.) 298–323 (Springer New York, 1994). https://doi.org/10.1007/978-1-4613-8333-8_9.
Yamagishi, T.-A. et al. Comparison of thermal and cholesteric mesophase properties among the three kind of hydroxypropylcellulose (HPC) derivatives. Polym. Bull. 32, 47–54 (1994).
Godinho, M. H., Gray, D. G. & Pieranski, P. Revisiting (hydroxypropyl) cellulose (HPC)/water liquid crystalline system. Liq. Cryst. 1–13 https://doi.org/10.1080/02678292.2017.1325018 (2017).
Godinho, M. H., Canejo, J. P., Feio, G. & Terentjev, E. M. Self-winding of helices in plant tendrils and cellulose liquid crystal fibers. Soft Matter 6, 5965 (2010).
Armon, S., Efrati, E., Kupferman, R. & Sharon, E. Geometry and mechanics in the opening of chiral seed pods. Science 333, 1726–1730 (2011).
Gerbode, S. J., Puzey, J. R., McCormick, A. G. & Mahadevan, L. How the cucumber tendril coils and overwinds. Science 337, 1087–1091 (2012).
Almeida, A. P. C. et al. Reversible water driven chirality inversion in cellulose-based helices isolated from Erodium awns. Soft Matter 15, 2838–2847 (2019).
Abraham, Y., Dong, Y., Aharoni, A. & Elbaum, R. Mapping of cell wall aromatic moieties and their effect on hygroscopic movement in the awns of stork’s bill. Cellulose 25, 3827–3841 (2018).
Fernandes, S. N. et al. Structural color and iridescence in transparent sheared cellulosic films. Macromol. Chem. Phys. 214, 25–32 (2013).
Wilts, B. D. & Saranathan, V. A literal elytral rainbow: tunable structural colors using single diamond biophotonic crystals in pachyrrhynchus congestus weevils. Small 14, 1802328 (2018).
Kinoshita, S., Yoshioka, S. & Miyazaki, J. Physics of structural colors. Rep. Prog. Phys. 71, 076401 (2008).
Mishra, M. Transformation of colourful pattern of eyespot in peacock wing. Curr. Sci. 107, 186–188 (2014).
Prum, R. O. & Williamson, S. Reaction–diffusion models of within-feather pigmentation patterning. Proc. R. Soc. Lond. B Biol. Sci. 269, 781–792 (2002).
Epstein, I. R. The consequences of imperfect mixing in autocatalytic chemical and biological systems. Nature 374, 321–327 (1995).
Epstein, I. R. & Xu, B. Reaction–diffusion processes at the nano- and microscales. Nat. Nanotechnol. 11, 312–319 (2016).
Turing, A. M. The chemical basis of morphogenesis. Philos. Trans. R. Soc. Lond. B. Biol. Sci. 237, 37–72 (1952).
Chagas, R., Silva, P., Fernandes, S. N., Zumer, S. & Godinho, M. H. Playing the blues, the greens and the reds with cellulose-based structural colours. Faraday Discuss. https://doi.org/10.1039/D0FD00020E (2020).
Gennes, P. G. de & Prost, J. The Physics of Liquid Crystals. (Clarendon Press, 1998).
Collings, P. J., Goodby, J. W. G. Introduction to Liquid Crystals: Chemistry and Physics. (CRC Press, 2020).
Liebert, T., Schnabelrauch, M., Klemm, D. & Erler, U. Readily hydrolysable cellulose esters as intermediates for the regioselective derivatization of cellulose; II. Soluble, highly substituted cellulose trifluoroacetates. Cellulose 1, 249–258 (1994).
Barsbay, M. et al. Verification of controlled grafting of styrene from cellulose via radiation-induced RAFT polymerization. Macromolecules 40, 7140–7147 (2007).
Parsons, G. E., Buckton, G. & Chatham, S. M. Comparison of measured wetting behaviour of materials with identical surface energies, presented as particles and plates. J. Adhes. Sci. Technol. 7, 95–104 (1993).
Hill, C. Simulating the Belousov-Zhabotinsky Reaction. https://scipython.com/blog/simulating-the-belousov-zhabotinsky-reaction/ (2017).
Cantrell, K., Erenas, M. M., de Orbe-Payá, I. & Capitán-Vallvey, L. F. Use of the hue parameter of the hue, saturation, value color space as a quantitative analytical parameter for bitonal optical sensors. Anal. Chem. 82, 531–542 (2010).
Weller, H. I. & Westneat, M. W. Quantitative color profiling of digital images with earth mover’s distance using the R package colordistance. PeerJ 7, e6398 (2019).
Acknowledgements
This work is co-financed by FEDER, European funds, through the COMPETE 2020 POCI and PORL, National Funds through FCT—Portuguese Foundation for Science and Technology and POR Lisboa2020, under the projects PIDDAC (POCI-01-0145-FEDER-007688, reference UIDB/50025/2020-2023) and PTDC/CTM-REF/30529/2017 (NanoCell2SEC) and Action European Topology Interdisciplinary Action (EUTOPIA CA17139). RS supported by NSF CMMI-1663041.
Author information
Authors and Affiliations
Contributions
M.H.G. supervised and directed this project. R.C., S.N.F., P.E.S.S. and M.H.G. prepared the samples and performed SEM and Vis spectroscopy. R.C. and S.N.F. made CD measurements and R.C. FTIR and DRX. S.N.F. performed contact angle and XPS measurements. P.E.S.S. performed time-lapse photography and the colour analysis. R.C., S.N.F., P.E.S.S. and M.H.G. performed POM measurements. R.S. and P.E.S.S. designed the numerical model and R.S., P.P., M.H.G. and P.E.S.S. contributed to the interpretation of results. M.H.G. wrote the manuscript, and all of the authors contributed to the improvement and editing of the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Communications Earth & Environment Materials thanks Jan Lagerwall and Mark Andrews for their contribution to the peer review of this work. Primary Handling Editor: John Plummer.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Silva, P.E.S., Chagas, R., Fernandes, S.N. et al. Travelling colourful patterns in self-organized cellulose-based liquid crystalline structures. Commun Mater 2, 79 (2021). https://doi.org/10.1038/s43246-021-00182-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-021-00182-7