Abstract
Intensive effort to tailor photophysics of lead-free perovskites is appealing in recent years. However, their combined electronic and optical property elucidations remain elusive. Here, we report spectroscopic observations of the coexistence Zhang-Rice singlet state and exotic electronic transitions in two-dimensional copper-based perovskites. Herein, several perovskites with different alkylammonium spacers are investigated to unravel their correlated electronic systems and optical responses. Namely, methylammonium, ethylammonium, phenylmethylammonium and phenethylammonium. Using temperature dependent high-resolution X-ray absorption spectroscopy, we observe distinct electronic features highlighting the impact of short spacer chains compared to long-conjugated ligands, demonstrating a pronounced 3d9 and 3d9L signature linewidth variation. Corroborated by density functional theory calculations, the transient dynamics evolution of copper-based hybrid perovskites is influenced by the strong interplay of electron-phonon interactions and geometric constrictions. This finding sheds light on tuning the electronic and optical properties of hybrid perovskites towards efficient photoactive-based devices.
Similar content being viewed by others
Introduction
Two-dimensional hybrid organic–inorganic perovskites (2D-HOIPs) materials have demonstrated promising progress in photovoltaics and light-emitting diodes applications, such as their excellent performance as active-light absorbers and carrier transporters1,2,3,4,5. These materials deserve special attention in the field of unconventional 2D hybrid materials due to their tunable dielectric confinements, charge carrier dynamics, and their structural diversities. Initially, the research progress is motivated by a large number of seminal papers in the 1980s and 1990s6,7,8,9. To date, several classes of 2D-HOIPs have emerged with a diversity concerning their structure-property relationships3,4,5,10.
An intrinsic quantum well structure in 2D-HOIPs is composed of ammonium cations connected to the halide ions of inorganic sheets via hydrogen bonding. The hybrid perovskite framework has unique alternation of bilayer chains of spacers comprising alkyl- or aromatic ammonium cations and inorganic perovskite layers held by corner-sharing [BX4]2− octahedrals9,11. B element represents typical metals such as lead or tin with formal oxidation state of 2+, and X− is a halide anion. The inorganic sheets have potentially active sites due to their high charge carrier mobility12. The organic spacer ligands that occupy the A-site of the crystal structure with tunable length afford superior hydrophobicity and large dielectric confinement13. As a result, the formation of quantum well-like structure manifests high excitonic binding energies at room temperature and high radiative decay rate2,5,7,14,15,16,17,18,19,20,21. Pressure, electric field, and temperature serve as potential external stimulus owing to the weak hydrogen-bonding interactions between organic and inorganic moieties, which are tunable via thermally activated motion of the cations.
A fundamental challenge in the advancement of 2D-HOIPs is the toxicity issue and material stability2,3,4. The environmental toxicity originates from the lead that occupies the B-site of 2D-HOIPs crystal structure, which is a roadblock in commercialization. In this regard, 2D lead-free halide perovskites are particularly useful for future commercial applications15,19. For example, Cortecchia and coworkers explored the optical properties of (CH3NH3)2CuClxBr4−x series by tuning Br/Cl ratio to widen the optical absorption to the near-infrared regime15. Polyakov et al.22 and Nugroho et al.23 investigated copper-based 2D-HOIPs with longer alkylammonium chains (C6H5CH2CH2NH3)2CuCl4, and they showed the coexistence of ferromagnetic and ferroelectric orders within a hybrid material. With regard to the unstable humidity issue, several strategies have been employed such as the replacement of hygroscopic methylammonium (MA) functional group with a hydrophobic cation in the A-site of 2D-HOIPs crystals such as butylammonium (BA)24 and phenethylammonium (PEA). The work of Li et al.19 involving the case of (PMA)2CuBr4 (PMA = C6H5CH2NH3+; phenylmethylammonium) suggests the importance of copper as the lead substitute that suitable for light-harvesting in thin-film solar cells.
Several experimental25,26 and theoretical27,28 studies have demonstrated that the organic ligand size of 2D-confined spacer layer plays a significant role in determining their charge carrier dynamics. In particular, Zhang-Rice singlet state has a crucial role in the low-energy signature of A-site ordered cuprate perovskites such as hole-doped high-Tc superconductivity29,30. Santoso et al.31 outline that a strong competition between spin singlet and triplet states occurs in the hole-doped cuprates, manifesting an anomalous spectral-weight transfer in their high-energy optical conductivity measurements31. Owing to the similar layered structure, the question arises as to whether the copper hybrid perovskites could exhibit such intriguing correlated electron-electron interactions. To date, a systematic study on the charge recombination profile as a function of alkylamonium spacers in a lead-free hybrid perovskite is still lacking.
Here, we systematically investigate the electronic transition across the unoccupied electronic state and emission properties of copper-based 2D-HOIPs with tunable insulating layers using high-resolution synchrotron X-ray absorption (XAS) and steady-state photoluminescence (PL) spectroscopies, supported by density functional theory (DFT) calculations. In this study, we unravel the correlation of the core-hole transition to its unoccupied states and the choice of ligand size. Apart from the conventional L2,3 absorption threshold peaks32, we attribute the emergence of four well-defined electronic transitions based on the XAS lineshape analyses. For example, the compounds containing short ligand such as MA and ethylammonium (EA) exhibit pronounced transitions originating from Cu 2p states to the respective 3d9L (~936.6 eV, where L denotes for chlorine hole), 3d8 configuration (~939.9 eV) and Cu 4s-3d hybridized states (~942.4 and ~946.0 eV). In addition, the admixture spin singlet and triplet states of these Cu-perovskite series is largely influenced by the annealing temperature. Furthermore, a photoinduced charge transfer dynamics investigation of A2CuCl4 compounds at the perovskite phase transition temperature suggests that different compositional ratio of free exciton and self-trapped exciton is achieved. The Stokes shifts of these compounds vary as the cation size increases, suggesting a modulation of the activation energy barrier between free exciton and self-trapped exciton states. DFT results reveal that the role of octahedral distortion is pronounced in (PMA)2CuCl4.
Results and discussion
Temperature-dependent XAS of copper-based hybrid perovskite with short chain spacers
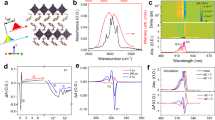
We perform temperature-dependent XAS measurements at the Cu L2,3 edge on (MA)2CuCl4 single crystal as depicted in Fig. 1a. Prior to examine the samples in the synchrotron measurements, we have characterized the structure, vibrational mode, and chemical state of the compounds (X-ray diffraction patterns, Raman spectra and X-ray photoemission spectroscopy) in Supplementary Figs. 1–3 respectively. The intense peak centered at ~932.9 eV is attributed to the Cu 2p3/2 → 3d transition (Cu L3), while the absorption peak at ~952.7 eV corresponds to the Cu 2p1/2 → 3d transition (Cu L2). These two peaks are the main features of the Cu L2,3 edge emerging from the 2p spin-orbit coupling interaction. Apart from those well-known absorption electronic transitions, we also observed other emergent peaks that centered at ~936.6 eV, ~939.9 eV, ~942.4 eV, and ~946.0 eV labeled as A1-A4, respectively. The first peak (A1) can be associated with the electronic transition from the Cu 2p states that resemble the signature of Zhang-Rice singlet state29,33,34,35.
Inset represent each of the optimized geometrical structure. a (MA)2CuCl4 absorption L-edge profile, indicating the coexistence of L2 and L3 absorption peak accompanied by the presence of d9 L and d9 signals. b (EA)2CuCl4 absorption L-edge with a pronounced spectral weight transfer. c (PMA)2CuCl4 absorption L-edge with strong suppression as the higher spectral feature are diminished. d (PEA)2CuCl4 absorption L-edge are depicted the L3 and d9 L competing interaction within the elevated temperatures. The temperature data represent 200 K (blue), 300 K (red), green (320 K), and magenta (340 K) respectively.
Here, we rationalize the observed peak due to the electronic transition of the ground state 3d9L to the cd10L excited state. L and c represent ligand hole and core hole, respectively. The second peak can be attributed to the typical signature of Cu in the high energy region (3d8 configuration) and the third peak correspond to the Cu 2p → 4s-3d transition36,37, while the fourth broaden peak is related to the electronic transition from the Cu 2p hybridized with the ligand p states to the Cu 4s-3d hybridized orbital38. As the samples were annealed at a higher temperature, we observed that the absorption intensities of the main features (Cu L2 and Cu L3 peaks) were decreased. However, this trend does not hold for the other emergent peaks, indicating that 3d9L, 3d8, and s-d hybridization are sensitive to the temperature variations. Here we notice that the line shape of 3d8 signature in (MA)2CuCl4 Cu L-edge XAS spectrum changed its intensity as the annealing temperature was lowered down to 200 K, whereas the core hole contribution (d9L) was slightly perturbed. Based on these findings, we attribute the spin singlet states to be prominently pronounced in the short chain spacer of copper perovskites.
We further discuss the evolution of emergent features of the Cu L3 and L2 edges in XAS spectra of (EA)2CuCl4 as shown in Fig. 1b. Interestingly, the absorption intensity of (EA)2CuCl4 has a substantial enhancement compared to the previous discussion on short chain spacer compounds. Particularly, these well-defined electronic transitions are strongly pronounced at 200 K. Thus, the intensities were gradually decreased when the annealing temperature reached ~340 K, coincided with the estimated transition temperature for Cu-series hybrid perovskites. Here we propose that the majority contribution originating from the spin triplet states rather than the singlet states within the experimental conditions. This effort introduces a strong and yet localized hybridization between 3d Cu and Cl 3p orbitals, accompanied by the weak coupling between the neighboring CuCl6 octahedron sheets. Structurally, the CH2 (methylene) moiety consists of two hydrogen atoms bound to a carbon atom. The covalent C–H bonding is dominated by the p character where the orbital is perpendicular with respect to the molecular plane, whereas the in-plane (σ-bond) direction is dominated by s character39. As the organic spacer is extended from MA to EA ligands, the extra sigma bond in the latter constructively increases its impact led to spectral changes as shown in the temperature-dependent XAS measurements. Based on these findings, we tentatively proposed that the additional –CH2 moiety span the organic ligand length inducing extra s states in this lead-free correlated hybrid perovskite electronic system.
Temperature-dependent XAS of copper-based hybrid perovskite with long chain spacers
We have performed a comparable XAS investigation on a longer conjugated organic spacer, namely, (PMA)2CuCl4 as shown in Fig. 1c. In contrast to (MA)2CuCl4 and (EA)2CuCl4 cases, the curvature of (PMA)2CuCl4 exhibited the weaken Zhang-Rice singlet states and featureless signals in the high energy range of 940–950 eV. Here, we consider that the absence of such signatures could be mediated by the substitution of a short chain spacer with a highly conjugated organic ligand. Moreover, the peak position of the Cu L3 and L2 features is shifted even further by ~0.4 eV to the higher energy compared to the corresponding features in (MA)2CuCl4. Here, we tentatively propose that mixed covalency character can be moderately controlled by increasing the ligand size of the organic spacer, thereby promoting strong localization on the core hole signals.
Interestingly, the incorporation of an extra CH2-chain onto the conjugated ligand spacer structure displayed a significant outcome as depicted in the temperature-dependent XAS measurements of (PEA)2CuCl4 in Fig. 1d (inset shown the corresponding structural arrangement). We notice that qualitatively, the line shape of the XAS spectra of (PEA)2CuCl4 is strikingly different compared to its counterpart ((PMA)2CuCl4), exhibiting a pronounced temperature-induced of Cu L3 intensity variation. Here, the curvature variation between L3 and d9L transitions strikingly depends on the temperature. For example, L3 signal is much more pronounced than that of d9L feature at 200 K (blue spectrum) and the absence of higher spectral signatures (beyond 940 eV). On the contrary, the reversal intensities on these signatures were observed at elevated temperatures. For example, d9L core holes are substantially increased with respect to the L3 features. We attribute these observations due to the competing interactions that arise between spin triplet and singlet states, which triggers the former to become dominant at 300 K and 340 K. Furthermore, these spectral weight transfer infers that Cu spins arrangements within the CuCl6 octahedron inducing local antiferromagnetic ordering at low temperature.
We further analyzed the full-width half maximum (FWHM) and peak positions to shed some light on the spectral weight transfer in this system as shown in Fig. 2a–d. For instance, we observe that the FWHM of d9 (blue square) and d9L (red circle) in short chain spacer (i.e. (MA)2CuCl4) increased as a function of temperatures as depicted in Fig. 2a, whereas the opposite trend was found in the long chain spacer (PMA)2CuCl4 as outlined in Fig. 2b. Similar behaviors were also pronounced in the peak positions profile shown in Fig. 2c, d. Interestingly, a plot of the integrated area of the short chains (Fig. 3a, b) and long chains (Fig. 3c, d) Cu-perovskites share comparable findings. It is obvious that temperature greatly influenced the proportion of respective electronic transitions, exhibiting abrupt spectral changes above 300 K. According to these extracted parameters, we believe careful consideration is required to shed some light on the role of mixed covalence states and spectral weight transfer governing the ground state d9L to the cd10 L excited state transitions. Such a finding could be useful to tailor the electronic properties of copper-hybrid perovskite using the organic ligand size effects5,16,19,26,27,40. In summary, we proposed that peculiar energetic transitions can be realized between the short versus long organic ligand spacer of copper-hybrid perovskite as schematically depicted in Fig. 3e. We further extend the investigations through optical measurement in the following sections.
The FWHM profile corresponds to the d9L (red circles) and d9 (blue squares) of (MA)2CuCl4 (a) and (PMA)2CuCl4 (b), respectively. The peak position variation corresponds to the d9L (top) and d9 (bottom) of (MA)2CuCl4 (c) and (PMA)2CuCl4 (d), respectively. Error bars are collected from the respective fitting results.
The evolution of d9L (red circles) and d9 (blue circles) of (MA)2CuCl4 (a), (EA)2CuCl4 (b), (PMA)2CuCl4 (c), and (PEA)2CuCl4 (d), respectively. Error bars are collected from the respective fitting results. (e) Schematic representation of spectral weight transfer of the short and long ligand spacers compounds. The arrows indicate the respective electronic transitions.
Optical response of copper-based hybrid perovskites as a function of temperatures
Steady-state PL measurements of these alkylammonium-based perovskite series suggest that the emission peak of (MA)2CuCl4 and (EA)2CuCl4 crystals do not vary significantly (Fig. 4a, b). On the contrary, the maxima of PL peak for the perovskite with a conjugated ligand spacer was blueshifted from 586 nm (2.12 eV) for (PMA)2CuCl4 to 537 nm (2.31 eV) for (PEA)2CuCl4 as depicted in Fig. 4c, d, respectively. This finding is in accordance with the previous reports on the lead iodide hybrid perovskite crystals25,40,41,42,43 and the corresponding theoretical works28,44,45,46. Furthermore, the FWHM of (PMA)2CuCl4 is determined to be ~48 nm, evidencing a narrow-band emission attributed to the recombination of free excitons12. On the other hand, the linewidth broadening of the other three cases shows typical FWHM in the range of 200 nm, which is comparable to the previous HOIPs reports15,40,47,48 and our recent work49. We associate that the occurrence of such broadband emission arises from the self-trapped excitons caused by strong carrier-phonon interaction within 2D-HOIPs structure25,41,42,43,50,51,52. The physical origin of such self-trapped excitons emission in 2D-alkylammonium copper halides is highly correlated to the Jahn-Teller effect resulted from the out-of-plane distortion within the Cu octahedra52,53. In addition, we also discuss further the absorption profile of the compounds in supplementary note 1 and Supplementary Fig. 4.
PL spectra and the deconvoluted excitonic signatures of (MA)2CuCl4 (a), (EA)2CuCl4 (b), (PMA)2CuCl4 (c), and (PEA)2CuCl4 (d), respectively. Raw PL data (black), donor bound exciton (red), free exciton (blue), self-trapped exciton (green), and fitting peak (cyan). Error bars are collected from the respective fitting results.
To shed some light on the excitonic recombination of the copper-based perovskites, the extracted integrated area from the temperature-dependent PL spectra of A2CuCl4 crystals are illustrated in Fig. 5. For example, the Gaussian fittings are implemented to deconvolute PL peaks with three components in Fig. 5a. For instance, we note that the PL measurement acquired in 200 K resulted in the first PL peak centered at 518 nm (FWHM = 102 nm and integrated area = 85050) and the second peak at 637 nm (FWHM = 247 nm and integrated area = 51252), respectively. The former signal corresponds to the formation of free-exciton emission, while the latter is considered as self-trapped exciton emissions. In addition, the red triangles correspond to the presence of donor-bound excitons. Here, we find that the free-exciton emission (blue squares, Fig. 5a–d) of alkylammonium and conjugated organic spacers do not change dramatically as a function of temperature. On the other hand, we observe that the corresponding self-trapped exciton emissions (green triangles) is slightly decreased close to 320 K for EA-, PMA-, and PEA-cases. Whereas the shortest chain (MA) displays a reasonable fluctuation at high temperature. Here, we reconcile that the self-trapping of photogenerated carriers within the CuCl6 octahedra is comprised of mutual interaction between emissive states and recombination pathways, which is much more feasible for the long spacers in these hybrid copper perovskites.
We further investigate the linewidth of the PL trends by comparing their FWHMs as a function of temperature (Fig. 6). In the case of free excitons signals, the FWHMs are gradually increasing for all samples. This can be rationalized due to the localized exciton at low temperature that thermally activated as temperature increases, which promotes the broadening of the spectral line shape. In contrast, self-trapped excitons emissions exhibit the absence of FWHM broadening as the temperature increases. With the exception, the longest chain compound in this study displays a reduction of ~50 nm in its FWHM. Moreover, the large Stokes shift can be realized between free-exciton and self-trapped exciton emissions. In addition, we note that such a Stoke difference becomes larger as the alkylammonium cation size increases (Supplementary Tables 1–4). For comparison, we include the extracted fitting parameters of donor bound excitons in Supplementary Tables 5 and 6 for alkyl-chains-ligand spacers and conjugated-chains-ligand spacers, respectively. Based on these findings, we consider that the organic spacer length of the A-site in copper-hybrid perovskites could be used to tune the activation energy barrier of the free excitons and self-trapped excitons states.
First principle calculations on the length-dependent of copper-based hybrid perovskites
To corroborate our experimental findings, we perform DFT calculations on (MA)2CuCl4, (EA)2CuCl4, (PMA)2CuCl4, and (PEA)2CuCl4. The optimized geometry, band structure, and projected density of states (PDOS) of each compound are summarized in Fig. 7. As previously discussed by Cortecchia et al.15, the lowest unoccupied molecular orbital (LUMO) which renders a conduction band in the minority spin is mainly comprised of Cu 3d orbital as Cu2+ involves an unpaired electron in its outer shell as outlined in Fig. 7a, b for (MA)2CuCl4 and (EA)2CuCl4, respectively. Here, we note that for (PMA)2CuCl4 and (PEA)2CuCl4 (Fig. 7c, d), there is a distinctive state above the LUMO originating from the C 2p orbital of the benzene ring. This indicates that the long organic spacers have more significant contributions to the charge carrier dynamics organic than the short ones46. In addition, the calculated electronic band gaps for (MA)2CuCl4, (EA)2CuCl4, (PMA)2CuCl4 and (PEA)2CuCl4 (1.83, 1.90, 1.85, and 1.89 eV, respectively) are in agreement with the UV-Vis absorption spectra and the calculated band structure (Supplementary Fig. 5). Therefore, we deduce that the chemical composition of the organic ligand in 2D-HOIPs structure does not change the band gaps significantly.
Table 1 summarizes the calculated lattice and geometrical parameters of (MA)2CuCl4, (EA)2CuCl4, (PMA)2CuCl4, and (PEA)2CuCl4 crystals. We find that the above parameters are in excellent agreement with the experimental values21,54,55,56. In this particular 2D-HOIPs structure, the coordinated Cu atoms to neighboring six Cl ligands form two type bonding, i.e., short and long equatorial Cu–Cl bonds that oriented perpendicular with respect to the apical (axial) Cu–Cl bonds. These bonds are strongly related to the formation of Cu–Cl–Cu bond angle, which indicates the presence of CuCl6 octahedron distortion and therefore act as a descriptor for a carrier lifetime of HOIPs28. It is generally accepted that a carrier lifetime of HOIPs can be predicted through the Cu–Cl–Cu angle as a parameter of the CuCl6 octahedron distortion. We note that the Cu−Cl−Cu angle of (PMA)2CuCl4 (157.2°) is the smallest among the studied compounds. Accordingly, (PMA)2CuCl4 is predicted to have the largest octahedral distortion and thus promotes the shortest carrier lifetime within the reported series. We also hypothesize that the previous discussion on the competing d9−d9L components and PL response resulted from direct consequence of the expansion of second equatorial bond length that more pronounced in (PMA)2CuCl4 crystals as schematically shown in Supplementary Fig. 6.
To strengthen our argument on the interplay of the electron-phonon couplings, we have performed molecular dynamics (MD) simulations to calculate the MSD for Cu, Cl, C atoms. As suggested by Gong et al.17, atomic displacements (essentially optical phonons) are important indicators of crystal rigidity, which is inversely proportional to the variation of electronic bandgap. Thus, this relation could be used to estimate the electron-phonon interactions within the two-dimensional perovskite structures. We have performed MD simulations to calculate the mean squared displacement (MSD) for Cl and Cu atoms, which respectively determine the valence band maxima and conduction band minima in the studied perovskites, along with a timeframe of 5 ps (Supplementary Fig. 7). For example, a hybrid perovskite crystal that exhibits a slow molecular motion leads to a greater rigidity, and thereby results in weaker electron-phonon interactions. According to our MD simulations, we found that (MA)2CuCl4 and (EA)2CuCl4 exhibit a lower MSD value (<2 Å2) than (PMA)2CuCl4 and (PEA)2CuCl4 (>2 Å2), inferring that the electron-phonon interactions in the short-spacer copper hybrid perovskite crystals are weak.
Conclusion
In conclusion, we summarize that the synchronous emergence of the structural transition, optical signature, and electronic modulation are present in the A2CuCl4 single crystals under variable temperature using combined photoluminescence and high-resolution synchrotron spectroscopies. The high-resolution XAS spectra at Cu L2,3 edge demonstrated that the implication of ligand size is clearly pronounced within the observed temperature range. Here, we observe peculiar linewidth variation of the d9 and d9L signature, involving the role of short-chain spacer (i.e. (MA)2CuCl4) as a function of temperatures. In the contrary, the opposite spectral weight transfer was found in the long-chain spacer (PMA)2CuCl4. Moreover, the reversal intensity ratio between d9L and L3 signal unambiguously suggests the presence of local-induced antiferromagnetic interaction between the neighboring Cu-inorganic sheets at 200 K.
Based on the temperature-dependent PL analyses, the hybrid compound with long conjugated organic ligand induces order-disorder structural phase transition resulting in the shift of emission peak close to room temperature. As a result, we observe large Stokes shift manifests large separation of free excitons and self-trapped excitons emission signals. In addition, the Stoke difference becomes larger as the organic spacer size increases. We attribute such optical response can be realized by tuning the activation energy barrier among the abovementioned defect states. This finding suggests that the geometric constriction argument promotes reduced structural fluctuations that unambiguously present in a longer conjugated organic space, thus it improves the carrier lifetime extensively. To strengthen the findings, DFT calculations and MD simulations shared similar insight in which the anomalous behavior is mainly influenced by the electronic properties of A2CuCl4 system due to the presence of large octahedral distortion. The future outcome from this study is promising since a tunable and yet correlated spin system can be realized via odd–even effects of the organic spacer. Further implication of this study is appealing to tailor the admixture spin singlet and triplet states towards the advancement of lead-free two-dimensional hybrid perovskites.
Methods
Synthetic growth of copper(II) hybrid-compounds
The method to grow (PEA)2CuCl4 perovskite single crystals were based on published literature57. A solution of copper (II) chloride dihydrate (CuCl2.2H2O, 1.70 g) in 10 mL of distilled water was mixed with 2-phenylethylamine hydrochloride (PEA, C8H12NCl, 3.15 g) containing 3–4 mL of 32% HCl. The mixture was stirred and heated up to 70 °C to achieve a homogeneous solution. After one hour, the solution was cooled down naturally to room temperature after which the crystallization emerged. This process was repeated until good-quality single crystals were obtained. A similar procedure was carried out to fabricate (PMA)2CuCl4, (EA)2CuCl4, and (MA)2CuCl4 by replacing the PEA precursor with PMA (phenylmethylamine hydrochloride, C7H10NCl, 2.86 g), EA (ethylamine hydrochloride, C2H8NCl, 1.67 g) and MA (methylamine hydrochloride CH6NCl, 1.35 g), respectively.
XAS measurements
Temperature-dependent X-ray absorption spectra at Cu L2,3 edge were examined within the photon energy range of 920-970 eV. A linearly polarized X-ray light was impinged onto a sample and the total electron yield method was implemented to collect the spectra. The measurements were performed under grazing incidence geometry, which can be varied by rotating the polar angle of the sample. The spectra were normalized to the integrated intensity spectra after subtracting an energy-independent background. The linear polarization factor of the X-ray beam was determined to be more than 90% with a photon energy resolution of 100 meV. XAS spectra were first normalized to the incident photon intensity (I0) monitored by a refocusing mirror. The penetration depth of soft X-ray measured with the total electron yield method is generally obtained in 2-4 nm range set by the mean free path of low energy (E < ~10 eV) secondary electrons created in the scattering process58. The temperature-dependent XAS measurements were carried out in the soft X-ray and ultraviolet (SUV) beamline of Singapore Synchrotron Light Source (SSLS)59.
PL and optical absorption measurements
Temperature-dependent PL measurements were performed at a temperature range of 200–350 K using free-space excitation and collection through a visible-near-infrared microscope objective (5×, NA = 0.15). The samples were excited with a ps-pulsed ytterbium fiber laser emitting at a high harmonic generation of 266 ± 1 nm wavelength with 10 MHz repetition rate. Photoluminescence spectra were detected using thermoelectric-cooled Avaspec HERO spectrometer. Absorption spectra were obtained using ultraviolet-visible light (UV-Vis) spectrometer (Shimadzu, Model UV-2450).
X-ray diffraction measurements
High-resolution X-ray diffractometry characterization for the samples was performed at the X-ray Demonstration and Development beamline at SSLS. All diffraction measurements were carried out at room temperature. X-ray diffractograms data acquisition was done in two-axis mode with a step size of 0.02° over a Bragg angle range of 10-80°.
High-resolution X-ray photoemission measurements
Room temperature X-ray photoemission experiments were carried out in an ultrahigh vacuum chamber with a typical base pressure of 1 × 10−10 mbar in the Surface, Interface, and Nanostructure Science beamline at the Singapore Synchrotron Light Source. The photon energy of 60 eV was used to determine the valence band spectra. The photoemission spectra were acquired in normal emission geometry and collected using a VG Scienta R4000 analyzer60,61.
Raman spectroscopy
The Raman vibration modes were measured using Alpha 300 R (WITec focus innovations) with an excitation wavelength of 532 nm and 37 μW continuous-wave laser at room temperature. The microscope objective has a numerical aperture of NA = 0.8 (Olympus 100×). The Raman microscope was operated at the diffraction limit with a laser spot size of fewer than 1 μm. The measurements were carried out in backscattering geometry.
DFT calculations
Spin-polarized calculations were performed with relaxed spin-multiplicity under the Kohn–Sham formulation62,63 as implemented in the Vienna Ab–initio Simulation Package (VASP)54,55. The projector augmented wave (PAW) method56,64 was employed to describe the interaction between ion cores and electrons. The electron exchange-correlation was treated by the generalized gradient approximation (GGA) based on the Perdew-Burke-Ernzerhof (PBE) functional65. A rotationally invariant GGA + U approach introduced by Dudarev et al.66 was used with an effective Hubbard parameter Ueff being 7.5 eV for the Cu d orbital, as suggested by Cortecchia et al15. The plane-wave basis sets with cut-off energy of 500 eV were employed for all calculations. Brillouin zone sampling centered at the Γ point was set to 2 × 2 × 2, 1 × 2 × 2, 2 × 2 × 1, and 2 × 2 × 1, respectively for (MA)2CuCl4, (EA)2CuCl4, (PMA)2CuCl4 and (PEA)2CuCl4. The conjugate gradient method was employed for cell optimizations and the calculations were considered to converge when the maximum forces on each atom were less than 0.01 eV/Å. During calculations, all atoms were allowed to fully relax. One monoclinic unit-cell of (MA)2CuCl4 and one orthorhombic unit-cell of the corresponding (EA)2CuCl4, (PMA)2CuCl4, and (PEA)2CuCl4 were used for the calculations. MD simulations were carried out with a time step of 1 fs within the NVT ensemble using the Nosé-Hoover thermostat as implemented in the VASP package. All atoms were allowed to equilibrate for 2 ps at a temperature of 300 K. Subsequent statistical sampling was then carried out for another 3 ps. Mean squared displacement (MSD) were obtained from the MD simulations using the following formula:
Data availability
All data generated or analyzed during this study are included in the published article and the Supplementary Information and are available from the corresponding authors upon reasonable request.
References
Mao, L. et al. Structural diversity in white-light-emitting hybrid lead bromide perovskites. J. Am. Chem. Soc. 140, 13078–13088 (2018).
Katan, C., Mercier, N. & Even, J. Quantum and dielectric confinement effects in lower-dimensional hybrid perovskite semiconductors. Chem. Rev. 119, 3140–3192 (2019).
Grancini, G. & Nazeeruddin, M. K. Dimensional tailoring of hybrid perovskites for photovoltaics. Nat. Rev. Mater. 4, 4–22 (2019).
deQuilettes, D. W. et al. Charge-carrier recombination in halide perovskites. Chem. Rev. 119, 11007–11019 (2019).
Cheng, P. et al. Ligand-size related dimensionality control in metal halide perovskites. ACS Energy Lett. 4, 1830–1838 (2019).
Day, P., Gillespie, R. J. & Day, P. Organic-inorganic layer compounds: physical properties and chemical reactions. Philos. T. R. Soc. A 314, 145–158 (1985).
Mitzi, D. B., Chondroudis, K. & Kagan, C. R. Design, structure, and optical properties of organic−inorganic perovskites containing an oligothiophene chromophore. Inorg. Chem. 38, 6246–6256 (1999).
Mitzi, D. B., Field, C. A., Harrison, W. T. A. & Guloy, A. M. Conducting tin halides with a layered organic-based perovskite structure. Nature 369, 467–469 (1994).
Calabrese, J. et al. Preparation and characterization of layered lead halide compounds. J. Am. Chem. Soc. 113, 2328–2330 (1991).
Straus, D. B. & Kagan, C. R. Electrons, excitons, and phonons in two-dimensional hybrid perovskites: connecting structural, optical, and electronic Properties. J. Phys. Chem. Lett. 9, 1434–1447 (2018).
Gao, Y. et al. Molecular engineering of organic–inorganic hybrid perovskites quantum wells. Nat. Chem. 11, 1151–1157 (2019).
Ishihara, T., Takahashi, J. & Goto, T. Optical properties due to electronic transitions in two-dimensional semiconductors (CnH2n+1NH3)2PbI4. Phys. Rev. B 42, 11099–11107 (1990).
Hong, X., Ishihara, T. & Nurmikko, A. V. Dielectric confinement effect on excitons in PbI4-based layered semiconductors. Phys. Rev. B 45, 6961–6964 (1992).
Willett, R. D., Gómez-García, C. J. & Twamley, B. Long-range order in layered perovskite salts – structure and magnetic properties of [(CH3)2CHCH2NH3]2CuX4 (X = Cl, Br). Eur. J. Inorg. Chem. 2012, 3342–3348 (2012).
Cortecchia, D. et al. Lead-free MA2CuClxBr4–x hybrid perovskites. Inorg. Chem. 55, 1044–1052 (2016).
Kamminga, M. E. et al. Confinement effects in low-dimensional lead iodide perovskite hybrids. Chem. Mater. 28, 4554–4562 (2016).
Gong, X. et al. Electron–phonon interaction in efficient perovskite blue emitters. Nat. Mater. 17, 550–556 (2018).
Jang, S. E., Kim, M. J. & Lim, A. R. Structural geometry of the layered perovskite-type (CH3CH2CH2NH3)2CuCl4 single crystal near phase transition temperatures. AIP Adv. 8, 105324 (2018).
Li, X. et al. (C6H5CH2NH3)2CuBr4: A lead-free, highly stable two-dimensional perovskite for solar cell applications. ACS Appl. Electron. Mater. 1, 2709–2716 (2018).
Marongiu, D., Saba, M., Quochi, F., Mura, A. & Bongiovanni, G. The role of excitons in 3D and 2D lead halide perovskites. J. Mater. Chem. C 7, 12006–12018 (2019).
Mauck, C. M. & Tisdale, W. A. Excitons in 2D organic-inorganic halide perovskites. Trends Chem. 1, 380–393 (2019).
Polyakov, A. O. et al. Coexisting ferromagnetic and ferroelectric order in a CuCl4-based organic–inorganic hybrid. Chem. Mater. 24, 133–139 (2012).
Nugroho, A. A. et al. Cross-type orbital ordering in the layered hybrid organic-inorganic compound (C6H5CH2CH2NH3)2CuCl4. Phys. Rev. B 94, 184404 (2016).
Tsai, H. et al. High-efficiency two-dimensional Ruddlesden–Popper perovskite solar cells. Nature 536, 312–316 (2016).
Zhang, S.-F., Chen, X.-K., Ren, A.-M., Li, H. & Bredas, J.-L. Impact of organic spacers on the carrier dynamics in 2D hybrid lead-halide perovskites. ACS Energy Lett. 4, 17–25 (2019).
Yin, J. et al. Tuning hot carrier cooling dynamics by dielectric confinement in two-dimensional hybrid perovskite crystals. ACS Nano 13, 12621–12629 (2019).
Leveillee, J. et al. Tuning electronic structure in layered hybrid perovskites with organic spacer substitution. Nano Lett. 19, 8732–8740 (2019).
Ghosh, D., Neukirch, A. J. & Tretiak, S. Optoelectronic properties of two-dimensional bromide perovskites: influences of spacer cations. J. Phys. Chem. Lett. 11, 2955–2964 (2020).
Meyers, D. et al. Zhang-Rice physics and anomalous copper states in A-site ordered perovskites. Sci. Rep. 3, 1834–1834 (2013).
Meyers, D. et al. Competition between heavy fermion and Kondo interaction in isoelectronic A-site-ordered perovskites. Nat. Commun. 5, 5818 (2014).
Santoso, I. et al. Unraveling local spin polarization of Zhang-Rice singlet in lightly hole-doped cuprates using high-energy optical conductivity. Phys. Rev. B 95, 165108 (2017).
Arramel et al. Electronic modulation in site-selective occupation of quasi-2D triangular-lattice Cs2CuCl4-xBrx perovskite probed by surface-sensitive characterization. ACS Appl. Mater. Interfaces 12, 4114–4122 (2020).
Grioni, M. et al. Studies of copper valence states with CuL3 x-ray-absorption spectroscopy. Phys. Rev. B 39, 1541–1545 (1989).
Chen, C. T. et al. Electronic states in La2-xSrxCuO4+δ probed by soft-x-ray absorption. Phys. Rev. Lett. 66, 104–107 (1991).
Bianconi, A. et al. Linearly polarized CuL3-edge x-ray-absorption near-edge structure of Bi2CaSr2Cu2O8. Phys. Rev. B 44, 10126–10138 (1991).
Carniato, S., Luo, Y. & Ågren, H. Theoretical Study of the Near-Edge Cu L X-ray Absorption Spectrum of Copper Phthalocyanine. Phys. Rev. B 63, 085105 (2001).
Stepanow, S. et al. Giant spin and orbital moment anisotropies of a Cu-phthalocyanine monolayer. Phys. Rev. B 82, 014405 (2010).
van der Laan, G., Pattrick, R. A. D., Henderson, C. M. B. & Vaughan, D. J. Oxidation state variations in copper minerals studied with Cu 2p X-ray absorption spectroscopy. J Phys. Chem. Solids 53, 1185–1190 (1992).
Harrison, J. F. Structure of methylene. Acc. Chem. Res. 7, 378–384 (1974).
Gan, L., Li, J., Fang, Z., He, H. & Ye, Z. Effects of organic cation length on exciton recombination in two-dimensional layered lead iodide hybrid perovskite crystals. J. Phys. Chem. Lett. 8, 5177–5183 (2017).
Cortecchia, D. et al. Broadband emission in two-dimensional hybrid perovskites: the role of structural deformation. J. Am. Chem. Soc. 139, 39–42 (2017).
Straus, D. B. et al. Longer cations increase energetic disorder in excitonic 2D hybrid perovskites. J. Phys. Chem. Lett. 10, 1198–1205 (2019).
Liu, G. et al. Influence of the organic chain on the optical properties of two-dimensional organic–inorganic hybrid lead iodide perovskites. ACS Appl. Electron. Mater. 1, 2253–2259 (2019).
Quarti, C., Marchal, N. & Beljonne, D. Tuning the optoelectronic properties of two-dimensional hybrid perovskite semiconductors with alkyl chain spacers. J. Phys. Chem. Lett. 9, 3416–3424 (2018).
Maheshwari, S., Savenije, T. J., Renaud, N. & Grozema, F. C. Computational design of two-dimensional perovskites with functional organic cations. J Phy Chem C 122, 17118–17122 (2018).
Madjet, M. E., Berdiyorov, G. R. & Ashhab, S. Effect of organic spacers on electronic, optical and transport properties of two-dimensional layered lead-halide perovskites. Comput. Mater. Sci. 169, 109130 (2019).
Braun, M., Tuffentsammer, W., Wachtel, H. & Wolf, H. C. Tailoring of energy levels in lead chloride based layered perovskites and energy transfer between the organic and inorganic planes. Chem. Phys. Lett. 303, 157–164 (1999).
Smith, M. D., Connor, B. A. & Karunadasa, H. I. Tuning the luminescence of layered halide perovskite. Chem. Rev. 119, 3104–3139 (2019).
Naradipa, M. A. et al. Spin correlated-plasmons at room temperature driven by electronic correlations in lead-free 2D hybrid organic-inorganic perovskites. J. Phys. Chem. C 124, 14272–14278 (2020).
Toyozawa, Y. Excitonic instabilites of deformable lattice from self-trapping to phase transition. Acta Phys. Pol. 87, 47–56 (1995).
Dohner, E. R., Jaffe, A., Bradshaw, L. R. & Karunadasa, H. I. Intrinsic white-light emission from layered hybrid perovskites. J. Am. Chem. Soc. 136, 13154–13157 (2014).
Smith, M. D., Jaffe, A., Dohner, E. R., Lindenberg, A. M. & Karunadasa, H. I. Structural origins of broadband emission from layered Pb–Br hybrid perovskites. Chem. Sci. 8, 4497–4504 (2017).
Zolfaghari, P., de Wijs, G. A. & de Groot, R. A. The electronic structure of organic–inorganic hybrid compounds: (NH4)2 CuCl4, (CH3NH3)2CuCl4 and (C2H5NH3)2 CuCl4. J. Phys. Condens. Matter. 25, 295502 (2013).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Arkenbout, A. H. Organic-inorganic hybrids: A route towards soluble magnetic electronics. PhD Thesis. University of Groningen (2010).
Stöhr, J. NEXAFS Spectroscopy. Springer-Verlag Berlin Heidelberg GmbH (1992).
Yu, X. J., Diao, C. Z., Venkatesan, T., Breese, M. B. H. & Rusydi, A. A soft x-ray-ultraviolet (SUV) beamline and diffractometer for resonant elastic scattering and ultraviolet-vacuum ultraviolet reflectance at the Singapore synchrotron light source. Rev. Sci. Instrum. 89, 113113 (2018).
Yu, X. et al. New soft X-ray facility SINS for surface and nanoscale science at SSLS. J. Electron. Spectrosc. 144-147, 1031–1034 (2005).
Yu, X. J., Chi, X., Wee, A. T. S., Rusydi, A. & Breese, M. B. H. A scripting LabVIEW based program for experiment automation in synchrotron radiation applications. Rev. Sci. Instrum. 90, 103902 (2019).
Kohn, W. & Sham, L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, A1133–A1138 (1965).
Hohenberg, P. & Kohn, W. Inhomogeneous electron gas. Phys. Rev. 136, B864–B871 (1964).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Dudarev, S. L., Botton, G. A., Savrasov, S. Y., Humphreys, C. J. & Sutton, A. P. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Phys. Rev. B 57, 1505–1509 (1998).
Pabst, I., Fuess, H. & Bats, J. W. Structure of monomethylammonium tetrachlorocuprate at 297 and 100 K. Acta, Cryst, C 43, 413–416 (1987).
Steadman, J. P. & Willett, R. D. The crystal structure of (CH5NH3)2CuCl4. Inorg. Chim. Acta 4, 367–371 (1970).
Kimishima, Y. Successive phase transitions in 2D-XY ferromagnet (C6H5CH2NH3)2/CuCl4. Jpn. J. Appl. Phys. 26, 867 (1987).
Acknowledgements
Xiaojiang Yu is appreciated for his technical support in the Singapore Synchrotron Light Source (SSLS). The authors acknowledge the Singapore Synchrotron Light Source (SSLS) for providing the facility necessary for conducting the research. The laboratory is a National Research Infrastructure under the National Research Foundation Singapore. This work is financially supported by several funding agencies. Thus, authors have acknowledged research grants from Ministry of Education, Singapore with numbers MOE Tier 3 (MOE2014-T3-1-004) and MOE Tier 2 (MOE2018-T2-1-088, MOE2016-T2-1-052, and MOE2019-T2-1-163) and MOE2019-T1-002-063. A. acknowledges funding support from NRF-NSFC grant R-144-000-405-281. M. H. M. acknowledges a research fund from Institut Teknologi Bandung through the “Riset Unggulan Pusat Penelitian ITB 2020” program. D. O. acknowledges 079 /SP2H/LT/DRPM/2021. The computations were carried out by using the high-performance computing facility at the Research Center for Nanoscience and Nanotechnology, Institut Teknologi Bandung.
Author information
Authors and Affiliations
Contributions
A.A. and A.R. conceived the project. M.A. and D.O. synthesized the perovskite single crystals. A.D.F., X.Y., C.S.T., C.D., and A.R. performed X-ray absorption spectroscopy measurements. M.D.B. carried out photoluminescence and optical absorption experiments. A.A., X.Y., and C.S.T. carried out X-ray photoemission spectroscopy measurements. A.A. and M.F.S. carried out Raman scattering experiments. M.H.M. performed density functional theory calculations. G.S. calculated MD simulations. H.W. and A.T.S.W. contributed to the fruitful discussions. All the authors were involved in the discussion and manuscript preparation. All authors have given their approval for the final version of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Communications Materials thanks the anonymous reviewers for their contribution to the peer review of this work. Primary Handling Editors: Aldo Isidori. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Arramel, A., Fauzi, A.D., Yin, X. et al. Ligand size effects in two-dimensional hybrid copper halide perovskites crystals. Commun Mater 2, 70 (2021). https://doi.org/10.1038/s43246-021-00175-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-021-00175-6