Abstract
The dehydration of gypsum to hemihydrate has been studied for decades because it is an important model reaction for understanding fluid-triggered earthquakes, and due to the global use of plaster of Paris in the construction industry. The dehydration kinetics of gypsum strongly depend on temperature and water vapour pressure. Here, we perform fast, time-resolved synchrotron X-ray scattering on natural alabaster samples, finding that a small elastic load accelerates the dehydration reaction significantly. The mechanical acceleration of the reaction consumes about 10,000 times less energy than that due to heating. We propose that this thermodynamically surprising finding is caused by geometry-energy interactions in the microstructure, which facilitate nucleation and growth of the new crystalline phase. Our results open research avenues on the fundamental thermo-mechanics of crystal hydrates and the interaction of stress and chemical reactions in crystalline solids with a wide range of implications, from understanding dehydration-triggered earthquakes to the energy-efficient design of calcination processes.
Similar content being viewed by others
Introduction
The calcium sulphate dihydrate gypsum (CaSO4·2H2O) is the most common sulphate evaporite mineral on our planet1. Sulphate evaporites play an important role in Earth’s sulphur cycle and are primary recorders of geochemical fluxes through time2,3. Upon heating, gypsum gradually loses its water, transforming into the hemihydrate, also known as bassanite, (CaSO4·0.5H20) and anhydrite (CaSO4). While gypsum and anhydrite deposits are common on Earth, bassanite is unstable at its surface1. However, bassanite, as well as gypsum, deposits have been detected on Mars, and their origin remains a matter of ongoing debate4,5,6,7. The gypsum-hemihydrate transformation has been long studied as a laboratory analogue for seismogenic dehydration reactions during subduction8,9 and as a model of metamorphic dehydration reactions per se10,11. Hemihydrate, often referred to as plaster of Paris, has been used by humans for centuries. The modern construction industry alone produces ~100 billion kg of hemihydrate per year globally by gypsum calcination7. It serves as binder in cement, mortars, and stucco, and orthopaedicians employ it for the immobilisation of fractured limbs12,13. In the US, 47% of the domestically mined and synthesised gypsum supplies are calcined to hemihydrate to be used as plaster14. Due to the vast scale of production, its high energy demands and the significant CO2 footprint of gypsum calcination (ca. 76 kg of CO2 per ton of gypsum15), it is desirable to improve the efficiency of the dehydration procedure7. All in all, there is a clear need to improve our understanding of the physical controls on the kinetics of the gypsum-hemihydrate transformation.
The rate of the gypsum-hemihydrate transformation is dominantly controlled by temperature, T, and the water vapour pressure in the reaction environment, pH2O16,17,18. A temperature increase causes an exponential increase in reaction rate \(\kappa\) according to the Arrhenius relation \(\kappa =A{{\rm{e}}}^{-E/\left({RT}\right)}\) where \(A\) is a reaction-specific constant, \(R\) is the universal gas constant, and \(E\) is the activation energy. Increasing pH2O in the sample environment slows down the evacuation of H2O from the crystalline phase and results in a negative correlation of pH2O with \(\kappa\)18. In contrast, the effect of mechanical stress on gypsum dehydration kinetics is not well understood. A single study on high-pressure dehydration of single crystals, conducted in the pressure range 343–1085 MPa using a diamond anvil cell under water-saturated conditions19, found that a pressure increase decreases the reaction rate. This result contrasts with the conclusions of a comprehensive study on the effects of confining pressure, pc, and pore-fluid pressure, pf, on dehydration kinetics of natural gypsum rock (Volterra alabaster)20, performed on cylindrical specimens (20 × 50 mm) in a triaxial stress apparatus. It turned out that the reaction rate is negatively correlated with pf, consistent with the rate-inhibiting impact of pH2O, whereas pc has a negligible effect.
Triaxial dehydration experiments are usually conducted under constant-stress load (often to >100 MPa20), which causes complex interactions between the transient hydraulic, chemical, and mechanical processes in gypsum samples20,21,22. Whereas without large confining stresses the shrinking of the denser dehydrated phase produces ~30% porosity, the dehydration-induced pore network collapses under high constant-stress load9. Therefore, the evolving drainage network loses connectivity, and micro-regions of high pore-fluid pressure can form, which in turn decelerate the reaction dramatically and possibly lead to hydraulic fracturing21,22. Under constant-stress boundary conditions it is thus difficult to separate the effect of mechanical stress on kinetics from the coupled chemo-hydraulic-mechanical processes. This is further compounded by the need to infer the progress of dehydration from proxies, usually the measured volume of expelled excess fluid20,21,22. This method is not sensitive enough to capture the onset of dehydration and generally leads to an underestimation of the dehydration rate11.
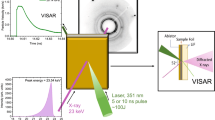
To overcome these challenges, we conducted in-situ experiments using time-resolved synchrotron X-ray scattering techniques specifically designed to investigate and quantify the impact of stress on the dehydration kinetics of the gypsum-hemihydrate transformation11. Dehydration of axially pre-stressed, heated discs of natural gypsum rock (Volterra alabaster) was monitored in a purpose-built loading cell while collecting 2D small- and wide-angle X-ray scattering patterns11 (SAXS/WAXS, Fig. 1). Experiments were performed at controlled temperature in the elastic differential pre-stress regime (Δσ), such that the resulting pore network could evolve freely, and the sample did not fracture macroscopically. Details of the pre-stress regime are discussed in Supplementary Note 1. Our experiments provide unambiguous evidence that dehydration kinetics and differential stress are coupled. For the examined dehydration temperatures of 129 °C and 142 °C, the pre-stressed samples dehydrate about two times faster than their low-stress equivalents (Fig. 2, Supplementary Table 1). 3D grain-scale numerical models demonstrate that the elastic differential pre-stress combined with internal stresses due to the elastic anisotropy of the gypsum grains produce substantial, geometrically controlled stress perturbations at the grain scale (Fig. 3). It is hypothesised that these stress perturbations explain the observed acceleration of the dehydration reaction, as predicted theoretically more than thirty years ago23.
Diffraction patterns at small and wide scattering angles are collected with two separate detectors. The SAXS detector covers the centre of transmitted beam masked by the beam stop (Fig. 2). The threaded piston is used to apply a small elastic pre-stress to the sample, approximating a constant-displacement load.
Upper row a, c, e, g: pairs of 2D SAXS and WAXS maps of unreacted Volterra alabaster for low- and high-stress experiments (see map titles) at T = 129 °C ± 2.5 °C (a, c) and T = 142 °C ± 2.5 °C (e, g). The colour scale maps the decadic logarithm of raw intensity in the interval [0; 6] where blue denotes low values and red high ones. Characteristic gypsum reflections are annotated and marked with white arrows, indexed according to space group C2/c32. Centre row b, d, f, h: pairs of 2D SAXS/WAXS maps for the reacted samples. Selected hemihydrate reflections are annotated and marked by white arrows, indexed in space group I231. i, j Conversion curves as a function of time showing reaction progress for low- (white circles) and high-stress (grey squares) experiments at T = 129 °C ± 2.5 °C on the left (i), and at T = 142 °C ± 2.5 °C on the right (j). Error bars for time and conversion fraction are smaller than the symbol size and thus not shown. Orange markers indicate datapoints at induction time (α = 0.05) and green ones those at the characteristic time (α = 0.63). The orange and green double arrows above the plot boxes indicate the differences in induction and characteristic times, respectively. The induction time is often interpreted as the time required for the formation of critical nuclei and growth to detectable size while the period thereafter involves crystal growth from those nuclei33,34. The characteristic time denotes the inverse of the kinetic rate constant for exponential conversion models35,36.
a Numerical simulation of grain-boundary normal contact stresses for a polycrystalline model cube with an edge length of 1 mm under a constant-displacement load (black arrow) equivalent to the one applied to our samples. For simplicity, a polygonal foam microstructure is used. Model grains have the anisotropic elastic properties of gypsum26 with randomly oriented crystallographic axes. Several model grains have been removed to unveil the model interior. Tensile stresses are negative and shown in blue colours. The white circle with the minus-sign marks a grain boundary at low angle to shortening under tensile loading. Compressive stresses are positive. The plus-sign in a white circle marks a grain boundary at high angle to the shortening direction, which accordingly is in compression. Completely white grain boundaries are located at the outer surfaces of the model cube and thus have no contact stress. b Visualisation of grain-boundary segments that formed incipient grain-boundary cracks. The colour scale is the same as in a and shows the opening displacement over the interval [2; 30] nm. As expected37, grain-boundary cracking commences at grain vertices and triple lines. From these locations, cracks preferentially propagate across grain interfaces sub-parallel to the loading direction.
Results
2D SAXS/WAXS patterns
We report the results of four dehydration experiments (Fig. 2, Supplementary Table 1). Two pre-stresses, low (hand-tight) and high (estimated Δσ <5 MPa in the sample centre, well below the unconfined compressive strength of 25 MPa of Volterra alabaster22), were used at two different dehydration temperatures, 129 °C and 142 °C (Fig. 2). For each temperature and pre-stress condition, a time series of 2D SAXS/WAXS patterns was acquired, recording X-rays scattered inside a small interrogation volume in the sample centre. The SAXS/WAXS patterns reflect the evolution of nano-structural features in the scale range from 0.15 to 23 nm, which covers characteristic Bragg reflections of gypsum and hemihydrate (Fig. 2a–h) as well as the development of nano-porosity and nano-crystallites of hemihydrate11. Analysis of Bragg reflections enabled in situ tracking of the lattice transformation during dehydration (Fig. 2i, j; see Methods for details).
For three experiments, gypsum fully converted to hemihydrate (Fig. 2c–h). Only the low-stress experiment at T = 129 °C retained ~1% of gypsum in the sample centre11 (Fig. 2a, b). The Bragg reflections of the unreacted samples form patchy rings (Fig. 2a, c, e, g), indicating random orientation of grains of a number insufficient to form a powder-like truly isotropic pattern24. The (020)-reflection of the gypsum sample used at T = 129 °C and low pre-stress exhibits a noticeable gap in the upper-left quadrant of the (020)-ring, indicating the local alignment of grains in this specific interrogation point (Fig. 2a). As a result of this alignment, local micro-strains, expressed by changes of the width and height of the azimuthally integrated growing hemihydrate (110)-peak24, lead to fluctuations of the 1D conversion curve (black circles in Fig. 2i). Azimuthal intensity variations along the hemihydrate (110)-ring are noticeable in Fig. 2b but perhaps not obvious because of the logarithmic colour scale. The conversion curve for a second, adjacent interrogation point of the same sample with a more uniform microfabric exhibits less fluctuations and shows similar kinetics (Supplementary Fig. 2) because the micro-strains are averaged out. The homogenisation of the Bragg rings in the product (Fig. 2b, d, f, h) indicates growth of smaller, randomly oriented hemihydrate grains, confirmed by ex-situ imaging of the samples (Supplementary Figs. 3 and 4). The high-intensity SAXS region around the beam stop contains scattering due to nano-pores, and in the reacting samples, to a smaller degree, also due to nano-crystallites of hemihydrate embedded in gypsum grains11. In the unreacted samples, the SAXS iso-intensity profiles are nearly circular (with aspect ratio ≤1.03), suggesting random orientation of nano-pores. The corresponding SAXS patterns of reacted samples display a significant increase in intensity caused by growth of nano-pores and nano-crystallites11. In the low-stress experiments, the iso-intensity profiles remain almost circular, with aspect ratios ≤1.05 (Fig. 2b, f). In contrast, their high-stress counterparts have an aspect ratio of ~1.16, which indicates preferential growth of anisotropic nano-pores and/or nano-crystallites along the radial real-space direction under the increased Δσ. The nano-scale tubular structures parallel to the long axes of the elongated hemihydrate grains (Supplementary Figs. 3 and 4) and radially propagating nano-scale voids inclined relative to the incident beam could be the physical cause of the observed anisotropic scattering pattern.
Dehydration kinetics
The striking impact of Δσ on kinetics is revealed by the conversion curves (Fig. 2i, j, see Methods for definition). At both temperatures, increased Δσ accelerates the dehydration reaction by a factor of about 2, as measured by the induction and characteristic times (Fig. 2i, j, Supplementary Table 1). Therefore, higher Δσ promotes both the formation and subsequent growth of nuclei. The conversion curve for T = 129 °C at high pre-stress is very similar to the one at T = 142 °C and low pre-stress. Thus, one can compare the energy needed to accelerate the dehydration reaction by a factor of 2, at T = 129 °C and low stress, through heating or elastic straining. Most significantly, accelerating the dehydration by heating turns out to be more than 10,000 times more expensive energetically than doing so via pre-stress (Supplementary Note 1). The dramatic impact of pre-stress on kinetics does neither depend on nor alter the microphysical dehydration mechanisms, as revealed by post-mortem analyses of scanning-electron microscope images (Supplementary Note 2, Supplementary Figs. 3 and 4).
Discussion
Why does a small differential stress Δσ accelerate dehydration? The answer probably lies in the microstructure of the material. Volterra alabaster contains randomly oriented gypsum grains25 with significant elastic anisotropy26. Nucleation of hemihydrate is common within the vacancy-rich water layer of the (010)-plane in the gypsum parent, especially where this plane intersects crystal edges16. Since the critical resolved shear stress on the (010)-plane is ca. 0.5 MPa at low confining pressure27, it is likely that suitably oriented (010)-planes slip slightly under pre-stress (Fig. 3a), which in turn may promote nucleation by producing new vacancies and vacancy clusters16. Moreover, any pre-stress loading results in heterogeneous grain-scale stresses caused by geometric mismatch of the anisotropically deforming, randomly oriented grains (Fig. 3, Supplementary Note 3). The resulting local contact stresses may be normal to grain boundaries, especially on interfaces at a high angle to the compression direction, whereas most grain boundaries sub-parallel to the pre-stress direction are under local tension (Fig. 3a) and may start to crack at higher Δσ (Fig. 3b). The observed anisotropy of the final SAXS iso-intensity patterns at high Δσ attests to stress-controlled formation of anisotropic nano-scale structures, such as radially growing inclined cracks or hollow hemihydrate nano-crystallites, in our samples. Increased normal stresses on grain boundaries enhance the chemical potential gradient and fluid pressure gradient locally, which can accelerate the transformation20,23,28,29. Therefore, we hypothesise that the high elastic pre-stress promotes local dissolution of gypsum at grain-interface regions with high contact stresses and facilitates subsequent transport to and precipitation near those with low or tensile contact stresses. This prediction can be tested by examining gypsum rocks with a strong crystallographic preferred orientation such as satin spar. In such materials, transformation kinetics should be less sensitive to pre-stress.
Our results imply that elastic stresses can accelerate dehydration reactions dramatically in crystalline solids with randomly oriented grains. This notion supports the call for the development of a thermodynamically consistent model for the coupling of stress and reaction kinetics in such materials28; it should also inspire a new class of kinetic experiments that explores the effect of small elastic stresses on mineral transformations systematically. Our results hint at a potentially ubiquitous geometric thermodynamic effect of a polycrystalline microstructure. Finally, this work should open new research avenues for the energy-efficient design of calcination processes for gypsum and other solids.
Methods
Starting material
We dehydrated discs of natural alabaster from Volterra, Italy, with a diameter of 10 mm and a thickness of 1 mm. Volterra alabaster is a standard material in experimental rock mechanics because of its small grain size, low porosity, and purity9,20,22,25. This alabaster consists of randomly oriented, subhedral, tabular gypsum grains with a mean grain size that varies on the scale of centimetres and is generally in the range of 45–123 μm25. A representative image of the unreacted alabaster is shown in Supplementary Fig. 4a.
Beamline set-up and data processing
We used the pinhole-geometry SAXS/WAXS beamline at the ANSTO Australian Synchrotron described in Kirby, et al.30. A 3 m-long, 22 mm-period in-vacuum undulator source (Kmax of 1.6 at 6.6 mm minimum insertion device gap) and a flat Si(111) double-crystal monochromator provide a photon flux of up to 1013 photons per second in the energy range from 5 to 20 keV. X-ray energy of 16 keV, corresponding to the photon wavelength of 0.775 Å, was used in all experiments. Focusing is achieved with a KB mirror pair with Si, Rh, and Pt stripes for harmonic rejection. Four monochromatic slits allow flexible adjustment of the collimation system to minimise parasitic scattering at different camera lengths. The vacuum SAXS camera can be adjusted to camera lengths between 60 and 720 cm. Its rear module contains the beamstop and the SAXS detector. The WAXS detector is located above the frontal nose cone of the SAXS camera. The 169 × 179 mm Pilatus 1 M and the 33 × 169 mm Pilatus 200 K (pixel size of 172 × 172 μm2), were used to collect 2D SAXS and WAXS scattering (diffraction) images in transmission mode. The sample-to-detector distances of 1.03 and 0.45 m, respectively (Fig. 1), were calibrated using silver behenate. This set-up covered the real-space size range of ca. [0.15; 1.0] nm on the WAXS detector, and ca. [0.3; 23] nm on the SAXS detector. The corresponding full range of the magnitude of the scattering vector q11 covered 2.2 × 10-2 \({\mathring{\rm{A}} }^{-1}\) to 4.1 \({\mathring{\rm{A}} }^{-1}\). In this configuration, the SAXS detector monitored the prominent (110)-reflection of hemihydrate while the WAXS detector captured the time evolution of the (020)- and (220)-reflections. The time evolution of these reflections served for tracking of the dehydration reaction, as explained below. 2D diffraction patterns were recorded as uncompressed 32-bit TIFF images. Since the obtained Bragg reflections were circular, 2D SAXS/WAXS images were transformed into 1D curves by azimuthal averaging using the scatterBrain IDL program (http://archive.synchrotron.org.au/aussyncbeamlines/saxswaxs/software-saxswaxs), developed at the SAXS/WAXS beamline at the ANSTO Australian Synchrotron. SAXS intensity curves were converted to absolute units. This procedure entailed correction for background signal through measurements of the empty cell, dark current, intensity normalisation for transmitted flux using a beam-stop detector, and intensity calibration against a glassy carbon standard. The calibrated 1D SAXS curves employed to produce the conversion curves in Fig. 2i, j are available as electronic supplement (Supplementary Data 1).
Cell loading and heating
For each experiment, a sample disc was placed into the cell centre before the remaining components (seal, spacer, and axial piston; Supplementary Fig. 1a) were assembled. Then, the piston was screwed carefully to a hand-tight state in low-stress experiments; additional tightening with a calibrated torque wrench was applied for high-stress experiments (Supplementary Note 1). The closed cell was mounted on a high-precision translation stage in the orientation shown in Fig. 1. Ambient humidity was not controlled, and the sample chamber contained air from the SAXS experimental hutch. The fluid ports of the cell remained closed during all experiments (port 1 was connected to a pressure transducer11), locking in the air surrounding the sample. In the radial directions, a gap of 1 cm remained between the sample disc and the cell wall, providing space for the evacuation of the liberated water. Three or five equidistant regions of interest were chosen on each disc, always including the disc centre and additional points along the horizontal radius. The beam spot size was 100 × 100 μm2 in all experiments but the one at T = 142 °C and low pre-stress, in which the spot size was 250 × 250 μm2. The larger beam size was the requirement of modified beamline hardware and explains the elevated scattering intensity seen in Fig. 2e, f. We found that the measured progress of transformation does not depend on the position of the region of interest on the sample under our experimental conditions11. Therefore, we only report data acquired for the central point here. Reference SAXS/WAXS patterns were measured at ambient conditions before heating. In the next step, the heater was switched on, and SAXS/WAXS patterns were recorded with an exposure time of 5 seconds per point, moving the sample stage successively in the horizontal direction relative to the stationary X-ray beam, starting at the disc centre and stepping radially outwards. Time increments needed to move between points ranged from 6 to 11 s. As a result, the average time interval between acquisition of successive SAXS/WAXS images in the sample centre amounted to ~30 s. Additional set-up details and the calibration of the heating system are presented in our recent review paper on time-resolved synchrotron X-ray transmission scattering experiments11. Supplementary Note 4 demonstrates experimentally that the application of the high pre-stress does not affect the heating history of the samples. The observed acceleration of the dehydration reaction is due to elastic pre-stress loading.
Tracking of the phase transformation
Here, we use the time evolution of the normalised intensity of the hemihydrate (110) reflection, indexed according to Ballirano, et al.31 at |q| = 1.0463 Å−1, tracked by the SAXS detector as measure for the conversion fraction \(\alpha \left(t\right)\):
where \(I\) denotes SAXS intensity and \(t\) is the time. The corresponding time evolution of the (020)- and (220)-reflections resolved in the WAXS detector yield the same results and are omitted for clarity. We demonstrate the validity of this method for quantifying the gypsum dehydration process in our methodological review paper11. All experiments proceeded to reaction completion except for the one at T = 129 °C and low pre-stress. Post-mortem powder XRD confirmed that 1% gypsum remained in the sample centre, as can also be seen qualitatively in the SAXS/WAXS images (Fig. 2b) and the post-mortem microstructural images (Supplementary Figs. 3 and 4). The data tables for the conversion curves plotted in Fig. 2i, j are provided in Supplementary Data 1 accompanying this article.
Scanning-electron microscopy (SEM)
SEM images (Supplementary Figs. 3 and 4) of the surfaces of uncoated reacted and unreacted samples were obtained with the Tescan Mira 3 Variable Pressure Field Emission SEM under low vacuum (40 Pa). We used an accelerating voltage of 10 kV, beam intensity index of 12, and a working distance between 9 and 14 mm. A mixed mode of backscattered-electron signal (70%) and secondary-electron signal (30%) helped to eliminate edge effects compared to imaging in pure secondary-electron mode.
Data availability
The azimuthally integrated, calibrated, time-series 1D SAXS curves underpinning the conversion curves shown in Fig. 2 and the processed data for the conversion curves as well are provided as electronic supplement (Supplementary Data 1). The authors will arrange for sharing of the uncalibrated, uncompressed 32-bit TIFF images from the SAXS/WAXS detectors upon reasonable request.
References
Chang, L. L. Y., Howie, R. A. & Zussman, J. Non-silicates: Sulphates, Carbonates, Phosphates, Halides 2nd edn, Vol. 5B (Geological Society of London, 1998).
Blättler, C. L. et al. Two-billion-year-old evaporites capture Earth’s great oxidation. Science https://doi.org/10.1126/science.aar2687 (2018).
Spencer, R. J. Sulfate minerals in evaporite deposits. Rev. Miner. Geochem. 40, 173–192 (2000).
Rapin, W. et al. Hydration state of calcium sulfates in Gale crater, Mars: identification of bassanite veins. Earth Planet. Sci. Lett. 452, 197–205 (2016).
Wray, J. J. et al. Identification of the Ca-sulfate bassanite in Mawrth Vallis, Mars. Icarus 209, 416–421 (2010).
Langevin, Y., Poulet, F., Bibring, J.-P. & Gondet, B. Sulfates in the north polar region of Mars detected by OMEGA/Mars express. Science 307, 1584 (2005).
Stawski, T. M. et al. Formation of calcium sulfate through the aggregation of sub-3 nanometre primary species. Nat. Commun. 7, 11177 (2016).
Heard, H. C. & Rubey, W. W. Tectonic implications of gypsum dehydration. GSA Bull. 77, 741–760 (1966).
Brantut, N. et al. Dehydration-induced damage and deformation in gypsum and implications for subduction zone processes. J. Geophys. Res. https://doi.org/10.1029/2011JB008730 (2012).
Bedford, J., Fusseis, F., Leclère, H., Wheeler, J. & Faulkner, D. A 4D view on the evolution of metamorphic dehydration reactions. Sci. Rep. 7, 6881 (2017).
Schrank, C. E. et al. Tracking metamorphic dehydration reactions in real time with transmission small- and wide-angle synchrotron X-ray scattering: the case of gypsum dehydration. J. Petrol. https://doi.org/10.1093/petrology/egaa041 (2020).
Sharma, H. & Prabu, D. Plaster of Paris: past, present and future. J. Clin. Orthop. Trauma 4, 107–109 (2013).
Van Driessche, A. E. S., Stawski, T. M., Benning, L. G. & Kellermeier, M. in New Perspectives on Mineral Nucleation and Growth: From Solution Precursors to Solid Materials (eds Alexander, E. S. Van Driessche, Matthias Kellermeier, Liane G. Benning, & Denis Gebauer) (Springer International Publishing, 2017).
U. S. Geol. Survey, (ed U.S. Department of the Interior) 200, https://doi.org/10.3133/mcs2020 (Washington, 2020).
Fořt, J. & Černý, R. Carbon footprint analysis of calcined gypsum production in the Czech Republic. J. Clean. Prod. 177, 795–802 (2018).
Fowler, A., Howell, H. G. & Schiller, K. K. The dihydrate-hemihydrate transformation in gypsum. J. Appl. Chem. 18, 366–372 (1968).
McAdie, H. G. The effect of water vapour upon the dehydration of CaSO4•2H2O. Can. J. Chem. 42, 792–801 (1964).
Preturlan, J. G. D., Vieille, L., Quiligotti, S. & Favergeon, L. Kinetics and mechanism of the dehydration of calcium sulfate dihydrate: a comprehensive approach for studying the dehydration of ionic hydrates under controlled temperature and water vapor pressure. J. Phys. Chem. C 124, 26352–26367 (2020).
Liu, C., Zheng, H. & Wang, D. The dehydration kinetics of gypsum at high pressure and high temperature. High Press. Res. 35, 273–281 (2015).
Llana-Fúnez, S., Wheeler, J. & Faulkner, D. R. Metamorphic reaction rate controlled by fluid pressure not confining pressure: implications of dehydration experiments with gypsum. Contrib. Mineral. Petrol. 164, 69–79 (2012).
Ko, S.-C., Olgaard, D. L. & Wong, T.-F. Generation and maintenance of pore pressure excess in a dehydrating system 1. Experimental and microstructural observations. J. Geophys. Res. 102, 825–839 (1997).
Olgaard, D. L., Ko, S.-C. & Wong, T.-F. Deformation and pore pressure in dehydrating gypsum under transiently drained conditions. Tectonophysics 245, 237–248 (1995).
Wheeler, J. The significance of grain-scale stresses in the kinetics of metamorphism. Contrib. Mineral. Petrol. 97, 397–404 (1987).
Lavina, B., Dera, P. & Downs, R. T. Modern X-ray diffraction methods in mineralogy and geosciences. Rev. Mineral. Geochem. 78, 1–31 (2014).
Fusseis, F. et al. Pore formation during dehydration of polycrystalline gypsum observed and quantified in a time-series synchrotron radiation based X-ray micro-tomography experiment. Solid Earth 3, 857–900 (2012).
Bass, J. D. in Mineral Physics and Crystallography: a Handbook of Physical Constants Vol. 2, AGU Reference shelf (ed Ahrens, T. J.) (American Geophysical Union, 1995).
Williams, S. C. The shear strength of gypsum single crystals on three cleavage planes. Tectonophysics 148, 163–173 (1988).
Wheeler, J. The effects of stress on reactions in the Earth: sometimes rather mean, usually normal, always important. J. Metamorph. Geol. 36, 439–461 (2018).
Gratier, J.-P., Dysthe, D. K. & Renard, F. in Advances in Geophysics Vol. 54 (ed Renata Dmowska) (Elsevier, 2013).
Kirby, N. M. et al. A low-background-intensity focusing small-angle X-ray scattering undulator beamline. J. Appl. Crystallogr. 46, 1670–1680 (2013).
Ballirano, P., Maras, A., Meloni, S. & Caminiti, R. The monoclinic I2 structure of bassanite, calcium sulphate hemihydrate (CaSO4 · 0.5H2O). Eur. J. Mineral. 13, 985–993 (2001).
Comodi, P., Zanazzi, P. F., Nazzareni, S. & Speziale, S. High-pressure behavior of gypsum: a single-crystal X-ray study. Am. Mineral. 93, 1530–1537 (2008).
Lasaga, A. C. Kinetic Theory in the Earth Sciences (Princeton University Press, 1998).
Ossorio, M., Van Driessche, A. E. S., Pérez, P. & García-Ruiz, J. M. The gypsum–anhydrite paradox revisited. Chem. Geol. 386, 16–21 (2014).
Milsch, H., Priegnitz, M. & Blöcher, G. Permeability of gypsum samples dehydrated in air. Geophys. Res. Lett. https://doi.org/10.1029/2011GL048797 (2011).
Ballirano, P. & Melis, E. Thermal behaviour and kinetics of dehydration of gypsum in air from in situ real-time laboratory parallel-beam X-ray powder diffraction. Phys. Chem. Miner. 36, 391–402 (2009).
Raghami, E., Schrank, C. & Kruhl, J. H. 3D modelling of the effect of thermal-elastic stress on grain-boundary opening in quartz grain aggregates. Tectonophysics https://doi.org/10.1016/j.tecto.2019.228242 (2019).
Acknowledgements
We are grateful for the support of the ANSTO, in providing the SAXS/WAXS beamline at the Australian Synchrotron used in this work. We also acknowledge the Central Analytical Research Facility (CARF) at the Queensland University of Technology for supporting the laboratory work outside the Synchrotron and thank the following colleagues for their help, training, and advice: Donald McAuley and Gus Luthje (sample preparation), Dr. Henry Spratt, Dr. Tony Raftery, and Dr. Tony Wang (XRD), and Dr. Chris East (SEM). Computational resources and services used in this work were provided by the eResearch Office of the Queensland University of Technology. The authors thank Elnaz Raghami for providing the mesh for the numerical model shown in Fig. 3, and Dr. Harald Milsch for supplying Volterra alabaster. K.R.L. acknowledges financial support by the University of New South Wales through grant no. SPF01.
Author information
Authors and Affiliations
Contributions
Conceptualisation: C.E.S., T.B., O.G., A.R., and K.R.L. Investigation: C.E.S., T.B., K.C.M.G., S.M., N.K., O.G., and A.R. Formal analysis: C.E.S., O.G., K.C.M.G., and A.R. Visualisation: C.E.S., K.C.M.G. Supervision: C.E.S., K.R.L., O.G. Project administration: C.E.S. Writing—original draft: C.E.S. Writing—review & editing: all authors. Funding acquisition: T.B., C.E.S., K.R.L.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Primary handling editor: John Plummer.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Schrank, C.E., Gaede, O., Blach, T. et al. Fast in-situ X-ray scattering reveals stress sensitivity of gypsum dehydration kinetics. Commun Mater 2, 51 (2021). https://doi.org/10.1038/s43246-021-00156-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-021-00156-9
This article is cited by
-
Effects of groundwater and distilled water on the durability of evaporitic rocks
Scientific Reports (2023)