Abstract
Controlling the crystallographic orientation of 3D photonic crystals is important as it determines the behavior of light propagating through the device. Blue phases self-assemble into unique soft 3D photonic crystals with chiral structures for circular-polarization selectivity, but it has remained a challenge to control its 3D orientation. Here, we show that the orientation of blue phases can be precisely controlled to follow a predefined pattern imprinted on a substrate by exploiting field-induced phase transitions. Obtaining the blue phase through the field-induced chiral nematic phase and tetragonal blue phase X results in a highly oriented blue phase I with the crystallographic [001] direction aligned along the surface anchoring. Our approach is applied to fabricating a Bragg-Berry hologram with omnidirectional circular-polarization selectivity, where the hologram is visible only for one circular-polarization under all incident angles. Such devices are difficult to fabricate using conventional optical materials, thereby demonstrating the potential of self-organizing soft matter for photonics.
Similar content being viewed by others
Introduction
The search for nanostructures with advanced light-matter interactions has both fundamental and practical significance. The ability to affect only a single polarization of an orthogonal polarization pair is a basic yet important functionality that is relevant to a wide range of applications, from displays to sensing. In particular, circular-polarization (CP) selectivity has drawn considerable interest in the past decade because of its relevance in nature and its potential for novel applications1. Various devices have been proposed with strong CP selectivity, based on artificially engineered photonic crystals2 and metasurfaces3,4. Gyroid photonic crystals with I4132 symmetry have been demonstrated to split a light beam into orthogonal CP components5. The Pancharatnam-Berry phase in subwavelength anisotropic nanostructures has led to a plethora of CP-selective diffractive optical elements (DOEs)6,7. In a Pancharatnam-Berry phase device, the CP of light incident on the device acquires an optical phase that is proportional to twice the orientation of the optic axis, as well as reversing its handedness. The light wavefront can thus be modified by controlling the distribution of the optic axis orientation, and the phase gradient is reversed for orthogonal CP components, enabling multiple functions to be integrated into a single device. However, while nanofabrication can confer nontrivial functionality onto thin substrates, their fabrication is costly, making scaling up a technological challenge.
The use of materials with intrinsic chirality is an alternative approach to realize CP-selective optical devices. To this end, liquid crystal blue phases are promising candidates as they self-organize into 3D periodic structures. Blue phases are formed by the so-called double twist cylinders (DTCs) of the liquid crystal molecules, and self-organize into chiral cubic structures with body-centered or simple cubic symmetry known as blue phase I and blue phase II, depending on the chiral twisting power and temperature8. They typically possess a lattice constant of a few hundred nm, giving rise to CP-selective Bragg reflection of incident light with the same CP as the helical structure9,10. Moreover, they can be switched by an electric field, making them useful as electro-optic switches. Because blue phases generally exhibit polycrystalline structures, various strategies have been proposed to control their crystallographic orientation, such as thermal control11, application of an electric field12,13, surface alignment14,15, and the use of nano-patterned substrates16,17. However, the applicability of the previous alignment methods was limited in that they succeeded in only controlling the orientation of a single crystallographic axis (resulting in an orientation that is not unique), or required fabrication of nanostructures. Although the alignment mechanism of blue phases is not fully understood owing to their complex structure, a facile means to direct their 3D orientation is much in need to accelerate their use in electro-optical applications.
In this paper, we present a facile and robust method to direct the self-assembly of blue phases through a field-assisted reorientation process. Specifically, we show that the body-centered blue phase I can be made to align its [110] crystal axis perpendicular to the substrate, and simultaneously, its [001] axis along the easy axis imprinted on the substrate. Our technique enables the orientation of blue phase I to be uniquely controlled and spatially patterned on a substrate, which, to our knowledge, has never been demonstrated before. Importantly, the mechanism of this directed self-assembly is clarified by studying field-induced phase transitions of blue phase I. Further, we demonstrate the potential of our approach by fabricating an omnidirectional CP-selective volume hologram, in which the encoded phase is played back only for a single CP at practically all angles of incidence. The hologram works by the Bragg-Berry effect, which is analogous to the Pancharatnam-Berry effect but coupled to Bragg reflection from a periodic anisotropic medium18. Previous Bragg-Berry holograms were fabricated almost exclusively with chiral nematic liquid crystals with a 1D helical structure19,20,21,22,23, and showed reduced CP selectivity for light propagating off-axis from the helical axis. Because of the cubic structure, blue phases show CP selectivity for much broader angles of incidence, which is supported through numerical calculations based on directly solving the Maxwell equations for the light wave. Our work represents a significant step towards the application of CP-selective optical elements due to its exceptionally wide acceptance angle, and demonstrates the potential of self-organizing soft matter for photonics, enabling functionality that is extremely challenging to realize by top-down nanofabrication of conventional materials.
Results
Field-assisted directed self-assembly of blue phase lattices
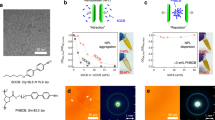
Many investigations on blue phase alignment focus on the crystal axis orientation along the substrate normal, referred to as the crystal plane orientation11,12,13,14,15,16,17. However, the orientation of a 3D crystal is uniquely defined by specifying the directions of two independent crystal axes. Here, we investigate field-induced phase transitions and show how they can be exploited to uniquely control the blue phase crystal orientation. Namely, we achieve (110) crystal plane orientation, and simultaneously direct the [001] crystal axis along the easy axis imprinted on a substrate (Fig. 1a). In the following, we refer to blue phase I with the (h k l) Miller plane oriented parallel to the substrate, as blue phase I(hkl).
a A schematic of blue phase (BP) I(110) and its crystal axes sandwiched by two glass substrates. b The design of azimuthal angle distribution, where each phase has a width of ~106 μm, and is varied with a step of 45°. The double-sided black arrows indicate the orientational easy axis. c POM image of BP I(211) before applying electric field. The inset shows the corresponding Kossel diagram. d POM images of field-induced phases at various electric fields. The POM images were taken in reflection mode between cross-polarizers. Scale bars in c and d: 200 μm. e Kossel diagrams of field-reoriented BP I(110) in regions with different easy axis directions. The double-sided white arrows and yellow dotted arrows indicate the orientational easy axis and the [001] crystal axis of BP lattices, respectively.
A sandwiched cell with a cell-gap of ~11 μm was prepared using ITO-coated glass substrates covered with a photoalignment layer to pattern the easy axis distribution illustrated in Fig. 1b. A blue phase material was injected in the patterned cell in the isotropic state, and cooled at a rate of 0.3 °C/min to a temperature where blue phase I appears (45.8 °C). Figure 1c shows a polarized optical microscope (POM) image, taken in reflection mode, of the as-prepared blue phase I cooled from the isotropic phase. The Kossel diagram, which is a 2D diffraction pattern for monochromatic converging light illuminated on the sample, indicates that the crystal plane orientation is (211) (see Supplementary Note 1 for principle of Kossel diagram observation). While the alignment pattern has some effect on the azimuthal orientation of the blue phase I(211), the alignment quality is not high, as can be seen from the non-uniformity in the direction of the domain boundaries. Figure 1d shows the evolution in the POM textures as a square electric field (1 kHz) is applied and gradually removed from the sample, at a rate of 0.05 V μm−1 per min. At a field of 7.3 V μm−1, the twist structure of the blue phase is completely unwound and the homeotropic alignment is obtained with a dark POM texture. As the electric field is reduced, a phase transition to the chiral nematic phase with a single-helix structure occurs at 7.0 V μm−1. Further decrease of the electric field leads to a phase transition at 2.7 V μm−1 to the blue phase X with centered tetragonal structure, and then to the orthorhombic blue phase I at 1.5 V μm−1, until finally reaching the cubic blue phase I at 0 V. As shown in Fig. 1e, the field-reoriented cubic blue phase I shows a two-fold Kossel pattern corresponding to (110) crystallographic plane orientation, and thus shows a different reflection color compared to blue phase I(211).
In the field-reoriented blue phase I(110), distinct boundaries are observed at the interface between regions with different surface anchoring directions. The azimuthal orientations in regions with different easy axes were characterized by observing the Kossel diagrams in each region (Fig. 1e). Clearly, the Kossel patterns are rotated by 45° in each striped region, reflecting the easy axis imprinted there (the angles of the Kossel pattern does not change within each area). Importantly, the [001] crystal axis is oriented along the easy axis, demonstrating that the azimuthal orientation of blue phase I(110) can be made to follow the easy axis imprinted on the surface through the field-assisted reorientation process. The slight variation in reflection color within the striped area is attributed to variations in the lattice constant, which can be improved by using a device with uniform cell thickness.
Two control experiments with different electric-field sequences were performed to clarify the mechanism of field-assisted self-assembly. Here, a cell with uniform easy axis was used. Starting from blue phase I(211) (Fig. 2a), the field intensity was first varied as shown in Fig. 2b, with field-induced phases homeotropic-chiral nematic-blue phase I without blue phase X. In this sequence, clear signs of alignment were observed in the chiral nematic phase at 4.5 V μm−1 (Fig. 2c), which, by the insertion of a reference retardation plate, was found to be composed of uniaxial helices with the helical axis pointing perpendicular to the easy axis (Supplementary Note 2). When the field was removed from this state, a blue phase I texture with two different reflection colors were observed (Fig. 2d). Observations of Kossel patterns revealed that the texture corresponded to either blue phase I(100) or blue phase I(110), and while the lattice planes were different, both had the [001] crystal axis parallel to the easy axis. The result implies that the chiral nematic phase causes the [001] axis of the succeeding blue phase I crystal to be aligned along the easy axis, but is unable to control the crystal plane orientation.
a POM image of blue phase (BP) I(211) before applying electric field, and corresponding Kossel diagram (inset). b Electric field sequence to obtain phases homeotropic–chiral nematic – BP I. c, d POM images of field-induced chiral nematic phase (c), and blue phase I with Kossel diagrams corresponding to two crystallographic planes shown in the inset (d). e Electric-field sequence to obtain phases homeotropic– BP X– BP I. f, g POM images of field-induced BP X (f) and BP I (g) with corresponding Kossel diagrams. Scale bar in a, c, d, f and g: 200 μm. The double-sided white arrows and yellow dotted arrows indicate the orientational easy axis and the [001] crystal axis of BP lattices, respectively.
The field sequence for the second control experiment was as shown in Fig. 2e, with field-induced phases homeotropic-blue phase X-blue phase I without the chiral nematic phase. By decreasing the field from 7.3 V μm−1 to 2.5 V μm−1, a red texture with a four-fold Kossel pattern was obtained, corresponding to the tetragonal blue phase X (Fig. 2f). Removing the field from blue phase X induced a transition into the cubic blue phase I with uniform reflection color over the entire cell (Fig. 2g). Kossel pattern observations revealed that the crystal plane of the field-induced blue phase I was (110); however, in this case, the azimuthal orientation was not unique but randomly varied within the sample (Fig. 2g, inset). This result implies that the blue phase X induces (110) crystal plane orientation of blue phase I, but the [001] crystal axis cannot be controlled.
The above results show that the chiral nematic phase and blue phase X act cooperatively to uniquely determine the blue phase I alignment; the chiral nematic phase controls the [001] crystal axis orientation, while blue phase X controls the (110) crystal plane orientation. When the chiral nematic phase is obtained from the homeotropic phase in a liquid crystal cell with uniform easy axis, the uniformly lying helix (ULH) texture with the helical axis lying in-plane, perpendicular to the easy axis is obtained (Fig. S2). This is because the molecules tend to align along the easy axis while the electric-field forces the molecules to tilt away from the substrate, causing the helical axis to become perpendicular to both of those directions. On the other hand, the DTC composing the blue phase I has a structure similar to the ULH in that the DTC has molecules roughly aligned parallel to the cylinder at the center, and the helical axis extending in the perpendicular direction. It is therefore likely that the DTC grows in the direction perpendicular to the helical axis in the ULH texture, or equivalently, along the easy axis on the substrate. In blue phase I, the DTCs are parallel to the [001] axis, which is consistent with the observed alignment behavior. We also note that the alignment of the chiral nematic helical axis and the [001] axis of blue phase I is probably universal, since the same alignment behavior has been reported in experiments performed in different geometries8,24.
The tetragonal blue phase X is a field-induced phase that is stabilized by applying an electric field along the [110] direction of blue phase I. Numerical simulations on this phase have shown that it can be obtained through a continuous reorganization from blue phase I(110)25,26. Thus, it is a natural consequence for blue phase I(110) to be obtained from blue phase X, as observed in experiment (Fig. 2g). However, because the preceding homeotropic phase has no twist structure that can direct the orientation of the blue phase crystals, the DTCs can grow in any direction, and thus the azimuthal orientation of blue phase I(110) is not uniquely determined.
The alignment of blue phases grown by temperature control depends on the liquid crystal structure preceding the blue phase and thus shows strong hysteresis27. The proposed alignment method is a robust solution to overcome the alignment hysteresis, because the alignment history is erased by unwinding the helix in the homeotropic phase. The alignment induced through the chiral nematic phase and blue phase X enables us to obtain the same alignment regardless of the initial blue phase I orientation. In Supplementary Note 3, we demonstrate the robustness of our approach by applying this alignment method to blue phase I with other lattice plane orientations, where blue phase I(110) with the [001] crystal axis along the easy axis is obtained for all cases.
Omnidirectional CP selectivity of blue phase I
The 3D helical structure of blue phases makes them attractive for CP-selective photonic applications that operate regardless of the direction of light propagation. However, despite the numerous works on the properties of blue phases as tunable photonic crystals, to the best of our knowledge, no previous study explicitly demonstrates the omnidirectional CP selectivity of blue phases. Here, we theoretically investigate the photonic band structure of blue phases, and experimentally confirm the results using a homogenously aligned, field-induced blue phase I(110).
Since we are interested in the Bragg reflection by the (110) planes as in the experiments, the Bloch vector k is chosen such that it satisfies the condition of Bragg reflection \(\left| {\mathbf{k}} \right| = | {{\mathbf{k}} + {\mathbf{G}}_{\left( {110} \right)}} |\), where G(khl) denotes the reciprocal lattice vector normal to the (hkl) planes and defined by \({\mathbf{G}}_{\left( {{\it{khl}}} \right)} = \frac{{{\mathrm{2}}\pi }}{a}( {h{\mathbf{e}}_x + k{\mathbf{e}}_y + l{\mathbf{e}}_z} )\), where a is the lattice constant and ej (j = x, y, z) is the unit vector along the j-direction. For comparison with experimental results that will be shown later, the band structures are presented in an unconventional manner; the horizontal axis shows the angle between k and the [110] crystal axis (denoted by α in the following), and the vertical axis indicates the wavelength in vacuum λvacuum = 2πc/ω, where c is the speed of light in vacuum, and ω is the eigenfrequency. As shown in Fig. 3a, b, considering the two-fold symmetry of blue phase I(110), the Bloch vector k is rotated around the [001] and \(\left[ {\bar 110} \right]\) crystal axes (from the initial condition pointing along [110]) for Fig. 3c, d, respectively, corresponding to paths parallel to the N-H and N-P directions in the first Brillouin zone of a bcc lattice [N, H, and P are points of high symmetry in reciprocal space, with coordinates N = (π/a)(0,1,1), H = (π/a)(0,0,2), and P = (π/a)(1,1,1)]. Eight bands from the largest λvacuum (or the smallest frequency) are plotted, and the pair of the 2nd and the 3rd bands and that of the 6th and 7th bands are almost indistinguishable in the resolution of Fig. 3c, d.
a, b A schematic of uniformly aligned blue phase (BP) I(110) describing the two rotation modes in real and reciprocal space. c, d Photonic bands in terms of the λvacuum and α, where the Bloch vector k is rotated around the [001] and \(\left[ {\bar 110} \right]\) crystal axes from the [110] crystal axis, respectively. e, f Polarization of the electric field for k. The vertical axis is such that it is 1 for perfect LCP, and 0 for RCP. g, h Calculated and i, j measured angular properties of Bragg reflection spectra upon LCP and RCP light illumination. Isolated bright spots in g are a numerical artifact. The incident angles are rotated around the [001] (g, i) and \(\left[ {\bar 110} \right]\) (h, j) crystal axes from the [110] crystal axis.
In Fig. 3c, the Fourier modes of the electric field of light dominating the 1st to 4th bands are those with the wavevectors k and k + G(110), corresponding to the Bragg reflection by the (110) planes, while the 5th to 8th bands are dominated by Fourier modes with \({\mathbf{k}} + {\mathbf{G}}_{\left( {10\overline 1 } \right)}\) and \({\mathbf{k}} + {\mathbf{G}}_{\left( {10\overline 1 } \right)} + {\mathbf{G}}_{\left( {002} \right)}\), thus involving the Bragg reflection by the (002) planes. The band structure in Fig. 3d is more complicated because the P point in the first Brillouin zone is involved. For incident angles below 36°, the Bragg reflection by the (110) planes is responsible for the 1st to 4th bands and shows a monotonic decrease in wavelength, but above the P point at α ~36°, the 1st to 4th bands and the 5th to 8th bands, which correspond to Bragg reflection involving both the (101) and the (011) planes, cross over. The behavior of the bands can be understood by identifying the relative orientations of the planes responsible for Bragg reflection as discussed in Supplementary Note 4. Figure 3e, f shows the polarization of the electromagnetic field for the Bloch wavevector, for the bands concerning the Bragg reflections by the (110) planes. The polarization of the 1st and 4th (also the 5th and 8th bands in Fig. 3f) is almost perfectly left-circular while that of the others is almost perfectly right-circular for a large range of α values, except around α ~42° in Fig. 3e and around α ~36° in Fig. 3f, where crossing of the bands occurs and other Fourier modes become non-negligible.
The opening of a band-gap for a single CP light for broad α values is indicative of omnidirectional selective reflection that does not disappear even at large off-axis propagation angles. Since photonic band calculations with bulk infinite structures do not exactly account for the selective reflection properties of experiments where samples with finite thickness are used, we also calculated the angular dependence of Bragg reflection spectra from a blue phase I(110) sample with a thickness of 6.04 μm-sandwiched between two glass substrates with a refractive index of 1.53. Similar to the photonic band structure, the incident angles are rotated around the [001] and \(\left[ {\bar 110} \right]\) crystal axes, and the reflectance is calculated for right- (R) and left- (L) CP incident light. As shown in Fig. 3g, h, the blue-shift in peak reflection wavelength and strong CP selectivity is clearly observed for both rotation modes, confirming the ability of blue phases to selectively reflect only a single CP light for broad range of incident angles.
The numerical results are validated by experimental data measured using a homogeneously aligned blue phase I(110), as shown in Fig. 3i, j [see Supplementary Note 4 for a discussion on the red-shifting bright band that appears in the calculations (above α ~36° in Fig. 3h), which is observed as a dark band in experiment (Fig. 3j)]. For light incidence from glass (n ~1.53), strong CP selectivity is confirmed for large incidence angles up to 45°. Considering refraction from air (n = 1.0), which limits the effective incident angle in the blue phase I(110) to ~40°, the CP selectivity is achieved for practically all angles of incidence on the (110) plane. This property is distinct from selective reflection of the 1D helical structure formed in the chiral nematic phase; because the helical structure deviates from the ideal sinusoidal profile for off-axis propagation, the CP selectivity is lost typically at angles greater than ~30°21,22. Another interesting property of selective reflection from blue phases is that the wavelength of Bragg reflection shows little dependence on the direction around which the crystal is rotated. This is due to the cubic symmetry of blue phase I, and is advantageous for applications, as we demonstrate in the omnidirectional CP-selective hologram below.
Omnidirectional CP-selective hologram based on the Bragg-Berry effect
The Bragg-Berry effect imparts a phase that is proportional to twice the azimuthal orientation of blue phase crystals, thereby enabling a full wave modulation of reflected wavefront by varying the crystal orientation from 0 − π18. Various CP-selective Bragg-Berry holograms have been proposed using the chiral nematic phase, but the CP selectivity is achieved only for limited incident angles21,22. Based on our findings—that the crystal orientation can be made to follow a pattern imprinted on a substrate, and that the Bragg reflection wavelength of blue phase I(110) shows little dependence on the rotation axis of light incidence—we demonstrate an omnidirectional CP-selective hologram that can only be played back using CP light even at large incident angles.
Figure 4a shows the target image for the hologram, which is the OSAKA UNIVERSITY mascot Dr. Wani. We used the Gerchberg-Saxton algorithm28,29 to obtain the optical phase information that was converted to the azimuthal orientation distribution (Fig. 4b) by multiplying a factor of 0.5. The blue phase mixture was filled in a 9-µm-sandwiched cell with the patterned azimuthal easy axis distribution, after which its alignment was achieved through the aforementioned method. Moreover, to use the fabricated hologram at room temperature, a small amount of photo-reactive monomer was added to the blue phase mixture and polymerized in-situ to prepare a polymer-stabilized blue phase (PSBP)30. The encoded hologram was played back by illuminating a super-continuum laser (NKT Photonics, SuperK COMPACT) controlled to have LCP or RCP (see Supplementary Note 5 for the laser setup).
Figure 4c shows the holographic images observed for LCP light propagating at 7° (yellow), 29° (green), and 40° (blue) in the blue phase; note that for light incident from air, these angles correspond to 10° (yellow), 49° (green), and 85° (blue), covering almost all accessible incident angles. In experiment, a triangular prism made of BK-7 was attached for the measurement of blue reflection, to increase the propagation angle. When the polarization is changed to RCP, the encoded image disappears for every angle, demonstrating the omnidirectional CP selectivity of the blue phase-based hologram. The conversion efficiency that is defined as the intensity ratio of the reflected light (without the zero-order intensity) with respect to the incident light was measured as ~54% for all angles of incidence. The dichroic ratio of hologram playback was approximately 85:1 for all angles.
The demonstrated device is a phase-hologram and its reflectance is due to the blue phase I(110) alignment, which is almost constant over the entire device. This enables a higher light-conversion efficiency compared to binary amplitude holograms that were previously demonstrated by spatially varying the reflection intensity through controlling only the crystal plane orientation15,17,31. The reduction of the conversion efficiency is mainly attributed to the small thickness of the blue phase, which causes low reflectance (~ 62% for LCP illumination), and imperfections in the orientation control of the blue phase lattices on the substrate, including the slight variations in lattice constants (~10 nm) as can be seen in Fig. 1d. The azimuthal easy axis in the demonstration was imprinted digitally, where the designed pattern was imprinted at 10° phase steps (corresponding to 18 phase levels) using a liquid crystal display (LCD) as a mask, with nominal pixel size of ~2.7 × 2.7 μm2 on the sample. While the results show that the blue phase lattice is capable of modulating its crystal orientation at this spatial resolution, the minimal size of oriented blue phase domains should depend on various parameters such as cell-gap and alignment layer used. We expect that alignment layers imposing strong surface anchoring will suppress the occurence of alignment imperfections. Optimization of such parameters, as well as using materials with larger birefringence will enable a higher reflectance, thus improving the overall efficiency.
Discussion
In summary, we proposed a facile and robust method to direct the macroscopic self-assembly of blue phase I crystals by exploiting field-induced phase transitions. We found that obtaining blue phase I through two field-induced intermediate phases enables the lattice orientation to be uniquely defined, with (110) crystal plane orientation, and [001] crystal axis orientation along the easy axis. The underlying concept is in understanding the effect of boundary conditions (surface alignment and external field) on different phases and inducing phase transitions in the correct order to control self-assembly. Because phase transitions are general phenomena, we believe that this concept can be applied to other soft systems as well. Based on the concept, we demonstrated a reflective hologram by spatial control of alignment, which shows a high degree of CP selectivity for practically all angles of light incidence. Although broadband CP selectivity has been demonstrated using metamaterials32, reflective metamaterials require an opaque (reflective) substrate, which makes our see-through type device based on Bragg reflection unique. On the other hand, while standard volume holograms operate by Bragg reflection, it is extremely difficult if not impossible to confer CP selectivity with wide acceptance angles using standard photopolymers. We believe that the blue phase-based Bragg-Berry hologram operating in a wide range of wavelengths can be achieved by using a polymer-stabilized blue phase with pitch distribution along the viewing direction33. We also expect that free-standing flexible holographic optical elements with the ability to tune their 3D photonic structures can be realized by photo-polymerizing mesogenic blue phase mixtures34,35. Our work will accelerate the development of advanced photonic applications with CP selectivity, and promote the investigation of fundamental optical properties of complex 3D soft matter. We believe future works exploiting the external field-tunability of blue phases36,37,38,39 or the capability of blue phases to act as templates40,41 will lead to intelligent photonic structures with tailored optical properties.
Materials and methods
Sample fabrication
The photoalignment agent (LIA-03, DIC) was spin-coated on two ITO-covered substrates to coat layer with thickness of ~100 nm. The alignment agent is based on an azobenzene, which sets the orientational easy axis perpendicular to the incident polarization. The sandwiched cells were prepared by assembling the two ITO-coated glass substrates using a photo-curable adhesive (NOA68T, Norland) containing ball spacers with nominal diameter of 8 μm.
The photo-patterning process to record the easy axis distribution for the stripe pattern (Fig. 1b) and the hologram (Fig. 4b) was performed using a home-made projection system19 consisting of a LCD projector (EPSON, ELP-820), a short-pass filter (475 nm), a rotatable half-wave plate, and a ×10 objective lens. The system exposed linear polarized (LP) light on the sandwiched cell over an area controlled by the electronic mask. The pixel resolution and size on the sample were 512 × 384 and 2.7 × 2.7 μm2, respectively, giving a pattered area of 1.3 × 1.0 mm2. The polarization angle of incident LP light was rotated at 45° increments for the striped pattern, and 10° increments for the hologram. The light dosage for patterning was 0.4 μJ per pixel.
The PSBP precursor was prepared by blending two types of host nematic liquid crystals (MLC-6849-100 and 5CB, both from Merck), a left-handed chiral dopant (S-5011, HCCH), a reactive mesogen (RM257, Merck), an isotropic monomer (12CA, Tokyo chemical industry Co. Ltd.), and a photoinitiator (IrgacureOxe04, BASF) at a weight ratio of 61.4:26.3:3.0:4.5:4.5:0.3. The ordinary (no) and extraordinary (ne) refractive indices and dielectric anisotropy (∆ε) of the two host nematic liquid crystals are no = 1.49, ne = 1.60, and ∆ε = 11.3 for MLC-6849-100, and no = 1.53, ne = 1.72, and ∆ε = 13.0 for 5CB, which are obtained from datasheet. The precursor was injected in the photo-patterned cell in the isotropic phase (55 °C), and cooled down to the temperature where blue phase I appears (45.8 °C), at a rate of 0.3 °C min−1. The temperature of the samples was controlled using a commercial hotplate (Linkam, LTS-350). For the field-assisted directed self-assembly process in Figs. 1, 3, and 4, a square wave electric field of 7.3 V µm−1 with a frequency of 1 kHz was applied between the ITO-coated glass substrates, and then gradually removed with a rate of 0.05 V µm−1 per min. After completely removing the electric field, the samples were photo-polymerized by illuminating UV light (365 nm, 10 mW cm−2) for 40 min30.
Observation of POM images and measurement of reflection spectrum for normal incidence
The crystal plane and azimuthal orientation of blue phase lattices were investigated by observation of POM images in reflection mode and Kossel diagrams. The reflection spectrum upon normal incidence was measured on the POM using a ×10 objective and an optical fiber coupled to a spectrometer (Hamamatsu, PMA-11).
Numerical calculations for optical properties of blue phase I(110)
For the orientation profile of blue phase I, we used the Landau-de Gennes theory describing the orientational order by a second rank tensor χij. We minimized the free energy functional
where the first three terms concern the strength of local orientational order, and the last two terms containing spatial derivatives represent the elastic energy. The length and the order parameter have been rescaled so that 4π is the natural pitch of the cholesteric helix, and only three dimensionless parameters τ (rescaled temperature), κ (rescaled elastic constant or reduced strength of chirality), and η (anisotropy of elasticity) appear as parameters representing the properties of the material. The sign of the chirality is determined by the sign of σ (|σ| = 1), and in the following calculations we chose σ = +1. However, the chirality of the liquid crystal used in experiments corresponds to σ = −1. Therefore, the results presented in the main text are the “mirror images” of the results of actual calculations. For the material parameters we chose τ = −1, κ = 0.7 and η = 1 for which blue phase I is the most stable. For further details, refer to ref. 42.
For optical calculations, the profile of the dielectric tensor εij is required. Here we assumed a linear relation between εij and χij, namely, \(\varepsilon _{ij} = \varepsilon _{iso}\delta _{ij} + \varepsilon _a\chi _{ij}\). We chose \(\varepsilon _{iso} = \left( {n_e^2 + n_o^2} \right)/3\), and \(\varepsilon _a = (n_e^2 - n_o^2)/\chi _{\mathrm{0}}\), where ne = 1.64 and no = 1.50 are the extraordinary and ordinary refractive indices, respectively, and χo is the degree of orientation order defined such that the orientation order in the bulk (not close to the defect) is \(\chi _{{ij}} = \chi _0\left( {n_in_j - \delta _{ij}/3} \right)\) (n is the director, a unit vector along the local liquid crystal alignment). For the photonic band calculations of bulk blue phase I obtained by minimizing Eq. (1), we solved the following Maxwell equation for non-magnetic materials in the frequency domain after the elimination of the electric field43,
where the time dependence of the magnetic field H(r) is given by e-iωt, c is the speed of light in vacuum, and \({^{\longleftrightarrow}{{\varepsilon^{ - 1}}}}\) is the inverse of the dielectric tensor \({\overleftrightarrow{\varepsilon}} = \varepsilon_{ij}\). We used the plane-wave expansion method43, in which the magnetic field for a given Bloch vector k is expanded as \({\mathbf{H}}_{\mathbf{k}}\left( {\mathbf{r}} \right) = \mathop {\sum}\nolimits_{\mathbf{G}} {{\mathbf{H}}_{\mathbf{k}}\left( {\mathbf{G}} \right)e^{i\left( {{\mathbf{k}} + {\mathbf{G}}} \right) \cdot {\mathbf{r}}}}\), where {G} is the set of the reciprocal lattice vectors. Now Eq. (2) becomes an eigenproblem for the set \(\left\{ {{\mathbf{H}}_{\mathbf{k}}\left( {\mathbf{G}} \right)} \right\}\), which was solved with the aid of an eigensolver PRIMME44. Note that the polarization presented in Fig. 3e, f is that of Hk(G = 0), the k-component of the magnetic field.
The reflection of light by a blue phase I(110) sample of finite thickness was calculated using the combination of plane-wave expansion in the lateral directions (x, y) and finite-difference discretization in the thickness direction (z)45. More specifically, we considered a system in which the liquid crystal of thickness L occupies the region –L/2 ≤ z ≤ L/2, and isotropic and homogeneous media with dielectric constant 2.34 are in z < –L/2 and z > L/2. We solved the Maxwell equation after the elimination of the magnetic field,
The electric field is expanded using the Bloch theorem as
where \({\mathbf{r}} = \left( {x,y,z} \right) = \left( {{\mathbf{r}}_ \bot ,z} \right)\), ez is the unit vector in the +z direction, \(\left\{ {{\mathbf{G}}_ \bot } \right\}\) is the set of reciprocal lattice vectors in the (x, y) plane, and Ei and ki are the electric field and the wavevector of the monochromatic incident light, respectively, with \({\mathbf{k}}_{{\mathrm{i}} \bot }\) being the (x, y) components of ki. The electric field inside the liquid crystal \({\mathbf{E}}_{\mathrm{2}}^{{\mathbf{G}}_ \bot }\left( z \right)\) is further discretized in the z direction with equal spacing. Now Eq. (3), together with appropriate boundary conditions, is reduced to a set of linear equations for \(\mathop {\sum}\nolimits_{{\mathbf{G}}_ \bot } {{\mathbf{E}}_{\mathbf{r}}^{{\mathbf{G}}_ \bot }\left( z \right)}\), \(\mathop {\sum}\nolimits_{{\mathbf{G}}_ \bot } {{\mathbf{E}}_{\mathrm{t}}^{{\mathbf{G}}_ \bot }\left( z \right)}\)and discretized \({\mathbf{E}}_{\mathrm{2}}^{{\mathbf{G}}_ \bot }\left( z \right)\), which was solved with the aid of LAPACK46, a standard software package for linear algebra. Further details are found in ref. 45. The reflectance shown in Fig. 3g, h is that for the regular reflection whose amplitude is \({\mathbf{E}}_{\mathbf{r}}^{{\mathbf{G}}_ \bot }\)with \({\mathbf{G}}_ \bot = 0\) in Eq. (4). The periodic structure of blue phase I obtained numerically by minimizing Eq. (1) was arranged such that its (110) plane is parallel to the xy-plane. Its thickness in the calculation was \(16\sqrt 2 a \approx 6.04\,{\mathrm{\mu m}}\), approximately half of the thickness of the experimental cell. Here, a = 267 nm is the lattice constant.
Let us comment that in the present calculation we solved Eq. (3) for the electric field because the treatment of the dielectric tensor \(\overleftrightarrow \varepsilon\) is easier, while in the photonic band calculation we resorted to Eq. (2) for the magnetic field because the zero-divergence condition, i.e., \(\left( {{\mathbf{k}} + {\mathbf{G}}} \right) \cdot {\mathbf{H}}_{\mathbf{k}}\left( {\mathbf{G}} \right) = 0\) in the present case, reduces the number of the independent components of \(\left\{ {{\mathbf{H}}_{\mathbf{k}}\left( {\mathbf{G}} \right)} \right\}\), in contrast to E that is not divergence-free.
Measurement of angular dependent Bragg reflection
A Xenon lamp was used to measure the angular dependence of Bragg reflection of the field-induced blue phase I(110). The light was illuminated on the sample after passing a polarizer and a quarter-wave plate to control its polarization. From the normal incidence where the light source was illuminated on the sample along [110] crystal axis, the reflection spectra were measured at various incidence angles by rotating the sample around the [001] and \(\left[ {\bar 110} \right]\) crystal axes, respectively. The reflected light from the sample was collected by an optical fiber connected to a spectrometer (Hamamatsu, PMA-11). For the measurement at incident angles over 30°, a BK-7 triangle prism was attached on the device through an index-matching oil to increase the incident angle accessible from air.
Data availability
The authors declare that the data supporting the findings of this study are available within the paper and its supplementary information files.
Code availability
The numerical codes employed for Fig. 3c–h are available from J.F. (fukuda.jun-ichi@phys.kyushu-u.ac.jp) upon reasonable request.
References
Gansel, J. K. et al. Gold helix photonic metamaterial as broadband circular polarizer. Science 325, 1513–1515 (2009).
Semnani, B., Flannery, J., Maruf, R. A. & Bajcsy, M. Spin-preserving chiral photonic crystal mirror. Light Sci. Appl. 9, 23 (2020).
Khorasaninejad, M., Ambrosio, A., Kanhaiya, P. & Capasso, F. Broadband and chiral binary dielectric meta-holograms. Sci. Adv. 2, e1501258 (2016).
Wen, D. et al. Helicity multiplexed broadband metasurface holograms. Nat. Commun. 6, 8241 (2015).
Turner, M. D. et al. Miniature chiral beamsplitter based on gyroid photonic crystals. Nat. Photonics 7, 801–805 (2013).
Pancharatnam, S. Generalized theory of interference and its applications. Proc. Indian Acad. Sci. A 44, 247–262 (1956).
Berry, M. V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. Lond. A. Math. Phys. Sci. 392, 45–57 (1984).
Tanaka, S. et al. Double-twist cylinders in liquid crystalline cholesteric blue phases observed by transmission electron microscopy. Sci. Rep. 5, 16180 (2015).
Coles, H. J. & Pivnenko, M. N. Liquid crystal ‘blue phases’ with a wide temperature range. Nature 436, 997–1000 (2005).
Yoshida, H. et al. Bragg reflection band width and optical rotatory dispersion of cubic blue-phase liquid crystals. Phys. Rev. E 94, 042703 (2016).
Chen, C.-W. et al. Large three-dimensional photonic crystals based on monocrystalline liquid crystal blue phases. Nat. Commun. 8, 727 (2017).
Chen, Y. & Wu, S.-T. Electric field-induced monodomain blue phase liquid crystals. Appl. Phys. Lett. 102, 171110 (2013).
Chen, M., Lin, Y.-H., Chen, H.-S. & Chen, H.-Y. Electrically assisting crystal growth of blue phase liquid crystals. Opt. Mater. Express 4, 953–959 (2014).
Kim, K. et al. A well-aligned simple cubic blue phase for a liquid crystal laser. J. Mater. Chem. C 3, 5383–5388 (2015).
Zheng, Z.-G. et al. Light‐Patterned crystallographic direction of a self‐organized 3D soft photonic crystal. Adv. Mater. 29, 1703165 (2017).
Martínez-González, J. A. et al. Directed self-assembly of liquid crystalline blue-phases into ideal single-crystals. Nat. Commun. 8, 15854 (2017).
Li, X. et al. Sculpted grain boundaries in soft crystals. Sci. Adv. 5, eaax9112 (2019).
Yoshida, H. & Kobashi, J. Flat optics with cholesteric and blue phase liquid crystals. Liq. Cryst. 43, 1–11 (2016).
Kobashi, J., Yoshida, H. & Ozaki, M. Planar optics with patterned chiral liquid crystals. Nat. Photonics 10, 389–392 (2016).
Rafayelyan, M. & Brasselet, E. Bragg-Berry mirrors: reflective broadband q-plates. Opt. Lett. 41, 3972–3975 (2016).
Kobashi, J., Yoshida, H. & Ozaki, M. Polychromatic Optical vortex generation from patterned cholesteric liquid crystals. Phys. Rev. Lett. 116, 253903 (2016).
Cho, S., Ono, M., Yoshida, H. & Ozaki, M. Bragg-Berry flat reflectors for transparent computer-generated holograms and waveguide holography with visible color playback capability. Sci. Rep. 10, 8201 (2020).
Chen, P. et al. Chirality invertible superstructure mediated active planar optics. Nat. Commun. 10, 2518 (2019).
Wang, C.-T., Liu, H.-Y., Cheng, H.-H. & Lin, T.-H. Bistable effect in the liquid crystal blue phase. Appl. Phys. Lett. 96, 041106 (2010).
Alexander, G. P. & Marenduzzo, D. Cubic blue phases in electric fields. Europhys. Lett. 81, 66004 (2008).
Alexander, G. P. & Yeomans, J. M. Numerical results for the blue phases. Liq. Cryst. 36, 1215–1227 (2009).
Takahashi, M. et al. Orientation of liquid crystalline blue phases on unidirectionally orienting surfaces. J. Phys. D Appl. Phys. 51, 104003 (2018).
Gerchberg, R. W. & Saxton, W. O. A practical algorithm for the determination of phase from image and diffraction plane pictures. Optik 35, 237–246 (1972).
Wyrowski, F. & Bryngdahl, O. Iterative Fourier-transform algorithm applied to computer holography. J. Opt. Soc. Am. A 5, 1058–1065 (1988).
Kikuchi, H. et al. T. Polymer-stabilized liquid crystal blue phases. Nat. Mater. 1, 64–68 (2002).
Zhou, K. et al. Light‐driven reversible transformation between self‐organized simple cubic lattice and helical superstructure enabled by a molecular switch functionalized nanocage. Adv. Mater. 30, 1800237 (2018).
Liu, Z. et al. Wang, Omnidirectional polarization beam splitter for white light. Opt. Express 27, 7673–7684 (2019).
Chen, C.-W. et al. Electric field-driven shifting and expansion of photonic band gaps in 3D liquid photonic crystals. ACS Photonics 2, 1524–1531 (2015).
Castles, F. et al. Stretchable liquid-crystal blue phase gels. Nat. Mater. 13, 817–821 (2014).
Yang, J. et al. Fabrication and photonic applications of large-domain blue phase films. J. Mater. Chem. C 7, 9460–9466 (2019).
Lin, T.-H. et al. Red, green and blue reflections enabled in an optically tunable self-organized 3D cubic nanostructured thin film. Adv. Mater. 25, 5050–5054 (2013).
Bisoyi, H. K. & Li, Q. Light-directing chiral liquid crystal nanostructures: from 1D to 3D. Acc. Chem. Res. 47, 3184–3195 (2014).
Wang, L. & Li, Q. Stimuli-directing self-organized 3d liquid-crystalline nanostructures: from materials design to photonic applications. Adv. Funct. Mater. 26, 10–28 (2016).
Guo, D.-Y. et al. Reconfiguration of three-dimensional liquid-crystalline photonic crystals by electrostriction. Nat. Mater. 19, 94–101 (2020).
Castles, F. et al. Blue-phase templated fabrication of three-dimensional nanostructures for photonic applications. Nat. Mater. 11, 599–603 (2012).
Jau, H.-C. et al. Optically rewritable dynamic phase grating based on blue-phase-templated azobenzene liquid crystal. Opt. Express 27, 10580–10585 (2019).
Fukuda, J., Yoneya, M. & Yokoyama, H. Simulation of cholesteric blue phases using a Landau–de Gennes theory: effect of an applied electric field. Phys. Rev. E 80, 031706 (2009).
Joannopoulos, J. D., Johnson, S. G., Winn, J. N. & Meade, R. D. Photonic Crystals: Modeling the flow of light. 2nd edn. (Princeton University Press, 2008).
Stathopoulos, A. & McCombs, J. R. PRIMME: PReconditioned Iterative MultiMethod Eigensolver: Methods and software description. ACM Trans. Math. Software 37(2), 21 (2010).
Fukuda, J., Okumura, Y. & Kikuchi, H. Calculation of confocal microscope images of cholesteric blue phases. Proc. SPIE 9769, 976906 (2016).
Anderson, E. et al. LAPACK Users’ Guide 3rd edn. (Society for Industrial and Applied Mathematics, 1999).
Acknowledgements
This work was supported by JSPS KAKENHI (JP17H02947, JP19H02581, JP20H00391, JP20H04672, JP20K21154), and MEXT Leading Initiative for Excellent Young Researchers. We thank Prof. Hirotsugu Kikuchi for providing blue phase materials used in the early stages of the study. We thank BASF Japan Ltd. for providing the photoinitiator, and DIC and JNC Corporation for providing the photoalignment material.
Author information
Authors and Affiliations
Contributions
S.C. designed and carried out the experiments. M.T. obtained initial results of blue phase alignment. J.F. carried out the simulation of photonic band structure and Bragg reflections of blue phases. H.Y. conceived and directed the study. M.O. supervised the study. All authors discussed the results and worked on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Primary handling editor: John Plummer
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cho, S., Takahashi, M., Fukuda, Ji. et al. Directed self-assembly of soft 3D photonic crystals for holograms with omnidirectional circular-polarization selectivity. Commun Mater 2, 39 (2021). https://doi.org/10.1038/s43246-021-00146-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-021-00146-x
This article is cited by
-
Directed crystalline symmetry transformation of blue-phase liquid crystals by reverse electrostriction
Nature Communications (2024)
-
Nanoscale three-dimensional fabrication based on mechanically guided assembly
Nature Communications (2023)
-
Pancharatnam–Berry phase reversal via opposite-chirality-coexisted superstructures
Light: Science & Applications (2022)
-
Enhanced 2D Photonic Crystal Sensor for High Sensitivity Sulfuric Acid (H2SO4) and Hydrogen Peroxide (H2O2) Detection
Silicon (2022)