Abstract
Transition metal dichalcogenide MoS2 is a two-dimensional material, attracting much attention for next-generation applications thanks to rich functionalities stemming from its crystal structure. Many experimental and theoretical works have focused on the spin-orbit interaction which couples the valley and spin degrees of freedom so that the spin-states can be electrically controllable. However, the spin-states of charge carriers and atomic vacancies in devices have not been yet elucidated directly from a microscopic viewpoint. Here, we report the spin-states in thin-film transistors using operando electron spin resonance spectroscopy. We have observed clearly different electron spin resonance signals of the conduction electrons and atomic vacancies, and distinguished the corresponding spin-states from the signals and theoretical calculations, evaluating the gate-voltage dependence and the spin-susceptibility and g-factor temperature dependence. This analysis gives deep insight into the MoS2 magnetism and clearly indicates different spin-scattering mechanisms compared to graphene, which will be useful for improvements of the device characteristics and new applications.
Similar content being viewed by others
Introduction
Since graphene was discovered in 2004, two-dimensional (2D) layered materials have attracted much attention. Among them, transition metal dichalcogenides (TMDs) denoted as MX2 have been extensively studied. TMDs, with their representative material MoS2, possess desired electrical and optical properties such as high mobility, circular-polarized light emission and flexibility, thus deserving wide investigation also in the field of valleytronics1,2,3,4. The synthesis of MoS2 and their new application have been discussed5,6. The bandgap in MoS2 single layer is direct, while it becomes indirect with increasing number of layers7. Since the nonzero bandgap exists in both the single layer and bulk, MoS2 is expected to be applicable in the thin-film devices as a next generation of graphene, the performance of which about the on/off ratio exceeds that with graphene because of a zero bandgap in graphene3,8,9,10. High electric field effect can be applied using ionic liquid, and the electric field-induced superconductivity, electrically switchable chiral light emission, and carrier spin relaxation in electrically doped MoS2 have been discussed in transistor structures with the ionic-liquid insulator11,12,13. It has been reported that the aforementioned properties are caused by the conduction- and valence-band splitting by the spin–orbit interaction (SOI)14,15,16, weak electronic localization, and spin–orbit scattering (SOS)17, discussed from the theoretical and experimental viewpoints. The spin states of atomic vacancies have been studied using the density functional theory (DFT)18,19,20. Although the spin-states investigation is an important issue for the fundamental understanding of MoS2 and applications of its magnetic properties, this matter in device structures under device operation has not been yet fully elucidated experimentally21.
Electron spin resonance (ESR) spectroscopy is useful for the spin-states study of the organic electronic devices, such as transistors, solar cells, and light-emitting diodes22,23,24. From the ESR study of graphene transistors, we have found a correlation between atomic vacancies and their conducting mechanisms25. That is, spins exist in the charge-neutral graphene due to atomic vacancies; however, when positive or negative gate voltage is applied, spins vanish and then the spin scattering of charge carriers decreases. Thus the electrically induced ambipolar spin vanishment is believed to contribute to the high carrier mobility in graphene25. Previous reports for MoS2 materials include the ESR and DFT studies of the atomic vacancies, antisites, impurities, etc. in MoS2 crystal and thin films18,19,20,21,26,27,28,29. For MoS2 transistors, the theoretical studies, fabrication methods, and device performance characterizations have been conducted3,4,8,10,11; however, operando ESR study of MoS2 devices has not been yet performed. Elucidation of the spin states of charge carriers and atomic vacancies is important for understanding the physical properties and functioning of MoS2 transistors.
Here we report MoS2 thin-film transistor spin states using the operando ESR. We have successfully observed several ESR signals, exhibiting various kinds of the electric field response, and identified their origins as derived from the conduction electrons or atomic vacancies. The ESR signal changes under the applied gate voltage are compared with the g-factor variation calculated with the gauge-including projector-augmented wave (GIPAW) method30. The temperature dependence of measured g-factors reflects the SOI and SOS and is compared to the theoretical results using the Mori–Kawasaki formula31. Therefore, these studies give an important information on the microscopic properties of MoS2 in the transistor structures. Compared to the previous ESR studies of MoS2 materials, the novel contribution of the present work is the spin-state investigation in MoS2 device structures under device operation.
Results
Device fabrication and characterization
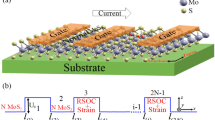
In this work, we used a device configuration called the side-gate structure, schematically presented in Fig. 1a with its cross-section in Fig. 1b. The MoS2 thin film was formed on the sapphire (Al2O3) substrate with a multi-step chemical vapor deposition (CVD) method32,33. The gate, source, and drain electrodes of Ni/Au (1/49 nm) were fabricated on Al2O3 or MoS2 with a vacuum deposition method. The insulating layer of the transistor structure was formed by the ion-gel electric double layers (EDLs), which enable to obtain a higher charge density at the low gate voltages than that of the conventional solid insulating layers34. The ion gel was formed on the polyethylene terephthalate (PET) substrate by drop casting and thermally annealed under the vacuum conditions. Then the whole system was annealed and laminated in the N2-filled glove box and wired using the Ag paste. The fabricated transistor was inserted into the ESR sample tube and sealed under He atmosphere, as presented in Fig. 1c. Details of the device fabrication method are described in the “Methods” section.
a Schematic diagram of the device structure of a MoS2 transistor used for ESR measurements. b Schematic cross-section of the device structure. c Schematic diagram of the MoS2 transistor in an ESR sample tube. d Transfer characteristic of the MoS2 transistor. The inset shows a plot of the transfer characteristics in logarithmic scale.
The spin states in the device were observed with the operando ESR spectroscopy using the liquid-He cryostat, which enables to perform measurements from 4 K to room temperature. The direction of the external magnetic field (H) was perpendicular to the MoS2 film plane unless otherwise stated. The gate voltage (VG) and drain voltage (VD) were controlled by an analyzer or a source meter, such that the operando ESR signals were measured simultaneously with the drain current (ID) and gate current (IG). Figure 1d shows the typical transfer characteristics of the fabricated device. The ID increased with the VG being positive and the n-type behavior was confirmed. The field-effect mobility μ = 6.6 cm2 V−1 s−1 and on/off ratio of 436 were obtained as the transistor parameters. The evaluated mobility and on/off ratio are lower than those of >100 cm2 V−1 s−1 and >104 reported in the previous works3,11. The reason may be ascribed to much longer channel length (500 μm) of our transistor than that (<15 μm) of the previous works because the mobility and on/off ratio are strongly affected by the charge transport across the grain boundaries of the MoS2 film in the transistor channel3,11. Another reason for the low mobility and on/off ratio may be attributed to the defectivity in the MoS2 film, as discussed later. The low mobility and on/off ratio, however, do not affect the ESR measurements because the ESR method does not require such charge transport. The reason of the use of such long channel length in the transistor structure is that we need a large active area of the transistor channel to improve the signal-to-noise ratio of the electrically induced ESR signal. The inset of Fig. 1d shows the transfer characteristics in logarithmic scale. The transistor in the forward scan is fully off at VG = 0 V. However, the transistor in the backward scan is not fully off at VG = 0 V, which may be ascribed to the slow relaxation of electric double layers due to ionic liquid in the ion gel in the side-gate transistor structure. “Methods” section contains more details of the characterization.
Operando spin observation of conduction electrons and atomic vacancies
Typical measured ESR spectra at VG = 2 and 0 V are presented in Fig. 2, where three kinds of signals: A, B, and C, are defined from the lowest applied magnetic field. We have measured the ESR spectra in the forward scan. That is, we have first measured the data at VG = 0 V, in other words, without the VG application, and then have measured the data at VG = 2 V. As shown in the inset of Fig. 1d, the transistor was in the off state at VG = 0 V in the forward scan. Thus the ESR spectra at VG = 0 V can be regarded as the background or reference data for the data at VG = 2 V. Other ESR spectra measured between VG = 2 and 0 V are similar to that at VG = 2 V except for electrically induced peak-to-peak ESR intensity, as discussed later. The signals with the opposite phase at around 306, 314, and 323 mT are due to a standard Mn2+ marker sample. We have confirmed that the signals at around 319 and 329 mT are attributed to the background signal of the ESR cavity resonator and the sapphire substrate, respectively.
a ESR spectra measured at a gate voltage (VG) of \(V_{\mathrm{G}} = 2\;{\mathrm{V}}\) and a drain voltage (VD) of VD = 1 V. b ESR spectra measured at \(V_{\mathrm{G}} = 0\;{\mathrm{V}}\) and VD = 1 V. Distortion of the baseline of the spectra at low temperatures, typically below 40 K, is due to the background signal of the ESR cavity resonator.
The spin states are clearly reflected in the ESR signals and vary due to the electron accumulation under applied VG, in “on” and “off” states. In addition, it is considered that the signals derived from the conduction electrons and atomic vacancies will exhibit different temperature dependencies. The former signals are expected to show the Pauli paramagnetism and the latter to obey the Curie law. Figure 2 shows a change of the signal intensity with VG. To analyze this effect in detail, we compared the ESR spectra with VG switched on and off and obtained the difference spectra shown in Fig. 3b, d, f. Figure 3a, c, e present the VG dependence of the ESR spectrum of Signal A, B, and C at a constant temperature, respectively, where the red and blue lines show the spectra at VG = 2 and 0 V, respectively. The data at VG = 2 and 0 V contain the background signal and baseline’s distortion due to the ESR cavity resonator. Figure 3b, d, f show the difference spectra of the Signals A, B, and C obtained by subtracting the signals at VG = 0 V from those at VG = 2 V. Since Signal A obtained at low temperatures overlapped with the background signal of the cavity resonator, we evaluated each difference after correcting the corresponding baseline signal. The intensity of Signal A increased with VG, and the difference spectrum with g-factor of 2.0546 ± 0.004 was observed at 5 K. The Signal B also increased with VG, and the difference spectrum with g = 2.0026 ± 0.004 was obtained at 40 K. In contrast, the Signal C with g = 1.9759 ± 0.004 was observed with VG = 0 V and its intensity decreased with VG; the decrease is demonstrated by the opposite phase of the difference spectrum as shown in Fig. 3f. The signal intensity and the signal position with respect to the external magnetic field have been calibrated by those of a Mn2+ marker standard sample. Therefore, it is demonstrated that these signals have different origins, because they show different g-factor and VG dependence. We have confirmed that the g-factor and ESR linewidth of the difference spectra do not depend on the VG for the region of 0 V < VG ≤ 2 V. Only the peak-to-peak ESR intensity monotonically depends on the VG, although the signal-to-noise ratio of the difference spectra is not so good for VG < 2 V. We do not discuss the VG dependence of the ESR intensity in this work in detail. Thus, for clear presentation of the difference spectra, we present the data at VG = 2 and 0 V as shown in Fig. 3.
The red lines show the spectra at VG = 2 V and VD = 1 V. The blue lines show the spectra at VG = 0 V and VD = 1 V. The data at VG = 2 and 0 V contain the background signal and baseline’s distortion due to the ESR cavity resonator. The green lines show the difference spectra obtained by subtracting the ESR spectra at VG = 0 V from that at VG = 2 V. These data almost do not contain the background signal and baseline’s distortion due to the ESR cavity resonator. a Enlarged view of the ESR spectra of Signal A at 5 K shown in Fig. 2. Baseline correction has been performed on the background signal from the ESR cavity resonator. b Difference ESR spectrum of Signal A shown in a. c, e Enlarged views of the ESR spectra of the Signals B and C shown in Fig. 2, respectively. d, f Difference ESR spectrum of the Signals B and C shown in c, e, respectively.
Further insight into the spin states such as degenerated conduction electrons or isolated spins and the SOI in MoS2 is drawn from the temperature dependence of the spin susceptibility (χ) and g-factor, respectively, evaluated from the difference spectra (Fig. 3b, d, f) obtained from the ESR spectra at VG = 2 and 0 V (Fig. 3a, c, e), which are presented in Fig. 4. The SOI determining the g-factor reflects whether the spin species are due to electrically induced charge carriers or localized charges in electrical devices. Specifically, the temperature dependence of χ is presented in Fig. 4a, c, e and of the g values in Fig. 4b, d, f for the Signals A, B, and C, respectively. The absolute value of χ for the Signals A, B, and C has been evaluated by doubly integrating the difference spectrum and comparing it with a Mn2+ marker sample with 5.6 × 1011 spins, respectively; the marker is attached to the inside wall of the ESR cavity resonator of the ESR system. Following, we derive the origins of the signals from the features of the g-factor and χ.
a, c, e Temperature dependence of the spin susceptibility (χ) of the Signals A, B, and C, respectively. In c, e, the plot of χT–T of the Signals B and C is shown, respectively. b, d, f Temperature dependence of the g-factor of Signals A, B, and C, respectively. The error bars in a, c, e and in b, d, f represent the errors from the double integral and baseline’s distortion of the difference ESR spectra shown in Fig. 3b, d, f, respectively.
Spin state of conduction electrons and theoretical calculation
We start with Signal A. χ shows almost no temperature dependence, as in Fig. 4a, and this behavior is clearly different from that of the Curie law (dotted line in Fig. 4a), which describes the isolated spins. Therefore, this signal is ascribed to be derived from the degenerated conduction electrons because no temperature dependence of the χ indicates Pauli paramagnetism that is derived from the degenerated electron systems. Moreover, the g-factor generally determined by the SOI decreased with temperature as in Fig. 4b. The g-factor shift by the intrinsic SOI has been calculated using the DFT method and the value at the zero temperature in the absence of SOS has been reported to be \(g \ast \sim 2.21\) (refs. 35,36), which is larger than our experimental result \((g\sim 2.055).\) This may imply that some spin states are isolated at atomic vacancies, while the majority of the spins may be located at the conduction band since the g-factors observed for the isolated spins are smaller than \(g\sim 2\), as discussed below. Since it has been reported that the spin-relaxation rate rises with increasing temperature17, the g-factor shift may originate from the SOS. In Supplementary Methods, Supplementary Table 1, and Supplementary Fig. 1, we theoretically considered a simple model of the monolayer MoS2, including the SOS and electron–phonon (e-ph) scattering, and assumed that the mechanism of the SOS was the Elliot–Yaffet type (EY) and D’yakonov–Perel’ (DP) type, existing in the presence of the magnetic field37. The SOS causes the spin relaxation induced by the SOI. This relaxation affects the spin states of conduction electrons, which change the characteristics of spintronic, valleytronic, and optoelectronic devices. The g-factor shift was derived from the calculation of the ESR response using the Mori–Kawasaki formula31,38. In Supplementary Fig. 1, we present a fit of the data in Fig. 4b to the aforementioned model, using the parameters for the SOS and e-ph scattering rate given in Supplementary Table 1. The result clearly shows that the SOS assisted by the e–ph interaction lowers the g-factor.
To further study the effect of the SOS, we have measured the temperature dependence of the peak-to-peak ESR linewidth \({\Delta}H_{{\mathrm{pp}}}\) of the difference spectrum of Signal A. As a result, a decrease of the \({\Delta}H_{{\mathrm{pp}}}\) from 1.9 mT at 5 K to 1.8 mT at 60 K has been observed (not shown). This result can be explained by the dominant DP spin relaxation compared to the EY spin relaxation at high temperatures because the DP spin relaxation narrows the ESR linewidth while the EY spin relaxation broadens the linewidth at high temperatures. This dominant DP spin relaxation compared to the EY spin relaxation is supported by the present theoretical calculation. That is, the calculated spin-relaxation time due to the DP type (approximately 4 × 10−7 s at 5 K and 8 × 10−7 s at 100 K) is shorter than that of the EY type (approximately 1 s at 5 K and 0.09 s at 100 K), and thus the DP spin relaxation dominantly determines the ESR linewidth because the linewidth is inversely proportional to the relaxation time.
We observed that the ESR signal lead to the different g-factor when the direction of the external magnetic field (H) was changed from the perpendicular to parallel with respect to the substrate plane. That is, the g-factor angular dependence with respect to the H direction was observed. When the angle between the H direction and the normal of the substrate plane increased from 0° (perpendicular) to 90° (parallel), the g-factor monotonically decreased from 2.0546 ± 0.004 to 1.9836 ± 0.004. Since the orbital angular momentum is different for two orientations of H, the g-factor measured in the system is confirmed to be determined by the SOI.
Spin states of different atomic vacancies
For Signal B, χ exhibits the decreasing temperature dependence, as shown in Fig. 4c. The inset of Fig. 4c shows the plot of χT–T of Signal B, which shows an almost constant behavior with respect to the temperature variation. This behavior is characteristic for the Curie law for the isolated spins (see dotted line in Fig. 4c), thus the signal is attributed to the atomic vacancies in the MoS2 thin films. As shown in Fig. 4d, the g-factor also decreased with temperature. In addition, the \({\Delta}H_{{\mathrm{pp}}}\) was obtained as 2.5 mT at 20 K and decreased monotonically to 0.8 mT at 60 K (not shown). Decreasing ESR linewidth with temperature indicates that the isolated spins are mobile, that is, the motional narrowing of the ESR linewidth. In this case, the SOS effect is believed to increase with temperature. Thus the SOS may contribute to the g-factor and lowers it with temperature, the same way as for Signal A.
For Signal C, akin to Signal B, a Curie law temperature dependence was observed, in which χ decreased with temperature, as shown in Fig. 4e (see dotted line in Fig. 4e). χ has been obtained from the ESR spectra at VG = 0 V because the difference ESR spectrum shows the opposite phase due to the decrease in the ESR intensity by the VG application (see Fig. 3f). The inset of Fig. 4e shows the plot of χT–T of Signal C, which shows an almost constant behavior with respect to the temperature variation, as observed for Signal B. Therefore, we ascribe this ESR signal to the isolated spins at atomic vacancies in the MoS2 films. No temperature dependence of the g-factor was observed, as shown in Fig. 4f. In addition, \({\Delta}H_{{\mathrm{pp}}}\) did not largely vary, changing from 1.7 to 2.0 mT in the range of 5–60 K (not shown). Therefore, the isolated spins are immobile (or localized), and the effect of the SOS may be small.
Identifications of atomic vacancies’ origins by DFT analysis
In order to investigate the atomic vacancy states in MoS2 in detail, being in the origin of Signals B and C, the DFT calculations were performed. Earlier works report several types of atomic vacancies, and among them, S, S2, MoS3, and MoS6 vacancies have been discussed as the defects that easily occur in MoS2 (refs. 18,19,39). Thus we focus on these four types of atomic vacancies. Supplementary Fig. 2 displays examples of calculated spin-density distribution around the above vacancies in the MoS2 monolayer, obtained with the DFT method, using the Quantum ESPRESSO package. To mimic the n-type operation of the ESR, in Supplementary Fig. 2, the spin densities correspond to the negatively charge-doped systems. We introduce the defects and electron doping to a monolayer (mL), bilayer (bL), trilayer (tL), and bulk material. For the bL, three configurations: A, B, and C, of the vacancy localization were considered, as shown in Supplementary Fig. 3. The electron-doping dependence of the magnetization was calculated for the mL, bL, tL, and bulk MoS2 without and with the vacancies, and it is presented in Supplementary Fig. 4. As shown in Supplementary Fig. 4, the MoS2 films with no vacancy or with S or S2 or MoS3 vacancy show no magnetization without electron doping (see Supplementary Fig. 4a–c). In contrast, the MoS2 films with MoS6 vacancy show the magnetization without electron doping (see Supplementary Fig. 4c). These results are useful for identifying the spin species of the observed ESR signals, as discussed later in detail. More detailed spin-density distribution maps are plotted in Supplementary Figs. 5–9. For the charge neutral defects, the local magnetization is non-vanishing only for the MoS6 vacancy. That is, the MoS6 vacancy in MoS2 has the diverse spin densities for spin up and spin down around the vacancy, and thus it has magnetization without electron doping (a non-vanishing state of spin), in other words, the electronic densities with spin up and spin down are different from each other (see Supplementary Figs. 2d, 4c, and 9), while other atomic vacancies in MoS2 in addition to pure MoS2 layers with no vacancy have equal spin densities for the spin up and spin down, and thus they have no magnetization without electron doping (a vanishing state of spin), in other words, the electronic densities with spin up and spin down are equal to each other (see Supplementary Fig. 4). This result has confirmed that the origin of Signal C is ascribed to the MoS6 vacancy, as discussed later. Under the electron doping, the spin density and magnetization decrease for the MoS6 vacancy (see Supplementary Figs. 2d, 4c, and 9). In contrast, for the remaining vacancies: S, S2, and MoS3, as well as the absence of the defects, the spin density and magnetization increase with weak electron doping (see Supplementary Figs. 2, 4, and 5–8).
As mentioned above, for the charge-neutral film, the calculated spin polarization vanishes for the cases of the S, S2, and MoS3 vacancies and no vacancy. This result agrees with the calculated electronic structures with non-vanishing bandgaps (Fig. 5a–d). In contrast, for the MoS6 vacancy, the bandgap disappeared for the spin down, indicating a semimetal state (as shown in Fig. 5e, f), which corresponds to the existence of magnetization even for the charge-neutral film.
a MoS2 with no vacancy. b MoS2 with the S vacancy. c MoS2 with the S2 vacancy. d MoS2 with the MoS3 vacancy. e, f MoS2 with the MoS6 vacancy for e spin-down and f spin-up case, respectively. When the electron doping is zero, no spin density or no magnetization is calculated for the cases of S, S2, and MoS3 vacancies, as shown in Supplementary Fig. 4. These results are further confirmed by the existence of the bandgap at the Fermi level with no spin density as shown in b–d. For the MoS6 vacancy, the bandgap is closed at the Fermi level depending on the spin direction as shown in e, f, which means a semimetal state. The color legend represents the projections of the bands on the Wannier functions localized at the Mo atoms.
We compare the experimental and calculated results. As can be seen from Fig. 3e, f, Signal C can be observed even without applied VG, and the signal intensity decreases with VG. From the DFT results shown in Supplementary Fig. 4c, only the MoS6 vacancy state is magnetic without electron doping among the vacancies that have been thought to occur easily in MoS2. Therefore, Signal C is reasonably ascribed to be derived from the MoS6 vacancy.
Contrary to Signal C, the intensity of Signal B increases with VG (see Fig. 3c, d). Since the magnetization increases with VG, three kinds of atomic vacancies: S, S2, and MoS3 can be a plausible origin of Signal B, examining the DFT results in Supplementary Fig. 4. To further identify the origin of this signal, the g-factors corresponding to these three vacancies were calculated, and the results are summarized in Fig. 6. Also, the g-factor shifts, with respect to the free-electron’s value (2.0023) in ppm units, and their dependence on the electron doping are shown in Supplementary Fig. 10. As shown in Fig. 6, the experimental g-factors of Signal B, of 1.987–2.003, agree with the corresponding numbers obtained from the GIPAW method for the S-vacancy case. Moreover, the g-factors calculated for the S2 and MoS3 vacancies do not coincide with the experimental values. Therefore, Signal B could be ascribed as associated with the S vacancy. The S vacancies are commonly observed using some techniques such as transmission electron microscope (TEM). In our study, we have assigned the origin of Signal B from the coincidence of not only the g-factor but also of the electron-doping dependence of the magnetization by ESR and DFT. That is, Signal B can be first observed with electrically induced electrons without the lattice distortion due to chemical doping. The previous ESR works have mainly studied films without electrically induced electrons without device structures, which may be the reason why the S vacancies have never been reliably observed in ESR.
The g-factor calculated for the S, S2, and MoS3 vacancies in the MoS2 supercell of size 12 × 12 × 1 unit, with 1–12 injected electrons, are collectively displayed. Purple area indicates the range of the observed g-factors of Signal B (g = 1.987–2.003). For the case of bilayer (bL), types A, B, and C are defined depending on the arrangement of atomic vacancies (see Supplementary Fig. 3). These g-factors are calculated for the direction of external magnetic field perpendicular to the MoS2 plane (z-axis) (see Supplementary Fig. 10). a All calculated g-factors for Signal B. b Enlarged view near the observed g-factors of Signal B (g = 1.987–2.003).
Recent ESR study of MoS2 films grown by metal organic vapor deposition and subsequently transferred on SiO2/Si has discussed the evidence of a process-induced Mo-vacancy (VMo)-related defect located at MoS2 grain edges or boundaries, which has reported the experimental g-factor of 1.9998 (ref. 40). The previous DFT study of point defects in MoS2 has reported the calculated g-values of S and Mo vacancies (VS and VMo) and antisites (SMo and MoS) as 2.031 for VS, 1.994 for VMo, 2.004 for SMo, and 2.065 for MoS, respectively20. The g-factor of the experimental and calculated values (1.9998 and 1.994) of the VMo are close to that of Signal C (g = 1.9759) under the non-doping state compared to those of other point defects. However, energy-dispersive X-ray spectroscopy (EDX) mapping of the MoS2 film used in our study shows that the atomic percentage of sulfur is smaller than the stoichiometric ratio of 2:1 for S:Mo in MoS2 (see Supplementary Table 2), which confirms the lack of sulfur in our films. Thus the VMo may be possibly excluded from the origin of Signal C of the MoS2 film fabricated by our multi-step CVD method. The amount of substitutional impurities is <1% per the MoS2 unit cell as confirmed by EDX mapping of the MoS2 film (see Supplementary Fig. 11), and thus substitutional impurities are excluded from the origins of the observed ESR signals because the observed spin concentration per the MoS2 unit cell is >2% (see “Evaluation of spin concentration” in “Methods”).
Discussion
Our results for the MoS2 thin films are compared with the previous ones for graphene. The mobility µ in graphene has been reported as about tens of thousands \({\mathrm{cm}}^2\;{\mathrm{V}}^{{\mathrm{ - 1}}}\;{\mathrm{s}}^{{\mathrm{ - 1}}}\) (ref. 41), to be compared with values of several hundred to a thousand \({\mathrm{cm}}^2\;{\mathrm{V}}^{{\mathrm{ - 1}}}\;{\mathrm{s}}^{{\mathrm{ - 1}}}\) for MoS2 (ref. 42). Since carbon atoms of graphene have four valence electrons and three C–C bonds due to the C3 symmetry, the carbon vacancy necessarily has one unpaired electron leading to a nonzero spin density43. In contrast, the unpaired electrons do not occur in MoS2 even if atomic vacancies: S, S2, and MoS3, are formed, as shown in this study. The reason may be as follows: Mo and S atoms have six and three Mo–S bonds, respectively, and six valence electrons. Thus S atom has three extra valence electrons, not used in the single bonds. For the S, S2, and MoS3 vacancies, three, six and nine electrons remain unpaired, respectively. These unpaired electrons can be coupled with counter electrons by three extra valence electrons of S, which leads to the spin-unpolarized state. For the electron doping, as described above, the spin density never vanishes and is believed to make an effect on the spin scattering of charge carriers, lowering the mobility. Contrary to MoS2, in graphene, the ambipolar spin vanishing under applied VG has been demonstrated and discussed to cause an improvement of the charge mobility by a suppression of the spin scattering of charge carriers25. That is, the spin species of a vacancy has magnetic dipolar interaction with the spin of a charge carrier, which disturbs the charge transport, while nonmagnetic vacancy does not have such interaction with a charge carrier that usually has a spin in semiconductor materials, which preserves the intrinsic mobility. Therefore, the investigations of the spin states of the atomic vacancies extend our knowledge on the mechanism of the high mobility emergence.
MoS2 thin-film transistors have been fabricated for the studies presented here, and the n-type transistor operation has been confirmed. The operando ESR measurements under electron doping have been performed with the variable VG and temperature. Three kinds of signals: Signals A, B and C, have been observed. Signals A and B increase and Signal C decreases with the applied VG, respectively. For Signal A, the spin susceptibility is almost independent of temperature, indicating that the origin of this signal can be ascribed to the degenerated conduction electrons. For Signals B and C, the spin susceptibility shows the Curie-like temperature dependence, which means that the origins of these signals can be ascribed to the isolated spins. To further investigate the ESR signal origins, the DFT and GIPAW calculations have been performed for four types of atomic vacancies: S, S2, MoS3, and MoS6, that are most likely to occur in MoS2. As a result, only MoS6 vacancy has a non-vanishing spin density without the electron doping, which enables us to identify Signal C origin to be associated with the MoS6 vacancy. In order to identify the origin of Signal B, the observed g-factor has been compared with that from the GIPAW calculations for S, S2, and MoS3 vacancies. As a result, only the g-factors calculated for the S vacancy agree with the ESR Signal B. Interestingly, the g-factors of Signals A and B show the temperature dependencies, which we assign to an effect of the SOS in MoS2 using the Mori–Kawasaki formula. In conclusion, the spin states of the conduction electrons and atomic vacancies (defects), being present in the MoS2 thin film, have been clarified in this study by the operando ESR measurement during the device operation, to our knowledge for the first time. This result gives a deep insight into our understanding of the spin states in MoS2 from the microscopic point of view and suggests a combined theoretical and experimental approach for other 2D TMDs. The previous ESR works have mainly studied MoS2 materials, where the spin states in MoS2 cannot be electrically controlled. In contrast, the present study reports the electrically controlled spin-state investigations in MoS2 with the device structure, which is more important to understand the behavior in MoS2 under device operation compared to the ESR studies of MoS2 materials without electrically doped charges. This is a novel point of our study compared to the previous ESR studies of MoS2 materials.
Methods
Fabrication of MoS2 thin film with multi-step CVD method
A sapphire (Al2O3) substrate (3 mm × 20 mm) was cleaned by ultrasonic with acetone and 2-propanol and then cleaned by ultraviolet ozone. A MoO3 (99.9%, Sigma Aldrich) thin film of 3 nm was fabricated on the sapphire substrate with a vacuum deposition method under \(1 \times 10^{ - 5}\) Pa. To crystalize the MoO3 film, the film was annealed at 325 °C for 120 min under O2 atmosphere at 200 sccm (standard cubic centimeter per minute). Sulfur powder was placed on a quartz boat, which was placed side by side with the MoO3 film in a quartz tube. The sulfur powder and the MoO3 film were heated at 275 and 550 °C, respectively, under N2 50 sccm at atmospheric pressure for 60 min, which sulfurized the MoO3 film to produce MoS2. An annealing treatment was performed at 1000 °C for 30 min under Ar 200 sccm atmosphere to improve the crystallinity. The characterization of the MoS2 film was performed by measuring the EDX mapping, cross-sectional TEM image, X-ray diffraction patterns, atomic force microscope image, and Raman spectra, which are presented in Supplementary Figs. 11–15 and Supplementary Table 2, respectively. These data confirm the thickness of 3 nm and the quality of the fabricated MoS2 film. The fabricated MoS2 with the 3-nm thickness corresponds to 5 layers with a lattice spacing of 0.62 nm32,33.
Fabrication of transistors with MoS2
Ni/Au (1/49 nm) layers were fabricated as electrodes on the MoS2 film on the sapphire substrate by a vacuum vapor deposition method with a very slow deposition rate of ≤0.1 Å s−1 using an ULVAC VPC-260F system. An ion-gel solution was fabricated with ionic liquid 1-ethyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide ([EMIM][TFSI]) (36 wt%) (Ionic Liquids Technologies, Inc.), an ABA triblock polymer poly(styrene-b-methylmethacylate-b-styrene) (3 wt%) (Polymer Source, Inc.), and a solvent ethyl acetate (61 wt%) (Wako Pure Chemical Industries, Ltd.); the solution was stirred for >1 day. The ionic liquid [EMIM][TFSI] has a cation EMIM+ and an anion TFSI−, which electrostatically attract each other. The EMIM+ and TFSI− are nonmagnetic without spin, which do not affect the spin states of the MoS2 film. The ion-gel layer was formed on an ultrasonically cleaned PET substrate (3 mm × 20 mm) by a drop-cast method, followed by a vacuum annealing treatment at 70 °C for >2 days. The reason for the formation of the ion-gel on the PET substrate is to remove the solvent ethyl acetate without the contact between the solvent and MoS2 film. The ion-gel insulating layer has an EDL and high ion conductivity44,45,46. The capacitance of the EDL is generally very large, causing a high charge-density state at low voltage and a high on/off ratio in transistor operation. After the vacuum annealing treatment, the ion-gel layer on the PET substrate and the MoS2 thin film on sapphire substrate were transferred into a glove box (O2 < 0.2 ppm, H2O < 0.5 ppm) and annealed at 70 °C for ≥2 h to remove the adsorbed moisture. The reason for the use of the Au electrodes is that Au is more stable than other metals under high electric filed at the interface with the ion-gel. The issue of the work–function difference can be overcome by the formation of the EDLs at the interface between the Au electrode and ion-gel44,45,46. A wiring was performed using a silver paste in the glove box, and finally the ion-gel layer was laminated on the MoS2 thin film. The fabricated transistor was placed into an ESR sample tube and sealed in it, where the inside of the sample tube was replaced with a He atmosphere. Supplementary Fig. 16 shows the photographs of the fabrication process of the transistor shown in Fig. 1a, c. We could not observe a clear change of the ESR signals of the MoS2 film by the electrode deposition, which indicates that the number of deposition-induced defects in the MoS2 film are negligibly smaller than that of the observed spin species in the MoS2 film. Thus we have confirmed no impact of device fabrication on our conclusions. The parts of the above-mentioned fabrication method have been described in the previous work25.
Measurements with device analyzer and ESR
Transfer characteristics were measured with a device analyzer (KEYSIGHT B1500A). The VD was fixed at 1 V and the VG was swept from 0 to 1.5 V, where the data were measured every 30 mV per 60 s at each point. ESR measurements were performed with a X-band ESR spectrometer (JEOL RESONANCE JES-FA200) equipped with a liquid-He temperature control system (temperature controller and cryostat) (JEOL RESONANCE ES-CT470) and a source meter (Keithley 2612A). The modulation amplitude of the ESR measurements was 0.3 mT.
Evaluation of spin concentration
For Signal B, the number of spins (Nspin) was evaluated by doubly integrating the difference ESR spectrum at 40 K and comparing it with a Mn2+ marker. Considering the Curie low and the temperature correction at room temperature (297 K), the Nspin was evaluated as Nspin = 8.84 × 1012. In the same way, the Nspin of Signal C was evaluated to be Nspin = 49.2 × 1012. The used active area of the transistor structure is \({\mathrm{0}}{\mathrm{.5}}\;{\mathrm{mm}} \times 12 \; {\mathrm{mm}} = {\mathrm{6}}{\mathrm{.0}}\;{\mathrm{mm}}^{\mathrm{2}} = {\mathrm{6}}.0 \,\times 10^{{\mathrm{ - 2}}}\;{\mathrm{cm}}^2\). Since the MoS2 thin film used in this experiment has five stacked layers, the spin concentration per the MoS2 unit cell is calculated to be approximately 3 and 16% for Signals B and C, respectively, using the lattice constant of MoS2 as 3.16 Å.
DFT calculations
DFT calculations were performed using the Quantum ESPRESSO package47, which is a plane-wave basis tool with the pseudopotentials describing the core electrons. For the g-tensor calculations, the norm-conserving GIPAW pseudopotentials were used48,49, with the energy cut-off 60 Ry. The g-tensor was obtained with the QE-GIPAW post-processing code30,50. The uniform mesh of k-points was set to \({\mathrm{12 \times 12 \times 1}}\) for the elementary cell, and \({{9\, \times 9 \times 1}}\) and \({{6\, \times 6 \times 1}}\) meshes for the \(3 \,\times 3 \times 1\) and \({{4\, \times 4 \times 1}}\) supercells, respectively. The vacuum separation between the periodic images of the 2D layers was set to 20 Å. We used the supercells of \(4{\mathrm{ \times }}4\) unit cells for the calculations with the defects. The distance between defects was 12.95 Å, while the chemical definition of the distance at which molecules do not interact is 10 Å. The comparison between the experimentally observed spin density and the defect density of the simulated material or the effect of the supercell size on the calculated results is an interesting issue because we can achieve high charge-density states by the ion-gel in the devices, which is in progress and will be reported in a separate paper.
The band structures were interpolated using the maximally localized Wannier functions51 implemented in the wannier90 tool52. The spin-polarization maps were plotted with the XCrySDen tool53.
Data availability
Data that support the findings of this study are available from the corresponding author upon reasonable request and can also be found at the following persistent repository: https://figshare.com/s/e08f7108e71b3dc9f631.
References
Song, I., Park, C. & Choi, H. C. Synthesis and properties of molybdenum disulphide: from bulk to atomic layers. RSC Adv. 5, 7495–7514 (2015).
Xiao, D. et al. Coupled spin and valley physics in monolayers of MoS2 and other group-VI dichalcogenides. Phys. Rev. Lett. 108, 196802 (2012).
Kim, S. et al. High-mobility and low-power thin-film transistors based on multilayer MoS2 crystals. Nat. Commun. 3, 1011–1017 (2012).
Wang, Q. H., Kalantar-Zadeh, K., Kis, A., Coleman, J. N. & Strano, M. S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 7, 699–712 (2012).
Choudhary, N., Patel, M. D., Park, J., Sirota, B. & Choi, W. Synthesis of large scale MoS2 for electronics and energy applications. J. Mater. Res. 31, 824–831 (2016).
Kumar, R. et al. A review on synthesis of graphene, h-BN and MoS2 for energy storage applications: recent progress and perspectives. Nano Res. 12, 2655–2694 (2019).
Splendiani, A. et al. Emerging photoluminescence in monolayer MoS2. Nano Lett. 10, 1271–1275 (2010).
Radisavljevic, B., Radenovic, A., Brivio, J., Giacometti, V. & Kis, A. Single-layer MoS2 transistors. Nat. Nanotechnol. 6, 147–150 (2011).
Ellis, J. K., Lucero, M. J. & Scuseria, G. E. The indirect to direct band gap transition in multilayered MoS2 as predicted by screened hybrid density functional theory. Appl. Phys. Lett. 99, 261908 (2011).
Yin, Z. et al. Single-layer MoS2 phototransistors. ACS Nano 6, 74–80 (2012).
Ye, J. T. et al. Superconducting dome in a gate-tuned band insulator. Science 338, 1193–1196 (2012).
Zhang, Y. J., Oka, T., Suzuki, R., Ye, J. T. & Iwasa, Y. Electrically switchable chiral light-emitting transistor. Science 344, 725–729 (2014).
Zhang, Y. J., Shi, W., Ye, J. T., Suzuki, R. & Iwasa, Y. Robustly protected carrier spin relaxation in electrostatically doped transition-metal dichalcogenides. Phys. Rev. B 95, 205302 (2017).
Cheiwchanchamnangij, T. & Lambrecht, W. R. L. Quasiparticle band structure calculation of monolayer, bilayer, and bulk MoS2. Phys. Rev. B 85, 205302 (2012).
Roldán, R. et al. Electronic properties of single-layer and multilayer transition metal dichalcogenides MX2 (M = Mo, W and X = S, Se). Ann. Phys. 526, 347–357 (2014).
Kormányos, A. et al. k·p theory for two-dimensional transition metal dichalcogenide semiconductors. 2D Mater. 2, 022001 (2015).
Neal, A. T., Liu, H., Gu, J. & Ye, P. D. Magneto-transport in MoS2: phase coherence, spin-orbit scattering, and the Hall factor. ACS Nano 7, 7077–7082 (2013).
Zhou, Y., Yang, P., Zu, H., Gao, F. & Zu, X. Electronic structures and magnetic properties of MoS2 nanostructures: atomic defects, nanoholes, nanodots and antidots. Phys. Chem. Chem. Phys. 15, 10385–10394 (2013).
Zheng, H. et al. Tuning magnetism of monolayer MoS2 by doping vacancy and applying strain. Appl. Phys. Lett. 104, 132403 (2014).
Houssa, M., Iordanidou, K., Pourtois, G., Afanas’ev, V. V. & Stesmans, A. Point defects in MoS2: comparison between first-principles simulations and electron spin resonance experiments. Appl. Surf. Sci. 416, 853–857 (2017).
Chiappe, D. et al. Controlled sulfurization process for the synthesis of large area MoS2 films and MoS2/WS2 heterostructures. Adv. Mater. Interfaces 3, 1–10 (2016).
Marumoto, K., Kuroda, S., Takenobu, T. & Iwasa, Y. Spatial extent of wave functions of gate-induced hole carriers in pentacene field-effect devices as investigated by electron spin resonance. Phys. Rev. Lett. 97, 256603 (2006).
Nagamori, T. & Marumoto, K. Direct observation of hole accumulation in polymer solar cells during device operation using light-induced electron spin resonance. Adv. Mater. 25, 2362–2367 (2013).
Sato, G. et al. Direct observation of radical states and the correlation with performance degradation in organic light-emitting diodes during device operation. Phys. Status Solidi A 215, 1700731 (2018).
Fujita, N. et al. Direct observation of electrically induced Pauli paramagnetism in single-layer graphene using ESR spectroscopy. Sci. Rep. 6, 34966 (2016).
Stesmans, A. et al. Paramagnetic intrinsic defects in polycrystalline large-area 2D MoS2 films grown on SiO2 by Mo sulfurization. Nanoscale Res. Lett. 12, 283 (2017).
Schoenaers, B., Stesmans, A. & Afanas’ev, V. V. The nitrogen acceptor in 2H-polytype synthetic MoS2: frequency and temperature dependent ESR analysis. Phys. Status Solidi C 14, 1700211 (2017).
Schoenaers, B., Stesmans, A. & Afanas’ev, V. V. Nitrogen acceptor in 2H-polytype synthetic MoS2 assessed by multifrequency electron spin resonance. J. Vac. Sci. Technol. A 36, 05G503 (2018).
Stesmans, A., Schoenaers, B. & Afanas’ev, V. V. Variations of paramagnetic defects and dopants in geo-MoS2 from diverse localities probed by ESR. J. Chem. Phys. 152, 234702 (2020).
Pickard, C. J. & Mauri, F. First-principles theory of the EPR g tensor in solids: defects in quartz. Phys. Rev. Lett. 88, 4 (2002).
Oshikawa, M. & Affleck, I. Electron spin resonance in S = 1/2 antiferromagnetic chains. Phys. Rev. B 65, 134410 (2002).
Heo, S., Hayakawa, R. & Wakayama, Y. Carrier transport properties of MoS2 field-effect transistors produced by multi-step chemical vapor deposition method. J. Appl. Phys. 121, 024301 (2017).
Jeong, Y. et al. Structural characterization and transistor properties of thickness-controllable MoS2 thin films. J. Mater. Sci. 54, 7758–7767 (2019).
Lee, J. et al. Ion gel-gated polymer thin-film transistors: operating mechanism and characterization of gate dielectric capacitance, switching speed, and stability. J. Phys. Chem. C 113, 8972–8981 (2009).
Pearce, A. J. & Burkard, G. Electron spin relaxation in a transition-metal dichalcogenide quantum dot. 2D Mater. 4, 025114 (2017).
Kormányos, A., Zólyomi, V., Drummond, N. D. & Burkard, G. Spin-orbit coupling, quantum dots, and qubits in monolayer transition metal dichalcogenides. Phys. Rev. X 4, 011034 (2014).
Žutić, I., Fabian, J. & Das Sarma, S. Spintronics: fundamentals and applications. Rev. Mod. Phys. 76, 323–410 (2004).
Mori, H. & Kawasaki, K. Theory of dynamical behaviors of ferromagnetic spins. Prog. Theor. Phys. 27, 529–570 (1962).
Zhou, W. et al. Intrinsic structural defects in monolayer molybdenum disulfide. Nano Lett. 13, 2615–2622 (2013).
Schoenaers, B. et al. Analysis of transferred MoS2 layers grown by MOCVD: evidence of Mo vacancy related defect formation. ECS J. Solid State Sci. Technol. 9, 093001 (2020).
Hwang, E. H., Adam, S. & Das Sarma, S. Carrier transport in two-dimensional graphene layers. Phys. Rev. Lett. 98, 186806 (2007).
Lembke, D., Bertolazzi, S. & Kis, A. Single-layer MoS2 electronics. Acc. Chem. Res. 48, 100–110 (2015).
Ma, Y., Lehtinen, P. O., Foster, A. S. & Nieminen, R. M. Magnetic properties of vacancies in graphene and single-walled carbon nanotubes. New J. Phys. 6, 68 (2004).
Panzer, M. J. & Frisbie, C. D. Exploiting ionic coupling in electronic devices: electrolyte-gated organic field-effect transistors. Adv. Mater. 20, 3176–3180 (2008).
Cho, J. H. et al. Printable ion-gel gate dielectrics for low-voltage polymer thin-film transistors on plastic. Nat. Mater. 7, 900–906 (2008).
Pu, J. et al. Highly flexible MoS2 thin-film transistors with ion gel dielectrics. Nano Lett. 12, 4013–4017 (2012).
Giannozzi, P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502 (2009).
Pickard, C. J. & Mauri, F. All-electron magnetic response with pseudopotentials: NMR chemical shifts. Phys. Rev. B 63, 245101 (2001).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Pickard, C. J. & Mauri, F. Nonlocal pseudopotentials and magnetic fields. Phys. Rev. Lett. 91, 196401 (2003).
Marzari, N., Mostofi, A. A., Yates, J. R., Souza, I. & Vanderbilt, D. Maximally localized Wannier functions: theory and applications. Rev. Mod. Phys. 84, 1419–1475 (2012).
Pizzi, G. et al. Wannier90 as a community code: new features and applications. J. Phys. Condens. Matter 32, 165902 (2020).
Kokalj, A. Computer graphics and graphical user interfaces as tools in simulations of matter at the atomic scale. Comput. Mater. Sci. 28, 155–168 (2003).
Acknowledgements
DFT calculations were performed in the Cyfronet Computer Centre using the Prometheus computer. This work was partially supported by JSPS KAKENHI Grant Numbers JP19K21955 and JP19K05201, by JST PRESTO, by The Hitachi Global Foundation, by The MIKIYA Science and Technology Foundation, by The Futaba Foundation, and by JST ALCA Grant Number JPMJAL1603, Japan.
Author information
Authors and Affiliations
Contributions
N.T. and K.M. conceived and designed this work. N.T., S.I., Y.Won, and K.M. fabricated all the devices, performed the experiments, and analyzed the data. M.W. performed the DFT calculations of g-factor and spin-density distribution. A.U. performed the calculation of the effective g-factor at finite temperature. N.T., S.H., Y.J., and Y.Wakayama fabricated all MoS2 thin films. N.T., M.W., A.U., and K.M. wrote the manuscript. K.M. supervised this work. All authors discussed the results and reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Primary handling editor: Aldo Isidori
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tsunetomo, N., Iguchi, S., Wierzbowska, M. et al. Spin-states in MoS2 thin-film transistors distinguished by operando electron spin resonance. Commun Mater 2, 27 (2021). https://doi.org/10.1038/s43246-021-00129-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-021-00129-y
This article is cited by
-
Investigating the operation mechanism of light-emitting electrochemical cells through operando observations of spin states
Communications Materials (2023)