Abstract
When a water drop is placed onto a soft polymer network, a wetting ridge develops at the drop periphery. The height of this wetting ridge is typically governed by the drop surface tension balanced by elastic restoring forces of the polymer network. However, the situation is more complex when the network is swollen with fluid, because the fluid may separate from the network at the contact line. Here we study the fluid separation and network deformation at the contact line of a soft polydimethylsiloxane (PDMS) network, swollen with silicone oil. By controlling both the degrees of crosslinking and swelling, we find that more fluid separates from the network with increasing swelling. Above a certain swelling, network deformation decreases while fluid separation increases, demonstrating synergy between network deformation and fluid separation. When the PDMS network is swollen with a fluid having a negative spreading parameter, such as hexadecane, no fluid separation is observed. A simple balance of interfacial, elastic, and mixing energies can describe this fluid separation behavior. Our results reveal that a swelling fluid, commonly found in soft networks, plays a critical role in a wetting ridge.
Similar content being viewed by others
Introduction
The wetting of soft solids plays a central role in a variety of natural functions, from the spreading of cellular aggregates1 to the adhesion of walking insects2. The ability to control wetting of soft materials is also of practical importance, for example in coatings3 and 3D printing4. Motivated by these biological and engineering applications, the concept of soft wetting has been given significant attention5,6,7,8,9,10,11,12,13,14. Yet, a fundamental understanding remains incomplete, especially when the soft polymeric surfaces are swollen with fluid.
When a water drop is placed onto a soft crosslinked solid, a wetting ridge develops around the drop periphery (Fig. 1a, b). The formation of the wetting ridge is driven by the drop’s surface tension while being resisted by the elasticity of the crosslinked network. However, if the soft solid is replaced by an immiscible fluid (e.g., oil), both liquids deform until they adopt the appropriate contact angles, defined by their interfacial tensions15,16. This liquid–liquid contact is commonly observed in slippery, lubricant-infused porous surfaces (SLIPS)17,18,19, which are traditionally textured surfaces infiltrated with an oil. Although many efforts have focused on the wetting of soft crosslinked solids and of SLIPS, less attention has been given to swollen networks, also known as gels or infused elastomers. These materials are crosslinked polymers swollen with a compatible fluid. When a drop is placed onto a swollen network, it is unclear if the surface creates a homogeneous wetting ridge, like for soft solids (Fig. 1b), or if the fluid interfacial tensions define the contact line, like for SLIPS (Fig. 1c). This illuminates a critical gap in our knowledge of soft wetting, given the fact that swollen networks are commonly implemented for soft (bio)materials applications. Moreover, wetting of soft surfaces is important for the development of slippery surfaces3,19,20,21, anti-icing surfaces22, self-lubricating surfaces23,24, surfaces for cell25,26 or drop27 patterning, and surfaces for controlling drop dynamics or coalescence28,29.
To study soft wetting, silicone elastomers (e.g., crosslinked polydimethylsiloxane, PDMS) with moduli on the order of a few kPa are often employed6,9,10,28,29,30. The mechanical properties are obtained by macroscopic rheological measurements and the material is assumed to behave as a homogenous solid6,27. However, this may not be sufficient for describing the wetting of swollen networks. PDMS elastomers typically possess uncrosslinked molecules inside the crosslinked network, which are effectively a fluid silicone oil that swells the network. This oily fluid is left over after crosslinking, and is likely a mix of linear, cyclic, and branched chains of unknown molecular weight31. Recently, Hourlier–Fargette et al. deposited water drops on vertical surfaces of stiff PDMS and measured their downward sliding velocity32. They found that the velocity drastically increases after a certain distance, and suggest that trace amounts of oily fluid inside the elastomer are pulled from the surface and encapsulate the drop; this effectively lubricates the drop. Others have also demonstrated that upon removing a water drop from a soft silicone surface, the wetting ridge relaxes and the dynamics appear to be affected by this oily fluid7,8. Moreover, the contact mechanics of soft silicone elastomers are also complicated by oily fluids in the material9,33,34. Despite progress in characterizing how drops interact with soft surfaces, a quantitative understanding of how crosslinking and swelling governs the wetting behavior is lacking.
In addition to materials aspects, being able to measure the shape of the wetting ridges is a prerequisite for understanding soft wetting. To visualize wetting ridges, several microscopy methods have been implemented, including high-speed optical imaging35, schlieren optics36, x-ray microscopy10, and confocal microscopy6,30. However, since the crosslinked network and the swelling fluid typically have similar chemical makeup, visualizing them separately is a non-trivial task. Moreover, wetting studies with in-situ visualization combined with control over both the degrees of crosslinking and swelling have not been reported, likely due to the combined challenges in imaging and sample preparation.
Here, we investigate the influence of both the degrees of crosslinking and swelling on the static wetting ridge of a soft and swollen network. Our study focuses on PDMS networks swollen with a low molecular weight fluid silicone oil or with hexadecane. By using confocal microscopy and fluorescent dyes, we show conclusively that fluid silicone oil can separate near the contact line of a water drop and a swollen network, while the network is also pulled up. This generates a pure liquid tip at a three-phase contact line of the drop, fluid, and air. We call the phenomenon where fluid separates from the network “fluid separation”. This fluid separation allows for mitigating the elastic energy penalty associated with pulling up the network, while still accommodating the surface tension of the water drop. We propose that fluid separation is driven by the spreading parameter (interfacial tensions), balanced by network elasticity and osmotic pressure. A simplified model suggests that fluid separation occurs in all cases of PDMS networks swollen with fluid silicone oil, even at moderate levels of swelling. However, when the network is swollen with hexadecane, which has a negative spreading parameter, fluid separation is not observed.
Results
Preparation of soft swollen surfaces
In our experiments, a water drop with a volume of V ~ 4 µl is placed onto soft PDMS surfaces with varying degrees of crosslinking (e.g., modulus) and swelling (i.e., the amount of fluid inside the network). To prepare our surfaces, we start with Sylgard 184 as our material system and modify the crosslinking by controlling the silicone base to the crosslinking agent mixing ratio. Surfaces are prepared with base to crosslinker ratios of 60:1 (lower modulus), 50:1, 40:1, and 30:1 (higher modulus). As with most soft commercial silicones, a significant fraction of poorly defined, oily fluid remains in the material after curing (as high as ~60% for 60:1). These oils are removed from the as-prepared state to obtain a dry network using a solvent extraction method37. To retain the thin film geometry required for wetting experiments, the extraction process is conducted on a bath of water using hexanes as a washing solvent, as described elsewhere (Supplementary Fig. 1)37. Briefly, PDMS is spin-coated onto a glass slide, which has already been coated with a water-soluble sacrificial layer. After curing, the PDMS film is released onto a bath of water and then submerged in excess hexane to allow for the oily fluid to migrate out of the network. After multiple washing steps, the hexanes are left to evaporate, leaving a thin, extracted, PDMS film. While it is possible that there is a minor amount of oil left in the network after extraction, it is expected to be negligible and play little role37,38. Therefore, we define the extracted PDMS film as the dry network.
After the extraction process, the dry network is swollen with a nonfunctional, low molecular weight (770 g mol−1) trimethylsiloxy-terminated linear silicone oil as our swelling fluid. There are several reasons for using this fluid to swell the crosslinked PDMS network. First, the network can be highly swollen in this fluid, due to its chemical compatibility. Second, the low molecular weight (and low viscosity) allows the system to reach an effective equilibrium more quickly than higher molecular weight oils. Third, silicone oil does not readily evaporate compared to other good solvents for PDMS (e.g., toluene). Finally, our work is motivated by wetting studies on soft silicone surfaces, which typically possess poorly-defined fluid silicone oil. The volumetric swelling ratio, defined as the swollen volume over the dry volume \(Q = V_{{\mathrm{swell}}}/V_{{\mathrm{dry}}}\), is controlled by adjusting the amount of fluid swollen into the network. The volume of the thin films is determined by capturing top-view images and measuring the areas, which is confirmed to be consistent with swelling experiments on macroscopic samples. To characterize the mechanical properties of the materials, rheological measurements on bulk samples are taken for the different degrees of crosslinking and swelling (Supplementary Fig. 2). For all the degrees of crosslinking, the measured moduli decrease with increasing swelling. These moduli are taken as the storage moduli at low frequency, where the rate-dependence is neglected (Supplementary Fig. 3). Note that we use Young’s modulus E to describe the modulus throughout this study. This is calculated from the shear storage modulus by assuming a Poisson’s ratio of v = 0.5, which is common for PDMS37,39,40,41.
In addition to the preparation and characterization of the materials, an important variable in soft wetting is the sample thickness. On the one hand, the underlying glass substrate can play a role in the wetting ridge when the film is thin6,42. On the other hand, a sample thickness of around 120 µm or less is best for obtaining high-resolution images with our confocal microscope. Therefore, the samples must be thin enough for quality imaging and thick enough to neglect the underlying glass substrate. By measuring the wetting ridge heights as a function of sample thickness using as-prepared 60:1 and 50:1 samples, we find that the thickness should be at least 50 µm to exclude sample thickness effects for a large 4 µl drop (Supplementary Fig. 4); this is in the range of others30,42. Since the film thicknesses decrease after extraction and increase after swelling, the initial spin-coating thickness must be chosen depending on the degree of crosslinking and the final desired swelling ratio (Q), noting that the maximum swelling ratio is a function of crosslinking (Supplementary Fig. 2). Accordingly, as-prepared films are first spin-coated to an initial thickness of ~25 to 90 µm and the final sample thicknesses for our wetting studies range from 50 to 110 µm.
Visualizing the wetting ridge
To visualize the swelling fluid and the crosslinked network at the wetting ridge, fluorescent dyes are incorporated into the material (Fig. 2a, b) and confocal microscopy is used to capture cross-sectional images. To capture these images, our confocal microscope scans an xz plane slice directly (where z is the vertical direction through the sample thickness), enabled by a piezo-driven objective. Confocal microscopy uses a laser with a particular wavelength to excite fluorophores and subsequently collects the emission by a photodetector within a specified wavelength range; this allows for precise control over which fluorophores are being excited and captured by the detectors. To visually separate the swelling fluid from the crosslinked network, two dyes with distinct emission spectra and no overlap are implemented. Independent, high sensitivity photodetectors are used to collect the emission of the two different dyes in two separate channels. Therefore, it is important that the two dyes do not have any overlap in the emission wavelength range, such that only one fluorophore is captured in each channel. Because the crosslinked network and the fluid molecules have near-identical chemical makeup, one dye is attached to the network. Bonding the fluorophore to the network prohibits the dye from dispersing into the fluid part of the material in the swollen state. A commercial fluorescein diacrylate is used as a green fluorophore (emission wavelength: λem ~ 520 nm in PDMS, Supplementary Fig. 5), which incorporates itself into the silicone network during crosslinking43. For the swelling fluid, we use a perylene monoimide (PMI) dye. The PMI is chemically modified to have a strong red shift in its absorption and emission (λem ~ 700 nm in PDMS, Supplementary Fig. 5), such that it does not overlap with the fluorescein. Spectra of the dyes in PDMS, obtained directly on the microscope, confirm the emission ranges of the fluorescein and PMI dyes in the actual PDMS environment of our experiment (Supplementary Fig. 5). Using this dye combination, we can simultaneously visualize the network (channel 1, Fig. 2c, d) and the fluid (channel 2, Fig. 2e, f) at the contact line. In the combined channel, which includes both channel 1 and channel 2 (Fig. 2g, h), the network appears yellow since the red and green colors are mixed. For the specific example in Fig. 2, the surface is a 60:1 material near its saturated swelling ratio and the macroscopic modulus is E ≈ 3 kPa (Supplementary Fig. 2). Note that for these cross-sectional images, an objective with a correction ring is used to correct z-axis distortion. To verify that confocal microscopy images are quantitative, we compare thickness measurements from confocal microscopy to optical profilometry as a second technique (Supplementary Fig. 6).
Schematics of (a) a water drop on a swollen surface, and (b) the PDMS elastomer, where the network is dyed with fluorescein and the silicone oil is dyed with PMI. c–h Schematics and corresponding confocal images of a wetting ridge for a swollen network with a water drop deposited on the surface. c, d Channel 1 shows the PDMS network (green), (e, f) channel 2 shows the silicone oil (red), and (g, h) the combination of channels 1 and 2 show both parts (yellow). Scale bars: 20 µm.
Wetting ridge measurements
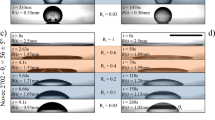
To study wetting ridges on swollen networks, the degree of swelling is varied from Q = 1 (dry) to saturation (maximum swelling) for the four different degrees of crosslinking (Sylgard 184 mixing ratios). Examples of wetting ridges for varying degrees of crosslinking and swelling are presented as a qualitative map in Fig. 3. Column A displays the dry samples that have been fully extracted. Images in the columns moving rightward display wetting ridges with increasing degrees of swelling. Column B displays wetting ridges for the maximum swelling cases. The rows show the different degrees of crosslinking from the lowest (60:1) in the top row to the highest (30:1) in the bottom row. Let us first consider the dry cases, where fluid separation is not possible. Since the surface tension of the water drop γw remains constant, the amount of network deformation is expected to be larger for softer networks. This is confirmed in column A of Fig. 3, illustrating the largest wetting ridge for 60:1 samples, which decreases as the degree of crosslinking increases toward 30:1. To describe the effect of swelling, consider the 60:1 samples as a first example (Fig. 3, top row). Upon swelling the network with lower swelling ratios, the height of the wetting ridge increases (Q ≈ 2.8 and 7.9). This is not surprising because E decreases with increasing Q (Supplementary Fig. 2). As Q is increased further, however, fluid clearly separates from the network (Q ≈ 13.4). By continuing to increase the degree of swelling towards saturation (column B), the amount of fluid separation increases. Qualitatively, the general trend of an initially increasing wetting ridge height followed by fluid separation is universal, regardless of the degree of crosslinking; this is illustrated in the 50:1, 40:1, and 30:1 rows of Fig. 3.
Each row of pictures from top to bottom corresponds to samples with a dry modulus ranging from 17 kPa to 234 kPa, and a base/crosslinker ratio from 60:1 to 30:1, respectively. Orange numbers inside each image indicate the degree of swelling and blue numbers indicate the macroscopic modulus. Column A and B display the dry and saturated conditions, respectively. Scale bar: 20 µm.
We also consider the macroscopic apparent contact angle (θapp) and the wetting ridge tip angle (θtip). The contact angle in the dry state (Q = 1), measured by a traditional goniometer (Fig. 4a), is constant at θapp(dry) = 111.9 ± 0.8° for all the degrees of crosslinking; this illustrates that contact angle is not strongly influenced by the degree of crosslinking in the dry state. In the range of the lower swelling ratios Q = 1 to Q ≈ 2, the contact angle precipitously decreases (Fig. 4b). Above Q ≈ 2, the contact angle remains nearly constant at θapp(swell) = 101.2 ± 1.1°, regardless of the crosslinking ratio (Fig. 4b). This suggests that at Q ≳ 2, a sufficient amount of fluid separates, which may play a governing role in defining the apparent contact angle. To see if the tip angle changes for different swelling cases, several xz profiles are overlaid with aligned tips. As illustrated in Fig. 4c, which includes 50:1 and 60:1 samples for situations with and without clear fluid separation, the tip angles θtip remain constant at around 71.5 ± 6.5°, at least to our level of precision. This is more clearly displayed in Fig. 4d, where the red data is for no clear fluid separation, purple is for a small amount of fluid separation, and green is for significant fluid separation (note that the network part of the green is out of view). Since θtip appears constant, regardless of the wetting ridge height, the angle at the tip is most likely governed by a constant interfacial tension. However, more experiments with higher resolution would be useful to better interpret this finding. In particular, the angles could be interpreted as not constant, if the angles were measured by extending the vertical length of the measurement zone (in which θtip would increase as red > purple > green). To attempt to focus on the very tip, we limit the angle measurement to a 1 µm zone at the tip. In general, the apparent contact angles (above Q ≈ 2) and the tip angles appear constant for the different degrees of crosslinking, pointing to the swelling fluid playing an important role in the wetting.
a–b The apparent contact angle for substrates with different degrees of swelling and base/crosslinker mixing ratios. Scale bar: 1 mm. c Examples of tip-aligned xz profiles for 50:1 and 60:1 samples, both with and without clear fluid separation. d Zoomed-in xz profiles for three samples with no fluid separation (red), a small amount of fluid separation (purple), and a significant amount of fluid separation (green). The open data points are for the fluid profile and the filled data points are for the network profile.
In addition to these angles, it is interesting to note that a flat zone develops at the fluid-network interface when fluid separation occurs, leading to three three-phase contact lines. As can be seen in the top rightmost image in Fig. 3 and the profiles in Fig. 4c, the flat zone is not completely horizontal. This is likely due to a difference in the interfacial tensions at the different contact lines. Since the water-fluid interfacial tension (right side of the flat zone, γwf = 43.2 mN m−1, Supplementary Fig. 7) is greater than the fluid-air surface tension (left side of the flat zone, γf = 19.7 mN m−1), it more strongly pulls up on the network, leading to a sloped network-fluid interface.
To quantify the wetting ridge, we measure the heights of both the network (hn) and the fluid (hf) relative to the unperturbed surface, as illustrated in Fig. 5a. For simplicity, hn is taken as the right side network height (i.e., the maximum network height). In Fig. 5b–d, both heights are plotted as a function of swelling for the different degrees of crosslinking. For the 60:1 material (Fig. 5b), hn (filled data points) and hf (open data points) remain nearly identical from Q = 1 to Q ≲ 7. In this lower swelling regime, the hn and hf both continue to increase as the swelling ratio is increased, and it is difficult to decern a difference between them if one exists. At Q ≈ 7, hf starts to clearly deviate from hn. As the swelling is increased even further, hn reaches a peak at ~15 µm and then starts to decrease, while hf continues to climb. Notably, this illustrates that at higher Q, the material expels fluid to allow the network to relax while accommodating the water drop. For the 50, 40, and 30:1 materials, the qualitative trends are similar, consistent with the images in Fig. 3. However, the quantitative values for both hn and hf differ for the different degrees of crosslinking. As the degree of crosslinking is increased, the overall magnitudes of both hf and hn decrease. For example, the peak network heights are ~15, 7, 3, and 1 µm for the 60:1 to 30:1 mixing ratios, respectively. In addition, the apparent transition of where clear fluid separation occurs is also shifted to lower swelling ratios.
a Example of a cross-sectional confocal image of a water drop on swollen 60:1 PDMS (hf and hn are the fluid and network tip heights relative to the unperturbed surface). Note that several images are stitched together to obtain a larger field of view. Scale bar: 20 µm. b–d Graphs of fluid height (hf, open data points) and network height (hn, filled data points) as a function of the degree of swelling (Q) with mixing ratios of (b) 60:1, (c) 50:1, (d) 40:1, and 30:1. e The network height for different degrees of swelling and crosslinking, where the solid curves are predictions given by ≈γw sin θ/E. Error bars denote standard deviations.
Network wetting ridge height
Commonly, the wetting ridge heights for soft solids are described by \(h_{\mathrm{n}} \approx \gamma _{\mathrm{w}}\sin \theta /E\), where θ is the contact angle10. Using measured values for the contact angle (Fig. 4b) and modulus (Supplementary Fig. 2), we overlay this calculated hn with our experimental results (Fig. 5e). The modulus is assumed to follow \(E = E_{{\mathrm{dry}}}{{\phi}} ^{0.56}\), which is consistent for a material system where the fluid likes to swell the network (Supplementary Fig. 2)44. Here, Edry is the measured modulus for dry samples and ϕ = 1/Q is the volume fraction of the polymer network. The calculated values reasonably predict the observed network height at lower swelling ratios. However, it cannot capture the network height for the cases where larger amounts of fluid separation are observed. This is also evident when plotting hn vs. E (Supplementary Fig. 8). Hence, this common relationship may be able to capture the wetting ridge heights at lower swelling ratios, as for prior studies10,45,46, but cannot capture hn when significant fluid separation occurs.
We propose two possible reasons for the peak in hn as a function of Q. First consider that when fluid separation does not occur (e.g., Q = 1), the network is being pulled up as a point load at the three-phase contact line of water, network, and air (Fig. 6a). Upon swelling the network, E decreases, such that one should expect a higher hn. However, if the fluid is expelled, then two separate forces exist pulling up on either side, which is the fluid-air surface tension (γf, left) and the water-fluid interfacial tension (γwf, right) (Fig. 6b, c). Hence, the two forces are separated by a distance, leading to two weaker forces pulling on the network. At lower swelling ratios, a very small amount of fluid separates, if at all. Therefore, the two forces from γf and γwf are close and may act together; this will lead to a hn that is higher than the dry case because of the lower modulus. Whereas at higher swelling ratios, the distance between the two forces becomes larger, and the two weaker forces may act at two points (Fig. 6c).
Confocal images show the surface/interfacial tensions pulling up the network for (a) dry, (b) low swelling ratio, and (c) high swelling ratio 60:1 samples. d Cross-sectional confocal images of four 50:1 samples with different levels of swelling and fluid separation, and (e) the corresponding profiles aligned at the network-fluid-water contact line on the right side. Interfacial tensions are shown as vectors with magnitude given in mN m−1. Scale bar: 20 µm.
A second possible reason for the peak in hn as a function of Q is due to a decrease in the network-fluid-water angle on the bottom right of the fluid separation zone (Fig. 6d, e). In order to compare the angles (α), several xz profiles are overlaid for 50:1 samples with the right angle aligned. When the degree of swelling increases (and more fluid separates), α decreases. The vertical force that pulls on the network is related to γwf sin α. Since α decreases with increasing fluid separation, the vertical force would also decrease. Therefore, hn first increases with Q due to a decreasing modulus, but then hn would decrease with Q when large fluid separation occurs due to a decreasing vertical force.
Proposed fluid separation mechanism
Here we seek out a simple, semi-quantitative model in an attempt to understand what drives fluid separation. First consider the case where a water drop is placed on a layer of immiscible oil, as often observed in SLIPS. Typically, the spreading parameter \({\it{S}} = \gamma _{\mathrm{w}} - (\gamma _{{\mathrm{wf}}} + \gamma _{\mathrm{f}})\) defines the “spreading power” (i.e., total vs. partial wetting). The oil lubricant cloaks the drop when the spreading parameter is positive47,48,49. Taking values from pendant drop measurements (Supplementary Fig. 7) for the interfacial tensions, which are consistent with literature50,51, S = 72.2 − (43.2 + 19.7) > 0; this means that in the absence of competing forces, the swelling fluid should cloak the drop. Since cloaking is not observed in our experiments, additional energies must be considered. Moreover, recent experiments from others also suggest that cloaking does not occur in static wetting on soft PDMS materials, probed by other means7,52. To rationalize this behavior, we hypothesize that while the interfacial tension of the drop pulls the network up and the fluid out, elastic energy and the energy of mixing between the network and fluid lead to a finite fluid height, hf, as illustrated in Fig. 7a. To describe fluid separation in a simplified manner, the interfacial energy is balanced by the elastic and mixing energies in equilibrium as \({\it{U}}_{{\mathrm{interfacial}}} = {\it{U}}_{{\mathrm{elastic}}} + {\it{U}}_{{\mathrm{mix}}}\). The elastic energy per unit volume for a deforming solid is given by integration of stress (σ) and strain (ε), \(U_{{\mathrm{elastic}}} \approx {\int} {\sigma \varepsilon }\). Assuming Hooke’s law is valid, this gives \({\it{U}}_{{\mathrm{elastic}}} = E\varepsilon ^2/2\). Strain is defined as \(\varepsilon = h_{\mathrm{n}}/t\), where t is the unperturbed sample thickness, such that the strain is defined in the vertical direction. This is an approximate global strain and not the true local strain around the tip since there is a complex relationship between the local and global stress and strain states that are not easily written analytically. The energy of mixing per unit volume Umix is related to the network volume fraction ϕ and the interaction parameter χ between the network and the swelling fluid. For simplicity, this is taken as the effective osmotic pressure derived from Flory-Huggins energy of mixing, \({\it{U}}_{{\mathrm{mix}}} = (k_{\mathrm{B}}T/b^3)(\ln \left( {1 - \phi } \right) + \phi + \chi \phi ^2)\), where kB is the Boltzmann constant, T is the temperature, and b is the Kuhn length53. Note that an exact value for χ is difficult to obtain. In addition to the enthalpic interactions, χ has also been shown to be a function of molecular weight, crosslinking density, and other factors54,55. Because of these complexities, an effective parameter χeff is used, which is expected to be in the range of 0.3–0.556. For Uinterfacial, we consider the spreading coefficient S as the driving force. From dimensional analysis, a length scale Δh arises as \({{U}}_{{\mathrm{interfacial}}} \sim {S/{\Delta}h}\), which is assumed to describe the height of the fluid separation, \({\Delta}{\it{h}} = {\it{h}}_f - {\it{h}}_n\) (Fig. 7a). Thus Δh may provide an idea of the fluid separation by rearranging the energy balance as:
a Schematic describing the balance of elastic, mixing, and interfacial energy. hn, hf, and Δh is also described in the schematic. b–e Plots of the experimental (filled black points) and theoretical (Eq. (1), orange open points and lines) separation heights as a function of the degree of swelling with mixing ratios of (b) 60:1, (c) 50:1, (d) 40:1, and (e) 30:1. Insets show zoomed-in data of lower swelling for clarity. f Separation height as a function of the degree of swelling of hexadecane swollen 60:1 PDMS. The dotted line is at Δh = 0. Error bars denote standard deviations.
To compare Eq. (1) to our experiments, we calculate the fluid separation height Δh using a Kuhn length of b = 1.4 nm44,57, and fitting an effective interaction parameter χeff, combined with measured values for the strain ε, moduli E, volume fractions ϕ, and interfacial tensions. The calculated values of Δh from Eq. (1) are overlaid with measured values for hf−hn in Fig. 7b–e. The data can be well fit to Eq. (1) except at very high swelling ratios, with χeff = 0.44 ± 0.04 for the different degrees of crosslinking. We suspect that the main reason for discrepancy at high swelling is associated with challenges in sample preparation of highly swollen thin films (which is also seen by the large error bars for hf at higher Q). At swelling ratios near saturation, there are likely small amounts of extra fluid on the surface, which would shift hf higher than expected. However, this does not affect measurements at swelling ratios below saturation, since the size of the films is directly measured. Nevertheless, the general trends of increasing Δh with increasing Q between our experiments and Eq. (1) are in agreement. This suggests that the fluid separation occurs due to a balance of the network elasticity, osmotic swelling pressure, and interfacial tensions.
Thus far, we have focused on PDMS networks swollen with fluid silicone oil having nearly identical chemistry. To test whether the underlying concept of Eq. 1 works for a different system, we performed a set of experiments using the 60:1 mixing ratio PDMS with hexadecane as the swelling fluid. Hexadecane is used because it swells PDMS (albeit with a much lower maximum swelling ratio), it does not readily evaporate, and it has a significantly different spreading power. For hexadecane, S = 72.2 − (49.5 + 27.5), where our measured hexadecane-water interfacial tension of 49.5 ± 0.3 is similar to literature58. Since S < 0, no fluid separation is expected to occur. Indeed, no fluid separation is observed below the saturated swelling ratio, as illustrated in Fig. 7f; the dotted line denotes zero fluid separation (also see Supplementary Fig. 9). Near the saturated swelling ratio, excess hexadecane droplets can be seen at the surface since it does not completely spread like fluid silicone oil (Supplementary Fig. 9). This supports our hypothesis that the large discrepancy between experiments and Eq. (1) near saturation is likely due to small amounts of excess fluid. The lack of fluid separation with the hexadecane swollen PDMS is consistent with Eq. (1), illustrating its generality.
Discussion
Here we call out our experimental results in Fig. 5, which suggested an abrupt transition of where fluid separation occurs. However, our proposed mechanism suggests that fluid separation should occur for all PDMS networks swollen with fluid silicone oil, even at lower swelling ratios. This inconsistency likely originates from the spatial resolution of confocal microscopy, which is on the order of several hundreds of nm, making it difficult to clearly visualize any separation at lower Q. For example, for the 60:1 samples at Q ≈ 3, Eq. (1) gives Δh ≈ 200 nm, which is not easily observed, whereas, for Q ≈ 7, Eq. (1) predicts Δh ≈ 2.5 µm, which is clearly visible. The apparent abrupt transition of fluid separation observed in the experiments should actually be a smooth transition governed by a balance of forces. This can be understood as follows: Because the network and fluid have favorable interactions, the network wants to retain the fluid. At low Q, the substrate imposes a high swelling pressure to keep the fluid inside the network, and the wetting ridge is dominated by the deformation of the overall gel (swollen network). At high Q, the drive for the network to retain fluid decreases because it already has a significant amount. This allows for the network to expel fluid at the contact line to mitigate the energy penalty of deforming the crosslinked network.
Our study is motivated by ongoing efforts in understanding how drops wet soft solids, as well as how drops behave on engineered slippery surfaces. Therefore, it is instructive to consider how our work fits into the framework of soft wetting and coatings development. For many studies, the wetting ridge is assumed to be described only by bulk mechanics while neglecting oils within the network59,60,61,62,63. However, we suggest here that fluid can come out at the tip of the contact line for swollen PDMS networks, even at moderate levels of swelling. Recently, Zhao et al. showed numerically that for a drop on a poroelastic substrate, the concentration of swelling fluid diverges near the contact line8. This is not inconsistent with our experiments, which show that fluid separation occurs to mitigate the elastic penalty at the contact line. However, the swelling fluid molecular weight is likely to play a role in both the static and dynamic wetting, which should be considered in future efforts.
Aside from drop wetting, our study is relevant for the adhesion of soft materials. For example, Berman et al. studied high-rate adhesive detachment of soft silicone elastomers from a small rigid sphere. They suggest that fluid inside the network generates a poroelastic behavior that needs to be considered in order to describe the detachment dynamics64. Elastowetting has also been considered for hydrogel materials and not limited to silicones. When a soft hydrogel sphere is placed onto a rigid surface, the sphere deforms and creates a foot near the contact line, analogous to a wetting ridge65,66. However, whether this foot is made up of mostly water or polymer is not well described. In these cases, we expect similar physics to our wetting results, except that one of the phases is non-deformable (i.e., the rigid underlying surface); this may also lead to more complex stress distributions that may need to be considered.
From an engineering perspective, swollen networks have been considered for slippery and repellent coatings (e.g., soft SLIPS). By crosslinking a PDMS network in the presence of a solvent, Urata et al. showed that the solvent can continuously leech out if the mixing energies are unfavorable; this lubricates the surface and enables easy sliding of drops24. In addition, Golovin and Tuteja developed a range of silicone elastomers for anti-icing and demonstrated that the performance is enabled by oily plasticizers (e.g., a swelling fluid)67. Although it was not explicitly studied, network deformation and fluid separation are likely important for both of these applications. Aside from soft surfaces, it has been shown for stiff, lubricant infused surfaces that the size of a lubricant wetting ridge is a function of the initial oil layer thickness68,69. Superficially, this may be analogous to the amount of fluid in a swollen network. However, these lubricant-infused, microporous surfaces do not possess mixing energy associated with the fluid-network interactions (e.g., χ) or a degree of crosslinking, which is needed to describe the wetting of soft and swollen surfaces.
In summary, we present an approach to visualize a crosslinked network and its swelling fluid separately by employing fluorescent molecules and confocal microscopy. Our experiments reveal that the static wetting ridge of a soft and swollen network can comprise both a region of network pullup and a region of pure fluid. Our calculation suggests that fluid separation occurs in all PDMS networks swollen with fluid silicone oil, although the size can be small at lower swelling ratios. The wetting ridge height of the crosslinked network increases initially with increasing swelling, but then decreases upon further swelling because more fluid is separated from the network; this allows the overall material system to mitigate the elastic energy penalty by balancing it with osmotic pressure. Using a PDMS network swollen with hexadecane, we also show that fluid separation does not occur when the swelling fluid has a negative spreading parameter. Our results clearly demonstrate the importance of considering the fluid inside of gels when investigating the wetting of soft surfaces, which are likely even more critical for dynamic cases. Overall, our study offers fundamental insight into soft wetting and poses many outstanding questions on how molecular architecture, chemical interactions, and nonlinear and complex strain states may all affect the wetting behavior of soft and swollen materials.
Methods
Preparation of swollen elastomer films
PDMS base fluorescence
Sylgard 184 (Dow) is used as our model polydimethylsiloxane (PDMS) elastomer. In order to visualize the crosslinked network, fluorescein dye is chemically incorporated into the PDMS network. Fluorescein O,O’-diacrylate (Sigma-Aldrich) is first dissolved in chloroform (ACS, VWR Chemicals) with a concentration of ~5 mg per gram of chloroform. The dye solution is then mixed with Sylgard 184 PDMS base with a fluorescein concentration of approximately ~400 μg per gram of PDMS base. The dyed base is kept in a desiccator under vacuum for ~4 days to remove residual solvent.
Silicone oil fluorescence
A red-shifted perylene monoimide (PMI) dye is utilized for the silicone oil. The perylene dye is synthesized via an N–H/C–H palladium-catalyzed domino reaction70. Details of the synthetic methods and characterization are given in Supplementary Note 1; for NMR spectra see Supplementary Figs. 10–11. The PMI powder is directly dissolved in the silicone oil (polydimethylsiloxane, trimethylsiloxy terminated, Mw: 770 g mol−1, Gelest) with a concentration of ~8 μg per gram of silicone oil. To dissolve the dye in the oil, the solution was agitated with a steel bar for 2 min until it was fully dissolved.
Thin PDMS film preparation
As-prepared PDMS elastomers are prepared using mixtures of 30:1, 40:1, 50:1, and 60:1 by weight of the dyed base and curing agent. The two parts are manually mixed with a steel bar by stirring for at least 5 min. The mixtures are then degassed under vacuum to remove trapped air bubbles for ~1 h. Thin PDMS films are then spin-coated onto a glass substrate. Before spin-coating PDMS, the glass slides (24 × 60 mm, VWR) are first cleaned by sonication in acetone (ACS, VWR Chemicals) for 15 min, and then cleaned in a UV-ozone chamber (Jelight) for 15 min. To aid in removing the thin PDMS film from the glass surface after curing, a sacrificial polyacrylic acid (PAA) (Mw: 1800 g mol−1, Sigma-Aldrich) layer is first spin-coated on the glass slide. The PAA is dissolved in water at a concentration of (30 mg g−1). The PAA solution is then spin-coated with a spin speed of 2500 r.p.m. for 60 s. Afterward, the substrates are left to dry under vacuum for 1 h. The PDMS mixture is then spin-coated onto the PAA-coated glass substrate with spin speed between 1500 to 3500 r.p.m. for 30 s to achieve a thickness range of 90 μm to 25 μm. The samples are then cured in a 65 °C pre-heated oven for 48 h.
For thin substrates, the thickness can play a role in the wetting behavior6,36,61. To determine a range where thickness effects are negligible, we measured the height of the water wetting ridge on as-prepared 60:1 and 50:1 samples with different thickness. We found the wetting ridge height to be independent of thickness when the thickness is larger than ~50 µm for 60:1 samples and ~40 µm for 50:1 samples, as shown in Supplementary Fig. 4. Therefore, all samples were prepared such that the final test samples have a thickness of at least 50 µm. It should be noted that the thicknesses change upon extracting free molecules or upon rewelling with the free fluid. Therefore, the initial spin-coated thickness for a given sample is chosen relative to the final desired swelling ratio. Thickness values were measured and verified both by confocal microscopy and by optical profilometry (Filmetrics Profilm 3D, Supplementary Fig. 6).
Extracting uncrosslinked molecules
The as-prepared soft PDMS (50:1 and 60:1) elastomers are rather sticky, making it challenging to fatten out a thin sample if it contacts itself or the container. In order to retain thin films after the extraction procedure, the interfacial extraction method, described elsewhere37, is used to remove uncrosslinked molecules that are initially present in the as-prepared samples. Briefly, the as-prepared samples are cut with a razor to a 1 cm by 0.5 cm size. They are then floated onto the surface of deionized water (VWR) in a glass petri dish. The PDMS films are released on the water surface by dissolving the sacrificial PAA underlayer. To extract the uncrosslinked PDMS chains, hexane was then carefully added to the Petri dishes to swell the network and allow uncrosslinked molecules to migrate into the surrounding media. During this procedure, the film remains at the hexane–water interface. The Petri dishes are then sealed with aluminum foil to keep hexane from evaporating. To minimize the concentration of free silicone chains in the surrounding hexane environment, the hexane is exchanged every two days. After three exchanges, the hexane is removed by syringe and micropipette, leaving the hexane-swollen PDMS film on the water surface. To dwell the sample and obtain a dry network, the Petri dishes are loosely covered with aluminum foil to slow the rate of hexane evaporation and the deswelling rate of film. After 24 h, the extracted film is left floating on the water surface.
Swelling with silicone oil and hexadecane
To systematically swell the sample with silicone oil, drops of PMI-dyed silicone oil or n-hexadecane (VWR) are added directly onto the extracted film when it is still floating on the water surface. The oil spontaneously swells into the thin film due to the affinity between silicone oil or hexadecane and the PDMS network. The degree of swelling is controlled by the volume of oil added. The petri dish is then sealed with aluminum foil for 1 week to allow the swelling to reach an equilibrium state. Thin-film samples are removed from the water surface and placed onto a glass slide. The glass slide is put under to vacuum for 1 day to remove any residual water or solvent.
Imaging via confocal microscopy
Images are captured on an inverted confocal microscope (Leica SP8) equipped with a ×40 objective with a correction ring (Leica). It should be noted that the correction ring is used to correct the z-direction height that can be stretched due to looking through the PDMS samples. The microscope is also equipped with a piezo objective kit (piezosystem jena) to capture faster cross-sectional images. Two lasers with wavelengths of 488 nm and 638 nm are utilized to excite the fluorescein and PMI dyes separately, and two high-sensitivity (HyD) detectors are used to collect emission wavelength ranges of 500–600 nm and 670–750 nm. A 4 μl water drop is placed on the sample and a cross-sectional image of the surface deformation is taken with a resolution of 1204 × 1204. The undisturbed surface line of the sample is identified by a flat surface far from the contact zone. For some samples with large deformations (e.g., 60:1), several images are taken along the x-axis and stitched together. The confocal images are analyzed using ImageJ software. The heights of oil and network are measured by the vertical distance between the flat surface and the highest tip of oil and network. The images are made binary to reduce color scattering and more clearly identify surface lines of each phase.
Characterization
Macroscale contact angle
A goniometer is used to measure the macroscopic static water contact angles on the PDMS elastomers. The goniometer pictures are analyzed with ImageJ and using Dropsnake to extract macroscale contact angle data.
Modulus
Due to the difficulty in measuring the modulus of thin-film samples, thick elastomer samples (thickness >0.5 mm) are prepared for testing by shear rheology. Samples are produced with as-prepared mixtures of 30:1, 40:1, 50:1, and 60:1 by weight of the Sylgard 184 base and curing agent. After mixing and degassing, the mixtures are then poured into a 35 mm diameter plastic Petri dish and cured in a 65 °C pre-heated oven for 48 h. To extract uncrosslinked molecules of these thick samples, the samples are immersed in a beaker of hexane for 1 week while exchanging solvent every two days. Afterward, the hexane-swollen sample is removed and allowed to dry at room temperature. A rheometer (TA Instruments Discovery HR-2) equipped with 8 mm aluminum parallel plates is used to measure the shear modulus of dry and swollen elastomers. The plates are scratched to help with mitigating slip at the boundaries. The shear modulus of highly swollen samples are tested to a strain of 1% at a frequency of 0.1 Hz and the dry and slightly swollen samples are tested to a strain of 1% at a frequency of 0.01 Hz (Supplementary Fig. 3). The strains used were confirmed to be in the linear region of a strain sweep up to 10% (Supplementary Fig. 12). The Young’s modulus (E) was calculated from the shear storage modulus (G) by assuming a Poisson’s ratio of 0.5 for incompressibility.
Swelling ratio
To quantify the amount of swelling, top view images of the films are obtained with a Nikon D610B camera equipped with a Tamron Sp Af 90 mmF/2.8Di Macro Lens while they are still floating on water. The area of the film before and after swelling and extraction is measured and the area ratio is calculated. The area ratio A is equal to the area of the swollen sample divided by dry (extracted) area, A = as/ad. Assuming the samples swell isotropically, the swelling ratio Q is then calculated as Q = A3/2.
Surface tension measurement
The pendant drop method is used to measure the surface tension of water, interfacial tension of water-silicone oil, and of water-hexadecane. A vertical needle with an outer diameter of 0.356 mm and an inner diameter of 0.178 mm is used to inject deionized water in the air, silicone oil, or hexadecane (Supplementary Fig. 7). The pendant drop pictures are analyzed with OpenDrop software71.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Douezan, S., Dumond, J. & Brochard-Wyart, F. Wetting transitions of cellular aggregates induced by substrate rigidity. Soft Matter 8, 4578–4583 (2012).
Labonte, D., Struecker, M. Y., Birn-Jeffery, A. V. & Federle, W. Shear-sensitive adhesion enables size-independent adhesive performance in stick insects. Proc. R. Soc. B Biol. Sci. 286, 20191327 (2019).
Wang, J. et al. Viscoelastic solid-repellent coatings for extreme water saving and global sanitation. Nat. Sustain 2, 1097–1105 (2019).
Roh, S., Parekh, D. P., Bharti, B., Stoyanov, S. D. & Velev, O. D. 3D printing by multiphase silicone/water capillary inks. Adv. Mater. 29, 1–7 (2017).
Cao, Z. & Dobrynin, A. V. Polymeric droplets on soft surfaces: from Neumann’s triangle to Young’s law. Macromolecules 48, 443–451 (2015).
Style, R. W. et al. Universal deformation of soft substrates near a contact line and the direct measurement of solid surface stresses. Phys. Rev. Lett. 110, 066103 (2013).
Xu, Q., Wilen, L. A., Jensen, K. E., Style, R. W. & Dufresne, E. R. Viscoelastic and poroelastic relaxations of soft solid surfaces. Phys. Rev. Lett. 125, 238002 (2020).
Zhao, M. et al. Growth and relaxation of a ridge on a soft poroelastic substrate. Soft Matter 14, 61–72 (2017).
Jensen, K. E. et al. Wetting and phase separation in soft adhesion. Proc. Natl. Acad. Sci. USA 112, 14490–14494 (2015).
Park, S. J. et al. Visualization of asymmetric wetting ridges on soft solids with X-ray microscopy. Nat. Commun. 5, 4369 (2014).
Andreotti, B. & Snoeijer, J. H. Statics and dynamics of soft wetting. Annu. Rev. Fluid Mech. 52, 285–308 (2020).
Schulman, R. D. & Dalnoki-Veress, K. Liquid droplets on a highly deformable membrane. Phys. Rev. Lett. 115, 1–5 (2015).
Seo, D. et al. The shape and dynamics of deformations of viscoelastic fluids by water droplets. J. Colloid Interface Sci 580, 776–784 (2020).
Coux, M. & Kolinski, J. M. Surface textures suppress viscoelastic braking on soft substrates. Proc. Natl Acad. Sci. USA 117, 32285–32292 (2020).
Neumann, A. W., Good, R. J., Hope, C. J. & Sejpal, M. An equation-of-state approach to determine surface tensions of low-energy solids from contact angles. J. Colloid Interface Sci 49, 291–304 (1974).
Butt, H., Graf, K. & Kappl, M. Physics and Chemistry of Interfaces. (Wiley-VCH, 2013).
Schellenberger, F. et al. Direct observation of drops on slippery lubricant-infused surfaces. Soft Matter 11, 7617–7626 (2015).
Daniel, D. et al. Origins of extreme liquid repellency on structured, flat, and lubricated hydrophobic surfaces. Phys. Rev. Lett. 120, 244503 (2018).
Wong, T. S. et al. Bioinspired self-repairing slippery surfaces with pressure-stable omniphobicity. Nature 477, 443–447 (2011).
Keiser, A., Keiser, L., Clanet, C. & Quéré, D. Drop friction on liquid-infused materials. Soft Matter 13, 6981–6987 (2017).
Mukherjee, R. et al. Oil-impregnated hydrocarbon-based polymer films. Sci. Rep. 8, 11698 (2018).
Yeong, Y. H., Wang, C., Wynne, K. J. & Gupta, M. C. Oil-infused superhydrophobic silicone material for low ice adhesion with long-term infusion stability. ACS Appl. Mater. Interfaces 8, 32050–32059 (2016).
Cui, J., Daniel, D., Grinthal, A., Lin, K. & Aizenberg, J. Dynamic polymer systems with self-regulated secretion for the control of surface properties and material healing. Nat. Mater. 14, 790–795 (2015).
Urata, C., Dunderdale, G. J., England, M. W. & Hozumi, A. Self-lubricating organogels (SLUGs) with exceptional syneresis-induced anti-sticking properties against viscous emulsions and ices. J. Mater. Chem. A 3, 12626–12630 (2015).
Zheng, W., Zhang, W. & Jiang, X. Precise control of cell adhesion by combination of surface chemistry and soft lithography. Adv. Healthc. Mater. 2, 95–108 (2013).
Sotiri, I. et al. Tunability of liquid-infused silicone materials for biointerfaces. Biointerphases 13, 06D401 (2018).
Style, R. W. et al. Patterning droplets with durotaxis. Proc. Natl Acad. Sci. USA 110, 12541–12544 (2013).
Karpitschka, S. et al. Liquid drops attract or repel by the inverted Cheerios effect. Proc. Natl Acad. Sci. USA 113, 7403–7407 (2016).
Roy, R., Seiler, R. L., Weibel, J. A. & Garimella, S. V. Droplets on soft surfaces exhibit a reluctance to coalesce due to an intervening wetting ridge. Adv. Mater. Interfaces 7, 2000731 (2020).
Gerber, J., Lendenmann, T., Eghlidi, H., Schutzius, T. M. & Poulikakos, D. Wetting transitions in droplet drying on soft materials. Nat. Commun. 10, 4776 (2019).
Nandi, S. & Winter, H. H. Swelling behavior of partially cross-linked polymers: a ternary system. Macromolecules 38, 4447–4455 (2005).
Hourlier-Fargette, A., Antkowiak, A., Chateauminois, A. & Neukirch, S. Role of uncrosslinked chains in droplets dynamics on silicone elastomers. Soft Matter 13, 3484–3491 (2017).
Pham, J. T., Schellenberger, F., Kappl, M. & Butt, H. J. From elasticity to capillarity in soft materials indentation. Phys. Rev. Mater. 1, 015602 (2017).
Glover, J. D. & Pham, J. T. Capillary-driven indentation of a microparticle into a soft, oil-coated substrate. Soft Matter 16, 5812–5818 (2020).
Van Gorcum, M., Andreotti, B., Snoeijer, J. H. & Karpitschka, S. Dynamic solid surface tension causes droplet pinning and depinning. Phys. Rev. Lett. 121, 208003 (2018).
Zhao, M. et al. Geometrical control of dissipation during the spreading of liquids on soft solids. Proc. Natl Acad. Sci. USA 115, 1748–1753 (2018).
Glover, J. D., McLaughlin, C. E., McFarland, M. K. & Pham, J. T. Extracting uncrosslinked material from low modulus sylgard 184 and the effect on mechanical properties. J. Polym. Sci. 58, 343–351 (2020).
Cai, L. H. et al. Soft Poly(dimethylsiloxane) elastomers from architecture-driven entanglement free design. Adv. Mater. 27, 5132–5140 (2015).
Du, P., Lin, I. K., Lu, H. & Zhang, X. Extension of the beam theory for polymer bio-transducers with low aspect ratios and viscoelastic characteristics. J. Micromech. Microeng. 20, 095016 (2010).
Wang, B. & Krause, S. Properties of dimethylsiloxane microphases in phase-separated dimethylsiloxane block copolymers. Macromolecules 20, 2201–2208 (1987).
Pritchard, R. H., Lava, P., Debruyne, D. & Terentjev, E. M. Precise determination of the Poisson ratio in soft materials with 2D digital image correlation. Soft Matter 9, 6037–6045 (2013).
Pericet-Camara, R. et al. Solid-supported thin elastomer films deformed by microdrops. Soft Matter 5, 3611–3617 (2009).
Clough, J. M., Creton, C., Craig, S. L. & Sijbesma, R. P. Covalent bond scission in the mullins effect of a filled elastomer: real-time visualization with mechanoluminescence. Adv. Funct. Mater. 26, 9063–9074 (2016).
Rubinstein, M. & Ralph H, C. Polymer Physics. (OUP Oxford, 2003).
Jerison, E. R., Xu, Y., Wilen, L. A. & Dufresne, E. R. Deformation of an elastic substrate by a three-phase contact line. Phys. Rev. Lett. 106, 186103 (2011).
Marchand, A., Das, S., Snoeijer, J. H. & Andreotti, B. Contact angles on a soft solid: from young’s law to Neumann’s law. Phys. Rev. Lett. 109, 1–5 (2012).
Preston, D. J., Song, Y., Lu, Z., Antao, D. S. & Wang, E. N. Design of lubricant infused surfaces. ACS Appl. Mater. Interfaces 9, 42383–42392 (2017).
Smith, J. D. et al. Droplet mobility on lubricant-impregnated surfaces. Soft Matter 9, 1772–1780 (2013).
Sett, S., Yan, X., Barac, G., Bolton, L. W. & Miljkovic, N. Lubricant-infused surfaces for low-surface-tension fluids: promise versus reality. ACS Appl. Mater. Interfaces 9, 36400–36408 (2017).
Banpurkar, A. G., Nichols, K. P. & MugeleF. Electrowetting-based microdrop tensiometer. Langmuir 24, 10549–10551 (2008).
Mchale, G., Orme, B. V., Wells, G. G. & Ledesma-aguilar, R. Apparent contact angles on lubricant-impregnated surfaces / SLIPS: from superhydrophobicity to electrowetting. Langmuir 35, 4197–4204 (2019).
Wong, W. S. Y. et al. Adaptive wetting of polydimethylsiloxane. Langmuir 36, 7236–7245 (2020).
Paul C, H. & Timothy P, L. Polymer Chemistry. (CRC Press, 2007).
Marzocca, A. J. Evaluation of the polymer-solvent interaction parameter χ for the system cured styrene butadiene rubber and toluene. Eur. Polym. J. 43, 2682–2689 (2007).
Horta, A. & Pastoriza, M. A. The interaction parameter of crosslinked networks and star polymers. Eur. Polym. J. 41, 2793–2802 (2005).
Milner, S. T., Lacasse, M. D. & Graessley, W. W. Why χ is seldom zero for polymer-solvent mixtures. Macromolecules 42, 876–886 (2009).
Gilra, N. et al. A SANS study of the conformational behaviour of linear chains in compressed and uncompressed end-linked elastomers. Macromolecules 34, 7773–7782 (2001).
Li, G., Prasad, S. & Dhinojwala, A. Dynamic interfacial tension at the oil/surfactant-water interface. Langmuir 23, 9929–9932 (2007).
Karpitschka, S. et al. Droplets move over viscoelastic substrates by surfing a ridge. Nat. Commun. 6, 7891 (2015).
Liang, H., Cao, Z., Wang, Z. & Dobrynin, A. V. Surface stresses and a force balance at a contact line. Langmuir 34, 7497–7502 (2018).
Pu, G. & Severtson, S. J. Dependence of wetting behavior on the thickness of highly viscoelastic films. J. Phys. Chem. C 115, 18729–18735 (2011).
Bostwick, J. B., Shearer, M. & Daniels, K. E. Elastocapillary deformations on partially-wetting substrates: Rival contact-line models. Soft Matter 10, 7361–7369 (2014).
Carré, A., Gastel, J.-C. & Shanahan, M. E. R. Viscoelastic effects in the spreading of liquids. Nature 379, 432–434 (1996).
Berman, J. D. et al. Singular dynamics in the failure of soft adhesive contacts. Soft Matter 15, 1327–1334 (2019).
Chakrabarti, A., Porat, A., Raphaël, E., Salez, T. & Chaudhury, M. K. Elastowetting of soft hydrogel spheres. Langmuir 34, 3894–3900 (2018).
Pham, J. T. et al. Spontaneous jumping, bouncing and trampolining of hydrogel drops on a heated plate. Nat. Commun. 8, 905 (2017).
Golovin, K. & Tuteja, A. A predictive framework for the design and fabrication of icephobic polymers. Sci. Adv. 3, e1701617 (2017).
Pham, Q. N., Zhang, S., Montazeri, K. & Won, Y. Droplets on slippery lubricant-infused porous surfaces: a macroscale to nanoscale perspective. Langmuir 34, 14439–14447 (2018).
Kreder, M. J. et al. Film dynamics and lubricant depletion by droplets moving on lubricated surfaces. Phys. Rev. X 8, 31053 (2018).
Zagranyarski, Y., Skabeev, A., Ma, Y., Müllen, K. & Li, C. Facile synthesis of annulated heterocyclic benzo[kl]acridine derivatives via one-pot N-H/C-H coupling. Org. Chem. Front. 3, 1520–1523 (2016).
Berry, J. D., Neeson, M. J., Dagastine, R. R., Chan, D. Y. C. & Tabor, R. F. Measurement of surface and interfacial tension using pendant drop tensiometry. J. Colloid Interface Sci. 454, 226–237 (2015).
Acknowledgements
We acknowledge financial support from the National Science Foundation KY-EPSCoR award 1849213 and the University of Kentucky startup funds.
Author information
Authors and Affiliations
Contributions
Z.C. performed the experiments, Z.C. and J.T.P. analyzed the results, and Z.C., S.M., and J.T.P. interpreted the results. A.S. synthesized dye molecules for the experiments. Z.C. and J.T.P. wrote the paper with support from S.M. and A.S.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Primary handling editor: Aldo Isidori
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cai, Z., Skabeev, A., Morozova, S. et al. Fluid separation and network deformation in wetting of soft and swollen surfaces. Commun Mater 2, 21 (2021). https://doi.org/10.1038/s43246-021-00125-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-021-00125-2
This article is cited by
-
Creasing in microscale, soft static friction
Nature Communications (2023)
-
Direct force measurement of microscopic droplets pulled along soft surfaces
Nature Communications (2022)