Abstract
Biological cilia generate fluid movement within viscosity-dominated environments using beating motions that break time-reversal symmetry. This creates a metachronal wave, which enhances flow efficiency. Artificially mimicking this behaviour could improve microfluidic point-of-care devices, since viscosity-dominated fluid dynamics impede fluid flow and mixing of reagents, limiting potential for multiplexing diagnostic tests. However, current biomimicry schemes require either variation in the hydrodynamic response across a cilia array or a complex magnetic anisotropy configuration to synchronise the actuation sequence with the driving field. Here, we show that simple modifications to the structural design introduce phase differences between individual actuators, leading to the spontaneous formation of metachronal waves. This generates flow speeds of up to 16 μm/s as far as 675 μm above the actuator plane. By introducing metachronal waves through lithographic structuring, large scale manufacture becomes feasible. Additionally, by demonstrating that metachronal waves emerge from non-uniformity in internal structural mechanics, we offer fresh insight into the mechanics of cilia coordination.
Similar content being viewed by others
Introduction
Magnetic micro-robots that can be actuated within fluids have grown into a thriving field of research due to their potential medical applications in drug delivery and microsurgery1,2,3. Due to the microscale dimensions of these robots, viscosity dominates over inertial motion, a regime characterized by a low Reynolds number. Within this regime, fluid flow around a fixed micro-robot depends solely on the forces that the micro-robot applies at any instant, not on the rate of force application. Consequently, fluids return to their unperturbed state if micro-robot actuation has time-reversal symmetry4: there is no net movement of fluid and no net displacement of the micro-robot. In order to introduce asymmetry into micro-robot actuation, many researchers have found inspiration from strategies employed by biological organisms. Mimicking strategies employed in biological microswimmers5,6,7, free-floating robots have been demonstrated to self-propel by rotating helical flagella1,2,3, generating travelling waves along flexible flagella8,9,10, controlling complex interactions between a colloidal swarm11,12, or asynchronously modulating shape during actuation13. Substrate-bound micro-robots frequently model biological cilia in order to generate fluid movement14,15,16,17.
Cilia are hair-like microstructures that protrude from the outer surface of biological cells and flex to move fluids and biomolecules along cell walls. Individually, cilia perform complex cyclical movements to break time-symmetry, combining a rotatory motion with an alteration of shape between the straight “effective” stroke and the bent “recovery” stroke18,19. Despite a lack of any internal coordination system, phase differences in the oscillatory actuation of neighbouring cilia generate pulses, called metachronal waves, that travel along the cell surface to enhance the efficiency of the generated flow19,20. Theoretical models indicate that the metachronal waves emerge from hydrodynamic interactions between cilia21,22,23.
Artificially reproducing the properties of cilia could generate more efficient flow generation in microfluidic applications. Several mechanisms have been proposed to create artificial cilia, including inducing electrostatic bending24, illumination of photo-active polymer flaps25, controlling acoustic resonance26 and pneumatic manipulation27. By far the most studied mechanism is magnetic actuation, in which columns typically formed from superparamagnetic particles15,16 or a polymer/magnetic particle composite14,17,28,29 are distorted by the presence of a magnetic field. While all these schemes mimic cilia in appearance, only a few are capable of producing metachronal waves as they actuate all cilia with the same phase. These schemes impose metachronal-like actuation under a uniform magnetic field by setting the magnetizations of individual cilia during fabrication. Use of millimetre-scale designs enables either the cilia28 or the substrate29 to be flexed prior to saturating the magnetization along a defined direction. Alternatively, several stages of magnetization alignment may be performed during microfabrication to effectively create a spatially varying anisotropy profile over the cilia array30. Each of these strategies predetermines the form of the metachronal wave according to the field strength and direction, while the speed of the wave is fixed by the field frequency.
A simpler approach to generating metachronal actuation is to modify the cilia length across the array31, although this has the drawback of also spatially varying the hydrodynamics of the component producing flow. Here, we take a different approach, modulating a part of the structure that influences actuation, but which produces negligible flow in its own right. We demonstrate that spatially varying the axle width of paddle-based magneto-elastic micro-robots enables metachronal waves to emerge spontaneously as the paddles rotate between bistable states defined by the field direction.
Results
Mechanical properties of paddle membranes
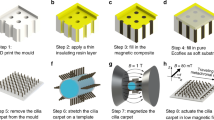
To establish the mechanical properties of the micro-robots, they were attached across a polydimethylsiloxane (PDMS) frame of 5 mm inner diameter and imaged in water under a uniaxial magnetic field. The micro-robots consisted of 10-µm-thick PDMS membranes divided into 650 µm × 500 µm cells, so that approximately 50 freestanding cells filled the 5 mm diameter frame. Each cell was composed of four 120 µm circular paddles with centre-to-centre spacing of 150 µm (Fig. 1a). Each paddle contained a hexagonal array of 6-µm-thick, 10 µm diameter Co–Ni–P cylinders with a pitch of 20 µm and was joined to a stiff frame by an axle of width w = 3–12 µm. Samples were imaged in a well filled with water to a height, h, above the membrane (Fig. 1b) with the axles aligned along the y-axis co-ordinate (Fig. 1a). Torque from the magnetic field (applied perpendicular to the axles, along the x-axis) caused the paddles to rotate on their axles.
a Schematic diagram of the whole membrane covering the frame, showing the approximate scaling of the cells to the inner diameter of the frame. The details show microscopy images of a single paddle cell within the membrane, highlighting critical dimensions of the active elements (w = 3–12 µm). Magnetic cylinders appear as dark circles. b Schematic cross-section of experimental arrangement.
Before considering how metachronal action can be introduced, we first demonstrate the basic paddle actuation. In cells containing four identical 3 µm axles, paddles rotated in unison due to the torque from a 15 Hz, 17.3 kA/m field (Fig. 2a–k and Supplementary Video 1). Differences in the response of individual paddles were negligible; with a maximum time delay of 0.18 ms between all paddles reaching a particular orientation (Supplementary Fig. 1). Reflections from otherwise dark contrast Co–Ni–P particles appeared as bright spots prior to the forward stroke (Fig. 2a), but were suppressed afterwards (Fig. 2e). This shows that the paddles had two stable orientations, at 0° under forward field (in the relaxed state) and rotated by almost 180° under reversed field (the metastable state). Figure 2k demonstrates that the paddle remained in the metastable state until a forward field was applied, indicating that the timescale of rotation due to elastic torsion, counteracted by fluid drag, was slow compared to the field frequency.
Sequence of images taken at the times indicated, showing a–e the forward and f–j the reverse rotation of four paddles (p1–p4) on identical 3-µm-wide axles during the application of a 15 Hz, 17.3 kA/m sinusoidal field. k Time-plot of individual paddle rotations and applied field for the cycle shown in a–j. l Effect of axle width and field amplitude on the maximum paddle rotation (15 Hz field). Data points are the average of three paddles in separate cells, error bars show standard deviation.
Each paddle displayed a systematic sense of rotation, although there was some variation in the sense of rotation between different paddles. Stray field interactions between the paddles would favour an opposite sense of rotation between neighbours, so may contribute to the rotation bias, but cannot solely be responsible for the pattern seen in Supplementary Video 1. Noting that any deviation from perfect parallel alignment between the paddle magnetization and the field would be sufficient to bias the rotation sense, we suggest that differences in rotation sense were introduced either by slight variations in out-of-plane magnetization texture or minor distortions in the membrane structure.
Competition between elastic torsion and the minimal magnetic torque as rotation approached 180° prevented complete symmetric rotation. Nevertheless, all fields achieved near-180° rotation except at the lowest fields (below 4 kA/m), which had slightly smaller maximum rotation (Fig. 2l). No change in rotation amplitude occurred under field frequencies between 1 and 35 Hz (at 11.2 kA/m, Supplementary Fig. 2), indicating that resonance does not play a role in actuation. Paddles on axles wider than 3 µm exhibited similar trends (Fig. 2l). However, the reduction in the maximum rotation achieved at fields below 4 kA/m became more pronounced as the axle width increased. Such reduced actuation was a consequence of the increased elastic torsion in wider axles. Therefore, while rotation was driven by the magnetic field, the structural design of the membrane provided an independent mechanism through which the actuation response could be modified.
Generation of metachronal actuation
To understand how time-reversal symmetry of paddle rotation could be broken to produce metachronal waves and therefore generate flow in a low Reynolds number environment, we developed a simplified model of the membrane, consisting of periodically repeating two-paddle cells (Fig. 3a and Supplementary Note 1). In the model, the membrane frame connecting the paddles was modelled as a series of non-magnetic beads (Fig. 3a, B1–4) joined by inflexible links to form a backbone structure. Each paddle was represented by two hard magnetic beads (Fig. 3a, P1–4) connected by inflexible links about a pivoting axis at B2 or B3. All links in the model were elastically stiff, producing negligible change in length under tension or compression. Building on our previous models of magnetically actuated swimmers32,33,34,35, we modelled the movement of the membrane in a fluid, but pinned its translational motion. Due to the restricted translational freedom, actuation that would otherwise produce propagation instead resulted in flow35,36. Torques produced by a magnetic field caused the magnetic beads to rotate around their respective paddle axes, with resultant flow due to each bead determined by Stokes’ law (the hydrodynamic resistance of the links was neglected). To describe the mechanical twisting of the paddle axles, rotation of each paddle around its pivot away from its rest position was resisted by a restoring elastic torsion proportional to a (non-dimensional) rotational stiffness. Each paddle was modelled with an individual rotational stiffness, l1 and l2, enabling the paddles to respond independently to the applied field.
a Geometry of a modelled cell, shown in cross-section with each paddle at a different rotation angle, θ. Solid lines represent the links within the paddles; dashed lines the links of the connecting backbone. Dots P1–4 are magnetic beads, dots B1–4 are non-magnetic beads and dot N shows the beginning of the next cell. Beads P1–4 are magnetized along their paddle orientation, as indicated by the arrows. b Modelled variation of x-axis flow with paddle 2 rotational stiffness, l2, at constant paddle 1 rotational stiffness l1 = 0.19 (this l1 reproduces the maximum rotation observed in the experimental axle of width w = 12 µm, see Supplementary Fig. 3). Data points highlight values of l2 when both paddles are identical (l2 = l1 = 0.19) and rotational stiffnesses corresponding to the mechanics of experimental axles w = 9 µm, 6 µm and 3 µm (l2 = 0.17, 0.15 and 0.13, respectively). c Illustration of dissimilar rotational stiffness generating non-reciprocal actuation, with left-hand paddles rotating by 60° (right-hand paddles by 45°) between time steps until rotated to near-180° and then returning to 0°. Time is represented by the arrow; the mirror symmetry in time of the driving field cycle is indicated by the solid line.
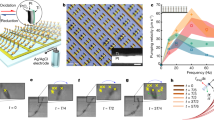
Microscopy time-sequence images showing actuation of a cell containing paddles on axles of width w = 12, 9, 6 and 3 μm during a forward and b reverse cycles under a 15 Hz, 1.9 kA/m field. Boxes highlight the movement phase for each paddle. c Time-plot of individual paddle rotations and applied field for the cycle shown in a and b. d Quantification of the phase differences between paddles on the same cell, measured as the delay in time between when the paddle on the 12-μm-wide axle reaches 90° rotation (during rotation to 0°) and when every other paddle reaches 90°.
Despite its simplicity, the model was able to reproduce experimental features of actuation and to predict design paradigms for generating flow in a low Reynolds number environment. When both paddles had identical rotational stiffness, the maximum paddle rotation depended on the field amplitude, in agreement with the mechanical experiments (Fig. 2l). Additionally, the magnitude of the rotational stiffness also influenced the largest actuation achieved (Supplementary Fig. 3). However, no flow was generated when the paddles had the same rotational stiffness (Fig. 3b), since the paddle actuation traced a path that was reciprocal in time. To produce a flow, it was necessary for the rotational stiffness of the paddles to differ (Fig. 3b).
Since elastic torsion is proportional to rotational stiffness, the two paddles with different rotational stiffness experienced different overall torque, even under identical magnetic torque. This led to phase differences between the time taken for each paddle to achieve a given rotation angle (Fig. 3c and Supplementary Video 2). As the magnetic torque is highly non-linear with time (being dependent on both the paddle rotation and a time-dependent field amplitude), small initial differences in torque were amplified to produce large phase difference between paddles. Fluid interactions between paddles and spring interactions via the backbone support had little causal effect on the emergence of a phase difference between paddles. Time symmetry between forward and reverse fields was broken because the field reversed direction while the paddle remained at near-180° rotation, causing rotation to be magnetically driven during the recovery stroke as well as the forward stroke (Supplementary Video 2). Whereas elastic torsion acted against the magnetic torque in the forward stroke, it acted in the same direction as the magnetic torque during the recovery stroke. Therefore, the phase differences between paddles were enhanced during the recovery stroke.
Analysis of the conditions under which the modelled paddle rotation reproduced the experimental measurements indicated that rotational stiffness was proportional to the axle width (Supplementary Fig. 3). Therefore, the model predicted that a graded axle width profile would be sufficient to enable flow generation. To test this experimentally, the actuation of a membrane containing cells with axles of width w = 3, 6, 9 and 12 μm was imaged under a 15 Hz, 1.9 kA/m field. During both the forward (Fig. 4a) and reverse (Fig. 4b) field cycles, the variation in the mechanical properties of the axles ensured that the paddles rotated sequentially to produce a metachronal wave throughout the membrane (Supplementary Video 3). The order of actuation was similar in the forward and reverse cycles, with the metachronal wave initiating at the 12 μm axle and propagating along the cell towards the 3 μm axle. Whereas paddles on identical axles rotated in unison (Fig. 2k), the variation of the rotational stiffness between the paddles in the graded axle width membrane introduced phase differences in the rotation angles of the paddles during actuation (Fig. 4c). To quantify the phase differences between the different paddles, we assessed the time delay to reach a specific angle, 90° (when returning to 0°) and found that the time delay decreased systematically with increasing axle width (Fig. 4d). Inhomogeneities in the sample meant there was a spread in the phase of paddles on nominally identical axles in different cells across the membrane, with around 1.5 ms standard deviation in the time delay for each axle width (Supplementary Fig. 4). Nevertheless, each individual cell followed a similar actuation sequence, such that Fig. 4 is representative of the average trend. Therefore, use of a graded axle width profile broke time-reversal symmetry in the membrane to produce non-reciprocal actuation.
Production of fluid movement
Having established the mechanism of actuation in the membranes, we now consider the effect of the actuation on the fluid around the membrane. Fluid motion generated by the graded axle width profile membrane (w = 3, 6, 9 and 12 μm within each cell) was measured from the motion of polystyrene tracer beads on the water surface (Supplementary Video 4). Whereas negligible bead motion occurred in the absence of an applied field (Fig. 5a and b), actuating the membrane generated persistent movement (Fig. 5c–f). Net flow (calculated from the average translation vector of the beads) was predominantly perpendicular to the axle axes, along the direction of deceasing axle width. Repeated measurements of the bead motion demonstrated that actuation under both high (17.4 kA/m, Fig. 5g) and low (1.9 kA/m, Fig. 5h) fields generated much faster flow than occurred prior to activation due to random drift. Since the enhanced flow speed was statistically significant (using a one-tailed paired t-test), it was unlikely to be caused by random fluctuations in surface flow, such as may be caused by temperature gradients, air currents or other environment factors. Indeed, the generation of a significant flow along the direction of decreasing axle width was in agreement with the modelled effect of inducing non-reciprocal actuation via a graded rotational stiffness profile (Fig. 3b).
a, b Still images of tracer beads before and c–f during application of a 15 Hz, 17.4 kA/m field at the time indicated (fluid height h = 544 µm). Ellipses highlight selected bead clusters and dashed lines demarcate 250 µm steps. g, h Statistical comparison of flow speed before and during application of g 17.4 kA/m and h 1.9 kA/m fields (15 Hz, h = 544 µm); * = p < 0.05 (one-tailed paired t-test), data bars are the average flow (error bars show standard deviation) from n = 3 separate field applications (individual data points; average flow for each field application measured from 50 beads). Effect of i field amplitude (at 15 Hz) and j frequency (at 11.2 kA/m) on flow speed at different h. The line in j is a linear fit to the h = 357 µm data for frequencies ≤ 20 Hz. Data obtained by calculating the magnitude of the average velocity vector from 58–187 beads, correcting for ambient drift by subtracting the average pre-field measurement (error bars derived from the standard deviation of the x- and y-components of the velocity vector).
Flow speed is a key performance indicator for many microfluidic applications, since it determines how fast fluid samples can be processed. We therefore measured how the net flow speed could be controlled using the amplitude and frequency of the applied field across a range of fluid heights. At a constant 15 Hz frequency, net flow speed was independent of the field amplitude (Fig. 5i), averaging 7.3 ± 2.5 μm/s. Since the field strength only alters the speed of disc rotation, not the sequence of actuation, the insensitivity demonstrates that the membrane actuated within the low Reynolds number regime. By contrast, increasing the field frequency generated progressive enhancement of the flow speed, following a linear trend up to 20 Hz (Fig. 5j). Despite not modifying the actuation sequence, proportional increases in flow speed with field frequency are consistent with low Reynolds number operation, assuming a similar amount of fluid was moved during each actuation cycle. Indeed, calculating the Reynolds number (Re) from the tangential velocity of the paddles13, flow was dominated by viscosity (Re < 1) up to 20 Hz, coinciding with the region of linear frequency dependence. At higher frequencies, the effects of inertia manifested in greater-than proportional increases in flow speed (Fig. 5j). Both Fig. 5i and j indicate that the flow speed produced by the membrane was largely unaffected by the fluid height, possibly due to the free surface at the top of our well (Fig. 1b). Therefore, the membrane is capable of generating significant flows within the low Reynolds number regime at heights compatible with microfluidic applications.
Discussion
Several features displayed by our membranes have potential uses in microfluidic point-of-care devices. The ability to generate flows with speeds up to 16 μm/s by tuning the field frequency potentially provides a mechanism to portion out fluid measures. Furthermore, insensitivity of flow speed to the fluid height above the membrane means that performance is tolerant towards variations in the volume of sample fluid provided by the user. This could facilitate the distribution of test samples among an array of biosensors for parallel diagnosis of multiple diseases.
On a more fundamental level, by tailoring the structural (elastic) profile of the axles within our membrane, we demonstrated an architecture in which metachronal waves were produced spontaneously. As such, the wave-generation mechanism was distinct from previous strategies of mimicking cilia motion, which either rely on imposing a pre-determined actuation sequence through the magnetic anisotropy profile37,38, or induce phase differences through progressively restricting movement of cilia along an array31. Considering the simplicity with which the structural profile can be controlled in a lithographically fabricated system, our method of producing metachronal waves could feasibly be adapted to induce complex flow patterns, such as a curved flow path, which would otherwise be difficult to achieve. Our membrane architecture could also provide insight into the spontaneous emergence of metachronal waves in biological cilia20, which has previously been attributed solely to the effects of hydrodynamic synchronization39. Given that our artificial system only displays metachronal waves when there is variation in the elastic properties of the actuating elements, our results highlight that internal structural mechanics may play a previously unrecognized role in the spontaneous generation of biological metachronal waves.
Methods
Sample fabrication
Magneto-elastic composite membranes were fabricated in three stages40. Initially, magnetically hard Co–Ni–P particles were deposited onto a glass/PMMA/Au substrate using photolithography with a 10-µm-thick AZ9260 resist and electrodeposition in an aqueous solution of 60 g/L of cobalt (II) sulfate heptahydrate (CoSO4·7H2O), 60 g/L of nickel (II) sulfate hexahydrate (NiSO4·6H2O), 3.9 g/L of sodium hypophosphite monohydrate (NaPO2H2·H2O) and 40 g/L of ammonium chloride (NH4Cl) at 30 °C. Secondly, a PDMS membrane was patterned by performing a further photolithographic step and spinning PDMS (Sylgard 184 PDMS base mixed in a 10:1 ratio with curing agent) at 7500 r.p.m. for 150 s. To maximize elasticity, the PDMS was cured at room temperature over 2 days41. Excess PDMS above the height of the photoresist was removed through reactive ion etching with SF6 (10 sccm) and O2 (2 sccm) under a 20-W power and 30 mTorr pressure. Finally, liberation of the membrane was achieved by using a nickel-compatible gold etchant to expose the sacrificial PMMA layer beneath the sample, adhering a supporting frame to the membrane with uncured PDMS (cured in situ) and soaking in acetone to dissolve the sacrificial PMMA layer. Residual gold on the membrane, left due to masking from the membrane itself, was removed by a second wash in nickel-compatible gold etchant. To define a consistent magnetization direction across the sample, the liberated structure was magnetized in an 80 kA/m field.
Actuation and flow speed measurement
For actuation measurements, samples were placed into 20 mm diameter well filled with water and imaged using a microscope incorporating a uniaxial Helmholtz coil that generated fields of 1.9–17.4 kA/m at frequencies of 5–35 Hz. Water height was calculated from the difference in focal position between the membrane and water surface. To resolve paddle rotation, membrane actuation was captured at 1500 frames per second (fps). Rotation angle was measured trigonometrically, as the inverse cosine of the projected paddle width during rotation, normalized to the maximum paddle width. Flow speed was measured using 15 µm diameter polystyrene beads that were added to the water surface. Bead motion was recorded at 200 fps, both prior to and during actuation. Net flow speed during field application was calculated as the magnitude of the average displacement vectors of 58–187 beads across the imaging area over a period of 15 s. Similarly, average flow prior to field application was measured from the drift of 50 beads over 4 s, enabling the net flow speeds to be drift-corrected. All measurements from images were performed manually using the ImageJ software.
Statistical analysis
To compare flow before and during actuation, the average flow speed from 50 beads was measured on n = 3 separate occasions under identical conditions (1.9 kA/m or 17.4 kA/m field at 15 Hz, h = 544 µm). On each occasion, flow was measured continuously from 4 s immediately before field application to 4 s after the field had been applied (on the same beads), ensuring that each measurement was independent and included a similar drift component before and during actuation, enabling a paired statistical test. Since induced flow could not be slower than the drift, all statistical comparisons were performed using a one-tailed paired t-test; differences between means were considered significant when p < 0.05.
Theoretical model
To investigate the mechanism of flow generation in the magneto-elastic membranes, we developed a minimal theoretical model based on our previous models of magnetic swimmers32,33,34,35. This is described in detail in Supplementary Note 1. Briefly, the model consists of eight beads within a unit cell, connected together via links in the arrangement shown in Fig. 3. Beads B1–4 form a backbone structure, with beads P1 and P2 connected to the backbone at bead B2 and similarly, beads P3 and P4 connected to bead B3. Therefore, the bead triplets P1-B2-P2 and P3-B3-P4 form two rotating paddles on the backbone structure. Beads P1-2 and P3-4 incorporate a magnetically hard magnetic moment aligned with their respective paddle orientations. The whole cell structure is repeated along the x-direction with periodic boundary conditions.
Solving the non-dimensionalized equation of motion for the system, movement of each bead is determined from spring, bending and fluidic interactions. Additionally, the magnetic moment of beads P1–4 mean they experience a magnetic torque due to an external elliptical magnetic field, which oscillates primarily in the x-direction with a small y-component to break the initial symmetry. Each link is treated as a high-stiffness elastic spring. Bending, described by misalignment of joined links, is resisted by a rotational stiffness that creates a restoring torque between the bead triplets describing the joint. Bead triplets describing misalignment between paddle 1 (paddle 2) and the backbone links have rotational stiffness l1 (l2). To make the paddles and backbone inflexible, bead triplets defining misalignment within each paddle (P1-B2-P2 and P3-B3-P4) and within the backbone are assigned a much greater rotational stiffness, lpaddle = lbackbone = 50. Fluidic forces acting on each bead due to drag from the surrounding fluid and flow from other beads are found using expansions that include the Stokes drag and the leading order fluid interaction term. Comparing the system with a pinned swimmer, the net movement of the beads corresponds to a flow generated in the opposite direction35,36.
Data availability
The datasets generated and analysed during the current study are available in the University of Exeter Repository, ORE (https://doi.org/10.24378/exe.2923).
Code availability
The MATLAB code used to model the effects of rotational stiffness on flow generated is available in the University of Exeter Repository, ORE (https://doi.org/10.24378/exe.2923).
References
Ghosh, A. & Fischer, P. Controlled propulsion of artificial magnetic nanostructured propellers. Nano Lett. 9, 2243–2245 (2009).
Qiu, F. M. et al. Magnetic helical microswimmers functionalized with lipoplexes for targeted gene delivery. Adv. Funct. Mater. 25, 1666–1671 (2015).
Peters, C., Hoop, M., Pane, S., Nelson, B. J. & Hierold, C. Degradable magnetic composites for minimally invasive interventions: device fabrication, targeted drug delivery, and cytotoxicity tests. Adv. Mater. 28, 533–538 (2016).
Purcell, E. M. Life at low Reynolds-number. Am. J. Phys. 45, 3–11 (1977).
Budrene, E. O. & Berg, H. C. Complex patterns formed by motile cells of escherichia-coli. Nature 349, 630–633 (1991).
Noji, H., Yasuda, R., Yoshida, M. & Kinosita, K. Direct observation of the rotation of F-1-ATPase. Nature 386, 299–302 (1997).
Polin, M., Tuval, I., Drescher, K., Gollub, J. P. & Goldstein, R. E. Chlamydomonas swims with two “gears” in a eukaryotic version of run-and-tumble locomotion. Science 325, 487–490 (2009).
Dreyfus, R. et al. Microscopic artificial swimmers. Nature 437, 862–865 (2005).
Jang, B. et al. Undulatory locomotion of magnetic multilink nanoswimmers. Nano Lett. 15, 4829–4833 (2015).
Khalil, I. S. M., Dijkslag, H. C., Abelmann, L. & Misra, S. MagnetoSperm: a microrobot that navigates using weak magnetic fields. Appl. Phys. Lett. 104, 223701 (2014).
Snezhko, A. & Aranson, I. S. Magnetic manipulation of self-assembled colloidal asters. Nat. Mater. 10, 698–703 (2011).
Garcia-Torres, J., Calero, C., Sagués, F., Pagonabarraga, I. & Tierno, P. Magnetically tunable bidirectional locomotion of a self-assembled nanorod-sphere propeller. Nat. Commun. 9, 1663 (2018).
Bryan, M. T. et al. Microscale magneto-elastic composite swimmers at the air-water and water-solid interfaces under a uniaxial field. Phys. Rev. Appl. 11, 044019 (2019).
Evans, B. A. et al. Magnetically actuated nanorod arrays as biomimetic cilia. Nano Lett. 7, 1428–1434 (2007).
Vilfan, M. et al. Self-assembled artificial cilia. Proc. Natl. Acad. Sci. USA 107, 1844–1847 (2010).
Babataheri, A., Roper, M., Fermigier, M. & Du Roure, O. Tethered fleximags as artificial cilia. J. Fluid Mech. 678, 5–13 (2011).
Belardi, J., Schorr, N., Prucker, O. & Ruhe, J. Artificial cilia: generation of magnetic actuators in microfluidic systems. Adv. Funct. Mater. 21, 3314–3320 (2011).
Brennen, C. & Winet, H. Fluid-mechanics of propulsion by cilia and flagella. Annu. Rev. Fluid Mech 9, 339–398 (1977).
Elgeti, J. & Gompper, G. Emergence of metachronal waves in cilia arrays. Proc. Natl. Acad. Sci. USA 110, 4470–4475 (2013).
Sanchez, T., Welch, D., Nicastro, D. & Dogic, Z. Cilia-like beating of active microtubule bundles. Science 333, 456–459 (2011).
Vilfan, A. & Julicher, F. Hydrodynamic flow patterns and synchronization of beating cilia. Phys. Rev. Lett. 96, 058102 (2006).
Osterman, N. & Vilfan, A. Finding the ciliary beating pattern with optimal efficiency. Proc. Natl. Acad. Sci. USA 108, 15727–15732 (2011).
Uchida, N. & Golestanian, R. Generic conditions for hydrodynamic synchronization. Phys. Rev. Lett. 106, 058104 (2011).
den Toonder, J. et al. Artificial cilia for active micro-fluidic mixing. Lab Chip 8, 533–541 (2008).
van Oosten, C. L., Bastiaansen, C. W. M. & Broer, D. J. Printed artificial cilia from liquid-crystal network actuators modularly driven by light. Nat. Mater. 8, 677–682 (2009).
Orbay, S., Ozcelik, A., Bachman, H. & Huang, T. J. Acoustic actuation of in situ fabricated artificial cilia. J. Micromech. Microeng. 28, 025012 (2018).
Milana, E., Gorissen, B., Peerlinck, S., De Volder, M. & Reynaerts, D. Artificial soft cilia with asymmetric beating patterns for biomimetic low-Reynolds-number fluid propulsion. Adv. Funct. Mater. 29, 1900462 (2019).
Lum, G. Z. et al. Shape-programmable magnetic soft matter. Proc. Natl. Acad. Sci. USA 113, E6007–E6015 (2016).
Gu, H. R. et al. Magnetic cilia carpets with programmable metachronal waves. Nat. Commun. 11, 2637 (2020).
Tsumori, F. et al. Metachronal wave of artificial cilia array actuated by applied magnetic field. Jpn. J. Appl. Phys. 55, 06GP19 (2016).
Hanasoge, S., Hesketh, P. J. & Alexeev, A. Metachronal motion of artificial magnetic cilia. Soft Matter 14, 3689–3693 (2018).
Ogrin, F. Y., Petrov, P. G. & Winlove, C. P. Ferromagnetic microswimmers. Phys. Rev. Lett. 100, 218102 (2008).
Gilbert, A. D., Ogrin, F. Y., Petrov, P. G. & Winlove, C. P. Theory of ferromagnetic microswimmers. Q. J. Mech. Appl. Math. 64, 239–263 (2011).
Bryan, M. T. et al. Emergent propagation modes of ferromagnetic swimmers in constrained geometries. J. Appl. Phys. 121, 073901 (2017).
Hamilton, J. K., Gilbert, A. D., Petrov, P. G. & Ogrin, F. Y. Torque driven ferromagnetic swimmers. Phys. Fluids 30, 092001 (2018).
Hamilton, J. K., Bryan, M. T., Gilbert, A. D., Ogrin, F. Y. & Myers, T. O. A new class of magnetically actuated pumps and valves for microfluidic applications. Sci. Rep. 8, 933 (2018).
Kim, J. et al. Programming magnetic anisotropy in polymeric microactuators. Nat. Mater. 10, 747–752 (2011).
Hines, L., Petersen, K., Lum, G. Z. & Sitti, M. Soft actuators for small-scale robotics. Adv. Mater. 29, 43 (2017).
Golestanian, R., Yeomans, J. M. & Uchida, N. Hydrodynamic synchronization at low Reynolds number. Soft Matter 7, 3074–3082 (2011).
Martin, E. L., Bryan, M. T., Pagliara, S. & Ogrin, F. Y. Advanced processing of micropatterned elasto-magnetic membranes. IEEE Trans. Magn. 55, 2900406 (2019).
Johnston, I. D., McCluskey, D. K., Tan, C. K. L. & Tracey, M. C. Mechanical characterization of bulk Sylgard 184 for microfluidics and microengineering. J. Micromech. Microeng. 24, 035017 (2014).
Acknowledgements
The work was funded by the European Union’s Horizon 2020 research and innovation programme grant 665440. The microscope with integrated Helmholtz coil was supplied by Platform Kinetics Ltd. E.L.M. was supported by the Engineering and Physical Sciences Research Council (EPSRC) Centre for Doctoral Training in Metamaterials (grant EP/L015331/1).
Author information
Authors and Affiliations
Contributions
M.T.B. and F.Y.O. conceived the experimental design. M.T.B. and A.P. fabricated the membranes. M.T.B. performed and analysed the experiments. E.L.M. and A.D.G. developed the theoretical model. E.L.M. produced the theoretical results. F.Y.O. supervised the project. M.T.B. wrote the manuscript and all authors edited it.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Primary handling editor: John Plummer.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bryan, M.T., Martin, E.L., Pac, A. et al. Metachronal waves in magnetic micro-robotic paddles for artificial cilia. Commun Mater 2, 14 (2021). https://doi.org/10.1038/s43246-021-00120-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-021-00120-7