Abstract
Conventional phase transitions are well understood in terms of the order parameter, based on the Landau–Ginzburg–Wilson theory. However, unconventional magnetic orders have been observed in clean systems such as MnSi. The unconventional magnetic orders of conduction electrons in the metallic phase has been observed for high-temperature superconductors and heavy fermion compounds. However, these unconventional magnetic orders have been limited to relatively low temperatures as quantum phase transitions. Here high-temperature magnetic short-range order is observed as one of the unconventional magnetic orders at temperatures up to 720 K in a noncentrosymmetric intermetallic antiferromagnet Mn3RhSi with a well-ordered lattice. The magnetic Mn ions form a hyperkagome network of corner-sharing triangles, where the spins are geometrically frustrated. The spin network is equivalent to that of a spin liquid and non-Fermi-liquid material, β-Mn. Our observation indicates that a metallic phase with magnetic short-range order exists at high temperatures.
Similar content being viewed by others
Introduction
Unconventional magnetic order of conduction electrons1 has been observed in a paramagnetic metallic state of MnSi under pressure by neutron diffraction2 and μSR measurements3. The similar unconventional magnetic order has been observed near the magnetic transition temperatures of inhomogeneous chiral-spin states in MnSi and FeGe4,5,6. As another case of unconventional magnetic order, solitonic spin liquid (SL) has been reported in an incommensurate magnetic phase of Fe1+yTe in a very narrow temperature range above the Néel temperature, as observed by a local magnetic probe, Mössbauer spectroscopy7. An inhomogeneous magnetic ordered state has also been observed in a triangular lattice magnet, α-NaMnO3, with nanometer-scale phase separation far below room temperature8,9. The origin of this order is attributed to local symmetry breaking by defects in the crystal structure. In addition, magnetic fragmentation has been reported for the spin ice compound Nd2Zr2O7 below 1 K10, where the tetrahedral network is known to break local symmetry for magnetic orderings, such as in an all-in-all-out structure. Manganese monoxide MnO11 with distorted face-centered cubic lattice of Mn is known as high-temperature magnetic short-range order (SRO) magnet. The magnetic diffuse scattering of SRO is observed up to 530 ± 20 K12 at the same Q-position as that of the long-range magnetic Bragg peak13. The temperature is much higher than the Néel temperature of about 120 K13.
These cases of unconventional magnetic order have been observed near critical points accompanied by symmetry breaking. The conditions may be close to multicritical points, as discussed by Belitz et al.1. These cases violate the Lifshitz condition in the Landau theory of second-order magnetic transitions as noncentrosymmetric magnetic ordering with the Dzyaloshinskii–Moriya (DM) interaction14,15,16 or incommensurate magnetic order7. Under the violation of the Lifshitz condition, we may expect an unconventional magnetic order due to an inhomogeneous order parameter. Thus far, however, the observed temperature ranges have been limited, where the ordered states are usually observed as a quantum phase transition at low temperatures.
Here, we report high-temperature magnetic SRO above the long-range magnetic transition temperature (TN = 190 K) in a noncentrosymmetric intermetallic antiferromagnet, Mn3RhSi, which is a novel compound with a β-Mn structure.
Results and discussion
According to structural refinements of the X-ray and neutron diffraction patterns at T = 293 K (Supplementary Note 1, Supplementary Figs. 1 and 2), the Mn atoms selectively occupy the 12-fold site (12b), similar to the Wyckoff 12d position of the β-Mn structure (Fig. 1a), whereas the Rh and Si atoms preferentially occupy two different 4-fold sites (4a) derived by splitting the Wyckoff 8c position of β-Mn, as previously observed for this compound family17,18,19. The 12-fold site is the magnetic moment site of β-Mn and forms a three-dimensional hyperkagome network as an ordered phase (Fig. 1a), whereas the Rh and Si atoms occupy non-magnetic sites in the β-Mn structure. In the case of β-Mn, the former 12-fold site is coordinated by near-neighbor (NN) Mn atoms with a distance of 2.66 Å, whereas the latter 8-fold site is surrounded by NN Mn atoms with a distance of 2.36 Å. The long and short bond lengths are consistent with the localized and itinerant natures of Mn 3d electrons at these sites, respectively20.
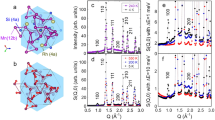
a Hyperkagome network of Mn magnetic sites in the cubic unit cell of Mn3RhSi. The 12b site of P213 is preferentially occupied by Mn magnetic moments. b Helical spin rod of triangular units along [111]. Vertical bonds correspond to the J5 ferromagnetic interaction described in ref. 21.
Below TN, the magnetic Bragg peaks, such as 100 and 110, develop (Supplementary Note 1, Supplementary Fig. 2). Those Q-positions are different from that of SRO in contrast to the case of MnO13. The refined long-range magnetic structure is shown in Fig. 1b, where each triangular unit consists of a 120° spin configuration accompanied by a small ferromagnetic component normal to the triangular plane. The triangle units form a helical spin rod along the [111] direction, which results in a geometrically frustrated hyperkagome structure. The Mn magnetic moment at T = 4 K is estimated as 2.61 ± 0.03 μB. In addition to the magnetic Bragg peaks, strong diffuse scattering is observed near Q = 1.7 Å−1, as shown in Fig. 2a. This scattering is not observed in the X-ray diffraction pattern in Fig. 2b or the electron diffraction patterns (Supplementary Note 2, Supplementary Fig. 3), confirming its magnetic origin. The Q position is precisely identical to the previously observed magnetic diffuse scattering position for SL in β-Mn0.8Co0.221 or spin glass (SG) in β-Mn1-xInx20. The original β-Mn is a well-known SL material with a three-dimensional hyperkagome network of triangular Mn spin units21. Non-Fermi-liquid (NFL) behavior is also indicated in β-Mn based on the exponent of the temperature dependence of the resistivity and the scaling of the dynamical spin susceptibility22. The magnetic diffuse scattering remains at T = 4 K, suggesting the coexistence of two types of magnetic orderings with different coherence lengths at different Q positions. The magnetic diffuse scattering intensity increases as the temperature increases up to TN. The integrated intensity is estimated as ~0.8 μB at 4 K and increases to ~1.3 μB at 300 K, based on the reverse Monte Carlo simulation reported in ref. 23 (Supplementary Note 3). However, the magnetic diffuse scattering remains at temperatures above TN, persisting to ~700 K, as shown in Fig. 3a. According to an isotropic short-range spin correlation model analysis (Supplementary Note 4), the SRO spin correlation primarily consists of an antiferromagnetic (AFM) correlation between the first NN spins and a ferromagnetic correlation between the fifth NN spins, as reported in ref. 21.
a Temperature dependence of the integrated magnetic diffuse scattering intensity near Q = 1.7 Å−1. The circles correspond to low-temperature cryostat measurements, the triangles correspond to cryofurnace measurements, and the diamonds correspond to furnace measurements. b Volume fraction of the magnetic short-range ordering component estimated from the normalized initial asymmetry. c Muon spin relaxation rate of the paramagnetic component, λ (μs−1). The data point for 320 K was obtained using ARGUS, whereas the other points were obtained using HiFi.
The observed diffuse scattering of Mn3RhSi can be attributed to a SRO. To estimate the volume fraction of the SRO in Mn3RhSi, μSR measurements were performed. μSR is a unique tool that can reveal the SRO volume fraction. This tool has been successfully applied for studies of phase separations in materials near the quantum phase transition3. In addition, the spin-lattice relaxation rate of μSR assists in our assessment of the magnetism20.
In Mn3RhSi, the SRO was observed as a decrease in the normalized initial asymmetry in the paramagnetic phase. The temperature dependence of the magnetic volume fraction over the whole volume is shown in Fig. 3b, following the estimation methods described in the methods (muon spin relaxation measurements). The volume begins to increase as the temperature decreases below 720 ± 21 K. In contrast, the muon spin relaxation rate, λ, of the remaining paramagnetic component exhibits Curie–Weiss behavior, as shown in Fig. 3c, where the Weiss temperature roughly corresponds to TN.
In the paramagnetic region, magnetic diffuse scattering appears gradually, with the μSR measurement showing a linear increase in SRO volume fraction with decreasing temperature. These different temperature dependences suggest that the magnetic moment in the SRO state gradually develops with decreasing temperature.
Based on the μSR measurement (Supplementary Note 5), the SRO volume fraction was 22.9% at T = 300 K. According to neutron diffraction measurements at T = 4 K, the ordered magnetic moment was 2.61 μB, whereas the magnetic moment of the diffuse scattering was approximately 0.8 μB. The total magnetic moment reaches 2.73 μB at 4 K. As the temperature increases to 300 K, only the magnetic moment of diffuse scattering remains at 1.3 μB. Based on the 22.9% SRO volume fraction at 300 K, the total magnetic moment is expected to decrease from 2.73 μB at 4 K to 1.31 μB at 300 K. This value of 1.31 μB is almost the same as the observed value of 1.3 μB by neutron diffuse scattering at 300 K. This coincidence suggests that the magnetic moment is transferred from the SRO to the long-range order at the other Q position on cooling below the Néel temperature.
One may suspect that the magnetic diffuse scattering may be induced by disorders such as local defects or elemental substitutions at individual sites in the crystal structure. In addition, not only the magnetic structure but also the crystal structure may be phase-separated, as observed in the triangular lattice magnet α-NaMnO38,9. The crystal structure of Mn3RhSi was studied by both neutron and X-ray diffraction measurements, and neither defects nor elemental disorders were identified in the range of 3σ (Supplementary Note 1, Supplementary Table 1). However, nuclear diffuse scattering may be included in Fig. 2a, as observed at Q = 0.8 Å−1 for β-Mn1-xInx20. In the case of Mn3RhSi, nuclear diffuse scattering at Q = 0.8 Å−1 is not observed in the X-ray diffraction pattern, as shown in Fig. 2b. Our electron diffraction measurement shows diffuse scattering peaks at {1/2 1/4 2} as the lowest reciprocal point, which corresponds to Q = 2.01 Å−1 (Supplementary Note 2, Supplementary Fig. 3). This diffuse scattering is not observed in the X-ray diffraction pattern of Fig. 2b, possibly due to its weak intensity. The diffuse scattering intensity significantly decreased from T = 100 K to 300 K, suggesting that the lattice strain may disappear above 300 K. Based on these results, we conclude that the SRO does not originate from disorder.
The SRO in this new compound, Mn3RhSi, is confirmed by a complementary use of neutron diffraction, X-ray diffraction, electron diffraction, and μSR measurements in this work. The SRO effect is manifested in the physical properties of Mn3RhSi as follows. The temperature dependence of the magnetic susceptibility of Mn3RhSi exhibits non-Curie–Weiss behavior over a wide temperature range from the long-range magnetic transition temperature (TN = 190 K) to ~700 K (Fig. 4a). The detailed study of the magnetic susceptibility is shown in Supplementary Note 6. As a possible origin of this non-Curie–Weiss behavior, one may consider a possible coupling of localized spins and conduction electrons as the Kondo effect in this compound. However, the low-temperature specific heat capacity does not show any significant enhancement of the electron mass, as illustrated in Fig. 4b. The estimated Sommerfeld constant γ is 12.18 ± 0.03 mJ Mn−1 K−2, while β-Mn is known as a heavy 3d electron material with a Sommerfeld constant of 70 mJ Mn−1 K−2 24. β-Mn shows a broad peak at ~140 K in the temperature dependence of the magnetic susceptibility, which may correspond to the Kondo temperature. Based on the specific heat results, we conclude that the Kondo effect is not the origin of this non-Curie–Weiss behavior. Some low-dimensional magnets also show a hump structure in the magnetic susceptibility, such as Bonner–Fisher-type magnets25. However, the present compound is a three-dimensional cubic magnet. The critical exponent of the temperature dependence of the Mn magnetic moment is close to 1/3, conforming to the classical model of a three-dimensional magnet. The solid line in Fig. 5 is a least-squares fit to the ordered magnetic moment based on the classical power-law function expressed as μ(T) = μ0 (1 − T/TN)β. The fitting gives a long-range magnetic transition temperature of 190.1 ± 0.2 K and a critical exponent β of 0.28 ± 0.03. The obtained transition temperature is consistent with that of the magnetic susceptibility measurement. The critical exponent suggests a second-order-type phase transition, with three-dimensional spin interactions corresponding to the Ising, XY, or Heisenberg model in Mn3RhSi26. This result excludes the possibility of Bonner–Fisher-type magnetic susceptibility in the paramagnetic region. Based on these results, the origin of the present non-Curie–Weiss temperature dependence can be attributed to the SRO effect.
a Temperature dependence of zero-field-cooled and field-cooled magnetic susceptibilities χ(= M/H) under a magnetic field of 3 kOe for a polycrystalline sample of Mn3RhSi. The crosses denote measurements in a high-temperature SQUID furnace. The inset shows the inverse magnetic susceptibility. The black solid line is a Curie–Weiss fit in the temperature range from 700 to 800 K. b Low-temperature specific heat capacity of Mn3RhSi. The electronic specific heat γ is estimated as 12.18 ± 0.03 mJ Mn−1 K−2, and the Debye temperature θD is 275.2 ± 0.2 K.
Similar ternary cubic compounds, such as Mn3TX (T = Co, Ir; X = Si, Ge)17,18,19, have primarily been characterized with respect to their crystallographic and long-range ordered magnetic structure. The published data are inconclusive regarding possible SRO in these series, but non-Curie–Weiss behavior and broad magnetic diffuse scattering signals in neutron powder diffraction patterns above the ordering temperature may warrant further research on these compounds. Results for the series of compounds with the β-Mn structure suggest that Mn3RhSi is located near a quantum critical point between a SL state and a long-range AFM ordered state, as shown in Fig. 6, where the long-range magnetic transition temperature decreases as the lattice constant decreases toward the quantum critical point. As the lattice constant decreases, the electronic bandwidth W increases. Therefore, the decrease in TN with decreasing U/W is consistent with the theoretical expectation for an AFM metal. However, some variations in TN are shown for the different systems in Fig. 6, suggesting that other parameters, such as the DM interaction, are required to describe this phase diagram. In this sense, there may be a quantum multicritical point1 that depends on the bandwidth, the DM interaction, and other parameters such as the Fermi surface topology. Our remarkable finding is the widely spread unconventional magnetic SRO up to 720 K, as illustrated in Fig. 6. Although this SRO state has not been confirmed in other compounds, magnetic diffuse scattering has been observed in β-Mn24, β-Mn0.8Co0.221, β-Mn1-xInx20, and β-Mn1-xAlx23. Notably, diffuse scattering occurs in β-Mn24, but the intensity decreases with decreasing temperature, and almost disappears at low temperatures. For β-Mn0.8Co0.2, however, the diffuse scattering intensity decreases with increasing temperature, and almost disappears at T = 200 K21. Therefore, the SRO transition temperature may be approximately 200 K for β-Mn0.8Co0.2. These results suggest that the SRO transition temperature rapidly decreases toward the quantum critical point, as illustrated in Fig. 6. Near the critical point, the family of β-Mn compounds exhibits NFL behavior22, as observed in MnSi4. Therefore, the phase diagram of Fig. 6 may include B20 family compounds. The SRO of MnSi at ambient pressure occurs at 1 K above the helical magnetic order temperature of 29 K4. For FeGe, the precursor region corresponds to ~2 K above the long-range magnetic order temperature of 278.2 K5, and the NFL behavior seems to disappear in the SG/AFM phase. Thus far, the SRO has a limited temperature range, possibly because of the weak DM interaction of 3d elements. The pseudogap state of cuprates may also be categorized as an unconventional magnetic ordered state of conduction electrons27. This issue is a central concept in condensed matter physics, accompanying Fermi surface reconstruction. The magnetic ordering of cuprates is suppressed by their low-dimensionality in addition to carrier doping, whereas the large superexchange coupling J leads to the development of unconventional magnetic order as the pseudogap state. In contrast, the magnetic ordering of Mn3RhSi with a large Mn magnetic moment is suppressed by geometrical frustration, where SRO appears at high temperatures. Here, the present finding of SRO in Mn3RhSi provides a novel platform for studying the unique properties of unconventional magnetic order over a wide temperature range.
Temperature results for the family of compounds with the β-Mn structure17,18,19,23 as a function of the cubic lattice parameter, in addition to Mn3RhSi (open and closed diamonds). The open circles with error bars present results for Mn3CoSi, Mn3IrSi, Mn3CoGe, Mn3IrGe, and their binary compounds17,18,19. The open triangles present results for β-Mn1-xAlx23. The result for the SL compound β-Mn occurs at 6.32 Å on the quantum critical point, where NFL behavior is observed22. SG behavior is observed in aluminum-doped β-Mn23, whereas the compound family of Mn3RhSi exhibits a long-range AFM transition.
Methods
Sample preparation and quality
Polycrystalline samples were prepared from stoichiometric amounts of high-purity powders of the constituent elements (99.9% pure Mn, 99.9% pure Rh, and 99.99% pure Si). The compounds were synthesized by a conventional arc melting method in an argon atmosphere. The polycrystals were sealed in an evacuated quartz tube, annealed at 900 °C for 3 days and 800 °C for 1 week, and subsequently quenched in water. The phase purity was examined by X-ray powder diffraction using a desktop diffractometer with Cu Kα radiation. No traces of impurity phases were found within the experimental accuracy. The chemical composition of the samples was verified by scanning electron microscopy and energy-dispersive X-ray spectroscopy (SEM/EDS) analysis. The SEM/EDS elemental mapping indicated a homogeneous distribution of atoms and an atomic ratio of Mn:Rh:Si = 58:21:22, which is consistent with the stoichiometric composition within an error of ~1%. Magnetization measurements were performed using a Superconducting Quantum Interference Device magnetometer at the CROSS-Tokai User Laboratory II. Specific heat measurements were performed with an AC capacitance bridge in a two-probe configuration.
Neutron diffraction experiments
Neutron powder diffraction data were collected on the Wide-Angle Neutron Diffractometer (WAND, HB-2C) installed at the High Flux Isotope Reactor (HFIR) at Oak Ridge National Laboratory (ORNL), employing Ge (113) reflection to produce a monochromatic neutron beam with a wavelength of 1.4827 Å. A 5.0-g powder sample was loaded into a vanadium can (7.5-mm inner diameter). Crystal and magnetic structure refinements were performed by the Rietveld method with the program FullProf28 and visualized with the software VESTA29. The magnetic form factor of the Mn atom was used in the analysis. Representational analysis was conducted using the program SARAh30 to identify a reasonable model for the symmetry-allowed magnetic structure.
The absolute magnetic diffuse scattering intensity was estimated using the method described in Supplementary Note 4, and the results were analyzed following the method described in Supplementary Note 5.
Muon spin relaxation measurements
The μSR experiments were performed using the HiFi and ARGUS spectrometers at the ISIS facility, Rutherford Appleton Laboratory. A polycrystalline ingot was cut and mounted in a light furnace for high-temperature measurements. The decay-positron asymmetry function was measured as a function of time, under zero field or under a longitudinal field of 10 mT, as shown in Supplementary Note 5.
The volume fraction shown in Fig. 3b was estimated from the normalized asymmetry as follows. The initial asymmetry is an instrumental parameter that can be obtained from a non-magnetic material, such as a silver foil. The asymmetry decreases in a magnetically ordered material over a short time, depending on the magnetic moment size. The decreasing time can be very short, on the order of 0.2 μs. In this case, the asymmetry can be observed as a sudden reduction near the zero time point using a pulsed muon spectrometer. The magnitude of the reduction in the spectrum is the ratio of the magnetically ordered volume because the muons randomly exhibit local magnetic ordering. The zero position of the zero magnetic moment was determined from the maximum initial asymmetry of the original time spectra at 700 K, which had a value of 20.8%. Therefore, in the normalized asymmetry graph, a value of 1 corresponds to the initial asymmetry of the time spectra at 700 K, and 0 indicates the minimum asymmetry of the time spectra at 300 K for up to 15 μs, considering the lower limit of the error bar. The minimum asymmetry was 14.1% in this case. The same approach was applied to normalize the time spectrum acquired at 320 K from a different spectrometer, which confirmed the repeatability of the data and analysis. It should be noted that the magnetic volume consists of the quasistatic magnetic moments in μSR time window below 0.1 meV.
Data availability
All relevant data are available from the authors on request.
Code availability
The program FullProf is distributed free of charge (https://www.ill.eu/sites/fullprof/). The software VESTA64 is distributed free of charge for academic users under the VESTA License (https://jp-minerals.org/vesta/jp/download.htm).
References
Belitz, D., Kirkpatrick, T. R. & Vojta, T. How generic scale invariance influences quantum and classical phase transitions. Rev. Mod. Phys. 77, 579–632 (2005).
Pfleiderer, C. et al. Partial order in the non-Fermi-liquid phase of MnSi. Nature 427, 227–231 (2004).
Uemura, Y. J. et al. Phase separation and suppression of critical dynamics at quantum phase transitions of MnSi and (Sr1-xCax)RuO3. Nature Physics 3, 29–35 (2007).
Pappas, C. et al. Chiral paramagnetic skyrmion-like phase in MnSi. Phys. Rev. Lett. 102, 197202 (2009).
Wilhelm, H. et al. Precursor phenomena at the magnetic ordering of the cubic helimagnet FeGe. Phys. Rev. Lett. 107, 127203 (2011).
Barla, A. et al. Pressure-induced inhomogeneous chiral-spin ground state in FeGe. Phys. Rev. Lett. 114, 016803 (2015).
Materne, Ph. et al. Solitonic spin-liquid state due to the violation of the Lifshitz condition in Fe1+yTe. Phys. Rev. Lett. 115, 177203 (2015).
Zorko, A., Adamopoulos, O., Komelj, M., Arčon, D. & Lappas, A. Frustration-induced nanometre-scale inhomogeneity in a triangular antiferromagnet. Nature Commun. 5, 3222 (2014).
Zorko, A. et al. Magnetic inhomogeneity on a triangular lattice: the magnetic-exchange versus the elastic energy and the role of disorder. Sci. Rep. 5, 9272 (2015).
Petit, S. et al. Observation of magnetic fragmentation in spin ice. Nature Phys. 12, 746–750 (2016).
Kostadinov, I. Z. & Patton, B. R. Second critical point in first order metal-insulator transitions. Phys. Rev. Lett. 101, 226407 (2008).
Hermsmeier, B., Osterwalder, J., Friedman, D. J. & Fadley, C. S. Evidence for a high-temperature short-range-magnetic-order transition in MnO(001). Phys. Rev. Lett. 62, 478–481 (1989).
Blech, I. A. & Averbach, B. L. Spin correlations in MnO. Physics 1, 31–44 (1964).
Dzyaloshinskii, I. E. Theory of helicoidal structures in antiferromagnets. I. nonmetals. Sov. Phys. JETP 19, 960–971 (1964).
Tolédano, J. C. & Tolédano, P. The Landau Theory of Phase Transitions (World Scientific, Singapore, 1987).
Bogdanov, A. N. & Yablonskii, D. A. Thermodynamically stable “vortices” in magnetically ordered crystals. The mixed state of magnets. Sov. Phys. JETP 68, 101–103 (1989).
Eriksson, T., Bergqvist, L., Nordblad, P., Eriksson, O. & Andersson, Y. Structural and magnetic characterization of Mn3IrGe and Mn3Ir(Si1-xGex): experiments and theory. J. Solid State Chem. 177, 4058–4066 (2004).
Eriksson, T. et al. Crystal and magnetic structure of Mn3IrSi. Phys. Rev. B 69, 054422 (2004).
Eriksson, T., Bergqvist, L., Andersson, Y., Nordblad, P. & Eriksson, O. Magnetic properties of selected Mn-based transition metal compounds with β-Mn structure: experiments and theory. Phys. Rev. B 72, 144427 (2005).
Stewart, J. R., Hillier, A. D., Hillier, J. M. & Cywinski, R. Structural and dynamical study of moment localization in β-Mn1-xInx. Phys. Rev. B 82, 144439 (2010).
Paddison, J. A. M. et al. Emergent frustration in Co-doped β-Mn. Phys. Rev. Lett. 110, 267207 (2013).
Stewart, J. R. et al. Non-Fermi-liquid behavior of electron-spin fluctuations in an elemental paramagnet. Phys. Rev. Lett. 89, 186403 (2002).
Stewart, J. R., Andersen, K. H. & Cywinski, R. Neutron polarization analysis study of the frustrated magnetic ground state of β-Mn1-xAlx. Phys. Rev. B 78, 014428 (2008).
Nakamura, H., Yoshimoto, K., Shiga, M., Nishi, M. & Kakurai, K. Strong antiferromagnetic spin fluctuations and the quantum spin-liquid state in geometrically frustrated β-Mn, and the transition to a spin-glass state caused by non-magnetic impurity. J. Phys.: Condens. Matter 9, 4701–4728 (1997).
Bonner, J. C. & Fisher, M. E. Linear magnetic chains with anisotropic coupling. Phys. Rev. 135, A640 (1964).
Campostrini, M., Hasenbusch, M., Pelissetto, A., Rossi, P. & Vicari, E. Critical exponents and equation of state of the three-dimensional Heisenberg universality class. Phys. Rev. B 65, 144520 (2002).
Li, Y. et al. Unusual magnetic order in the pseudogap region of the superconductor HgBa2CuO4+δ. Nature 455, 372–375 (2008).
Rodríguez-Carvajal, J. Recent advances in magnetic structure determination by neutron powder diffraction. Physica B 192, 55–69 (1993).
Momma, K. & Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 44, 1272–1276 (2011).
Wills, A. S. A new protocol for the determination of magnetic structures using simulated annealing and representational analysis (SARAh). Physica B 276–278, 680–681 (2000).
Acknowledgements
The neutron scattering experiment at ORNL was supported in part by the U.S.–Japan Cooperative Program on Neutron Scattering. A portion of this research was performed using resources at the ORNL HFIR and was sponsored by the Scientific User Facilities Division, Office of Basic Energy Sciences, U.S. Department of Energy. This work was supported by a Grant-in-Aid for Scientific Research (C) (No. 25390133) from the Japan Society for the Promotion of Science. The μSR measurements were performed under experiment proposal numbers (RB) 1870002 (ARGUS), 1710085 (HIFI), and 1670538 (CHRONUS & ARGUS). We also appreciate technical support provided by Paul McIntyre, Adam Sears, and Chris Goodway at ISIS.
Author information
Authors and Affiliations
Contributions
The polycrystalline Mn3RhSi sample was synthesized by H.Y. The neutron diffraction patterns were analyzed by H.Y., whereas the μSR spectra were analyzed by D.P.S. with the help of I.W. Neutron diffraction patterns were collected by H.Y., M.H., M.F., S.C., and J.F., and μSR spectra were acquired by D.P.S., J.L., A.B., L.C., and I.W. The magnetic susceptibility was measured by M.I. and H.Y. The specific heat capacity was measured by Y.Y. The chemical composition of Mn3RhSi was analyzed by K.K. using EDS. Electron diffraction measurements based on transmission electron microscopy were performed by A.K. and S.M. This paper was written by S.S. and H.Y., with input from the remaining authors. This research project was organized by S.S. All authors have approved this paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yamauchi, H., Sari, D.P., Watanabe, I. et al. High-temperature short-range order in Mn3RhSi. Commun Mater 1, 43 (2020). https://doi.org/10.1038/s43246-020-0042-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-020-0042-1
This article is cited by
-
Spiral spin cluster in the hyperkagome antiferromagnet Mn3RhSi
Communications Physics (2023)
-
Muon spin spectroscopy
Nature Reviews Methods Primers (2022)
-
Frustration-driven magnetic fluctuations as the origin of the low-temperature skyrmion phase in Co7Zn7Mn6
npj Quantum Materials (2021)