Abstract
Thin films are ubiquitous in modern technology and highly useful in materials discovery and design. For achieving optimal extrinsic properties, their microstructure needs to be controlled in a multi-parameter space, which usually requires too high a number of experiments to map. Here, we propose to master thin film processing microstructure complexity, and to reduce the cost of microstructure design by joining combinatorial experimentation with generative deep learning models to extract synthesis-composition-microstructure relations. A generative machine learning approach using a conditional generative adversarial network predicts structure zone diagrams. We demonstrate that generative models provide a so far unseen level of quality of generated structure zone diagrams that can be applied for the optimization of chemical composition and processing parameters to achieve a desired microstructure.
Similar content being viewed by others
Introduction
Thin films are of high importance both in modern technology as they are used as building elements of micro- and nanosystems but also in macroscopic applications where they add functionalities to bulk materials. Furthermore, they play a major role in materials discovery and design1,2. Next to composition and phase constitution, the microstructure of thin films is decisive for their properties. The microstructure depends on synthesis conditions and the material itself. Microstructure is important for extrinsic properties, determines functionality and its optimization leads to significant performance enhancement3,4,5,6,7. Successful synthesis, e.g., magnetron sputtering, of thin films needs to master many process parameters (e.g., power supply usage: (direct current (DC), radio frequency (RF), high power impulse magnetron sputtering (HiPIMS))8,9, pressure, bias, gas composition, setup, and geometry) which determine plasma conditions and affect film growth10,11. However, the selection of process parameters, especially for the deposition of new materials, is still mostly based on the scientists’ expertise and intuition and these parameters are usually optimized empirically. The film growth and the resulting microstructure at a fixed temperature is primarily determined by the relative flux of all particles in the gas phase, e.g., gas ions, metal ions, neutrals, thermalized atoms, arriving at the substrate12,13. Additional influencing factors are the substrate geometry14, the interaction strength between the film and the substrate15 and the films crystallographic properties16. Further, film microstructure is strongly dependent on the energy introduced into the growing surface by energetic ion bombardment17,18. The role of particle–surface interactions in altering film growth kinetics with respect to microstructure is not yet fully understood.
The need to predict microstructures from process parameters has inspired the development of structure zone diagrams (SZD, also referred to as structure zone models), first introduced by Movchan and Demchishin for evaporated films19. SZD are abstracted, graphical representations of the occurrence of possible polycrystalline thin-film microstructures (similar structural features) in dependence on processing parameters (e.g., homologous temperature Tdep/Tmelt). SZD are not purely phenomenological since their design includes fundamental knowledge about structure forming mechanisms. Kusano recently showed the validity of structure zone diagrams with respect to optimizing film deposition conditions of refractory metals and refractory metal oxides20. The simplicity of SZD, which enables estimation of process-dependent microstructures, is also their main drawback, as the actual process parameter space is much larger than what is covered in a classical SZD. Especially with compositionally complex materials, the quality of predictions from simple SZD is limited.
Refined versions of the initial SZD were introduced for magnetron sputtered films: Homologous temperature and sputter pressure21, homologous temperature and ion bombardment22, level of contamination23, reactive gas to metal flux ratio24, extreme shadowing conditions25. Classical SZD for sputtering roughly categorize microstructures into four structure zones (I, T, II, and III)21. More subzones can be identified based on adatom mobility conditions which influences crystalline texture26. Although SZD are useful and popular, they only have a very limited predictive capability since they are based on many generalizations and assumptions, e.g., the pressure is a proxy for the constitution of the incoming particle flux (kinetic energy, ratio of ion-to-growth flux, flux composition). Several revised SZD have in common that they are either strongly abstracted27 or materials specific28. Classical SZD relate processing to microstructure, however only for single elements or binary systems and using system-specific deposition process parameters like gas pressure or substrate bias, which are almost impossible to transfer between deposition systems. In order to identify an ideal microstructure for desired properties, classic SZD are helpful as they give the researchers a hint of likely microstructures, but empirical studies are still required, which require extensive experimental efforts.
To improve the predictive quality of SZDs, multiple input parameters (e.g., incoming particle flux, ion energy, temperature, discharge properties like peak power density and duty cycle, chemical composition, etc.) should be considered conjointly, leading to several challenges, e.g., the visualization of a multidimensional parameter space. Anders proposed to include plasma parameters and thickness information (deposition, etching)27. His SZD keeps three axes, including two generalized axes (temperature, energy) and the third axis film thickness27. However, the generalized axes include unknown factors, i.e., the formula for the calculation of generalized temperature and energy axes. In order to overcome the limitations of SZD, computational methods could be applied. The goal is to achieve a reliable prediction of complex, realistic microstructures based on given properties like composition and relevant process parameters. Microstructures can be predicted by simulations, e.g., kinetic Monte Carlo29,30,31,32,33 or molecular dynamic simulation34,35, which depend on selection of model architectures, the selection of initial values and are computationally expensive. The interpretation of the overlap between simulation and experimental results remains to be performed by human assessment. A physical model for an accurate calculation of the microstructure from process parameters needs integrated cross-disciplinary models that cover the plasma discharge at the target, transport of plasma species to the substrate and atomistic processes on the surface and in the volume of the film. Although progress has been made in various areas (electron36,37 particle transport38, plasma-surface interaction39, DFT40), a unified model is still unattainable today.
If physical models do not exist, instead of applying atomistic calculations, machine learning can provide surrogate models bridging the gap between process parameters and resulting microstructure. Machine learning evolved as a new category for microstructure cluster analysis41,42, microstructure recognition43,44,45, defect analysis46, materials design47, and materials optimization48. Generative deep learning models are able to produce new data based on hidden information in training data49. The two most popular models are variational autoencoders (VAE)50 and generative adversarial neural networks (GAN)51. VAEs were applied to predict optical transmission spectra from scanned pictures of oxide materials and vice versa52, for molecular design53 and for microstructures in materials design53,54,55. Noraas et al. proposed to use generative deep learning models for material design to identify processing–structure–property relations and predict microstructures56.
Many thin films in science and technology have a multinary composition and processing variations lead to an “explosion” of combinations which all would need to be tested to find the best processing condition leading to the optimal microstructure. In order to reduce the cost of microstructure design, we apply machine learning of experimental thin-film SEM surface images and conditional parameters (chemical composition and process parameters). The results are visualized in the form of generative-structure zone diagrams that can be utilized in order to select process parameters and chemical composition to achieve a desired thin film microstructure.
Results and discussion
Our approach
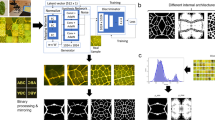
Two generative models are investigated: a VAE and a conditional GAN (cGAN). The VAE model provides an overview and interpretation of similarities and variations in the dataset by dimensionality reduction and clustering. The generative abilities of the cGAN are applied to conditionally predict microstructures based on conditional parameters. Furthermore, the general ability of deep learning models to generate specialized SZDs based on a limited number of observations is demonstrated. This approach predicts realistic process–microstructure relations with a generative model being trained on experimental observations only. Our approach handles complexity by (I) performing a limited set of experiments, using “processing libraries” to efficiently generate comprehensive training datasets; (II) training deep learning models to handle SEM microstructure images, (III) visualization of the similarities between different synthesis paths, and (IV) predictions of microstructures for new parameters from relations found in the training data. We select a material system from the class of transition metal nitrides, which are applied as hard protective coatings, Cr–Al–O–N57, for training and evaluation of our models. Cr–Al–O–N and subsystems (e.g., Al–Cr–N, CrN) have been the subject of many studies58,59,60,61. Our Cr–Al–O–N dataset, efficiently created from materials and processing libraries, in total containing 123 samples, includes variations of six conditional parameters, covering different combinations of compositional (Al concentration (Al), O-concentration (O) in Cr1-x–Alx–Oy–N) and process parameters (deposition temperature (Td), average ion energy (EI), degree of ionization (Id) and deposition pressure (Pd)). Id is a design parameter which is related to the ratio of ion flux and the total growth flux of all deposited particles. In order to provide a sufficient quantity of data, 128 patches with size 128 × 128 px2 were extracted randomly from each SEM image (see Methods). All depositions were carried out in one sputter system (ATC 2200, AJA International), therefore the geometrical factors that usually change between different deposition equipment is not present. As thin film microstructure is also thickness dependent, all analyzed samples are in a similar thickness range (800–1300 nm) and exhibit a fully developed microstructure.
To be able to study synthesis–processing–structure relationships, usually a large number of synthesis processes need to be carried out to create a sufficiently large dataset, which is time consuming. To substantially lower the number of necessary synthesis processes, we use combinatorial sputtering of thin-film materials libraries. We introduce the concept of “processing libraries” (PL): These are comparable to materials libraries, but, instead of a composition variation, PL comprise thin films synthesized using a set of different synthesis parameters, at either a constant materials composition, or additionally for different compositions (see Methods). The samples in a PL are subject to predetermined variations of the conditional parameters (EI, Id, Td, Pd, Al, O). The film growth develops to a microstructure, which is characterized by geometrically different surface features in terms of size, shape, and density. For a comprehensive study of possible microstructures, we exploit the process parameter space for synthesis conditions and repeat these processes for different chemical compositions. Film microstructures are usually assessed by surface and cross-sectional SEM images. Since high quality cross-sectional images are experimentally expensive and their interpretation is complicated, we focus on topographic surface images, as these are more comparable and describable. Surface morphology in terms of grain size and feature shapes can be used to correlate growth conditions and surface diffusion processes with resulting crystallographic orientation26.
Process–composition–microstructure relations
In order to inspect the dataset, we train a VAE with a regression model that uses the sampling layer (z) of the VAE as an input to predict the conditions (see Methods). The model optimizes simultaneously on microstructure images and conditional parameters and achieves a well-structured and dense representation (latent space embedding). The 64-dimensional latent space is further dimensionally-reduced by kernel principle component analysis (kPCA) with a radial basis function (RBF) kernel62 in order to provide graphical visualization in 2D. If the microstructure, composition and process parameters correlate, the images should cluster in the VAE latent space.
Figure 1 shows the first two components of the kPCA latent space representation of the validation set. The axes (kPCA 1, kPCA 2) have no actual physical meaning: they are rather a rough expression of how the VAE recognizes images and the conditional parameter space and joins them in a dense layer. Each microstructure image is plotted at its position in the dimensionally-reduced latent space embedding of the VAE. The images cluster in regions of similar sizes and shapes. A coarse-facetted surface morphology is observed at kPCA 1 = −0.1 and kPCA 2 = −0.3. With increasing kPCA 1 and kPCA 2 the feature size decreases. With values of kPCA 1 < 0, mainly facetted grains are observed, while for kPCA 1 > 0 the features become more fine-grained and nanocrystalline.
Patches created from experimental SEM surface images are plotted at their position in the dimensionally-reduced latent space. A continuous variation of microstructures is observed with respect to similarity of feature size and shape (e.g., featureless, fine-grained, oriented-facetted, smooth-facetted, coarse-facetted).
This qualitative overview of the microstructures in the dataset is now correlated to chemical composition and process characteristics: Fig. 2 shows the microstructure images plotted at their latent space position and the position of each sample in the latent space with their respective color-coded composition or process parameters. This visualizes the interplay between conditional parameters and their significance on microstructural features.
We now address the effect of each deposition parameter in order to provide a discussion baseline for the trends that are created by the prediction of the cGAN model. Samples with different levels of O-contamination are separated in latent space and show a clear trend in feature size (Fig. 2e). O leads to nucleation sites for O-phases in the fcc Cr–Al–N phase. The growth of the fcc Cr–Al–N phase can be inhibited by these O-phases23. Figure 2c shows a similar trend for Al63. A solid solution for Cr1−x–Alx–N with up to 70 at.% Al is known60, whereas between 50 and 70 at.% Al, hcp AlN precipitates64. The maximum solubility of Al in fcc CrN depends on process parameters65. The formation of a second phase, hcp AlN, at higher Al could be the reason of decreasing grain size with increasing Al. An increase in Td (Fig. 2b) leads to an increase in feature size. The feature shapes change from fine granular to sharp facetted grains and at high Td to coarse-facetted grains with relatively flat surfaces due to higher diffusion rates28. An increase in EI (Fig. 2d) above a certain threshold leads to a smoother surface as kinetic bombardment flattens facets and in extreme cases a featureless surface is observed. In addition, surface mobility is kinetically enhanced by ion bombardment66. An increase in EI and Id can cause a higher nucleation density and a decreased grain size67. These effects are most significant at low Td where diffusion is limited. At Td > 400 °C the effect is reduced due to higher diffusion. Oriented facets are observed up to Td = 400 °C which is a result of the by 27° inclined cathodes and low diffusion26. At higher Td the facets are randomly oriented which is an effect of higher adatom diffusivity. An increasing Pd (not shown) leads to an increase in gas atoms or molecules per volume and thereby to a decrease in mean free path68. Particles experience more collisions during their path from the target surface to the substrate and thereby lose energy. In addition, Id and the ratio of gas ions to target ions increases, which influences surface kinetics. This illustrates the complex interplay between process parameters, composition and resulting microstructure. Also, it shows the usefulness of dimensionality reduction to gain an overview of complex datasets. The identified trends correlate well with results from literature.
Prediction of microstructures from conditional parameters
The decoder part of the VAE could be applied to generate images from the latent representation, but the quality is unsatisfactory due to known limitations of VAEs69 (please review example code for VAE predictions). In contrast, GAN models are known to be able to produce photorealistic images70. To predict microstructures from the six conditional parameters, we train a cGAN model71. In order to categorize the level of prediction, we need to define what the model can learn from the experimental dataset. A reconstruction of a microstructure from the training set provides the baseline. Figure 3 compares experimental images to their predicted counterparts by their particle size distribution. The cGAN generates these microstructure images using two inputs only: conditional parameters and a latent sub-space with random noise. It should be noted that the cGAN is not trained to generate an exact copy of the original image. The histograms in Fig. 3 contain particle counts from 100 images patches of both experimental and predicted images. The generated images generally show a good reproduction of the experimental images in terms of feature size and shape. Even contrast variations on facets are reproduced. Figure 3f shows an exception, where locally, smaller features are generated on top of otherwise large smooth grain surfaces. This relates to the problem that the image patches only show small fractions of these large grains and the microstructure of 800 °C deposited samples strongly differs from all other images. In Fig. 3a, b, e, the generated images are nearly indistinguishable from their experimental counterparts. The facet shapes in Fig. 3a are not as sharp as in the experimental images and the facets in Fig. 3d show more curvature compared with the original images. However, the reproduced features can still be identified as facetted and the feature sizes match well. The generated image in Fig. 3d appear blurred and show less contrast than the experimental image. A low contrast in the experimental images of these smooth dense microstructures might affect the training of the model.
Particle size distributions and examples of SEM surface microstructure images (blue frame) and cGAN-generated images (green frame) of the training set for the same conditional parameters; results are shown for a a Cr–N film deposited without intentional heating; b, e Cr–Al–O–N films with 10 at.% O-contamination, deposited at 200 and 600 °C, respectively; c a Cr–Al–N thin film deposited at 500 °C; d, f Cr–O–N films with 3 at.% O-contamination that were deposited at 500 and 800 °C, respectively. The conditional parameters of the shown images are summarized in the table.
Machine learning models can only learn from information provided to them. Interpolations are reasonable while extrapolations are more challenging. For example, a microstructure prediction for a sample with high Al at Td = 1000 °C would fail, as a phase decomposition is expected which leads to a (for the model) unpredictable microstructure. The training set libraries were synthesized at selected basic process conditions (e.g., constant Td, EI, Al, or O) and contain a variation of one or two additional parameters. Therefore, the complete dataset has only limited intersections and extensions into other conditions. For example, a variation of EI between 40 and 200 eV was only carried out for samples deposited at 500 °C. In order to predict a sample deposited at Td = 100 °C and EI = 200 eV, a transfer of the EI trend on the Td trend is required. To validate the predictive capabilities of the model, new microstructure images are generated for extensions of a chosen base condition. A CrN sample (Td = 20 °C, EI = 1 eV, Id = 0.1, Pd = 0.5, Al = 0 at.%, O = 0 at.%) provides the base condition (Fig. 4, orange frame). The sample exhibits a triangular facetted morphology. Figure 4 visualizes how the microstructure of the initial sample changes when only a single condition is changed at a time and the other parameters stay constant. Experimental structures synthesized with the same or similar process parameters (closest experimental condition) are compared. The trends from Fig. 2 for the different conditional parameters are reproduced by the model. In the example, Al and O lead to a refinement of the microstructure, EI leads to smoother facets, and Td increases the grain size.
Predictions (blue frame) are based on the experimental microstructure of Cr–N deposited at room temperature (orange frame) with corresponding conditional parameters. The changed parameter for each predicted or experimental image (green frames) is indicated while all other parameters stay constant. If an experimental counterpart with identical conditional parameters is missing, the closest related experimental image is selected and the additional change in conditional parameters is marked above the image (e.g., +480 °C).
To validate the cGAN prediction quality on unseen conditions, microstructures from experimental test samples which were not included in the training set are predicted. Cr1−xAlxN samples grown at 500 °C from the training set were deposited at <10 eV (0 V substrate bias) and >100 eV (−100 V substrate bias) for different Al. As an example, the cGAN predicts images for the variation of Al at 40 eV (Fig. 5). This requires an interpolation of EI. At 0 V bias, the faceted microstructure changes to a fine-grained microstructure with increasing Al. The same trend is observed at −100 V bias but the facets of Cr-rich samples are smoother and denser. With increasing Al, the microstructure becomes featureless. The prediction matches both trends. In direct comparison to the experimental counterparts, the facets of Cr-rich samples are less pronounced. Al-rich samples are almost indistinguishable from the test set images. These results show that the cGAN produces good results for interpolations within the dataset.
The data shows the effect of bias voltage (EI) and Al concentration on the surface microstructure. The blue box contains images from the experimental test set. The red dashed box shows cGAN predictions for the exact conditions of the experimental test set. The green boxes show images from the experimental training set.
Finally, a SZD is generated by the cGAN. The advantage of this generative SZD (gSZD) is that it can be produced as required. In a 2D representation, two parameters can be varied while the remaining four parameters are selected constant. Figure 6a shows a gSZD for a variation of Al and Td at constant values for the remaining parameters (constant O = 1 at.%, EI = 40 eV, Id = 1.0, Pd = 0.5 Pa). Al and Td are varied randomly between 0–60 at.% and 20–600 °C, respectively. The predicted image patches are plotted at positions according to their input conditions. Hence, patches overlay and appear as a continuous diagram. A clear variation of the microstructure in dependence of Td and Al is observed. Figure 6b shows the CNN-predicted structure class in dependence of Td and Al (average over 100× variations of the random latent variable per (Td, Al)-step). The structure changes with increasing Td from oriented-facetted to facetted. An increase in Al leads to a change from facetted to a fine-grained structure. The remaining parameters (O, Id, EI) vary in the experimental data, while they are kept constant in the gSZD. A variation of Al and Td was experimentally realized at 10 at.% O while samples with a variation of EI were deposited at 500 °C and contain 0 at.% O. Thus, the model combines (I) the structural refinement with increasing Al and (II) the trend that this refinement is inhibited with increasing Td. In other words, a higher Td is necessary at high Al to obtain a similar feature size and shape as compared with Cr-rich compositions without O and Al. For the gSZD these can be interpreted in the following way. In general, an increase in Al leads to a refinement of the microstructure due to changes in adatom surface mobility conditions72 and second phase formation which inhibits crystal growth23. This trend is most significant at low temperatures, where diffusion is limited. With increasing temperature, the facetted structure extends to higher Al. An increase in feature size with Td is observed. The observed trends change to a finer structure when O is increased stepwise (not shown) and facets are smoothed out by an increase of EI to 200 eV (Fig. 6c). In addition, a featureless microstructure is observed at high Al and low Td. These results are consistent with conclusions from literature, which means that the cGAN model is able to correctly capture trends from an inhomogeneously distributed dataset and perform qualitative predictions by combining the learned information.
a gSZD generated by the cGAN model for a variation of Al und Td. The remaining conditional parameters were chosen to be Id = 1.0, EI = 40 eV, O = 1 at%, Pd = 0.5 Pa. Panel b shows the average probability and standard deviation of the predicted microstructure classes of the gSZD by the CNN. The dashed blue lines indicate the technological boundary of the use case. Panel c shows the predicted microstructure classes for an increased EI of 200 eV.
Definition of conditions for thin films with optimized microstructures
Finally, by combination of domain knowledge and the new gSZD, we are able to design a composition-process-window to create films for a desired application. The cGAN model is applied to predict microstructures for a variation of two conditional parameters (e.g., Al and Td). The microstructure classifier model is used to determine the microstructure class for the predicted images. For an example application of hard protective coatings for polymer injection molding or extrusion tools73, the tribological performance needs to be optimized, requiring films with a dense, smooth or fine-grained microstructure. Physical boundaries are provided by the maximum values of Al and Td (blue boundaries in Fig. 6b, c). Td is limited by the temper diagram of cold work steel AISI 420 (X42Cr13, 1.2083). To avoid tempering of the substrate, the maximum Td should be lower than 450 °C. Al is limited by the formation of hcp AlN above 50 at.% Al, which would lead to a reduction in hardness74. To achieve a fine-grained film, Al should be as high as possible, according to the gSZD (Fig. 6a). In addition, Td should be as high as possible in order to reduce grain boundary porosity. With an included uncertainty (standard deviation in Fig. 6b), the new composition-process-window (“window of opportunity”) can be selected from Fig. 6b according to the desired microstructure (e.g., fine-grained). In Fig. 6c the microstructure probability is shown for an increased EI of 200 eV. Under this high EI condition, the process window for a fine-grained microstructure is increased and a deposition at higher Td and supposedly higher grain boundary density can be conducted while a secure distance to the precipitation boundary of hcp-AlN is retained.
In summary, we applied combinatorial synthesis methods to create materials and process libraries of the Cr–Al–O–N system in order to observe the influence of composition and process parameters on the resulting microstructural properties. Our training set of samples from the Cr–Al–O–N system covers variations in the directions of previous SZD (Td, Pd, Id, EI, O) and an additional compositional variation of Al. A generative neural network (cGAN) was trained on SEM surface images to predict microstructures based on the input of composition and process parameters. The model reproduces the observed trends in the dataset. Furthermore, we were able to validate the predictive capabilities on test data, which requires an interpolation of conditional parameters. A microstructure classifier model and particle size distribution analysis are used to validate the predictions of the cGAN. A transfer of trends from sampled regions to un-sampled regions was demonstrated in a new generative SZD. The gSZD shows the expected microstructure of thin films for a variation of Al concentration and deposition temperature, which will be useful for the optimization of TM–Al–N (TM = transition metal) thin films. The observed microstructure predictions in the gSZD are consistent with observations from literature. A so far unseen level of predictive quality in the scope of SZD is observed which will lead to an acceleration in the development and optimization of thin films with a desired microstructure. Further this approach could be extended to other materials in thin film and bulk form.
Methods
Sample synthesis
Sample synthesis is performed in a multi-cathode magnetron sputter chamber (ATC 2200, AJA International). All samples are deposited reactively with an Ar/N2 flux ratio of 1 and a total gas flux of 80 sccm. The deposition pressure is controlled automatically by adjusting the pumping speed. Two confocal aligned cathodes (Al, Cr) facing the substrate lead to a continuous composition gradient of the two base materials, which results in a materials library. The substrate is heated with a resistive heater. In order to create a PL, an in-house made step heater is used to heat five substrates simultaneously at five different temperatures in the range from 200 to 800 °C, thereby covering a large temperature range of typical SZDs within a single PL28. PLs with a continuous variation of plasma parameters, e.g., EI and Id are synthesized by sputtering from two confocally aligned magnetrons which are operated by different power supplies. One cathode is powered by DC, the other one by HiPIMS (high power impulse magnetron sputtering). The substrate is placed centered below the two cathodes. A similar concept was chosen by Greczynski et al.75. The pulsed HiPIMS discharge produces a one magnitude larger number of ionized species and higher ion energies compared with a DC discharge76. An additional substrate bias is applied in some cases to further accelerate ions and increase EI. By placing the substrate in the center below the two inclined cathodes, the travel distance of the ionized species of the HiPIMS discharge increases towards the substrate positions next to the DC cathode. The ions thermalize due to collisions with other plasma species and loose energy. This effect is amplified by the angular distribution of the sputtered species77. Consequently, the ratio of ions per deposited atom as well as the average ion energy are different along the 100-mm diameter substrate. In order to achieve a homogenous film thickness, the DC power is reduced to match the typically lower deposition rate of the HiPIMS powered cathode. A variation in the degree of ionization is achieved by a variation of the sputter frequency at constant average power in HiPIMS processes. An increase in frequency leads to a decrease in target peak power density which leads to a decrease in Id and a small decrease (up to 3 eV) in EI. The O-concentration in several of the discussed samples are contaminations from residual gas outgassing from the deposition equipment, which is especially present at elevated temperatures (>600 °C).
Thin film characterization
The chemical composition (Al/Cr) is determined by EDX (Inca X-act, Oxford Instruments). The O-concentration is determined by XPS (Kratos Axis Nova) for a subset of the samples. All films are stoichiometric by the definition (Al + Cr)/(O + N) = 1. The stoichiometry is validated for additional samples that are deposited under similar process conditions (not shown) by RBS measurements, within a 5 at.% error. SEM images are taken in a Jeol 7200F using the secondary electron detector at ×50,000 magnification at an image size of 1280 × 960 pixels. The SEM images are histogram-equalized using contrast limited adaptive histogram equalization (CLAHE)78.
Plasma properties
EI was calculated from retarding field energy analyzer measurements of a previous study79 that were carried out at five measurement positions along the 100 mm substrate area in three reactive co-deposition processes of Al and Cr at 100, 200, and 400 Hz sputter frequency at 0.5 Pa. If a substrate bias was applied, an additional ion energy was added to the total ion energy (e.g., EI + 40 eV bias). To estimate Id, the ratio of total ion flux and growth flux was calculated. Unknown values for conditions that were not measured are estimated by extrapolation. The ion-to-growth flux ratios are normalized over the dataset. These values provide only a rough estimation that covers the known trends from literature and our own investigations. It should be noted that we consider Id a physics-informed descriptor, rather than a physical property.
Data handling
Our dataset contains 123 individual samples. The 1280 × 960 px2 images locally contain characteristic microstructure features that are distributed repeatedly over the image. Patches are extracted at random points of each image. Each of the extracted patches cover a large enough range to represent the characteristic microstructure of the synthesis condition. We choose a patch size of 128 × 128 px2 and scale them by a factor of 2 into 64 × 64 px2 to speed up computations. The images patches have a pixel density of 0.27 px/nm. A total of 128 patches are cropped per each image which results in an average pixel shift of 10 and 7.5 px per patch (1280/128, 960/128). The training data therefore contains more than 10,000 different image patches depending on the train-test split. For the VAE, the complete dataset is split randomly at a ratio of 70:30 (train:validation). In case of the cGAN, a test set (13 out of 123 original SEM images) for the conditions (described in Fig. 5) is removed from the dataset.
Machine learning models
The VAE model consist of three models, an encoder, a decoder, and a regression model. Encoder and decoder represent the variational autoencoder (VAE) part of the model. The image patches of size (64 × 64 × 1) provide the input and the output of the VAE. The encoder consists of five convolution building blocks which comprise a 2D convolutional layer that is followed by batch normalization, a Leaky ReLU activation function and a dropout layer. The filter sizes are 32, 64, 128, 128, and 128. The kernel size is 4 × 4. The output of the last convolutional layer is flattened and connected to two dense layers (µ and σ) with 64 dimensions. These are passed to a sampling layer (z) which samples the latent space according to the formula: z = μ + αεeσ/2. ε is a random normal tensor with zero mean and unit variance and has the same shape as µ. α is a constant which is set to 1 during training and otherwise to 0. The decoder reflects the structure of the encoder. The output of the sampling layer is passed into a dense layer with 512 neurons which is reshaped to match the shape of the last convolutional layer. The layer is passed to five building blocks which comprise a 2D convolutional layer followed by batch normalization, Leaky ReLU activation, dropout and an upsampling layer. The filter sizes of the convolutional layers are 128, 128, 128, 64, and 32. An additional convolutional layer with filter size 1 provides the output of the decoder. A regression model takes the output of the sampling layer z as an input and outputs the conditional parameters. The regression model has four dense layers with dimensions 20, 20, 20, 6 and ReLU activation, an input layer with 64 dimensions and an output layer with 6 dimensions and linear activation function. The VAE and the regression model are simultaneously trained using the Adadelta optimizer80. The VAE loss is provided by the sum of the Kullback–Leibler divergence and the image reconstruction binary cross entropy. The loss of the regression model is calculated by the mean squared error. The losses of VAE and regression model are weighted 1:10,000 in order to provide a well-structured latent space.
The generative adversarial network consists of two parts: a generator and a discriminator. The generator network has two inputs, a 16-dimensional latent space (intrinsic parameters) and six conditional physical parameters (extrinsic). The latent space input layer is followed by a dense layer with 32768 neurons and Leaky ReLU activation function and then reshaped into a 16 × 16 layer with 128 channels. The conditional input layer is followed by 256 dense layers with linear activation function and reshaped into a 16 × 16 matrix with one channel. Two reshaped 16 × 16 matrices are combined together and followed by two convolutional-transpose layers with Leaky ReLU activation functions, with an upscaling factor of 2 and 128 filters for each layer. The last layer is convolutional with hyperbolic tangent activation and 64 × 64 × 1 shaped of output. The discriminator network also has two inputs, the six conditional physical parameters and a 64 × 64 × 1 input image. As in the generator network the conditional input layer is converted into a 64 × 64 × 1 matrix with one dense layer and concatenated with the input image. This is followed by two convolutional layers with 128 channels and a downscaling factor of 2, which results in a 16 × 16 × 128 matrix. A flattening layer is followed by a dropout layer with a dropout factor = 0.4 and a dense output layer with sigmoid activation function. The same conditional extrinsic physical parameters were fed into both the generator and the discriminator. The discriminator model has a binary cross-entropy loss function and an Adam optimizer81 with a learning rate equal to 0.0002, and beta_1 equal to 0.5. The loss function for the generator is approximated by the negative discriminator, in a spirit of adversarial network training. The training procedure consists of consecutive training of the discriminator on small batches of real and fake images with corresponding conditional physical parameters and generator training on randomly generated points from latent space and realistic extrinsic parameters.
Two metrics are introduced that provide qualitative and quantitative comparison of conditionally generated and experimental images. The type of microstructure features is identified by a convolutional neural network (CNN) classifier and particle analysis is performed using the ImageJ particle analyzer.
The classifier is trained to categorize microstructures in six classes (featureless, fine-grained, oriented-facetted, smooth-facetted, facetted, and coarse-facetted). The model consists of three convolutional blocks consisting of a convolutional layer followed by a ReLU activation and a max pooling layer. The output of the third convolutional block is flattened and followed by a dense layer with 64 neurons and ReLU activation, followed by a dropout layer with rate 0.5. The final output layer is a dense layer with 4 neurons and softmax activation function. The complete dataset is split train and test set at a ratio of 4:1. The train set is further split into a train and validation set at a ratio of 7:3. The model is trained using the Adam optimizer81 and converges after ~13 epochs. The validation and test accuracies are ~93–95%.
Particle analysis is performed on experimental and conditionally generated images. A Gaussian filter is applied to reduce noise in the images. Afterward a threshold is applied and the images are transformed into a binary mask, followed by watershed segmentation and ImageJ particle analyzer. Hundred patches per conditions are analyzed. The histogram of the feret diameter measurement (equivalent to particle size or grain size) is evaluated.
Data availability
The datasets generated and analyzed during the current study are available through Harvard Dataverse under the following link: https://doi.org/10.7910/DVN/LEPSJW82. Additional information is provided from the corresponding author on reasonable request.
Code availability
Example code is accessible through Github under the following link: https://github.com/lbanko/generative-structure-zone-diagrams. Additional information is provided by the corresponding author on reasonable request.
References
Alberi, K. et al. The 2019 materials by design roadmap. J. Phys. D: Appl. Phys. 52, 13001 (2018).
Ludwig, A. Discovery of new materials using combinatorial synthesis and high-throughput characterization of thin-film materials libraries combined with computational methods. npj Comput. Mater. 5, 70 (2019).
Greczynski, G., Jensen, J., Böhlmark, J. & Hultman, L. Microstructure control of CrNx films during high power impulse magnetron sputtering. Surf. Coat. Technol. 205, 118–130 (2010).
Pan, T. S. et al. Enhanced thermal conductivity of polycrystalline aluminum nitride thin films by optimizing the interface structure. J. Appl. Phys. 112, 44905 (2012).
Wang, X. C., Mi, W. B., Chen, G. F., Chen, X. M. & Yang, B. H. Surface morphology, structure, magnetic and electrical transport properties of reactive sputtered polycrystalline Ti1−xFexN films. Appl. Surf. Sci. 258, 4764–4769 (2012).
Zalnezhad, E., Sarhan, A. A. D. & Hamdi, M. Optimizing the PVD TiN thin film coating’s parameters on aerospace AL7075-T6 alloy for higher coating hardness and adhesion with better tribological properties of the coating surface. Int. J. Adv. Manuf. Technol. 64, 281–290 (2013).
Zgrabik, C. M. & Hu, E. L. Optimization of sputtered titanium nitride as a tunable metal for plasmonic applications. Opt. Mater. Express 5, 2786 (2015).
Lundin, D., Minea, T. & Gudmundsson, J. T. High Power Impulse Magnetron Sputtering. Fundamentals, Technologies, Challenges and Applications (2020).
Sarakinos, K., Alami, J. & Konstantinidis, S. High power pulsed magnetron sputtering. A review on scientific and engineering state of the art. Surf. Coat. Technol. 204, 1661–1684 (2010).
Depla, D. & Mahieu, S. Reactive Sputter Deposition (Springer, 2008).
Kouznetsov, V., Macak, K., Schneider, J. M., Helmersson, U. & Petrov, I. A novel pulsed magnetron sputter technique utilizing very high target power densities. Surf. Coat. Technol. 122, 290–293 (1999).
Kay, E., Parmigiani, F. & Parrish, W. Microstructure of sputtered metal films grown in high-and low-pressure discharges. J. Vac. Sci. Technol. A 6, 3074–3081 (1988).
Ferreira, F., Oliveira, J. C. & Cavaleiro, A. CrN thin films deposited by HiPIMS in DOMS mode. Surf. Coat. Technol. 291, 365–375 (2016).
Hopwood, J. Ionized physical vapor deposition of integrated circuit interconnects. Phys. Plasmas 5, 1624–1631 (1998).
Sarakinos, K. A review on morphological evolution of thin metal films on weakly-interacting substrates. Thin Solid Films 688, 137312 (2019).
Greene, J. E. Chapter 12—Thin Film Nucleation, Growth, and Microstructural Evolution: An Atomic Scale View. In Handbook of Deposition Technologies for Films and Coatings (pp. 554–620). William Andrew Publishing (2010).
Harper, J. M. E., Cuomo, J. J., Gambino, R. J. & Kaufman, H. R. Modification of thin film properties by ion bombardment during deposition. Nuc. Instrum. Meth. B 7, 886–892 (1985).
Viloan, R. P. B. et al. Bipolar high power impulse magnetron sputtering for energetic ion bombardment during TiN thin film growth without the use of a substrate bias. Thin Solid Films 688, 137350 (2019).
Movchan, B. A. & Demchishin, A. V. Structure and properties of thick condensates of nickel, titanium, tungsten, aluminum oxides, and zirconium dioxide in vacuum. Fiz. Metal. Metalloved 28, 653–660 (1969).
Kusano, E. Structure-zone modeling of sputter-deposited thin films: a brief review. Appl. Sci. Converg. Technol. 28, 179–185 (2019).
Thornton, J. A. The microstructure of sputter‐deposited coatings. J. Vac. Sci. Technol. A 4, 3059–3065 (1986).
Messier, R., Giri, A. P. & Roy, R. A. Revised structure zone model for thin film physical structure. J. Vac. Sci. Technol. 2, 500–503 (1984).
Barna, P. B. & Adamik, M. Fundamental structure forming phenomena of polycrystalline films and the structure zone models. Thin Solid Films 317, 27–33 (1998).
Petrov, I., Barna, P. B., Hultman, L. & Greene, J. E. Microstructural evolution during film growth. J. Vac. Sci. Technol. 21, S117–S128 (2003).
Mukherjee, S. & Gall, D. Structure zone model for extreme shadowing conditions. Thin Solid Films 527, 158–163 (2013).
Mahieu, S., Ghekiere, P., Depla, D. & Gryse, Rde Biaxial alignment in sputter deposited thin films. Thin Solid Films 515, 1229–1249 (2006).
Anders, A. A structure zone diagram including plasma-based deposition and ion etching. Thin Solid Films 518, 4087–4090 (2010).
Stein, H. et al. A structure zone diagram obtained by simultaneous deposition on a novel step heater. A case study for Cu2O thin films. Phys. Status Solidi A 212, 2798–2804 (2015).
Bouaouina, B. et al. Nanocolumnar TiN thin film growth by oblique angle sputter-deposition. Experiments vs. simulations. Mater. Des. 160, 338–349 (2018).
Wang, P., He, W., Mauer, G., Mücke, R. & Vaßen, R. Monte Carlo simulation of column growth in plasma spray physical vapor deposition process. Surf. Coat. Tech. 335, 188–197 (2018).
Savaloni, H. & Shahraki, M. G. A computer model for the growth of thin films in a structure zone model. Nanotechnology 15, 311 (2003).
Nita, F., Mastail, C. & Abadias, G. Three-dimensional kinetic Monte Carlo simulations of cubic transition metal nitride thin film growth. Phys. Rev. B 93, 349 (2016).
Lü, B., Almyras, G. A., Gervilla, V., Greene, J. E. & Sarakinos, K. Formation and morphological evolution of self-similar 3D nanostructures on weakly interacting substrates. Phys. Rev. Mater. 2 https://doi.org/10.1103/PhysRevMaterials.2.063401 (2018).
Müller, K. ‐H. Stress and microstructure of sputter‐deposited thin films: molecular dynamics investigations. J. Appl. Phys. 62, 1796–1799 (1987).
Sangiovanni, D. G. Copper adatom, admolecule transport, and island nucleation on TiN(0 0 1) via ab initio molecular dynamics. Appl. Surf. Sci. 450, 180–189 (2018).
Krüger, D. & Brinkmann, R. P. Interaction of magnetized electrons with a boundary sheath. Investigation of a specular reflection model. Plasma Sources Sci. Technol. 26, 115009 (2017).
Krüger, D., Trieschmann, J. & Brinkmann, R. P. Scattering of magnetized electrons at the boundary of low temperature plasmas. Plasma Sources Sci. Technol. 27, 25011 (2018).
Trieschmann, J. et al. Combined experimental and theoretical description of direct current magnetron sputtering of Al by Ar and Ar/N2 plasma. Plasma Sources Sci. Technol. 27, 54003 (2018).
Music, D. et al. Correlative plasma-surface model for metastable Cr-Al-N. Frenkel pair formation and influence of the stress state on the elastic properties. J. Appl. Phys. 121, 215108 (2017).
Music, D., Geyer, R. W. & Schneider, J. M. Recent progress and new directions in density functional theory based design of hard coatings. Surf. Coat. Tech. 286, 178–190 (2016).
DeCost, B. L., Francis, T. & Holm, E. A. Exploring the microstructure manifold. Image texture representations applied to ultrahigh carbon steel microstructures. Acta Mater. 133, 30–40 (2017).
Kitahara, A. R. & Holm, E. A. Microstructure cluster analysis with transfer learning and unsupervised learning. Integr. Mater. Manuf. Innov. 7, 148–156 (2018).
Bulgarevich, D. S., Tsukamoto, S., Kasuya, T., Demura, M. & Watanabe, M. Pattern recognition with machine learning on optical microscopy images of typical metallurgical microstructures. Sci. Rep. 8, 2078 (2018).
Kondo, R., Yamakawa, S., Masuoka, Y., Tajima, S. & Asahi, R. Microstructure recognition using convolutional neural networks for prediction of ionic conductivity in ceramics. Acta Mater. 141, 29–38 (2017).
Chowdhury, A., Kautz, E., Yener, B. & Lewis, D. Image driven machine learning methods for microstructure recognition. Comput. Mater. Sci. 123, 176–187 (2016).
Rovinelli, A., Sangid, M. D., Proudhon, H. & Ludwig, W. Using machine learning and a data-driven approach to identify the small fatigue crack driving force in polycrystalline materials. npj Comput. Mater. 4, 963 (2018).
Moot, T. et al. Material informatics driven design and experimental validation of lead titanate as an aqueous solar photocathode. Mater. Discov. 6, 9–16 (2016).
Cao, B. et al. How to optimize materials and devices via design of experiments and machine learning: demonstration using organic photovoltaics. ACS Nano 12, 7434–7444 (2018).
Salakhutdinov, R. Learning deep generative models. Annu. Rev. Stat. Appl. 2, 361–385 (2015).
Kingma, D. P. & Welling, M. Auto-encoding variational bayes. In Proceedings of the 2nd International Conference on Learning Representations (ICLR), arXiv preprint arXiv:1312.6114 (2013).
Goodfellow, I. et al. In Advances in Neural Information Processing Systems (eds. Ghahramani, Z., Welling, M., Cortes, C., Lawrence, N. D. & Weinberger, K. Q.) 2672–2680 (Curran Associates, Inc., 2014).
Stein, H. S., Guevarra, D., Newhouse, P. F., Soedarmadji, E. & Gregoire, J. M. Machine learning of optical properties of materials–predicting spectra from images and images from spectra. Chem. Sci. 10, 47–55 (2019).
Gomez-Bombarelli, R. et al. Automatic chemical design using a data-driven continuous representation of molecules. ACS Cent. Sci. 4, 268–276 (2018).
Yang, Z. et al. Microstructural materials design via deep adversarial learning methodology. J. Mech. Des. 140 https://doi.org/10.1115/1.4041371 (2018).
Li, X. et al. (eds.). A Deep Adversarial Learning Methodology for Designing Microstructural Material Systems (2018).
Noraas, R., Somanath, N., Giering, M. & Olusegun, O. O. In AIAA Scitech 2019 Forum (American Institute of Aeronautics and Astronautics, 2019).
Stueber, M., Diechle, D., Leiste, H. & Ulrich, S. Synthesis of Al–Cr–O–N thin films in corundum and f.c.c. structure by reactive r.f. magnetron sputtering. Thin Solid Films 519, 4025–4031 (2011).
Hofmann, S. & Jehn, H. A. Oxidation behavior of CrNx and (Cr, Al)Nx hard coatings. Materials and Corrosion 41, 756–760 (1990).
Kunisch, C., Loos, R., Stüber, M. & Ulrich, S. Thermodynamic modeling of Al-Cr-N thin film systems grown by PVD. Zeitschrift fur Metallkunde 90, 847–852 (1999).
Sugishima, A., Kajioka, H. & Makino, Y. Phase transition of pseudobinary Cr–Al–N films deposited by magnetron sputtering method. Surf. Coat. Technol. 97, 590–594 (1997).
Bobzin, K. et al. Mechanical properties and oxidation behaviour of (Al, Cr) N and (Al, Cr, Si) N coatings for cutting tools deposited by HPPMS. Thin Solid Films 517, 1251–1256 (2008).
Schölkopf, B., Smola, A. & Müller, K.-R. (eds). Kernel Principal Component Analysis (Springer, 1997).
Grochla, D. et al. Time- and space-resolved high-throughput characterization of stresses during sputtering and thermal processing of Al–Cr–N thin films. J. Phys. D: Appl. Phys. 46, 84011 (2013).
Mayrhofer, P. H., Music, D., Reeswinkel, T., Fuß, H.-G. & Schneider, J. M. Structure, elastic properties and phase stability of Cr1–xAlxN. Acta Mater. 56, 2469–2475 (2008).
Bagcivan, N., Bobzin, K. & Theiß, S. (Cr1−xAlx)N: a comparison of direct current, middle frequency pulsed and high power pulsed magnetron sputtering for injection molding components. Thin Solid Films 528, 180–186 (2013).
Hultman, L., Sundgren, J. ‐E., Greene, J. E., Bergstrom, D. B. & Petrov, I. High‐flux low‐energy (≂20 eV) N+2 ion irradiation during TiN deposition by reactive magnetron sputtering: effects on microstructure and preferred orientation. J. Appl. Phys. 78, 5395–5403 (1995).
Michely, T. & Krug, J. Islands, mounds and atoms (Springer Science & Business Media, 2012).
Hecimovic, A., Burcalova, K. & Ehiasarian, A. P. Origins of ion energy distribution function (IEDF) in high power impulse magnetron sputtering (HIPIMS) plasma discharge. J. Phys. D: Appl. Phys. 41, 95203 (2008).
X. Hou, L. Shen, K. Sun & G. Qiu (eds). Deep feature consistent variational autoencoder. In 2017 IEEE Winter Conference on Applications of Computer Vision (WACV) (IEEE, 2017).
Ledig, C. et al. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 4681–4690 (2017).
Mirza, M. & Osindero, S. Conditional Generative Adversarial Nets. In Advances in neural information processing systems, 2672–2680, arXiv preprint arXiv:1411.1784 (2014).
Tholander, C., Alling, B., Tasnádi, F., Greene, J. E. & Hultman, L. Effect of Al substitution on Ti, Al, and N adatom dynamics on TiN(001), (011), and (111) surfaces. Surf. Sci. 630, 28–40 (2014).
Bagcivan, N., Bobzin, K., Brögelmann, T. & Kalscheuer, C. Development of (Cr, Al) ON coatings using middle frequency magnetron sputtering and investigations on tribological behavior against polymers. Surf. Coat. Technol. 260, 347–361 (2014).
Reiter, A. E., Derflinger, V. H., Hanselmann, B., Bachmann, T. & Sartory, B. Investigation of the properties of Al1−xCrxN coatings prepared by cathodic arc evaporation. Surf. Coat. Technol. 200, 2114–2122 (2005).
Greczynski, G. et al. A review of metal-ion-flux-controlled growth of metastable TiAlN by HIPIMS/DCMS co-sputtering. Surf. Coat. Technol. 257, 15–25 (2014).
Bohlmark, J. et al. The ion energy distributions and ion flux composition from a high power impulse magnetron sputtering discharge. Thin Solid Films 515, 1522–1526 (2006).
Horwat, D. & Anders, A. Spatial distribution of average charge state and deposition rate in high power impulse magnetron sputtering of copper. J. Phys. D: Appl. Phys. 41, 135210 (2008).
Zuiderveld, K. in Graphics Gems IV 474–485 (1994).
Banko, L. et al. Effects of the ion to growth flux ratio on the constitution and mechanical properties of Cr1-x-Alx-N thin films. ACS Comb. Sci. 21, 782–793 (2019).
Zeiler, M. D. ADADELTA: an adaptive learning rate method. Preprint at https://arxiv.org/abs/1212.5701 (2012).
Kingma, D. P. & Ba, J. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations (ICLR), arXiv preprint arXiv:1412.6980 (2014).
Banko, L. & Ludwig, A. Cr-Al-O-N thin film SEM surface microstructure images. Harvard Dataverse, V1; https://doi.org/10.7910/DVN/LEPSJW (2020).
Acknowledgements
This study was funded by the German Research Foundation (DFG) as part of the Collaborative Research Centre TRR87/3 “Pulsed high power plasmas for the synthesis of nanostructured functional layers” (SFB-TR 87), project C2. We acknowledge ZGH (Zentrum für Grenzflächendominierte Höchstleistungswerkstoffe, Ruhr-Universität Bochum) for SEM and XRD measurements. We acknowledge Detlef Rogalla at RUBION, Ruhr-Universität Bochum, for RBS measurements. The authors thank Alan Savan for cross-reading the paper.
Author information
Authors and Affiliations
Contributions
L.B. developed the concept, deposited the samples and adapted the machine learning models, L.B. and A.L. wrote the main parts of the paper, Y.L. contributed the code of the machine learning models and coded the cGAN model and helped to develop the machine learning methodology, D.G. and D.N. were involved in preparation and analysis of materials and processing libraries, R.D. supervised the development of the machine learning methods. All authors contributed to the writing of the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Banko, L., Lysogorskiy, Y., Grochla, D. et al. Predicting structure zone diagrams for thin film synthesis by generative machine learning. Commun Mater 1, 15 (2020). https://doi.org/10.1038/s43246-020-0017-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-020-0017-2
This article is cited by
-
Semantic segmentation in crystal growth process using fake micrograph machine learning
Scientific Reports (2024)
-
Development of Process-Structure Linkage Using Conditional Generative Adversarial Networks
Metallurgical and Materials Transactions A (2024)
-
Combinatorial synthesis for AI-driven materials discovery
Nature Synthesis (2023)
-
Machine learning-assisted high-throughput exploration of interface energy space in multi-phase-field model with CALPHAD potential
Materials Theory (2022)
-
Identification of microstructures critically affecting material properties using machine learning framework based on metallurgists’ thinking process
Scientific Reports (2022)