Abstract
The mechanical response of polycrystalline materials to an externally applied load and their in-service performance depend on the local load partitioning among the constituent crystals. In hexagonal close-packed polycrystals such load partitioning is significantly affected by deformation twinning. Here we report in-situ compression-tension experiments conducted on magnesium specimens to measure the evolution of grain resolved tensorial stresses and formation and annihilation of twins. More than 13000 grains and 1300 twin-parent pairs are studied individually using three-dimensional synchrotron X-ray diffraction. It is shown that at the early stages of plasticity, the axial stress in twins is higher than that of parents, yet twins relax with further loading. While a sign reversal is observed for the resolved shear stress (RSS) acting on the twin habit plane in the parent, the sign of RSS within the majority of twins stays unchanged until twin annihilation during the load reversal. The variations of measured average stresses across parents and twins are also investigated.
Similar content being viewed by others
Introduction
The development or use of light-weight high-strength alloys is essential for reducing carbon emissions in various industrial sectors. As the potential light-weight structural materials for automotive or aerospace industries, wrought magnesium-based alloys have received significant attention over the last two decades1,2,3,4,5. Understanding deformation mechanisms and improving the ductility of magnesium alloys at room temperature have been at the centre of many studies because during manufacturing, it is necessary to form the metal alloy to a specific shape. The crystal structure of magnesium alloys is hexagonal close-packed (HCP) where there is a lack of “easy” slip systems along the crystal c-axis, limiting ductility. Tension along the crystal c-axis is usually accompanied by the formation of tensile twins, while tension perpendicular to the crystal c-axis results in the movement of dislocations on the basal or prism planes, i.e. slip6. Twinning is the reorientation of a crystal domain with respect to a habit plane, common between the parent and the twin crystals. It is an important deformation mechanism in many strategic high-value metal alloys such as magnesium, zirconium, and titanium7,8,9,10. The performance of these alloys is significantly affected by load sharing between the twin and parent crystals at micro- or nano-scales.
The measurement of load partitioning between parent and twin pairs has been a challenging endeavour. For measuring internal stresses that develop between grains, a family of grains, or twin-parent pairs, diffraction-based techniques are mainly used11,12,13. For example, neutron or synchrotron X-ray diffraction has been used to measure the evolution of lattice strains in the family of twin and parent grains that can diffract the incident beam14,15,16. Such measurement for a wrought magnesium alloy was primarily done by Clausen et al.17 where they used in situ neutron diffraction to study the evolution of lattice strains in clusters of twin and parent grains. It was shown that the c-axis of the newly nucleated twins was in tension, although the macroscopic load was compressive and nearly parallel to the twin c-axis. While substantial information has been extracted from these experiments, particularly for developing materials models at micro-scales18,19,20,21, there are two main challenges. First, there is a need to carefully measure and calibrate the initial lattice spacing, called d0, in the absence of macroscopic loads22. Although the determination of “true” d0 might be straightforward for parent grains, in textured materials there may be no twin to calibrate the initial d0 in the direction that twins will nucleate, i.e. the c-axis of the twins. This will have a major impact on the values of the measured lattice strains for twins. Second, since lattice strain is the homogenized elastic strain for many diffracting grains, some crucial information about the interaction between individual twins and parents might be lost. Attempts have been made to use higher resolution techniques, e.g. differential aperture X-ray microscopy (DAXM), to measure internal elastic strains in individual twin and parent pairs23,24. With DAXM, it is possible to measure stress variations within parent or twin grains, but so far only one or two twin-parent pairs have been studied with this technique. The complexity in deconvoluting diffraction spots increases drastically with the number of grains satisfying the diffraction condition. Only recently DAXM was used to measure stress variations within about 30 grains25. High angular resolution electron backscatter diffraction technique (HR-EBSD) is also used to measure the variation of elastic strains and lattice rotations within many twin-parent pairs of HCP polycrystals26,27. While such strain variations can be measured every 20 nm, this method also suffers from the d0 problem and only grains located at the specimen surface can be investigated.
In comparison to DAXM, many grains can be simultaneously measured with three-dimensional synchrotron X-ray diffraction (3D-XRD), but at the expense of losing spatial variations of stresses within grains28,29. Following the observations reported by Clausen et al.17, 3D-XRD was used to measure the stress tensor in a single twin-parent pair of a textured MgAZ31 specimen under uniaxial compression. Aydiner et al.30 reported that the nucleated twin is compressed along the loading direction, but carries less load than the corresponding parent. This measurement has been used as the benchmark for developing constitutive models assuming that twins are generally relaxed20,31,32. With the use of DAXM, however, Balogh et al.24 showed that the measured axial strain within two twins and their common parent grain were compressive, yet the smaller twin went through a compressive strain that was two times higher than its corresponding parent. In addition, 3D-XRD is recently used to measure the stress tensor in the twins that nucleate at the early stages of plasticity in a pure zirconium specimen under a tensile load33. Results of this measurement have indicated that the nucleated twins are relatively stressed at the onset of plasticity. No attention was given to the evolution of stress within twins during annihilation.
In this paper, 3D-XRD is used to measure the centre of mass (COM), average orientation, elastic strain, stress, and relative volume of more than 13,000 grains from two magnesium specimens deformed in situ. Post-processing codes are developed to match grains from each measurement step, find nucleated twins and their corresponding parents, and track them throughout the experiment. More than 1300 twin-parent pairs are identified and are used to unequivocally determine the relationship between the measured stresses within the twins and parents. The measured microstructures were subsequently imported into a crystal plasticity fast Fourier transform (CP-FFT) model to investigate the origin of the observed trends.
Results
3-D experiment and crystal plasticity model
Magnesium specimens were cut from a rolled MgAZ31 plate with the geometry shown in Supplementary Fig. 1. The coordinate system used in this paper is such that Z is parallel to the loading direction (LD) as well as the plate rolling direction, X is parallel to the X-ray beam direction (BD), and Y or transverse direction (TD) is defined by the cross product of the other two axes. This coordinate system is also shown in Supplementary Fig. 1. The magnesium plate was initially annealed at 500 °C for 4 h to create equiaxed grains with an average grain size of approximately 50 µm. Initial texture measurement, with a Bruker D8 Discover powder diffractometer, indicated that most of the crystal c-axis are oriented towards the plate’s normal direction (Supplementary Fig. 2). To monitor the formation and annihilation of twins, magnesium specimens were cut such that all parent grains have their c-axis perpendicular to the LD, i.e. parallel to the BD, so that during the compressive loading steps, twins nucleate with their c-axis towards the LD while during the subsequent tensile loading steps, twins annihilate.
Finite element analysis was used to determine the geometry of the samples such that they did not buckle before yielding. Two specimens were deformed in situ to (a) confirm the repeatability of our experimental data and (b) to determine the limit at which the specimen would buckle. The 3D-XRD experiment was done at ID-11, the European Synchrotron Radiation Facility (ESRF), using a monochromatic X-ray beam of 50.239 keV energy. Specimens were mounted on an ADMET deformation rig to apply uniaxial compressive and tensile load while collecting diffraction patterns. The macroscopic applied load was measured by a load cell attached to the tensile rig, while the macroscopic strain was measured by strain gauges attached to the specimens. The detector was positioned at 182.9 mm from the specimen so that 14 complete diffraction rings can be collected to index grains following the procedure explained in “Methods”.
For the Mg-2 specimen, diffraction patterns were collected at zero applied load (Preload), Onset of Plasticity, and two more steps in the plastic zone. The Mg-2 specimen, which was tested first, buckled at a compressive stress of −70 MPa during pattern collection. The details of the experiment and results for this specimen are provided in Supplementary Table 1. Only compressive stress was applied to Mg-2. For the first two loading steps, the beam height was set to 100 µm, but due to the formation of twins and possible overlapping of diffraction patterns, the beam height was reduced to 50 µm and then to 25 µm in steps 3 and 4, respectively. Except for the last step, more than 4000 grains were indexed in the probed volume. In the last step, a clear buckling was observed during the compressive loading and only 1392 grains were indexed before dismissing the measurement. In addition, another sample was made for measuring macroscopic stress–strain curve ex situ. It was observed that the yield stress in a monotonic compression test was about −35 MPa.
For the Mg-1 specimen, the same steps were followed, but the specimen was only loaded to −54 MPa of applied stress to avoid buckling. The details of the experiment and results for this specimen are provided in Table 1 and in Fig. 1. For this specimen, diffraction patterns were collected at the preload and two steps during compressive loading that are named as Onset-C and Plasticity-C. As shown in Table 1, more than 8000 grains were measured in the probed volume of 0.95 × 0.93 × 1.03 mm3 during the compressive loading steps. Further, the measured 3D grain map of the specimen confirmed that Mg-1 did not buckle at the maximum applied stress of −54 MPa as shown in Supplementary Fig. 3. After collecting patterns at Plasticity-C, the specimen was unloaded to near zero applied stress (Unload) and then reloaded to the tensile stress of 25 MPa (Reload-T). The last two steps are to study the mechanism of detwinning. Since the load reversal experiment was done on the Mg-1 specimen, all of the results presented in this manuscript are those obtained for Mg-1 unless otherwise stated. The results for Mg-2 specimen are provided in the supplementary file.
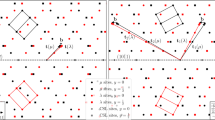
(a) Measured and calculated macroscopic stress–strain curve, (b) measured 3D grain map and stress in the loading direction at the unload step, (c) reconstructed 3D grain map for CP-FFT modelling. The measured (0002) pole figures at (d) Preload, (e) Plasticity-C, and (f) Reload-T steps. In (e) and (f) grains are colour coded with respect to their stresses in the loading direction (LD) and the size of each circle is proportional to the measured relative volume for the grain. (g) The measured distribution of β at each loading step. β is the misorientation between the basal plane normal of each indexed crystal and the loading direction. (h) A 3D view of the matched twin-parent pairs at the Plasticity-C step. Grains are colour coded with respect to their β angle.
As shown in Table 1, at the preload step and on average, 141 peaks were assigned to each grain. These peaks were used to calibrate single-crystal parameters, i.e., more than 1.1 million diffraction peaks were analyzed and used to calibrate single-crystal parameters following the method explained in “Methods”. The “stress-free” lattice parameters were extracted assuming that there was no significant residual stress in the specimen and that, sample preparation did not induce discernible plasticity within the crystals. Although, the specimens were heat treated and recrystallized before the experiment to reduce residual stresses as much as possible. In addition, the peaks recorded at preload did not show any visible evidence of plasticity. The fitted parameters were subsequently used to calculate the stress tensor within each grain during compressive and tensile loading steps. All in all, more than 7.4 million diffraction peaks from Mg-1 and Mg-2 are analyzed to study individual twins and parents. In Table 1, the weighted average of the stresses measured for all grains is provided and compared to the macroscopic applied stress. The measured relative volume for each grain was used as the weight function. Considering the values of the error bars, all components of the stress tensor are close to zero except for σ33 where the grain-weighted average values are very close to the macroscopic stresses calculated from the load cell. It is also shown in Table 1 that the average errors for the measured centre-of-mass (COM) of all grains across all steps do not exceed 6.2 μm which is less than 13% of the average grain size. Since relative volumes can be extracted from peak intensities, the average grain size is determined to be ~50 µm at the preload assuming that grains are spherical and are space filling.
An overview of the results obtained for Mg-1 is shown in Fig. 1. The measured in situ stress–strain curve is shown in Fig. 1a and is compared with the results of the CP-FFT modelling. An example of the measured 3D grain map and stresses are shown in Fig. 1b. It can be seen that upon unloading from Plasticity-C, the axial stress σ33 of grains vary between ±40 MPa. Grains located in the centre of the probed volume were used to reconstruct the 3D microstructure shown in Fig. 1c and import into a CP-FFT model. The steps followed for meshing the microstructure and the constitutive equations used in CP-FFT modelling are provided in Methods. As shown in Fig. 1a, the axial stress is overestimated by the model during the load reversal, at Reload-T. The main reason for this is that only isotropic hardening is considered by the present model. Specifically, the model assumes that the resistance of a slip system remains unchanged when the load direction is reversed. However, during the compression steps, some internal stresses may be generated due to microscopically inhomogeneous plastic deformation, which may lead to kinematic hardening. For simplicity, this aspect is ignored here.
The measured pole figures at the Preload, Plasticity-C, and Reload-T steps are shown in Fig. 1d–f. In Fig. 1e, f, each circle represents a grain with the size of the circle being proportional to the measured relative volume of the grain. In the presented pole figures, grains are colour coded by their measured stresses along the loading direction (σ33). It can be seen that initially, no grains have their c-axis along the loading direction. With compression loading to Plasticity-C, many twins nucleate with their c-axis parallel to the loading direction. While the measured σ33 at the preload is nearly zero (Table 1), at Plasticity-C it varies between −20 MPa and −100 MPa. After unloading and applying a tensile stress (Reload-T), the population of twins reduces indicating that detwinning happened. To clearly see the formation and annihilation of twins, the propensity of the misorientation between the loading direction and the crystal c-axis, β, measured for all grains of each loading step is shown in Fig. 1g. To calculate the propensity of β, the number of grains in each β range is divided by the total number of grains measured at each loading step (as provided in Table 1). It can be seen that only 2.8% of the grains have their β < 40° at the Preload, but this population increases to 3.5% at the Onset-C and subsequently to 11.2% at Plasticity-C. This increase is an indication of the formation of twins. Upon unloading and then reloading, the population of grains with β < 40° decreases to 10.6% and 8.5%, respectively. This is an indication of detwinning during Unload and Reload-T. Twinning and detwinning were further confirmed by tracking the measured diffraction peaks of the twins, an example of which is provided in the supplementary file.
Since twins nucleate during compressive loading and annihilate during tensile reloading, codes were developed to find twin-parent pairs of each measurement step. For the Mg-1 specimen, 10 layers of the gauge volume were measured during Preload and Onset-C, and 20 layers during the rest of the steps. After adding and merging layers to reconstruct the 3D maps, grains of each step were cross-correlated with those of the previous step to determine the common grains. The unmatched grains are the potential “twins” that nucleated between the steps. The layer in which the twin was nucleated was then identified and procedures were developed to search for the possible parents among the neighbouring grains of the twin. A parent is identified when (I) the distance between twin and parent is less than the summation of their radii, (II) the misorientation between basal plane normals of the twin and parent is 86.4°±1.5°, and (III) the misorientation between the normals to the twin \(\left\{ {10\bar 12} \right\}\) habit plane from twin and parent is less than 1.5°. For condition (I), the measured COM for twin and parent are used to calculate the distance between twin and parent. An example of measured twin-parent pairs is shown in Fig. 1h, with the plane projections shown in Supplementary Fig. 3. To determine the size of the smallest twin indexed in the experiment, it is assumed that twins are lenticular and cut through the parent. Hence, twin thickness can be defined as \({{t}}_{\mathrm{T}} = \frac{{4{{V}}_{\mathrm{T}}}}{{\pi {{D}}_{\mathrm{P}}^2}}\), where VT is the volume of the twin and DP is the diameter of its corresponding parent grain. The thinnest indexed twin at Onset-C had a thickness of 0.22 μm. If it was assumed to be spherical, this twin would have a diameter of 23.6 μm.
Evolution of stress: compressive loading
The evolution of σ33 stress component in individual parents and twins for all measured steps is shown in Fig. 2a, b. The measured average values of all grains of each set are illustrated with the solid green lines and the shaded regions represent the full width at half maximum of σ33 measured for all grains. These results indicate that during the compression loading step, the average stress of twins along the loading direction is higher than those of the parents. To further investigate this observation, the measured σ33 of twins are plotted as a function of those of parent grains. As shown in Fig. 2c, at the onset of plasticity, on average, σ33 of twins is about 10.6 MPa higher than those of parent grains. However, with further loading to Plasticity-C (Fig. 2d), this difference drops to 8.4 MPa. The measured average values are illustrated with the red circles with the crosses showing the average error bars calculated for each population.
The measured σ33 in (a) parent grains and (b) twins. The shaded region represents the full width at half maximum (FWHM) of σ33 distribution. The measured σ33 in twins as a function of the measured σ33 in the corresponding parents for (c) Onset-C and (d) Plasticity-C steps. Measured stress normal to the twin habit plane at (e) Onset-C and (f) Plasticity-C steps. Measured resolved shear stress on the twin habit plane in the twinning direction at (g) Onset-C and (h) Plasticity-C steps. (i) The simulated stress–strain curves of twins and parents from CP-FFT. The dotted lines in (c)–(h) are for clarity and to show when the parameter of the vertical axis becomes equal to that of the horizontal axis and the circles with their crosses represent the stress values and their corresponding error bars.
For developing constitutive equations and modelling the localized interactions between twin and parent pairs, assumptions are mainly imposed on the shear and normal stresses that act on the twin habit plane17,34. In HCP crystals, there are six variants of the \(\left\{ {10\bar 12} \right\}<\bar 1011> \) twinning system. With the procedure developed for matching twin-parent pairs, it was possible to determine the twin variant and hence, to determine the normal stress to the twin habit plane (σNormal) and the resolved shear stress acting on the habit plane in the twinning direction (τRS). Since the average tensorial stress in a twin is measured separately from that of the corresponding parent, it is now possible to investigate the relationship between σNormal and τRS of twins with those of parents. In all figures, the normal to the habit plane and shear direction from the parent grain is used to project stresses into a given direction. In Fig. 2e, f, the measured σNormal in twins are plotted as a function of σNormal in parents at Onset-C and Plasticity-C, respectively. It can be seen that the average σNormal measured for the population of the twins is very close to that measured in parents. However, τRS in twins are collectively higher than those of parents at the Onset-C (Fig. 2g), even with considering error bars. At this step, the measured τRS of twins is on average 16.6 MPa higher than that of parents, but this difference drops to 14.5 MPa with proceeding to Plasticity-C (Fig. 2h) with the associated errors of ±6.7 MPa and ±8.7 MPa, respectively. At Plasticity-C, some of the bigger twins now have their τRS closer to, or even less than, τRS of parents. A 3D view of τRS for twin-parent pairs is shown in Supplementary Fig. 3. It is worth noting that the error bars calculated for twins are slightly higher than those for parents because on average, the number of peaks assigned to twins is less than those assigned to parent grains. For example, at Plasticity-C, on average 105 and 153 peaks are, respectively, assigned to twins and parents. Nevertheless, the calculated differences are higher than the error bars, reinforcing the reported trends. The minimum number of peaks used to index grains in any of the loading steps was 60, which is high enough to allow for indexing grains with high confidence. The extracted errors for each twin and parent grain are provided in Supplementary Fig. 4.
In Fig. 2i, the average stress–strain curve calculated for all twins using CP-FFT are compared to that of parent grains. Simulation results indicate that, in the investigated strain range [−0.28%, 0.1%], twinning is the predominant deformation mode. Because of the initial texture, twin Schmid factor for twinning systems is relatively high and such systems are easily activated during the compression loading. Though the Schmid factor does not allow considering the impact of internal stresses, it provides a global indicator of whether twinning systems are likely to be activated or not. Here, crystallographic slip systems provide only minor contribution to the macroscopic plastic strain. Also, at the early stage of nucleation and thickening, twins will be harder than their corresponding parents, yet they become softer with growing in size (see supplementary Table 2 and Fig. 5). Specifically, though plasticity is allowed to happen in twin domains, crystallographic slip systems are generally not activated during the loading. Indeed, the resolved shear stresses acting on basal and prismatic slip systems in twinned crystals are quite low in comparison with the critical shear stresses. As a result, the behaviour of twinned grains is quasi-elastic, which makes them harder to deform than parent grains. In addition, since the applied strain is quite small, the effects of rate sensitivity parameters used in the model are minimum. Although rate sensitivity parameters may affect the values calculated in the vicinity of grain boundaries, such localized variations are generally homogenized during grain averaging.
The average of σ33 for the predicted population of twin and parent pairs from CP-FFT are provided in the supplementary Table 2. It is shown that, on average, σ33 in twins at Onset-C are 6 MPa higher than their corresponding parents, but this difference reduces to zero at Plasticity-C. This follows the trends captured in the experiment, but the difference in the calculated axial stress between the twins and parents is not as large as that measured. The likely explanation is that twin/parent interfaces are not considered in the current model. Indeed, the formation of these interfaces may participate in strain hardening35, by limiting dislocation glide in the vicinity of twins. As a result, when deforming a twinned grain, the twin and its immediate surrounding are harder to deform than the region away from the twin boundary, hence experience higher flow stresses. Considering this contribution to strain hardening would require knowing the position of twin/parent interfaces, using a measurement method such as DAXM. As discussed in35, the effects of interface can be studied within the framework of the phase-field method, which allows tracking twin/parent interfaces.
Evolution of stress: unload and reload
The Mg-1 specimen was unloaded to nearly zero macroscopic stress and then reloaded to 25 MPa tensile stress to investigate the annihilation of twins. The measured stresses for the Unload and Reload-T steps are shown in Fig. 3. It is shown that the average σ33 calculated for twins at Unload is −12.9 MPa while that of parents is 4.5 MPa. Upon removing the applied compressive stress, the size of the twins reduces- an observation confirmed with the analysis of diffraction peaks captured for some selected twins (see for example Supplementary Fig. 6). This means that the reduction of twin size increases the difference between σ33 in twin and parent. While σ33 in parents follows the sign of the macroscopic stress, the average σ33 in twins stays negative. This observation was further reinforced at Reload-T, where the average σ33 calculated for parents is 22.3 MPa while that of twins is −0.6 MPa. At this step, many twins annihilated and those that remained were greatly reduced in size. Interestingly, during unload and with the reduction in twin size, the model predicts that the average stress within twins fall under the average stress from parents—a phenomenon captured in the experiment.
Measured σ33 in twins as a function of measured σ33 in the corresponding parents for (a) Unload and (b) Reload-T steps. (c) Measured stress normal to the twin habit plane for twins that did not annihilate. Measured resolved shear stress on the twin habit plane in the twinning direction for (d) twins that did not annihilate and (e) twins that detwinned. (f) The measured relative volumes of the twins at Plasticity-C. The circles with their crosses represent the stress values and their corresponding error bars.
To understand the mechanism of detwinning, the measured twins at Plasticity-C are categorized into two groups: those that detwinned between Plasticity-C and Reload-T steps, and those that did not, i.e. they were indexed at Reload-T. The measured σNormal and τRS for both cases at Unload and Reload-T are shown in Fig. 3c–e. It is shown that during unload and tensile reload, the σNormal calculated in twins are similar to those measured for parents (Fig. 3c and Supplementary Fig. 3). On the other hand, for the twins that did not annihilate, the calculated τRS in the twins at Unload and Reload-T, on average, are respectively 22 MPa and 27 MPa higher than those of parents (Fig. 3d). Similar trends are observed for the twins that annihilated (Fig. 3e). Given that twin size decreases upon unloading and subsequent tensile reloading of the sample, these data suggest that the difference between τRS of parent and twin increases with decreasing twin size. This observation is supported by tracking the measured relative volume of twins. In Fig. 3f, it is shown that the twins that annihilated were relatively smaller than those that did not. These relative volumes are measured at Plasticity-C.
In addition, in Fig. 3d, e it is shown that, while the τRS in the parents are negative at Reload-T, it is still positive within the twins. This suggests that negative τRS in the parent grain does not necessarily lead to twin annihilation; in fact, this experiment reveals that for annihilating twins, τRS within the twin should become zero or even negative. A 3D map of the measured τRS for twin-parent pairs at Reload-T is also provided in Supplementary Fig. 3.
Discussion
In order to confirm the trends reported in this paper for Mg-1, results obtained for Mg-2 specimen are investigated. In Supplementary Fig. 7, it is shown that by applying compressive stress, twins nucleate with their c-axis oriented towards the LD. While a few twins nucleate at Onset-C, many more twins are formed at Plasticity-C1. The measured stresses for twin and parent pairs are analyzed and presented in Supplementary Fig. 8. It is shown that for both the Onset-C and Plasticity-C1 steps, both σ33 and τRS in twins are higher than those in their parents. It is further shown that σNormal in the twin and parent are very close. All of these results are consistent with those measured for Mg-1 and confirm the repeatability of the results reported in this paper.
It is generally believed that slip activity in the neighbouring grain can activate nucleation of a twin in magnesium36,37. These observations are generally done using higher resolution techniques, for example with the use of electron backscatter diffraction technique. In this paper, the possible role of slip transfer38 from a neighbouring grain on the nucleation of twins is investigated the details of which can be found in Supplementary Fig. 9. In brief, attentions are given to the twins captured at Plasticity-C while slip activity in the neighbouring grains is investigated at Onset-C. This is to ensure that a slip system was active in a neighbouring grain before the twin nucleation event. While our data show that it was possible that some of the low Schmid factor twins nucleated due to slip transfer, the recorded frequency of this event is not high enough to solidify any conclusion. Higher resolution techniques, such as diffraction contrast tomography8,39, that can provide details of grain boundaries in 3D are required.
This paper provides some evidence that twins are more stressed than their corresponding parents at the early stages of plasticity. The specimens were deformed such that twins form with their c-axis along the compressive loading direction. Due to the lack of easy slip systems along the crystal c-axis, the HCP crystal is plastically hard when a compressive load is applied in this direction. Previous measurements conducted on Mg and Zr have indicated that when the c-axis of twins is perpendicular to the loading direction, they are generally relaxed40,41. Although these measurements are not done in the early stages of plasticity, they both indicate that the existence of easy slip systems within the twin can lead to relaxation. A previous experiment conducted, with the use of DAXM, on two twins located within the same parent indicated that the smaller twin was more stressed than the corresponding parent24. The measured data presented here confirm such observation. Results shown in Fig. 2g, h, suggest that the relaxation of twins increases with twin size. This may be the reason that stresses reported by Aydiner et al.30 for the two reported twins are lower than their corresponding parent. Further, the reported observation in this study is consistent with the results of crystal plasticity numerical simulations reported by Siska et al.42 and Barnett et al.43 where it is shown that τRS within thin twins are relatively closer to zero or even positive at the vicinity of the twin tip right after nucleation. Due to the dynamic nature of twinning, stresses measured within twins using 3D-XRD are for after nucleation; that is, twins nucleated first and after further loading, they are detected and indexed at Onset-C. The experimental data presented in this paper suggest that with loading after nucleation, τRS within the thin twins quickly shifts toward positive values because of twin size effects as well as the lack of plasticity.
Most recently, the state of the tensorial stresses within the twins that nucleate at the early stages of plasticity in a pure zirconium specimen is measured using 3D-XRD33. In this experiment, the c-axis of the parent grains are oriented towards and perpendicular to the tensile loading direction. Hence, during the tensile loading experiment, twins form with their c-axis perpendicular to the loading direction. In contrast to the current experiment, the twins of the zirconium experiment are favourably aligned for plastic deformation by slip on the prism and basal systems. Hence, on average, the recorded stress for twins at the beginning of plasticity onset is reported to be 16 MPa less than their corresponding parents, yet this difference increases with further loading. Both zirconium and magnesium experiments indicate that twins are hard at the first step they are captured, yet they relax with further loading. Although in the magnesium experiment twins are shown to develop higher axial stresses than their corresponding parents.
In sections 2 and 3, the average stress within twins and parents during the compression-tension test were compared. It is worth noting that the averages for each population are provided without considering the effects of grain volumes. In Table 2, the weighted averages of the discussed stress components are provided along with those reported in the previous sections. The measured relative volumes of the grains are used as the weight function. It can be seen that at Onset-C and Plasticity-C, σ33 and τRS within twins are on average higher than those from the corresponding parents, regardless of using the weight function. In addition, σNormal in twins are close to that of parents. In order to check if the reported averages are affected by any possible bias in the data, the distribution of σ33 for twins and parents is investigated. Supplementary Fig. 10 shows the histograms of σ33 measured in twins and parents at Onset-C and Plasticity-C. It can be seen that the averages provided in Table 2 are correct descriptors of the experimental data. In addition, the measured average axial elastic strain (\(\varepsilon _{33}^e\)) for twin and parents are provided in Table 2. This is to ensure that the uncertainty in the elastic modulus of magnesium does not affect the conclusions made. It can be seen that \(\varepsilon _{33}^e\) follows the trends reported for the axial stress. That is, at Onset-C and Plasticity-C, the magnitudes of \(\varepsilon _{33}^e\) in twins are, on average, higher than those in parents, but their differences reduce from Onset-C to Plasticity-C. Errors extracted for each axial strain component are provided in Supplementary Fig. 4. The average errors associated with the measurement of \(\varepsilon _{33}^e\) in both twins and parents are nearly 1E−4 since many diffraction peaks were assigned to the indexed grains. This further reinforces the trends reported for stress relationship in twins and parents.
Although it is shown that σNormal in twins are close to those from the corresponding parents, it is not possible to clearly discuss the local force equilibrium and strain compatibility in the vicinity of twin and parent grain boundaries. Indeed, since the 3D-XRD technique does not allow estimating the total strain field, the compatibility of the strain field cannot be evaluated. In addition, for a twin/parent interface, static equilibrium requires the normal and tangential components of the stress tensor to be the same on both sides of the interface. However, the spatial resolution of the 3D-XRD technique used here is not high enough to estimate the stress state close to the twin/parent interface, i.e. only the grain-averaged stress tensors can be estimated.
In order to further confirm the results reported in this paper, two twin-parent pairs are studied in detail (Fig. 4). Since the height of the X-ray beam used in our experiment was comparable to the average grain size, it was possible to track twin and parent pairs that spanned multiple layers in the z-direction. This allows the study of the variation of stress across parents and twins during the formation and annihilation of twins. The first example of such a case is shown in Fig. 4a–c. In these figures, the parent grain is shown with circles and the twin with squares. The size of the circles and squares is proportional to the measured relative volumes and their colours are proportional to the measured location along the z-axis, as shown by the colour bar. Since the height of the X-ray beam was reduced to half at Plasticity-C, the parent grain spans four measured layers, while it spans two layers at Onset-C. The twin was detected at Plasticity-C and spans two layers. In Fig. 4a it is shown that while σ33 of parent at Plasticity-C varies between −62.8 MPa and −44.1 MPa, the measured σ33 of twin varies from −83 to −80 MPa. This confirms our observation for higher σ33 in twins and also indicates that the variation of σ33 within the twin is much smaller than that of the parent. Upon unload, σ33 of the parent varies between ±5.5 MPa while σ33 of the twin remains negative. At this step, σ33 in the north part of the twin, which has a smaller volume, becomes closer to zero. With further loading, the north part of the twin annihilates while the south part of the twin only shrinks in size. The measured resolved shear stresses τRS for this pair is shown in Fig. 4b. It can be seen that at Plasticity-C, τRS for the twin measured in both layers are higher than those of the parent but decreases with unloading and reloading. Interestingly, while the measured τRS in the portion of the parent that corresponds to the north part of the twin is −14.3 MPa, τRS in that part of the twin is still positive at Unload; however, with progressing towards Reload-T, this portion of twin annihilates while the south part of the twin shrinks. This observation further reinforces the condition for the annihilation of twins where τRS within the twin should become equal or less than zero, not necessarily within the parent. The measured normal stress to the twin habit plane is shown in Fig. 4c. It is shown that the measured σNormal within the twin in the two measured layers are close to the σNormal measured for the parent. In addition, Fig. 4a–c provides an example of a large grain with lower σ33 comparing to its twin. One reason for having lower stresses in large grains is that the localized stresses that occur at the vicinity of grain boundaries might be averaged out during homogenization. However, it should be noted that the data presented in Fig. 2c, d are for all twin-parent pairs, regardless of the parent grain size.
The evolution of σ33, the shear stress in twinning direction, and the normal stress acting on twin habit plane for (a-c) the first twin-parent pair and (d-f) the second pair. Parent grains are shown with circles, twins with squares, and each marker represent a portion of the grain measured with 3D-XRD. Markers are colour coded with respect to their measured position along the loading direction (Z) and arrows show the sequence of loading.
The evolution of stress in the second twin-parent pair is shown in Fig. 4d–f. Similarly, the twin was detected at Plasticity-C, yet with lower σ33 comparing to the portion of the parent measured in the same layer. At this loading step, however, τRS within twin is 14.5 MPa higher than that of parent. While upon unloading and tensile reloading τRS of the parent becomes negative, τRS of the twin remains positive and this twin does not fully annihilate. The measured σNormal for this pair is also shown in Fig. 4f where the measured σNormal within twin is initially higher, yet becomes equal to σNormal of the parent at Reload-T.
The results shown in Fig. 4 indicate that there is a stress heterogeneity within twin or parent grains and that τRS within twins stay positive until twin annihilation. We observe that twins with smaller size experience higher σ33 compared to their parents, although this higher stress is balanced with the parent grains and other surrounding grains to result in an average stress equal to the macroscopic one (as shown in Table 1).
Conclusions
The evolution of tensorial stress within twin and parent pairs during a load reversal experiment is investigated. Magnesium specimens were firstly compressed such that twins formed with their c-axis parallel to the loading direction. This was followed by a tensile load to study the mechanism of detwinning. It was shown that with 3D-XRD it was possible to capture twin-parent pairs and track them across loading steps. With the matching procedure developed here, it was possible to determine the twin habit plane, and hence, measure the normal (σNormal) and resolved shear stress (τRS) acting on the habit plane. It was shown that during loading, unloading, and reloading σNormal of twins stay close to those of parents. Further, at the early stages of plasticity and on average, grain-resolved stress along the loading direction (σ33) is higher in twins relative to parents. This is because twins behave quasi-elastic with minimum slip activity. With further loading and increase in the twin size, the difference in σ33 from twin and parent is reduced. It was shown that twins form with higher τRS relative to their parent yet relax with further loading. Upon load reversal, τRS within the majority of twins were positive until full annihilation, while τRS of parents can be negative. This suggests that positive τRS within twins help prevent full twin annihilation during a load reversal. Further, detwinning was observed during unload, even before the start of tensile reload.
Methods
3D-XRD experiment and data analysis
The experiment was conducted at ID-11 of the European Synchrotron Radiation Facility (ESRF), Grenoble, France. The specimens were mounted on an ADMET rig where the strain was applied at the rate of 5.5 × 10−5 1/s. The macroscopic force was measured by a 500 N load cell at the precision of 1mN. During the experiment minimum creep was recorded; for example at Plasticity-C the recorded strain was −3000µε before pattern collection and −2831µε at the end of pattern collection. At each loading step, in order to measure tensorial stress for each grain, specimens were rotated from −53° to 53° and then from −234.5° to −125.5° with 0.25° rotation increment while collecting diffraction patterns. Diffraction patterns were collected on a 2048 × 2048 pixels director with the pixel size of 47.2 µm. Python codes were developed to post-process the collected diffraction patterns using ImageD11 and the subroutines embedded in Fable (https://github.com/FABLE-3DXRD). After calculating the background image and subtracting it from diffraction patterns, peasksearch was done by applying a series of threshold intensity level of the form 50 × 2n (for 0 < n < 8). This means that when n = 8 and n = 0 were used, only peaks with intensities higher than 12800 and 50 were analyzed. This allows for separating high-intensity peaks first, and then move towards the low-intensity ones. Once diffraction peaks were identified, they were indexed by looking for expected angular relationship between peaks falling on the different Debey–Sherrer rings. At this stage, it was possible to tune single-crystal parameters at the Preload to calculate a “zero” stress for each measured layer. The procedure for extracting the “stress-free” lattice parameters is explained in supplementary file where an example of indexed peaks at preload is shown in Supplementary Fig. 11. Error bars are extracted using FITALLB44. Once single-crystal parameters were fitted for Preload, they were used, without alteration, to index grains from all other measurement steps. The 3D grain maps were then reconstructed by adding and merging measured layers. For the Mg-1 specimen, 10 layers were measured at Preload, and Onset-C, then with a reduction in X-ray beam height, 20 layers were measured at Plasticity-C, and Unload, and 14 layers at Reload-T. For the Mg-2 specimen, 10 layers were measured at Preload, and Onset-C, then with a reduction in the X-ray beam height, 20 and 16 layers were measured at Plasticity-C1 and Plasticity-C2 steps, respectively.
After reconstructing 3D grain maps, the rigid body movement of the specimen was calculated by locating common grains across loading steps. The common grains are those that more than six of their neighbours could be identified between any two steps. The measured COMs of the common grains were used to correct the rigid body movements45. At this stage, it was possible to compare grains from each loading step and match them. The unmatched grains are considered as possible twins that formed between the previous and current loading step. The twins also have their crystal c-axis oriented towards the loading direction. Once the possible twins are identified, their corresponding parents were determined by checking the local neighbourhood of the twin in the layer that the twin was found.
Crystal plasticity fast Fourier transform (CP-FFT)
To conduct the CP-FFT simulations, a volume element has first been extracted from the measured 3D grain map of the Mg-1 specimen obtained at Preload46. To reconstruct the volume element, a weighted Voronoï tessellation has been performed with 400 seeds, corresponding to grains located in the centre of the probed volume. The weight (respectively position) of each seed is given by the cube root of the volume (respectively centre of mass) of the corresponding grain. For the application of the spectral (i.e. FFT) method47 the volume element, which is shown in Fig. 1c, has been discretized into 1283 voxels. The volume of a voxel is about 13 µm3. Each voxel is treated as a composite material consisting of seven different constituents, i.e. the parent crystal and the six possible twin variants. At the voxel scale, the seven constituents are assumed to undergo the same stress state. For a voxel with stress state \(\bar \sigma\), the stress state \(\sigma _\alpha\) in the αth constituent is
This assumption allows calculating the effective stiffness tensor \(\bar S\) and effective plastic strain tensor \(\overline {\varepsilon ^p}\) of each voxel with:
where \(\varphi _\alpha\), \({\mathbf{S}}_\alpha\) and \({\mathbf{\upvarepsilon }}_\alpha ^p\) are, respectively, the volume fraction, the compliance tensor, and the plastic strain tensor of the αth constituent. For parent constituents, the plastic strain tensor is the sole result of crystallographic slip on basal, prismatic and 2nd order pyramidal slip systems. For twin variants, the same slip systems are considered but the additional contribution of the shear strain associated with twinning is also accounted for. The viscoplastic flow rule proposed by Méric et al.48 is used to evaluate the shear strain rate \(\dot \gamma _\alpha ^s\) associated with each slip system s:
where \(\tau _\alpha ^s\) is the resolved shear stress, \(r_\alpha ^s\) is the CRSS, and K and M are material parameters. A linear isotropic hardening rule is used for the evolution of the CRSS, that is:
where H is the isotropic hardening modulus and A is the interaction matrix. In the present work, no distinction is made between self- and latent hardening (Ast=1). For each twin variant, the evolution of the twin volume fraction is described with a similar rate-dependent formulation. Nevertheless, in contrast with the formulation used for crystallographic slip, the distinction is made between twinning and detwinning by using different CRSS for these two situations.
The initial CRSS and viscosity parameters associated with the different slip modes are given in Table 3. The values of the CRSS and the isotropic hardening modulus, which is the same for all slip systems, have been selected to match the experimental stress–strain curve. The ratios between the CRSS of different slip modes are the same as those obtained by Clausen et al.17 for the same alloy. It is worth mentioning that, in contrast with that of twinning, the initial CRSS for detwinning is zero. This allows considering that the nucleation of a twin, which necessitates the creation of an interface, requires higher shear stresses than for detwinning.
Data availability
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Code availability
The codes used for post-processing diffraction data can be found at https://github.com/FABLE-3DXRD/
References
Agnew, S. R. & Duygulu, Ö. Plastic anisotropy and the role of non-basal slip in magnesium alloy AZ31B. Int. J. Plast. 21, 1161–1193 (2005).
Wang, H. et al. Crystal plasticity modeling and neutron diffraction measurements of a magnesium AZ31B plate: effects of plastic anisotropy and surrounding grains. J. Mech. Phys. Solids. 135, 103795 (2019).
Barnett, M. R., Ghaderi, A., Quinta Da Fonseca, J. & Robson, J. D. Influence of orientation on twin nucleation and growth at low strains in a magnesium alloy. Acta Mater. 80, 380–391 (2014).
Liu, Y. et al. Three-dimensional character of the deformation twin in magnesium. Nat. Commun. 10, 1–7 (2019).
Nagra, J. S. et al. A new micromechanics based full field numerical framework to simulate the effects of dynamic recrystallization on the formability of HCP metals. Int. J. Plast. 125, 210–234 (2020).
Proust, G., Tomé, C. N., Jain, A. & Agnew, S. R. Modeling the effect of twinning and detwinning during strain-path changes of magnesium alloy AZ31. Int. J. Plast. 25, 861–880 (2009).
Dunne, F. P. E. Fatigue crack nucleation: mechanistic modelling across the length scales. Curr. Opin. Solid State Mater. Sci. 18, 170–179 (2014).
Nervo, L., King, A., Fitzner, A., Ludwig, W. & Preuss, M. A study of deformation twinning in a titanium alloy by X-ray diffraction contrast tomography. Acta Mater. 105, 417–428 (2016).
Kumar, M. A., Beyerlein, I. J., Mccabe, R. J. & Tome, C. N. Grain neighbour effects on twin transmission in hexagonal close-packed materials 1. Nat. Commun. 7, 13826 (2016).
Bieler, T. R., Wang, L., Beaudoin, A. J., Kenesei, P. & Lienert, U. In situ characterization of twin nucleation in pure Ti using 3D-XRD. Metall. Mater. Trans. A: Phys. Metall. Mater. Sci. 45, 109–122 (2014).
Sedmak, P. et al. Grain-resolved analysis of localized deformation in nickel-titanium wire under tensile load. Science 353, 559 (2016).
Simons, H. et al. ferroelectrics. Nat. Mater. 17, 814–819 (2018).
Abdolvand, H., Wright, J. & Wilkinson, A. J. Strong grain neighbour effects in polycrystals. Nat. Commun. 9, 171 (2018).
Zhang, H. et al. Multi-scale mechanisms of twinning-detwinning in magnesium alloy AZ31B simulated by crystal plasticity modeling and validated via in situ synchrotron XRD and in situ SEM-EBSD. Int. J. Plast. 119, 43–56 (2019).
Muránsky, O., Barnett, M. R., Carr, D. G., Vogel, S. C. & Oliver, E. C. Investigation of deformation twinning in a fine-grained and coarse-grained ZM20 Mg alloy: Combined in situ neutron diffraction and acoustic emission. Acta Mater. 58, 1503–1517 (2010).
Xu, F., Holt, R. A. & Daymond, M. R. Modeling lattice strain evolution during uniaxial deformation of textured Zircaloy-2. Acta Mater. 56, 3672–3687 (2008).
Clausen, B., Tomé, C. N., Brown, D. W. & Agnew, S. R. Reorientation and stress relaxation due to twinning: Modeling and experimental characterization for Mg. Acta Mater. 56, 2456–2468 (2008).
Mareau, C. & Daymond, M. R. Micromechanical modelling of twinning in polycrystalline materials: Application to magnesium. Int. J. Plast. 85, 156–171 (2016).
Abdolvand, H. & Daymond, M. R. Internal strain and texture development during twinning: comparing neutron diffraction measurements with crystal plasticity finite-element approaches. Acta Mater. 60, 2240–2248 (2012).
Arul Kumar, M., Kanjarla, A. K., Niezgoda, S. R., Lebensohn, R. A. & Tomé, C. N. Numerical study of the stress state of a deformation twin in magnesium. Acta Mater. 84, 349–358 (2015).
Sangid, M. D. Coupling in situ experiments and modeling—opportunities for data fusion, machine learning, and discovery of emergent behavior. Curr. Opin. Solid State Mater. Sci. 24, 100797 (2019).
Withers, P. J. & Webster, P. J. Neutron and synchrotron X-ray strain scanning. Strain. 37, 19–33 (2001).
Arul Kumar, M. et al. Deformation twinning and grain partitioning in a hexagonal close-packed magnesium alloy. Nat. Commun. 9, 4761 (2018).
Balogh, L. et al. Spatially resolved in situ strain measurements from an interior twinned grain in bulk polycrystalline AZ31 alloy. Acta Mater. 61, 3612–3620 (2013).
Hayashi, Y., Setoyama, D., Hirose, Y., Yoshida, T. & Kimura, H. Intragranular three-dimensional stress tensor fields in plastically deformed polycrystals. Science. 366, 1492–1496 (2019).
Guo, Y., Abdolvand, H., Britton, T. B. & Wilkinson, A. J. Growth of {112¯2} twins in titanium: a combined experimental and modelling investigation of the local state of deformation. Acta Mater. 126, 221–235 (2017).
Abdolvand, H. & Wilkinson, A. J. Assessment of residual stress fields at deformation twin tips and the surrounding environments. Acta Mater. 105, 219–231 (2016).
Poulsen, H. F. et al. Jensen, Three-dimensional maps of grain boundaries and the stress state of individual grains in polycrystals and powders. J. Appl. Crystallogr. 34, 751–756 (2001).
Margulies, L., Winther, G. & Poulsen, H. F. In situ measurement of grain rotation during deformation of polycrystals. Science 291, 2392–2394 (2001).
AydIner, C. C. et al. Evolution of stress in individual grains and twins in a magnesium alloy aggregate. Phys. Rev. B: Condens. Matter Mater. Phys. 80, 1–6 (2009).
Ardeljan, M., Beyerlein, I. J. & Knezevic, M. Effect of dislocation density-twin interactions on twin growth in AZ31 as revealed by explicit crystal plasticity finite element modeling. Int. J. Plast. 99, 81–101 (2017).
Abdolvand, H. & Wilkinson, A. J. On the effects of reorientation and shear transfer during twin formation: comparison between high resolution electron backscatter diffraction experiments and a crystal plasticity finite element model. Int. J. Plast. 84, 160–182 (2016).
Abdolvand, H., Louca, K., Mareau, C., Majkut, M. & Wright, J. On the nucleation of deformation twins at the early stages of plasticity. Acta Mater. 196, 733–746 (2020).
Mareau, C. & Daymond, M. R. Study of internal strain evolution in Zircaloy-2 using polycrystalline models: Comparison between a rate-dependent and a rate-independent formulation. Acta Mater. 58, 3313–3325 (2010).
Basinski, Z. S., Szczerba, M. S., Niewczas, M., Embury, J. D. & Basinski, S. J. The transformation of slip dislocations during twinning of copper-aluminum alloy crystals. Rev. Metall. Cah. D’Informations Tech. 94, 1037–1043 (1997).
Jonas, J. J. et al. The role of strain accommodation during the variant selection of primary twins in magnesium. Acta Mater. 59, 2046–2056 (2011).
Khosravani, A. et al. Nucleation and propagation of { 1 0 1 ¯ 2 } twins in AZ31 magnesium alloy. Acta Mater. 100, 202–214 (2015).
Werner, E. & Prantl, W. Slip transfer across grain and phase boundaries. Acta Metall. 38, 533–537 (1990).
Proudhon, H. Pelerin, M. King, A. & Ludwig, W. In situ 4D mechanical testing of structural materials: the data challenge. Curr. Opin. Solid State Mater. Sci. 24,100834 (2020).
Abdolvand, H. et al. On the deformation twinning of Mg AZ31B: A three-dimensional synchrotron X-ray diffraction experiment and crystal plasticity finite element model. Int. J. Plast. 70, 77–97 (2015).
Abdolvand, H., Majkut, M., Oddershede, J., Wright, J. P. & Daymond, M. R. Study of 3-D stress development in parent and twin pairs of a hexagonal close-packed polycrystal: Part i - In-situ three-dimensional synchrotron X-ray diffraction measurement. Acta Mater. 93, 246–255 (2015).
Siska, F., Stratil, L., Cizek, J., Ghaderi, A. & Barnett, M. Numerical analysis of twin thickening process in magnesium alloys. Acta Mater. 124, 9–16 (2017).
Barnett, M. R., Stanford, N., Ghaderi, A. & Siska, F. Plastic relaxation of the internal stress induced by twinning. Acta Mater. 61, 7859–7867 (2013).
Oddershede, J. et al. Determining grain resolved stresses in polycrystalline materials using three-dimensional X-ray diffraction. J. Appl. Crystallogr. 43, 539–549 (2010).
Louca, K. & Abdolvand, H. Accurate determination of grain properties using three-dimensional synchrotron X-ray diffraction: A comparison with EBSD. Materials Characterization 110753 (2020).
Abdolvand, H., Wright, J. P. & Wilkinson, A. J. On the state of deformation in a polycrystalline material in three-dimension: Elastic strains, lattice rotations, and deformation mechanisms. Inter. J. Plasticity 106, 145–163 (2018).
Lebensohn, R. A., Kanjarla, A. K. & Eisenlohr, P. An elasto-viscoplastic formulation based on fast Fourier transforms for the prediction of micromechanical fields in polycrystalline materials. Int. J. Plast. 32-33, 59–69 (2012).
Méric, L., Cailletaud, G. & Gaspérini, M. F.E. calculations of copper bicrystal specimens submitted to tension-compression tests. Acta Metall. Mater. 42, 921–935 (1994).
Acknowledgements
The authors acknowledge the ESRF for allocating beamtime for experiment MA-3613. This research was supported by a Discovery Grant (#RGPIN/04969-2017) from the Natural Sciences and Engineering Research Council (NSERC) of Canada.
Author information
Authors and Affiliations
Contributions
H.A. and C.M. designed and planned the experiment. H.A., C.M., M.M., and J.W. conducted the experiment. K.L., H.A., M.M., and J.W. post-processed the collected diffraction data. K.L. and H.A. analyzed the experimental results and C.M. conducted CP-FFT numerical modelling. H.A. wrote the first draft, and all authors contributed to the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Primary handling editor: John Plummer
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Louca, K., Abdolvand, H., Mareau, C. et al. Formation and annihilation of stressed deformation twins in magnesium. Commun Mater 2, 9 (2021). https://doi.org/10.1038/s43246-020-00105-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-020-00105-y