Abstract
Fundamental dynamic processes at the electronic contact interface, such as carrier injection and transport, become pivotal and significantly affect device performance. Time-resolved photoemission electron microscopy (TR-PEEM) with high spatiotemporal resolution provides unprecedented abilities of imaging the electron dynamics at the interface. Here, we implement TR-PEEM to investigate the electron dynamics at a coplanar metallic 1 T′-MoTe2/semiconducting 2H-MoTe2 heterojunction. We find the non-equilibrium electrons in the 1 T′-MoTe2 possess higher energy than those in the 2H-MoTe2. The non-equilibrium photoelectrons collapse and relax to the lower energy levels in the order of picoseconds. The photoexcited electrons transfer from 1 T′-MoTe2 to 2H-MoTe2 with at a rate of ~0.8 × 1012 s−1 (as fast as 1.25 ps). These findings contribute to our understanding of the behavior of photoexcited electrons in heterojunctions and the design of in-plane optoelectronic devices.
Similar content being viewed by others
Two-dimensional (2D) semiconducting materials become particularly attractive in next-generation electronic device applications due to their atomic thickness and nonzero bandgap. In the way to the scaling in integrated circuits, the electrical contacts that connect to the 2D semiconductors become specifically critical and significantly affect the electronic and optoelectronic devices’ performance. As the pristine surface of the 2D material has no dangling bonds, it is difficult to form strong interfacial bonds with metal, thereby increasing the contact resistance. The traditional method to reduce the contact resistance for silicon is to decrease the depletion region width by locally doping near the metal–silicon junction, which is invalid in 2D devices. The devices based on 2D materials were usually fabricated using direct metal electrode deposition that can introduce defects and impurities, which leads to a reduction in device performance1. Recently, contacting 2D semiconductors through seamless coplanar 2D metal, such as metallic 1 T-MoS2/semiconducting 2H-MoS2 (ref. 2), metallic 1 T′-MoTe2/semiconducting 2H-MoTe2 (refs. 3,4,5,6,7), metallic VS2/semiconducting 2H-MoS2 (ref. 8), and metallic Co-intercalated SnS2/semiconducting Cu-intercalated SnS2 (ref. 9) has been developed. This seamless coplanar 2D metal/semiconductor structures via the covalent bonds, for instance, the heterojunction made of 1 T′/2H-MoTe2, can significantly reduce the contact resistance. Besides, efforts toward constructing high-performance 2D electronic and optoelectronic devices require an understanding of the carrier dynamics fundamentally, which would help design the miniature devices with the ever-increasing demand for faster speed or lower low-energy consumption. Since in modern electronics, carriers transport in the in-plane structures in most of the semiconductor devices, it is of great significance to image the in-plane carriers injection and transport in the 2D limit. However, the carriers dynamics at the coplanar 2D metal/semiconductor interface with the high spatiotemporal resolution is still rare.
In the past decades, many techniques have been developed to study the dynamics of photocarriers simultaneously in space and time with high resolution, such as transient absorption10,11 and scanning ultrafast electron microscopy12,13, etc. In contrast, the time-resolved photoemission electron microscopy (TR-PEEM) method can simultaneously access the evolution of electrons on the time, space, and energy, providing a direct way to image the electrons’ behavior at the nanoscale. Recently, the TR-PEEM technique has been applied to image the dynamics of surface plasmon14,15,16,17,18,19,20,21,22,23, the transport and recombination of carriers in bulk24,25,26,27, atomically thin semiconductors28,29,30,31, and vertical type-II semiconductor heterostructure29. Lateral modulation of electronic and optical properties of the in-plane structures is necessary for planar devices with high-density integration potentials in modern electronics10. Hence, it is of great opportunity to image carrier dynamics of the in-plane metallic 1 T′-MoTe2/semiconducting 2H-MoTe2 heterojunction. Such coplanar structures provide an ideal platform to study the relaxation and motion of photoexcited electrons in the 2D limit.
In this study, we investigated the electron dynamics in energy, time, and space dimensions at a coplanar 1 T′/2H-MoTe2 heterojunction by employing the TR-PEEM technique. The nonequilibrium photoexcited electrons distributed and evolved heterogeneously near the heterojunction interface. The photoexcited electrons in the 1 T′-MoTe2 region possessed higher energy compared with those in the 2H-MoTe2 region. And the energy of nonequilibrium electrons collapsed and relaxed rapidly to the lower energy levels on picoseconds time scale. At the metal/semiconductor interface, the photoexcited electrons in the 1 T′-MoTe2 region decay faster than that of the 2H-MoTe2 region. That could be due to the charge transport or energy transfer with a rate of ~0.80 × 1012/s. The results are useful for the design and fabrication of high-performance in-plane 2D electronic and optoelectronic devices.
Results
Imaging the heterojunction by steady-state PEEM
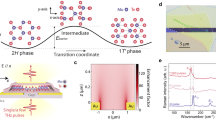
To investigate the carrier dynamics of the coplanar 1 T′/2H-MoTe2 heterojunction, we employed the low-energy electron microscopy (LEEM)/PEEM (Elmitec GmbH) system equipped with an energy analyzer and pump–probe technique (details in “Methods” section)22,32,33,34,35,36,37, as shown in Fig. 1a. The coplanar thin film 1 T′/2H-MoTe2 heterojunction was synthesized via a chemical vapor deposition method through a phase-engineered process (see details in the “Methods” section)38. In short, a 1.5 nm thick Mo film was firstly prepared on the p-type Si substrate via magnetron sputtering. Then, the MoTe2 films were grown by tellurizing the Mo film at 620 °C. During the tellurization, 1 T′ phase polycrystalline MoTe2 film with Te vacancies formed firstly. Then, the solid-to-solid phase transformation from 1 T′- to 2H-MoTe2 occurred and diffused into circles (Fig. 1b). The phase transformation results in single-crystalline 2H-MoTe2 circles seamlessly connected by the polycrystalline 1 T′-MoTe2 background (see Raman mapping in Supplementary Fig. 1a, b)5,7,38. The phase (Supplementary Fig. 1c) and electron backscatter diffraction map (Supplementary Fig. 1d) of the circled 2H-MoTe2 shows a uniform and single contrast, indicating a single-crystalline domain. The high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) was employed to resolve the in-plane atomic arrangements of a typical 1 T′/2H-MoTe2 interface (Fig. 1c), where an atomically smooth interface transition with seamless contact was confirmed. The seamless 2D metal/semiconductor heterojunction provides an exceptionally smooth coplanar structure to study the electrons’ motion and dynamics by the TR-PEEM method.
a Schematic of the TR-PEEM setup, where the 410 nm and 273 nm pulsed lasers were used as the pump and probe beams, respectively. “Δt” indicates the time delay of pump–probe pulsed lasers. b Optical image of the MoTe2 grown on a p-type silicon substrate (p-Si), scale bar is 100 μm. c The HAADF-STEM image (scale bar is 1 nm), as well as the schematic lattice of the 1 T′/2H-MoTe2 interface. d Steady-state PEEM image of the heterojunction with a FOV of ~100 μm illuminated by the 410 nm pulsed laser (laser-PEEM at 410 nm). Scale bar is 25 μm. e Steady-state PEEM image of the blue circled region in d with a FOV of ~20 μm illuminated by the 410 nm pulsed laser. Scale bar is 5 μm. f PEI versus the laser fluence on a logarithmic scale. I indicates the laser fluence. Error bars are ±0.1.
At first, the steady-state PEEM was performed to image the heterostructures under a 410 nm (3.02 eV) pulsed laser (the fluence of ~28 μJ/cm2) with a field of view (FOV) of ~100 μm and ~20 μm (Fig. 1d, e), we can see that the 2H-MoTe2 region appears to be much brighter than the 1 T′-MoTe2 region. The steady-state PEEM image illuminated by a 273 nm (4.54 eV) pulsed laser (Supplementary Fig. 1e, the fluence of ~0.44 μJ/cm2) shows similar results like that by the 410 nm pulsed laser. Besides, the laser fluence dependences (Fig. 1f) of the integrated photoemission intensity (PEI) exhibit linear fluence dependence (~I1.05) and near quadratic fluence dependence (~I1.83) for the 273 nm and 410 nm laser, respectively. The fluence dependence from solely 1 T′- or 2H-MoTe2 regions shows similar results (Supplementary Fig. 1f, g). These results indicate that one-photon or two-photon processes determined mainly the photoemission under 273 nm or 410 nm pulsed laser illuminations, respectively. We discussed the photoemission process in detail (Supplementary Fig. 2).
Energy distribution of photoexcited electrons
To resolve the spatial energy distribution of the photoexcited electrons, we used the energy-resolved mode by filtering the electrons at specific kinetic energies before imaging29,39. With this capability, we can obtain a series of steady-state PEEM images of the spatial distribution of electrons at different photoelectron energies. For example, under the 410 nm laser illumination (Fig. 2a), we did not observe any photoelectrons in the 1 T′ region when the kinetic energy was <0.4 eV. In contrast, most of the photoexcited electrons came from the 2H region. As the kinetic energy increased to >0.4 eV, the photoelectrons began to appear in the 1 T′ region. When the kinetic energy increased further to >1.2 eV, we can observe fewer electrons in the 2H region, while most of the photoelectrons distributed in the 1 T′ region. The 273 nm pulsed laser resulted in similar spatial energy distributions (Supplementary Fig. 3). We noted that the valence band maximum (VBM) of the few-layer 2H-MoTe2 locates at the Γ point, and the conduction band minimum (CBM) locates at the valley between the Γ and K points40,41,42 (Supplementary Fig. 2). For the semiconducting 2H-MoTe2, the minimum energy required to ionize an electron is the energy difference between the vacuum energy level and the VBM around the Γ point. For the metallic 1 T′-MoTe2, since its Fermi energy crosses the allowed energy bands, the minimum energy required to ionize an electron is the energy difference between the vacuum energy level and the Fermi energy around the Γ point. In the coplanar heterojunction, the photoelectron kinetic energy from the 1 T′-MoTe2 is higher than that from the 2H-MoTe2 (Fig. 2b, c). So the Fermi energy of the 1 T′-MoTe2 is above (higher energy level) the VBM of the 2H-MoTe2. Furthermore, we performed the low-energy electron reflectivity spectroscopy with the LEEM method, which helps to determine the band alignment (Fig. 2d). We obtained an energy difference of ΔE0 = 0.18 eV in the vacuum energy level (work function) between the 1 T′- and 2H-MoTe2. The result confirmed a higher work function of the 1 T′-MoTe2 than that of the 2H-MoTe2. The higher work function of the 1 T′-MoTe2 is preferable for the ohmic contact of the p-type 2H-MoTe2, which is consistent with our previous transport data38,43.
a PEEM images recorded at different energies under the illumination of 410 nm pulsed laser. Scale bar is 5 μm. b Normalized photoelectron spectroscopy illuminated by the 273 nm pulsed laser with a fluence of ~0.27 μJ/cm2. c Normalized photoelectron spectroscopy illuminated by the 410 nm pulsed laser with a fluence of ~28 μJ/cm2. “E–E0” indicates the kinetic energy of the photoemission electrons. d Electron reflectivity curves measured by the LEEM, indicating the work function of 1 T′-MoTe2 is about ~0.18 eV higher than that of the 2H-MoTe2.
Photoelectrons relaxation dynamics by TR-PEEM
The TR-PEEM with energy-resolved mode can provide the evolution of photoexcited electrons in time, space, and energy dimensions simultaneously. To elucidate the distribution of nonequilibrium photoelectrons in energy and space, as well as their relaxation dynamics, we pumped the samples with a 410 nm (3.02 eV) pulsed laser at normal incidence. Then, we probed the nonequilibrium electrons with a 273 nm (4.54 eV) pulsed laser with a time delay Δt. At the instant of photoexcitation (Δt = 0), the PEI is the highest, and the energy distribution is broadest. For instance, some photoelectrons had kinetic energy ~3 eV (Fig. 3a). As the time delay increases, the PEI decreases, and the energy distribution of photoemission electrons becomes narrower, and the electrons populate more at lower energy levels. As the time delay increases >1.4 ps, the PEI reduces to the background level. We noted that all photoelectrons spectra had been substrated a background spectrum recorded at the time delay of −1 ps (Supplementary Fig. 4a, b show the original spectra). In the 2D mapping image (Fig. 3b, Supplementary Fig. 4c), we can see that the PEI decreases, and the energy collapses to the low-energy levels rapidly (indicated by the white arrow) as the time delay increases. The relaxation of nonequilibrium photoelectrons is shown schematically in Fig. 3c, i.e., the hot electrons could lose their energy to the lattice on a subpicosecond time scale44.
a Typical energy-resolved photoelectron spectra recorded at various time delays. b Mapping of photoemission (PE) intensity versus the delay time and relative energy. The energy of the photoelectron collapses to the low-energy levels rapidly (white arrow). c Schematic of energy distribution evolution of the photoexcited electrons. “E–E0” indicates the kinetic energy of the photoemission electrons. “Δt” indicates the time delay of pump–probe pulsed lasers.
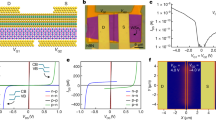
To unravel the spatial dependence of the carrier dynamics, we recorded the PEEM images as a function of pump–probe time delay. In these measurements, the pump and probe fluences are fixed at 28 μJ/cm2 and 0.27 μJ/cm2, respectively. We focused on the dynamics of four representative regions, i.e., the T and H regions (both far away from the heterojunction), and JT/JH regions (near the heterojunction), as shown in Fig. 4a. The normalized time traces of the PEI for the 1 T′- (T region) and the 2H-MoTe2 (H region) are shown in Fig. 4b. In both areas, the PEI increases sharply at the instant of photoexcitation and then followed by two distinct relaxation processes. The normalized time traces can be well-fitted with two exponential decays convolving with the instrument response function, expressed as, \({\mathrm{PEI}}(t) = \left( {A_1e^{ - t/\tau _1} + A_2e^{ - t/\tau _2}} \right) \otimes G({\Delta}tr)\), where τ1 (τ2) is the fast (slow) decay time, G(Δtr) is Gaussian instrumental resolution function, and Δtr is the time resolution of the TR-PEEM system (~200 fs). With that, the fast decay time τ1 of ~0.33 ps with the relative weights A1 of ~85% (0.14 ps/85%), and slow decay time τ2 of ~3.0 ps with the relative weights A2 of ~15% (~1.0 ps/15%) were obtained for the pristine 2H (1 T′) MoTe2, respectively. The fast decay time τ1 of a few hundreds of femtoseconds should arise from the hot electron relaxation via electron–phonon interactions44,45. The slow decay time τ2 could be related to nonradiative electron–hole recombinations (such as Auger recombination or many-body interactions)46. To analyze the results more quantitatively, we used the rate equation analysis (for details see Supplementary Note 1, Supplementary Fig. 5, Supplementary Fig. 6). Then, we obtained the fast decay rate k1H of 2.52 × 1012/s and the slow decay rate γH of 0.042 cm2/s for the 2H-MoTe2 (also k1T of 4.52 × 1012/s and γT of 0.065 cm2/s for the 1 T′-MoTe2)11,28,47,48,49.
a PEEM images excited by the pulsed laser (Laser-PEEM; top) and the scale bar is 8 μm. Schematic of spatially resolved measured regions (bottom). Pristine 1 T′-MoTe2, 2H-MoTe2, and heterojunction regions are labeled as T, H, and J, respectively. b, c Time traces of the PEIs for the T (green), H (orange), and J (magenta for JT and brown for JH) regions. Inset: zoomed-in curve within ~2 ps. d, e Comparisons of the PEI’ time traces between T (H) region and JT (JH) region. The results of the PEIs were averaged of five measurements.
Dynamics of photoexcited electrons at the heterojunction
We imaged the photoelectrons at the heterojunction region by the TR-PEEM (Supplementary Fig. 7). For comparison, we plot the PEIs from the JH and JT regions near the heterojunction, as a function of time delay (Fig. 4c). At the instant of photoexcitation (Δt = 0), we see an increased photoelectron simultaneously in both regions. As shown in the inset of Fig. 4c, we can see that the JH region has longer electrons accumulation time than that of the JT region. The PEI of the JH region is still increasing (extends to 0.2 ps), when the PEI of the JT region has started to decrease (indicated by the arrows, inset of Fig. 4c). To show these clearly, we compared the relaxation lifetimes of the MoTe2 at the JT (JH) junction regions with those at the pristine T (H) regions (far away from the junction) in Fig. 4d, e. The longer electron accumulation time of the JH region should mainly result from the charge or energy transfer from the JT region to the JH region. Because of the electron or energy transfer, there are additional channels to deplete the electrons in the JT region. As time delay increases further, the PEIs eventually decrease in both the JT and JH regions.
The normalized time traces can also be well-fitted by two exponential decays. We obtained that the τ1 (τ2) of the JT region decreases from 0.15 ps (1.18 ps) to 0.12 ps (0.50 ps) compared to the pristine T region (Fig. 4d; the relative weights of the fast and slow decay processes, A1/A2, is 89%/11% for the JT region). Reversely, due to the additional supply of the excited electrons, the electrons lifetime in the JH region τ1 (τ2) increases from 0.33 ps (3.00 ps) to 0.48 ps (5.72 ps) compared to the pristine H region (Fig. 4e; the weights of the fast and slow decay processes, A1/A2, is 79%/21% for the JH region). At the junction region, the fast decay τ1 owing to the free “hot” electrons still has a high weight ratio, which implies the “hot” electrons should dominate the transfer process. We noted that the excitons could impact the transfer process following photoexcitation (at least in the 2H phase). We think that the thermal effect and photon-induced surface voltage effect in the experiments should decrease the excitonic effect in such an indirect few-layer semiconductor with small exciton binding energy50,51,52. But it is hard to isolate precisely the contribution of the excitonic effect in the present situation. We have discussed the exciton binding energy of the few-layer MoTe2 in detail (Supplementary Note 2). Furthermore, the transfer mechanisms could attribute to the charge transport or the energy transfer. In the scheme of the charge transport, the electrons can transfer from the 1 T′ to the 2H phase, and the holes transfer from the 2H to the 1 T′ phase. Such metal/semiconductor band alignment can be supported by the Kelvin probe force microscopy38. Regarding the energy transfer scheme, it could also contribute to the dynamics. For example, the dielectric coupling effect at a metal/semiconductor interface directly induce a generation of hot electrons in the semiconductor substrate53. More efforts are still needed to reveal the contribution of the charge transport and/or energy transfer in the dynamic processes.
Discussion
To illustrate the possible probe range in the band diagram, we drew the probe window of the band structure that can be probed by the 4.54 eV photon (details in Supplementary Note 3). Fig. 5 shows the calculated electronic band structure of a bilayer MoTe2, which is similar to that of a few-layer MoTe2 (refs. 40,41,54). After the photoexcitation by the 3.02 eV (410 nm) pump light, for the 1 T′-MoTe2 (Fig. 5a), the electrons around Γ point near the Femi energy level jump to the higher energy levels; for the 2H-MoTe2 (Fig. 5b), the electrons in the VBM near Γ point jump to the conduction bands and then relax to the CBM (the valley between the Γ and K points). All of these photoexcited electrons are accessible by the 4.54 eV photon in the PEEM measurements (purple shaded area). The excited electrons in the 1 T′-MoTe2 region possess higher energy compared with that in the 2H-MoTe2, as shown in Fig. 2. The photoexcited electrons in the 1 T′ region could transfer to the 2H region crossing the heterojunction interface besides relaxing to lower energy state (magenta arrows). At the same time, the dynamic equilibrium would build up because the transfer of the photoexcited carriers leads to the accumulation of electrons (holes) in the 2H (1 T′) region. That would result in the formation of internal electric fields that impede further charge transfer.
The calculated band structures of bilayer 1 T′-MoTe2 in a and 2H-MoTe2 in b. The purple shaded areas show the band structurse that are accessible by the 4.54 eV photoionization probe. The top red and brown circles indicate the electrons, and the bottom blue circles indicate the holes. The black arrows indicate the 3.02 eV photoexcitation. The magenta dashed arrows stand for the electrons’ relaxation process.
According to the above discussions, a modified rate equation at the coplanar 1 T′/2H-MoTe2 heterojunction can be expressed as:
where τtr is the lifetime of transfer rate from the 1 T′ region to the 2H region, N and M are the electron densities of the 1 T′, and 2H-MoTe2, k1H, k1T, γH, and γT are assumed to the same as the pristine regions. Then, the transfer rate ktr = 1/τtr = 0.8 × 1012/s (τtr = 1.25 ps) is obtained by using Runge–Kutta methods (Supplementary Note 4, Supplementary Fig. 6). This result means that the response time of photoexcited hot carriers could be about picoseconds. The obtained transfer rate ktr is with the same order of magnitude as that in 10-nm-sized graphene quantum dots/MoS2 heterostructure55. Such fast response time is a benefit for high-speed optoelectronic devices. The electrons transfer rate could also be explained by the Marcus theory, which is determined by the driving force, the density of state in acceptor, electronic coupling, reorganization energy, and Fermi occupancy factor, etc.56,57.
In conclusion, we investigated the ultrafast relaxation process of the electrons at the in-plane 1 T′/2H-MoTe2 heterojunction by using the TR-PEEM method in detail. We measured the relaxation rate of the photoexcited electrons in pristine 1 T′ (2H) MoTe2 and the transfer rate at the 1 T′/2H-MoTe2 interface. The metal/semiconductor interface modified the relaxation behavior of the nonequilibrium on picoseconds time scale. We employed the modified relaxation rate equations to analyze the electron dynamic behaviors at the heterojunction. And we obtained the time scale of ~1.25 ps for the photoexcited electrons transferring from 1 T′-MoTe2 to 2H-MoTe2 by using the Runge–Kutta methods. We also discussed the transfer process mechanism and the factors that could influence it. These findings of the dynamics of the electron are instructive for future coplanar electronics and optoelectronics. In the future, combining with the in-plane electrical field, the TR-PEEM could image the majority injection and drift at the contact, and excess carriers ambipolar transport in the coplanar pn junction. That is crucial to gain further understanding of the fundamental processes of the semiconductor devices in the 2D limit.
Methods
Sample preparations
The MoTe2 thin films (with a thickness of ~4.2 nm (ref. 38)) were synthesized by tellurizing the Mo film at atmospheric pressure, using a horizontal hot wall tube furnace equipped with mass flow controllers and a vacuum pump. Mo films were deposited on p-type silica (resistitviy of ~0.05 Ω cm) substrates through magnetron sputtering. The substrates were placed facedown on an alumina boat containing Te powders placed at the center of the heating zone in a one-inch quartz tube. After evacuating the quartz tube to <1 mTorr, we flowed Ar gas at a maximum rate until the pressure reached atmospheric pressure. At atmospheric pressure, Ar and H2 flowed at rates of 4 and 5 standard cubic centimeters per minute (sccm), respectively. The furnace was ramped to 650 °C in 15 min and was kept for various times to synthesize different phase films. At a short growth time of 5 min, the Mo thin film was fully tellurized and formed 1 T′-MoTe2. When the growth time increased to 30 min, some 2H-MoTe2 circles (diameter ~80 μm to ~200 μm) randomly distributed on the background of the 1 T′-MoTe2 film. After the reactions, we let the furnace cool to room temperature naturally. Once the sample had grown, it was sent to the preparation chamber (PCH) with an ultrahigh vacuum (~10−10 Torr) of PEEM immediately. Before measurements, the sample was outgassed and annealed at 110 °C for 0.5 h in PCH with an ultrahigh vacuum (<2 × 10−9 Torr).
Time-resolved photoemission electrons microscopy
The photoemission electron measurements were based on a LEEM/PEEM system (Elmitec GmbH) with an energy analyzer (energy resolution ~150 meV) enabled non-scanning and high-resolution imaging. In the pump and probe setup, the femtosecond near-infrared pulses (820 nm, pulse duration of ~100 fs, repetition rate of ~80 MHz) output from a Ti:sapphire femtosecond laser system (Mai Tai HP, Spectra-Physics) were used to pump the optical parametric oscillator (OPO; Inspire Auto 100, Spectra-Physics). The second-harmonic generation (410 nm/3.02 eV) part was used as pump pulses. And the third-harmonic generation (273 nm/4.54 eV) of the residual fundamental pulse from OPO was used as the probe pulses with time delay. The pump and probe pulse illuminated the sample collinearly at normal incidence. These two pulses were combined and focused on the sample surface at normal incidence. Spot diameter of pump pulse (410 nm/3.02 eV) and probe pulse (273 nm/4.54 eV) were about ~150 μm and ~60 μm, respectively. At each time delay, the image acquisition time was set at 0.15 s and average fourfolds. Due to the influence of nonlinear crystal, the pulse durations broaden; therefore, the temporal resolution of the system is ~200 fs.
Data availability
The authors declare that all the data supporting the findings of this study are available within the paper and its Supplementary Information.
References
Zhang, Q. et al. Simultaneous synthesis and integration of two-dimensional electronic components. Nat. Electronics 2, 164–170 (2019).
Kappera, R. et al. Phase-engineered low-resistance contacts for ultrathin MoS2 transistors. Nat. Mater. 13, 1128–1134 (2014).
Sung, J. H. et al. Coplanar semiconductor-metal circuitry defined on few-layer MoTe2 via polymorphic heteroepitaxy. Nat. Nanotechnol. 12, 1064–1070 (2017).
Suyeon Cho et al. Phase patterning for ohmic homojunction contact in MoTe2. Science 349, 625–628 (2015).
Wang, Y. et al. Structural phase transition in monolayer MoTe2 driven by electrostatic doping. Nature 550, 487–491 (2017).
Empante, T. A. et al. Chemical vapor deposition growth of few-layer MoTe2 in the 2H, 1T′, and 1T phases: tunable properties of MoTe2 films. ACS Nano 11, 900–905 (2017).
Zhang, X. et al. Low contact barrier in 2H/1T′ MoTe2 in-plane heterostructure synthesized by chemical vapor deposition. ACS Appl. Mater. Interfaces 11, 12777–12785 (2019).
Leong, W. S. et al. Synthetic lateral metal-semiconductor heterostructures of transition metal disulfides. J. Am. Chem. Soc. 140, 12354–12358 (2018).
Gong, Y. et al. Spatially controlled doping of two-dimensional SnS2 through intercalation for electronics. Nat. Nanotechnol. 13, 294–299 (2018).
Bellus, M. Z. et al. Photocarrier transfer across monolayer MoS2-MoSe2 lateral heterojunctions. ACS Nano 12, 7086–7092 (2018).
Sun, D. et al. Observation of rapid exciton-exciton annihilation in monolayer molybdenum disulfide. Nano Lett. 14, 5625–5629 (2014).
Najafi, E., Scarborough, T. D., Tang, J. & Zewail, A. Four-dimensional imaging of carrier interface dynamics in p-n junctions. Science 347, 164 (2015).
Liao, B. et al. Photo-excited hot carrier dynamics in hydrogenated amorphous silicon imaged by 4D electron microscopy. Nat. Nanotechnol. 12, 871–876 (2017).
Spektor, G. et al. Revealing the subfemtosecond dynamics of orbital angular momentum in nanoplasmonic vortices. Science 355, 1187–1191 (2017).
Marsell, E. et al. Nanoscale imaging of local few-femtosecond near-field dynamics within a single plasmonic nanoantenna. Nano Lett. 15, 6601–6608 (2015).
Gong, Y. et al. Ultrafast imaging of surface plasmons propagating on a gold surface. Nano Lett. 15, 3472–3478 (2015).
Lemke, C. et al. Spatiotemporal characterization of SPP pulse propagation in two-dimensional plasmonic focusing devices. Nano Lett. 13, 1053–1058 (2013).
Zhang, L. et al. Imaging of surface plasmon polariton fields excited at a nanometer-scale slit. Phys. Rev. B 84, 245442 (2011).
Melchior, P. et al. Optical near-field interference in the excitation of a bowtie nanoantenna. Phys. Rev. B 83, 235407 (2011).
Yang, J. et al. Manipulation of the dephasing time by strong coupling between localized and propagating surface plasmon modes. Nat. Commun. 9, 4858 (2018).
Putnam, W. P. et al. Optical-field-controlled photoemission from plasmonic nanoparticles. Nat. Phys. 13, 335–339 (2016).
Da̧browski, M. et al. Multiphoton photoemission microscopy of high-order plasmonic resonances at the Ag/vacuum and Ag/Si interfaces of epitaxial silver nanowires. ACS Photonics 3, 1704–1713 (2016).
Kubo, A. et al. Femtosecond imaging of surface plasmon dynamics in a nanostructured silver film. Nano Lett. 5, 1123–1127 (2005).
Fukumoto, K. et al. Femtosecond time-resolved photoemission electron microscopy for spatiotemporal imaging of photogenerated carrier dynamics in semiconductors. Rev. Sci. Instrum. 85, 083705 (2014).
Fukumoto, K., Yamada, Y., Koshihara, S.-y. & Onda, K. Lifetimes of photogenerated electrons on a GaAs surface affected by nanostructural defects. Appl. Phys. Express 8, 101201 (2015).
Wong, E. L. et al. Pulling apart photoexcited electrons by photoinducing an in-plane surface electric field. Sci. Adv. 4, eaat9722 (2018).
Fukumoto, K., Yamada, Y., Onda, K. & Koshihara, S.-y Direct imaging of electron recombination and transport on a semiconductor surface by femtosecond time-resolved photoemission electron microscopy. Appl. Phys. Lett 104, 053117 (2014).
Wang, L. et al. Unraveling spatially heterogeneous ultrafast carrier dynamics of single-layer WSe2 by femtosecond time-resolved photoemission electron microscopy. Nano Lett. 18, 5172–5178 (2018).
Man, M. K. et al. Imaging the motion of electrons across semiconductor heterojunctions. Nat. Nanotechnol. 12, 36–40 (2017).
Fukumoto, K. et al. Ultrafast electron dynamics in twisted graphene by femtosecond photoemission electron microscopy. Carbon 124, 49–56 (2017).
Yang, J. et al. Engineering ultrafast carrier dynamics at the graphene/GaAs interface by bulk doping level. Adv. Opt. Mater. 7, 1900580 (2019).
Sun, Q. et al. Dissecting the few-femtosecond dephasing time of dipole and quadrupole modes in gold nanoparticles using polarized photoemission electron microscopy. ACS Nano 10, 3835–3842 (2016).
Yu, H. et al. Exploring coupled plasmonic nanostructures in the near field by photoemission electron microscopy. ACS Nano 10, 10373–10381 (2016).
Razinskas, G. et al. Normal-incidence PEEM imaging of propagating modes in a plasmonic nanocircuit. Nano Lett. 16, 6832–6837 (2016).
Lecarme, O., Sun, Q., Ueno, K. & Misawa, H. Robust and versatile light absorption at near-infrared wavelengths by plasmonic aluminum nanorods. ACS Photonics 1, 538–546 (2014).
Yang, J. et al. Spatial evolution of the near-field distribution on planar gold nanoparticles with the excitation wavelength across dipole and quadrupole modes. Photonics Res. 5, 187–193 (2017).
Neff, A. et al. Imaging nanoscale morphology of semiconducting polymer films with photoemission electron microscopy. Adv. Mater. 29, 1701012 (2017).
Xu, X. et al. Millimeter-scale single-crystalline semiconducting MoTe2 via solid-to-solid phase transformation. J. Am. Chem. Soc. 141, 2128–2134 (2019).
Keyshar, K. et al. Experimental determination of the ionization energies of MoSe2, WS2, and MoS2 on SiO2 using photoemission electron microscopy. ACS Nano 11, 8223–8230 (2017).
Sankar, R. et al. Polymorphic layered MoTe2 from semiconductor, topological insulator, to Weyl semimetal. Chem. Mater. 29, 699–707 (2017).
Qian, X., Liu, J., Fu, L. & Li, J. Quantum spin Hall effect in two-dimensional transition metal dichalcogenides. Science 346, 1344–1347 (2014).
Zhang, H. et al. Resolving deep quantum-well states in atomically thin 2H-MoTe2 flakes by nanospot angle-resolved photoemission spectroscopy. Nano Lett. 18, 4664–4668 (2018).
Xu, X. et al. Scaling-up atomically thin coplanar semiconductor-metal circuitry via phase engineered chemical assembly. Nano Lett. 19, 6845–6852 (2019).
Dai, Y. M. et al. Ultrafast carrier dynamics in the large-magnetoresistance material WTe2. Phys. Rev. B 92, 161104 (2015).
Nie, Z. et al. Ultrafast carrier thermalization and cooling dynamics in few-layer MoS2. ACS Nano 8, 10931–10940 (2014).
Li, Y. et al. Ultrafast carrier dynamics in two-dimensional transition metal dichalcogenides. J. Mater. Chem. C 7, 4304–4319 (2019).
Yuan, L. et al. Exciton dynamics, transport, and annihilation in atomically thin two-dimensional semiconductors. J. Phys. Chem. Lett. 8, 3371–3379 (2017).
Kumar, N. et al. Exciton-exciton annihilation in MoSe2 monolayers. Phys. Rev. B 89, 125427 (2014).
Froehlicher, G., Lorchat, E. & Berciaud, S. Direct versus indirect band gap emission and exciton-exciton annihilation in atomically thin molybdenum ditelluride (MoTe2). Phys. Rev. B 94, 085429 (2016).
Wang, F. et al. Observation of excitons in one-dimensional metallic single-walled carbon nanotubes. Phys. Rev. Lett. 99, 227401 (2007).
Arora, A. et al. Interlayer excitons in a bulk van der Waals semiconductor. Nat. Commun. 8, 639 (2017).
Komsa, H.-P. & Krasheninnikov, A. V. Effects of confinement and environment on the electronic structure and exciton binding energy of MoS2 from first principles. Phys. Rev. B 86, 241201 (2012).
Tan, S. et al. Plasmonic coupling at a metal/semiconductor interface. Nat. Photonics 11, 806–812 (2017).
Pawlik, A. S. et al. Thickness dependent electronic structure of exfoliated mono- and few-layer 1T′−MoTe2. Phys. Rev. Mater. 2, 104004 (2018).
Shan, H. et al. Electron transfer and cascade relaxation dynamics of graphene quantum dots/MoS2 monolayer mixed-dimensional Van der Waals heterostructures. Mater. Today 24, 10–16 (2019).
MARCUS, R. A. On the theory of oxidation-reduction reactions involving electron transfer. I. J. Chem. Phys. 24, 966–978 (1956).
Anderson, N. A. & Lian, T. Ultrafast electron transfer at the molecule-semiconductor nanoparticle interface. Rev. Phys. Chem 56, 491–519 (2005).
Acknowledgements
This work was supported by the National Key Research and Development Program of China (grant no. 2018YFB2200401 and 2018YFA0306900) and the National Natural Science Foundation of China (grant nos. 91950111, 61521004, 11527901, and 91850111). We acknowledge Electron Microscopy Laboratory in Peking University for the use of Cs corrected electron microscope.
Author information
Authors and Affiliations
Contributions
G.L. conceived and designed the research. A.H. performed the measurements and data analysis. Y.Y. and X.X. prepared the sample. W.L. and Z.X. assisted in PEEM experiments. S.X. calculated the electronic structure for MoTe2. B.H. performed the TEM measurements under the direction of P.G. S.W., Q.G., and Q.S. discussed paper writing. A.H., Y.Y., and G.L. wrote the paper. All authors discussed the results and data analysis.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hu, A., Xu, X., Liu, W. et al. Relaxation and transfer of photoexcited electrons at a coplanar few-layer 1 T′/2H-MoTe2 heterojunction. Commun Mater 1, 61 (2020). https://doi.org/10.1038/s43246-020-00062-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-020-00062-6