Abstract
Waveguide integrated optical modulators in the mid-infrared wavelength range are of significant interest for molecular spectroscopy. This is because on-chip synchronous detection can improve the performance of detection systems and can also be used for free-space communications where optical modulators working in atmospheric transparency windows are needed. Here we report optical modulation in a mid-infrared photonic circuit, reaching wavelengths larger than 8 µm. Optical modulation in the wavelength range from 5.5 to 11 µm is shown, relying on a broadband Ge-rich graded-SiGe platform. This demonstration experimentally confirms the free-carrier absorption effect modeling. These results pave the way towards efficient high-performance electrically-driven integrated optical modulators in the mid-infrared wavelength range.
Similar content being viewed by others
Introduction
The mid-infrared (mid-IR) wavelength range, spanning from 2 to 20 µm, is of tremendous interest as it covers the molecular fingerprint of many molecules, such as alkanes or greenhouse gasses, and thereby it can be used to unambiguously detect the molecular composition of a broad variety of gases, liquids, or solids in a non-intrusive way. Moreover, the mid-IR range hosts both atmospheric transparency windows, at wavelengths between 3 and 5 µm and between 8 and 13 µm. Photonics integrated circuits (PICs) operating at those wavelengths are thus expected to have a major impact in a broad variety of high impact applications1, such as environmental monitoring2, astronomy3, hazard detection4, industrial processes control5, medical diagnostics6,7, thermal imaging8, or free-space telecommunications9.
Among the different solutions explored to develop an integrated platform at these wavelengths, silicon (Si) photonics can have a major impact by leveraging the reliable and high-volume fabrication technologies already developed for microelectronic integrated circuits. Interestingly, germanium (Ge), already used in Si photonics, is a prime candidate to extend the operating wavelength of Group IV-based PICs beyond 8 µm, potentially up to 15 µm1,10,11,12. A whole set of passive building blocks have already been developed using different Ge- and SiGe-based platforms, such as wavelength multiplexers, fiber couplers, resonators, or polarization rotators13,14,15,16,17,18,19,20,21. As a next step for the development of mid-IR PICs, active devices must be achieved. More specifically, the development of an optical modulator on these Ge- or SiGe-based platforms would open exciting perspectives in the context of free-space communications, since it could pave the road for a plethora of applications from short-distance access network to satellite communications. Moreover, spectroscopic detection systems would also benefit from the development of an integrated mid-IR modulator, as detection sensitivity can be greatly enhanced via synchronous detection.
A large variety of high-speed optical modulators have been demonstrated using free carrier plasma dispersion effect in the near-IR wavelength range22. The extension of this effect to the mid-IR has been theoretically evaluated first in Si23 and then in Ge24. Interestingly, the plasma dispersion effect was predicted to become more efficient at longer wavelengths. Electro-optic modulation has thus been experimentally demonstrated using diodes embedded in silicon-on-insulator or germanium-on-silicon waveguides25,26,27,28. Most of these demonstrations have been reported in the 2–3.8-µm wavelength range, while the development of mid-IR modulators at longer wavelength is still at its infancy with only one recent preliminary demonstration of electro-absorption modulation at 8 µm29. All-optical modulation has also been demonstrated based on free carrier absorption in the 2–3.2-μm wavelength range30.
The development of high-performance integrated optical modulator in the mid-IR range reaching the fingerprint region beyond 6 µm and the long-wave infrared (LWIR) regime beyond 8 µm still requires a careful evaluation and analysis of the electro-optic effects in SiGe materials. In that sense, experimental demonstrations now appear to be essential to confirm current models for the design of electrically driven mid-IR optical modulators.
In this work, we report the demonstration of optical modulation in mid-IR PICs reaching wavelengths >8 µm. Optical modulation in a wide wavelength range, spanning from 5.5 to 11 µm wavelength, is shown relying on a broadband Ge-rich graded SiGe platform previously reported in ref. 31. This demonstration reaching the LWIR regime is used to experimentally confirm the effectiveness of free-carrier absorption effect24.
Results
Sample description
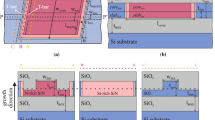
This work relies on Ge-rich graded SiGe waveguides, similar to the ones reported in ref. 31. As seen in Fig. 1, the layer stack is formed by an 11-µm-thick graded layer, in which the Ge fraction increases linearly from pure Silicon (Si) up to Si0.21Ge0.79, followed by a 2-µm-thick Si0.2Ge0.8 constant composition layer. This structure allows a smooth transition from pure Si to Ge-rich material while minimizing the threading dislocation density due to lattice mismatch. Since the refractive index increases linearly with the Ge content in the SiGe alloy, the mode is confined to the upper part of the epitaxial layer. As an illustration of the mode confinement effect, the normalized field intensity profile is plotted as a function of the vertical axis (z-axis) for different wavelengths between 1.33 and 11 µm (right side of Fig. 1). Such ultra-wideband light confinement is a unique property directly related to the refractive index gradient effect and 1.5-cm-long rib waveguides have been fabricated as described in the “Methods” section. To efficiently couple the light from the free-space optical set-up to the PIC, 50 µm-wide and 1-mm-long waveguides are used as the input/output of the circuit, followed by 2-mm-long linear transitions to 7-µm-wide waveguides.
Cut view of the epitaxial layer: on top of the Si wafer the epitaxial stack is formed by an 11-µm-thick graded layer, in which the Ge fraction increases linearly from pure Si up to Si0.21Ge0.79, followed by a 2-µm-thick Si0.2Ge0.8 constant composition layer. The profile of Ge fraction along z-axis is reported on the left part. The normalized field profile in z-axis is reported on the right part, for 1.33, 5.5, and 11 µm wavelengths, illustrating wideband mode confinement in the upper part of the epitaxial layer.
Experimental evidence of optical modulation
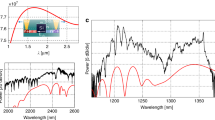
The goal of the experiment is to observe the effect of free carrier concentration variations on the optical absorption of Ge-rich SiGe waveguides in the mid-IR wavelength range. To generate free carriers, the waveguides are optically pumped with a near-infrared (NIR) laser at 1.33 µm wavelength. The pump wavelength is selected so that its photon energy is above the indirect bandgap energy of Si0.2Ge0.8 where most of the NIR beam is confined. Light is thus absorbed by interband absorption, generating free carriers along the waveguide. A tunable mid-IR laser beam is coupled simultaneously in the waveguide, using a free-space beam splitter (BS) to combine both beams. The effect of free carrier absorption can thus be evaluated in an all-optical modulation configuration. The scheme of the experimental set-up is shown in Fig. 2 and is further detailed in “Methods” section. The power of the NIR beam is swept to achieve different densities of free carrier in the waveguide.
An NIR beam at 1.33 µm is amplified by a semiconductor optical amplifier (SOA), coupled to free space and superposed with a tunable mid-IR beam thanks to a beam splitter (BS). An NIR camera is used to adjust the input coupling and the mid-IR output beam can be seen in a mid-IR camera thanks to a flipping mirror. The NIR amplitude is modulated by actuating manually a shutter in the optical path before the BS. The output mid-IR signal is collected in a mercury cadmium telluride (MCT) photodetector (PD) and a lock-in amplifier is used to improve the signal-to-noise ratio.
To evaluate the effect of the free carriers on the absorption of the mid-IR beam, the NIR beam is modulated by actuating manually a shutter in the optical path before the BS. An example of measurement on the lock-in amplifier is reported on Fig. 3. In this example, the shutter has been actuated 8 times, and the modulation of the mid-IR signal at a wavelength of 11 µm is clearly seen at each actuation, with clear on/off level separation. A typical figure of merit for optical signals modulated in amplitude on two levels is the modulation depth (MD) that is defined in Eq. (1), where Poff and Pon are the optical powers on the two levels. Experimentally, MD can be evaluated from Voff and Von that are the mean values of the voltage measured on the lock-in amplifier for each level.
All-optical modulation at 11 µm wavelength is reported using a 12-mW pump beam at 1.33 µm wavelength. The voltage at the lock-in amplifier that is proportional to the mid-IR beam power is reported as a function of time, while the NIR pump is mechanically switched on or off by the use of an external shutter. The modulation of the mid-IR signal is seen at each actuation, with clear on/off level separation. The mean values of the measured voltages for both levels (Voff and Von) are deduced from this measurement and are used to calculate the MD.
A set of measurements is carried out by tuning the mid-IR laser wavelength from 5.5 to 11 µm and for 3 values of the NIR pump powers at 1.33 µm (4, 8, and 12 mW estimated in the waveguide). The experimental results are plotted in Fig. 4. As expected, it can be seen that the MD increases when the near-IR beam power increases. Moreover, the MD first increases with the wavelength of the mid-IR signal, but then a saturation and even a slight decrease of MD is observed for wavelength values beyond 9.5 µm. While the increase of the MD with the wavelength is easily explained by the enhancement of the plasma dispersion effect as predicted by ref. 24, the evolution of MD at longer wavelength will be further explained by the modeling of free carrier absorption in this all-optical modulation scheme.
All-optical MD as a function of the signal wavelength for different NIR pump powers (wavelength of 1.33 µm). Experimental data (dots) show a good agreement with the modeling (solid lines): when the wavelength increases, first the modulation depth (MD) increases but then a saturation and even a slight decrease of MD is observed for wavelength values beyond 9.5 µm. Furthermore, MD increases with the pump power. The error bars in the experimental data correspond to the variation of the measured modulation depth, when repeating the measurement ten times.
Modeling of free carrier absorption in Ge-rich SiGe waveguides
Once all-optical modulation reaching the LWIR regime in Ge-rich SiGe waveguides is experimentally demonstrated, it is interesting to evaluate the free carrier concentration profile in the waveguide and to compare the experimental results with the modeling of free carrier absorption effect in the mid-IR. A proper understanding of the physical effects and a good match between theory and experiment would thus be of major importance for further design of efficient electrically driven mid-IR integrated modulator.
The modeling of the free carrier absorption effect will be detailed below. It relies on (i) the modeling of the free carrier concentration in the waveguide, (ii) the calculation of the absorption coefficient as a function of the wavelength along the waveguide and (iii) the evaluation of Pon and Poff, the power at the output of the waveguide with and without the presence of the NIR pump.
The modeling of the semiconductor carrier distribution uses the model proposed in ref. 32. An NIR beam at 1.33 µm wavelength propagating in (x) direction is the source of photons that generates the free carriers inside the waveguide by interband absorption. In the absence of any electrical field applied, the free carriers can undergo either free carrier recombination (described by the recombination lifetime τ) or carrier diffusion. In the (y,z) plane, the free carrier distribution is described by a two-dimensional Gaussian distribution G(y,z) with a standard deviation R (µm). If the diffusion length is larger than the NIR input beam that generates the carriers, the value of R is estimated as the carrier diffusion length \(L_D = \sqrt {D\tau }\). Finally, the excess carrier density Δn(x,y,z) is thus given by the following equation:
where τ is the free carrier recombination lifetime, D is the ambipolar diffusion coefficient33, α is the NIR absorption coefficient, Φ0 is the incident photon flux, G(y,z) is the normalized Gaussian distribution function describing the free carrier distribution in the (y,z) plane with standard deviation R, and x is the position along the propagation axis. Φ0 can be calculated from the input power by \({\it{\Phi }}_0 = \frac{{P_{{\mathrm{NIR}}}}}{{h\,c/\lambda _{{\mathrm{NIR}}}}}\), where PNIR is the power of the NIR beam, h is the Plank constant, c is the light speed in vacuum, and λNIR is the wavelength of the NIR beam.
Assuming a surface recombination rate S0 at x = 0 and a free carrier density that vanishes at x = +∞ as boundary conditions32, the carrier density can be calculated as:
Free carriers are generated by the optical absorption at 1.33 µm wavelength and most of this absorption occurs in the Si0.2Ge0.8 top constant composition layer. The absorption coefficient is thus 20 cm−134. The ambipolar diffusion coefficient can be estimated to be 65 cm2 s−1 [ref. 33, http://www.ioffe.ru/SVA/NSM/Semicond/]. In terms of recombination velocity at the input surface, we use values that have been reported for Ge surface35, i.e., S0 = 250 cm s−1 . The carrier recombination time can strongly vary with growth conditions and fabrication process. We thus decided to fit this value by comparing the experimental measurements and the simulation results, both shown in Fig. 4. A value of τ = 15 ns is obtained, which is consistent with the results reported in ref. 30, where a value of τ of 18 ns has been estimated for Ge-on-Si waveguides. The corresponding carrier diffusion length is thus 10 µm. This value has been used as the standard deviation R of the free carrier distribution G(y,z), as it is larger than the NIR beam spot size.
Based on these data, carrier density distribution along the propagation axis can be calculated with Eq. (3) at any (y,z) position. The electron and hole concentrations in the center of the normalized Gaussian distribution G(y,z) and along x-axis are reported in Fig. 5 for different values of the NIR powers. The maximal carrier concentration in the waveguide entrance is 3.9 × 1015 cm−3 for 12 mW input power. The carrier distribution decays rapidly along the propagation direction up to negligible values after a few millimeters of propagation. This indicates that the NIR beam is strongly absorbed as soon as it is coupled in the PIC, which implies that most of the modulation will then occur in the 50-µm-wide, 1-mm-long input waveguide.
Once the carrier distributions are obtained, the absorption coefficient due to free carriers can be estimated. As most of the optical mode propagates in the Ge-rich part of the epitaxial growth, the model developed in ref. 24 is used, where the effect of free carrier on the optical absorption is evaluated for Ge. Absorption variation is thus given by the following equation where c1(λ), c2(λ), c3(λ), and c4(λ) are obtained from ref. 24.
The absorption coefficient increase due to free carriers along the propagation direction can be deduced from Eq. (4), using the calculated carrier density distribution. The result is reported in Fig. 6 for an input pump power of 12 mW. As expected, the absorption mainly occurs in the first millimeter of propagation. The absorption coefficient increase is also reported as a function of the wavelength in the inset of Fig. 6, using a carrier concentration of 3.9 × 1015 cm−3 for electrons and holes. A strong increase of the absorption coefficient is observed between 5 and 9 µm, but it suffers from a saturation for wavelengths >9 µm.
Absorption coefficient due to free carriers along the propagation direction (x-axis) at the center of the (y,z) Gaussian distribution for a pump power of 12 mW and for different mid-IR wavelengths. Inset: absorption coefficient increase as a function of the wavelength for a carrier density of 3.9 × 1015 cm−3, calculated by Eq. (4) and considering the parameters c1(λ), c2(λ), c3(λ), and c4(λ) reported in ref. 24 for Ge.
To evaluate the modulation of the mid-IR signal, light confinement of the mid-IR beam must be considered. As most of the absorption occurs in the first millimeter of propagation, i.e., in the 50-µm-wide waveguide, a non-uniform Gaussian distribution in z and y direction is used, considering different values for the vertical and horizontal standard deviation (Rmid-z and Rmid-y, respectively). In the vertical direction, the mode size and position strongly depend on the wavelength (right side of Fig. 1). Numerical simulations are thus used to estimate both Rmid-z(λ) and the position of the optical mode center in the vertical direction. In the lateral dimension, the confinement is much lower because of the 50-µm-wide input waveguides. Thus the beam size is roughly given by the spot size at the output of the coupling lens. Rmid-y is then estimated experimentally with a camera at the waveguide output, and a value of 12 µm at 5.5 µm wavelength is obtained. For larger wavelengths, the following relation is used: \(R_{{\mathrm{mid}} - y}\left[ {\upmu {\mathrm{m}}} \right] = R_{5.5\,\upmu {\mathrm{m}} - y}\sqrt {\lambda _{{\mathrm{mid}}}\left[ {\upmu {\mathrm{m}}} \right]/5.5}\), where λmid [μm] is the signal wavelength and R5.5 μm–y takes a value of 12 µm.
It can be noted that, when the mid-IR wavelength increases, the larger mid-IR beam and its deeper vertical displacement in the graded layer are both responsible for the reduction of the overlap between the beam and the free carrier distributions, leading to a reduction of MD.
Finally, the evolution of the power at mid-IR wavelengths along the propagation direction can be calculated by integrating the mid-IR signal distribution with the locally calculated free-carrier-based absorption coefficient. Typical propagation loss of 2.5 dB cm−131 is also considered all along the waveguide and added to the free-carrier-based absorption. As an example, the evolution of the power inside the waveguide is reported in Fig. 7 at 11 µm wavelength. Without NIR pump, the mid-IR power experiences a long exponential decay due to the constant propagation losses. With 12 mW pump at 1.33 µm, the effect of the free carriers can be seen at the waveguide entrance by a stronger power decrease in the first millimeter. Then the slope of the transmission as a function of the length becomes equal to the case without free carriers, meaning that only the contribution from classical propagation loss can be seen. From this calculation, the MD can be obtained by evaluating Pon and Poff at the waveguide output.
Evolution of the power of the signal at 11 µm wavelength, along the propagation direction, when a 12-mW NIR beam at 1.33 µm is applied (blue) or not (orange). 2.5 dB cm−1 propagation losses are considered in both cases. The effect of the free carriers can be seen in the first millimeter, by an increase of the losses. The modulation can be deduced at the waveguide output.
This method has been applied for different mid-IR wavelength from 5.5 to 11 µm and for different NIR pump power (4, 8, and 12 mW). The results are plotted as solid lines in Fig. 4 together with the experimental measurements in dots.
A good agreement between experiments and simulations can be observed overall, while the slight variations at low wavelengths are expected to be due to modeling assumptions, such as the estimation of the mid-IR beam size in the lateral direction. However, the modeling reproduces the evolution of MD with the signal wavelength, i.e., a strong increase of MD with the wavelength from 5 to 9.5 µm, followed by a saturation and even a decrease of MD beyond 9.5 µm. This evolution is explained by a combination of both the saturation of the plasma dispersion effect modeled in ref. 24 and reported in the inset of Fig. 6 and a reduction of the overlap between carriers and the mid-IR beam when the wavelength increases, as previously discussed. This experiment is the first experimental demonstration of free carrier absorption effect over such a wide mid-IR spectral range.
Discussion
This work reports the first experimental demonstration of optical modulation in a mid-IR PIC carried out in LWIR regime, up to 11 µm. The reported modulation performances are modest in term of MD for a continuous wave (CW) pump power of 4–12 mW, but this is easily explained by the decrease of free carrier concentration inside the waveguide along the propagation. Interestingly, experimental results are in a good alignment with free carrier electro-absorption predictions24, which is a first step toward the realization of efficient high-performance electrically driven integrated optical modulator in the mid-IR range. Indeed, the use of a PIN or PN diode embedded in the waveguide to inject free carriers all along the modulator active region can be envisaged. Free carrier concentration variations in the range of 1016 cm−3 can then be expected. Absorption variation around Δα = 6 cm−1 can then be predicted at 8 µm wavelength, allowing to expect >5 dB extinction ratio for a 2-mm-long modulator.
These result paves the way toward the design of efficient mid-IR modulators and confirm the huge potential of Ge-based photonic circuits as a promising platform for the integration of mid-IR photonics functions, as it could benefit from low loss waveguides and compact photonics structures, together with the integration of active devices, such as optical modulator. The realization of complete functional systems in the mid-IR and LWIR paves the way for a plethora of applications, from mid-IR spectroscopy, sensing, to free-space telecommunications.
Methods
Fabrication
The epitaxial growth is performed on a silicon wafer by low-energy plasma-enhanced chemical vapor deposition at a rate of 5–10 nm s−1. Then a set of straight waveguides are fabricated by laser lithography and reactive-ion inductively coupled plasma etching. The typical waveguide width is 7 µm and the etching depth is 3.8 µm. These dimensions have been measured with a scanning electron microscope. To efficiently couple the light from the free-space optical set-up to the PIC, 50-µm-wide and 1-mm-long waveguides are used as the input/output of the PIC, followed by 2-mm-long linear transition to the 7-µm-wide waveguide.
Measurement set-up
The scheme of the experimental set-up is shown in Fig. 2. We use a pulsed quantum-cascade tunable laser from 5.5 up to 11 µm wavelength range, with a repetition rate of 100 kHz and duty cycle of 5%. The mean power varies with the wavelength, with a maximum value of 30 mW at 6.25 µm. The mid-IR beam is spatially superposed with a CW 1.33 µm wavelength laser beam, thanks to a BS. The NIR laser is first amplified by a semiconductor optical amplifier (SOA) and then sent to free space by a collimator lens. Both beams are coupled together in and out of the PIC thanks to broadband ZnSe aspheric lenses. The NIR power is swept by variation of the SOA current to achieve different free carrier concentrations in the waveguide. It is evaluated by measuring the power of the NIR beam with a broadband power-meter before coupling to the sample and estimating 5 dB of coupling loss. The measurement is reported for 4, 8, and 12 mW coupled on-chip, evaluated mid-IR-modulated signal is collected from the waveguide output, and sent to a mercury cadmium telluride detector. A lock-in amplifier triggered by the pulsed mid-IR laser is used for signal-to-noise ratio improvement. The output voltage of the lock-in amplifier is thus proportional to the power of the collected mid-IR beam. A mid-IR camera is also placed thanks to a flipping mirror to ensure a correct alignment and coupling.
Data availability
The data supporting the findings of this study are available from the corresponding author upon reasonable request.
References
Soref, R. Mid-infrared photonics in silicon and germanium. Nat. Photonics 4, 495–497 (2010).
Michel, A. P., Miller, D. J., Tao, L., Stanton, L. & Zondlo, M. A. Long-path quantum cascade laser-based sensor for methane measurements. J. Atmos. Oceanic Technol. 33, 2373–2384 (2016).
Labadie, L. & Wallner, O. Mid-infrared guided optics: a perspective for astronomical instruments. Opt. Express 17, 1947–1962 (2009).
Chang, Y.-C. et al. Cocaine detection by a mid-infrared waveguide integrated with a microfluidic chip. Lab. Chip 12, 3020–3023 (2012).
Reich, G. Near-infrared spectroscopy and imaging: basic principles and pharmaceutical applications. Adv. Drug Deliv. Rev. 57, 109–1143 (2005).
Rehman, S., Movasaghi, Z., Darr, J. A. & Rehman, I. U. Fourier transform infrared spectroscopic analysis of breast cancer tissues; identifying differences between normal breast, invasive ductal carcinoma, and ductal carcinoma in situ of the breast. Appl. Spectrosc. Rev. 45, 355–368 (2010).
Depciuch, J. et al. Application of Raman spectroscopy and infrared spectroscopy in the identification of breast cancer. Appl. Spectrosc. 70, 251–263 (2016).
Zhang, D. et al. Depth-resolved mid-infrared photothermal imaging of living cells and organisms with submicrometer spatial resolution. Sci. Adv. 2, 1600521 (2016).
Su, Y. et al. 10 Gbps DPSK transmission over free-space link in the mid-infrared. Opt. Express 26, 34515 (2018).
Zhang, L., Agarwal, A., Kimerling, L. & Michel, J. Nonlinear Group IV photonics based on silicon and germanium: from near-infrared to mid-infrared. Nanophotonics 3, 247–268 (2014).
Marris-Morini, D. et al. Germanium-based integrated photonics from near- to mid-infrared applications. Nanophotonics 7, 1781–1793 (2018).
Osman, A. et al. Suspended low-loss germanium waveguides for the longwave infrared. Opt. Lett. 43, 5997–6000 (2018).
Malik, A. et al. Germanium-on-silicon mid-infrared arrayed waveguide grating multiplexers. IEEE Photon. Technol. Lett. 25, 1805–1808 (2013).
Troia, B. et al. Germanium-on-silicon Vernier-effect photonic microcavities for the mid-infrared. Opt. Lett. 41, 610–613 (2016).
Liu, Q. et al. On-chip Bragg grating waveguides and Fabry-Perot resonators for long-wave infrared operation up to 8.4 µm. Opt. Express 26, 34366–34372 (2018).
Ramirez, J. M. et al. Broadband integrated racetrack ring resonators for long-wave infrared photonics. Opt. Lett. 44, 407–410 (2019).
Xiao, T. et al. Mid-infrared high-Q germanium microring resonator. Opt. Lett. 43, 2885–2888 (2018).
Alonso-Ramos, C. et al. Germanium-on-silicon mid-infrared grating couplers with low-reflectivity inverse taper excitation. Opt. Lett. 41, 4324–4327 (2016).
Radosavljevic, S., Kuyken, B. & Roelkens, G. Efficient 5.2 µm wavelength fiber-to-chip grating couplers for the Ge-on-Si and Ge-on-SOI mid-infrared waveguide platform. Opt. Express 25, 19034–19042 (2017).
Koshkinbayeva, A. et al. Impact of non-central input in N x M mid-IR arrayed waveguide gratings integrated on Si. IEEE Photon. Technol. Lett. 28, 2191–2194 (2016).
Vakarin, V. et al. Ultra-wideband Ge-rich silicon germanium mid-infrared polarization rotator with mode hybridization flattening. Opt. Express 27, 9838 (2019).
Reed, G. T., Mashanovich, G., Gardes, F. Y. & Thomson, D. J. Silicon optical modulators. Nat. Photonics 4, 518–526 (2010).
Nedeljkovic, M., Soref, R. & Mashanovich, G. Z. Free-carrier electrorefraction and electroabsorption modulation predictions for silicon over the 1–14-μm infrared wavelength range. IEEE Photon. J. 3, 1171–1180 (2011).
Nedeljkovic, M., Soref, R. & Mashanovich, G. Z. Predictions of free-carrier electroabsorption and electrorefraction in germanium. IEEE Photon. J. 7, 1–14 (2015).
Van Camp, M. et al. Demonstration of electrooptic modulation at 2165nm using a silicon Mach-Zehnder interferometer. Opt. Express 20, 28009–28016 (2012).
Thomson, D. et al. Optical detection and modulation at 2µm-2.5µm in silicon. Opt. Express 22, 1825–10830 (2014).
Kang, J., Takenaka, M. & Takagi, S. Novel Ge waveguide platform on Ge-on-insulator wafer for mid-infrared photonic integrated circuits. Opt. Express 24, 11855 (2016).
Mashanovich, G. et al. Group IV mid-infrared photonics. Opt. Mat. Express 8, 2276 (2018).
Li, T. et al. Ge-on-Si modulators operating at mid-infrared wavelengths up to 8 µm. Photon. Res. 7, 828–836 (2019).
Shen, L. et al. Mid-infrared all-optical modulation in low-loss germanium-on-silicon waveguides. Opt. Lett. 40, 268–271 (2015).
Ramirez, J. M. et al. Graded SiGe waveguides with broadband low-loss propagation in the mid infrared. Opt. Express 26, 870–877 (2018).
Rosencher, E. & Vinter B. in Optoelectronique Ch. 11 (Dunod, 2002).
McKelvey, J. P. in Solid State and Semiconductor Physics Ch. 10 (R. E. Krieger, 1966).
Braunstein, R., Moore, A. R. & Herman, F. Intrinsic optical absorption in germanium-silicon alloys. Phys. Rev. 109, 695–710 (1958).
Stevenson, D. T. & Keyes, R. J. Measurements of recombination velocity at germanium surfaces. Physica 20, 1041–1046 (1954).
Acknowledgements
This work was supported by the European Research Council (ERC) under the European Union’s Horizon 2020 (No. 639107 - INsPIRE). The fabrication of the device has been performed in the Platforme de Micro-Nano-Technologie/C2N, which is partially funded by the “Conseil Général de l’Essonne.” This work was partly supported by the French RENATECH network. A. Ballabio and A. Barzaghi acknowledge financial support by the TEINVEIN project funded by POR FESR 2014-2020 (ID: 242092). J.F. acknowledges financial support by the European Union Horizon 2020 FET project microSPIRE (ID: 766955).
Author information
Authors and Affiliations
Contributions
J.M.R. proposed the experiment. M.M.-B. and D.M.-M. developed the theoretical model and data analysis. J.F., A. Ballabio, A. Barzaghi, and G.I. carried out the epitaxial growth. M.M.-B., V.V., D.B., Q.L. and X.L.R. fabricated the structures. M.M.-B. and L.D. performed the measurements. M.M.-B., C.A.-R., G.I., L.V., and D.M.-M. discussed the results and wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Montesinos-Ballester, M., Vakarin, V., Ramirez, J.M. et al. Optical modulation in Ge-rich SiGe waveguides in the mid-infrared wavelength range up to 11 µm. Commun Mater 1, 6 (2020). https://doi.org/10.1038/s43246-019-0003-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-019-0003-8