Abstract
How to control the global temperature rise within 1.5 °C in the post-COVID-19 era has attracted attention. Road transport accounts for nearly a quarter of global CO2 emissions, and the related sulfur dioxide (SO2) emissions also trigger air pollution issues in population-intensive cities and areas. Many cities and states have announced a timetable for phasing out urban-based fossil fuel vehicles. By combining a Markov-chain model with a dynamic stochastic general equilibrium (DSGE) model, the impacts of on-road energy structural change led by phasing out fossil fuel vehicles in the road transportation sector are evaluated. The impact of automobile emissions (both CO2 and SO2) on the environment is evaluated, taking into consideration of variation between cities, regions, and countries. Two other major driving forces in addition to CO2 emissions reduction in promoting fossil fuel vehicles’ transition toward net-zero carbon are identified and analyzed with multiple different indicators. Under the framework of the DSGE model, climate policy instruments’ effects on economic development, energy consumption, and their link to economic and environmental resilience are evaluated under exogenous shocks as well.
Similar content being viewed by others
Introduction
United Nations Secretary-General António Guterres recently called for stronger ambitions in nationally determined contributions (NDCs) around the world in the 26th Conference of the Parties (COP26). Limiting global average temperature increases to 1.5 degrees requires a 45% reduction in carbon dioxide (CO2) emissions in 2030, according to the Intergovernmental Panel on Climate Change (IPCC). Among all sectors, transport typically accounts for the majority of oil demand and is closely related to air pollution issues in population-intensive cities and areas1. Since transportation emissions contribute to about 23% of total energy-related CO2 emissions worldwide2 and approximately 72% from road transport3, more than twelve countries planned to phase out fossil fuel vehicles and eventually banned their sales4 for transport sector decarbonization. Although transport demand has significantly decreased since the outbreak of COVID-19 and its demand drop contributed the largest share to the decline in 2020 emissions5, the recovery of global transport activity is an important bellwether for the rebound in global oil demand and in global CO2 emissions6,7.
The concept of banning the sale of gasoline vehicles was first proposed by the Netherlands and is scheduled to be fully implemented in 2025. Since then, Ireland, Slovenia, Israel, France, Sri Lanka, the United Kingdom, Sweden, and China have all announced plans to ban the sale of gasoline vehicles8,9,10,11. Under these circumstances, the Ministry of Industry and Information Technology (MIIT) announced that China will support cities and regions to become pilots for the banning sale of fossil energy vehicles when the conditions are sufficient. This is consistent with the requirement of 30–60 dual carbon goals. China’s transport sector is responsible for ~10% of national CO2 emissions12, and it is also a substantial source of air pollution4,13. To alleviate the cities’ pressure on energy and the environment and promote the upgrading of the automobile industry, it is imperative to ban the sale of gasoline vehicles14. In addition, oil consumption in China is highly dependent on imports, while geopolitical risks (GPRs) may lead to safety issues and uncertainties15,16.
However, a retaliatory growth of CO2 emissions was found in the post-COVID-19 era through the short- and long-term analysis7. A rebound in the consumption of motor gasoline was found in May 202017. Since the emission reductions associated with the pandemic are only temporary, the CO2 emissions may skyrocket again in reviving economies. Since China is the first major economy to show recovery after a slowdown induced by the COVID-19 pandemic18, hereafter, balancing economic growth with energy use and CO2 emissions reduction is still an important issue confronting China.
Carbon neutrality in the post-COVID-19 era requires new pathways and solutions to meet the energy demands previously met by fossil energy19,20. In addition, restraining oil consumption is important for countries facing a shortage of oil resources21,22 for energy security and environmental protection. Many countries in the world are experiencing a shortage of oil resources and depend on imports, for example, the European Union, Japan, Korea, India, and China. Taking China as an example, external oil dependence has exceeded 70% in three consecutive years. Since oil consumption by vehicle usage accounts for ~60% of total oil consumption in China, from this perspective, the deactivation of fossil fuel vehicles has its own internal driving force for these countries. The decarbonization of the transportation sector requires a massive transformation that involves promoting and increasing renewable shares in the vehicle fuel mix23, and electric vehicles are considered to be the main method to solve these problems24,25. Solutions to mitigate conventional vehicles’ CO2 emissions and SO2 emissions in the urban area can be categorized into banning fossil fuel vehicles and promoting electric vehicles and other renewable energy vehicles. These changes, along with investments in complementary infrastructure such as charging stations, make electric vehicles viable substitutes for many modes of transportation in cities and regions. However, the transition to electrification has moved slower than expected, and many potential adverse effects have arisen during this transition to BEVs, generally involving the range, initial investment, and charging equipment insufficiency. Regarding transportation carbon emissions, policy instruments represented by personal carbon trading schemes are still under discussion26,27. The costs of these policy instruments remain unknown28.
A successful transition toward a net-zero economy and the achievement of carbon neutrality in the transportation sector of population-intensive areas, such as urban areas, require the scaling up of low-carbon vehicle investment and the divestment of carbon-intensive vehicle investments and production29. For the transportation sector, banning the sale of fossil fuel vehicles to achieve the upcoming stringent carbon emissions reduction targets is imperative10, i.e., carbon peak by 2030 and carbon neutrality by 2060. Since 2005, China has become the world’s largest vehicle-producing country, with nearly 25% of total global vehicle production. Whether it undertakes the common but differentiated responsibilities (CBDR) determined by the Kyoto Agreement or actively responds to the more radical carbon emission reduction target proposed by COP26, cities and regions in China need to pay more attention to the impact of fossil fuel vehicles.
Therefore, we explore the macroeconomic effects of different emission reduction policy instruments in China by applying a static comparison method using both deterministic and stochastic general equilibrium models. Based on the analysis of road transport energy demand, related emissions, and its impact on economic development and resilience, we also compare the related emissions with those of other countries, such as the United States, Japan, the European Union, and India. Although the notion of “resilience” was first used in physical, engineering, and organizational science, it has recently gained popularity in economics and regional analysis30, especially since the outbreak of COVID-19. Most research focuses on the resilience of cities and entrepreneurs. For example, Hardaker et al. studied the resilience of city retailers under the shock of COVID-1931. Cheng et al. evaluated Chinese cities’ resilience in terms of spatial-temporal evolution32.
Additionally, we explore the role of different policy instruments under the deterministic economy and with consideration of exogenous stochastic shocks in the future through a dynamic stochastic general equilibrium model. Such an integrated strategy considering the demands in fossil fuel vehicles and their related energy consumption, especially the shortage of oil resources in many countries represented by China, can be viewed as an early entry point to address carbon emission mitigation, sulfur dioxide emissions impact on the environment quality and human health in population-intensive urban areas, and national energy security challenges.
Results
Demand analysis by transport mode and vehicle powertrain
The types of transport modes among cities and regions can be categorized into four different uses, such as railways, roads, waterways, and civil aviation. To clarify the significance of fossil energy, especially fuel oil demand, we use the Markov-Chain prediction model to predict how transport demand will change in the future from the perspective of the rotation volume of both freight and passengers.
According to the results, a significant change in road transport has occurred since the outbreak of the COVID-19 pandemic. An unusual decreasing trend in the rotation volume of both freight and passengers in road transport and a significant increase in railway volume indicates that people prefer to avoid road use and choose railway travel instead. Given the significant decrease in the total volume of both passengers and shipments, we can infer that people prefer to stay at home instead of travel compared to the years before COVID-196, conducting trips only if they are necessary (visiting parents during the spring festival, for example). The proportion of convenient and efficient travel is increasing. This is also a representation of the policy launched in the 14th Five-Year Plan for National Economic and Social Development and Vision 2035 of the People’s Republic of China about road transition to railway and waterway.
Although transport demand has significantly decreased since the outbreak of COVID-19 and its demand drop contributed the largest share to the decline in 2020 emissions5, the recovery of global transport activity is an important bellwether for the rebound in global oil demand and in global CO2 emissions33. In the future, the long-term fluctuation of the epidemic and the overall trend of economic growth after the epidemic are expected to coexist for a long time Fig. 1. This also shows the inseparable and interrelated relationship between transportation demand, travel activities, and economic growth.
Figure 1 depicts the forecasting results of the four types of transport mode probability transition processes (i.e., railway, road, waterway, and civil aviation) from 2030 to 2060, categorized by end-use. The pie charts (first and second column) depict the predicted share of each type of demand of transport mode to the total volume of turnover in 2030 and 2060. Partial future demand in civil aviation (freight transport) and waterway is not clearly shown in the pie chart because their share is under 1%. The fourth column depicts the visualization of the average probability transition matrix corresponding to each type of rotation volume, where the x-axis and y-axis denote four states and each state’s transition probability, respectively. The fifth column depicts the visualization of the discrete-time Markov-chain state transition matrix. The higher the transition probability, namely heading to 1, the color closer to blue. The smaller the transition probability, the color closer to red.
Based on the types of powertrain, vehicles can be categorized into conventional fossil fuel vehicles (FFVs) and new energy vehicles (NEVs). NEVs can be divided into three different types, namely, battery electrical vehicles (BEVs), plug-in hybrid electrical vehicles (PHEVs), and fuel cell vehicles (FCVs), by the accessibility of data. The period of the dataset is from 2013 to 2018. We can predict each type of vehicle consumption ratio to the total vehicle consumption from 2030 to 2060 by applying a Markov-chain forecasting model. The predicted results are depicted at a 10-year interval in Fig. 2.
Figure 2 depicts the forecasting results of the four types of vehicle consumption for the total sale of vehicles (i.e., FFVs, BEVs, PHEVs, and FCVs) from 2030 to 2060, categorized by powertrain type. The vehicle powertrain is denoted by “vpt”. The pie charts (col. 1 and 2) depict the consumption ratio of each type of powertrain to the total sales of vehicles from 2030 to 2060. Partial future demand for FCVs is not clearly shown in the pie charts because their share is under 1%. In the third column, the upper right subplot depicts the visualization of the average probability transition matrix corresponding to each type of powertrain, where the x-axis and y-axis denote four states and each state’s transition probability, respectively. And the lower right subplot depicts the visualization of the state transition matrix. The higher the transition probability, namely heading to 1, the color closer to blue. The smaller the transition probability, the color closer to red.
The results show that the ratio of FFVs and NEVs generally decreases and increases, respectively. Among the NEVs, BEV and PHEV demand increases smoothly, while the share of FCVs accounts is too small to play an important role in vehicle transition in the next four decades. The increase in NEVs is connected to the stimulus policies launched by the Chinese government in recent years. By employing subsidies in purchasing NEVs and investing in the charging station, the two most-watched concerns of consumers in choosing NEVs instead of FFVs are being eliminated.
According to the estimation results of Lin and Du34, the share of the transportation sector in urban areas accounts for ~60% of the total consumption of crude oil. Based on the Markov-chain forecast model, we can predict that demand in FFVs will be ~87% and 66% in 2030 and 2060, respectively. Compared to the level in 2020, the corresponding decrease amount in terms of the total sales of vehicles is ~8.09% and 31.53%. Using the energy consumption inventory data of CEADs, we can calculate the total CO2 emissions reduction by the structural change in vehicles in terms of the powertrain.
Energy shortage in transport becomes a driving force
The additional transport fuel consumption mainly comes from demand in the transportation sector. Although China has employed a state-centered approach toward energy security, which has led to cooperation with its neighboring countries, the sophisticated bi- or multilateral political relationship faces considerable uncertainty.
China became the largest importer of oil–gas resources in the world in 2019. Since 2015, the additional consumption of the raw material of transport fuel has depended entirely on imports. It is centralized in comparison to coal, which is commonly used for power generation. Oil is frequently used as automobile fuel, and its consumption patterns are decentralized. And it is strongly related to transportation and other domestic consumption fields, so the policy application points are different. Although the ratio of new energy vehicles in the car market has grown dramatically in recent years35, it accounted for only 5.4% in 2020. Therefore, fossil fuels in the transportation sector still play an important role, which is related to consumption habits36,37.
In addition, China is highly dependent on oil imports, generating potential risk because each country in the international market competes with each other. The Markov-based energy prediction model can capture this shared competition when the sum of all the participants equals one.
Based on BP energy statistical data from 2020, the main importers of oil in the world, such as China, the United States, Europe, India, and Japan, are considered. For the period 2010 to 2019, the share of each country or region in each year can be calculated. Based on the prediction results of the Markov-based model, the future import share of the countries and regions mentioned above can be obtained. In contrast to other linear forecasting methods, the Markov-chain-based model can capture competition in the share of imports among importers in the global market. Assuming no major change in global total oil exports and relatively steady growth in the economy, the predicted share of raw material for transport fuel imports for China would be 42.7% in 2030 when there are no exogenous constraints. However, this increasing share on the demand side cannot be satisfied by the international oil market, given geopolitical risk and supply capacity.
Therefore, triggering a structural transition from fossil fuel vehicles toward new energy vehicles, especially for the urban areas with intensive populations and a large amount of private car possession, is of great benefit to alleviate this potential imbalance between supply and demand in fuel oil. In other words, the imbalance between supply and demand in the future can also become an internal driving force for phasing out fossil fuel vehicles.
The variation among cities and regions for CO2 emissions of fossil fuel vehicles
In fact, the initial driving force for countries that brought up phasing out FFVs is to reduce carbon dioxide emissions. CO2 emissions of the transportation sector account for the second rank of the total emissions for a country, but its impact has a wide range and involves consumption habits. Since China is a country with a large population and a vast territory, variations between cities and regions become a significant factor in analyzing energy transitions in the transportation sector. To date, the majority of previous studies have focused on the country level rather than the possible urban or regional impact, and the key point in reducing transport emissions remains unknown. To determine the importance of phasing out fossil fuel vehicles with the consideration of regional heterogeneity, using regional microdata to analyze these issues is important and helpful in improving the accuracy of policy instrument designations.
Both Figs. 3 and 4 depict the carbon emissions intensity of cities’ and provinces’ transportation sectors. These two figures, however, are calculated using different methodologies. In Fig. 3, the road transportation emissions are divided by the GDP of each province or city. In Fig. 4, the road transportation emissions are divided by the transportation sector’s GDP. A significantly higher deviation and fluctuation are shown in Fig. 3 than in Fig. 4. The original data resources come from the CEADs database, which contains cities and provinces’ energy inventory from 2003 to 2019. The energy inventory data of each year contain 30 sheets corresponding to 30 cities and provinces in China in constraint of data accessibility.
Figure 3 depicts the results of the cities and provincial carbon emission intensity of China’s transportation sector from 2003 to 2019. The numbers from 1 to 30 denote thirty cities or provinces in China in the constraint of data accessibility. Please refer to Supplementary Table 1 in the supplementary information file to obtain the corresponding name of each city or province represented as numbers in Fig. 3.
Figure 4 depicts road transportation-related CEI by the transportation sector’s GDP rather than the total GDP of China. The x-axis and y-axis represent the 30 cities or provinces and year, respectively. The z-axis represents the carbon intensity of road transportation. Please refer to Supplementary Table 2 in the Supplementary Information file to obtain the corresponding name of each city or province represented as a number in Fig. 4.
Figure 3 presents an overview of cities’ and provinces’ carbon emission intensity (CEI) of road transport in China from 2003 to 2019. As shown, a pronounced discrepancy in the level of CEI is represented among cities and regions. During this period, the three provinces with the highest CEI values were Yunnan, Xinjiang, and Guangxi; their average CEI values reached as high as 3.011, 2.897, and 2.649 tons per ten thousand yuan, respectively. The three cities or provinces with the lowest CEI values were Hebei, Beijing, and Shanghai, with average CEI values equal to 0.671, 0.701, and 0.742 tons per ten thousand yuan, respectively. When using the GDP of the corresponding province or city as the denominator for the road transport CEI calculation, however, given the comparatively lower level of economic development in Yunnan, Xinjiang, and Guizhou, these three provinces become the regions with the highest CEI but with a lower level of private car ownership.
Furthermore, we use the GDP of the transportation sector as the denominator for the road transport CEI, and the results are shown in Fig. 4. Using this method, the three provinces with the highest average CEI values are Yunnan, Inner Mongolia, and Ningxia, which indicates that these three provinces need to consume more energy and transport capacity per unit GDP. This is also indicated that these three cities or provinces’ economic benefits of the transportation sector is relatively low. In addition, Ningxia, Yunnan, and Inner Mongolia belong to a sparsely populated area in China. The differences between vast land and sparse population or road mileage may cause these three places to cost more energy to reach amenities than in a dense city.
From the perspective of promoting cities and provincial economic development, the road transport CEI reflects a significant regional heterogeneity in energy efficiency regardless of the direct effect or indirect effect. Furthermore, banning the sale of fossil fuel vehicles in cities and provinces may generate greater impacts for regions with comparatively lower economic development levels. Therefore, variation among cities and regions must be considered during the designation of policy instruments for promoting the transition to transportation mode by phasing out fossil fuel vehicles.
Analysis of SO2 emissions intensity of fossil fuel vehicles in cities and regions
Different from the impact of CO2 emissions on global climate change, the pollutant emissions represented by sulfur dioxide (SO2) generated from fossil fuel vehicles mainly affect the environmental quality and resident health of cities and their surrounding areas. In the existing literature, SO2 per capita is commonly used as the SO2 emission intensity, especially at the regional or provincial level, for comparison.
Figure 5 depicts the trends of cities and provincial SO2 emissions per capita from 2004 to 2019 every five years. From the perspective of comparison, a significant increase in the SO2 emissions intensity has been shown across the 30 provinces in China. In 2009, the limitation of the concentration was less than 0.05 tons per ten thousand people, while in 2019, this limitation was increased to 0.16 tons per ten thousand people. In 2003, there were three provinces with SO2 concentrations higher than 0.01 tons per ten thousand people: Hebei, Guangdong, and Guangxi Zhuang Autonomous Region. In 2019, there were 16 provinces with SO2 intensity higher than 0.01 tons per ten thousand people, and two of them were higher even than 0.05 tons per ten thousand people. Further analysis indicates that this increasing trend results from local economic growth and a rapidly increasing amount of total vehicle ownership. Fossil fuel vehicles account for the majority of the total vehicle ownership, especially in urban-based areas. SO2 emissions can have a negative impact on local residents’ health conditions in cities or provinces, and improve the corresponding health cost.
Considering that the sulfur dioxide emissions of road transportation are more concentrated in the central urban areas, the SO2 intensity can be better represented by emissions per unit road mileage and emissions per unit area. Therefore, we calculated and compared the SO2 emissions per unit road mileage and unit area in five of the top largest private car-owned cities in China to obtain the pollution impact of sulfur dioxide emissions on central cities. The results are shown in Figs. 6 and 7.
Figure 7 depicts a distribution trend in total road transportation of CO2 (on the left) and SO2 (on the right), respectively. The x-axis denotes the time period from 2003 to 2019. The y-axis denotes 30 cities and provinces of China by the constraint of data accessibility. The original resource of road transport energy consumption is the energy inventory list in the CEADs database. Please refer to Supplementary Table 3 in the Supplementary Information file to obtain the corresponding name of each city or province represented as a number in Fig. 7.
In fact, road transport SO2 emissions are generated when fossil fuel vehicles run on roadways38,39. It lacks realistic meaning to use the total population or private car ownership as the denominator to calculate the SO2 intensity. Therefore, a rational indicator to represent road transport SO2 emissions is of significant importance. As shown in Fig. 6, the road transport SO2 intensity is calculated using the total roadway mileage (on the left) and the total land area of the administrative division (on the right) as the denominator. Both subfigures show a similar trend for each city over time, which indicates that using these two variables as the denominator to obtain the road transport SO2 intensity is rational. When referring to the size of the bubble, Shanghai and Guangzhou have the largest SO2 intensity compared to the other three cities. For each city, the road transport SO2 intensity changes little over time, which indicates a sophisticated connection among the economic growth rate, roadway construction, urban expansion, and FFVs increase. This five-city sample can clearly reflect the sophisticated connections among these variables.
Compared to the initial driving force of banning the sale of FFVs is CO2 emissions reduction, the reduction of SO2 emissions generated by FFVs would become big cities’ driving force of phasing out FFVs, especially for those with a large amount of private vehicle ownership. This is because SO2 emissions would exacerbate people’s health conditions and lower the surrounding environmental quality in resident-density areas. These negative impacts cannot be eliminated by the three-way catalytic converter, which focuses on converting NOx, CnHm, and CO into harmless and nontoxic N2, H2O, and CO2. In addition, sulfur-containing automobile exhaust may damage TWC converters and poison them. This negative effect can increase the emissions of NOx, CO, and CnHm if the TWC converter becomes invalid and further dampen the environmental quality. On the other hand, the usual technical in SO2 emission reduction is to decrease its share during the processing period, and it is common to reach the level of less than 10 μg per gram (the level of element sulfur <10 μg per gram). However, any further increase in the decreased degree would increase the production cost and be technically difficult to achieve. From the perspective of economic development, however, the improvement in the resident living level is bound to prospectively increase the ownership of private vehicles. Hence, a phase-out of FFVs and a ban on the sale of them eventually would be the reasonable choice for solving the dilemma confronted by us, especially for large cities and metropolises. In addition, the constraint on SO2 emissions would become an important grasp for these cities and areas to fulfill the transition in transport mode from FFVs.
Urban and regional road transport emissions and economic growth
In fact, urban and regional road transport emissions have a close connection with economic development. First, we analyze the total road transport CO2 and SO2 emissions in 30 cities and provinces of China. Trends in both emissions show an increasing trend over time, which is consistent with empirical evidence from the urban and provincial levels.
A distribution trend in regional (30 cities and provinces) total road transport CO2 emissions and SO2 emissions from 2003 to 2019 in China (see Fig. 7) shows a similar trend over time. Along the x-axis, the general trend of all 30 cities and provinces shows an upward trend over time. This is consistent with the trend in regional economic development.
We use the static comparison method and rearrange the expression of each variable by substitution into the terms of share to the total output and labor supply in terms of the labor–leisure ratio (dt) as follows.
We can obtain the expression of the effective shadow price equation as follows.
Equation (5) denotes that the effective shadow price value is connected with emissions per capita and permits allocations corresponding to each policy scenario.
First, we compare how the steady state changes under each policy scenario by abstract variables from its dynamics and eliminate the time subscript t. We assume that \(\hat \kappa \equiv 1/\left( {1 + \delta } \right)\) and substitute this equation into Eq. (1). Therefore, the steady state of each variable is given by:
We assume that there are four different policy scenarios and that each of them contains only one policy instrument at a time. Using a static comparative method, we can obtain the steady state of each variable under each policy scenario and further evaluate the policy’s effect on the economy from a deterministic perspective. The four policy scenarios we consider here are no policy, emission intensity, emission tax, and emission cap, which are policy instruments that have received a wide range of attention and discussion.
We assume that there is no-policy scenario, which can be regarded as a benchmark of the following static comparison analysis. Under this circumstance, the budget constraint of emissions no longer exists (\(\phi = 0,\hat \phi = 0\)). Then, we have \(k = \hat \kappa \alpha\), m = γ, \(c = 1 - \gamma - \delta \hat \kappa \alpha\), and \(d = 1 - \alpha - \gamma /\eta \left( {1 - \gamma - \delta \hat \kappa \alpha } \right)\). Then, we can solve d to obtain \(H = \left( {1 - \alpha - \gamma } \right)/\left[ {\eta \left( {1 - \gamma - \delta \hat \kappa \alpha } \right) + 1 - \alpha - \gamma } \right]\). Solving for the steady state of the total output, we can obtain that \(Y = Z^{\frac{1}{{1 - \alpha - \gamma }}}\left( {\hat \kappa \alpha } \right)^{\frac{\alpha }{{1 - \alpha - \gamma }}}\left( \gamma \right)^{\frac{\gamma }{{1 - \alpha - \gamma }}}H\).
It is worth noting that under the benchmark scenario, the steady state of the total output share of consumption, capital stock, labor supply, and emissions intermediate inputs are not connected to the productivity variable or the share of leisure time to the whole day of time.
The second policy scenario we would like to analyze is the emission intensity. Assuming that the intensity target is μ, we can obtain the emission constraint as in A(Y) = μY, AY = μ = m. Then, we have\(m = \gamma \left( {1 + \hat \phi \mu } \right)/\left( {1 + \hat \phi } \right) = \mu\), from which we can derive the expression of the shadow price value \(\hat \phi\) as follows.
Equation (7) is also invariant to the productivity factor. After rearranging and substituting, we can obtain the steady state expression for capital, labor supply, consumption, and emission intermediate inputs as follows.
Under the constraint of an intensity target, the steady-state capital, consumption share to the total output, and steady-state labor–leisure ratio is invariant to the productivity factor.
The third policy scenario we would like to analyze is the emission cap. Since the emission intermediate input we consider here consists of both CO2 and SO2 emissions, we can intuitively infer that the SO2 and CO2 emissions are generated from fossil fuel vehicles if the representative agent owns a car for production. With an emission cap, M is a constant, and \(A\left( Y \right) = \bar M\), which indicates that AY = 0. Then, the steady-state capital, labor–leisure ratio, consumption, and emission intermediate input can be expressed as follows.
It is noted that the steady state of capital is constant and equals the same level as in the no-policy scenario. In addition, the steady-state consumption and labor–leisure ratio are identical to the same level as in the no-policy scenario. All the variables in this circumstance (Eq. (9)) is invariant to the productivity factor, while the effective shadow price of emissions is connected to the productivity factor as follows.
In other words, the effective shadow price of emissions increases as long as there is an improvement in the productivity factor. A lift in the level of \(\hat \phi\) indicates an increase in the price level of the emission permit and generates an additional cost per unit of emission. Since there is a procyclical trend in the shadow price of emissions, each variable in Eq. (12) shows procyclical or countercyclical trends differ from those of the no-policy scenario or the emission intensity scenario.
Taking road transport emissions as an example, we can intuitively understand the impact of an emission cap on the economy. As mentioned above, many countries have planned to phase out fossil fuel vehicles and eventually ban their sale. Therefore, we assume that part of the emission cap corresponds to the emission level generated by FFVs at the time of banning the sale of FFVs. Assuming that the share of energy consumption by FFVs is ψ, if the emission intermediate input corresponds to the total energy consumption in the economy, we can obtain the emissions generated by FFVs to be ψM. Therefore, the emission cap scenario is fit into the question of banning the sale of fossil fuel vehicles.
The fourth policy scenario is emission tax, with all the revenues conserved into a lump-sup transfer to the representative consumer. Letting the price of per unit emission remain fixed, we can obtain \(\hat \phi = \tau\). Then, we can obtain the steady state capital, labor–leisure ratio, consumption, and emission intermediate input as follows.
With the emissions price fixed, the labor supply and the total output shares of consumption, capital, and emissions are all invariant to productivity changes, as in the no-policy and intensity target scenarios. For the comparison of the steady state of variables under each policy scenario, please refer to Supplementary table 4 in the Supplementary Information file for more details. To numerically understand the abovementioned analytical analysis, we use the calibration method to set values for all the parameters. For more details on the parameter values, please refer to Supplementary Table 5 for more information. Different from Fischer and Springborn40, who selected values of parameters according to postwar economic development in the United States, we select the key parameter values according to China’s economy according to the existing literature.
The comparison results show that there is no difference between emission cap and emission tax when there is no uncertainty. Therefore, we choose energy tax for policy assessment and compare it with the business-as-usual scenario under the exogenous shocks.
Figure 8 depicts the impulse response of variables to exogenous shocks under both the no-policy (business-as-usual, BAU) and energy tax (ET) scenarios. In general, variables under the ET scenario have a lower growth rate in their corresponding level compared to those under the BAU scenario, which implies that any policy instrument would dampen economic development to some degree. Under the energy tax scenario, the road transport energy consumption fluctuates less than it does under the BAU scenario, which indicates that although a one-unit standard deviation of the energy price shock would decrease each variable in the economy system, since the total energy consumption would decrease when launching an energy tax, the fluctuations would be smoothed correspondingly. Since the total consumption of energy has decreased, the impact of the exogenous shock is smoothed to some degree (compared to the BAU scenario). This is consistent with the direction of expectation. It is reasonable to infer that with the improvement in the substitution rate of new energy vehicles to fossil fuel vehicles, the on-road fuel consumption will decrease, enhancing the ability of the economy to adjust to the effects of adverse unexpected shocks, commonly known as economic resilience.
The two policy scenarios are no policy (red line) and an energy tax (blue line). The x-axis and y-axis represent the time period since the shock happens and the deviation of each variable from their steady state in percentage. All the variables (a–h) are represented in deviation from their steady state in logarithmic format.
Road transport emissions compared to other countries
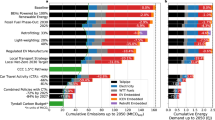
Compared with other countries, as illustrated in Figs. 9, 10, this study facilitates a better understanding of China’s FFV development and the level of its related emissions, including both CO2 emissions and SO2 emissions. In general, the development and expansion of road construction represented by the total length of roadway mileage show different trends in different countries. The faster the construction and expansion of a country’s roadway developed, the higher the road transport SO2 emissions generated. In addition, there is a positive relationship between economic development and road transport CO2 emissions as well as SO2 emissions in developing countries, while this relationship reverses in developed countries or regions.
The data include the following: SO2 emissions, calculated according to the oil consumption used as motor gasoline in each country, and roadway mileage, using public road mileage as the measure. The top four energy consumption countries are selected as the sample for comparison. The x-axis and the y-axis represent the year and roadway mileage in kilometers, respectively. The z-axis represents the road transport SO2 emissions.
As shown in Fig. 9, a panoramic figure of the comparison of road transport CO2 emissions generated by fossil fuel vehicles and economic development is compared among China, the United States, the European Union, Japan, and India. These five countries or regions are the top five largest energy consumption and economic development countries in the world. It is apparent that the United States’s total road transport CO2 emissions are the highest among other countries, which is closely connected to the idea of the United States as a country on wheels. This is partly because China and India are developing countries and possess lower levels of private cars compared to the United States and the European Union. China’s road transport CO2 emissions have exceeded those of the EU since 2015. The projection of the y-axis and z-axis represents the connection between economic development and road transport CO2 emissions. India has the highest growth rate in road transport CO2 emissions along with economic development, and China has the second highest growth rate. Given the rapid development in economic growth in China and India and their vast total population, it can be inferred that the total road transport CO2 emissions will grow rapidly. Although road transport only ranks second in each country’s total CO2 emissions, phasing out fossil fuel vehicles is important for the heading carbon neutrality target for each country.
In Fig. 10, a panoramic figure of the comparison of road transport SO2 emissions generated by fossil fuel vehicles and roadway mileage development is compared among China, the United States, Japan, and India. These four countries have comparatively large energy consumption and impact other countries worldwide. It is apparent that the United State’s total road transport SO2 emissions are the highest among other countries, which is closely connected to the United States possessing the largest amount of private car ownership. Currently, there is a shortage of rational indicators for SO2 emissions intensity generated by road transport energy. The projection of the y-axis and z-axis represents the connection between roadway development and road transport SO2 emissions. Along with the increase in roadway mileage, China’s total SO2 emissions generated by road transport have the fastest growth rate, and India has the second fastest growth rate. This is connected to rapid economic growth and the vast population. Japan’s road mileage stays at almost the same level among all these years because of its constrained land area. However, the total road transport SO2 emissions are in a growth trend, which indicates that Japan’s road transport fuel is growing too, while the United States has a decreasing trend. In fact, road transport SO2 emissions are generated only when fossil fuel vehicles are operating on public roads, which has a deep impact on the environmental quality of areas with high population density, such as urban-based areas. Therefore, from the perspective of reducing SO2 emissions in densely populated urban-based areas and improving urban environmental quality, compared with the United States and other developed countries with high car ownership per thousand people, phasing out and banning the sale of fossil fuel vehicles will eventually have a great internal driving force even in most developing countries, such as China and India, which have lower car ownership per thousand people.
Discussion
The greater ambition of national independent donation (NDC) to control the temperature rise within 1.5 °C worldwide, called for by COP26, will lead to more in-depth discussions on carbon emission reduction control. The banning sales of fossil fuel vehicles involve reducing nearly a quarter of global carbon dioxide emissions and air pollution in densely populated areas. Taking China as an example, this step will be helpful for achieving the requirements of 30–60 dual carbon targets and alleviating the shortage of transportation fuels.
Based on the forecasting results of the Markovian model, the results show an unusual decreasing trend in the rotation volume of both freight and passengers in road transport and a significant increase in railways, indicating that people prefer to avoid road traffic and choose railways instead. This is also a representation of the new policy launched in China’s fourteen-fifth planning regulation about road transition to railway and waterway, which reflects the effectiveness of policy instruments in the transformation of transportation mode and road transportation energy structure. In addition, unexpected events such as COVID-19 have an influential impact on transportation demand.
The results of the regional (30 cities and provinces) carbon intensity of the transportation sector when using the added value of the transportation sector of each city or province as a denominator show that Yunnan, Inner Mongolia, and Ningxia had the highest CEI values from 2003 to 2019. Furthermore, when the GDP of each city or province is used as the denominator, Yunnan, Xinjiang, and Guangxi are the top three provinces and cities with the highest CEI value in the transportation sector. This indicates significant heterogeneity among different regions, similar to other countries with multiple regions and vast territories. The urban and regional carbon intensity of the transportation sector has a high connection with the freight car possession volume.
In the future, the long-term fluctuation of the COVID-19 epidemic and the overall trend of economic growth after the epidemic will coexist for a long time and result in a strong demand for transportation. The demand shares of FFVs and NEVs, respectively show a downward and upward trend overall. Among the new energy vehicles, the demand for BEVs and PHEVs is growing steadily, while the share of FCVs accounted for is too small to play an important role in vehicle transformation in the next 40 years. By encouraging vehicle substitution through appropriate policies, the possible fluctuations of this dramatic carbon emission reduction strategy of the transportation sector can be smoothed under the condition of meeting the mobility needs of residents.
In fact, aside from reducing CO2 emissions to combat global climate change, reducing the impact of sulfur-containing automobile exhaust on local residents who live in densely populated urban areas and alleviating the tense supply–demand relationship of fuel oil in the international oil market should be a significant driving force in the near future. Based on the analysis through the theoretical model, different policy instruments could promote the transition to fossil fuel vehicles. A comparison of four different policy scenarios at their steady state indicates that all of the climate policies dampen economic development compared to the BAU scenario. Furthermore, we find that an energy tax can alleviate exogenous shocks’ impact on the economy by decreasing the consumption of energy and road transport. For countries with vast territories, there is regional heterogeneity in both economic development and the level of fossil fuel vehicle ownership. Hence, variation among cities and regions should be treated as an essential factor during the process of policy designation and implementation, and treating different cities and regions differently, such as phased, differentiated, and gradually implemented policies and measures, could profit the local economy to cope with unexpected shocks and enhance economic resilience. With economic growth, the vehicle ownership of developing countries such as China and India are bound to increase greatly. With reference to the situation of developed countries and regions such as the United States, the European Union, and Japan, we should conduct comprehensive research, carry out a transformation layout in advance and formulate corresponding policies and measures in combination with our own actual situation, which can promote the great changes in the transportation field of phasing out fossil fuel vehicles.
In the future, the policy of phasing out fossil fuel vehicles and banning their sale can eventually contribute to emissions mitigation and reduction in fossil fuel consumption. The energy consumption corresponding to the reduced emissions accounts for 10% of the total energy, which is equivalent to carbon dioxide emission reduction (~1 billion tons) and sulfur dioxide emission reduction in central urban areas (~3000 tons). This is of significant importance to improve the urban atmospheric environment and benefit the health of residents. In addition, the oil supply–demand of 400–600 million tons for road transportation fuel can be alleviated, and the positive effect of phasing out traditional fossil energy vehicles can be fully displayed.
Methods
Provincial carbon emission intensity and sulfur dioxide intensity of road transport
Since the carbon emission intensity (CEI) (defined as the ratio of carbon emissions to GDP) is regarded as one of the important indicators in carbon emissions reduction by the Chinese government, the CEI of road transport is calculated using the following method. This paper employs panel data of 30 Chinese provinces and municipalities during the period from 2003 to 2019 to consider the accessibility and comprehensiveness of the datasets, which can be defined using both Eq. (12) and Eq. (13).
Here, CEI denotes the carbon emission intensity in the transportation sector, EMc represents the total CO2 emissions of the transportation sector, and TSOV stands for the GDP of the transportation sector, which can be obtained from Chinese statistical yearbooks at the provincial level. The subscript i and t represent the ith province or city and t year, respectively.
Considering the characteristics of the transportation sector, the calculation is divided into two parts: domestic carbon emissions and net import carbon emissions. Domestic carbon emissions are emissions directly generated by vehicles produced by domestic enterprises. The net import carbon emissions are emissions generated by net imports of vehicles. Domestic carbon emissions in the transportation sector can be calculated using the following equation. The energy used by the transport sector is separated into nine types, including coal, coke, crude oil, fuel oil, gasoline, diesel, natural gas, and electricity. The CO2 emissions can be calculated as follows.
where CEt denotes the total CO2 emissions of the transport sector at time t. Subscript i represents the ith type of on-road fuel. Ei,t is the energy consumption of the ith type of on-road fuel in year t. ζi represents the carbon emission factor of the ith type of on-road fuel.
In addition, phasing out conventional fossil energy vehicles can alleviate the pressure of energy savings and air pollution. Using the sulfur intensity as one of the measurements of SO2 emissions of the transportation sector, the calculation method can be expressed as follows, where ϕs denotes the sulfur content of oil with the unit of μg per gram.
The Markov-chain model and vehicle structural prediction by type
The Markov-chain model denotes a stochastic process. A stochastic process is a family of random variables {X(t), t ∈ T} defined on a given probability space S, indexed by the parameter t, where t belongs to an index set T. Specifically, a transfer process is called a Markov-chain when the conditional probability satisfies Eq. (16):
where S is the collection of all possible values that the random variables of the stochastic process may assume. If \(P\left\{ {X_{n + 1} = s_{n + 1}|X_0 = s_0,X_1 = s_1,X_2 = s_2, \ldots ,X_n = s_n} \right\} > 0\) is applicable for any positive integer n ∈ N and any state s1,s2,…,sn∈S, the values assumed by a random variable Xn are called “states”. Equation (3) denotes that the state at moment n + 1 is dependent on only the state at moment n. It is a significant feature of a Markov process that the future state is merely associated with the current state and does not rely on the previous state41. This characteristic is known as the “nonaftereffect” property42 or “memoryless” property. For all i,j∈Sn, the Markov-chain one-step transition probability matrix is defined in Eq. (17), which denotes a state transition from moment n to moment n + 1.
When the transition probability is independent of n, the Markov-chain becomes a homogeneous Markov-chain, which is the most commonly used random process. Hereafter, the one-step transition probability matrix is defined in Eq. (18), and pij(n) becomes pij.
Under this assumption, the k step transition probability is calculated by Eq. (19) as follows:
According to the assumption of the Chapman–Kolmogorov equation, if the initial probability distribution vector is P0, the probability distribution of the state after k periods can be calculated by Eq. (20). For more information about Chapman–Kolmogorov assumption, please refer to the supplementary notes in the Supplementary Information file
The variation in the energy consumption structure is identified as a stochastic process41,43. A Markov-chain model is employed to forecast vehicle consumption by powertrains in China from 2020 to 2060, with the initial input data period from 2011 to 2019. Assume the state space S contains all the historical vehicle consumption state vectors Si, which can be described as \(S_i = \{ {S_{ff}\left( i \right),S_p^{nev}\left( i \right),S_{hyb}^{nev}\left( i \right),S_{fb}^{nev}\left( i \right)} \}\). The four elements \(S_{ff}\left( i \right),S_p^{nev}\left( i \right),S_{hyb}^{nev}\left( i \right)\) and \(S_{fb}^{nev}\left( i \right)\) in Si represent the initial state for each type of powertrain, namely, fossil fuel vehicles, pure electric vehicles, hybrid plug-in electric vehicles, and fuel battery electric vehicles, respectively, and take each type of powertrain consumption ratio to the total vehicle consumption as the measurement index.
The calculations of the transition probability matrix are the most critical procedure during the Markov-based model prediction process41,43. The position transition matrix comprises transition probabilities that each type of energy’s share in the primary energy consumption changes or the status quo. The one-step transition probability matrix is shown in Eq. (21):
where the main diagonal elements denote the original share probability of the four types of vehicle consumption, the row elements indicate the conversion probability for each subcategory, and the column elements represent the switching probability from other subcategories.
If available, vehicle and energy consumption data in this paper are from the Chinese Statistical Yearbook (CSY). Based on historical data from 2003 to 2019, the prediction of vehicle consumption from 2020 to 2060 is performed in three steps. First, suppose the initial state of the vehicle consumption structure by their powertrains is in 2011. Second, the one-step transition probability matrix44 is calculated annually with 1 year as the time interval. Third, the average probability transition matrix is calculated. The average transition matrix can be obtained by means of Eq. (22).
The main diagonal element equals 1 when a type of energy has a higher ratio of primary energy consumption at time t + 1 than at time t. In other words, the conversion probability of this type of energy is 1.
Dynamic stochastic general equilibrium model
To evaluate how different policy instruments affect the economy and energy-related emissions, we first consider a determined economy. Consider a simple Robinson Crusoe economy with reference to Fischer and Springborn40. Let C be the consumption good, K be the capital stock, H be the labor supply, l be the leisure time, and M be the polluting intermediate good. In this context, M includes CO2 and SO2 emissions. The representative agent obtains utility in period t equal to U(Ct, 1 − Ht) from consuming goods and spending leisure time. Therefore, the utility function can be represented as follows.
We take the format of logarithm with additive with the reference to Hansen45. The total output Y is a Cobb–Douglas function of capital, labor supply, and pollution intermediate inputs (including road transport emissions), adjusted by a productivity factor Z with an expected value of 1, where the total output can be expressed as follows.
We assume that the capital accumulation follows the following dynamic rule as in Kt+1 = (1 − δ)Kt + It, where It denotes the gross investment and δ is the depreciated rate. This indicates that during each period, capital depreciates at rate δ and is augmented by gross investment. The total output is allocated among consumption, investment, and pollution intermediate goods (C + I + M ≤ Y), which is an important budget constraint in this model. Following the assumptions in Fischer and Springborn40, the level of polluting intermediate inputs and the level of emissions are used interchangeably in the following analysis. The emissions constraint represents M ≤ At(Y), where A(•) is a function of permit allocation and varies over time. The Lagrangian function for maximizing the expected lifetime utility is as follows.
The representative agent is assumed to make a decision in period t based on all the information available at time t, which indicates that there is no asymmetry in the information accessibility. In Eq. (25), β represents the discount factor, λt is the shadow price of the national income identity, and ψt is the shadow value of the emissions constraint. The maximization problem actually depicts the discounted sum of utility along with the infinite lifetime of the representative agent. Under this determined economy scenario, any additional revenue generated by the policy is conserved within the system as lump-sum transfers. According to the Lagrangian function, we can obtain the first-order conditions of each variable as follows:
Where At,Y represents a first-order derivative of At with respect to Yt.
Based on the DSGE framework above, we further introduce return on capital, labor income, and energy consumption instead of emission intermediates to evaluate the reaction of energy consumption to exogenous shocks and energy price fluctuations.
The representative enterprises wish to maximize their net profit, i.e., the total revenue from output minus the production cost.
where the price of final products is normalized to one, Yt represents the total output, and wt t and rt denote the wage rate and the capital return, respectively. Under a complete competition factor market, the capital return equals the interest rate. \(P_t^e\) is the energy price.
where superscripts s and c denote emissions of sulfur dioxide and carbon dioxide, respectively, Et denotes the total consumption of energy, ψ is the share of on-road fuel to the total energy consumption, and ξt represents the share of nonfossil fuel consumption to the total energy use by vehicles at time t. Assume that energy price \(P_t^e\) follows an AR (1) process:
All the parameters used in the DSGE framework are calibrated and the corresponding values are provided in Supplementary Table 5. Besides, all the abbreviations used in this study are displayed with their meaning in Supplementary Table 6.
Reporting summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Data Availability
The datasets generated during and/or analyzed during the current study are available from the corresponding author upon reasonable request. Part of the data were publicly dataset as follows, the CEADs dataset are available at https://www.ceads.net/. The Chinese energy statistical yearbook is proprietary and is thus not freely available. The provincial and city-level population data were available at https://data.stats.gov.cn/easyquery.htm?cn=E0103. The road mileage data of the United States is from the US Department of transportation, available at http://www.fhwa.dot.gov/policyinformation/statistics.cfm. The road mileage data of India is from the Ministry of Road Transport & Highways, Government of India, which is available at https://morth.nic.in/sites/default/files/Annual%20Report%20-%202021%20%28English%29_compressed.pdf. Oil product’s final consumption by sector is from the IEA World Energy Balances available at https://www.iea.org/data-and-statistics/data-product/world-energy-statistics-and-balances.
Code availability
The code aggregated and/or analyzed during the current study are available from the corresponding author upon reasonable request.
References
Li, C. & Managi, S. Contribution of on-road transportation to PM2. 5. Sci. Rep. 11, 1–12 (2021).
Creutzig, F. et al. Transport: a roadblock to climate change mitigation? Science 350, 911–912 (2015).
Axsen, J., Plötz, P. & Wolinetz, M. Crafting strong, integrated policy mixes for deep CO2 mitigation in road transport. Nat. Clim. Chang. 10, 809–818 (2020).
Holland, S. P., Mansur, E. T. & Yates, A. J. The electric vehicle transition and the economics of banning gasoline vehicles. Am. Econ. J. Econ. Policy 13, 316–344 (2021).
International Energy Agency (IEA). Global energy review: CO2 emissions in 2020. https://www.iea.org/articles/global-energy-review-co2-emissions-in-2020 (2021).
Griffiths, S., Del Rio, D. F. & Sovacool, B. Policy mixes to achieve sustainable mobility after the COVID-19 crisis. Renew. Sustain. Energy Rev. 143, 110919 (2021).
Wang, Q. & Wang, S. Preventing carbon emission retaliatory rebound post-COVID-19 requires expanding free trade and improving energy efficiency. Sci. Total Environ. 746, 141158 (2020).
Brand, C. & Anable, J. ‘Disruption’and ‘continuity’in transport energy systems: the case of the ban on new conventional fossil fuel vehicles. In European Council for an Energy Efficient Economy (ECEEE) Summer Study 2019 Proceedings 1117–1127 (2019).
International Energy Agency (IEA). Global EV outlook 2020, IEA, Paris. https://www.iea.org/reports/global-ev-outlook-2020 (2020).
Rinscheid, A., Pianta, S. & Weber, E. U. Fast track or Slo-Mo? Public support and temporal preferences for phasing out fossil fuel cars in the United States. Clim. Policy 20, 30–45 (2020).
Dong, F., Li, K., Li, Y., Liu, Y. & Zheng, L. Factors influencing public support for banning gasoline vehicles in newly industrialized countries for the sake of environmental improvement: a case study of China. Environ. Sci. Pollut. Res. 29, 43942–43954 (2022).
Li, W., Li, H., Zhang, H. & Sun, S. The analysis of CO2 emissions and reduction potential in China’s transport sector. Math. Probl. Eng. 2016, (2016).
Plötz, P., Axsen, J., Funke, S. A. & Gnann, T. Designing car bans for sustainable transportation. Nat. Sustain. 2, 534–536 (2019).
Liu, Y. & Dong, F. What are the roles of consumers, automobile production enterprises, and the government in the process of banning gasoline vehicles? Evidence from a tripartite evolutionary game model. Energy 238, 122004 (2022).
Wang, K.-H., Su, C.-W. & Umar, M. Geopolitical risk and crude oil security: a Chinese perspective. Energy 219, 119555 (2021).
Liu, Y., Han, L. & Xu, Y. The impact of geopolitical uncertainty on energy volatility. Int. Rev. Financ. Anal. 75, 101743 (2021).
Tian, X., An, C., Chen, Z. & Tian, Z. Assessing the impact of COVID-19 pandemic on urban transportation and air quality in Canada. Sci. Total Environ. 765, 144270 (2021).
Wang, Q. & Zhang, F. What does the China’s economic recovery after COVID-19 pandemic mean for the economic growth and energy consumption of other countries? J. Clean. Prod. 295, 126265 (2021).
Stern, P. C. et al. Opportunities and insights for reducing fossil fuel consumption by households and organizations. Nat. Energy 1, 1–6 (2016).
Zhang, S. & Chen, W. Assessing the energy transition in China towards carbon neutrality with a probabilistic framework. Nat. Commun. 13, 1–15 (2022).
Li, M. Peak oil, the rise of China and India, and the global energy crisis. J. Contemp. Asia 37, 449–471 (2007).
Adekoya, O. B. Revisiting oil consumption-economic growth nexus: Resource-curse and scarcity tales. Resour. Policy 70, 101911 (2021).
Binsted, M. An electrified road to climate goals. Nat. Energy 7, 9–10 (2022).
Salpakari, J., Rasku, T., Lindgren, J. & Lund, P. D. Flexibility of electric vehicles and space heating in net zero energy houses: an optimal control model with thermal dynamics and battery degradation. Appl. Energy 190, 800–812 (2017).
Lin, B. & Wu, W. The impact of electric vehicle penetration: A recursive dynamic CGE analysis of China. Energy Econ 94, 105086 (2021).
Fawcett, T. Personal carbon trading: a policy ahead of its time? Energy policy 38, 6868–6876 (2010).
Fuso Nerini, F., Fawcett, T., Parag, Y. & Ekins, P. Personal carbon allowances revisited. Nat. Sustain. 4, 1025–1031 (2021).
Peng, W. et al. The surprisingly inexpensive cost of state-driven emission control strategies. Nat. Clim. Chang. 11, 738–745 (2021).
Acemoglu, D., Aghion, P., Bursztyn, L. & Hemous, D. The environment and directed technical change. Am. Econ. Rev. 102, 131–166 (2012).
Martin, R. Regional economic resilience, hysteresis and recessionary shocks. J. Econ. Geogr. 12, 1–32 (2012).
Hardaker, S., Appel, A. & Rauch, S. Reconsidering retailers’ resilience and the city: a mixed method case study. Cities 128, 103796 (2022).
Cheng, T., Zhao, Y. & Zhao, C. Exploring the spatio-temporal evolution of economic resilience in Chinese cities during the COVID-19 crisis. Sustain. Cities Soc. 84, 103997 (2022).
Yang, C., Hao, Y. & Irfan, M. Energy consumption structural adjustment and carbon neutrality in the post-COVID-19 era. Struct. Chang. Econ. Dyn. 59, 442–453 (2021).
Lin, B. & Du, Z. Can urban rail transit curb automobile energy consumption? Energy Policy 105, 120–127 (2017).
Dong, F. & Liu, Y. Policy evolution and effect evaluation of new-energy vehicle industry in China. Resour. Policy 67, 101655 (2020).
Hackbarth, A. & Madlener, R. Consumer preferences for alternative fuel vehicles: a discrete choice analysis. Transp. Res. Part D Transp. Environ. 25, 5–17 (2013).
Creutzig, F. et al. Towards demand-side solutions for mitigating climate change. Nat. Clim. Chang. 8, 260–263 (2018).
Yan, S. & Wu, G. SO2 emissions in China–their network and hierarchical structures. Sci. Rep. 7, 1–11 (2017).
Yang, M., Ma, T. & Sun, C. Evaluating the impact of urban traffic investment on SO2 emissions in China cities. Energy Policy 113, 20–27 (2018).
Fischer, C. & Springborn, M. Emissions targets and the real business cycle: Intensity targets versus caps or taxes. J. Environ. Econ. Manage. 62, 352–366 (2011).
Li, W. & Lu, C. The multiple effectiveness of state natural gas consumption constraint policies for achieving sustainable development targets in China. Appl. energy 235, 685–698 (2019).
Li, P., Liu, F. & Li, C. Markov-based forecasting model for enterprise human resources internal supply. in 2018 International Conference on Computer Science, Electronics and Communication Engineering (CSECE 2018) 427–430 (Atlantis Press, 2018).
Wang, F., Wu, L. & Yang, C. Driving factors for growth of carbon dioxide emissions during economic development in China. Econ. Res. J. 45, 123–136 (2010).
Ashouri, M. J. & Rafei, M. How do energy productivity and water resources affect air pollution in Iran? New evidence from a Markov Switching perspective. Resour. Policy 71, 101986 (2021).
Hansen, G. D. Indivisible labor and the business cycle. J. Monet. Econ. 16, 309–327 (1985).
Acknowledgements
The authors acknowledge financial support from the National Natural Science Foundation of China (72073010, and 71521002), the Science and Technology Program of Zhejiang Province of China (2022C35060), the Technology Innovation Program of Beijing Institute of Technology (2022CX01013), and the Joint Development Program of the Beijing Municipal Commission of Education. The usual disclaimer applies.
Author information
Authors and Affiliations
Contributions
C.Y. designed the study. C.Y. and H.W. performed the analysis. C.Y. and Y.G. prepared the manuscript. All authors (C.Y., H.W., Y. G., Y.H., and Z.W.) participated in the writing of the manuscript. Y.H. and Z.W. coordinated and supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yang, C., Wu, H., Guo, Y. et al. Promoting economic and environmental resilience in the post-COVID-19 era through the city and regional on-road fuel sustainability development. npj Urban Sustain 2, 33 (2022). https://doi.org/10.1038/s42949-022-00078-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42949-022-00078-6
This article is cited by
-
Covid, cities, and sustainability: a reflection on the legacy of a global pandemic
npj Urban Sustainability (2023)