Abstract
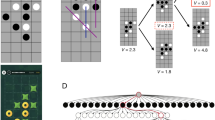
The Rubik’s cube is a prototypical combinatorial puzzle that has a large state space with a single goal state. The goal state is unlikely to be accessed using sequences of randomly generated moves, posing unique challenges for machine learning. We solve the Rubik’s cube with DeepCubeA, a deep reinforcement learning approach that learns how to solve increasingly difficult states in reverse from the goal state without any specific domain knowledge. DeepCubeA solves 100% of all test configurations, finding a shortest path to the goal state 60.3% of the time. DeepCubeA generalizes to other combinatorial puzzles and is able to solve the 15 puzzle, 24 puzzle, 35 puzzle, 48 puzzle, Lights Out and Sokoban, finding a shortest path in the majority of verifiable cases.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The environments for all puzzles presented in this paper, code to generate labelled training data and initial states used to test DeepCubeA are available through a Code Ocean compute capsule (https://doi.org/10.24433/CO.4958495.v1)44.
References
Lichodzijewski, P. & Heywood, M. in Genetic Programming Theory and Practice VIII (eds Riolo, R., McConaghy, T. & Vladislavleva, E.) 35–54 (Springer, 2011).
Smith, R. J., Kelly, S. & Heywood, M. I. Discovering Rubik’s cube subgroups using coevolutionary GP: a five twist experiment. In Proceedings of the Genetic and Evolutionary Computation Conference 2016 789–796 (ACM, 2016).
Brunetto, R. & Trunda, O. Deep heuristic-learning in the Rubik’s cube domain: an experimental evaluation. Proc. ITAT 1885, 57–64 (2017).
Johnson, C. G. Solving the Rubik’s cube with learned guidance functions. In Proceedings of 2018 IEEE Symposium Series on Computational Intelligence (SSCI) 2082–2089 (IEEE, 2018).
Korf, R. E. Macro-operators: a weak method for learning. Artif. Intell. 26, 35–77 (1985).
Arfaee, S. J., Zilles, S. & Holte, R. C. Learning heuristic functions for large state spaces. Artif. Intell. 175, 2075–2098 (2011).
Korf, R. E. Finding optimal solutions to Rubik’s cube using pattern databases. In Proceedings of the Fourteenth National Conference on Artificial Intelligence and Ninth Conference on Innovative Applications of Artificial Intelligence 700–705 (AAAI Press, 1997); http://dl.acm.org/citation.cfm?id=1867406.1867515
Korf, R. E. & Felner, A. Disjoint pattern database heuristics. Artif. Intell. 134, 9–22 (2002).
Felner, A., Korf, R. E. & Hanan, S. Additive pattern database heuristics. J. Artif. Intell. Res. 22, 279–318 (2004).
Bonet, B. & Geffner, H. Planning as heuristic search. Artif. Intell. 129, 5–33 (2001).
Schmidhuber, J. Deep learning in neural networks: an overview. Neural Netw. 61, 85–117 (2015).
Goodfellow, I., Bengio, Y., Courville, A. & Bengio, Y. Deep Learning Vol. 1 (MIT Press, 2016).
Sutton, R. S. & Barto, A. G. Reinforcement Learning: An Introduction Vol. 1 (MIT Press, 1998).
Bellman, R. Dynamic Programming (Princeton Univ. Press, 1957).
Puterman, M. L. & Shin, M. C. Modified policy iteration algorithms for discounted Markov decision problems. Manage. Sci. 24, 1127–1137 (1978).
Bertsekas, D. P. & Tsitsiklis, J. N. Neuro-dynamic Programming (Athena Scientific, 1996).
Hart, P. E., Nilsson, N. J. & Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern. 4, 100–107 (1968).
Pohl, I. Heuristic search viewed as path finding in a graph. Artif. Intell. 1, 193–204 (1970).
Ebendt, R. & Drechsler, R. Weighted A* search—unifying view and application. Artif. Intell. 173, 1310–1342 (2009).
McAleer, S., Agostinelli, F., Shmakov, A. & Baldi, P. Solving the Rubik’s cube with approximate policy iteration. Proceedings of International Conference on Learning Representations (ICLR) (PMLR, 2019).
Silver, D. et al. A general reinforcement learning algorithm that masters chess, shogi and Go through self-play. Science 362, 1140–1144 (2018).
Rokicki, T. God’s Number is 26 in the Quarter-turn Metric http://www.cube20.org/qtm/ (2014).
Korf, R. E. Depth-first iterative-deepening: an optimal admissible tree search. Artif. Intell. 27, 97–109 (1985).
Rokicki, T. cube20 https://github.com/rokicki/cube20src (2016).
Rokicki, T., Kociemba, H., Davidson, M. & Dethridge, J. The diameter of the Rubik’s cube group is twenty. SIAM Rev. 56, 645–670 (2014).
Culberson, J. C. & Schaeffer, J. Pattern databases. Comput. Intell. 14, 318–334 (1998).
He, K., Zhang, X., Ren, S. & Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 770–778 (IEEE, 2016).
Kociemba, H. 15-Puzzle Optimal Solver http://kociemba.org/themen/fifteen/fifteensolver.html (2018).
Scherphuis, J. The Mathematics of Lights Out https://www.jaapsch.net/puzzles/lomath.htm (2015).
Dor, D. & Zwick, U. Sokoban and other motion planning problems. Comput. Geom. 13, 215–228 (1999).
Guez, A. et al. An Investigation of Model-free Planning: Boxoban Levels https://github.com/deepmind/boxoban-levels/ (2018).
Orseau, L., Lelis, L., Lattimore, T. & Weber, T. Single-agent policy tree search with guarantees. In Advances in Neural Information Processing Systems (eds Bengio, S. et al.) 3201–3211 (Curran Associates, 2018).
Brüngger, A., Marzetta, A., Fukuda, K. & Nievergelt, J. The parallel search bench ZRAM and its applications. Ann. Oper. Res. 90, 45–63 (1999).
Korf, R. E. Linear-time disk-based implicit graph search. JACM 55, 26 (2008).
Moore, A. W. & Atkeson, C. G. Prioritized sweeping: reinforcement learning with less data and less time. Mach. Learn. 13, 103–130 (1993).
Newell, A. & Simon, H. A. GPS, a Program that Simulates Human Thought Technical Report (Rand Corporation, 1961).
Fikes, R. E. & Nilsson, N. J. STRIPS: a new approach to the application of theorem proving to problem solving. Artif. Intell. 2, 189–208 (1971).
Anthony, T., Tian, Z. & Barber, D. Thinking fast and slow with deep learning and tree search. In Advances in Neural Information Processing Systems (eds Guyon, I. et al.) 5360–5370 (Curran Associates, 2017).
Wilt, C. M. & Ruml, W. When does weighted A* fail? In Proc. SOCS (eds Borrajo, D. et al.) 137–144 (AAAI Press, 2012).
Ioffe, S. & Szegedy, C. Batch normalization: accelerating deep network training by reducing internal covariate shift. In Proceedings of International Conference on Machine Learning (eds Bach, F. & Blei, D.) 448–456 (PMLR, 2015).
Glorot, X., Bordes, A. & Bengio, Y. Deep sparse rectifier neural networks. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics (eds Gordon, G., Dunson, D. & Dudík, M.) 315–323 (PMLR, 2011).
Kingma, D. P. & Ba, J. Adam: a method for stochastic optimization. In Proceedings of International Conference on Learning Representations (ICLR) (eds Bach, F. & Blei, D.) (PMLR, 2015).
Samadi, M., Felner, A. & Schaeffer, J. Learning from multiple heuristics. In Proceedings of the 23rd National Conference on Artificial Intelligence (ed. Cohn, A.) (AAAI Press, 2008).
Agostinelli, F., McAleer, S., Shmakov, A. & Baldi, P. Learning to Solve the Rubiks Cube (Code Ocean, 2019); https://doi.org/10.24433/CO.4958495.v1
Acknowledgements
The authors thank D.L. Flores for useful suggestions regarding the DeepCubeA server and T. Rokicki for useful suggestions and help with the optimal Rubik’s cube solver.
Author information
Authors and Affiliations
Contributions
P.B. designed and directed the project. F.A., S.M. and A.S. contributed equally to the development and testing of DeepCubeA. All authors contributed to writing and editing the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1–7
Rights and permissions
About this article
Cite this article
Agostinelli, F., McAleer, S., Shmakov, A. et al. Solving the Rubik’s cube with deep reinforcement learning and search. Nat Mach Intell 1, 356–363 (2019). https://doi.org/10.1038/s42256-019-0070-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s42256-019-0070-z
This article is cited by
-
Spatial planning of urban communities via deep reinforcement learning
Nature Computational Science (2023)
-
New directions in fitness evaluation: commentary on Langdon’s JAWS30
Genetic Programming and Evolvable Machines (2023)
-
Analyzing neural network behavior through deep statistical model checking
International Journal on Software Tools for Technology Transfer (2023)
-
Quantum reinforcement learning
Quantum Information Processing (2023)
-
The flip-flop neuron: a memory efficient alternative for solving challenging sequence processing and decision-making problems
Neural Computing and Applications (2023)