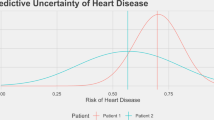
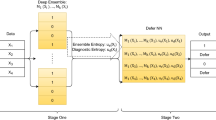
Medicine, even from the earliest days of artificial intelligence (AI) research, has been one of the most inspiring and promising domains for the application of AI-based approaches. Equally, it has been one of the more challenging areas to see an effective adoption. There are many reasons for this, primarily the reluctance to delegate decision making to machine intelligence in cases where patient safety is at stake. To address some of these challenges, medical AI, especially in its modern data-rich deep learning guise, needs to develop a principled and formal uncertainty quantification (UQ) discipline, just as we have seen in fields such as nuclear stockpile stewardship and risk management. The data-rich world of AI-based learning and the frequent absence of a well-understood underlying theory poses its own unique challenges to straightforward adoption of UQ. These challenges, while not trivial, also present significant new research opportunities for the development of new theoretical approaches, and for the practical applications of UQ in the area of machine-assisted medical decision making. Understanding prediction system structure and defensibly quantifying uncertainty is possible, and, if done, can significantly benefit both research and practical applications of AI in this critical domain.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout
Similar content being viewed by others
References
Oberkampf, W. L. & Roy, C. J. Verfication and Validation in Scientific Computing (Cambridge Univ. Press, Cambridge, 2010).
National Research Council Evaluation of Quantification of Margins and Uncertainties: Methodology for Assessing and Certifying the Reliability of the Nuclear Stockpile (National Academies Press, Washington DC, 2009).
Zuk, O., Hechter, E., Sunyaev, S. R. & Lander, E. S. The mystery of missing heritability: Genetic interactions create phantom heritability. Proc. Natl Acad. Sci. USA 109, 1193–1198 (2012).
Choi, J. D. & Lee, J.-S. Interplay between epigenetics and genetics in cancer. Genomics Inform. 11, 164–173 (2013).
Kermany, D. S. et al. Identifying medical diagnoses and treatable diseases by image-based deep learning. Cell 172, 1122–1131 (2018).
Esteva, A. et al. Dermatologist-level classification of skin cancer with deep neural networks. Nature 542, 115–118 (2017).
Mar, V. & Soyer, H. Artificial intelligence for melanoma diagnosis: How can we deliver on the promise? Ann. Oncol. 29, 1625–1628 (2018).
Weng, S. F., Reps, J., Kai, J., Garibaldi, J. M. & Qureshi, N. Can machine-learning improve cardiovascular risk prediction using routine clinical data? PLoS One 12, e0174944 (2017).
Bychkov, D. et al. Deep learning based tissue analysis predicts outcome in colorectal cancer. Sci. Rep. 8, 3395 (2018).
Xiao, C., Ma, T., Dieng, A. B., Blei, D. M. & Wang, F. Readmission prediction via deep contextual embedding of clinical concepts. PLoS One 13, e0195024 (2018).
Rajkomar, A. et al. Scalable and accurate deep learning with electronic health records. npj Digit. Med. 1, 18 (2018).
Coley, C. W., Barzilay, R., Jaakkola, T. S., Green, W. H. & Jensen, K. F. Prediction of organic reaction outcomes using machine learning. ACS Cent. Sci. 3, 434–443 (2017).
Hsu, E., Klemm, J., Kerlavage, A., Kusnezov, D. & Kibbe, W. Cancer moonshot data and technology team: Enabling a national learning healthcare system for cancer to unleash the power of data. Clin. Pharmacol. Ther. 101, 613–615 (2017).
Fillon, M. Making sense of the mountains of new cancer data. J. Natl Cancer Inst. 109, djx020 (2017).
Geraci, J. et al. Applying deep neural networks to unstructured text notes in electronic medical records for phenotyping youth depression. Evid. Based Ment. Health 20, 83–87 (2017).
Zhou, Y. et al. Resource-efficient neural architect. Preprint at https://arxiv.org/abs/1806.07912 (2018).
Gal, Y. & Ghahramani, Z. Dropout as a bayesian approximation: Representing model uncertainty in deep learning. Preprint at https://arxiv.org/abs/1506.02142 (2015).
Zhang, C., Bengio, S., Hardt, M., Recht, B. & Vinyals, O. Understanding deep learning requires rethinking generalization. Preprint at http://arxiv.org/abs/1611.03530 (2016).
Arpit, D. et al. A closer look at memorization in deep networks. Preprint at https://arxiv.org/abs/1706.05394 (2017).
Zhang, C., Vinyals, O., Munos, R. & Bengio, S. A study on overfitting in deep reinforcement learning. Preprint at http://arxiv.org/abs/1804.06893 (2018).
Cawley, G. C. & Talbot, N. L. C. On over-fitting in model selection and subsequent selection bias in performance evaluation. J. Mach. Learn. Res. 11, 2079–2107 (2010).
Brahma, P. P., Wu, D. & She, Y. Why deep learning works: A manifold disentanglement perspective. IEEE Trans. Neural Netw. Learn. Sys. 27, 1997–2008 (2016).
Raghu, M., Gilmer, J., Yosinski, J. & Sohl-Dickstein, J. SVCCA: Singular vector canonical correlation analysis for deep learning dynamics and interpretability. Preprint at https://arxiv.org/abs/1706.05806 (2017).
Brahma, P. P., Huang, Q. & Wu, D. O. Structured memory based deep model to detect as well as characterize novel inputs. Preprint at http://arxiv.org/abs/1801.09859 (2018).
Yu, Y., Qu, W., Li, N. & Guo, Z. Open-category classification by adversarial sample generation. Preprint at http://arxiv.org/abs/1705.08722 (2017).
Ge, Z., Demyanov, S., Chen, Z. & Garnavi, R. Generative openmax for multi-class open set classification. Preprint at http://arxiv.org/abs/1707.07418 (2017).
Acknowledgements
This manuscript has been in part co-authored by UT-Battelle, LLC, under contract no. DE-AC05-00OR22725.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Begoli, E., Bhattacharya, T. & Kusnezov, D. The need for uncertainty quantification in machine-assisted medical decision making. Nat Mach Intell 1, 20–23 (2019). https://doi.org/10.1038/s42256-018-0004-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s42256-018-0004-1
This article is cited by
-
Slideflow: deep learning for digital histopathology with real-time whole-slide visualization
BMC Bioinformatics (2024)
-
Uncertainty-aware deep-learning model for prediction of supratentorial hematoma expansion from admission non-contrast head computed tomography scan
npj Digital Medicine (2024)
-
Uncertainty-aware deep learning for trustworthy prediction of long-term outcome after endovascular thrombectomy
Scientific Reports (2024)
-
Denoising OCT videos based on temporal redundancy
Scientific Reports (2024)
-
Enhancing a deep learning model for pulmonary nodule malignancy risk estimation in chest CT with uncertainty estimation
European Radiology (2024)