Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Perspective
  • Published:

Rigor with machine learning from field theory to the Poincaré conjecture

Nature Reviews Physics (2024)Cite this article

Subjects

Abstract

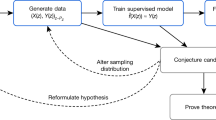
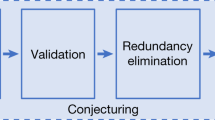
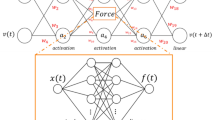
Despite their successes, machine learning techniques are often stochastic, error-prone and blackbox. How could they then be used in fields such as theoretical physics and pure mathematics for which error-free results and deep understanding are a must? In this Perspective, we discuss techniques for obtaining zero-error results with machine learning, with a focus on theoretical physics and pure mathematics. Non-rigorous methods can enable rigorous results via conjecture generation or verification by reinforcement learning. We survey applications of these techniques-for-rigor ranging from string theory to the smooth 4D Poincaré conjecture in low-dimensional topology. We also discuss connections between machine learning theory and mathematics or theoretical physics such as a new approach to field theory motivated by neural network theory, and a theory of Riemannian metric flows induced by neural network gradient descent, which encompasses Perelman’s formulation of the Ricci flow that was used to solve the 3D Poincaré conjecture.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Moves and singularities of ribbon knots.
Fig. 2: Performance comparison of the TRPO, A3C and RW algorithms on the unknotting problem.

Similar content being viewed by others

References

  1. Jumper, J. et al. Highly accurate protein structure prediction with AlphaFold. Nature 596, 583–589 (2021).

    Article  ADS  Google Scholar 

  2. Carleo, G. et al. Machine learning and the physical sciences. Rev. Mod. Phys. 91, 045002 (2019).

    Article  ADS  Google Scholar 

  3. Ruehle, F. Data science applications to string theory. Phys. Rept. 839, 1–117 (2020).

    Article  ADS  MathSciNet  Google Scholar 

  4. He, Y. Machine Learning in Pure Mathematics and Theoretical Physics (World Scientific, 2023).

  5. Athalye, A., Engstrom, L., Ilyas, A. & Kwok, K. Synthesizing robust adversarial examples. Proc. Mach. Learn. Res. 80, 284–293 (2018).

    Google Scholar 

  6. Athalye, A., Carlini, N. & Wagner, D. Obfuscated gradients give a false sense of security: circumventing defenses to adversarial examples. Preprint at https://arxiv.org/abs/1802.00420 (2018).

  7. Gukov, S., Halverson, J., Manolescu, C. & Ruehle, F. Searching for ribbons with machine learning. Preprint at https://doi.org/10.48550/arXiv.2304.09304 (2023).

  8. Neal, R. M. Bayesian Learning for Neural Networks. PhD thesis, Univ. Toronto (1995).

  9. Jacot, A., Gabriel, F. & Hongler, C. Neural tangent kernel: convergence and generalization in neural networks. In 32nd Conference on Neural Information Processing Systems (eds Garnett, R. et al.) 1–10 (2018).

  10. Lee, J. et al. Wide neural networks of any depth evolve as linear models under gradient descent. J. Statist. Mech. 2020, 124002 (2019).

    Article  Google Scholar 

  11. Demirtas, M., Halverson, J., Maiti, A., Schwartz, M. D. & Stoner, K. Neural network field theories: non-Gaussianity, actions, and locality. Mach. Learn. Sci. Technol. 5, 015002 (2023).

    Article  ADS  Google Scholar 

  12. Perelman, G. The entropy formula for the Ricci flow and its geometric applications. Preprint at https://doi.org/10.48550/arXiv.math/0211159 (2002).

  13. Hamilton, R. S. Three-manifolds with positive Ricci curvature. J. Differ. Geom. 17, 255–306 (1982).

    MathSciNet  Google Scholar 

  14. Gauthier, T., Kaliszyk, C., Urban, J., Kumar, R. & Norrish, M. TacticToe: learning to prove with tactics. J. Automat. Reason. 65, 257–286 (2018).

    Article  MathSciNet  Google Scholar 

  15. Szegedy, C. (ed.). A Promising Path Towards Autoformalization and General Artificial Intelligence (Springer, 2020).

  16. Wu, Y. et al. Autoformalization with large language models. Preprint at https://doi.org/10.48550/arXiv.2205.12615 (2022).

  17. Lample, G. et al. HyperTree proof search for neural theorem proving. Preprint at https://doi.org/10.48550/arXiv.2205.11491 (2022).

  18. Hales, T. C. Developments in formal proofs. Asterisque Exp. No. 1086, 387–410 (2015).

  19. Alama, J., Heskes, T., Kühlwein, D., Tsivtsivadze, E. & Urban, J. Premise selection for mathematics by corpus analysis and kernel methods. J. Automat. Reason. 52, 191–213 (2014).

    Article  MathSciNet  Google Scholar 

  20. Blanchette, J. C., Greenaway, D., Kaliszyk, C., Kühlwein, D. & Urban, J. A learning-based fact selector for Isabelle/HOL. J. Automat. Reason. 57, 219–244 (2016).

    Article  MathSciNet  Google Scholar 

  21. Nagashima, Y. Simple dataset for proof method recommendation in Isabelle/HOL (dataset description). In Intelligent Computer Mathematics: 13th International Conference 297–302 (ACM, 2020).

  22. Piotrowski, B., Mir, R. F. & Ayers, E. Machine-learned premise selection for lean. Preprint at https://doi.org/10.48550/arXiv.2304.00994 (2023).

  23. Carifio, J., Halverson, J., Krioukov, D. & Nelson, B. D. Machine learning in the string landscape. J. High Energy Phys. 09, 157 (2017).

    Article  ADS  MathSciNet  Google Scholar 

  24. He, Y.-H. Deep-learning the landscape. Phys. Lett. B 774, 564–568 (2017).

    Article  ADS  Google Scholar 

  25. Krefl, D. & Seong, R.-K. Machine learning of Calabi-Yau volumes. Phys. Rev. D 96, 066014 (2017).

    Article  ADS  MathSciNet  Google Scholar 

  26. Ruehle, F. Evolving neural networks with genetic algorithms to study the string landscape. J. High Energy Phys. 08, 038 (2017).

    Article  ADS  MathSciNet  Google Scholar 

  27. Davies, A. et al. Advancing mathematics by guiding human intuition with ai. Nature 600, 70–74 (2021).

    Article  ADS  Google Scholar 

  28. Craven, J., Jejjala, V. & Kar, A. Disentangling a deep learned volume formula. J. High Energy Phys. 06, 040 (2021).

    Article  ADS  MathSciNet  Google Scholar 

  29. Craven, J., Hughes, M., Jejjala, V. & Kar, A. Learning knot invariants across dimensions. SciPost Phys. 14, 021 (2023).

    Article  ADS  MathSciNet  Google Scholar 

  30. Brown, G. et al. Computation and data in the classification of Fano varieties. Preprint at https://doi.org/10.48550/arXiv.2211.10069 (2022).

  31. Mishra, C., Moulik, S. R. & Sarkar, R. Mathematical conjecture generation using machine intelligence. Preprint at https://doi.org/10.48550/arXiv.2306.07277 (2023).

  32. Cranmer, M. D. et al. Discovering symbolic models from deep learning with inductive biases. In Advances in Neural Information Processing Systems 33 (NeurIPS, 2020).

  33. Silver, D. et al. Mastering the game of Go without human knowledge. Nature 550, 354–359 (2017).

    Article  ADS  Google Scholar 

  34. Silver, D. et al. Mastering chess and shogi by self-play with a general reinforcement learning algorithm (2017). Preprint at https://doi.org/10.48550/arXiv.1712.01815 (2017).

  35. Strogatz, S. One giant step for a chess-playing machine. The New York Times https://www.nytimes.com/2018/12/26/science/chess-artificial-intelligence.html (2018).

  36. Klaewer, D. & Schlechter, L. Machine learning line bundle cohomologies of hypersurfaces in toric varieties. Phys. Lett. B 789, 438–443 (2019).

    Article  ADS  MathSciNet  Google Scholar 

  37. Brodie, C. R., Constantin, A., Deen, R. & Lukas, A. Topological formulae for the zeroth cohomology of line bundles on del Pezzo and Hirzebruch surfaces. Compl. Manif. 8, 223–229 (2021).

    Article  MathSciNet  Google Scholar 

  38. Brodie, C. R., Constantin, A., Deen, R. & Lukas, A. Index formulae for line bundle cohomology on complex surfaces. Fortsch. Phys. 68, 1900086 (2020).

    Article  ADS  MathSciNet  Google Scholar 

  39. Brodie, C. R., Constantin, A., Deen, R. & Lukas, A. Machine learning line bundle cohomology. Fortsch. Phys. 68, 1900087 (2020).

    Article  ADS  MathSciNet  Google Scholar 

  40. Brodie, C. R. & Constantin, A. Cohomology chambers on complex surfaces and elliptically fibered Calabi-Yau three-folds. Preprint at https://doi.org/10.48550/arXiv.2009.01275 (2020).

  41. Bies, M. et al. Machine learning and algebraic approaches towards complete matter spectra in 4d F-theory. J. High Energy Phys. 01, 196 (2021).

    Article  ADS  MathSciNet  Google Scholar 

  42. Halverson, J., Nelson, B. & Ruehle, F. Branes with brains: exploring string vacua with deep reinforcement learning. J. High Energy Phys. 06, 003 (2019).

    Article  ADS  MathSciNet  Google Scholar 

  43. Cole, A., Krippendorf, S., Schachner, A. & Shiu, G. Probing the structure of string theory vacua with genetic algorithms and reinforcement learning. In 35th Conference on Neural Information Processing Systems (NeurIPS, 2021).

  44. Krippendorf, S., Kroepsch, R. & Syvaeri, M. Revealing systematics in phenomenologically viable flux vacua with reinforcement learning. Preprint at https://doi.org/10.48550/arXiv.2107.04039 (2021).

  45. Abel, S., Constantin, A., Harvey, T. R. & Lukas, A. String model building, reinforcement learning and genetic algorithms. In Nankai Symposium on Mathematical Dialogues (iNSPIRE, 2021).

  46. Abel, S., Constantin, A., Harvey, T. R. & Lukas, A. Evolving heterotic gauge backgrounds: genetic algorithms versus reinforcement learning. Fortsch. Phys. 70, 2200034 (2022).

    Article  ADS  MathSciNet  Google Scholar 

  47. Constantin, A., Harvey, T. R. & Lukas, A. Heterotic string model building with monad bundles and reinforcement learning. Fortsch. Phys. 70, 2100186 (2022).

    Article  MathSciNet  Google Scholar 

  48. Hughes, M. C. A neural network approach to predicting and computing knot invariants. J. Knot Theory Ramif. 29, 2050005 (2020).

    Article  MathSciNet  Google Scholar 

  49. Sundararajan, M., Taly, A. & Yan, Q. Axiomatic attribution for deep networks. In Proc. 34th International Conference on Machine Learning (eds Precup, D. & Teh, Y. W.) Vol. 70, 3319–3328 (PMLR, 2017).

  50. Hass, J., Lagarias, J. C. & Pippenger, N. The computational complexity of knot and link problems. J. ACM 46, 185–211 (1999).

    Article  MathSciNet  Google Scholar 

  51. Kuperberg, G. Knottedness is in NP, modulo GRH. Adv. Math. 256, 493–506 (2014).

    Article  MathSciNet  Google Scholar 

  52. Lackenby, M. The efficient certification of knottedness and Thurston norm. Adv. Math. 387, 107796 (2021).

    Article  MathSciNet  Google Scholar 

  53. Gukov, S., Halverson, J., Ruehle, F. & Sułkowski, P. Learning to unknot. Mach. Learn. Sci. Technol. 2, 025035 (2021).

    Article  Google Scholar 

  54. Alexander, J. W. A lemma on systems of knotted curves. Proc. Natl Acad. Sci. USA 9, 93–95 (1923).

    Article  ADS  Google Scholar 

  55. Ri, S. J. & Putrov, P. Graph neural networks and 3-dimensional topology. Mach. Learn. Sci. Tech. 4, 035026 (2023).

    Article  Google Scholar 

  56. Gukov, S., Halverson, J., Manolescu, C. & Ruehle, F. An algorithm for finding ribbon bands. GitHub https://github.com/ruehlef/ribbon (2023).

  57. Williams, C. K. In Advances in Neural Information Processing Systems 295–301 (1997).

  58. Yang, G. Tensor programs I: wide feedforward or recurrent neural networks of any architecture are Gaussian processes. In Advances in Neural Information Processing Systems 32 (NeurIPS, 2019).

  59. Roberts, D. A., Yaida, S. & Hanin, B. The Principles of Deep Learning Theory: an Effective Theory Approach to Understanding Neural Networks (Cambridge Univ. Press, 2022).

  60. Halverson, J., Maiti, A. & Stoner, K. Neural networks and quantum field theory. Mach. Learn. Sci. Tech. 2, 035002 (2021).

    Article  Google Scholar 

  61. Halverson, J. Building quantum field theories out of neurons. Preprint at https://doi.org/10.48550/arXiv.2112.04527 (2021).

  62. Osterwalder, K. & Schrader, R. Axioms for Euclidean green’s functions. Commun. Math. Phys. 31, 83–112 (1973).

    Article  ADS  MathSciNet  Google Scholar 

  63. Erbin, H., Lahoche, V. & Samary, D. O. Non-perturbative renormalization for the neural network-QFT correspondence. Mach. Learn. Sci. Tech. 3, 015027 (2022).

    Article  Google Scholar 

  64. Grosvenor, K. T. & Jefferson, R. The edge of chaos: quantum field theory and deep neural networks. SciPost Phys. 12, 081 (2022).

    Article  ADS  MathSciNet  Google Scholar 

  65. Banta, I., Cai, T., Craig, N. & Zhang, Z. Structures of neural network effective theories. Preprint at https://doi.org/10.48550/arXiv.2305.02334 (2023).

  66. Krippendorf, S. & Spannowsky, M. A duality connecting neural network and cosmological dynamics. Mach. Learn. Sci. Technol. 3, 035011 (2022).

    Article  ADS  Google Scholar 

  67. Maiti, A., Stoner, K. & Halverson, J. in Machine Learning in Pure Mathematics and Theoretical Physics Ch. 8, 293–330 (2023).

  68. Halverson, J. & Ruehle, F. Metric flows with neural networks. Preprint at https://doi.org/10.48550/arXiv.2310.19870 (2023).

  69. Anderson, L. B. et al. Moduli-dependent Calabi-Yau and SU(3)-structure metrics from machine learning. J. High Energy Phys. 05, 013 (2021).

    Article  ADS  MathSciNet  Google Scholar 

  70. Douglas, M. R., Lakshminarasimhan, S. & Qi, Y. Numerical Calabi-Yau metrics from holomorphic networks. In Proc. 2nd Mathematical and Scientific Machine Learning Conference Vol. 145, 223–252 (PMLR, 2022).

  71. Jejjala, V., Mayorga Pena, D. K. & Mishra, C. Neural network approximations for Calabi-Yau metrics. J. High Energy Phys. 08, 105 (2022).

    Article  ADS  MathSciNet  Google Scholar 

  72. Larfors, M., Lukas, A., Ruehle, F. & Schneider, R. Learning size and shape of Calabi-Yau spaces. In Fourth Workshop on Machine Learning and the Physical Sciences (2021).

  73. Larfors, M., Lukas, A., Ruehle, F. & Schneider, R. Numerical metrics for complete intersection and Kreuzer–Skarke Calabi–Yau manifolds. Mach. Learn. Sci. Tech. 3, 035014 (2022).

    Article  Google Scholar 

  74. Gerdes, M. & Krippendorf, S. CYJAX: a package for Calabi-Yau metrics with JAX. Mach. Learn. Sci. Tech. 4, 025031 (2023).

    Article  Google Scholar 

  75. Yau, S.-T. On the Ricci curvature of a compact Kähler manifold and the complex Monge-Ampére equation, I. Commun. Pure Appl. Math. 31, 339–411 (1978).

    Article  Google Scholar 

  76. Calabi, E. On Kähler Manifolds with Vanishing Canonical Class 78–89 (Princeton Univ. Press, 2015).

  77. Donaldson, S. K. Some numerical results in complex differential geometry (2005). Preprint at https://doi.org/10.48550/arXiv.math/0512625 (2005).

  78. Yang, G. Tensor programs II: neural tangent kernel for any architecture. Preprint at https://doi.org/10.48550/arXiv.2006.14548 (2020).

  79. Cotler, J. & Rezchikov, S. Renormalization group flow as optimal transport. Phys. Rev. D https://doi.org/10.1103/physrevd.108.025003 (2023).

  80. Berman, D. S. & Klinger, M. S. The inverse of exact renormalization group flows as statistical inference. Preprint at https://doi.org/10.48550/arXiv.2212.11379 (2022).

  81. Berman, D. S., Klinger, M. S. & Stapleton, A. G. Bayesian renormalization. Mach. Learn. Sci. Technol. 4, 045011 (2023).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

S.G. is supported in part by a Simons Collaboration Grant on New Structures in Low-Dimensional Topology and by the Department of Energy grant DE-SC0011632. J.H. is supported by National Science Foundation CAREER grant PHY-1848089. F.R. is supported by the National Science Foundation grants PHY-2210333 and startup funding from Northeastern University. The work of J.H. and F.R. is also supported by the National Science Foundation under Cooperative Agreement PHY-2019786 (The NSF AI Institute for Artificial Intelligence and Fundamental Interactions).

Author information

Authors and Affiliations

  1. Richard N. Merkin Center for Pure and Applied Mathematics, California Institute of Technology, Pasadena, CA, USA

    Sergei Gukov

  2. Dublin Institute for Advanced Studies, Dublin, Ireland

    Sergei Gukov

  3. Department of Physics, Northeastern University, Boston, MA, USA

    James Halverson & Fabian Ruehle

  4. The NSF AI Institute for Artificial Intelligence and Fundamental Interactions, Cambridge, USA

    James Halverson & Fabian Ruehle

  5. Department of Mathematics, Northeastern University, Boston, MA, USA

    Fabian Ruehle

Authors
  1. Sergei Gukov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. James Halverson
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Fabian Ruehle
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

The authors contributed equally to all aspects of the article.

Corresponding authors

Correspondence to James Halverson or Fabian Ruehle.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Reviews Physics thanks Marika Taylor, Sven Krippendorf and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gukov, S., Halverson, J. & Ruehle, F. Rigor with machine learning from field theory to the Poincaré conjecture. Nat Rev Phys (2024). https://doi.org/10.1038/s42254-024-00709-0

Download citation

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1038/s42254-024-00709-0

Search

Advanced search

Quick links

Nature Briefing AI and Robotics

Sign up for the Nature Briefing: AI and Robotics newsletter — what matters in AI and robotics research, free to your inbox weekly.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing: AI and Robotics