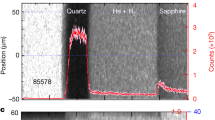
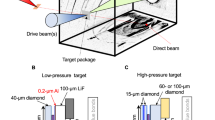
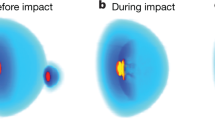
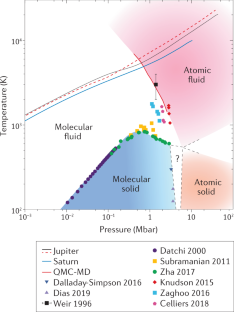
Abstract
Materials at high pressures and temperatures are of great interest for planetary science and astrophysics, warm dense-matter physics and inertial confinement fusion research. Planetary structure models rely on an understanding of the behaviour of elements and their mixtures under conditions that do not exist on Earth; at the same time, planets serve as natural laboratories for studying materials at extreme conditions. The topic of dense hydrogen is timely given the recent accurate measurements of the gravitational fields of Jupiter and Saturn, the current and upcoming progress in shock experiments, and the advances in numerical simulations of materials at high pressure. In this Review we discuss the connection between modelling planetary interiors and the high-pressure physics of hydrogen and helium. We summarize key experiments and theoretical approaches for determining the equation of state and phase diagram of hydrogen and helium. We relate this to current knowledge of the internal structures of Jupiter and Saturn, and discuss the importance of high-pressure physics to their characterization.
Key points
-
Modelling planetary interiors relies on a profound knowledge of the behaviour of materials at high pressures and temperatures. For the gas giant planets, these materials are hydrogen and helium.
-
Progress in high-pressure experiments using diamond anvil cells and shock waves is critical for understanding hydrogen under extreme conditions and for calibrating theoretical models
-
Simulations of hydrogen at high pressure are essential to understand fundamental physical problems such as its rich phase diagram; assist the experimental realization and interpretation of new materials; and predict its behaviour for parameters at which experiments cannot be performed.
-
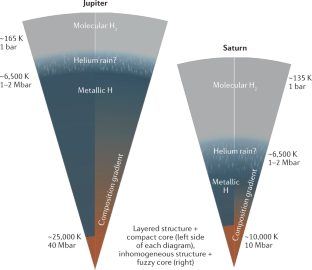
Jupiter and Saturn are expected to have complex interiors in which hydrogen metallizes and helium separates from hydrogen. The full understanding of these processes is still a major challenge in high-pressure physics.
-
Although the structure and evolution of gas giant planets are dominated by hydrogen and helium, the planets contain other, heavier elements and can have complex interiors that include composition gradients and inhomogeneous regions.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$99.00 per year
only $8.25 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout
Similar content being viewed by others
References
McMahon, J. M., Morales, M. A., Pierleoni, C. & Ceperley, D. M. The properties of hydrogen and helium under extreme conditions. Rev. Mod. Phys. 84, 1607–1653 (2012).
Wigner, E. & Huntington, H. B. On the possibility of a metallic modification of hydrogen. J. Chem. Phys. 3, 764–770 (1935).
Helled, R., Anderson, J. D., Podolak, M. & Schubert, G. Interior models of Uranus and Neptune. Astrophys. J. 726, 15 (2011).
Ashcroft, N. W. Metallic hydrogen: a high-temperature superconductor? Phys. Rev. Lett. 21, 1748–1749 (1968).
Babaev, E., Sudbø, A. & Ashcroft, N. A superconductor to superfluid phase transition in liquid metallic hydrogen. Nature 431, 666 (2004).
Goncharov, A. Phase diagram of hydrogen at extreme pressures and temperatures; updated through 2019 (Review article). Low Temp. Phys. 46, 97–103 (2020).
Weir, S., Mitchell, A. & Nellis, W. Metallization of fluid molecular hydrogen at 140 GPa (1.4 Mbar). Phys. Rev. Lett. 76, 1860 (1996).
Goncharov, A. F., Mazin, I. I., Eggert, J. H., Hemley, R. J. & Mao, H.-k Invariant points and phase transitions in deuterium at megabar pressures. Phys. Rev. Lett. 75, 2514–2517 (1995).
Dias, R. P. & Silvera, I. F. Observation of the Wigner–Huntington transition to metallic hydrogen.Science 355, 715–718 (2017).
Datchi, F., Loubeyre, P. & LeToullec, R. Extended and accurate determination of the melting curves of argon, helium, ice (H2O), and hydrogen (H2). Phys. Rev. B 61, 6535–6546 (2000).
Deemyad, S. & Silvera, I. F. Melting line of hydrogen at high pressures. Phys. Rev. Lett. 100, 155701 (2008).
Dzyabura, V., Zaghoo, M. & Silvera, I. F. Evidence of a liquid–liquid phase transition in hot dense hydrogen. Proc. Natl Acad. Sci. USA 110, 8040–8044 (2013).
Zaghoo, M., Salamat, A. & Silvera, I. F. Evidence of a first-order phase transition to metallic hydrogen. Phys. Rev. B 93, 155128 (2016).
Zaghoo, M. & Silvera, I. F. Conductivity and dissociation in liquid metallic hydrogen and implications for planetary interiors. Proc. Natl Acad. Sci. USA 114, 11873–11877 (2017).
Dubrovinsky, L. et al. The most incompressible metal osmium at static pressures above 750 gigapascals. Nature 525, 226–229 (2015).
Loubeyre, P., Occelli, F. & Dumas, P. Synchrotron infrared spectroscopic evidence of the probable transition to metal hydrogen. Nature 577, 631–635 (2020).
Goncharov, A. F. & Struzhkin, V. V. Comment on ‘‘Observation of the Wigner–Huntington transition to metallic hydrogen’’. Science 357, eaam9736 (2017).
Liu, X.-D. & Dalladay-Simpson, P. & Howie, R. T. & Li, B. & Gregoryanz, E. Comment on ‘‘Observation of the Wigner–Huntington transition to metallic hydrogen”. Science 357, eaan2286 (2017).
Loubeyre, P., Occelli, F. & Dumas, P. Comment on: ‘‘Observation of the Wigner–Huntington transition to metallic hydrogen’’. Preprint at http://arxiv.org/abs/1702.07192 (2017).
Eremets, M. & Drozdov, A. Comments on the claimed observation of the Wigner–Huntington transition to metallic hydrogen. Preprint at https://arxiv.org/abs/1702.05125 (2017).
Geng, H. Y. Public debate on metallic hydrogen to boost high pressure research. Matter Radiat. Extremes 2, 275 (2018).
Silvera, I. & Dias, R. Response to comment on ‘‘Observation of the Wigner–Huntington transition to metallic hydrogen”. Science 357, eaan1215 (2017).
Silvera, I. & Dias, R. Response to critiques on observation of the Wigner–Huntington transition to metallic hydrogen. Preprint at http://arxiv.org/abs/1703.0306 (2017).
Howie, R. T., Dalladay-Simpson, P. & Gregoryanz, E. Raman spectroscopy of hot hydrogen above 200 GPa. Nat. Mater. 14, 495–499 (2015).
Dalladay-Simpson, P., Howie, R. T. & Gregoryanz, E. Evidence for a new phase of dense hydrogen above 325 gigapascals. Nature 529, 63–67 (2016).
Eremets, M., Troyan, I. & Drozdov, A. Low temperature phase diagram of hydrogen at pressures up to 380 GPa. A possible metallic phase at 360 GPa and 200 K. Preprint at http://arxiv.org/abs/1601.04479 (2016).
Dias, R. P., Noked, O. & Silvera, I. F. Quantum phase transition in solid hydrogen at high pressure. Phys. Rev. B 100, 184112 (2019).
Eremets, M. I., Drozdov, A. P., Kong, P. & Wang, H. Semimetallic molecular hydrogen at pressure above 350 GPa. Nat. Phys. 15, 1246–1249 (2019).
Gregoryanz, E. et al. Everything you always wanted to know about metallic hydrogen but were afraid to ask. Matter Radiat. Extremes 5, 038101 (2020).
Dias, R. P. & Silvera, I. F. Observation of the Wigner–Huntington transition to metallic hydrogen. Science 355, 715–718 (2017).
Nellis, W. Ultracondensed Matter by Dynamic Compression (Cambridge Univ. Press, 2017).
Nellis, W. J. Dense quantum hydrogen. Low Temp. Phys. 45, 294–296 (2019).
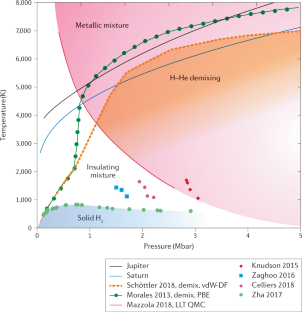
Knudson, M. et al. Direct observation of an abrupt insulator-to-metal transition in dense liquid deuterium. Science 348, 1455–1460 (2015).
Celliers, P. M. et al. Insulator–metal transition in dense fluid deuterium. Science 361, 677–682 (2018).
Mochalov, M. A. et al. Quasi-isentropic compressibility of deuterium at a pressure of ~12 TPa. JETP Lett. 107, 168–174 (2018).
Brygoo, S. et al. Analysis of laser shock experiments on precompressed samples using a quartz reference and application to warm dense hydrogen and helium. J. Appl. Phys. 118, 195901 (2015).
Miller, J. E. et al. Streaked optical pyrometer system for laser-driven shock-wave experiments on omega. Rev. Sci. Instrum. 78, 034903 (2007).
Knudson, M. D. & Desjarlais, M. P. High-precision shock wave measurements of deuterium: evaluation of exchange-correlation functionals at the molecular-to-atomic transition. Phys. Rev. Lett. 118, 035501 (2017).
Knudson, M. D. et al. Probing the interiors of the ice giants: shock compression of water to 700 GPa and 3.8 g/cm3. Phys. Rev. Lett. 108, 091102 (2012).
Millot, M. et al. Nanosecond X-ray diffraction of shock-compressed superionic water ice. Nature 569, 251 (2019).
Eremets, M. I. & Trojan, I. Evidence of maximum in the melting curve of hydrogen at megabar pressures. JETP Lett. 89, 174–179 (2009).
Subramanian, N., Goncharov, A. F., Struzhkin, V. V., Somayazulu, M. & Hemley, R. J. Bonding changes in hot fluid hydrogen at megabar pressures. Proc. Natl Acad. Sci. USA 108, 6014–6019 (2011).
Zha, C.-s, Liu, H., Tse, J. S. & Hemley, R. J. Melting and high P−T transitions of hydrogen up to 300 GPa. Phys. Rev. Lett. 119, 075302 (2017).
Zha, C.-S., Liu, Z., Ahart, M., Boehler, R. & Hemley, R. J. High-pressure measurements of hydrogen phase IV using synchrotron infrared spectroscopy. Phys. Rev. Lett. 110, 217402 (2013).
Mott, N. F. The transition to the metallic state. Phil. Mag. 6, 287–309 (1961).
Ohta, K. et al. Phase boundary of hot dense fluid hydrogen. Sci. Rep. 5, 16560 (2015).
Ross, M., Ree, F. & Young, D. The equation of state of molecular hydrogen at very high density. J. Chem. Phys. 79, 1487–1494 (1983).
Saumon, D., Chabrier, G. & Van Horn, H. An equation of state for low-mass stars and giant planets. Astrophys. J. Suppl. Ser. 99, 713 (1995).
Chabrier, G., Mazevet, S. & Soubiran, F. A new equation of state for dense hydrogen–helium mixtures. Astrophys. J. 872, 51 (2019).
Ross, M. Linear-mixing model for shock-compressed liquid deuterium. Phys. Rev. B 58, 669–677 (1998).
Kerley, G. I. Equations of state for hydrogen and deuterium. Sandia National Laboratories report SAND 2003–3613 (SAND, 2003).
Caillabet, L., Mazevet, S. & Loubeyre, P. Multiphase equation of state of hydrogen from ab initio calculations in the range 0.2 to 5 g/cc up to 10 eV. Phys. Rev. B 83, 094101 (2011).
Militzer, B. & Hubbard, W. B. Ab initio equation of state for hydrogen–helium mixtures with recalibration of the giant-planet mass–radius relation. Astrophys. J. 774, 148 (2013).
Militzer, B. Equation of state calculations of hydrogen–helium mixtures in solar and extrasolar giant planets. Phys. Rev. B 87, 014202 (2013).
Becker, A. et al. Ab initio equations of state for hydrogen (H-REOS. 3) and helium (He-REOS. 3) and their implications for the interior of brown dwarfs. Astrophys. J. Suppl. Ser. 215, 21 (2014).
Brush, S., Sahlin, H. & Teller, E. Monte Carlo study of a one-component plasma. I. J. Chem. Phys. 45, 2102–2118 (1966).
Morales, M. A., McMahon, J. M., Pierleoni, C. & Ceperley, D. M. Nuclear quantum effects and nonlocal exchange-correlation functionals applied to liquid hydrogen at high pressure. Phys. Rev. Lett. 110, 065702 (2013).
Allen, M. P. & Tildesley, D. J. Computer Simulation of Liquids (Clarendon, 1987).
Pierleoni, C., Ceperley, D. M. & Holzmann, M. Coupled electron–ion Monte Carlo calculations of dense metallic hydrogen. Phys. Rev. Lett. 93, 146402 (2004).
Payne, M. C., Teter, M. P., Allan, D. C., Arias, T. A. & Joannopoulos, J. D. Iterative minimization techniques for ab initio total-energy calculations: molecular dynamics and conjugate gradients. Rev. Mod. Phys. 64, 1045–1097 (1992).
Alavi, S.Book review: Ab initio Molecular Dynamics. Basic Theory and Advanced Methods. By Dominik Marx and Jürg Hutter. Angew. Chem. Int. Ed. 48, 9404–9405 (2009).
Andersen, H. C. Molecular dynamics simulations at constant pressure and/or temperature. J. Chem. Phys. 72, 2384–2393 (1980).
Martyna, G. J., Tobias, D. J. & Klein, M. L. Constant pressure molecular dynamics algorithms. J. Chem. Phys. 101, 4177–4189 (1994).
Bussi, G., Donadio, D. & Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 126, 014101 (2007).
Ceperley, D. M. & Alder, B. J. Ground state of solid hydrogen at high pressures. Phys. Rev. B 36, 2092–2106 (1987).
Cao, J. & Voth, G. A. The formulation of quantum statistical mechanics based on the Feynman path centroid density. I. Equilibrium properties. J. Chem. Phys. 100, 5093–5105 (1994).
Ceperley, D. M. Path integrals in the theory of condensed helium. Rev. Mod. Phys. 67, 279–355 (1995).
Pierleoni, C., Morales, M. A., Rillo, G., Holzmann, M. & Ceperley, D. M. Liquid–liquid phase transition in hydrogen by coupled electron–ion Monte Carlo simulations. Proc. Natl Acad. Sci. USA 113, 4953–4957 (2016).
Car, R. & Parrinello, M. Unified approach for molecular dynamics and density-functional theory. Phys. Rev. Lett. 55, 2471–2474 (1985).
Hohenberg, P. & Kohn, W. Inhomogeneous electron gas. Phys. Rev. 136, B864–B871 (1964).
Kohn, W. & Sham, L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, A1133–A1138 (1965).
Burke, K. Perspective on density functional theory. J. Chem. Phys. 136, 150901 (2012).
Cohen, A. J., Mori-Sánchez, P. & Yang, W. Challenges for density functional theory. Chem. Rev. 112, 289–320 (2011).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Scandolo, S. Liquid–liquid phase transition in compressed hydrogen from first-principles simulations. Proc. Natl Acad. Sci. USA 100, 3051–3053 (2003).
Lorenzen, W., Holst, B. & Redmer, R. First-order liquid–liquid phase transition in dense hydrogen. Phys. Rev. B 82, 195107 (2010).
Vorberger, J., Tamblyn, I., Militzer, B. & Bonev, S. A. Hydrogen–helium mixtures in the interiors of giant planets. Phys. Rev. B 75, 024206 (2007).
Tamblyn, I. & Bonev, S. A. Structure and phase boundaries of compressed liquid hydrogen. Phys. Rev. Lett. 104, 065702 (2010).
Morales, M. A., Pierleoni, C., Schwegler, E. & Ceperley, D. M. Evidence for a first-order liquid–liquid transition in high-pressure hydrogen from ab initio simulations. Proc. Natl Acad. Sci. USA 107, 12799–12803 (2010).
Bonev, S., Schwegler, E., Galli, G. & Ogitsu, T. A quantum fluid of metallic hydrogen suggested by first-principles calculations. Nature 431, 669 (2004).
Pickard, C. J. & Needs, R. J. Structure of phase III of solid hydrogen. Nat. Phys. 3, 473 (2007).
Liu, H., Zhu, L., Cui, W. & Ma, Y. Room-temperature structures of solid hydrogen at high pressures. J. Chem. Phys. 137, 074501 (2012).
Magda˘u, I. B. & Ackland, G. J. Identification of high-pressure phases III and IV in hydrogen: simulating Raman spectra using molecular dynamics. Phys. Rev. B 87, 174110 (2013).
Pickard, C. J., Martinez-Canales, M. & Needs, R. J. Density functional theory study of phase IV of solid hydrogen. Phys. Rev. B 85, 214114 (2012).
Naumov, I. I., Hemley, R. J., Hoffmann, R. & Ashcroft, N. Chemical bonding in hydrogen and lithium under pressure. J. Chem. Phys. 143, 064702 (2015).
Monserrat, B. et al. Structure and metallicity of phase V of hydrogen. Phys. Rev. Lett. 120, 255701 (2018).
Morales, M. A. et al. Phase separation in hydrogen–helium mixtures at Mbar pressures. Proc. Natl Acad. Sci. USA 106, 1324–1329 (2009).
Lorenzen, W., Holst, B. & Redmer, R. Demixing of hydrogen and helium at megabar pressures. Phys. Rev. Lett. 102, 115701 (2009).
Becke, A. D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 38, 3098–3100 (1988).
Monserrat, B., Ashbrook, S. E. & Pickard, C. J. Nuclear magnetic resonance spectroscopy as a dynamical structural probe of hydrogen under high pressure. Phys. Rev. Lett. 122, 135501 (2019).
Monserrat, B., Needs, R. J., Gregoryanz, E. & Pickard, C. J. Hexagonal structure of phase III of solid hydrogen. Phys. Rev. B 94, 134101 (2016).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 118, 8207–8215 (2003).
Dion, M., Rydberg, H., Schröder, E., Langreth, D. C. & Lundqvist, B. I. Van der Waals density functional for general geometries. Phys. Rev. Lett. 92, 246401 (2004).
Lee, K., Murray, É. D., Kong, L., Lundqvist, B. I. & Langreth, D. C. Higher-accuracy van der Waals density functional. Phys. Rev. B 82, 081101 (2010).
Azadi, S. & Ackland, G. J. The role of van der Waals and exchange interactions in high-pressure solid hydrogen. Phys. Chem. Chem. Phys. 19, 21829–21839 (2017).
Knudson, M. D., Desjarlais, M. P., Preising, M. & Redmer, R. Evaluation of exchange-correlation functionals with multiple-shock conductivity measurements in hydrogen and deuterium at the molecular-to-atomic transition. Phys. Rev. B 98, 174110 (2018).
Azadi, S. & Foulkes, W. M. C. Fate of density functional theory in the study of high-pressure solid hydrogen. Phys. Rev. B 88, 014115 (2013).
Mazzola, G., Helled, R. & Sorella, S. Phase diagram of hydrogen and a hydrogen–helium mixture at planetary conditions by quantum Monte Carlo simulations. Phys. Rev. Lett. 120, 025701 (2018).
Clay, R. C. et al. Benchmarking exchange-correlation functionals for hydrogen at high pressures using quantum Monte Carlo. Phys. Rev. B 89, 184106 (2014).
Schöttler, M. & Redmer, R. Ab initio calculation of the miscibility diagram for hydrogen–helium mixtures. Phys. Rev. Lett. 120, 115703 (2018).
Rillo, G., Morales, M. A., Ceperley, D. M. & Pierleoni, C. Optical properties of high-pressure fluid hydrogen across molecular dissociation. Proc. Natl Acad. Sci. USA 116, 9770–9774 (2019).
Foulkes, W. M. C., Mitas, L., Needs, R. J. & Rajagopal, G. Quantum Monte Carlo simulations of solids. Rev. Mod. Phys. 73, 33–83 (2001).
Clay, R. C. III, Holzmann, M., Ceperley, D. M. & Morales, M. A. Benchmarking density functionals for hydrogen–helium mixtures with quantum Monte Carlo: energetics, pressures, and forces. Phys. Rev. B 93, 035121 (2016).
Chen, J., Ren, X., Li, X.-Z., Alfè, D. & Wang, E. On the room-temperature phase diagram of high pressure hydrogen: an ab initio molecular dynamics perspective and a diffusion Monte Carlo study. J. Chem. Phys. 141, 024501 (2014).
Azadi, S., Monserrat, B., Foulkes, W. M. C. & Needs, R. J. Dissociation of high-pressure solid molecular hydrogen: a quantum Monte Carlo and anharmonic vibrational study. Phys. Rev. Lett. 112, 165501 (2014).
Drummond, N. D. et al. Quantum Monte Carlo study of the phase diagram of solid molecular hydrogen at extreme pressures. Nat. Commun. 6, 7794 (2015).
Azadi, S., Singh, R. & Kühne, T. D. Nuclear quantum effects induce metallization of dense solid molecular hydrogen. J. Comput. Chem. 39, 262–268 (2018).
Attaccalite, C. & Sorella, S. Stable liquid hydrogen at high pressure by a novel ab initio molecular-dynamics calculation. Phys. Rev. Lett. 100, 114501 (2008).
Mazzola, G., Yunoki, S. & Sorella, S. Unexpectedly high pressure for molecular dissociation in liquid hydrogen by electronic simulation. Nat. Commun. 5, 3487 (2014).
Mazzola, G., Zen, A. & Sorella, S. Finite-temperature electronic simulations without the Born–Oppenheimer constraint. J. Chem. Phys. 137, 134112 (2012).
Zen, A., Luo, Y., Mazzola, G., Guidoni, L. & Sorella, S. Ab initio molecular dynamics simulation of liquid water by quantum Monte Carlo. J. Chem. Phys. 142, 144111 (2015).
Mazzola, G. & Sorella, S. Accelerating ab initio molecular dynamics and probing the weak dispersive forces in dense liquid hydrogen. Phys. Rev. Lett. 118, 015703 (2017).
Delaney, K. T., Pierleoni, C. & Ceperley, D. M. Quantum Monte Carlo simulation of the high-pressure molecular–atomic crossover in fluid hydrogen. Phys. Rev. Lett. 97, 235702 (2006).
Morales, M. A., Pierleoni, C. & Ceperley, D. M. Equation of state of metallic hydrogen from coupled electron–ion Monte Carlo simulations. Phys. Rev. E 81, 021202 (2010).
Tubman, N. M., Liberatore, E., Pierleoni, C., Holzmann, M. & Ceperley, D. M. Molecular–atomic transition along the deuterium Hugoniot curve with coupled electron–ion Monte Carlo simulations. Phys. Rev. Lett. 115, 045301 (2015).
Luo, Y., Zen, A. & Sorella, S. Ab initio molecular dynamics with noisy forces: validating the quantum Monte Carlo approach with benchmark calculations of molecular vibrational properties. J. Chem. Phys. 141, 194112 (2014).
Lin, F. et al. Electrical conductivity of high-pressure liquid hydrogen by quantum Monte Carlo methods. Phys. Rev. Lett. 103, 256401 (2009).
Mazzola, G. & Sorella, S. Distinct metallization and atomization transitions in dense liquid hydrogen. Phys. Rev. Lett. 114, 105701 (2015).
Zaghoo, M., Husband, R. J. & Silvera, I. F. Striking isotope effect on the metallization phase lines of liquid hydrogen and deuterium. Phys. Rev. B 98, 104102 (2018).
Davis, P. et al. X-ray scattering measurements of dissociation-induced metallization of dynamically compressed deuterium. Nat. Commun. 7, 11189 (2016).
McWilliams, R. S., Dalton, D. A., Mahmood, M. F. & Goncharov, A. F. Optical properties of fluid hydrogen at the transition to a conducting state. Phys. Rev. Lett. 116, 255501 (2016).
Clay, R. C., Desjarlais, M. P. & Shulenburger, L. Deuterium Hugoniot: pitfalls of thermodynamic sampling beyond density functional theory. Phys. Rev. B 100, 075103 (2019).
Geng, H. Y., Wu, Q., Marqués, M. & Ackland, G. J. Thermodynamic anomalies and three distinct liquid–liquid transitions in warm dense liquid hydrogen. Phys. Rev. B 100, 134109 (2019).
Holzmann, M. et al. Theory of finite size effects for electronic quantum Monte Carlo calculations of liquids and solids. Phys. Rev. B 94, 035126 (2016).
Cheng, B., Mazzola, G. & Ceriotti, M. Evidence for supercritical behavior of high-pressure liquid hydrogen. Preprint at http://arxiv.org/abs/1906.03341 (2019).
Soubiran, F. & Militzer, B. Miscibility calculations for water and hydrogen in giant planets. Astrophys. J. 806, 228 (2015).
Wilson, H. F. & Militzer, B. Rocky core solubility in Jupiter and giant exoplanets. Phys. Rev. Lett. 108, 111101 (2012).
Ancilotto, F., Chiarotti, G. L., Scandolo, S. & Tosatti, E. Dissociation of methane into hydrocarbons at extreme (planetary) pressure and temperature. Science 275, 1288–1290 (1997).
Chau, R., Hamel, S. & Nellis, W. J. Chemical processes in the deep interior of Uranus. Nat. Commun. 2, 203 (2011).
Cytter, Y. et al. Transition to metallization in warm dense helium–hydrogen mixtures using stochastic density functional theory within the Kubo–Greenwood formalism. Phys. Rev. B 100, 195101 (2019).
Loubeyre, P., Le Toullec, R. & Pinceaux, J. P. Binary phase diagrams of H2–He mixtures at high temperature and high pressure. Phys. Rev. B 36, 3723–3730 (1987).
Loubeyre, P., Letoullec, R. & Pinceaux, J. A new determination of the binary phase diagram of H2–He mixtures at 296 K. J. Phys. Condens. Matter 3, 3183 (1991).
Lim, J. & Yoo, C.-S. Phase diagram of dense H2−He mixtures: evidence for strong chemical association, miscibility, and structural change. Phys. Rev. Lett. 120, 165301 (2018).
Turnbull, R. et al. Reactivity of hydrogen–helium and hydrogen–nitrogen mixtures at high pressures. Phys. Rev. Lett. 121, 195702 (2018).
Stevenson, D. J. & Salpeter, E. E. The dynamics and helium distribution in hydrogen–helium fluid planets. Astrophys. J. Suppl. 35, 239–261 (1977).
Stevenson, D. J. & Salpeter, E. E. The phase diagram and transport properties for hydrogen–helium fluid planets. Astrophys. J. Suppl. 35, 221–237 (1977).
Morales, M. A. et al. Phase separation in hydrogen–helium mixtures at Mbar pressures. Proc. Natl Acad. Sci. USA 106, 1324–1329 (2009).
Soubiran, F., Mazevet, S., Winisdoerffer, C. & Chabrier, G. Optical signature of hydrogen–helium demixing at extreme density–temperature conditions. Phys. Rev. B 87, 165114 (2013).
Guillot, T. The interiors of giant planets: models and outstanding questions. Annu. Rev. Earth Planet. Sci. 33, 493–530 (2005).
Fortney, J. J. et al. in Saturn in the 21st Century (eds. Baines, K.,Flasar, F.,Krupp, N. & Stallard, T.) p. v (Cambridge Univ. Press, 2018).
Militzer, B., Soubiran, F., Wahl, S. M. & Hubbard, W. Understanding Jupiter’s interior. J. Geophys. Res. Planet. 121, 1552–1572 (2016).
Helled, R. & Guillot, T. Internal Structure of Giant and Icy Planets: Importance of Heavy Elements and Mixing, 44 (Springer, 2018).
Helled, R. The Interiors of Jupiter and Saturn, 175 (Oxford Univ. Press, 2018).
Leconte, J. & Chabrier, G. A new vision of giant planet interiors: impact of double diffusive convection. Astron. Astrophys. 540, A20 (2012).
Leconte, J. & Chabrier, G. Layered convection as the origin of Saturn’s luminosity anomaly. Nat. Geosci. 6, 347–350 (2013).
Debras, F. & Chabrier, G. New models of Jupiter in the context of Juno and Galileo. Astrophys. J. 872, 100 (2019).
Vazan, A., Helled, R. & Guillot, T. Jupiter’s evolution with primordial composition gradients. Astron. Astrophys. 610, L14 (2018).
Marley, M. S., Gómez, P. & Podolak, M. Monte Carlo interior models for Uranus and Neptune. J. Geophys. Res. 100, 23349–23354 (1995).
Podolak, M., Podolak, J. I. & Marley, M. S. Further investigations of random models of Uranus and Neptune. Planet. Space. Sci. 48, 143–151 (2000).
Helled, R., Schubert, G. & Anderson, J. D. Empirical models of pressure and density in Saturn’s interior: implications for the helium concentration, its depth dependence, and Saturn’s precession rate. Icarus 199, 368–377 (2009).
Guillot, T. & Gautier, D. in Treatise on Geophysics. 2nd edn. Volume 10, 529–557 https://www.elsevier.com/books/treatise-on-geophysics/schubert/978-0-444-53802-4 (2015).
Helled, R. et al. in Protostars and Planets VI (eds Beuther, H. et al.) 643 (2014).
Fortney, J. J. & Hubbard, W. B. Phase separation in giant planets: inhomogeneous evolution of Saturn. Icarus 164, 228–243 (2003).
Mankovich, C., Fortney, J. J. & Moore, K. L. Bayesian evolution models for Jupiter with helium rain and double-diffusive convection. Astrophys. J. 832, 113 (2016).
Vazan, A., Helled, R., Podolak, M. & Kovetz, A. The evolution and internal structure of Jupiter and Saturn with compositional gradients. Astrophys. J. 829, 118 (2016).
Püstow, R., Nettelmann, N., Lorenzen, W. & Redmer, R. H/He demixing and the cooling behavior of Saturn. Icarus 267, 323–333 (2016).
Debras, F. & Chabrier, G. New models of Jupiter in the context of Juno and Galileo. Astrophys. J. 872, 100 (2019).
Bolton, S. J. et al. Jupiter’s interior and deep atmosphere: the initial pole-to-pole passes with the Juno spacecraft. Science 356, 821–825 (2017).
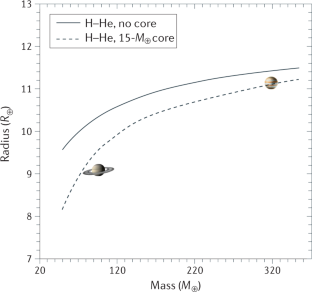
Iess, L. et al. Measurement of Jupiter’s asymmetric gravity field. Nature 555, 220–222 (2018).
Wahl, S. M. et al. Comparing Jupiter interior structure models to Juno gravity measurements and the role of a dilute core. Geophys. Res. Lett. 44, 4649–4659 (2017).
Nettelmann, N. Low- and high-order gravitational harmonics of rigidly rotating Jupiter. Astron. Astrophys. 606, A139 (2017).
Guillot, T. et al. A suppression of differential rotation in Jupiter’s deep interior. Nature 555, 227–230 (2018).
Helled, R. & Stevenson, D. The fuzziness of giant planets’ cores. Astrophys. J. Lett. 840, L4 (2017).
Iess, L. et al. Measurement and implications of Saturn’s gravity field and ring mass. Science 364, aat2965 (2019).
Militzer, B., Wahl, S. & Hubbard, W. B. Models of Saturn’s interior constructed with an accelerated concentric Maclaurin spheroid method. Astrophys. J. 879, 78 (2019).
Helled, R. & Guillot, T. Interior models of Saturn: including the uncertainties in shape and rotation. Astrophys. J. 767, 113 (2013).
Galanti, E. et al. Saturn’s deep atmospheric flows revealed by the Cassini Grand Finale gravity measurements. Geophys. Res. Lett. 46, 616–624 (2019).
Fuller, J. Saturn ring seismology: evidence for stable stratification in the deep interior of Saturn. Icarus 242, 283–296 (2014).
Helled, R. The Interiors of Jupiter and Saturn, 175 (Oxford Univ. Press, 2018).
Lühr, H., Wicht, J., Gilder, S. A. & Holschneider, M. Magnetic Fields in the Solar System, Vol. 448 (Springer, 2018).
French, M. et al. Ab initio simulations for material properties along the Jupiter adiabat. Astrophys. J. Suppl. 202, 5 (2012).
Liu, J., Goldreich, P. M. & Stevenson, D. J. Constraints on deep-seated zonal winds inside Jupiter and Saturn. Icarus 196, 653–664 (2008).
Cao, H. & Stevenson, D. J. Zonal flow magnetic field interaction in the semi-conducting region of giant planets. Icarus 296, 59–72 (2017).
Gastine, T., Wicht, J., Duarte, L. D. V., Heimpel, M. & Becker, A. Explaining Jupiter’s magnetic field and equatorial jet dynamics. Geophys. Res. Lett. 41, 5410–5419 (2014).
Jones, C. A. A dynamo model of Jupiter’s magnetic field. Icarus 241, 148–159 (2014).
Wicht, J., Gastine, T., Duarte, L. D. V. & Dietrich, W. Dynamo action of the zonal winds in Jupiter. Astron. Astrophys. 629, A125 (2019).
Duer, K., Galanti, E. & Kaspi, Y. Analysis of Jupiter’s deep jets combining Juno gravity and time-varying magnetic field measurements. Astrophys. J. Lett. 879, L22 (2019).
Connerney, J. E. P. et al. A new model of Jupiter’s magnetic field from Juno’s first nine orbits. Geophys. Res. Lett. 45, 2590–2596 (2018).
Moore, K. M. et al. A complex dynamo inferred from the hemispheric dichotomy of Jupiter’s magnetic field. Nature 561, 76–78 (2018).
Dougherty, M. K. et al. Cassini magnetometer observations during Saturn orbit insertion. Science 307, 1266–1270 (2005).
Dougherty, M. K. et al. Saturn’s magnetic field from the Cassini Grand Finale orbits. In AGU Fall Meeting Abstracts, Vol. 2017, U22A-02 (2017).
Cao, H. et al. The landscape of Saturn’s internal magnetic field from the Cassini Grand Finale. Icarus 344, 113541 (2020).
Cao, H., Russell, C. T., Wicht, J., Christensen, U. R. & Dougherty, M. K. Saturn’s high degree magnetic moments: evidence for a unique planetary dynamo. Icarus 221, 388–394 (2012).
Drozdov, A., Eremets, M., Troyan, I., Ksenofontov, V. & Shylin, S. Conventional superconductivity at 203 kelvin at high pressures in the sulfur hydride system. Nature 525, 73–76 (2015).
Liu, H., Naumov, I. I., Hoffmann, R., Ashcroft, N. & Hemley, R. J. Potential high-Tc superconducting lanthanum and yttrium hydrides at high pressure. Proc. Natl Acad. Sci. USA 114, 6990–6995 (2017).
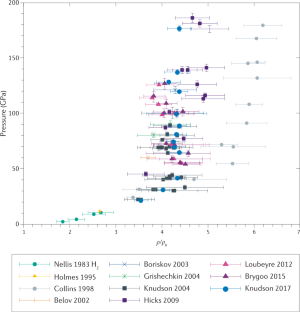
Nellis, W. J. et al. Equation of state data for molecular hydrogen and deuterium at shock pressures in the range 2–76 GPa (20–760 kbar). J. Chem. Phys. 79, 1480–1486 (1983).
Holmes, N. C., Ross, M. & Nellis, W. J. Temperature measurements and dissociation of shock-compressed liquid deuterium and hydrogen. Phys. Rev. B 52, 15835–15845 (1995).
Collins, G. W. et al. Measurements of the equation of state of deuterium at the fluid insulator–metal transition. Science 281, 1178 (1998).
Belov, S. I. et al. Shock compression of solid deuterium. J. Exp. Theor. Phys. Lett. 76, 433–435 (2002).
Boriskov, G. V. et al. Shock-wave compression of solid deuterium at a pressure of 120 GPa. Dokl. Phys. 48, 553–555 (2003).
Grishechkin, S. K. et al. Experimental measurements of the compressibility, temperature, and light absorption in dense shock-compressed gaseous deuterium. J. Exp. Theor. Phys. Lett. 80, 398–404 (2004).
Knudson, M. D. et al. Principal Hugoniot, reverberating wave, and mechanical reshock measurements of liquid deuterium to 400 GPa using plate impact techniques. Phys. Rev. B 69, 144209 (2004).
Hicks, D. G. et al. Laser-driven single shock compression of fluid deuterium from 45 to 220 GPa. Phys. Rev. B 79, 014112 (2009).
Loubeyre, P. et al. Extended data set for the equation of state of warm dense hydrogen isotopes. Phys. Rev. B 86, 144115 (2012).
Miguel, Y., Guillot, T. & Fayon, L. Jupiter internal structure: the effect of different equations of state. Astron. Astrophys. 596, A114 (2016).
Acknowledgements
The authors thank the anonymous referees for comments that helped to improve the manuscript. The authors also acknowledge support from W. Nellis, F. Soubrian, S. Sorella, D. Stevenson, N. Nettelmann, J. J. Fortney, Y. Miguel, S. Müller, C. Valletta and A. Cumming. R.H. acknowledges support from the Swiss National Science Foundation (SNSF grant 200020_188460) and thanks the members of the Juno science team for discussions. R.R. acknowledges support by the Deutsche Forschungsgemeinschaft via the projects FOR 2440 and SPP 1992.
Author information
Authors and Affiliations
Contributions
All authors contributed to all aspects of this article.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Helled, R., Mazzola, G. & Redmer, R. Understanding dense hydrogen at planetary conditions. Nat Rev Phys 2, 562–574 (2020). https://doi.org/10.1038/s42254-020-0223-3
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s42254-020-0223-3