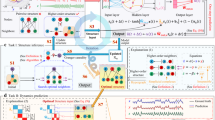
Abstract
Non-linear dynamical systems describe numerous real-world phenomena, ranging from the weather, to financial markets and disease progression. Individual systems may share substantial common information, for example patients’ anatomy. Lately, deep-learning has emerged as a leading method for data-driven modeling of non-linear dynamical systems. Yet, despite recent breakthroughs, prior works largely ignored the existence of shared information between different systems. However, such cases are quite common, for example, in medicine: we may wish to have a patient-specific model for some disease, but the data collected from a single patient is usually too small to train a deep-learning model. Hence, we must properly utilize data gathered from other patients. Here, we explicitly consider such cases by jointly modeling multiple systems. We show that the current single-system models consistently fail when trying to learn simultaneously from multiple systems. We suggest a framework for jointly approximating the Koopman operators of multiple systems, while intrinsically exploiting common information. We demonstrate how we can adapt to a new system using order-of-magnitude less new data and show the superiority of our model over competing methods, in terms of both forecasting ability and statistical fidelity, across chaotic, cardiac, and climate systems.
Similar content being viewed by others
Introduction
Dynamical systems describe natural phenomena, such as atmospheric convection1, physiological processes2, and financial markets3. For decades, scientists have been developing tools for predicting, analyzing, and controlling the future state of dynamical systems. With the advent of high computing power and abundant data, machine-learning has become a popular approach to discover models of dynamical systems directly from data4,5,6,7,8, with deep-learning at the forefront9,10. Lately, Koopman spectral theory11,12,13 has emerged as a dominant approach for data-driven modeling of dynamical systems7,14, representing non-linear dynamics through the action of a linear operator, known as the Koopman operator (KO), by lifting measurements from the state-space to an observable-space. This linear representation is amenable to treatment by provably optimal methods for prediction, analysis, and control of dynamical systems, based on the comprehensive theory developed for linear operators7.
While machine learning has been successful in approximating system dynamics, prior works mostly focused on single-system settings6,7,8,9,10,15,16. However, in the case of multiple systems, learning a separate model per system forfeits the chance to exploit shared information. Alternatively, training a single model for all systems does not accommodate different systems’ varying behaviors.
An important case is that of chaotic systems with the mixing property, such as the Lorenz attractor. While such systems are not globally linearizable in finite dimensions, there exists a semiconjugacy allowing to linearize the system on a part of state space17. While no homeomorphic transformation will linearly encapsulate the global dynamics of the Lorenz system, the Koopman operator can provide a transformation that extends local neighborhoods where a linear model is valid to the full basin around fixed points of the system, as prior works have shown6,7,8,18. One can then ask whether jointly learning multiple approximations from different state trajectories might produce superior approximation globally.
Here, we consider this multi-system case, where all systems possess similar or identical dynamics, with the intent of exploiting shared information, while remaining system- (or neighborhood-) specific. For clarity, in the context of multiple trajectories with identical dynamics multi-system means multi-neighborhood. Hence, our goal is to jointly learn a set of interrelated linear dynamics operators, one per system (or neighborhood of a single system), with shared components. For this purpose, we define linearly interrelated dynamics as follows:
Definition 1 Let \(\{{{{{{{{{\mathcal{F}}}}}}}}}_{1},\ldots ,{{{{{{{{\mathcal{F}}}}}}}}}_{M}\}\) be a collection of discrete-time dynamical systems with the state in \({{\mathbb{R}}}^{n}\). We say that the systems have linearly interrelated dynamics if there exists an invertible coordinate transformation \(\varphi :{{\mathbb{R}}}^{n}\to {{\mathbb{R}}}^{k}\) and a set of k × k matrices \({\{{{{{{{{{\boldsymbol{K}}}}}}}}}_{i}\}}_{i = 1}^{M}\) such that \({{{{{{{{\mathcal{F}}}}}}}}}_{m}={\varphi }^{-1}{\circ}\;\, {{{{{{{{\boldsymbol{K}}}}}}}}}_{m}\circ\;\, \varphi\).
In other words, the systems can be globally linearized by the same coordinate transformation, but will have individual linear dynamics in that representation space. This definition is different from that of other notions of coupled dynamics (e.g., coupled oscillators). Specifically, in our definition different systems do not act on each other, but can simply be jointly linearly decomposed (for details see “Multi-systems setting” subsection in the “Methods”). Additionally, throughout this work, by saying that the above holds approximately, we mean that φ and K is a reduced real representation of \({{{{{{{\mathcal{F}}}}}}}}\). Recent works somewhat similar to ours are19,20. However, in both works the authors suggest deriving joint linear dynamics for the evolution of measurements from multiple modalities (i.e., various states) of the same system, and do not consider the case of multiple systems.
In contrast, we learn a single transformation to a joint coordinate system, in which the dynamics of multiple systems are linearly interrelated. We use auto-encoders (AE)21 to learn a single-state embedding for all systems. Then, in the representation space, we learn a k-dimensional approximation of each system’s individual dynamics. Specifically, we represent each system’s time propagation as:
where \({{{{{{{{\boldsymbol{x}}}}}}}}}_{t}^{m}\in {{\mathbb{R}}}^{n}\) denotes the state of system m at time t, and ϕ and ψ denote the learned transformations, parameterized by deep neural networks (DNN), mapping between the state space and the representation space. The factorized form Km = ABmC for the linear propagator in the representation space is motivated by22 due to its implicit rank regularization. Thus, the only system-specific component is Bm (see Fig. S1 for schematic view).
Previous works have employed time-delayed embeddings6,8,16, where the time-delayed measurements were used as the representation. Instead, we learn the representation automatically through the encoder ϕ, and then approximate a propagator that represents the dynamics of the temporal differences of these representation:
where (Δx)t ≔ xt − xt−1 denotes the temporal difference operator and I is the identity operator. We term this formulation as the residual mode.
In what follows, we refer to the proposed framework in both the direct and the residual modes as to Model of Interrelated Dynamical Systems (MIDST). We compare MIDST to competing methods and show its superiority both in terms of forecasting accuracy and statistical fidelity to the future states. We demonstrate that single-system models fail to utilize shared information between interrelated systems. Specifically, in the case of the Lorenz system, where dynamics approximations are only locally valid, we show that, unsurprisingly, the forecasting ability of competing methods degrades as the number of different trajectories increases, while MIDST’s performance improves monotonically. We demonstrate how MIDST’s formulation allows us to adapt our model to new systems (or neighborhoods) using an order-of-magnitude less new samples. Finally, we show that MIDST significantly improves the prediction accuracy of chaotic and climate systems, while also being the only method to estimate with high statistical fidelity the future states of the effect of side-effects of anti-arrhythmogenic drugs in different patients.
Results
We report prediction errors via the Mean Absolute Scaled Error (MASE) metric, defined as:
where \({\hat{{{{{{{{\boldsymbol{x}}}}}}}}}}_{t}=\psi ({{{{{{{\boldsymbol{K}}}}}}}}\phi ({{{{{{{{\boldsymbol{x}}}}}}}}}_{t-1}))\) is the prediction made by the model, and xt is the target value at time t. The numerator represents the average prediction error of the model, and the denominator represents the average prediction error of a naïve predictor (MASE = 1 indicates that the two perform similarly).
We compare MIDST in the direct (MIDST-D) and residual (MIDST-R) formulations to five competing models: (1) Extended Dynamic Mode Decomposition (EDMD)23; (2) Measure Preserving Extended Dynamic Mode Decomposition (mpEDMD)8; (3) ResNet5024 in a temporal convolutional network configuration25; (4) a Universal Linear Embedding (ULE)9; and (5) Consistent Koopman (CK)10. We use an identical AE model for ULE, CK and our MIDST model, with the only difference being the representation of the linear propagator Km.
While the EDMD and mpEDMD methods can theoretically utilize multiple trajectories from a single system, ULE and CK were not designed for the multi-system settings. To extend these single-system methods to multi-system settings, we conducted an ablation study on the degree of dynamics sharing between different systems (Fig. S2, which can be found in the Supplementary Results section, similarly to all other Figures and Tables labeled with the prefix “S”). Specifically, we explored three levels of sharing: (1) no dynamics sharing, i.e., a different model per system; (2) sharing the entire model across systems, which is equivalent to the single-system case; (3) sharing the AE, and the left (A) and right (C) components of each propagator representation (only possible in MIDST). Based on the results of the ablation study, we extended the ULE and CK models through sharing a single AE for all systems (i.e., learning a shared coordinates transformation), while retaining separate per-system KOs. We refer to these extended models as Joint ULE (J-ULE) and Joint CK (J-CK), respectively.
Chaotic attractors
The Lorenz attractor1 is a simplified mathematical model for atmospheric convection that is chaotic, meaning differently initialized systems generate significantly different state trajectories. To evaluate MIDST, we generated M multiple trajectories with different initializations and identical dynamics. Each trajectory was partitioned into three sets: train, validation, and test. The initial 70% of each trajectory were used for training, the following 10% were used as a validation set, and the last 20% comprised the test set. The state-vector at each time t includes the (x, y, z) coordinates, and the goal is to predict the next H coordinates given T = 64 previous states (64 was chosen arbitrarily). A gap of T = 64 temporal states was maintained between each set to prevent information leakage. Except when specified otherwise, all experiments were performed on systems with the original parameters used by Lorenz1 (\(\sigma =10,\rho =28,\beta =\frac{8}{3}\)).
An obvious implicit assumption is that, given enough samples different state trajectories from the same system should yield similar dynamics approximations. However, in many real-life cases, and also with mixing chaotic systems, one cannot even hope to obtain the true dynamics represented by a finite-dimensional linear system. The Lorenz system, for example, has no point spectrum, hence it is not globally linearizable17, and while prior works obtained local linear approximations6,8,18, the effect of the sampled trajectory on the system approximation was not discussed.
Here, we jointly learn multiple dynamics approximations using MIDST on different trajectories from the same Lorenz system. After obtaining the different approximations, we test their forecasting capability on a newly generated trajectory. Figure 1a presents how by jointly learning multiple approximations using MIDST, we achieve order-of-magnitude improvement in terms of forecasting accuracy against all baseline methods. Additionally, Fig. 1b shows an order-of-magnitude lower error scores for MIDST compared to all other baselines, both on the originally learned systems, and on the new one, where we ablate over the available number of training samples, and where MIDST still outperforms every other model, in both the low- and high-data regimes.
a Average Mean Absolute Scaled Error (MASE) scores of MIDST and competing models. For the two analytical models (EDMD and mpEDMD) we have used time-delay embeddings as the observable-coordinates, as was done in refs. 6,8. b Average MASE scores of the fine-tuned models on a new attractor instance on an increasing training-set size. ResNet is trained entirely on the new dynamics; J-ULE and J-CK utilize pre-trained auto-encoder, and newly trained dynamics; MIDST-R utilizes a pre-trained and fixed auto-encoder and the A and C matrices, while we only train the Bm component. In all figures, Naïve refers to the naïve predictor (always have a value of 1). Shaded areas mark the 1σ confidence intervals.
Figure S2 ablates over the various sharing schemes. It shows that, unsurprisingly, a separate model per trajectory (MIDST-Disjoint) results in similar performance across all trajectories, while the prediction error of a single model (MIDST-Single) monotonically increases with the number of trajectories. Importantly, the two shared MIDST variants (MIDST-D and MIDST-R) show improvement as the number of trajectories increases, with MIDST-R outperforming all other variants.
In turn, Fig. 2 exemplifies how despite all trajectories having identical dynamics, each KO approximation performs noticeably differently on a newly generated trajectory. Figure 2a shows that different KO approximations are indeed mostly valid in a basin around the system’s fixed points, despite each local environment being slightly different for each approximation. In contrast, Fig. 2b shows a considerable difference in the areas in which each approximation breaks, i.e., despite all approximations being jointly obtained using the same algorithm from trajectories following the same dynamics, each different approximation breaks in different neighborhoods of the system’s state space.
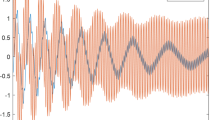
To validate that MIDST indeed exploit shared information, we evaluated a pre-trained MIDST-R model on a new trajectory. We compared three approaches: (1) training only the new system component (i.e., a new B matrix) while keeping the pre-trained AE maps ϕ, ψ and the matrices A, C fixed; (2) training a completely new K = ABC while using a fixed pre-trained AE; and (3) training an entirely new model. Each model was trained on an increasing number of samples to estimate the sample complexity for learning the new dynamics approximation. Figure 3 shows predictions from each model and highlights qualitative differences, while Fig. S3 reports the overall mean MASE scores. The results demonstrate that without optimizing shared components, the pre-trained AE and dynamics components enabled MIDST to significantly outperform the other two variants. To further examine the effects of MIDST on the learned dynamics approximations, we computed the average effective rank of the linear time propagator26 in each method (ResNet and J-ULE were excluded since ResNet does not approximate a linear propagator, and J-ULE generates a different approximation for each different sample). The effective rank of a matrix A represents the average number of significant dimensions in the range of A26, which in our context, can be considered as the “effective dimension” of the representation space. Figure S4 shows that MIDST is the only method in which the effective rank of K is affected by adding more trajectories (or systems), leading to improved results, while all other methods remain invariant to the addition of new trajectories.
GT denotes ground-truth; Fresh-start denotes a newly trained MIDST model; Pre-trained auto-encoder (AE) denotes a fixed pre-trained AE and a newly trained propagator K; Pre-trained AE + Dynamics denotes training only the B matrix in the propagator. a Predictions are for horizon H = 1 across the entire test set. b Zoom-in on the right blue box. c Auto-regressive predictions for H = 20 (displaying first 15 points for clarity), zoom-in on the left blue-box. Colors correspond to Lyapunov time (i.e., \(\frac{1}{{\lambda }_{L}}\), where λL ≈ 0.905646 is the largest Lyapunov exponent of the Lorenz system). Importantly, note that while a macro view shows no visible differences (a), by utilizing previously learned dynamics (i.e., dynamics sharing), our model forecasts are both more accurate for H = 1 (b and Fig. S3), and better encapsulate the true system dynamics when applied auto-regressively for longer time-horizons (c). Specifically, c shows that the only model actually obeying the true system dynamics for more than a single prediction step, is the one utilizing dynamics sharing.
In Fig. S5, we present the scaled average mean absolute error (sMAE) for the prediction horizon H = 20 (such a long horizon was chosen in order to reach the point of divergence for all models), where predictions for each step h ≥ 1 were generated in an autoregressive manner. By using the pre-trained AE and the A, C dynamics components (Pre-trained AE + Dynamics), the model outperformed training an entirely new model (52.1% lower sMAE) and training a new specific K approximation for the new system neighborhood (71.7% lower sMAE). We also tested MIDST on groups of Lorenz attractors with different parameters, i.e., similar systems with different dynamics, and on groups of completely different and unrelated systems. In both cases, MIDST outperformed any other competing method. Figures S6 and S7 respectively show the results for these experiments. Note that we did not include the EDMD and mpEDMD methods since these models are not suitable to handle trajectories from different systems (and indeed utterly failed to generate meaningful predictions). Figure S8 reports the effect of the representation dimension k, showing that MIDST’s performance improves monotonically as k increases, up to a performance limit. Finally, there is the question of stability of the learned system. While indeed an important aspect, our reliance on DNNs renders a proper analytical analysis impractical. However, to still obtain a measure of how stable MIDST is, we estimated the largest Lyapunov exponent (LLE) and compared it to that of the J-CK model. In Fig. S9, we show that not only does MIDST produce more stable dynamics approximations (Fig. S9a), but also that it produces a model with an LLE value that is closer to the true LLE of the Lorenz system (Fig. S9b).
Arrhythmogenic treatments
When modeling stochastic dynamical systems, correctly predicting the statistical behavior of future states can be more important than exact point-wise predictions. Thus, we aim to demonstrate MIDST’s superior fidelity to the statistical behavior of future state trajectories. To this end, we modeled the cardiac dynamics of different patients under the effect of different anti-arrhythmogenic treatments. Long QT syndrome (LQTS) is a cardiac condition that affects the repolarization of the heart, as represented in an electrocardiogram (ECG) by the QT interval27. LQTS is diagnosed by ECG when observing a corrected QT (QTc) interval ≥ 460 [msec]28. LQTS increases the risk of a ventricular arrhythmia known as Torsade de Pointes, which can result in sudden cardiac death29. Drug-induced QT prolongation is a known cause of increased mortality risk30, and currently, there are no widely available clinical tools for predicting which individuals are at greatest risk31.
Here, we predicted the length of future QT intervals under five different anti-arrhythmic treatments. We considered each treatment as a different dynamical system. Each treatment was administered to each of 21 patients. Short ECG recordings were taken 30 min prior to treatment administration, as well as at 15 fixed time points post-treatment. The state vector was composed of 13 clinical and ECG-derived measurements (for details, see the “Data availability” section). Given six initial measurements, for a given patient and treatment, we predicted the next 10 future QT and RR states (RR represents the temporal interval between consecutive heartbeats), from which we obtained the QTc values. We then estimated under which treatment the patient is predicted to suffer from a drug-induced QTc-prolongation event, defined as having at least one future QTc interval exceeding 460 milliseconds. Hence, and given our initial motivation for this section, here we report, in addition to MASE scores, on goodness-of-fit statistical tests between future ground-truth values and predictions and standard statistics for binary classification tasks. Due to the small number of points in each trajectory (six), we excluded the EDMD and mpEDMD models from this section, as they could not be properly evaluated.
Figure 4a demonstrates the benefits of having partially shared dynamics (MIDST-R) compared to a single model (MIDST-Single), with MIDST-R achieving 60% improvement in F1-Score. Figure 4b compares MIDST-R to competing models. MIDST-R achieved an F1-score improvement of 292% and 208% compared to ResNet and J-CK, respectively, and an improvement of 217% in specificity compared to J-ULE.
a Comparison between MIDST-Single and MIDST-R. b Comparison between ResNet, J-ULE, J-CK, and MIDST-R. For complete numerical results see Table S1.
Figures S10 and S11 showcase the stronger statistical fidelity of MIDST-R predictions by comparing the histogram of predicted QTc lengths to that of ground-truth values. We performed an Epps-Singleton (ES) goodness-of-fit test32 between predicted QTc lengths and ground-truth lengths. The null hypothesis claims that the two samples were generated by the same underlying probability distribution, i.e., rejection of the null indicates that predicted QTc values are not similarly distributed as ground-truth values. Figure S10 clearly shows that MIDST is the only method that properly captures the statistical behavior of QTc dynamics. MIDST’s predictions are the only ones for which the null could not be significantly rejected (p = 0.43), while the null was significantly rejected for all other methods (p ≤ 0.05). Figure S11 presents a similar comparison between MIDST-R and MIDST-Single, showing that the null is also significantly rejected for the single model (p = 0.02). Surprisingly, Table S2 demonstrates that almost all models have performed similarly in terms of average MASE scores, highlighting that while the accuracy of point-wise predictions for each model was similar, it does not necessarily translate to capturing the true statistical behaviors of these stochastic systems.
Sea surface temperature
In this section, we focused on highly periodical systems that exhibit non-stationary structures. The National Oceanic and Atmospheric Administration (NOAA) has made a series of sea surface temperature (SST) measurements available to the public in the Optimum Interpolation SST V2 dataset33. The state of each dynamical system is represented as a time series of SST in fixed locations.
We trained a MIDST model to predict future SSTs at 50 different locations across two oceans, corresponding to 50 interrelated systems (for more details, see the “Data availability” section). At each time point t, the model was provided with a trajectory of state vectors, consisting of the average weekly temperatures of 16 adjacent locations from the previous T = 16 weeks, and then predicted the next H weeks (the numbers of regions, adjacent locations per state vector and previous state-vectors to consider were all chosen arbitrarily).
Figure 5 demonstrates how the single-system model (MIDST-Single) fails in the multi-system setting. Instead of making an accurate prediction for each separate system, it consistently fails across all systems. It has a significant phase shift when compared to individual systems and overestimate the lower and underestimate the higher SST values. In contrast, MIDST-R generates high-fidelity predictions while maintaining the correct phase and amplitude for each individual system. Figure S12 shows that MIDST also outperform all other models, scoring a 25.3% average MASE reduction over MIDST-Single, and an order-of-magnitude improvement compared to EDMD and mpEDMD.
a Average Prediction error of every state (i.e., specific location for which SST is monitored), positioned on its appropriate location on the globe. Colors indicate the absolute error in degrees Celsius. b Predicted SST values vs. ground truth (GT), plotted across time. For clarity, we only visualize one state trajectory from each ocean. Predictions are for H = 1. MIDST-Single has a single AE and linear propagator for all 50 systems, while MIDST-R shares the AE and the A and C components.
Discussion
Koopman operator theory and its application with deep learning have led to considerable improvements in our ability to perform data-driven modeling of non-linear dynamical systems. However, in many cases, obtaining the true KO is not possible, and we are left with only finite-dimensional approximations that may still be useful to describe the dynamics at least in a neighborhood of the state space. Here we have shown that these approximations highly depend on the specific state trajectories based on which they are obtained, regardless of whether they have originated from the same dynamical systems or not. Furthermore, the question of how to use an approximation of one system to improve that of another was also largely unaddressed. We presented a framework named MIDST, which we have shown is capable of producing improved data-driven dynamics approximations, whether by considering multiple trajectories of the same systems, or those of different interrelated systems. We showed that not only is MIDST superior to existing methods, but that it is the only method that noticeably benefits from jointly learning multiple dynamics approximations for either different neighborhoods of the same systems, or for different systems altogether. Thus, we hope MIDST can enable better modeling of important real-life, non-linear dynamical systems.
Methods
The Koopman operator
Koopman theory has gained popularity as a theoretically sound and, recently, also data-driven method for representing non-linear dynamics in terms of a linear operator7,11,12,13,14,17. This theory posits that for any dynamical system \({{{{{{{\mathcal{F}}}}}}}}\) there exists a (potentially infinitely-dimensional) linear operator \({{{{{{{\mathcal{K}}}}}}}}\), known as the Koopman operator (KO), which completely describes \({{{{{{{\mathcal{F}}}}}}}}\)17. More specifically, we consider a discrete-time dynamical system \({{{{{{{{\boldsymbol{x}}}}}}}}}_{t+1}={{{{{{{\mathcal{F}}}}}}}}({{{{{{{{\boldsymbol{x}}}}}}}}}_{t})\) with a real-valued n-dimensional state initialized at \({{{{{{{{\boldsymbol{x}}}}}}}}}_{0}\in {{\mathbb{R}}}^{n}\). The time propagator \({{{{{{{\mathcal{F}}}}}}}}:{{\mathbb{R}}}^{n}\to {{\mathbb{R}}}^{n}\) is often referred to as the system’s “dynamics”. Let the state be observed through a real-valued scalar readout y = G(xt) with \(G:{{\mathbb{R}}}^{n}\to {\mathbb{R}}\). The observable trajectory can therefore be expressed as \({y}_{t}=G({{{{{{{{\mathcal{F}}}}}}}}}^{t}({{{{{{{{\boldsymbol{x}}}}}}}}}_{0}))\), where the family of flow maps \({{{{{{{{\mathcal{F}}}}}}}}}^{t}:{{{{{{{\boldsymbol{x}}}}}}}}\to ({{{{{{{\mathcal{F}}}}}}}}\circ\;\, ...\circ\;\, {{{{{{{\mathcal{F}}}}}}}})({{{{{{{\boldsymbol{x}}}}}}}})\) applies a t-times composition of \({{{{{{{\mathcal{F}}}}}}}}\) to the initial state vector.
The idea of Koopman representation is to define a dual dynamical system in which the roles of x0 and G are switched. The state of the dual system is the space of observables, \({G}_{t}:{{\mathbb{R}}}^{n}\to {{\mathbb{R}}}^{k}\) and the dynamics are given by the family of flow maps \({{{{{{{{\mathcal{K}}}}}}}}}^{t}:G\to G\circ\;\, {{{{{{{{\mathcal{F}}}}}}}}}^{t}\), with G0 = G. The generator of the flow, \({{{{{{{\mathcal{K}}}}}}}}={{{{{{{{\mathcal{K}}}}}}}}}^{1}:G\to G\circ\;\, {{{{{{{\mathcal{F}}}}}}}}\) is often referred to as the Koopman operator. The dual dynamical system is observed through a linear sampling operator \({{{{{{{{\mathcal{S}}}}}}}}}_{{{{{{{{{\boldsymbol{x}}}}}}}}}_{0}}:G\to G({{{{{{{{\boldsymbol{x}}}}}}}}}_{0})\in {\mathbb{R}}\), yielding \({y}_{t}=G({{{{{{{{\mathcal{F}}}}}}}}}^{t}({{{{{{{{\boldsymbol{x}}}}}}}}}_{0}))=({{{{{{{{\mathcal{K}}}}}}}}}^{t}{G}_{0})({{{{{{{{\boldsymbol{x}}}}}}}}}_{0})={G}_{t}({{{{{{{{\boldsymbol{x}}}}}}}}}_{0})={{{{{{{{\mathcal{S}}}}}}}}}_{{{{{{{{{\boldsymbol{x}}}}}}}}}_{0}}({G}_{t})\). Note that even in the case of a fully observable primal, the observability of the dual is limited by the null-space of \({{{{{{{{\mathcal{S}}}}}}}}}_{{{{{{{{{\boldsymbol{x}}}}}}}}}_{0}}\) that depends on the primal initial conditions34.
The Koopman operator admits an eigendecomposition with the eigenfunctions satisfying \(\lambda \Phi ={{{{{{{\mathcal{K}}}}}}}}\Phi =\Phi \circ\;\, {{{{{{{\mathcal{F}}}}}}}}\). Any finite subset of eigenfunctions Φ = (Φ1, ..., Φk) spans an invariant subspace in the sense that for every G ∈ sp(Φ), its time propagation \({{{{{{{\mathcal{K}}}}}}}}G\) stays in the subspace. Thus, \({{{{{{{\boldsymbol{\Phi }}}}}}}}:{{\mathbb{R}}}^{n}\to {{\mathbb{R}}}^{k}\) and the k × k diagonal matrix Λ = diag(λ1, ..., λk) constitute a linear representation of the primal dynamical system in the sense that \({{{{{{{\boldsymbol{\Phi }}}}}}}}({{{{{{{{\mathcal{F}}}}}}}}}^{t}({{{{{{{\boldsymbol{x}}}}}}}}))=({{{{{{{{\mathcal{K}}}}}}}}}^{t}{{{{{{{\boldsymbol{\Phi }}}}}}}})({{{{{{{\boldsymbol{x}}}}}}}})={{{{{{{{\boldsymbol{\Lambda }}}}}}}}}^{t}{{{{{{{\boldsymbol{\Phi }}}}}}}}({{{{{{{\boldsymbol{x}}}}}}}})\). Furthermore, for any regular linear transformation, Ψ(x) = MΦ(x) defined by an invertible k × k matrix \({{{{{{{\boldsymbol{M}}}}}}}},{{{{{{{\boldsymbol{\Psi }}}}}}}}({{{{{{{{\mathcal{F}}}}}}}}}^{t}({{{{{{{\boldsymbol{x}}}}}}}}))=({{{{{{{{\mathcal{K}}}}}}}}}^{t}{{{{{{{\boldsymbol{M}}}}}}}}{{{{{{{\boldsymbol{\Phi }}}}}}}})({{{{{{{\boldsymbol{x}}}}}}}})={{{{{{{\boldsymbol{M}}}}}}}}{{{{{{{{\boldsymbol{\Lambda }}}}}}}}}^{t}{{{{{{{\boldsymbol{\Phi }}}}}}}}({{{{{{{\boldsymbol{x}}}}}}}})={{{{{{{\boldsymbol{M}}}}}}}}{{{{{{{{\boldsymbol{\Lambda }}}}}}}}}^{t}{{{{{{{{\boldsymbol{M}}}}}}}}}^{-1}{{{{{{{\boldsymbol{\Psi }}}}}}}}({{{{{{{\boldsymbol{x}}}}}}}})\). If, furthermore, Ψ is injective, we can write xt = Ψ−1(MΛtM−1Ψ(x0)). Ψ can be thus thought of as a non-linear coordinate transformation globally linearizing the primal system.
While for many systems (e.g., chaotic systems with the mixing property) such an exact finite-dimensional transformation does not exist, essentially all Koopman representation-based methods attempt to find an approximation thereof in the form of a parametric state encoder z0 = ϕθ(x0) mapping the initial state into some latent representation, a linear propagator zt = Ktz0 in that representation, and a parametric decoder \({{{{{{{{\boldsymbol{x}}}}}}}}}_{t}={{{{{{{{\boldsymbol{\psi }}}}}}}}}_{{{{{{{{\boldsymbol{\theta }}}}}}}}}({{{{{{{{\boldsymbol{z}}}}}}}}}_{t}),{{{{{{{{\boldsymbol{\psi }}}}}}}}}_{{{{{{{{\boldsymbol{\theta }}}}}}}}}\, \approx \, {{{{{{{{\boldsymbol{\phi }}}}}}}}}_{{{{{{{{\boldsymbol{\theta }}}}}}}}}^{-1}\) mapping the latent vector back into the original state space, where, K serves as a reduced real representation of the KO. In such cases, the approximate relation \({{{{{{{{\boldsymbol{\psi }}}}}}}}}_{{{{{{{{\boldsymbol{\theta }}}}}}}}}\circ\;\, {{{{{{{\boldsymbol{K}}}}}}}}\circ\;\, {{{{{{{{\boldsymbol{\phi }}}}}}}}}_{{{{{{{{\boldsymbol{\theta }}}}}}}}}\approx {{{{{{{\mathcal{F}}}}}}}}\) still holds.
Multi-systems setting
Consider multiple dynamical systems \({\{{{{{{{{{\mathcal{F}}}}}}}}}_{m}\}}_{m = 1}^{M}\), where for each time t, each mth system \({{{{{{{{\mathcal{F}}}}}}}}}_{m}\) is described through a fully-observable state vector \({{{{{{{{\boldsymbol{x}}}}}}}}}_{t}^{m}\in {{\mathbb{R}}}^{n}\). For example, let there be a group of M patients, let n be the number of clinical measurements obtained from each patient, at each time t, such that the dynamical system \({{{{{{{{\mathcal{F}}}}}}}}}_{m}\) represent the evolution of the clinical state of the mth patient. Because all patients share similar anatomy and physiology, we can expect similar dynamics to determine the clinical dynamics of each patient.
A straightforward condition for the existence of “shared” dynamics can be defined as follows:
Definition 2 Let \(\{{{{{{{{{\mathcal{F}}}}}}}}}_{1},...,{{{{{{{{\mathcal{F}}}}}}}}}_{M}\}\) be a collection of systems, all in \({{\mathbb{R}}}^{n}\), and each with a respective Koopman representation \(\{{{{{{{{{\mathcal{K}}}}}}}}}_{1},...,{{{{{{{{\mathcal{K}}}}}}}}}_{M}\}\). We say that the systems have shared dynamics if they share an eigenbasis, that is, there exists a mapping \({{{{{{{\boldsymbol{\Phi }}}}}}}}:{{\mathbb{R}}}^{n}\to {{\mathbb{R}}}^{k}\) and a set of k × k diagonal matrices \({\{{{{{{{{{\boldsymbol{\Lambda }}}}}}}}}_{m}\}}_{m = 1}^{M}\) such that \({{{{{{{\boldsymbol{\Phi }}}}}}}}({{{{{{{{\mathcal{F}}}}}}}}}_{m}({{{{{{{\boldsymbol{x}}}}}}}}))=({{{{{{{{\mathcal{K}}}}}}}}}_{m}{{{{{{{\boldsymbol{\Phi }}}}}}}})({{{{{{{\boldsymbol{x}}}}}}}})={{{{{{{{\boldsymbol{\Lambda }}}}}}}}}_{m}{{{{{{{\boldsymbol{\Phi }}}}}}}}({{{{{{{\boldsymbol{x}}}}}}}})\) for all m’s.
This immediately leads to the following
Proposition 1 \(\{{{{{{{{{\mathcal{F}}}}}}}}}_{1},...,{{{{{{{{\mathcal{F}}}}}}}}}_{M}\}\) have shared dynamics if and only if they commute, i.e., for every pair \(i,j,{{{{{{{{\mathcal{F}}}}}}}}}_{i}\circ\;\, {{{{{{{{\mathcal{F}}}}}}}}}_{j}={{{{{{{{\mathcal{F}}}}}}}}}_{j}\circ\;\, {{{{{{{{\mathcal{F}}}}}}}}}_{i}\) and, correspondingly, \({{{{{{{{\mathcal{K}}}}}}}}}_{i}{{{{{{{{\mathcal{K}}}}}}}}}_{j}={{{{{{{{\mathcal{K}}}}}}}}}_{j}{{{{{{{{\mathcal{K}}}}}}}}}_{i}\).
The proof is trivial (see the MIDST section in the Supplementary Methods). By allowing the shared non-linear embedding to be a linear transformation of the eigenspace spanned by Φ, we further allow the individual linear dynamics to be represented as Km = ABmC as in Definition 1.
Furthermore, in many cases, we do not even have access to these unknown underlying rules. Instead, we have state trajectories measured from each system. However, even when the underlying dynamics are identical, state trajectories may seem wildly different, due to the different sampling operator \({{{{{{{{\mathcal{S}}}}}}}}}_{{{{{{{{{\boldsymbol{x}}}}}}}}}_{0}}\) which depends on the initial state x0. Yet, in many cases, we can still reasonably assume that trajectories from different systems obey similar dynamical rules. For example, when studying physiological changes in different patients, analyzing stocks in the same market sector, or modeling similar climate systems in different geographical locations. As such, we wish to model the specific dynamics of each system directly from observed state trajectories, while also utilizing information from trajectories of other similar systems. Our approach is similar in spirit to that of collaborative filtering35, which can be thought of as the process of filtering information among multiple data sources, to enable maximal utilization of the data contained in each source. And indeed, one can always test the empirical validity of this assumption by attempting to learn a linear propagator for \({{{{{{{{\mathcal{F}}}}}}}}}_{M+1}\) based on the observables space learned for \(\{{{{{{{{{\mathcal{F}}}}}}}}}_{1},\ldots ,{{{{{{{{\mathcal{F}}}}}}}}}_{M}\}\).
MIDST
In prior works, a finite-dimensional linear representation of the dynamical system was either derived analytically36,37, learned based on a given, pre-determined, set of state-to-observable transformations5, optimized for under specific structural constraints9, or learned directly via unconstrained optimization10. We also opted for learning such a representation through unconstrained optimization but in an indirect manner. We decomposed the linear propagator in the representation space as the product of three k × k matrices, K = ABC, where we directly optimize A, B, C. This factorization serves two purposes: firstly, it induces an implicit rank regularization which enables learning richer models, as opposed to when using an explicit norm-based regularization, whenever A, B, and C are optimized through a stochastic gradient descent (SGD) algorithm22. This leads to a model, referred to as Deep Matrix Factorization (DMF), which can generalize better22; and, it specifies K in a way that directly enables us to tie together the dynamics of different systems. Note that Arora et al.22 proved convergence to a solution with minimal nuclear norm under the assumptions that all sub-matrices (i.e., A, B, C) commute, which we do not enforce, however, it was also conjectured that it suffices to initialize the matrices to an arbitrary full-rank matrix22,38 (which we do).
Additionally, even when the DMF model does not converge to the minimal nuclear norm solution, it still induces rank regularization22. Thus, even though we may not know a priori what the optimal dimensionality k for the propagator approximation is, we can set k to be sufficiently large, and by specifying K in factorized form, we will obtain a rank-regularized solution for it. This can be directly observed in Fig. S8, in which the approximation of the KO improves monotonically, as we increase k, up to a k ≈ 10, beyond which the approximation neither improves nor deteriorates. Of course, in many cases, including both conservative and dissipative cases, the KO is not compact and the system does not admit a finite-dimensional linear representation39. Regardless, practical uses still necessitate finite-dimensional approximations, and we find that in practice our construction leads to better results compared to competing methods.
Furthermore, while there are works addressing (under certain assumptions) the construction of potentially non-compact KO39, data-driven DL-based methods9,10 perform better, while learning a rank-regularized approximation of the linear propagator.
For predicting the future state of system m with horizon h > 1, we can write14:
Note that although Kh for a linear propagator literally means power h, unless otherwise specified (such as in Fig. 3), we follow Lusch et al.9, and define h different propagators, where each \({{{{{{{{\boldsymbol{K}}}}}}}}}_{m}^{h}={{{{{{{{\boldsymbol{A}}}}}}}}}^{h}{{{{{{{{\boldsymbol{B}}}}}}}}}_{m}^{h}{{{{{{{{\boldsymbol{C}}}}}}}}}^{h}\) advances the observable functions by h steps, with h denoting an index rather than power.
Residual dynamics
Denoting by zt = ϕ(xt) the state representation at time t, the direct mode MIDST formulation propagates zt forward in time by K (or Kh if a longer horizon is sought), and then maps zt+1 = Kzt back to the state space by xt+1 = ψ(zt+1).
However, we can also write zt+1 = Δzt+1 − zt, with Δzt+1 = zt+1 − zt being the one-step temporal difference, and apply the propagator to the difference, Δzt+1 = KΔzt, leading to \({{{{{{{{\boldsymbol{x}}}}}}}}}_{t+1}=\psi \left(({{{{{{{\boldsymbol{K}}}}}}}}\Delta +{{{{{{{\boldsymbol{I}}}}}}}})\phi ({{{{{{{{\boldsymbol{x}}}}}}}}}_{t})\right)\). Applying the same reasoning to bigger time delays yields:
By comparing Eq. (5) above to the direct mode equation \({{{{{{{{\boldsymbol{x}}}}}}}}}_{t+1}=\psi \left({{{{{{{{\boldsymbol{K}}}}}}}}}^{t+1}\phi ({{{{{{{{\boldsymbol{x}}}}}}}}}_{0})\right)\) we can immediately observe the implicit meaning of our alternative formulation: in the direct mode, a propagator with eigenvalues bigger than 1 will quickly diverge, while if all the eigenvalues are smaller than 1, it will converge to a fixed point. In the residual mode, eigenvalues bigger than 1 will still diverge, however, propagators with spectral radius bounded by 1 will exhibit stable behavior dominated by the slow modes of K for long time horizons.
One can also see a potential relation between our residual formulation and prior works approximating the KO using time-delayed Hankel matrices6,15. A Hankel matrix is a square matrix, in which each ascending skew-diagonal from left to right is constant. Prior works approximated the KO using a Hankel matrix of time-delayed states, as opposed to directly from the states themselves. Similarly, by applying our learned propagator in the residual mode, we learn a KO for the time-delayed observables.
Arrhythmogenic treatments
Data was obtained from the publicly available PhysioNet database40,41. The database consists of 22 ECG recordings from healthy subjects partaking in a randomized, double-blind, 5-period crossover clinical trial. The purpose of the trial was to compare the effects of four known QT prolonging drugs, versus placebo, on both electrophysiological and clinical parameters (for details see the “Data” subsection in the Supplementary Methods).
Sea surface temperature
SST measurements were obtained from the publicly available National Oceanic and Atmospheric Administration (NOAA) database33. The data used includes weekly mean temperature, on a one-degree grid, of the sea surface as measured by satellites, from 31/12/1989 to 17/04/2022. Weeks are defined to be centered on Wednesday (for details see the “Data” subsection in the Supplementary Methods).
Statistical analysis
The ES goodness-of-fit test was computed using SciPy42. Evaluation of the statistical metrics reported in the anti-arrhythmogenic treatment experiments were computed using Scikit-Learn43. Evaluation of the MASE scores was performed using custom Python implementation.
Data availability
Strange attractors: in order to generate trajectories for the Lorenz attractors we used the equations originally discovered by Lorenz1. For the experiment simulating learning of entirely different systems, we also generated trajectories from the Sprott44, and Wang-Sun45 chaotic systems (for details see the “Data” subsection in the Supplementary Methods). Arrhythmogenic treatments: the data for the arrhythmogenic treatments experiments was taken from the following public database in Physionet: “ECG Effects of Ranolazine, Dofetilide, Verapamil, and Quinidine”40,41, which is available at the following link: https://physionet.org/content/ecgrdvq/1.0.0/ (for details see the “Data” subsection in the Supplementary Methods). Sea surface temperature: the data for the sst experiments was taken from the public Optimum Interpolation SST V2 dataset from the National Oceanic and Atmospheric Administration33, which is available at the following link: https://psl.noaa.gov/data/gridded/data.noaa.oisst.v2.html (for details see the “Data” subsection in the Supplementary Methods).
Code availability
Complete code implementation and partial datasets are publicly available at the following github repository: https://github.com/YonatanElul/midst.git (see additional implementation details in the “Model architecture, training & implementation” subsection in the Supplementary Methods).
References
Lorenz, E. N. Deterministic nonperiodic flow. J. Atmos. Sci. 20, 130–141 (1963).
Govindan, R. B., Narayanan, K. & Gopinathan, M. S. On the evidence of deterministic chaos in ECG: surrogate and predictability analysis. Chaos Interdiscip. J. Nonlinear Sci. 8, 495 (1998).
Hommes, C. H. Financial markets as nonlinear adaptive evolutionary systems. Quant. Financ. 1, 149–167 (2001).
Schmidt, M. & Lipson, H. Distilling free-form natural laws from experimental data. Science 324, 81–85 (2009).
Brunton, S. L., Proctor, J. L., Kutz, J. N. & Bialek, W. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl Acad. Sci. USA 113, 3932–3937 (2016).
Brunton, S. L., Brunton, B. W., Proctor, J. L., Kaiser, E. & Nathan Kutz, J. Chaos as an intermittently forced linear system. Nat. Commun. 8, 1–34 (2017).
Brunton, S. L., Budišić, M., Kaiser, E. & Kutz, J. N. Modern Koopman theory for dynamical systems. SIAM Rev. 64 https://doi.org/10.1137/21M1401243 (2022).
Colbrook, M. J. The mpEDMD algorithm for data-driven computations of measure-preserving dynamical systems. SIAM J. Numer Anal. 61 https://doi.org/10.1137/22M1521407 (2023).
Lusch, B., Kutz, J. N. & Brunton, S. L. Deep learning for universal linear embeddings of nonlinear dynamics. Nat. Commun. 9, 4950 (2018).
Azencot, O., Erichson, N. B., Lin, V. & Mahoney, M. Forecasting sequential data using consistent Koopman autoencoders. In Proceedings of the 37th International Conference on Machine Learning, Vol. 119 (eds III, H. D. & Singh, A.) 475–485 (PMLR, 2020).
Koopman, B. O. Hamiltonian systems and transformation in Hilbert space. Proc. Natl Acad. Sci. 17, 315–318 (1931).
Mezić, I. & Banaszuk, A. Comparison of systems with complex behavior. Phys. D Nonlinear Phenom. 197, 101–133 (2004).
Mezić, I. Spectral properties of dynamical systems, model reduction and decompositions. Nonlinear Dyn. 41, 309–325 (2005).
Budišić, M., Mohr, R. & Mezić, I. Applied Koopmanism. Chaos 22, 047510 (2012).
Črnjarić-Žic, N., Maćešić, S. & Mezić, I. Koopman operator spectrum for random dynamical systems. J. Nonlinear Sci. 30, 2007–2056 (2019).
Wanner, M. & Mezić, I. Robust approximation of the stochastic Koopman operator. http://arxiv.org/abs/2011.00078 (2020).
Mezić, I. Koopman operator, geometry, and learning of dynamical systems. Not. Am. Math. Soc. 68, 1 (2021).
Giannakis, D. Data-driven spectral decomposition and forecasting of ergodic dynamical systems. Appl. Comput. Harmon. Anal. 47, 338–396 (2019).
Williams, M. O., Rowley, C. W., Mezić, I. & Kevrekidis, I. G. Data fusion via intrinsic dynamic variables: an application of data-driven Koopman spectral analysis. Europhys. Lett. 109, 40007 (2015).
Qian, S., Chou, C. A. & Li, J. S. Deep multi-modal learning for joint linear representation of nonlinear dynamical systems. Sci. Rep. 12, 1–10 (2022).
Hinton, G. E. & Salakhutdinov, R. R. Reducing the dimensionality of data with neural networks. Science 313, 504–507 (2006).
Arora, S., Cohen, N., Hu, W. & Luo, Y. Implicit regularization in deep matrix factorization. In Advances in Neural Information Processing Systems, Vol. 32 (eds Wallach, H. et al.) (Curran Associates, Inc., 2019).
Williams, M. O., Kevrekidis, I. G. & Rowley, C. W. A data-driven approximation of the Koopman operator: extending dynamic mode decomposition. J. Nonlinear Sci. 25, 1307–1346 (2015).
He, K., Zhang, X., Ren, S. & Sun, J. Deep residual learning for image recognition. In 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (2016).
Bai, S., Kolter, J. Z. & Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. http://arxiv.org/abs/1803.01271 (2018).
Roy, O. & Vetterli, M. The effective rank: a measure of effective dimensionality. In 2007 15th European Signal Processing Conference, 606–610 (2007).
Levine, E. et al. Congenital long QT syndrome: considerations for primary care physicians. Clevel. Clin. J. Med. 75, 591–600 (2008).
Members, A. F. et al. 2015 ESC guidelines for the management of patients with ventricular arrhythmias and the prevention of sudden cardiac death: the Task Force for the Management of Patients with Ventricular Arrhythmias and the Prevention of Sudden Cardiac Death of the Europe. EP Europace 17, 1601–1687 (2015).
Trinkley, K. E., Page, R. L. N., Lien, H., Yamanouye, K. & Tisdale, J. E. QT interval prolongation and the risk of torsades de pointes: essentials for clinicians. Curr. Med. Res. Opin. 29, 1719–1726 (2013).
Briasoulis, A., Agarwal, V. & Pierce, W. J. QT prolongation and Torsade de pointes induced by fluoroquinolones: infrequent side effects from commonly used medications. https://pubmed.ncbi.nlm.nih.gov/22156660/ (2011).
Tomaselli Muensterman, E. & Tisdale, J. E. Predictive analytics for identification of patients at risk for QT interval prolongation: a systematic review. Pharmacotherapy 38, 813–821 (2018).
Goerg, S. J., Kaiser, J. & Bundesbank, D. Nonparametric testing of distributions-the Epps-Singleton two-sample test using the empirical characteristic function. Stata J. 9, 454–465 (2009).
Reynolds, R. W., Rayner, N. A., Smith, T. M., Stokes, D. C. & Wang, W. An improved in situ and satellite SST analysis for climate. J. Clim. 15, 1609–1625 (2002).
Bamieh, B. A short introduction to the Koopman representation of dynamical systems. https://arxiv.org/abs/2205.08048v1 (2022).
Herlocker, J. L., Konstan, J. A., Terveen, L. G. & Riedl, J. T. Evaluating collaborative filtering recommender systems. ACM Trans. Inf. Syst. 22, 5–53 (2004).
Schmid, P. J. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28 (2010).
Williams, M. O., Kevrekidis, I. G. & Rowley, C. W. A data-driven approximation of the Koopman operator: extending dynamic mode decomposition. J. Nonlinear Sci. http://arxiv.org/abs/1411.2260 (2014).
Gunasekar, S., Woodworth, B. E., Bhojanapalli, S., Neyshabur, B. & Srebro, N. Implicit regularization in matrix factorization. In Advances in Neural Information Processing Systems 30 (NIPS, 2017).
Mezić, I. On numerical approximations of the Koopman operator. Mathematics 10, 1180 (2022).
Johannesen, L. et al. Differentiating drug-induced multichannel block on the electrocardiogram: randomized study of dofetilide, quinidine, ranolazine, and verapamil. Clin. Pharmacol. Ther. 96, 549–558 (2014).
Goldberger, A. L. et al. PhysioBank, PhysioToolkit, and PhysioNet components of a new research resource for complex physiologic signals. (2014).
Virtanen, P. et al. SciPy 1.0: fundamental algorithms for scientific computing in Python. Nat. Methods 17, 261–272 (2020).
Pedregosa, F. et al. Scikit-learn: machine learning in Python. J. Mach. Learn. Res. 12, 2825–2830 (2011).
Sprott, J. C. A dynamical system with a strange attractor and invariant tori. Phys. Lett. A 378, 1361–1363 (2014).
Wang, Z., Sun, Y., van Wyk, B. J., Qi, G. & van Wyk, M. A. A 3-D four-wing attractor and its analysis. Braz. J. Phys. 39, 547–553 (2009).
Viswanath, D. Lyapunov exponents from random Fibonacci sequences to the Lorenz equations. 126. https://ecommons.cornell.edu/items/82d8f293-1b91-40f9-a6f5-8070b3a70467 (1998).
Acknowledgements
This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme, grant agreements No. 863839 and No. 101037643 (ILIAD), from the Israeli Science Foundation, grant No. 191/18, and from Israel Ministry of Science and Technology.
Author information
Authors and Affiliations
Contributions
Y.E. and A.M.B. conceived of the presented idea, and developed the theory. E.R. and A.B. helped in developing parts of the theory. Y.E. implemented the code, performed the experiments and computations, and produced the figures. Y.E. and A.M.B. have written the manuscript. E.R., A.S., Y.Y. and A.M.B. have reviewed and edited the manuscript. A.S., Y.Y. and A.M.B. have supervised the work.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Elul, Y., Rozenberg, E., Boyarski, A. et al. Data-driven modeling of interrelated dynamical systems. Commun Phys 7, 141 (2024). https://doi.org/10.1038/s42005-024-01626-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-024-01626-5
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.