Observation of a phase space horizon with surface gravity water waves

Abstract

In 1974, Stephen Hawking predicted that quantum effects in the proximity of a black hole lead to the emission of particles and black hole evaporation. At the very heart of this process lies a logarithmic phase singularity which leads to the Bose-Einstein statistics of Hawking radiation. An identical singularity appears in the elementary quantum system of the inverted harmonic oscillator. In this Letter we report the observation of the onset of this logarithmic phase singularity emerging at a horizon in phase space and giving rise to a Fermi-Dirac distribution. For this purpose, we utilize surface gravity water waves and freely propagate an appropriately tailored energy wave function of the inverted harmonic oscillator to reveal the phase space horizon and the intrinsic singularities. Due to the presence of an amplitude singularity in this system, the analogous quantities display a Fermi-Dirac rather than a Bose-Einstein distribution.

Introduction

When a massive star collapses, a black hole¹ is born. During the collapse, the matter is compressed to an infinitesimal small volume of infinite density leading to a singularity in spacetime, surrounded by a domain where gravity is strong enough to capture light. This area is bounded by an event horizon dividing spacetime into two disjunct regions.

Since light cannot escape, one might think that black holes are black¹. However, Hawking^2,3 postulated that a black hole emits radiation with a spectrum governed by the Bose-Einstein distribution and similar to that of a black body. This phenomenon is a direct consequence^4,5,6 of quantum field theory and the curvature of spacetime at the event horizon of the black hole. Essential for the so-called Hawking radiation is a logarithmic phase singularity^7,8 in the mode functions of the quantized light field. Indeed, the characteristic Bose-Einstein distribution is a consequence⁸ of the Fourier transform of this phase, as was already discussed back in 1974 in the seminal paper of Hawking².

In order to study quantum effects of this type, access to a black hole is not mandatory. Many analog systems such as negative-frequency waves^9,10,11,12, Bose–Einstein condensates¹³, optical fibers¹⁴, and shallow water waves¹⁵ are experimentally accessible. While the focus of these works lies on the observation of effects similar to Hawking radiation, here we are interested in the measurement of its origin^8,16, that is, of the logarithmic phase singularity in a mode function close to an event horizon. For this purpose, we exploit an analogy between a black hole and an inverted harmonic oscillator^17,18. The energy eigenfunctions of this system also display¹⁹ a horizon with a logarithmic phase singularity, however, now in phase space. Since this phenomenon only takes place in specific phase space variables, we use the free time evolution of these energy wave functions to bring out the effects of this phase space horizon most clearly. This technique also allows us to show experimentally that for the inverted harmonic oscillator, the energy distribution associated with this horizon is of the Fermi–Dirac rather than Bose–Einstein type.

In our article, we use the one-dimensional inverted harmonic oscillator as a system to study black hole physics. For this purpose, we describe its inherent properties such as the phase space horizons, the logarithmic phase singularity, as well as the Fermi–Dirac distribution. We demonstrate how a free propagation of its quantum-mechanical energy eigenfunctions enables an observation of these features in position space. We present an experiment based on a classical analog of a quantum system by employing surface gravity water waves^20,21. Our measurements confirm the predicted horizon as well as the associated singularities and allow us to extract the Fermi–Dirac distribution.

Results and discussion

Phase space horizons, logarithmic phase singularity, and Fermi–Dirac distribution

We start by reviewing the classical dynamics of a particle moving in an inverted parabolic potential. As shown in Fig. 1a (bottom), for energies E below the top of the barrier, that is, E < 0, the particle is reflected, whereas for energies above, that is, E > 0, it is transmitted. When the energy is equal to the maximum of the barrier, that is, E = 0, the particle approaches the top and cannot cross over to the other domain.

Fig. 1: Emergence of a horizon in phase space and an amplitude singularity in the free time evolution of an energy eigenstate of the inverted harmonic oscillator.

a Phase space trajectories of classical particles (top) approaching a parabolic barrier V(x) (bottom) from the left (right) are represented by the blue (green) and red (orange) hyperbolas. Depending on their energy E the particles are transmitted (E > 0) or reflected (E < 0). For E = 0, they define a horizon in phase space (black), which separates the different energy domains. b Phase space representation of a quantum particle (top) with energy ε corresponding to the energy wave function, Eq. (1), as a function of position x and momentum p. In the neighborhood of the classical trajectory corresponding to the energy E = ℏωε, the corresponding Wigner function ${W}_{\phi ,\varepsilon }^{+}(x,p)$ has a dominant maximum (red). In contrast to a classical particle, the Wigner function covers two domains in phase space due to tunneling. The horizons confine the Wigner function to one half-plane in phase space. We show the corresponding position distribution $| {\phi }_{\varepsilon }^{+}(x){| }^{2}$ (bottom) resulting from integration over the momentum variable. The time evolution of such a Wigner function in the absence of any potential is governed by a sheering in phase space. c At a particular time $t={t}_{c}^{+}$ an amplitude singularity emerges in the position distribution while the horizon at x = 0 separates vanishing from non-vanishing parts. d At later times $t \, > \, {t}_{{{{{{{{\rm{c}}}}}}}}}^{+}$ the singularity disappears, and the position distribution extends again over the complete x-axis.

This particular dynamic gives rise to four disjunct regions in phase space, which are separated by the lines p = mωx and p = −mωx, as depicted in Fig. 1a (top). Here we have introduced the position x and the momentum p of the particle, while m and ω denote its mass and the steepness of the parabolic potential, respectively. The line p = mωx separates particles coming from the left from particles coming from the right, and thus corresponds to a horizon in phase space.

However, the line p = −mωx also represents a horizon in phase space. This fact stands out most clearly in Fig. 1(b), where we present the corresponding quantum picture¹⁷ of the energy eigenfunction

$${\phi }_{\varepsilon }^{+}(x)\equiv {{{{{{{{\mathcal{N}}}}}}}}}_{+}(\varepsilon ){D}_{-1/2-{{{{{{{\rm{i}}}}}}}}\varepsilon }\left(2{{{{{{{{\rm{e}}}}}}}}}^{-{{{{{{{\rm{i}}}}}}}}3\pi /4}\kappa x\right)$$

(1)

of the inverted harmonic oscillator with a positive energy eigenvalue ε, by depicting the corresponding Wigner function^19,22${W}_{\phi ,\varepsilon }^{+}={W}_{\phi ,\varepsilon }^{+}(x,p)$. Here ${{{{{{{{\mathcal{N}}}}}}}}}_{+}$ and D_ν denote the normalization constant and the parabolic cylinder function²³. Moreover, the scaling parameter κ ensures that the argument of D_ν is dimensionless. For more details, we refer to the Methods section.

The Wigner function ${W}_{\phi ,\varepsilon }^{+}$ vanishes in a half-plane of phase space separated by the horizon p = −mωx, is constant along all classical trajectories in the other half-plane and, in particular, along the horizon, while displaying a dominant positive maximum (red domain) in the neighborhood of the trajectory corresponding to the eigenvalue ε. It oscillates between positive and negative values for trajectories (yellow and blue hyperbolic bands) determined by energies larger than the eigenvalue, but decays with oscillations for trajectories (light blue and yellow domains) governed by negative energies reaching into the classically non-accessible quadrant. At the bottom, we display the probabilities in the position variable x obtained by integration of the Wigner function over the momentum p at a given coordinate.

We emphasize that the energy eigenfunction ${\phi }_{\varepsilon }^{+}={\phi }_{\varepsilon }^{+}(x)$ in position representation defined by Eq. (1) does not give any indication of a singular behavior. However, as shown in the Methods section, a logarithmic phase singularity and an amplitude singularity manifest¹⁹ themselves in a specific representation of the corresponding state.

To uncover these features, we now make use of the free time evolution²⁴, which translates to a sheering in phase space as shown in the transition from Fig. 1b–d. The situation in Fig. 1c depicts the moment ${t}_{c}^{+}\equiv 1/\omega$ in time, where the Wigner function is constrained to the right side of x = 0. In this case, the position density is restricted to positive values of x only, with an inverse square-root amplitude and a logarithmic phase singularity as expressed by the wave function

$${\phi }_{\varepsilon }^{+}\left(x,{t}_{{{{{{{{\rm{c}}}}}}}}}^{+}\right)={\left(2\pi | x| \right)}^{-1/2}{{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}\varepsilon \log \left\vert \kappa x\right\vert +{{{{{{{\rm{i}}}}}}}}\varphi }\Theta \left(\kappa x\right)\,,$$

(2)

where φ is a phase and Θ denotes the Heaviside step function.

The square-root amplitude singularity in this probability amplitude is a consequence of integrating the constant Wigner function at x = 0 over the momentum. For more details, we refer to the Methods section. At a later time, shown in Fig. 1d, the probability density returns to the domain x < 0, and covers again the complete coordinate axis.

Next, we recall that the Bose–Einstein statistics of the Hawking radiation is a consequence^8,19 of the Fourier transform of the logarithmic phase singularity. In order to obtain its analog for the inverted harmonic oscillator, we could make use of the backward propagation of the wave function ${\phi }_{\varepsilon }^{+}(x)$ until the critical time ${t}_{c}^{-}=-1/\omega$. Instead, we consider here the forward propagation of the energy eigenfunction ${\psi }_{\varepsilon }^{+}(x)\equiv {\left[{\phi }_{\varepsilon }^{+}(x)\right]}^{* }$ determined by the complex conjugate of Eq. (1), which also allows us to extract the analog distribution for the inverted harmonic oscillator. Here the vanishing and non-vanishing parts of the corresponding Wigner function are separated by the horizon p = mωx in phase space.

As demonstrated in the Methods section, when we propagate the wave function ${\psi }_{\varepsilon }^{+}={\psi }_{\varepsilon }^{+}(x)$ up to the critical time ${t}_{c}^{+}$, we obtain the Fermi–Dirac distribution²⁵$F(\varepsilon )\equiv {[1+\exp (2\pi \varepsilon )]}^{-1}$ determining the transmission and reflection coefficients T(ε) = F(−ε) and R(ε) = F(ε) of the inverted harmonic oscillator from the expression

$${\left\vert {\psi }_{\varepsilon }^{+}(x,{t}_{{{{{{{{\rm{c}}}}}}}}}^{+})\right\vert }^{2}={(2\pi | x| )}^{-1}\left[R(\varepsilon )\Theta \left(\kappa x\right)+T(\varepsilon )\Theta \left(-\kappa x\right)\right]\,.$$

(3)

For a given energy ε, the steepness of the position distribution associated with the simple pole at x = 0 determines R and T, and thus F. Indeed, positive x-values yield R(ε) while negative ones lead to T(ε). We find the dependence of R and T, and thus of F on ε, by propagating wave functions corresponding to different energies.

Experimental observation with surface gravity water waves

In order to observe the predicted phenomena¹⁹ of a logarithmic phase singularity and a Fermi–Dirac distribution in the reflection and transmission coefficients of the inverted harmonic oscillator, we take advantage of the concept of analog experiments^14,26,27 and utilize the analogy between the propagation of quantum-mechanical waves and surface gravity water waves^20,21,28. In the co-moving frame with group velocity c_g, the water waves are governed by a wave equation that corresponds to the Schrödinger equation, where time and space are interchanged. This analogy enables us to transfer the wave properties of the quantum-mechanical problem to purely classical waves²⁹. Moreover, in contrast to a quantum system, we can measure simultaneously their amplitude and phase²⁰. For a more detailed discussion of the quantum analogy of surface gravity water waves, we refer to ref. ²¹ and the Methods section.

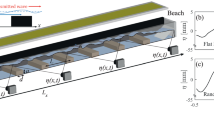
Figure 2 shows a schematic illustration of our experimental setup. A wave maker at one end of the water tank, which is 5 m long, 0.4 m wide, and 0.19 m deep, creates the initial wave packet that propagates along the water tank. Four capacitance type of wave gauges record the surface elevation, which corresponds to the complex envelope $A\equiv | A| \exp ({{{{{{{\rm{i}}}}}}}}{\varphi }_{A})$. Hence, the imaginary part of A follows²⁹ from the Hilbert transform³⁰ of the real-valued elevation, see Methods section for more details.

Fig. 2: Experimental setup for generating wave packets of surface gravity water waves and measuring their propagation dynamics in both amplitude and phase.

Illustration of a laboratory water wave tank measuring 5 m in length, 0.4 m in width, and 0.19 m in depth. The tank is constructed with a transparent glass sidewall and base, enclosed in an aluminum frame, and mounted on eight shock-absorbing legs for stability. A computer-controlled wave maker at one end generates water waves, while a wave energy absorbing beach at the opposite end minimizes residual reflections. Wave dynamics within the tank can be observed from all angles due to the tank’s transparency. The instantaneous elevation of the water surface is monitored by four-wave gauges mounted on a movable bar, facilitating precise wave field analysis.

In our experiments, we modulate the envelope of the surface gravity water wave to achieve the desired wave packet by the real function $h(t,x=0)\equiv {a}_{0}| A(t)| \cos ({\Omega }_{0}t+{\varphi }_{A})$, where a₀ is the amplitude of the carrier wave with frequency Ω₀. In the Methods section, we present a comprehensive discussion on the generation of the truncated state A = A(t). Within this context, we have already made the necessary interchange between time t and position x, in accordance with the requirements of the water wave equation.

We measured the time-dependent elevations of the wave at different positions in the tank and stored them in a computer. The data recorded at the end of the canal was sent to the wave maker for a new excitation based on the previous measurement³¹. This process was repeated 4 times, enabling to achieve an effective propagation distance of 11 m in a 5 m long water tank.

In Fig. 3a, b, we compare and contrast the numerical simulation and the experimental results for the envelope of this free propagation. We prepare a surface gravity water wave corresponding to the wave packet, Eq. (1), with ε = 0.25 at x = 0. The free propagation of this wave packet leads to focusing at x = 10.4 m (red spot), indicating the amplitude singularity. From the raw data of the wave packets exemplified by (i) and (ii) and measured at the two positions indicated in (d) by arrows, we reconstruct the amplitude (c) and the phase (d) of the wave packet along the horizontal axis t = x/c_g. Here, dots represent experimentally obtained values and the blue lines are numerical solutions of the truncated initial envelope with the same temporal truncation length as used in the experiments. The red curves represent analytical expressions outlined in the Methods section.

Fig. 3: Experimental observation of a horizon in phase space giving rise to amplitude and logarithmic phase singularities in surface gravity water waves.

The free propagation of the energy eigenfunction of the inverted harmonic oscillator determined by Eq. (1) with ε = 0.25 displays in the simulation (a) as well as in the experiment (b) a singularity at t = x/c_g and x = 10.4 m, indicated by the orange arrows. Bright and dark colors represent large and small values of the elevation, as indicated by the color bars on the right side. Our analysis is based on the raw data exemplified in (i) and (ii), yielding the amplitude (c) and the phase (d) of the water wave along the horizontal axis at t = x/c_g. The experimental data (white dots), together with simulations (blue) and analytical predictions (red) given by Eq. (2), show both an amplitude and a logarithmic phase singularity at x = 10.4 m. In e, f, we display the transverse amplitude and phase at x = 10.4 m and compare the observation (black), simulation (blue), and analytical predictions (red). The horizon at t = x/c_g separates a vanishing amplitude (t < x/c_g) from non-vanishing contributions (t > x/c_g), which also display an amplitude and a logarithmic phase singularity.

These results bring out most clearly the square-root singularity in the amplitude as well as the onset of logarithmic phase singularity. They not only manifest themselves along the spatial axis but also in the orthogonal direction, as shown in Fig. 3e, f, where the black curves represent the experimental values of amplitude and phase while the blue and red curves correspond to the simulation and analytical expressions, respectively. However, we note that in a truncated system, the expected growth does not exhibit full divergence. Rather, the amplitude peak tends to exhibit a smoother or flattened profile. Moreover, the phase singularity in such a system is influenced by truncation. In the context of an infinite wave packet, one would anticipate the logarithmic phase singularity to manifest as a clear divergence. However, the inherent finiteness of a truncated wave packet restricts this manifestation. Further details and methodologies associated with this observation can be found in the Methods section.

Our system also allows us to deduce the dependence of the reflection and transmission coefficients³² on the energy reminiscent of the Fermi–Dirac distribution²⁵ F displayed in Fig. 4. For this purpose, we prepare the complex conjugate of the wave function defined by Eq. (1), and consider the propagation along the canal up to the position x = 10.4 m where the singularity emerges, and measure the transverse distribution of the amplitude envelope. For a fixed energy ε, we observe the amplitudes exemplified in Fig. 4a, c for the energies ε = −0.4 and ε = 0.4. This procedure applied to different energies yields the experimental values (open circles) in Fig. 4b which agree well with the theoretical prediction (solid lines) of the Fermi–Dirac distribution.

Fig. 4: Experimental observation of the Fermi-Dirac distribution with surface gravity water waves.

The free propagation of the energy eigenfunction of the inverted harmonic oscillator, determined by the complex conjugate of Eq. (1), results in an amplitude singularity at x = 10.4 m and t = x/c_g. In a we display the amplitude singularity for an initial wave packet below the parabolic barrier (ε = −0.4). We present the observation (black) together with the simulation (blue) and the analytical prediction (red). The transmission and reflection coefficients T(ε) and R(ε) are extracted following Eq. (3) from the measured amplitude at x = 10.4 m by fits along the transverse coordinate for t < x/c_g and t > x/c_g, respectively. b We recover the dependence of T (green) and R (orange) on ε by varying the energy of the initial wave packet. Here the open circles represent the experimentally obtained values in comparison to the analytical expressions (solid lines), given by R(ε) = F(ε) and T(ε) = F(−ε) where $F(\varepsilon )\equiv {[1+\exp (2\pi \varepsilon )]}^{-1}$ represents the Fermi–Dirac distribution. c For an initial wave packet above the parabolic barrier (ε = 0.4), we observe a mirror image of a at t = x/c_g for the analytical prediction (red) and numerical simulation (blue) leading to the symmetry of the transmission T and reflection coefficient R with respect to the energy eigenvalue ε = 0.

Conclusions

In our article we have employed the similarity of the wave equations for quantum and surface gravity water waves to bring out the essence of Hawking radiation. Indeed, in our experiment, we observe the fingerprint of the logarithmic phase singularity emerging analogously at the event horizon of a black hole. For this purpose, we take advantage of the phase space horizons of the inverted harmonic oscillator. Here the logarithmic phase singularity manifests itself in the corresponding energy eigenfunctions and appears in phase space variables, that are not easily accessible. We emphasize that the observation of this effect does not require the presence of a potential barrier, but instead a free propagation of appropriately tailored initial wave packets. Although we are only able to prepare truncated wave packets our experimental results allow a clear identification of amplitude and phase singularities as appearing in an ideal system.

We point out that a square-root amplitude singularity is absent in the mode functions of the light field around the black hole. For this reason, we have observed a Fermi–Dirac rather than a Bose–Einstein distribution governing the transmission and reflection coefficients of the inverted harmonic oscillator.

These insights open pathways to another branch of experiments in black hole analogs that will propel our understanding of Hawking radiation. At the same time, many open questions emerge, and it suffices to mention only three: What would be an analog experiment to simulate the particle creation³ in the ergosphere of a rotating black hole? Is there a deeper connection between the singularities and spin? Could black hole physics open a window toward the spin-statistics theorem^33,34?

Methods

In this section we briefly summarize elements of the quantum description¹⁹ of the inverted harmonic oscillator crucial for our article, and review key properties of surface gravity water waves²⁰. In addition, we provide an extensive overview of the experimental techniques which were used to perform the experiments.

We start by re-deriving the amplitude and the logarithmic phase singularities in the energy wave functions of the inverted harmonic oscillator expressed in rotated phase space variables. Then, we recall the corresponding Wigner functions as well as the reflection and transmission coefficients. Moreover, we demonstrate that the singularities manifest themselves in space and time during the free propagation of these wave functions. We also address the limitations observed in truncated Weber wave packets.

We then turn to the discussion of the experimental details. In particular, we introduce the Schrödinger-like wave equation for surface gravity water waves and outline the conditions under which it is valid. Subsequently, we delve into the methods of extracting phase and amplitude data using the Hilbert transform, and present the primary features of our experimental setup, such as the water tank, the computer-controlled wave maker, and the use of capacitance-type wave gauges. The section concludes with a summary of the experimental protocol to generate and observe truncated Weber wave packets and their properties.

Energy wave functions

The quantum inverted harmonic oscillator of mass m and steepness ω is described by the Hamiltonian

$$\hat{H}\equiv \frac{{\hat{p}}^{2}}{2m}-\frac{1}{2}m{\omega }^{2}{\hat{x}}^{2}$$

(4)

where the position operator $\hat{x}$ and the momentum operator $\hat{p}$ satisfy the familiar commutation relation $[\hat{x},\hat{p}]=i\hslash$.

Next, we introduce the dimensionless operators

$$\hat{\xi }\equiv \sqrt{\frac{m\omega }{2\hslash }}\left(\hat{x}-\frac{\hat{p}}{m\omega }\right)$$

(5)

and

$$\hat{\eta }\equiv \sqrt{\frac{m\omega }{2\hslash }}\left(\hat{x}+\frac{\hat{p}}{m\omega }\right),$$

(6)

satisfying the commutation relation $[\hat{\xi },\hat{\eta }]={{{{{{{\rm{i}}}}}}}}$.

The operators $\hat{\xi }$ and $\hat{\eta }$ are intimately related to the familiar annihilation and creation operators $\hat{a}$ and ${\hat{a}}^{{{{\dagger}}} }$ of the standard harmonic oscillator by the transformation ω → iω and an overall phase factor. Hence, $\hat{\xi }$ and $\hat{\eta }$ are Hermitian operators whereas $\hat{a}$ and ${\hat{a}}^{{{{\dagger}}} }$ are non-Hermitian ones.

In terms of $\hat{\xi }$ and $\hat{\eta }$, the Hamiltonian given by Eq. (4) takes the symmetric form

$$\hat{H}=-\frac{\hslash \omega }{2}\left(\hat{\xi }\hat{\eta }+\hat{\eta }\hat{\xi }\right).$$

(7)

Subsequently, the familiar eigenvalue equation

$$\hat{H}\left\vert \varepsilon \right\rangle =\hslash \omega \varepsilon \left\vert \varepsilon \right\rangle$$

(8)

determines the energy eigenstates $\left\vert \varepsilon \right\rangle$ corresponding to the dimensionless energy eigenvalue ε.

According to Eq. (7), the projection Φ_ε(η) ≡ 〈η∣ε〉 of the energy eigenstate $\left\vert \varepsilon \right\rangle$ onto the eigenstates $\left\vert \eta \right\rangle$ of the operator $\hat{\eta }$, Eq. (6), allows us to express the eigenvalue equation, Eq. (8), as the differential equation¹⁹

$$\eta \frac{{{{{{{{\rm{d}}}}}}}}}{{{{{{{{\rm{d}}}}}}}}\eta }{\Phi }_{\varepsilon }(\eta )=\left(-\frac{1}{2}+{{{{{{{\rm{i}}}}}}}}\varepsilon \right){\Phi }_{\varepsilon }(\eta )$$

(9)

which is solved by the two orthogonal functions

$${\Phi }_{\varepsilon }^{\pm }(\eta )\equiv \frac{1}{\sqrt{2\pi }}{\left\vert \eta \right\vert }^{-\frac{1}{2}}{{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}\varepsilon \log \left\vert \eta \right\vert }\Theta (\pm \eta ),$$

(10)

where Θ denotes the Heaviside step function.

Analogously, the ξ-representation Ψ_ε(ξ) ≡ 〈ξ∣ε〉 of an energy eigenstate $\left\vert \varepsilon \right\rangle$ with regard to an eigenstate $\left\vert \xi \right\rangle$ of the operator $\hat{\xi }$ given by Eq. (5) is determined by the differential equation

$$\xi \frac{{{{{{{{\rm{d}}}}}}}}}{{{{{{{{\rm{d}}}}}}}}\xi }{\Psi }_{\varepsilon }(\xi )\equiv \left(-\frac{1}{2}-{{{{{{{\rm{i}}}}}}}}\varepsilon \right){\Psi }_{\varepsilon }(\xi )$$

(11)

which yields the set of orthogonal solutions

$${\Psi }_{\varepsilon }^{\pm }(\xi )=\frac{1}{\sqrt{2\pi }}{\left\vert \xi \right\vert }^{-\frac{1}{2}}{{{{{{{{\rm{e}}}}}}}}}^{-{{{{{{{\rm{i}}}}}}}}\varepsilon \log \left\vert \xi \right\vert }\Theta (\pm \xi ).$$

(12)

Expressed in the rotated phase space coordinates η and ξ, the horizons inherent in the stationary states of the inverted harmonic oscillator stand out most clearly. In fact, both sets of linearly independent solutions ${\Phi }_{\varepsilon }^{\pm }$ and ${\Psi }_{\varepsilon }^{\pm }$ in η- and ξ-representation, respectively, have a similar functional dependence, differing only by the sign in front of ε. These energy eigenfunctions display a square-root amplitude singularity which is a consequence of the canonical commutation relation, and a logarithmic phase singularity at the horizons in phase space at η = 0 and ξ = 0, respectively, expressed by the Heaviside step function Θ.

We note that in ξ-representation each energy eigenstate $\left\vert \varepsilon \right\rangle$ can be expressed as a superposition of the eigenfunctions ${\Psi }_{\varepsilon }^{+}$ and ${\Psi }_{\varepsilon }^{-}$. Analogously, in η-representation $\left\vert \varepsilon \right\rangle$ can be decomposed into a superposition of the eigenfunctions ${\Phi }_{\varepsilon }^{+}$ and ${\Phi }_{\varepsilon }^{-}$. Moreover, we emphasize that the horizon and the logarithmic phase singularity in the energy eigenfunctions only become apparent in the coordinates ξ and η.

In fact, in position representation, the energy eigenfunctions

$${\phi }_{\varepsilon }^{\pm }(x)\equiv {{{{{{{{\mathcal{N}}}}}}}}}_{+}(\varepsilon ){D}_{-1/2-{{{{{{{\rm{i}}}}}}}}\varepsilon }\left(\pm 2{{{{{{{{\rm{e}}}}}}}}}^{-{{{{{{{\rm{i}}}}}}}}3\pi /4}\kappa x\right)$$

(13)

and

$${\psi }_{\varepsilon }^{\pm }(x)\equiv {{{{{{{{\mathcal{N}}}}}}}}}_{-}(\varepsilon ){D}_{-1/2+{{{{{{{\rm{i}}}}}}}}\varepsilon }\left(\pm 2{{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}3\pi /4}\kappa x\right)$$

(14)

corresponding to Eqs. (10) and (12), respectively, do not display a logarithmic phase singularity nor a horizon. Instead, these functions are governed by a parabolic cylinder function²³ D_ν(z) and a normalization factor

$${{{{{{{{\mathcal{N}}}}}}}}}_{\pm }(\varepsilon )\equiv \frac{\Gamma \left(\frac{1}{2}\pm {{{{{{{\rm{i}}}}}}}}\varepsilon \right)}{\sqrt{2}\pi }{\kappa }^{1/2}{{{{{{{{\rm{e}}}}}}}}}^{\varepsilon \pi /4}\,.$$

(15)

Here, we have introduced the scaling factor

$$\kappa \equiv \sqrt{\frac{m\omega }{2\hslash }}\,.$$

(16)

Finally, we point out that the horizons in the inverted harmonic oscillator become evident in a phase space representation. Indeed, in complete analogy to the energy eigenfunctions ${\Psi }_{\varepsilon }^{\pm }$ and ${\Phi }_{\varepsilon }^{\pm }$, the Wigner functions^17,22

$${W}_{\Phi ,\varepsilon }^{\pm }(\xi ,\eta )=\frac{1}{2\pi }{w}_{\varepsilon }(\xi \eta )\,\Theta (\pm \eta )$$

(17)

and

$${W}_{\Psi ,\varepsilon }^{\pm }(\xi ,\eta )=\frac{1}{2\pi }{w}_{\varepsilon }(\xi \eta )\,\Theta (\pm \xi )$$

(18)

with the weight function¹⁹

$${w}_{\varepsilon }(h)=\frac{1}{\pi }\int\nolimits_{-1}^{1}{{{{{{{\rm{d}}}}}}}}y\,\frac{\exp \left(-{{{{{{{\rm{i}}}}}}}}\varepsilon \log \left\vert \frac{1+y}{1-y}\right\vert \right)}{\sqrt{1-{y}^{2}}}{{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}2hy}$$

(19)

display a horizon in phase space. Consequently, the Wigner function ${W}_{\Phi ,\varepsilon }^{+}$ corresponding to the wave function ${\Phi }_{\varepsilon }^{+}$, Eq. (10), vanishes on the half plane η < 0, while it depends only on the product ξη in the other half plane η > 0. Analogously, the Wigner function ${W}_{\Psi ,\varepsilon }^{+}$ corresponding to the wave function ${\Psi }_{\varepsilon }^{+}$, Eq. (12), vanishes on the half plane ξ < 0, while it depends only on the product ξη in the other half-plane ξ > 0.

Moreover, by making use of the c-number relations for ξ and η corresponding to Eqs. (5) and (6), we are able to obtain the Wigner functions

$${W}_{\phi ,\varepsilon }^{\pm }(x,p)\equiv {W}_{\Phi ,\varepsilon }^{\pm }\left[\sqrt{\frac{m\omega }{2\hslash }}\left(x-\frac{p}{m\omega }\right),\sqrt{\frac{m\omega }{2\hslash }}\left(x+\frac{p}{m\omega }\right)\right]$$

(20)

and

$${W}_{\psi ,\varepsilon }^{\pm }(x,p)\equiv {W}_{\Psi ,\varepsilon }^{\pm }\left[\sqrt{\frac{m\omega }{2\hslash }}\left(x-\frac{p}{m\omega }\right),\sqrt{\frac{m\omega }{2\hslash }}\left(x+\frac{p}{m\omega }\right)\right]$$

(21)

in terms of the position x and the momentum p.

Free propagation

Next, we consider the free propagation of an arbitrary energy eigenfunction

$${\varphi }_{\varepsilon }(x)\equiv {c}_{+}{\phi }_{\varepsilon }^{+}(x)+{c}_{-}{\phi }_{\varepsilon }^{-}(x)$$

(22)

of the inverted harmonic oscillator, expressed as a superposition of the orthogonal energy eigenfunctions ${\phi }_{\varepsilon }^{\pm }$, Eq. (13), with complex coefficients c_± that satisfy the normalization condition ∣c₊∣² + ∣c₋∣² = 1. Consequently, the time-evolved wave function φ = φ(x, t) is obtained as solution of the Schrödinger equation

$${{{{{{{\rm{i}}}}}}}}\hslash \frac{\partial }{\partial t}\varphi (x,t)=-\frac{{\hslash }^{2}}{2m}\frac{{\partial }^{2}}{\partial {x}^{2}}\varphi (x,t)$$

(23)

with the initial condition φ(x, 0) ≡ φ_ε(x).

In the following we demonstrate that the function φ(x, t) reveals an amplitude as well as a phase singularity at the times ${t}_{c}^{\pm }\equiv \pm 1/\omega$.

Indeed, the solution of Eq. (23) given by the Fresnel transform

$$\varphi (x,t)=\sqrt{\frac{m}{2\pi {{{{{{{\rm{i}}}}}}}}\hslash t}}\int\,{{{{{{{\rm{d}}}}}}}}{x}_{{{{{{{{\rm{i}}}}}}}}}\,\exp \left[\frac{{{{{{{{\rm{i}}}}}}}}m}{2\hslash t}{\left(x-{x}_{{{{{{{{\rm{i}}}}}}}}}\right)}^{2}\right]{\varphi }_{\varepsilon }\left({x}_{{{{{{{{\rm{i}}}}}}}}}\right)$$

(24)

takes the explicit form

$$ \varphi (x,t)= \\ {\left| 1-{(\omega t)}^{2}\right | }^{-\frac{1}{4}}\exp \left(-\frac{{{{{{{{\rm{i}}}}}}}}\varepsilon }{2}\log \left| \frac{1+\omega t}{1-\omega t}\right | -\frac{{{{{{{{\rm{i}}}}}}}}m}{2\hslash t}\frac{{(\omega t)}^{2}}{1-{(\omega t)}^{2}}{x}^{2}\right){\varphi }_{\varepsilon }\left(\frac{x}{\sqrt{\left\vert 1-{(\omega t)}^{2}\right\vert }}\right)$$

(25)

for ${t}_{{{{{{{{\rm{c}}}}}}}}}^{-} \, < \, t \, < \, {t}_{{{{{{{{\rm{c}}}}}}}}}^{+}$, being valid for any energy eigenfunction φ_ε.

For $t \, > \, {t}_{c}^{+}$ we instead obtain the expression

$$ \varphi (x,t)= \\ {\left| 1-{(\omega t)}^{2}\right| }^{-\frac{1}{4}}\exp \left(-\frac{\pi \varepsilon }{2}-\frac{{{{{{{{\rm{i}}}}}}}}\pi }{4}-\frac{{{{{{{{\rm{i}}}}}}}}\varepsilon }{2}\log \left| \frac{1+\omega t}{1-\omega t}\right| -\frac{{{{{{{{\rm{i}}}}}}}}m}{2\hslash t}\frac{{(\omega t)}^{2}}{1-{(\omega t)}^{2}}{x}^{2}\right){\varphi }_{\varepsilon }\left(\frac{-{{{{{{{\rm{i}}}}}}}}x}{\sqrt{\left| 1-{(\omega t)}^{2}\right| }}\right)$$

(26)

which holds again for any energy eigenfunction φ_ε. We point out that Eq. (25) is reminiscent of the one obtained²⁴ for the free time evolution of a symmetric energy eigenfunction of the standard harmonic oscillator.

In addition, at the center x = 0, the wave packet

$$ \varphi (0,t)= \\ {\left| 1-{(\omega t)}^{2}\right| }^{-\frac{1}{4}}\exp \left(-\frac{{{{{{{{\rm{i}}}}}}}}\varepsilon }{2}\log \left| \frac{1+\omega t}{1-\omega t}\right| \right){\varphi }_{\varepsilon }(0)\left\{\begin{array}{ll}1\hfill\quad &\,{{\mbox{for}}}\,-{t}_{{{{{{{{\rm{c}}}}}}}}}^{-} < t < {t}_{{{{{{{{\rm{c}}}}}}}}}^{+}\\ \exp \left(-\frac{\pi \varepsilon }{2}-\frac{{{{{{{{\rm{i}}}}}}}}\pi }{4}\right) &\,{{\mbox{for}}}\,\hfill t > {t}_{{{{{{{{\rm{c}}}}}}}}}^{+},\hfill\end{array}\right.$$

(27)

displays both an amplitude and a phase singularity at time $t={t}_{{{{{{{{\rm{c}}}}}}}}}^{\pm }$.

So far, we have only studied the behavior of the wave function φ(x, t) for ${t}_{c}^{-} \, < \, t \, < \, {t}_{c}^{+}$ and $t \, > \, {t}_{c}^{+}$, that is, before and after the emergence of the singularity. In order to examine the wave function in the limit $t\to {t}_{{{{{{{{\rm{c}}}}}}}}}^{\pm }$, we now analyze different options for the initial energy eigenfunction φ_ε at t = 0. Indeed, we demonstrate that (i) for ${\varphi }_{\varepsilon }={\phi }_{\varepsilon }^{+}$, Eq. (13), a horizon and the logarithmic phase singularity is revealed at $t={t}_{c}^{+}$, while (ii) for ${\varphi }_{\varepsilon }={\psi }_{\varepsilon }^{+}$, Eq. (14), we are able to extract the transmission and reflection coefficients of the inverted harmonic oscillator at time $t={t}_{c}^{+}$, which are reminiscent of the Fermi–Dirac distribution.

The horizon and the logarithmic phase singularity

In order to transfer the horizon and the logarithmic phase singularity of the inverted harmonic oscillator hidden in the variables η and ξ to the position coordinate, we consider the free time evolution of a particular energy eigenstate $\left\vert \varepsilon \right\rangle$, whose η-representation ${\Phi }_{\varepsilon }^{+}(\eta )$ is given by Eq. (10). For this purpose, we prepare at t = 0 the energy eigenfunction

$${\phi }_{\varepsilon }^{+}(x)\equiv {{{{{{{{\mathcal{N}}}}}}}}}_{+}(\varepsilon ){D}_{-1/2-{{{{{{{\rm{i}}}}}}}}\varepsilon }\left(2{{{{{{{{\rm{e}}}}}}}}}^{-{{{{{{{\rm{i}}}}}}}}3\pi /4}\kappa x\right)$$

(28)

defined by Eq. (13), where the normalization constant ${{{{{{{{\mathcal{N}}}}}}}}}_{+}(\varepsilon )$ is given by Eq. (15).

In the limit $t\to {t}_{{{{{{{{\rm{c}}}}}}}}}^{+}$, we obtain according to Eqs. (25) and (26) the probability amplitude

$${\phi }_{\varepsilon }^{+}\left(x,{t}_{{{{{{{{\rm{c}}}}}}}}}^{+}\right)=\frac{{{{{{{{{\rm{e}}}}}}}}}^{-{{{{{{{\rm{i}}}}}}}}\pi /8}}{\sqrt{2\pi | x| }}{{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}{(\kappa x)}^{2}/2+{{{{{{{\rm{i}}}}}}}}\varepsilon \log \left\vert \kappa x\right\vert }\Theta \left(\kappa x\right)$$

(29)

and consequently, the probability density

$${\left| {\phi }_{\varepsilon }^{+}\left(x,{t}_{{{{{{{{\rm{c}}}}}}}}}^{+}\right)\right| }^{2}=\frac{1}{2\pi | x| }\Theta \left(\kappa x\right).$$

(30)

Indeed, at the time $t={t}_{{{{{{{{\rm{c}}}}}}}}}^{+}$ we are able to observe the logarithmic phase singularity as well as the horizon of the energy wave function ${\Phi }_{\varepsilon }^{+}$, Eq. (10), in the position variable x. Moreover, apart from a phase quadratic in x, the overall form of the propagated wave function given by Eq. (29) is reminiscent of the initial wave function ${\Phi }_{\varepsilon }^{+}$ in the η-coordinate given by Eq. (10).

We emphasize that a similar treatment for ${\Psi }_{\varepsilon }^{\pm }$ reveals a logarithmic phase singularity and a horizon in the position coordinate at $t={t}_{{{{{{{{\rm{c}}}}}}}}}^{-}$, which is obtained by a free time evolution backward in time.

Influence of truncation parameter

We emphasize that in an idealized scenario, the infinite extension of the energy eigenfunctions of the inverted harmonic oscillator employed as an initial wave packet leads to singularities in both amplitude and phase during free propagation. However, in a realistic experimental setup, an infinite wave packet is unattainable and thus must be truncated. For the sake of simplicity, we employ for the truncation a rectangular window of width 2γ leading us to the initial wave function

$${\phi }_{\varepsilon }^{+}(x;\gamma )\equiv \Theta (\gamma -\kappa | x| ){\phi }_{\varepsilon }^{+}(x)$$

(31)

prepared at time t = 0.

This truncation has consequences for the singularity appearing at time $t={t}_{c}^{+}$ in the free propagation ${\phi }_{\varepsilon }^{+}(x,t;\gamma )$ of the initial wave function ${\phi }_{\varepsilon }^{+}(x;\gamma )$ as shown in Fig. 5. The truncation of the wave packet imposes finite boundaries, which inherently limits the growth of the wave amplitude. In a theoretical infinite wave packet, the amplitude could grow without bound, leading to a singularity. When truncated, this growth is stymied, and instead of a true divergence, a smoothing or flattening of the amplitude peak may be observed. In order to bring this out most clearly, we show again in Fig. 6a the influence of the truncation parameter on the amplitude at $t={t}_{c}^{+}$ for the chosen parameters.

Fig. 5: Influence of the truncation of the initial wave packet ${\phi }_{\varepsilon }^{+}(x;\gamma )$ on the amplitude for three values of the truncation parameter γ.

For finite values of γ, that is, a truncated initial Weber wave packet, illustrated here for a γ = 5 and b γ = 10, the singularity at x = 0 is smoothed out. Only for γ = ∞ in c we obtain a divergence at $t={t}_{c}^{+}$ and x = 0, indicating the amplitude singularity.

Fig. 6: Influence of the truncation of the initial wave function on the amplitude and phase singularity.

At time $t={t}_{c}^{+}$, we display the a amplitude $| {\phi }_{\varepsilon }^{+}(x,t={t}_{c}^{+};\gamma ){| }^{2}$ and b phase ${\vartheta }_{\epsilon }^{+}(x,t={t}_{c}^{+};\gamma )$ of the propagated wave packet with truncation parameter γ as a function of the position x. For γ = ∞ (red), we obtain the ideal case displaying both singularities. For the truncation parameters γ = 5 (blue) and γ = 10 (black) the singularities are blurred and the respective values become finite.

A similar behavior is observed for the phase singularity as indicated by Fig. 6b. In an infinite wave packet, the logarithmic phase singularity would manifest itself as a divergence, but the finite nature of a truncated wave packet constrains this behavior. The result is a tempered, less pronounced phase shift, which still follows a logarithmic trend but without exhibiting a clear singularity.

Fermi–Dirac distribution

Next, we show that the free time evolution not only reveals the inherent horizon and logarithmic phase singularity of the inverted harmonic oscillator, but also the characteristic transmission and reflection coefficients of the parabolic barrier. For this purpose, we make use of the energy wave functions ${\Psi }_{\varepsilon }^{\pm }$, Eq. (12), which display a logarithmic phase singularity and a horizon in the ξ-representation.

According to Eq. (14), we thus prepare at time t = 0 the initial wave function

$${\psi }_{\varepsilon }^{+}(x)\equiv {{{{{{{{\mathcal{N}}}}}}}}}_{-}(\varepsilon ){D}_{-1/2+{{{{{{{\rm{i}}}}}}}}\varepsilon }\left(2{{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}3\pi /4}\kappa x\right)\,,$$

(32)

where the normalization factor ${{{{{{{{\mathcal{N}}}}}}}}}_{-}(\varepsilon )$ is given by Eq. (15).

At time $t={t}_{{{{{{{{\rm{c}}}}}}}}}^{+}$, the time-evolved wave function

$${\psi }_{\varepsilon }^{+}(x,{t}_{{{{{{{{\rm{c}}}}}}}}}^{+})={S}_{+}(\varepsilon ){\Delta }_{\varepsilon }^{+}(x)+{S}_{-}(\varepsilon ){\Delta }_{\varepsilon }^{-}(x)$$

(33)

is governed by the position-dependent functions

$${\Delta }_{\varepsilon }^{\pm }(x)\equiv \frac{{\kappa }^{1/2}}{\sqrt{2\pi }}{{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}{(\kappa x)}^{2}/2-{{{{{{{\rm{i}}}}}}}}\pi /8}{\left\vert \kappa x\right\vert }^{-1/2+{{{{{{{\rm{i}}}}}}}}\varepsilon }\Theta \left(\pm \kappa x\right)$$

(34)

with energy-dependent coefficients

$${S}_{\pm }(\varepsilon )\equiv \frac{\Gamma \left(\frac{1}{2}-{{{{{{{\rm{i}}}}}}}}\varepsilon \right)}{\sqrt{2\pi }}\exp \left[\mp \left(\frac{\varepsilon \pi }{2}+\frac{{{{{{{{\rm{i}}}}}}}}\pi }{4}\right)\right]\,.$$

(35)

Consequently, the function ${\psi }_{\varepsilon }^{+}(x,{t}_{{{{{{{{\rm{c}}}}}}}}}^{+})$ consists of two distinct contributions in the domains x < 0 (−) and x > 0 (+), which are separated by a singularity at x = 0.

In terms of the probability density

$${\left| {\psi }_{\varepsilon }^{+}(x,{t}_{{{{{{{{\rm{c}}}}}}}}}^{+})\right| }^{2}=\frac{1}{2\pi | x| }\left[\frac{\Theta \left(\kappa x\right)}{1+{{{{{{{{\rm{e}}}}}}}}}^{2\pi \varepsilon }}+\frac{\Theta \left(-\kappa x\right)}{1+{{{{{{{{\rm{e}}}}}}}}}^{-2\pi \varepsilon }}\right],$$

(36)

the respective regions in position are associated with either the transmission coefficient

$$| {S}_{-}(\varepsilon ){| }^{2}=\frac{1}{1+{{{{{{{{\rm{e}}}}}}}}}^{-2\pi \varepsilon }}\equiv T(\varepsilon ),$$

(37)

or the reflection coefficient

$$| {S}_{+}(\varepsilon ){| }^{2}=\frac{1}{1+{{{{{{{{\rm{e}}}}}}}}}^{2\pi \varepsilon }}\equiv R(\varepsilon )$$

(38)

of the parabolic scattering potential. Consequently, by propagating the energy eigenfunction ${\psi }_{\varepsilon }^{+}$ for different values of ε during the time $t={t}_{{{{{{{{\rm{c}}}}}}}}}^{+}$, we uncover the characteristic transmission and reflection coefficients³² T and R of the inverted harmonic oscillator.

At this point, it is worthwhile mentioning that T(ε) and R(ε) resemble a particular quantum statistics, namely the Fermi–Dirac¹⁹ distribution. In fact, it is the presence of the amplitude singularity in addition to the logarithmic phase singularity in the energy eigenfunction of the inverted harmonic oscillator that results in the positive sign in the denominator of T and R. In contrast, disregarding the amplitude singularity and solely retaining the logarithmic phase singularity leads to a negative sign in the denominator, being reminiscent of the Bose–Einstein statistics.

Surface gravity water waves

In a frame moving with the group velocity c_g, the evolution of the slowly varying complex-valued envelope A ≡ A(τ, ζ) of a surface gravity water wave follows from the wave equation

$${{{{{{{\rm{i}}}}}}}}\frac{\partial A}{\partial \zeta }=\frac{{\partial }^{2}A}{\partial {\tau }^{2}},$$

(39)

reminiscent^29,35,36 of the Schrödinger equation (23) of a free particle, where A takes over the role of the wave function φ and the substitutions t → ζ, x → τ, ℏ → 1, m → 1/2, and i → − i have been applied in regard to the quantum-mechanical case.

The scaled dimensionless variables ζ and τ are related to the propagation coordinate x and the time t for the surface gravity water waves by $\zeta \equiv {s}_{0}^{2}{k}_{0}x$ and $\tau \equiv {s}_{0}{\Omega }_{0}(x/{c}_{g}-t)$. The carrier wave number k₀ and the angular carrier frequency Ω₀ satisfy the deep-water dispersion relation ${\Omega }_{0}^{2}={k}_{0}g$ with g being the gravitational acceleration, and define the group velocity c_g ≡ Ω₀/2k₀. The parameter s₀ ≡ k₀a₀ characterizing the wave steepness is assumed to be small (s₀ ≪ 1) in the linear regime.

Phase and amplitude from Hilbert transform

The time-dependent elevation

$$h(x,t)={a}_{0}A(x,t)\cos [{\Omega }_{0}t-{k}_{0}x+{\varphi }_{A}(x,t)]\equiv {a}_{0}{u}_{x}(t)$$

(40)

of the water surface at any point x in the tank involves the envelope function, characterized by the amplitude A(x, t) and the phase φ_A(x, t), which both vary slowly with respect to the carrier wave of frequency Ω₀.

The Hilbert transform³⁰

$${v}_{x}(s)\equiv \frac{1}{\pi }\int\nolimits_{-\infty }^{\infty }{{{{{{{\rm{d}}}}}}}}t\,\frac{{u}_{x}(t)}{s-t}$$

(41)

of the real-valued function u_x(t) reduces in our case to

$${v}_{x}(t) \, \approx \, A(x,t)\sin [{\Omega }_{0}t-{k}_{0}x+{\varphi }_{A}(x,t)].$$

(42)

Using the Euler formula, we can define the complex function:

$${z}_{x}(t)\equiv {u}_{x}(t)+{{{{{{{\rm{i}}}}}}}}{v}_{x}(t)=A(x,t)\exp [{{{{{{{\rm{i}}}}}}}}{\varphi }_{{A}_{{{{{{{{\rm{tot}}}}}}}}}}(x,t)]$$

(43)

with the total phase ${\varphi }_{{A}_{{{{{{{{\rm{tot}}}}}}}}}}(x,t)\equiv {\Omega }_{0}t-{k}_{0}x+{\varphi }_{A}(x,t)$ and thereby obtain the amplitude

$$A(x,t)=\sqrt{{u}_{x}{(t)}^{2}+{v}_{x}{(t)}^{2}}$$

(44)

and phase

$${\varphi }_{A}(x,t)={\varphi }_{{A}_{{{{{{{{\rm{tot}}}}}}}}}}(x,t)-{\Omega }_{0}t+{k}_{0}x=\arctan \left(\frac{{v}_{x}(t)}{{u}_{x}(t)}\right)-{\Omega }_{0}t+{k}_{0}x$$

(45)

of the envelope function directly from the measured function u_x(t) and its Hilbert transform v_x(t).

To numerically compute the Hilbert transform from the measured surface elevation data, we use the Matlab toolbox function ’hilbert’.

Experimental facility

The experimental facility consists of three essential ingredients (i) a wave tank, (ii) a wave maker, and (iii) wave gauges. In this section, we summarize important details.

Surface gravity water wave tank

Our experiments were performed in a 5 m long, 0.4 m wide, and 0.19 m deep laboratory wave tank, as illustrated in Fig. 2. The wave tank is encompassed by an aluminum extrusion frame and supported by eight shock-absorbing legs. The sidewalls and base of the wave tank are made of transparent glass to permit flow visualization of the wave field and the observation of the waves from all angles. At each end of the test section, openings in the tank floor permit tank filling and discharging via particle filter. Prior to each experiment, the water surface was cleaned to remove any surface film that could influence the results. The use of transparent glass allowed the observation of the water’s surface from above, and capacitance-type sensors were inserted into the test section at any distance from the inlet. The measuring equipment, power supplies, and sensors are supported by the instruments carriage, which is constructed of aluminum extrusions and affixed on a rail along the test section. The position of the carriage along the test section at the intended fetch and the input at the wave maker are the controlled experimental parameters.

In our experiments, we have used the carrier frequency Ω₀ = 15 rad/s and the initial amplitude a₀ = 2.0 mm. Moreover, k₀ satisfies the deep-water condition²¹ k₀d > π, where d = 0.19 m denotes the depth of the tank and the corresponding steepness is s₀ < 0.04 guaranteeing the validity of the linear Schrödinger equation. More details on the experimental setup can be found in refs. ^20,36.

Computer-controlled wave maker

A mechanical wedge-type wave maker (Linmot T01-72/420-1ph) is used to generate surface gravity water waves. It is composed of a wedge-shaped plate, a motor or actuator, a frame to hold the wedge, and a water tank. The wedge plate is mounted on the frame, and the frame is positioned above the water tank. The motor or actuator is connected to the wedge plate, which is positioned at the surface of the water and moves back and forth in a reciprocating motion. As the wedge plate moves, it creates a disturbance in the water, which generates waves that propagate outwards from the wedge. The size and frequency of the waves can be adjusted by changing the amplitude and frequency of the wedge’s motion.

The initial envelope of the surface water gravity wave is determined by the quantum-mechanical energy eigenfunctions of the inverted harmonic oscillator. Therefore, the wave packet generated by the wave maker reads

$$h(t,x=0)={a}_{0}| A(t)| \cos \left[{\Omega }_{0}t+{\varphi }_{A}(t)\right],$$

(46)

with the carrier frequency Ω₀ = 15 rad/s and the initial amplitude a₀ = 2 mm. Here A = A(t) and φ_A = φ_A(t) represent the amplitude and phase of the eigenfunctions obtained from Eqs. (13) and (14). For this purpose we make use of the substitutions as defined previously in order to translate quantum-mechanical variables to the formalism of surface gravity water waves.

Then, the time-dependent elevation of the wave was measured using wave gauges at different positions in the tank and stored in a computer. This data was numerically truncated at the location of the next temporal slit, and was then sent to the wave maker for a new excitation based on the previous measurement. In this way, we were able to cascade several slits in the time domain and observe the effect of diffractive guiding.

Capacitance-type wave gauges

We utilize a capacitive wave gauge transducer consisting of a 0.3 mm thin tantalum wire coated with a uniform thin layer of tantalum oxide. Before the measurement of the surface wave height using wave gauges, the calibration of the wave sensor is performed in three steps: (i) we first set the vertical position of the wire wave gauge in such a way that the mean water level is approximately in the middle of the wire. (ii) We perform automatic calibration of the wave gauge using a lab-view-made routine by submerging the wave sensor at different depths and recording the mean voltage for 5 s for each depth. (iii) Finally, a polynomial fit is applied to the recorded data in order to find out the dependence between measured height H[mm] and the gauge voltage and verify visually the fitted calibration polynomial as shown in Fig. 7. We note that the analysis of the relationship between height and voltage in capacitor type wave gauges, the precision of measurements was evaluated by employing statistical error calculations based on five separate measurements for each data point. This approach ensured that the estimated errors reflect the variability inherent in the experimental setup and measurement process. Notably, the resulting error bars were found to be smaller than the symbols representing the data points on the plotted graph.

Fig. 7: Set of calibration curves for the four capacitance wave gauges.

Comprehensive calibration curves for four distinct capacitance wave gauges, detailing measurements across six different heights (H) in millimeters (mm) and their respective recorded voltages (V) in volts. Each data point is derived from an average of five separate measurements at each height to ensure accuracy and reliability. This experimental data undergoes an analysis through linear regression methods to establish the relationship between height and voltage accurately. To evaluate the precision of these measurements, statistical error calculations were employed, which factored in the variability inherent in the experimental setup and the measurement process. Notably, the calculated error bars, indicative of measurement precision, were found to be significantly smaller than the symbols used to represent the data points on the graph, underscoring the high degree of accuracy in the experimental findings.

Experimental protocol

In this section, we outline the experimental protocol to generate the truncated Weber wave packets and observe the singularities appearing in Eq. (10). In particular, we discuss the propagation along the wave tank, and its recording and transformation into a full complex wave function. The iterative procedure is repeated until the observation of a singularity in both amplitude and phase.

We proceed in the following steps:

• (i) Generation of truncated Weber wave packet. The Weber wave packet defined by Eq. (1) is not normalizable. For the experiment, we had to truncate them to a finite duration in time. The temporal window of truncation was carefully chosen based on experimental constraints and theoretical predictions. In Fig. 8, we show the full wave packet (black curve) and the truncated Weber wave packet (red). The truncated Weber wave packet was generated by the computer-controlled wave maker.

  Fig. 8: Illustration of the truncated initial wave packet for surface gravity water waves.

  

  Full initial envelope waveform based on Eq. (1) for ε = 0.25 (black solid lines) and the truncated one for a truncation window of 50 s (red solid lines).

• (ii) Propagation and recording. The so-generated truncated Weber wave packet was then allowed to propagate along the carefully controlled water tank. The height of the propagating wave packet, that is the real part, was recorded using the high-resolution wave gauges positioned at specific locations along the tank discussed before.

• (iii) Translation into complex wave function. Each recorded real part of the wave packet envelope was then translated into a full complex wave function using the Hilbert transform discussed above.

• (iv) Reconstructing and sending back to the wave maker. The wave packet was then propagated to the final point, x_f, recorded, and recreated again at the wave maker.

• (v) Iterative procedure and singularity observation. This entire process was repeated iteratively—each time observing the properties of the propagated, transformed, and re-sent wave packet. The iteration was continued until we observed a singularity in both the amplitude and phase of the wave packet. The criteria for the observation of a singularity were based on a combination of theoretical predictions and experimental viability.