Introduction

With the development of quantum computers new encryption methods become necessary to enable secure communication. Quantum key distribution (QKD) guarantees security based on the principles of quantum mechanics, where any eavesdropping attempt leaves an unavoidable fingerprint on the measurement results which would otherwise provide a shared random key1,2. Photonic entanglement distribution among remote quantum nodes is the key element for quantum information exchange over long distances3. Fiber-based quantum channels are desirable for practical use, building on existing network technology, but are vulnerable to losses which limit the distance for point-to-point links to about 100 km. Without the need for trusted nodes, the most promising way at present to establish long-distance quantum communication is based on modular quantum repeaters4. Experimental realizations of quantum repeaters are extremely difficult and subject to ongoing research efforts5,6. The major experimental challenge is to develop elementary quantum repeater nodes with efficient fiber connectivity and, at the same time, access to long-lived quantum memories in order to reach transmission rates and state transfer fidelities that enable practical use over long distance. The first demonstrations of quantum repeater nodes containing the necessary elements were recently demonstrated based on diamond technology7.

Color centers in diamonds are among the most promising platforms to realize quantum repeater nodes8,9,10,11. Pioneering work was done with negatively charged nitrogen-vacancy (NV−) centers. A recent breakthrough marks the implementation of quantum network protocols in three-node entanglement-based quantum networks12, where two-node entangled Bell state fidelity reaches 80 % with entangling rates of about 9 Hz. Three-node heralded Greenberger–Horne–Zeilinger (GHZ) state preparation reaches a state fidelity of 53.8% and entanglement swapping across three nodes 58.7% with rates of 25 mHz12. While all quantum repeater elements are established13,14, scaling to multiple nodes for long distances requires significant improvements. In particular, coherent photon emission and detection require higher efficiency in order to maintain entanglement fidelity over long-distance links at high rates. A solution is spin-photon interfaces with Purcell-enhanced coherent photon interaction. Therefore, the optical transition of the NV− center can, for example, be coupled to the mode of a Fabry-Perot (FP) microcavity15,16,17.

Group IV color centers and, in particular, the negatively charged silicon vacancy (SiV−) center, are an attractive alternative to NV− centers. The D3d symmetry enables spectrally stable, optical transitions and indistinguishable photons without Stark tuning18. High brightness and a large Debye–Waller factor lead to an intrinsically higher rate of coherent photon exchange. Its electron spin coherence time reaches 13 ms at mK-temperatures19 and access to nuclear spins20 potentially enables second-long memory times. But building an efficient spin–photon interface mode-matched to Gaussian optics still remains an outstanding challenge, where fast coherent optical manipulation is blocked by inefficient light-matter interaction due to the high refractive index of the diamond host. Various approaches rely on the implementation of tapered fibers21, bullseye antennas22, and inverse-designed couplers in diamond23, partly in combination with an optical resonator21 in order to enhance the internal efficiency and bandwidth of the color center. Likewise raising technical demands, operating at sub-Kelvin temperatures for long spin-coherence times requires dilution refrigerators.

As a solution, we propose to work with SiV− centers in nanodiamonds (NDs) coupled to the mode of an optical FP microcavity. It has been shown that coherence times can be extended by suppressing phonon processes as it was done by engineering the strain of the SiV− center24,25,26. Another approach is the locally modified phonon density of states (pDOS) which could increase the operation temperature to a few Kelvin when the SiV− center is localized inside an ND27, making dilution refrigerators redundant. At the same time, the small size of NDs, smaller than the optical wavelength, enables integration into open resonators with low scattering loss15,28,29,30. Therefore, SiV− centers in NDs with their optical transitions coupled to the mode of an optical resonator offer a promising spin–photon interface for quantum repeater applications.

In pioneering experiments, SiV− centers in NDs31 and in diamond membranes (DMs)32, as well as germanium vacancy (GeV−) centers in DMs33, were coupled to the mode of fiber-based cavities at room temperature. Breakthroughs in the realization of stable FP cavities at cryogenic temperatures34,35,36,37,38,39,40,41,42 enabled cavity coupling of SiV− centers at low temperatures43. Integrated platforms have been developed for microwave control of the NV− center electron spin inside open FP microcavities44, but SiV− center electron spin access inside open resonators is yet to be demonstrated. At the same time, coherent optical driving and a significant Purcell-enhancement that shortens the optical lifetime are required. All these elements are essential for an efficient quantum repeater node and need to be implemented simultaneously.

Here, we realize such a spin–photon interface by coupling individual optical transitions of single SiV− centers in an ND to the mode of an open microcavity at cryogenic temperatures. We demonstrate coherent optical driving with Rabi-frequencies of 330 MHz, significant lifetime shortening yielding Purcell factors well above 1, and all-optical initialization and readout of the electronic spin in the presence of a strong magnetic field. Therefore, we establish a promising platform to serve as a quantum repeater node that is passively stable and enables efficient mode-matching of the fundamental Gaussian TEM mode to fiber networks.

Results and discussion

Nanodiamond placement and cavity coupling

NDs with ingrown SiV− centers are pre-characterized using confocal spectroscopy (see the “Methods” section). Despite an inhomogeneous distribution in NDs, SiV− centers with the same transition frequency can be identified reliably45,46. Utilizing atomic force microscope (AFM)-based pick-and-place technique45,47 (Fig. 1a), candidate NDs of small size, here 200−300 nm, and spectrally stable SiV− centers are placed in the curved mirror of the FP microcavity. The hemispherical cavity is optimized towards small mode volume V and high coupling strength. The spherical mirror consists of a small radius of curvature RoC ≈ 8 μm, fabricated with focused ion beam milling pioneering techniques48,49,50. Both mirrors are symmetrically coated with distributed Bragg reflectors (DBRs). The transmission T = 500 ppm at wavelength λ = 737 nm corresponds to a coating-limited finesse of \({{{{{{{{\mathcal{F}}}}}}}}}_{{{{{{{{\rm{ideal}}}}}}}}}\approx 6300\). The experimentally achieved finesse is on average \({{{{{{{{\mathcal{F}}}}}}}}}_{\exp }=3500\pm 500\) and \({{{{{{{\mathcal{F}}}}}}}}=2700\pm 500\), respectively, before and after placing the ND. From this we estimate the scattering losses on the ND to be 85 ppm. For NDs below the size of 200 nm we find strongly reduced scattering (see the “Methods” section). We optimize the system towards high passive stability with a moderate finesse and small mode volume, avoiding the high mechanical stability demands and advanced locking of high-finesse open cavities39 whilst resulting in a reasonable high-quality factor Q on the order of 20k. Furthermore, we operate the open cavity in direct contact with the liquid He-bath, providing significantly higher cooling power than systems based on thermal conduction.

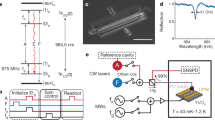
Fig. 1: Assembling the coupled nanodiamond-microcavity system and optical measurements at 4 K.
figure 1

a A pre-characterized nanodiamond (ND) is picked with an Atomic Force Microscope (AFM) and placed in the hemispherical Fabry–Perot mirror. For excitation, a laser on resonance with the zero-phonon line and the cavity is used. For detection, the phonon sideband (PSB) is collected. LHe liquid Helium, DBR distributed Bragg reflector. b A subsequent AFM scan reveals the ND inside the mirror structure with a radius of curvature of 8 μm indicated by blue-dashed lines. c Resonant photoluminescence excitation (PLE) through the cavity mode yields SiV− side-band emission modulated by individual cavity modes shown for two different cavity lengths. The resonant excitation light (yellow solid line) is filtered before entering the detection fiber (green dashed line). The phonon side-band couples to TEM00 and higher order modes (solid blue and red lines). d At the cavity length with the laser light coupled to the fundamental mode of number m = 8, an auto-correlation measurement g(2)(τ) on the emission shown in c reveals a single photon emission with g(2)(0) < 0.5. Data points are plotted with blue dots, technical noise with gray dots, and the fit is shown in a red solid line. e The power-broadened PLE linewidth of ≈340 MHz (scanning speed ≈ 180 MHz s−1) yields a spectral long-term stability within ±24 MHz (standard deviation σ of the peak center, black circle) over 90 s. The peak height demonstrates a stable frequency overlap between the emitter, cavity, and laser light. Single scan and integrated data are shown with red and blue dots, fitted with red and blue solid lines.

Full size image

Positioning the ND at the center of the concave mirror enables highly accurate alignment of the SiV− center with a precision limited by the ND size to the hemispherical mirror structure with access to its rotational degrees of freedom45, which could be used for further alignment of the SiV dipole axis with the cavity axis and with the external magnetic field. This bears the advantage of a fixed emitter–cavity coupling without the need to scan the plane mirror in the xy-directions. Spectral overlap can be optimized in-situ by tuning the cavity length in the z-direction. Following this approach, a more compact FP system with reduced complexity, enhanced stability and better scalability can be designed. A subsequent AFM scan verifies the successful transfer of the ND to the center of the curved mirror (Fig. 1b), well within the beam waist of the cavity mode (≥1.2 μm) without further optimization. The size of the ND yields 300 nm in lateral dimension and 200 nm in height. The SiV− center is then resonantly excited via the fundamental TEM00-mode of order m with laser light at a wavelength of λlas ≈ 736.7 nm. Mode m−1 is located at a longer wavelength and couples to the phonon side-band emission. The obtained emission spectra at 4 K are shown in Fig. 1c for two different cavity lengths while keeping the same excitation wavelength λlas. In the idealized case of a planar resonator, the mode wavelength is given by \({\lambda }_{{m}}=\frac{2}{m}L\), where L describes the effective distance between the two mirrors. For two neighboring TEM00 modes this results in \(\frac{{\lambda }_{m-1}}{{\lambda }_{m}}=\frac{m}{(m-1)}\). For the two mentioned spectra with a known length difference \(\Delta L\approx \frac{3}{2}{\lambda }_{{{{{{{{\rm{las}}}}}}}}}\), we find m = 8 and m = 11 in agreement with ΔL. Note that the fundamental TEM00-modes with orthogonal polarization are degenerate, enabling independent control of the light polarization.

A second-order auto-correlation measurement yields g(2)(0) = 0.33 ± 0.06 without background correction, shown in Fig. 1d, and proves single photon emission through the cavity modes under resonant excitation. The two peaks marked in gray arise from optical cross-talk between the detectors, which is resolved in later measurements (see Supplementary Note 3).

When cooled in the liquid Helium bath, narrow spectral lines become apparent in the photoluminescence excitation (PLE) scans. Individual, slightly power-broadened line scans reveal linewidths γ below 300 MHz as expected for Fourier-transform (FT) limited lines for SiV− centers (Fig. 1e). The PLE scans on the emitter-cavity system disclose long-term stability, where individual line-scans differ less than the FT-limited linewidth on timescales of 90 s. The microcavity length is not actively stabilized throughout the scans. Instead, the mechanical stability arises from the passive stability of the setup that persists even when operating in the liquid Helium bath. An estimation of the maximum length fluctuation shows that the microcavity length changes by less than one linewidth, corresponding to 160 pm (see Supplementary Note 1).

Cavity-enhanced, coherent optical driving of individual SiV− centers

An optical transition on resonance with the cavity mode results in a modified spontaneous decay rate. The reduction of the excited state lifetime τ is described by the Purcell-factor

$${F}_{{{{{{{{\rm{P}}}}}}}}}=\frac{{\tau }_{{{{{{{{\rm{free}}}}}}}}}}{{\tau }_{{{{{{{{\rm{cav}}}}}}}}}}=1+\xi {f}_{{{{{{{{\rm{P}}}}}}}}},$$
(1)

where τfree and τcav are the emitter lifetimes in free space and in the cavity, respectively, and ξ is the off-resonant branching ratio. fP can be calculated as

$${f}_{{{{{{{{\rm{P}}}}}}}}}=\frac{3}{4{\pi }^{2}}\frac{{\lambda }^{3}}{{n}^{3}}\frac{Q}{V}$$
(2)

with the light wavelength λ and the refractive index n of the medium inside the microcavity. For our system, Q is primarily limited by the broader cavity resonances \(\delta {\nu }_{{\rm {cav}}}=\frac{c}{{{{{{{{\mathcal{F}}}}}}}}\lambda m}\). For m = 10, we calculate the linewidth of the cavity to be δνcav ≈ 15 GHz, thus δνcav ≈ 100 × FWHMemitter. The fundamental cavity mode volume \(V=\frac{\pi }{4}L{\omega }_{0}^{2}\) is determined by Gaussian beam properties. With an emitter placed on the curved mirror, the dependency of V on the length L deviates from the case of an emitter on the flat side by a reduced field maximum (see Supplementary Note 4). In contrast to the case of an emitter located on the flat side, FP strongly depends on L, as shown in Table 1, and grows monotonically for shorter lengths. In a real system, additional factors such as limited quantum efficiency, branching ratio, dipole location, and orientation need to be accounted for. The coupling in our system is reduced by a factor of 1.58 as compared to an emitter located on the flat side but with the aforementioned advantages for the assembled cavity system.

Table 1 Microcavity parameters for two effective lengths.
Full size table

In the experiment, we choose the mode m = 8 and drive the emitter’s transition from Fig. 1 at various powers above and below saturation, revealing its saturation behavior as shown in Fig. 2a, with a saturation power PSat = 0.7 μW which is comparable to values measured in other works51,52. The count rate is comparable to values reached for nitrogen-vacancy centers coupled to an FP resonator17. A full width at half maximum linewidth of 168 MHz is reached at 0 power. Repeating this measurement yields an averaged linewidth of 153 ± 11 MHz (Fig. 2b). For longer cavity lengths, the averaged linewidth reduces to 128 ± 21 MHz with a minimal linewidth measured of 107 MHz at m = 11. This suggests that the free-space emitter linewidth lies close to the FT-limit of SiV− centers in the range of 90−100 MHz. Assuming an FT-limited emitter linewidth, the ratio shown in Eq. (1) can be reformulated as

$$\frac{{\gamma }_{{{{{{{{\rm{cav}}}}}}}}}}{{\gamma }_{{{{{{{{\rm{free}}}}}}}}}}=\frac{{\tau }_{{{{{{{{\rm{free}}}}}}}}}}{{\tau }_{{{{{{{{\rm{cav}}}}}}}}}}.$$
(3)
Fig. 2: Purcell-enhancement and coherent optical driving of the SiV− centers transition at 4 K.
figure 2

a Peak count rates (blue) and linewidth (red) from photoluminescence excitation (PLE) scans with varying laser excitation power at the shortest accessible cavity mode m = 8. The linewidth extrapolated to zero power yields 168 MHz. The error bars correspond to the 95% confidence interval of the fit. The inset shows respective PLE scans for the highest (green) and lowest (yellow, scaled by 23) optical power. b Zero-power linewidth averaged for multiple measurements at three different cavity lengths (blue dots) with standard deviation. The Purcell-factor is extracted from fits with the free-space linewidth as a free parameter (green dashed line) and fixed to 90 MHz (red solid line). c Resonant g(2)(τ)-measurement (blue dots) under strong drive reveals an optical lifetime of τ = 1.0 ± 0.5 ns and a Rabi-frequency ΩR/2π = 330 ± 50 MHz (from fit in red solid line). The red-shaded area displays the confidence interval. A fit using a three-level model for bunching (green line) does not represent the data well. The error is the standard deviation (shot noise).

Full size image

The zero-power extracted linewidths for the SiV− center coupled at different cavity lengths are fit with two different bounds, as shown in Fig. 2b. The first fit marks an upper bound with a free-space linewidth of 18 MHz, corresponding to a long lifetime τfree = 9 ns as it has been reported for NDs53 and predicts a Purcell-factor of 8.6. Usually, excited state lifetimes of 1.5-2.2 ns are reported18,52. Therefore, we also fit with the free-space linewidth fixed to 90 MHz, corresponding to τfree = 1.77 ns, and extrapolate FP = 1.61 ± 0.06. The difference in the extrapolated Purcell-factors could arise from an increasing suppression of emission into the side band as the effective cavity length shortens, as studied in detail for NV− centers in ref. 15. Therefore, we assume our extracted Purcell-factor of 1.61 marks a lower bound.

A resonant, second-order auto-correlation measurement (Fig. 2c) with a high excitation power of 7 μW measured before the lens coupling into the resonator, yields a power-broadened linewidth of 433 ± 8 MHz and reveals coherent optical driving of the system. The arising Rabi-oscillations are fit with a resonant g(2)(τ)-model, yielding an optical lifetime τ = 1.0 ± 0.5 ns and a Rabi-frequency ΩR/2π = 330 ± 50 MHz. Bunching due to shelving can be excluded as a corresponding three-level model is not able to fit the data well as the green fitting curve suggests. Additional information to the g(2) measurements can be found in Supplementary Note 3. τ = 1.0 ns corresponds to a homogeneous linewidth of about 160 MHz (marked yellow in Fig. 2b), in agreement with this cavity length. The optical coherence is governed by the lifetime τ0 of the SiV− center. Slow variations in the effective excitation power during data acquisition might add minor dephasing.

The ideal Purcell-factor for our cavity could reach up to 620 (see Table 1). Deviations from the ideal case include low quantum efficiency (order of 0.059) and off-resonant branching ratio (0.32554), which together reduce the limit of the theoretically possible Purcell-factor by 60 times. An imperfect overlap of dipole and cavity field further reduces FP experimentally.

The β-factor

$$\beta =\frac{{F}_{{{{{{{{\rm{P}}}}}}}}}-1}{{F}_{{{{{{{{\rm{P}}}}}}}}}}$$
(4)

quantifies the fraction of excited state population, that decays through coherent coupling into the microcavity mode. With the extrapolated value of FP = 1.61, we estimate β ≈ 38% as a lower bound. This value fundamentally limits the efficiency as a spin–photon interface, but can be further raised by improving emitter–cavity coupling and \({{{{{{{\mathcal{F}}}}}}}}\) of the cavity. As the system operates in the bad cavity regime, the cooperativity C is closely linked to our value of FP and can be calculated as C = FP−138, for which we find C ≈ 0.6.

All-optical spin initialization and readout

We now initialize and read out the electronic spin state all-optically via the cavity mode. Therefore, we split the spin–orbit states by applying a magnetic field of variable strength and resonantly address the resulting spin–cycling transitions, labeled as C2 and C3 in Fig. 3a. The cavity mode (m = 8) is in resonance with the SiV− centers optical transition shown in Figs. 1 and  2. PLE scans at magnetic fields of B = 0, 2.1 and 3.2 T reveal the field-dependent splitting into the two spin-cycling transitions C2 and C3, shown in Fig. 3b. The splitting of the spin-conserving transition is a result of strain25 and alignment between the magnetic field and SiV− center axis. We attribute the reduced brightness with increasing magnetic field to a prolonged lifetime of the electron spin state as compared to the lifetime of the orbital state. Consequently, optically pumping for the duration of the spin lifetime \({T}_{1}^{{{{{{{{\rm{spin}}}}}}}}}\) yields a reduced brightness.

Fig. 3: All-optical initialization of the SiV− center electron spin at 4 K.
figure 3

a Energy level diagram with and without external magnetic field (B) applied along the cavity axis showing splitting of transitions A through D. In an external magnetic field, the spin is initialized in the up-state by optical pumping on the spin-conserving transition C3. P state population, τinit initialization time constant, \({T}_{1}^{{{{{{{{\rm{spin}}}}}}}}}\) spin lifetime. b The magnetic field (B) dependent photoluminescence excitation signal shows the splitting of transition C into the spin-conserving transitions C2 and C3. For better visibility, the scans (data points as blue, red, and green dots with respective fits as blue, red, and green lines) are offset by 0.4 kc/s. The inset shows the relative peak position over the field strength. c When pulsing on resonance with C3 and registering the number of time-resolved photon events (blue line), the exponential decay (red fit) of the fluorescence signal indicates the initialization in the spin-up state (0.2 ns bin width). d A sequence of 750 ns-long laser pulses separated by an increasing waiting time by increments of 75 ns yields the recovery into the equilibrium state (0.8 ns bin width). e The amplitude A of an exponential fit with offset H to the decaying signal of every pulse is plotted against increasing waiting time (blue dots) revealing an electron spin lifetime of \({T}_{1}^{{{{{{{{\rm{spin}}}}}}}}}=350\pm 40\) ns (fit in red).

Full size image

In order to access the spin state at B = 3.2 T, we apply 400 ns long laser pulses resonant to C3 at the relative frequency Δν ≈ 0.6 GHz, shown in Fig. 3c. The exponential fit to the fluorescence signal yields an initialization time τinit ≈ 67 ± 6 ns, on which the system is pumped into the spin-up state. The fidelity of the electron spin initialization is extracted to 80 ± 4% by comparing the counts at the beginning and at the end of the pulse55. We assume, that the system is initially in an equal distribution of spin-up and spin-down. After optical pumping the system is preferably in spin-up state, decreasing the fluorescence signal on transition C3 accordingly (see the “Methods” section). To determine the recovery time we vary the waiting time of consecutive 750 ns-long pulses with an increment of 75 ns, as depicted in Fig. 3d. An exponential fit on the fluorescence pulse heights yields a lifetime of \({T}_{1}^{{{{{{{{\rm{spin}}}}}}}}}=350\pm 40\,{{{{{{{\rm{ns}}}}}}}}\) (Fig. 3e). \({T}_{1}^{{{{{{{{\rm{spin}}}}}}}}}\) can reach values in the ms-range or higher and is typically limited by mixing of the spin states in the case of non-perfect magnetic field alignment55,56, which we can not precisely control in our setup. The spin relaxation, \(1/{T}_{1}^{{{{{{{{\rm{spin}}}}}}}}}\), and initialization with speed 1/τinit are two competing processes on similar timescales in the initialization process. Therefore, we assume this to be the main limiting factor of the spin initialization fidelity. This is in agreement with Fig. 3c, where the two measurements were performed at different excitation powers, resulting in a slower initialization speed and lower fidelity. We did not observe the spin–flipping transitions, C1 and C455, which are required for accessing the spin coherently through optical driving. Possible causes are either reduced fluorescence in strong magnetic fields, making the usually weaker spin–flipping transitions hardly detectable, or that the spin–flipping transitions are forbidden due to the orientation of the defect57.

Besides the application as a quantum repeater node, our platform might prove valuable as a sensor for high magnetic fields in larger magnets. Furthermore, microscopic magnetic samples can be sensed on the flat mirror with fine resolution in xy. From the fit accuracy of the B-field dependent splitting in Fig. 3b, we estimate a sensitivity of 180 ± 60 mT Hz−1/2 to determine dc-field strengths in high magnetic fields, here done at 3.2 T. For comparison, the NV− center reaches dc-magnetic field sensitivities of 40 nT Hz−1/2, seven orders of magnitude below the sensitivity of our system58. However, magnetometry with NV− centers has limitations in high-field sensing. Typically, microwaves with frequencies on the order of 100 GHz are necessary for strong fields, requiring broadband tunable sources and compatible waveguides59. Instead, our system requires a tunable laser, thus keeping additional technical expenses low. By utilizing the resonator setup, it is possible to achieve high count rates in a compact design without the need for employing high numerical aperture (NA) objectives. In the future, the sensitivity can be enhanced by employing NDs with lower strain and by improving the B-field alignment. Potential applications are discussed in more detail in Supplementary Note 5.

Conclusions

Summarizing, we introduce a passively stable emitter-cavity platform based on a single SiV− center coupled to the mode of an FP microcavity with the prospect of serving as a building block for a quantum repeater. We coherently drive individual optical transitions through the cavity mode with a Rabi-frequency of ΩR/2π = 330 ± 50 MHz. The resulting lifetime shortening yields a Purcell-factor of 1.61 as a lower bound. We further demonstrate all-optical, electron-spin initialization with an initialization time constant of τinit ≈ 67 ns and a fidelity of 80% at equilibrium. The observed spin lifetime of \({T}_{1}^{{{{{{{{\rm{spin}}}}}}}}}=350\,{{{{{{{\rm{ns}}}}}}}}\) in a strong magnetic field of 3.2 T is limited by field misalignment.

The compact geometry of the system allows mounting it in a vector magnet where, with a well-aligned magnetic field, electron spin lifetimes in the ms-range and coherence times in the μs-range become feasible at liquid Helium temperatures20. As a result, a higher level of fidelity can be achieved in spin initialization. Furthermore, access to nuclear spin opens the possibility for longer quantum storage times with coherence times well beyond millisecond timescales19,20,26. In addition, by further optimizing placement through nanomanipulation and the ND shape and size, improved coupling parameters and reduced scattering losses and thus, higher Purcell-factors are within reach60,61. Increasing the finesse to \({{{{{{{\mathcal{F}}}}}}}}=10.000\) (\({{{{{{{\mathcal{F}}}}}}}}=50.000\)), photon extraction efficiencies of β = 69% (β > 90%) and Purcell-factors above FP = 3 (FP = 12) are predicted for a short cavity length (see Supplementary Note 4). Therefore, we believe this platform will be capable of tackling the two main obstacles for quantum repeater applications, namely low operation bandwidth and rapid quantum memory dephasing.

Our work delivers experimental input to theoretical protocol developments62,63 towards high secret key transmission rates over long distances exceeding hundreds of kilometers. Connecting many such quantum repeater nodes will overcome the limitations of direct quantum information transmission and lead to extended quantum networks.

Methods

Nanodiamond fabrication and characterization

In the following, we describe the fabrication and optical characterization of the NDs and their precise placement in the mirror structure by means of AFM-based nanomanipulation. NDs with SiV− centers were created by the mixture of naphthalene (C10H8) and tetrakis(trimethylsilyl)silane (C12H36Si5) under a high pressure and high temperature (HPHT) treatment, analogous to previous work47. Purification and carbon removal were performed with the acid mixture of HNO3, HClO4, and H2SO4. Final ultrasonic treatment and washing of the NDs form crystals in the size between 40 and 500 nm, as shown in the scanning electron microscope image in Fig. S6c.

Subsequently, the NDs with ingrown SiV− centers are first studied at ambient conditions with confocal spectroscopy, e.g. in terms of spectral and temporal stability. Suitable NDs with sizes below 300 nm are selected and placed in the curved mirror of the microresonator using the AFM-based pick and place technique47. We estimate the rate of success for an ND transfer to be on the order of 50–70%. The fluorescence scan displayed in Fig. S6a shows the spatial emission profile of the ND used for this work under green excitation (532 nm) and before the placement in the cavity. The respective spectrum which was acquired in order to identify the presence of SiV− centers in the ND is shown in Fig. S6b. For this acquisition a narrow-band optical filter centered close to 737 nm was used (Semrock, 740/13 BrightLine HC).

Comparing the spectra of SiV− centers in an ND in freespace at 4 K and the cavity, good coupling of the TEM00 mode to the sideband becomes apparent (see Fig. S6d). While the freespace sideband emission is barely visible in the spectrum at long wavelengths, emission into the cavity mode is still distinct up to a wavelength of up to 840 nm. It may be interesting to note that the mirror reflectivity decreases from 800 nm upwards, reaching a down to 8-fold lower finesse at 840 nm. The strain of the SiV− centers in this sample varies between a ground state splitting of 50 GHz up to multiples of 100 GHz.

Cavity mirrors

For the cavity mirrors DBRs, coated by Laseroptik GmbH onto silica substrates, were employed. The reflectivity for an ideal lossless case is R = 1−T. This can be used to calculate the ideal finesse

$${{{{{{{\mathcal{F}}}}}}}}\approx \frac{{\pi R}^{1/2}}{1-R}$$
(5)

The spherical mirror structure was produced by focused ion beam milling (FIB). With this method, variable sizes and RoCs between 8 and 35 μm with surface roughnesses down to below 0.2 nm can be achieved. The structure is milled into a conical substrate with a tip diameter \({{\emptyset}}\approx 200\,{\rm {\mu}} {{{{{{{\rm{m}}}}}}}}\). Thus, short cavity lengths are possible even in case of a slight relative tilt between the two mirrors. The FIBed structures on this sample usually yield maximum values of \({{{{{{{\mathcal{F}}}}}}}}\approx 3000-4000\), not at the nominal limit given by the coating design (6300). Therefore, we assume that our overall systems quality is limited by remaining absorption in the dielectric material, imperfections in the structure shape and surface roughness associated with the FIB milling process, as well as losses attributed to scattering at the ND interface. Assuming an average \({{{{{{{\mathcal{F}}}}}}}}=3500\) before ND placement, the scattering losses per round trip due to the ND equal \({{{{{{{\mathcal{L}}}}}}}}=85\,{\rm {ppm}}\). Decreasing the ND size will reduce scattering losses at the diamond interface in future experiments. Investigation of the scattering introduced by NDs has shown that 100 nm-sized NDs typically have no noticeable impact on cavities with \({{{{{{{\mathcal{F}}}}}}}}=6000\). In principle, the shape of the ND has to be taken into account as well in order to predict its precise impact on the quality of the resonator mode. This is a complex topic as many potential shapes need to be taken into account. However, our observations indicate that the primary factor for the scattering probability is the size of the ND, particularly when crossing a critical size of \(\frac{\lambda }{2n}\). Other works have demonstrated that there is no significant scattering for \({{{{{{{\mathcal{F}}}}}}}}=30{{{{{{{\rm{k}}}}}}}}\) when employing NDs61. CO2 fabricated structures will allow \({{{{{{{\mathcal{F}}}}}}}}\) up to 100k−200k. As a result, values of \({{{{{{{\mathcal{F}}}}}}}}\) up to 100k are feasible for our system with a highly reflective coating and suitable NDs.

The microresonator is centered within a monolithic titanium frame in which the cavity mirrors are mounted. While the curved mirror is mounted directly on the frame, the flat mirror is mounted on a xyz-scanner stage consisting of Attocube nanopositioners from the ANP series, allowing for full tunability of the cavity. In this work, only the z-scanner is used. A second xyz-scanner is used to optimize the cavity coupling by an aspheric lens (Asphericon: AHL10-08-P-U-780, f = 8 mm, NA = 0.55) that focuses through the mirror substrate onto the structures.

Optical setup

For resonant excitation and probing the finesse at 742 nm an actively stabilized Ti:sapphire ring laser (Sirah: Matisse 2 TS) was used. No further green light is necessary to spectrally stabilize the transition, as it is commonly done for PLE measurements in free-space, which minimizes additional optics and alignment. Pulsed excitation was employed by a field programmable gate array (FPGA) which controls a fiber-pigtailed amplitude electro-optical modulator (Jenoptik: AM705). The laser light is guided to the resonator through a single mode fiber (IVG Fiber: SM CU600PSC) and overlapped with the collection path, which is in reflection, with a wedge prism (Edmund Optics: 0.5° Nom. 12.5 mm Dia. VIS–NIR, N-BK7 Wedge Prism).

Before the collection and after the excitation fiber filters were mounted to clean up fiber fluorescence and prevent laser coupling into the collection fiber. For the measurements, a 740/13BP filter after the single-mode fiber and a 730 Notch filter (Semrock: 740/13 BrightLine HC; Chroma: single notch filter 730 nm—zet 730NF) were placed in the optical paths. When the cooperativity C > 1 and purely resonant excitation and detection schemes become feasible, the optical filters can be removed.

The described optics including the cavity, the lens and filters are mounted to the titanium setup and are positioned inside a helium bath cryostat (Oxford). Above mentioned excitation and detection fibers provide optical access to the cavity. Misalignment occuring during the cooling process is compensated with the xyz-positioning unit stack holding the lens in front of the resonator and an xy-positioning unit stack on which the detection fiber is mounted (Attocube: 2x ANPx101). A discussion on the detection efficiency can be found in Supplementary Note 2. For detection, the collected light from the multimode fiber (Thorlabs: MM FG050LGA) is detected in freespace with two single photon counting modules (Excelitas: SPCMAQRH-14). With flip mirrors the signal could be switched to a Si avalanche photodetector (Thorlabs: APD120A2/M) or a spectrometer (Princeton Instr., SpectraPro HRS-500) with the here used 150 grooves/mm. Correlation measurements were performed with a Time Tagger Ultra module (Swabian Instruments GmbH).

Finesse

The finesse \({{{{{{{\mathcal{F}}}}}}}}\) value cited in this article was measured by focussing monochromatic (Δλ ≈ 30−40 kHz) laser light onto the cavity and measuring the reflected light intensity while scanning the length of the cavity by tuning the z-position of the nanopositioner piezo. By definition

$${{{{{{{\mathcal{F}}}}}}}}=\frac{{\nu }_{{{{{{{{\rm{FSR}}}}}}}}}}{\delta {\nu }_{{{{{{{{\rm{FWHM}}}}}}}}}}$$
(6)

where νFSR is the free spectral range (spacing between the resonances) of the cavity and δνFWHM is the full width at half maximum of the resonances, both in the frequency domain. This is translated to the spatial domain when the frequency of the light is kept constant and instead the length of the cavity is swept. For large \({{{{{{{\mathcal{F}}}}}}}}\) it follows that

$${{{{{{{\mathcal{F}}}}}}}}=\frac{{L}_{{{{{{{{\rm{FSR}}}}}}}}}}{\delta {L}_{{{{{{{{\rm{FWHM}}}}}}}}}},$$
(7)

where LFSR is the spacing of the resonances and δLFWHM is their full width at half maximum, both in the spatial domain. Exemplary data is shown in Fig. S7 from which the finesse can be determined.

Spin initialization

The spin initialization was done by resonant excitation of a spin-cycling optical transition inside a magnetic field. Within the 750 ns duration of such an initializing laser pulse, the spin state on resonance with the laser pulse gets depopulated. We pulsed on one transition and used the ratio of pulse amplitude Htotal = A + H and equilibrium signal height H to calculate the state fidelity

$$f=1-\frac{H}{2(A+H)}$$
(8)

of the initialization. We assume a thermal equilibrium state distributed 50/50 between the spin-up and the spin-down state. The slow initialization on the order of 70 ns of the spin state can be attributed to a low effective excitation power. We attribute this to be the main cause for the spin initialization fidelity below 1. Background from dark counts of the single photon counting modules accumulated during the measurement. This was corrected by subtraction of the average counts received outside the pulse times.