Abstract
Nitrogen vacancy (NV) centers are a major platform for the detection of nuclear magnetic resonance (NMR) signals at the nanoscale. To overcome the intrinsic electron spin lifetime limit in spectral resolution, a heterodyne detection approach is widely used. However, application of this technique at high magnetic fields is yet an unsolved problem. Here, we introduce a heterodyne detection method utilizing a series of phase coherent electron nuclear double resonance sensing blocks, thus eliminating the numerous Rabi microwave pulses required in the detection. Our detection protocol can be extended to high magnetic fields, allowing chemical shift resolution in NMR experiments. We demonstrate this principle on a weakly coupled 13C nuclear spin in the bath surrounding single NV centers, and compare the results to existing heterodyne protocols. Additionally, we identify the combination of NV-spin-initialization infidelity and strong sensor-target-coupling as linewidth-limiting decoherence source, paving the way towards high-field heterodyne NMR protocols with chemical resolution.
Similar content being viewed by others
Introduction
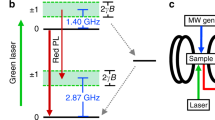
Nuclear magnetic resonance (NMR) is one of the most powerful analytical tools in medicine, chemistry, material science and physics1. Various attempts have been made to increase the sensitivity of the method to decrease the required sample sizes from millimeter to the micro- or even nanoscales2. One of the promissing avenues is the use of optically addressable paramagnetic centers, e.g. NV centers in diamond as sensors (illustrated in Fig. 1a). By combining high fidelity readout and long coherence times, NV centers provide an excellent platform for sensing of NMR signals. The optically detectable electron spin of the NV center allows for single electron spin detection at room temperature. Such single electron spins or a small ensemble of electron spins are used as nanoscale probes of their local environment, e.g. the magnetic field of a set of nuclei. Experiments rely on the observation of (modified) electron spin echo envelope modulation signals (ESEEM), e.g. using dynamical decoupling sequences such as Carr-Purcell-Meiboom-Gill (CPMG) and Knill dynamical decoupling3. In these techniques the precessing nuclear spins generate a time varying magnetic field at the location of the spin via the off-diagonal hyperfine coupling elements (\({B}_{z}=B(\langle {I}_{x}\rangle ,\langle {I}_{y}\rangle \cos ({\omega }_{L}t))\)4. This time varying field is detected by these pulse sequences, if. e.g. the pulse spacing in a CPMG sequence is exactly commensurate with ωL. These techniques were extended to correlation type sequences, e.g. 5 pulse ESEEM5,6, or correlation CPMG sequences7, with the possibility to increase the available correlation time to the ancillary nuclear spin memory lifetime used in the experiment6,8. However, in all of these techniques an intrinsic quantum sensor spin relaxation time T1 is the fundamental limit of the achievable spectral resolution for NMR signals. One method to overcome the limitation imposed by the quantum sensor T1 decay is the use of sequential measurements9,10,11,12 (see Fig. 1b). Each measurement is composed of electron spin initialisation, coherent interaction with the target nuclear spin during the electron pulse sequence and optical electron spin readout. Here one uses the fact that nuclear oscillations persist longer than the NV electron T1. Rather than probing this oscillations with a single run of an electron spin detection sequence, one can use multiple of those measurement runs and sample the nuclear oscillation in a phase coherent manner (see Fig. 1b). This technique has become state of the art in high resolution methods denoted as quantum heterodyne (qdyne) or coherent averaged synchronised readout (CASR)13, which has demonstrated a spectral resolution only limited by the external clock used to synchronize the pulse sequence. However, this technique requires the repeated application of MW-π-pulses to the electron spin, which need to be faster than the corresponding nuclear Larmor frequency to avoid a severe loss of sensitivity4. At a field of 3 T for example, the Larmor frequency of a proton spin is 120 MHz. Application of the sequential measurement scheme would thus require the application of pulses on the NV electron spin with pulse length well below 8 ns, which is technically hard to achieve. As a result, the conventional qdyne detection schemes are intrinsically difficult to extend to high magnetic fields, where however chemical shift and J-coupling resolution14 is easiest. Further on, at high-field NMR the thermal polarization becomes comparable to the statistical polarization already in smaller sample volumes, which would allow overcoming the diffusion limit of spectral resolution.
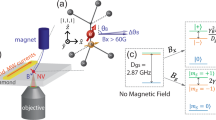
a The Nitrogen vacancy (NV) center with its internal 13C is studied as a model for a nano-scale surface Nuclear Magnetic Resonance (NMR) experiment with a diamond sensor. The target nuclei is coupled to the sensor via the longitudinal and transversal hyperfine coupling matrix elements Azz and Azx. b In the qdyne measurement schemes the nuclear precession is consequently probed by the electron spin during the measurement periods Mn. In our electron-nuclear-double-resonance quantum heterodyne (ENDOR qdyne) protocol the transverse polarization Ix of the nuclear spin is transferred to the z-axis with a \((\frac{\pi }{2})\) radio frequency (RF) pulse. The nuclear polarization along the z-axis can then be sensed by preparing the sensor electron spin in the superposition state with a \({(\frac{\pi }{2})}_{x}\) pulse and letting it evolve under the effective Hamiltonian \({\hat{S}}_{z}\otimes {\hat{I}}_{z}\), before a second pulse is applied and the sensor is read out. Afterwards the nuclear polarization along the z-axis is transferred back to Ix via a second RF pulse. Taking the polarization transfer of the nuclear spin due to the RF pulses into account, the effective Hamiltonian of the measurement is given by \({\hat{S}}_{z}\otimes {\hat{I}}_{x}\). In conventional qdyne schemes the (oscillating) transverse polarization of the nuclear spin is sensed directly via microwave (MW) pulse intensive dynamical decoupling (DD) sequences. In our experiment the Knill Dynamical Decoupling (KDD) sequence is used.
Recently, a heterodyne sensing principle was applied to high frequency signals, e.g. in the microwave band. By utilizing the interaction of an oscillating microwave field with the spin in the rotating frame, the signal is correlated to the phase of the external ref. 15,16,17.
In this work, we utilize this effect for a proof-of-principle heterodyne detection of NMR signals at moderate fields (B = 0.25 T). Rather than probing the nuclear Ix and Iy components which give rise to fast oscillating signals, we use a phase coherent radio frequency (RF) pulse to convert both components to Iz. The method proposed and investigated in this work combines previously used electron-nuclear double resonance (ENDOR) methods12,18 with time efficient signal sampling through quantum heterodyne measurements9,10,13. Additionally, we experimentally study the NMR spectral resolution of the protocol and outline its practical application.
Results and discussion
An isolated nuclear spin in a magnetic field B precesses freely around the z-axis with the Larmor frequency ωL = γNB, where γN denotes the nuclear gyromagnetic ratio. As a result, information about ωL can be obtained from the oscillating expectation value of the nuclear spin-1/2 operators \({\hat{I}}_{x}\) and \({\hat{I}}_{y}\). In a classical qdyne detection scheme the phase information of the time-evolution of e.g. \(\langle {\hat{I}}_{x}\rangle\) is sensed by the electronic sensor spin via dynamical decoupling (DD) sequences (see Fig. 1b). These sequences generate an effective Hamiltonian of the form \({\hat{H}}_{{{{{{{{\rm{eff}}}}}}}}}\propto {\hat{S}}_{z}\otimes {\hat{I}}_{x}\), where \({\hat{S}}_{z}\) is the electron spin operator19. This however requires the application of pulses on the timescale of the Larmor frequency ωL, which for protons easily reaches values larger than 100 MHz and hence requires DD pulses with lengths < 10 ns. As of today, this is technically very hard to achieve. In this work, we circumvent the necessity for pulse-intensive DD sequences by mapping the phase information of \(\langle {\hat{I}}_{x}\rangle\) to \(\langle {\hat{I}}_{z}\rangle\) with a 3π/2 pulse to the nuclear spin prior to the sensing step. Subsequently, information of \(\langle {\hat{I}}_{z}\rangle\) can be sensed by the sensor spin via the effective Hamiltonian of the hyperfine interaction \({\hat{H}}_{{{{{{{{\rm{eff}}}}}}}}}=2\pi {A}_{zz}{\hat{S}}_{z}{\hat{I}}_{z}\). Besides being a static interaction, a further advantage is, that unlike for the direct sensing of \(\langle {\hat{I}}_{x}\rangle\), a rich variety of doubly dressed sensing protocols like ENDOR, DEER5 or the recently developed DDRF20 sequences can be applied during the sensing period. After the sensing sequence and successive readout of the electron spin, the nuclear spin is rotated back into the x-y-plane by application of another π/2 pulse, before beginning the next precession period. To enable the correct back-rotation of the nuclear spin into the x-y-plane, the measurement protocol requires a nuclear phase acquisition of β = 2πk (k = integer) during the sensing period. This objective can be accomplished by either resonantly driving the nuclear spin or introducing additional RF π pulses to refocus it during this time. A direct comparison of the DD-based and ENDOR qdyne pulse sequences is shown in Fig. 1. In our experiment a phase coherent RF source with frequency ωi is employed to realize the RF pulses, which effectively translates the nuclear system to the rotating frame of the RF source and converts the precession frequency down, yielding the heterodyne response illustrated in Fig. 2. After a free precession period τfid and the first π/2 pulse of the n-th measurement cycle 〈Iz〉 is given by
By measuring this value weakly21,22 with the measurement strength α, the phase information (ωL − ωi)τfid is mapped onto the sensor spin with
where the back action of the measurement has been neglected. As a result the Larmor frequency of the target spin can be recovered from the readout of \({\hat{S}}_{z}\) of the sensor spin. A more detailed explanation of the theoretical background of our method and the effects of backaction on our experiment are presented in Supplementary note 2.
The heterodyne detection schemes compares the phase of the Larmor precession of the target spin (blue line) with the phase of the coherent RF driving source (red line). During the free precession time τfid the nuclear spin acquires a phase of Δωτfid, where Δω is the detuning of the RF frequency from the Larmor frequency. The phase information (incorporated in 〈Ix〉, dark-green line) is then transferred to the Iz (green line) and read out via the sensor spin (yellow line) during the time τsens, before being transferred back to Ix. The application of a coherent RF source enables the effective down-conversion of the nuclear Larmor frequency from ωL to Δω. The evolution of the nuclear spin (red arrow) during one representative iteration of the measurement sequence, consisting of free evolution, first RF pulse, sensing period and second RF pulse, is also visualized in the bottom panel.
Weak measurement of a single 13C nuclear spin
To demonstrate the ENDOR qdyne experiment we probe the spin dynamics of a single weakly coupled 13C nucleus in the vicinity of the NV center in a proof-of-principle experiment. The coupling strength between the 13C and the NV sensor reflects the coupling conditions which are also found for sample nuclei on the diamond surface. The interaction of the single 13C with the NV is given by the hyperfine interaction via a long range dipolar coupling of \(\hat{H}=2\pi {A}_{zx}{\hat{S}}_{z}{\hat{I}}_{x}+2\pi {A}_{zz}{\hat{S}}_{z}{\hat{I}}_{z}\). Experimentally the Azx interaction is used to initialize the 13C nuclear spin via the polarization exchange sequence (pulse-pol)23, while the Azz term is responsible for the signal acquired with our NV center via the proposed scheme. We study a 13C with hyperfine coupling Azz = 6 kHz. This nucleus was chosen as the coupling is sufficient to get a weak signal within the decoherence time of the sensor (\({T}_{2}^{* }=50\,\mu {{{{{{{\rm{s}}}}}}}}\)), while still being smaller than the nuclear Rabi frequency \({\Omega }_{{}^{13}{{{{{{{\rm{C}}}}}}}}}=15\,{{{{{{{\rm{kHz}}}}}}}}\). The latter, allows robust RF control of the nuclear spin with respect to the NV center charge and spin state infidelities. The proof of principle experiment follows the sequence shown in Fig. 3a. Due to the limited coherence time of the nuclear carbon spin, the introduction of additional RF π pulses (33 μs) into measurement sequence would result in an insufficient number of data points to extract the nuclear spin precession from the experimental data. As a result the experiment is performed with a resonant RF source. The 13C is initialized via the pulse-pol scheme23 and is prepared in the superposition state \(\vert {+}_{{{{{{{{\rm{y}}}}}}}}}\rangle\) with a (π/2)ref-pulse from the coherent RF source. After a free precession time, the spin is rotated to the measurement basis Iz via a second pulse (3π/2)ref+Φ, where the phase of the following pulses are cycled with a shift of Φ along the z-axis to move the demodulation frequency to 1/4 of the sampling frequency. The 13C 〈Iz〉 is mapped with a Ramsey sequence onto the NV sensor spin 〈Sz〉, which is optically readout. The 13C is rotated back with (π/2)ref+Φ. The protocol is repeated M times. A detailed description of the experimental design and the data analysis is provided in Supplementary Note 3. In Fig. 3b the experimental result from the described sequence is shown. Fourier transformation of the obtained ENDOR qdyne signal yields a 13C Larmor frequency of 2.336 ± 0.018 kHz, with a signal decay rate of Γ = 0.6 ± 0.1 kHz. The nuclear 13C signal is therefore at the expected frequency 2.368 kHz and decays with a rate of Γ = 0.6 ± 0.1 kHz, where the associated spectrum is visualized in Fig. 3c. To further characterize the heterodyne response of our measurement sequence, we also applied it to the 14N within the NV center (see Supplementary note 2). In the following we analyze the obtained linewidth and compare it to the conventional qdyne measurement (see Fig. 4a, b).
a Sensing sequence of the proof of principle experiment. The 13C spin is hyperpolarized with the pulse-pol sequence before the nuclear spin precession is initiated with a (π/2)ref pulse from the reference RF source. The nuclear spin evolves freely during τfid (10 μs) and gets rotated to the z-basis with a second (π/2)ref pulse from the same source. The z-component of the polarization is measured with a Ramsey sequence on the sensor spin ((π/2)x − (π/2)y) during τsens (15 μs) and the sensor spin is readout with a laser pulse at time Ti. Finally the nuclear spin is rotated back with a (3π/2)ref pulse, continuing its free evolution. The Rabi period of the applied RF pulses is 66 μs. Inclusion of the repolarization time (2.5 μs), readout time (1.9 μs) and an additional wait time (10 μs) after the RF pulse leads to a sampling time of 105.5 μs. b Experimental measurement of the nuclear evolution under the protocol above at resonance. The experimental time trace (blue) is fitted by an exponentially decaying cosine (orange). For the proof of principle the free evolution of the target spin was implemented as a phase shift in the 3π/2 pulse with Φ = π/2, leading to a normalized signal periodicity of 4 × 105.5 μs. The decay rate of the signal is Γ = 0.6 ± 0.1 kHz. The spectrum of the signal with a peak at 2.368 kHz is shown in c (blue) alongside the Fourier spectrum of the fit (green) and the residuals of the fit (orange) from b.
a Conventional dynamical decoupling (DD) -based heterodyne detection protocol22,34. The 13C spin is hyperpolarized with the pulsepol sequence and the nuclear spin precession is initiated with a (π/2)ref pulse from the reference radio frequency (RF) source. The nuclear spin evolves freely while interacting with the sensor spin through a Knill-Dynamical-Decoupling (KDD) sequence during the sensing block (blue) and the free evolution time τfid (see Fig. 1b). The sensor is readout with a laser pulse and a wait time is added to adjust the total sequence time (see Supplementary Note 4). This block is repeated M times. b Conventional quantum heterodyne (qdyne) signal (blue) from the sequence above with a decay rate of Γ = 1.4 ± 0.3 kHz from the exponentially decaying cosine fit (orange). c Comparison of the measurement back-action corrected lifetimes for different NV-13C pairs with conventional qdyne (blue) and electron-nuclear-double-resonance (ENDOR) qdyne (orange). The lowest decay rate of 27 ± 9 Hz appears in the NV-13C pair with Azz ≤ 70 Hz.
Linewidth and projected spectral resolution
Magnetic resonance spectroscopy relies on high spectral resolution which is typically achieved by qdyne experiments on weakly coupled nuclear spins9. Our qdyne experiment relies on a modified ENDOR experiment and measures nuclear spins with a rather large hyperfine coupling. Therefore we discuss the impact of coupling strength on the NMR linewidth. We quantify our spectral resolution in comparison to conventional dynamical decoupling based qdyne (conventional qdyne). The interaction between electron and nuclear spin is determined by a static Azz component and the oscillating component Azx. At high magnetic fields along the z-axis Azz is the dominant term. To quantify the impact of the coupling strength on the observed linewidth, Fig. 4c shows an experimental comparison between ENDOR qdyne and the conventional qdyne. We investigated 13C nuclei with different Azz couplings.
The decay constant of the conventional qdyne was measured to be Γ = 1.4 ± 0.3 kHz and agrees well with the decay rate of the ENDOR qdyne measurement on the same nuclear spin. As both methods show similar decay rates, we performed an investigation of its origin by studying the decoherence across a large range of Azz couplings with the conventional qdyne. In Fig. 4c, we compared four 13C nuclei and find that the three 13C nuclei with Azz > 3 kHz show a decay rate of about 1 kHz, while only the 13C nucleus with Azz ≤ 0.07 kHz, also discussed in ref. 24,25, shows a decay rate of 27 ± 9 Hz.
We now discuss the observed decay, i.e. the NMR linewidth. In a diamond crystal with 0.01 % 13C concentration one expects an intrinsic NMR linewidth of around 10 Hz. In our experiments however, we detect linewidth between 1000 to 27 Hz, depending on the hyperfine coupling. There are multiple effects that cause the observed increase in NMR linewidth. The sequential measurement scheme is based on multiple readout and initialisation sequences during the whole measurement cycle. These sequences involve laser pulses which excite the NV electron spin. In the excited state the electron spin wavefunction is markedly different which causes a change in Azz hyperfine interaction of the 13C nucleus16. Although the resulting phase error is small because of the short lifetime of the excited state the accumulated total phase error may be substantial because the sequence involved multiple readout steps. Next, charge state switching of the NV between measurements is a possible mechanism. Upon optical excitation the charge and hence spin state of the NV changes between NV− (S = 1) and NV0 (S = 1/2). The known fast nuclear spin relaxation in NV08 and the drastic change in spin quantum number leads to a marked increase in nuclear spin relaxation time. Lastly, the initialisation infidelity of the NV− electron spin state26 can shorten the lifetime27 of the nuclear spin coherence. The pulse sequence is designed such that the NV center is initialized in the ms = 0 state at the beginning of each probing of the nuclear spin state (see Fig. 3a). Any false initialization, which happens with a probability of p = 1 − f will result in the nuclear spin picking up a large phase error. Here f denotes the fidelity for the initialization process into the spin state ms = 0 (f ≈ 0.9). During the time τmeas between successive measurements shown in Fig. 1b the effective change in the nuclear Larmor frequency is 6.0 kHz which results in a phase difference of Azzτmeas = 0.63 rad with the probability 1 − f. When averaging the recorded nuclear spin precession over multiple measurement cycles, the random phase shifts introduce a decay of the coherent nuclear precession, yielding an exponentially decaying cosine signal with an effective decay rate Γ, given by
as derived in Supplementary note 5. A quantitative study of the relation between decay rate Γ and the measurement time τmeas is given in Supplementary note 6. Some insight on the importance of the three mechanisms come from an analysis of Fig. 4c. The figure shows the measured nuclear spin relaxation rate as a function of the nuclear hyperfine coupling. The first two mechanisms scale with \({({A}_{zz})}^{2}\), as they originate from a random walk, and therefore cannot explain the observed functional behaviour. Only the decoherence mechanism based on spin initialisation infidelity is in the right order of magnitude ( ≈ 1 kHz for Azz = 6 kHz, τmeas = 105 μs and f = 0.9) and shows a functionality which is similar to the observed dependence, see Supplementary note 5.
Independent of the exact description of the mechanisms for decoherence, the comparison between conventional qdyne and ENDOR qdyne yields that the spectral resolution limits are similar. We find that qdyne, can measure very small Azz → 0, resulting in a sensor unlimited spectral resolution below 30 Hz. Such small couplings are hard to reach by ENDOR qdyne because for measurements on single nuclear spins the phase provided by Azzτsens needs to be large enough to result in a sufficient change in the electron spin sensor readout signal. As we are using an electron spin Ramsey sequence the time for acquiring this phase is limited by the electron \({T}_{2}^{* }\), i.e. around 10 μs. The resulting phase difference is too small to be detected for small Azz couplings. This is intrinsically different from the DD detection of NMR where the interaction time is around 1ms. However, in the case of a small ensemble of nuclear spins, the ENDOR qdyne could be advantageous (see Fig. 5). Distant ensembles of weakly coupled nuclear spins are desirable for high spectral resolutions in nanoscopic surface NMR experiments. In these cases the Azz coupling strength typically coincides with the performance range of ENDOR qdyne. For example, an Azz coupling below 70 Hz is reached when the 13C (1H) is ≈4.5 nm (≈7 nm) away from the NV center along the z axis. The loss of coupling strength and therefore signal size has to be compensated by sensing an ensemble of nuclear spins with an ensemble of NV centers, as already applied with conventional qdyne in ref. 13,28.
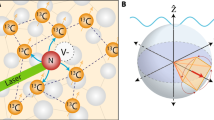
a Schematic of the extension of the sensing scheme to sample detection. Only the target spins with sufficient Azz coupling (red spins) will be detected by our measurement scheme. b Relation between implantation depth of the NV centers and the detected linewidth. By increasing the depth of the NV centers, the dipolar coupling via Azz decreases, resulting in a decreasing linewidth of the ENDOR qdyne protocol (see Eq. (3)). For example, a linewidth of 1 Hz is predicted at dNV = 4.2 nm for 1H target spins (grey line). However, as the Azz coupling decreases, the number of detected target spins has to increase to maintain sufficient signal quality. The orange lines represent the necessary number of detected 1H target spins to reach a SNR of 3 in a 10 min measurement cycle with 100 points. For the case of dNV = 4.2 nm104 target spins in the detection volume are sufficient if a NV ensemble of 1000 sensor spins is used. This can easily be achieved, as the dashed orange line shows the number of 1H target spins of a water sample in the detection volume of the sensor when thermal polarization in a 3 T bias field is considered.
A detailed investigation into the trade-off between achieved sensitivity and magnetic susceptibility for our system is given in Supplementary note 6.
Conclusions
In summary we presented a nanoscale NMR protocol that is based on a heterodyne measurement via double resonance. Hereby the advantages of heterodyne sensing schemes are adjusted to enable application in high-field scenarios. We showed weak measurements of a single 13C nuclear spin with our protocol. The extracted linewidth was compared to conventional qdyne methods and we found that the linewidth is intrinsically limited. Finally we discussed the effective sensitivity of heterodyne sensing and the service costs involved. The experimental demonstration of the proposed protocol under high magnetic fields to verify the predicted advantage over DD-based methods requires further work.
Double resonance qdyne is particular interesting for nano- to micron-scale NMR sensing scenarios, outlined in Figs. 1a and 5. In this scenario, an ensemble of nuclear spins is coupled to the NV sensor spins13,28. This means that the linewidth is not affected by the hyperfine dynamics like in our demonstrator experiment and the same spectral resolution as conventional qdyne can be achieved. In the future, ENDOR qdyne could be combined with echo-type measurement schemes18 or homo- and heteronuclear decoupling sequences29 improving the spectral resolution for solids and dipolar interacting samples. The removed constraints on the microwave power allow us to apply this method to high magnetic fields, e.g. optical detected magnetic resonance with NVs at 8 T30. A high magnetic field leads to an increased thermal polarization equal to larger signals or equivalently reduced sensing volumes14. Additionally, the sensitivity to chemical shifts increases, allowing to study of proteins or short-lived molecules31. In the preparation of the manuscript, we became aware of a similar theoretical work32. In the future, the measurement block of our protocol could be extended to the more advanced double resonance schemes e.g. proposed in the recent work32 and combined with multidimensional sequences (e.g. COSY33).
Methods
Experimental setup
The experiments were conducted with a confocal room temperature single NV setup depicted in Supplementary Fig. 1. The NV is excited in the phonon sideband with a green 520 nm laser. This initializes and readouts the NV electron spin state. The red fluoresence of the NV is detected with an avalanche photo diode (APD) before passing through a wedged mirror, a pinhole 50 μm and a long pass filter 650 nm. The diamond sample is a 2 mm × 2 mm × 80 μm, (111)-oriented polished slice from a 12C - enriched (99.995 %) diamond crystal. The crystal was grown by the temperature gradient method under high-pressure high-temperature conditions at 5.5 GPa and 1350 ∘C, using high-purity Fe-Co-Ti solvent and high-purity 12C-enriched solid carbon. The single NV centers were created from intrinsic nitrogen by irradiaton with 2 MeV electrons at room temperature with a total fluence of 1.3 ⋅ 1011 cm−1 and annealed at 1000 ∘C (for 2 h in vacuum). The typical lifetimes for the NV centers in this slice are \({T}_{2}^{* }=50\,\mu s\) and T2 ≈ 300 μs15,21. The diluted 13C bath in the latice leads to a electron \({T}_{2}^{* }\) time of 50 μs and usually only one 13C is significantly coupled to a single NV center. The nuclear and electron spins are manipulated with an arbitrary waveform generator, able to sample 12 GSamples/s, with two channels. The MW channel is amplified with a Hughes-Traveling Wave Tube 8010H amplifier (TWT, max. 7 MHz Rabi frequency), while the RF channel is amplified with Amplifier Research 150A250. They are combined with a combiner before the both connect to the coplanar waveguide where the diamond is glued to. We use a 3 axis piezo-positioner stage (range 100 × 100 × 25 (μm)3) from npoint. This allows us to keep a single NV in focus. The setup of the experiment is visualized in Supplementary Note 1.
For the proof of principle we searched for a single NV center with a moderate 13C with Azz coupling with a stimulated echo sequence8. Moderate means that the coupling is smaller than the RF Rabi frequency for 13C of 15 kHz, while still being strong enough coupled to address it within the \({T}_{2}^{* }\) time. We found NV#5 which has a coupling of Azz = 6 kHz. For the comparison of the natural linewidth we studied other NV centers within the 100 × 50 × 5 (μm)3 volume. A list of all used variables can be found in Supplementary Note 7.
Data availability
Data supporting the findings of this study are available in a public data repository under following link: https://doi.org/10.18419/darus-3728.
References
Ernst, R. R. Nuclear magnetic resonance fourier transform spectroscopy. Biosci. Rep. 12, (1992).
Casey, W. H., Wang, Z., Brandt, N. & Curro, N. The promise of optical nmr spectroscopy for experimental aqueous geochemistry. Am. J. Sci. 320, 533–545 (2020).
Souza, A. M., Álvarez, G. A. & Suter, D. Robust dynamical decoupling. Philos. Trans. R. Soc. A: Math., Phys. Eng. Sci. 370, 4748–4769 (2012).
Casanova, J., Wang, Z.-Y., Schwartz, I. & Plenio, M. B. Shaped pulses for energy-efficient high-field nmr at the nanoscale. Phys. Rev. Appl. 10, 044072 (2018).
Schweiger, A. & Jeschke, G. Principles of pulse electron paramagnetic resonance (Oxford University Press on Demand, 2001).
Laraoui, A. et al. High-resolution correlation spectroscopy of 13c spins near a nitrogen-vacancy centre in diamond. Nat. Commun. 4, 1651 (2013).
Staudacher, T. et al. Nuclear magnetic resonance spectroscopy on a (5-nanometer) 3 sample volume. Science 339, 561–563 (2013).
Pfender, M. et al. Nonvolatile nuclear spin memory enables sensor-unlimited nanoscale spectroscopy of small spin clusters. Nat. Commun. 8, 1–12 (2017).
Schmitt, S. et al. Submillihertz magnetic spectroscopy performed with a nanoscale quantum sensor. Science 356, 832–837 (2017).
Boss, J. M., Cujia, K., Zopes, J. & Degen, C. L. Quantum sensing with arbitrary frequency resolution. Science 356, 837–840 (2017).
Zaiser, S. et al. Enhancing quantum sensing sensitivity by a quantum memory. Nat. Commun. 7, 1–11 (2016).
Aslam, N. et al. Nanoscale nuclear magnetic resonance with chemical resolution. Science 357, 67–71 (2017).
Glenn, D. R. et al. High-resolution magnetic resonance spectroscopy using a solid-state spin sensor. Nature 555, 351–354 (2018).
Schwartz, I. et al. Blueprint for nanoscale nmr. Sci. Rep. 9, 1–11 (2019).
Meinel, J. et al. Heterodyne sensing of microwaves with a quantum sensor. Nat. Commun. 12, 1–8 (2021).
Chu, Y. et al. Precise spectroscopy of high-frequency oscillating fields with a single-qubit sensor. Phys. Rev. Appl. 15, 014031 (2021).
Staudenmaier, N., Schmitt, S., McGuinness, L. P. & Jelezko, F. Phase-sensitive quantum spectroscopy with high-frequency resolution. Phys. Rev. A 104, (2021).
Mamin, H. et al. Nanoscale nuclear magnetic resonance with a nitrogen-vacancy spin sensor. Science 339, 557–560 (2013).
Ma, W.-L. & Liu, R.-B. Angstrom-resolution magnetic resonance imaging of single molecules via wave-function fingerprints of nuclear spins. Phys. Rev. Appl. 6, 024019 (2016).
Bradley, C. E. et al. A ten-qubit solid-state spin register with quantum memory up to one minute. Phys. Rev. X 9, 031045 (2019).
Pfender, M. et al. High-resolution spectroscopy of single nuclear spins via sequential weak measurements. Nat. Commun. 10, 1–8 (2019).
Cujia, K., Boss, J. M., Herb, K., Zopes, J. & Degen, C. L. Tracking the precession of single nuclear spins by weak measurements. Nature 571, 230–233 (2019).
Schwartz, I. et al. Robust optical polarization of nuclear spin baths using hamiltonian engineering of nitrogen-vacancy center quantum dynamics. Sci. Adv. 4, eaat8978 (2018).
Meinel, J. et al. Quantum nonlinear spectroscopy of single nuclear spins. Nat. Commun. 13, 5318 (2022).
Vorobyov, V. V. et al. Transition from quantum to classical dynamics in weak measurements and reconstruction of quantum correlation. Phys. Rev. A 107, 042212 (2023).
Song, Y. et al. Pulse-width-induced polarization enhancement of optically pumped nv electron spin in diamond. Photonics Res. 8, 1289–1295 (2020).
Maurer, P. C. et al. Room-temperature quantum bit memory exceeding one second. Science 336, 1283–1286 (2012).
Liu, K. S. et al. Surface nmr using quantum sensors in diamond. Proc. Natl Acad. Sci. 119, (2022).
Waugh, J. S., Huber, L. M. & Haeberlen, U. Approach to high-resolution nmr in solids. Phys. Rev. Lett. 20, 180 (1968).
Fortman, B. et al. Electron–electron double resonance detected nmr spectroscopy using ensemble nv centers at 230 ghz and 8.3 t. J. Appl. Phys. 130, 083901 (2021).
Lovchinsky, I. et al. Nuclear magnetic resonance detection and spectroscopy of single proteins using quantum logic. Science 351, 836–841 (2016).
Munuera-Javaloy, C., Tobalina, A. & Casanova, J. High-resolution nmr spectroscopy at large fields with nitrogen vacancy centers. Phys. Rev. Lett. 130, 133603 (2023).
Smits, J. et al. Two-dimensional nuclear magnetic resonance spectroscopy with a microfluidic diamond quantum sensor. Sci. Adv. 5, eaaw7895 (2019).
Cujia, K. S., Herb, K., Zopes, J., Abendroth, J. M. & Degen, C. L. Parallel detection and spatial mapping of large nuclear spin clusters. Nat. Commun. 13, 1260 (2022).
Acknowledgements
We acknowledge financial support by European Union’s Horizon 2020 research and innovation program ASTERIQS under grant No. 820394, European Research Council advanced grant No. 742610, SMel, Federal Ministry of Education and Research (BMBF) project MiLiQuant and Quamapolis, the DFG (FOR 2724), the Max Planck Society, and the Volkswagentiftung.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
J.M. and V.V. came up with the initial idea of the experiment, and designed the experiment. J.M., V.V., M.K. and J.W. performed the initial experiment, J.M., V.V. and J.W. analyzed the experimental data, J.M., R.M. and V.V. performed additional required experiments and numerical simulations. D.D. provided theoretical support. H.S., S.O. and J.I. manufactured and characterised the diamond sample. V.V., J.M., R.M and J.W. wrote the text of the manuscript. All authors read and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks Jeong Hyun Shim and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Meinel, J., Kwon, M., Maier, R. et al. High-resolution nanoscale NMR for arbitrary magnetic fields. Commun Phys 6, 302 (2023). https://doi.org/10.1038/s42005-023-01419-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-023-01419-2
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.