Abstract
Recent findings of structural glasses with extremely high kinetic and thermodynamic stability have attracted much attention. The question has been raised as to whether the well-known, low-temperature “glassy anomalies” (attributed to the presence of two-level systems [TLS] and the “boson peak”) persist or not in these ultrastable glasses of much lower configurational entropy. To resolve previous contradictory results, we study a particular type of ultrastable glass, TPD, which can be prepared by physical vapor deposition in a highly-stable state with different degrees of layering and molecular orientation, and also as a conventional glass and in crystalline state. After a thorough characterization of the different samples prepared, we have measured their specific heat down to 0.4 K. Whereas the conventional glass exhibits the typical glassy behaviour and the crystal the expected Debye cubic dependence at very low temperatures, a strong depletion of the TLS contribution is found in both kinds of ultrastable glass, regardless of their layering and molecular ordering.
Similar content being viewed by others
Introduction
After more than one century of intense research, the phenomenon of the glass transition (the solidification of a liquid without crystallization) and many of the physical properties of glasses continue to be the subject of controversy and lively discussions1,2,3,4,5,6,7,8,9,10,11,12,13,14.
Glasses are liquids that have been supercooled out of thermodynamic equilibrium, avoiding crystallization. The glass transition in the laboratory is a kinetic transition. However, when thermodynamic magnitudes are measured, the glass transition looks like a second-order phase transition, with finite discontinuities in second derivatives of the Gibbs free energy, such as the specific heat. Hence, in contrast to the first-order divergence for the melting of a crystal, glass transitions are typically observed as a jump in heat capacity with a small overshoot depending on the employed heating rate. Nonetheless, there are complicated unsolved questions related to this apparent phase transition. For instance, if one cools the liquid at a slower rate, the deviation from the equilibrium curve occurs at a lower glass-transition temperature Tg. This is a serious problem to consider it a proper phase transition temperature. Furthermore, since the glass is in a non-equilibrium state, it exhibits time-dependent relaxation. So, by isothermal annealing of a glass below Tg (or simply by aging at room temperature), the thermodynamic magnitudes can be relaxed to lower, more stable values.
There is not a unique, widely accepted theory of the glass transition. The essential reason of the problem is probably that the glass transition is a complex combination of kinetics and thermodynamics. There is, nevertheless, a very useful framework often employed for interpreting the complex phenomenology of glasses and supercooled liquids: the potential-energy landscape (PEL)15,16, illustrated, for instance, in Fig. 3 of ref. 17. In brief, the PEL is a schematic topographic view of the potential-energy hypersurface of any glass-forming material. It is plenty of local minima and saddle points for thermal energies below the melting point (Tm) of the crystalline state, which is associated with the absolute energy minimum. Much has been speculated about the existence of an “ideal glass” which should correspond to the best and most stable possible glass achievable, associated with the lowest relative minimum, of course still above the energy of the crystalline absolute minimum. Moreover, this "ideal glass" may well correspond to the limiting case of zero configurational entropy of a liquid eventually supercooled down to the Kauzmann temperature18, where an underlying thermodynamic phase transition might occur.
Besides the abovementioned supercooled-liquid to glass-state transition and related relaxational effects at higher temperatures, also in the solid state at very low temperatures the situation is complex and not well understood. It is well likely that the origin of such complexity is that most of the “anomalous” glassy features are interrelated. Among the particular physical properties of non-crystalline solids, one of the most conspicuous issues is that of the low-temperature properties of glasses (comprising thermal, vibrational, acoustic or dielectric properties), unexpectedly very different from those found in their crystalline counterparts, and at the same time very similar among themselves. For instance, the specific heat at the lowest temperatures is dominated by a linear term ascribed to the existence of tunneling states or two-level systems (TLS) in glasses, whereas the thermal conductivity exhibits a quadratic T2 dependence, followed by a plateau, both behaviors clearly deviating from the Debye theory fulfilled by crystalline solids1,14. Most of these properties are independent of the type of substance or its chemical bonding, hence the usual reference to “universal properties of glasses”1,2,14,19. These “anomalies” were initially only ascribed to structural glasses, i.e., amorphous solids, but soon other materials such as mixed crystals or orientationally-disordered crystals (often also named as “orientational glasses”), and even many other more or less disordered crystals, were found to exhibit this ubiquitous and striking “glassy behavior” at low temperatures14.
Since the 1970’s, many experiments were devoted to investigating whether those low-temperature anomalous excitations would gradually decrease or even disappear, when decreasing enthalpy and entropy of the glass by means of typical annealing or aging stabilization processes. Due to the obvious limitations of time (many millions of years are expected to be necessary to stabilize a glass with minimal entropy), the obtained results from those modest thermal treatments were usually unclear or even contradictory.
Nevertheless, highly-stable glasses have recently been identified or prepared, raising interest and hope of successfully addressing these issues. Previous works on amorphous silicon films reported20 an absence of the glassy features at low temperatures mentioned above, that were later shown to be dependent on deposition conditions21,22. Furthermore, ultrastable glasses obtained by physical vapor deposition (PVD) of typically organic molecular substances, by employing particular deposition rates (~0.1 nm/s) and temperatures (≈0.85 Tg), were demonstrated to exhibit extremely high thermodynamic and kinetic stability17,23,24,25,26. Then, specific-heat measurements of ultrastable indomethacin (IMC) glasses prepared by PVD were published27, where the linear term attributed to TLS was completely suppressed in samples deposited under high stability conditions, while a usual linear term was observed for samples of the same material with ordinary deposition conditions. This behavior has been recently supported by swap Monte Carlo computer simulations, which have found a depletion of the TLS in computer glasses with increasing stability28,29. Nonetheless, the very nature of computer glasses is not straightforwardly related to that of real structural glasses.
It should be noted, however, that there is a notable exception to this behavior in highly stable glasses. A significant linear coefficient on the specific heat at the lowest temperatures, ascribed to the “universal” presence of TLS in glasses, was found to persist invariant in geologically hyperaged glasses of amber (a typical polymer glass)30,31,32, when comparing the pristine samples (up to 110 My aged) to the rejuvenated samples. One possible difference to take into account between standard glasses and PVD glasses is that the former are essentially homogeneous and isotropic, whereas the latter typically exhibit anisotropic packing and layered structures33,34,35,36 that can play a role in different properties37,38,39,40,41,42. In fact, the anisotropy of IMC ultrastable glasses was argued in ref. 27 as a possible origin of the suppression of TLS in opposition to the case of highly-stable amber glasses.
Beyond the fundamental interest of this topic in condensed matter physics, the presence and behavior of TLS in disordered solids have recently been found most relevant for quantum technological applications, such as superconducting qubits for quantum computation or gravitation wave detectors43,44,45,46,47. Specifically, the major source of noise and decoherence in superconducting circuits typically made from aluminum or niobium, comes from the losses generated by these TLS or atomic tunneling excitations within the amorphous oxide layers encasing them.
Therefore, the natural conclusion is that more experiments on this matter are needed, mainly where the issue of anisotropy or any other variable deemed relevant could be controlled independently. To shed light on this issue, we have identified a substance, namely N,N—bis(3-methylphenyl)_N,N-bis(phenyl)-benzidine (TPD), an organic molecular solid, where various relevant parameters can be tuned separately. Besides, it presents a very convenient Tg slightly above room temperature48,49.
Results and discussion
As described in Methods more in detail, we have studied TPD glasses grown by PVD in three different conditions: anisotropic glass with the highest stability (deposited at 285 K); isotropic glass but also with high stability (deposited at 300 K); and isotropic, conventional glass (deposited at Tg = 333 K). Control samples grown simultaneously with the ones for low-temperature measurements were characterized by Differential scanning calorimetry (DSC), X-ray diffraction (XRD), ultraviolet/visible (UV/Vis) spectroscopy and high-resolution Brillouin spectroscopy (HRBS).
Differential scanning calorimetry
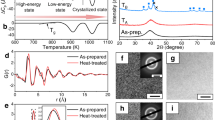
Figure 1 shows the calorimetric scans obtained at 10 K/min from the two most stable samples, deposited at 285 K (0.85 Tg) and 300 K (0.9 Tg), respectively. The small difference in the onset of devitrification (built by intersection of the dashed lines as shown) of the sample grown at 0.9 Tg (Ton = 360 K) with respect to the one grown at 0.85 Tg (Ton = 363.3 K) indicates its slightly lower kinetic stability. The left wing of the devitrification peak of the 285 K sample is caused by the front transformation initiating at the many surfaces that emerge from cracking when the Al foil is wrapped to fit it in the Al pan. This is more evident in the more stable glass due to its retarded bulk glass transition temperature. The respective second upscans, measured after the previous heating to 380 K and immediate cooling down at −10 K/min, are also shown, which correspond to the conventional glass state, where the devitrification onset Ton shifts down about 30 K and the big overshoot due to the huge enthalpy release characterizing stable glasses has disappeared, as expected.
DSC curves for stable glasses deposited at 0.85 Tg (black lines) and 0.9 Tg (red lines), where Tg is the glass transition temperature. Both first upscans at 10 K/min up to 380 K −exposing the thermodynamic history of the stable glass− and second upscans −after the sample has transformed into the conventional glass by cooling the liquid at −10 K/min− are depicted. The corresponding devitrification temperatures Ton of each case (assessing the degree of kinetic stability) are graphically shown.
X-ray diffraction
The glassy nature of the sample and the presence of layering was investigated by Wide angle X-ray Scattering (WAXS) as shown in Fig. 2. The most remarkable feature of the XRD spectra is the difference in the intensity and position of the low-angle peak (vertical dotted blue lines) located at around 2θ ≈ 5−6° from samples grown at 285 and 300 K. This peak has been related to the existence of layering in the z direction50. The sample grown at 0.9 Tg has the peak maximum at 2θ = 5.340° which accounts for an average vertical distance of 16.55 Å, while the sample grown at 0.85 Tg has the maximum at 6.15° which translates into 14.35 Å of vertical separation. The low-angle feature of the former Tdep = 300 K sample is also more intense which may be indicative of stronger layering in this sample. We note that the conventional glass exhibits a similar diffraction pattern to that of the sample grown at 285 K (0.85 Tg) in terms of intensity, with the lowest angle peak maximum at 2θ = 5.340°. This is indicative of a similar level of layering as the most stable glass.
Ultraviolet/visible spectroscopy
For TPD, two main electronic transitions can be observed in the UV-Vis spectra, at 355 nm (3.50 eV) and 315 nm (3.95 eV), as shown in Fig. 3a. The lower energetic transition is associated to the HOMO-LUMO transition. The HOMO state of the molecule is electronically distributed along the molecule, having contributions from the amines, the biphenyl core and the C rings at the peripheral ends of the molecule. The LUMO of this low energetic transition is heavily centered on the biphenyl core, implying that the transition dipole moment of the molecule will be oriented along the long axis of the molecule. On the other hand, the higher energetic transition comprises two almost degenerated transitions, arising from HOMO-(LUMO + 2) and HOMO-(LUMO + 3). In this case, (LUMO + 2) and (LUMO + 3) are electronically localized at the peripheral C rings of the molecule. This transition has two different associated transition dipole moments, both oriented in the perpendicular plane of the long axis and having opposite directions51,52. For this reason, the intensity of this transition at 355 nm (3.50 eV) is used to determine the molecular orientation of the molecule in comparison to an isotropic sample. The absorption of this electronic transition is associated to the degree of horizontal orientation of the molecules with respect to the substrate.
a Ultraviolet/Visible spectra for glasses grown at different deposition temperatures as indicated in the legend. See Sample preparation in Methods for more details. b Solid black squares (left scale): Sz obtained from UV/Vis spectra of samples grown at temperatures spanning 235 to 333 K. Open black squares: Sz values measured by ellipsometry in refs. 50,55. Solid red squares (right scale): devitrification onset temperature (Ton) measured by calorimetry on TPD glasses grown at different deposition temperatures. Solid stars correspond to samples obtained by cooling from the liquid state. Dashed lines are guides to the eye. The uncertainty in the Sz value is obtained from the standard deviation of three absorption measures per each deposition temperature, after error propagation of the maximum absorption value in the UV-Vis spectra.
We use the order parameter, Sz, to quantify the degree of orientation of the molecules53,54,55. Sz is generally derived from the angle between the transition dipole moment and the surface normal, θ, but can be simplified to a simple fraction between absorbances56:
where \(A\) is the absorption of the deposited film and \({A}_{{iso}}\) is the absorption of a film that has exactly the same number of molecules as the original one, but randomly oriented. This is obtained after annealing the vapor deposited film during 30 s at 350 K (Tg + 27 K) in Ar atmosphere. A value of Sz = −0.5 corresponds to a transition dipole moment of the molecule aligned parallel to the substrate, then indicating horizontal orientation of the molecule; Sz = 0 means that the molecules are randomly oriented, and Sz = 1 that molecules are preferentially aligned with the long axis perpendicular to the substrate.
According to Fig. 3b the sample grown at the lowest temperature has an order parameter Sz (UV/Vis) of −0.029 while for the one grown at 0.9 Tg is −0.002. This indicates that the sample grown at 0.85 Tg has on average a slightly larger face-on orientation with molecules lying with their long axis parallel to the substrate compared to the sample deposited at 300 K that is much more isotropic, as also shown from HRBS experiments in Supplementary Fig. 2a. These results are slightly lower but compatible with previous ellipsometry (open squares in Fig. 3b) and Grazing-Incidence Wide-Angle X-ray Scattering measurements on TPD or closely related organic semiconductor molecules50,55.
Overall, the thermokinetic and structural investigation of the two stable samples leads to the following conclusions: samples grown at 0.85 Tg have slightly larger thermodynamic and kinetic stability, lower layering (similar to the conventional glass) but more molecular anisotropy towards face-on orientation with respect to the sample grown at Tdep = 300 K (0.9 Tg), which is essentially isotropic, as depicted in Fig. 3b.
Sound velocity
In Fig. 4, longitudinal (vL) and transverse (vT) sound velocity for the three different glasses, determined from HRBS measurements down to low temperatures, are presented. As usual, transverse sound waves give much weaker Brillouin peaks with lower frequency shifts, thereby resulting in more scattered data points than for longitudinal sound waves. Data obtained from both cooling and heating runs (same symbols with slightly different colors) are depicted together, showing good reproducibility.
Sound velocity as a function of temperature for the differently prepared glasses, as indicated in the legend: a longitudinal sound velocity vL; b transverse sound velocity vT. In the case of the conventional glass the darker symbols represent a cooling run and the less dark ones represent a heating run. In the case of the anisotropic ultrastable glasses (USG), both symbols (darker and less dark ones) represent two different cooling runs. It is to be stressed that data in anisotropic glasses refers only to the sound velocity measured in the direction of the acoustic vector (see the Sound velocity subsection for more details). Errors associated with the data points are calculated from the frequency error values obtained from the non-linear fits to the peaks in the Brillouin spectra and are below 1% for vL and about 2.5% for vT, making them smaller than the symbols in the plot.
It is important to stress at this point that HRBS measurements do not average in all three directions of the sample as calorimetric methods do. HRBS measures the elastic properties in the direction of the acoustic wave vector (see Supplementary Fig. 1). If the sample under study is really isotropic, as usually canonical glasses are, this difference in averaging will become irrelevant, but if the sample is anisotropic, then discrepancies can arise, because the averaging is different. Therefore, the absolute values for the different samples in Fig. 4, especially for the more anisotropic glass (0.85 Tg), must be taken with caution.
The testing of the elastic isotropy in the sample/substrate plane of a TPD sample grown at 300 K is shown in Supplementary Fig. 2a. It is to see that there is no relevant indication of anisotropy in the longitudinal phonon, the data show random dispersion about f 110A = 7.859 ± 0.013 GHz. The acoustic wave vector performed a circular path in the plane with 10° steps. The 2αA scattering geometry was used, with a scattering angle of 55º (2α = 110º). Supplementary Fig. 2b shows the film TPD sample with the schematics of the different directions of the q2αA in the sample/substrate plane.
Not surprisingly, the most stable glass (the rather anisotropic ultrastable glass deposited at 0.85 Tg) exhibits the hardest elastic constants, i.e., the highest sound velocities, whereas the conventional glass (the one deposited at Tg) has the lower. Interestingly, the intermediate glass grown at 300 K (0.9 Tg) behaves closer to the latter than to the former. It seems, therefore, that the molecular orientation in the structural network plays a more leading role to determine the sound velocity than the degree of stability53. This finding will be supported by the specific heat data to be discussed below.
Low-temperature specific heat
Specific-heat Cp data, obtained after low-temperature measurements of the heat capacity employing the thermal-relaxation method and carefully subtracting the contribution of the addenda (see Methods), are presented in Figs. 5−7. We have measured the specific heat for three different glasses grown as thin films on 1 cm2 sapphire substrates, following the procedure detailed in Methods. In every case, three twin samples were put together on the calorimetric cell to triplicate the sample mass and improve the sensitivity of the measurement. As a useful reference, the material in crystalline state, in powder as received, was measured too. Additionally, another crystal sample and another ultrastable glass grown at 0.85 Tg had been previously measured in a higher temperature range, employing a standard 4He cryostat (see all raw data, after subtracting the corresponding addenda, in Supplementary Fig. 3). As can be seen, the overlap between the net data from the two different setups under so many different conditions is good, further supporting the accuracy of these measurements. Cp data shown in Figs. 5−7 are therefore the result of statistically averaging many experimental data points, from different experimental runs. The final precision, that can be envisaged from the data scatter in the most demanding Cp/T 3 representation used in Fig. 5, can be estimated to be better than 5%. Of course, the real accuracy in absolute value of the specific heat data, which is influenced by the subtracted, significant contribution of the addenda, could be above that value, but it is a systematic error that hardly affects the comparison among the different samples measured.
Specific heat for the three different glasses (conventional, isotropic ultrastable glass and anisotropic ultrastable glass) and the reference crystal of TPD (see the symbols in the legend) plotted in a Debye-reduced Cp/T 3 plot. Error associated with the data points was calculated using one standard deviation and is of the size of the data points.
Specific-heat data below 2 K for the three different glasses and the reference crystal of TPD (see the symbols in the legend) in a Cp/T vs T 2 plot. Dashed lines show the corresponding least-squares fits: quadratic, below 2 K for the glasses; linear, below 1 K for the crystal. Error associated with the data points was calculated using one standard deviation and is of the size of the data points.
Glassy specific-heat excess (subtracting its value for the crystal state) for the three different glasses (see legend) in: a Cp/T 3 representation; b Cp/T vs T 2 representation at the lowest temperatures. Dashed lines show the least squares linear fits performed to determine the corresponding linear coefficients.
As mentioned above, in Fig. 5 the whole of our specific-heat data is plotted as Cp/T 3 versus temperature in a log scale. This is the well-known Debye-reduced plot, where deviations from the expected cubic behavior for crystals at the lowest temperatures are more easily observed and analyzed. Nevertheless, data appear noisier than in other representations due to the T 3 factor in the denominator.
The TPD crystal shows the expected Cp ∼ T3 Debye law, at least below 2 K, with a shallow hump at 4 K, usually ascribed to a van-Hove singularity for transverse acoustic phonons in crystals. Strikingly, the rather anisotropic and most ultrastable glass (deposited at 0.85 Tg) exhibits a very similar behavior in Cp, although with a ≈30% higher magnitude, which is attributable to the lower elastic constants in the glass state. In particular, the depletion of the TLS density (i.e., the absence of an upturn in Cp/T 3 at very low temperatures) confirms the previous observation in ultrastable glasses of IMC27. Oppositely, the isotropic and ordinary glass (deposited at Tg) shows the typical glassy behavior, with a clear upturn in Cp/T 3 below 1 K featuring the presence of TLS and a significant boson peak below 3 K, even better defined than for the conventional glass of IMC27. In addition, we have measured the glass film deposited at 0.9 Tg, which corresponds to a highly stable glass (albeit somewhat less stable than the 0.85 Tg one, see Fig. 1) but fully isotropic. This intermediate glass exhibits a temperature dependence below 1 K near to cubic, that is, the TLS contribution is almost negligible, while above 1 K its specific heat is very similar to that of the conventional glass. Therefore, the degree of stability appears to control the density of TLS, whereas the more-or-less anisotropic structure of the molecular network seems to influence the elastic constants (see Fig. 4), and hence the lattice dynamics and the Cp/T 3 vibrational background (see Fig. 5).
The previous analysis referred to Fig. 5 can be complemented by means of the also usual Cp/T vs T 2 plot for the data at the lowest temperatures, as done in Fig. 6. By employing this representation, the linear-term coefficients, if any, can be directly determined from linear or quadratic least-squares fits57,58. Besides the numerical fits, whose obtained coefficients are presented in the central column of Table 1, the linear coefficient Cp is visualized as the intercept of Cp/T curves with the ordinate axis in Fig. 6. Only the isotropic, conventional glass has a significant linear coefficient, ascribed to a typical density of TLS, whereas the stable glasses show a clear depletion of TLS, especially the most stable glass deposited at 0.85 Tg, for which its presence is null within experimental error, as in the crystal state.
In order to enhance and better visualize the glassy features of the specific heat, we have subtracted the reference crystal value from the total Cp(T) of each glass sample, as depicted in Fig. 7. The left panel (a) shows this glassy excess ΔCp,glassy over the crystal curve in the Cp/T 3 plot, while the right panel (b) shows the lowest-temperature data in a Cp/T vs T 2 plot.
In Fig. 7a, we can observe the typical glassy behavior for the conventional glass, while the anisotropic, stable glass shows a flat excess ΔCp,glassy/T 3 signaling a mere difference in the cubic Debye coefficient relative to the crystal one. In the intermediate case (the more isotropic but still stable glass at 0.9 Tg), a weak upturn in ΔCp,glassy/T 3 below 1 K is seen, together with a “boson peak” very similar to that of the conventional glass, both in position and height. In Fig. 7b, the corresponding data are plotted as ΔCp,glassy/T vs T 2 to scrutinize more precisely the behavior at the lowest temperatures. The linear fits performed below 1.4 K (dashed lines) are also shown in Table 1 (right column) and show a good agreement with the previous ones (central column) using a different approach.
Conclusions
In summary, we have thoroughly studied several key properties of a glass-forming substance, TPD, where both its degree of thermodynamic and kinetic stability, and its degree of structural/optical anisotropy can be dramatically varied. Specifically, we have performed calorimetric experiments, both around the glass transition and at low temperatures, as well as elastoacoustic and structural characterization measurements. In particular, three representative and clearly different glass states of TPD have been studied, depending on the deposition temperature of the PVD films. The glass deposited at 285 K (0.85 Tg) is anisotropic, where the molecules are preferentially oriented parallel to the substrate, and exhibits the strongest stabilization as indicated by a large +30 K shift in the devitrification temperature Ton, compared to the conventional glass. It also shows some layering, though less than the other stable glass, and of the same magnitude that the conventional glass, which implies at least that the existence of layering is not the only reason for the different properties of the ultrastable glass. Brillouin measurements of longitudinal and transverse sound velocities at low temperatures show that the most stable glass (deposited at 0.85 Tg) has the highest values among the studied TPD glasses, and hence the lowest Debye level, in agreement with Cp/T 3 data at low temperature. Furthermore, this 0.85 Tg ultrastable glass lacks TLS within experimental error, as it was also observed in the ultrastable glass of IMC27. On the contrary, the ordinary or conventional glass (grown at Tg) exhibited the expected glassy features, namely a linear term in the specific heat due to the presence of TLS and a boson peak Cp/T 3 slightly below 3 K.
However, the most novel finding in this work has been obtained from preparing and studying an intermediate glass state (the glass deposited at 0.9 Tg), which is almost as stable as the 0.85 Tg one, but almost as isotropic as the conventional glass. Interestingly, it shows a linear term in Cp much smaller than that of the conventional glass, although not strictly zero within experimental error, what we attribute to the slightly lesser stability than the 0.85 Tg glass. In short, the density of TLS appears to inversely correlate with the degree of stability and is independent of the anisotropy. However, the vibrational Debye-like background of Cp dominating above 1 K of this isotropic/stable glass, is very similar to that of the conventional glass, but clearly higher than that of the anisotropic glass of 0.85 Tg. Hence this vibrational background around the boson peak seems to be governed by the molecular ordering influencing the network structure, rather than by the degree of stability, oppositely to the TLS contribution.
Finally, it can be remarked that our better understanding of the key variables that deplete the amount of TLS in amorphous solids is expected to be very useful in the field of superconducting circuits and quantum technologies, which are currently much limited by the losses due to tunneling states present in the amorphous parts employed in those devices43,44,45,46,47.
Methods
Sample preparation
TPD (N,N—bis(3-methylphenyl)_N,N-bis(phenyl)-benzidine, Tg = 333 K and Tm = 440 K) crystalline powders with 99% purity were purchased from Sigma-Aldrich and used as received. The films were thermally evaporated and deposited at three different substrate temperatures, 285 K (0.85 Tg), 300 K (0.9 Tg), and 333 K (Tg), within a high vacuum chamber with a base pressure of 1 × 10−8 Torr. An effusion cell filled with TPD powder was heated to achieve a deposition rate of 0.20 ± 0.05 nm/s, as measured by a quartz crystal microbalance. Once the substrate temperature was stabilized and the desired growth rate attained, the shutter was removed to start depositing onto several 1 × 1 cm2 sapphire substrates (Sigma Aldrich). Films around 50 μm thick were produced to enhance the signal-to-noise ratio in the low-temperature heat capacity measurements. After deposition the samples were stored in vacuum for few days at a temperature of 4 °C and shipped from Barcelona to Madrid for the low-temperature measurements. Control samples were grown simultaneously on aluminum substrates and checked by calorimetry just before the low-T measurement for the determination of the thermodynamic stability of the glass, on silicon wafers (with native oxide) for the study of molecular layering with XRD and on quartz substrates (from Ossila) for UV/Vis analysis devoted to the determination of molecular orientation of the as-grown glasses. Two of the selected deposition temperatures (285 K and 300 K) were determined with the intention to have samples of comparable stability but different molecular orientation and layering according to previous reports17,26,35. The third deposition temperature (333 K) was chosen to prepare a conventional glass, isotropic and much less stable than the others (see Fig. 3b), as a reference. The sample grown at Tdep =333 K is equivalent, from the thermodynamic (onset and fictive temperature) and structural (XRD and Sz parameter) points of view to a conventional (−10 K/min) liquid-cooled glass. Additionally, the low-temperature specific heat of the reference crystal state was also measured.
Calorimetric characterization
DSC was carried out in a Perkin-Elmer 7 DSC with a heating rate of 10 K/min in samples of thickness ≈15 μm and total mass around 8−12 mg deposited on Al foil. The first scan corresponds to the as-deposited state, while the second upscan is characteristic of a sample that has been heated up to the liquid state at 380 K and subsequently cooled down at −10 K/min. The strong variation of the onset of devitrification (Ton) and the enthalpy overshoot between both vapor-deposited and liquid-cooled glasses (see Fig. 1) is related to the enhanced kinetic and thermodynamic stability of these ultrastable glasses.
Structural characterization
The glassy nature of the sample and the presence of layering was investigated by WAXS. Measurements were carried out in an X-Pert diffractometer from Phillips in the Bragg–Brentano configuration with Cu Kα radiation. The samples were scanned in Bragg–Brentano geometry from 2θ = 3° to 30° with an angular step of 0.05° and time per point of 20 s for both samples. The average molecular orientation of the samples was inferred from the variation of the UV/Vis spectra measured in thinner (100−200 nm thick) samples, through the order parameter, Sz, calculated as reported elsewhere56,59, see Fig. 3. The Sz value of the sample deposited directly at Tdep = 333 K (in the liquid state) and a conventional glass obtained from the liquid (square and star black symbols in Fig. 3b, respectively) are both isotropic within the experimental uncertainty. This technique provides information about the electronic transitions in the range of ultraviolet-visible wavelengths. As each electronic transition has associated a transition dipole moment, the molecular orientation of the glass may yield variations on the intensity of the transition.
Brillouin light scattering
Temperature dependent measurements of the longitudinal and transverse acoustic phonons have been performed by means of HRBS. Due to the sample geometry (film of about 5 μm on Si substrate) the scattering geometry applied in these experiments was the 2αA scattering geometry. Supplementary Fig. 1 shows the schematics of this scattering geometry. The most important point is that the reflecting substrate acts as a virtual light source, introducing the 2αA scattering geometry that is confined in the sample/substrate plane60. This scattering geometry allows the observation of the longitudinal and transverse phonons, whereas in the pure Backscattering geometry the transverse phonons in principle do not couple to the electromagnetic field of the incoming light.
As it is shown in Supplementary Fig. 1, the acoustic wave vector q2αA is related to the scattering angle (2α) as:
being α the angle of incidence and λ0 the laser wavelength. It is not dependent on the refractive index of the sample. Thus, the sound velocities are given by:
where fL,T is the measured Brillouin frequency shift of the longitudinal (L) or transverse (T) phonons.
Low-temperature specific heat
Heat capacity of the different samples was measured in the temperature range 0.4−8 K employing a 3He cryostat. Some complementary measurements for a crystal and an ultrastable glass of TPD were previously performed in a standard 4He cryostat between 2 and 20 K, showing good agreement with the others despite so many different experimental conditions, as can be observed in Supplementary Fig. 3, where all raw data are depicted together. In all cases the thermal relaxation method was used27,61, with the samples placed on the sapphire substrate (1 inch diameter) of the calorimetric cell, with a small, carefully measured amount of Apiezon N grease. More details of our calorimetric methods at low temperatures can be found in refs. 62,63. For these experiments, a 1 kΩ resistor chip (used as a heater) and a thermal sensor were also fixed on the sapphire support in very good thermal contact with the samples. The calorimetric cell was connected to the controlled thermal sink through a thin PtW wire, chosen to have relaxation times of tens of seconds.
For the lower temperature measurements in the 3He cryostat, a RuO2 thermal sensor was selected to minimize its contribution to the total heat capacity. A radiation shield of polished metal was put surrounding the calorimetric setup to allow this to reach temperatures around 0.3 K. The contribution of the addenda (slightly below 50% of the total heat capacity at 2 K, though gradually increasing below 1 K) was carefully measured and subtracted to obtain the specific heat of the corresponding material. To improve the sensitivity of the heat capacity measurements, three samples grown simultaneously were measured together, so triplicating the sample mass, for each case. Additionally, many different experimental runs were performed to improve data statistics. Smoothed statistical-averaged data from the whole of datasets shown in Supplementary Fig. 3 are presented in Fig. 5.
Data availability
All data are available in the main text or the supplementary materials, as well as from the corresponding author on reasonable request.
References
Phillips, W. A. (ed.). Amorphous Solids: Low Temperature Properties, (Springer, Berlin,1981).
Yu, C. C. & Leggett, A. J. Low temperature properties of amorphous materials: through a glass darkly. Comments Cond. Mat. Phys. 14, 231 (1988).
Elliott, S. R. Physics of Amorphous Materials, 2nd edn. (Longman, Harlow, Essex, 1990).
Anderson, P. W. Through the glass lightly. Science 267, 1615 (1995).
Gutzow, I. & Schmelzer, J. The Vitreous State (Springer, Berlin, 1995).
Angell, C. A., Ngai, K. L., McKenna, G. B., McMillan, P. F. & Martin, S. W. Relaxation in glassforming liquids and amorphous solids. J. Appl. Phys. 88, 3113 (2000).
Debenedetti, P. G. & Stillinger, F. H. Supercooled liquids and the glass transition. Nature 410, 259 (2001).
Donth, E. The Glass Transition, (Springer, Berlin, 2002).
Binder, K. & Kob, W. Glassy Materials and Disordered Solids, (World Scientific, Singapore, 2005).
Cavagna, A. Supercooled liquids for pedestrians. Phys. Rep. 476, 51 (2009).
Wolynes, P. G. & Lubchenko V. (eds.). Structural glasses and supercooled liquids: theory, experiment, and applications, (Wiley, New York, 2012).
Ediger, M. D. & Harrowell, P. Perspective: supercooled liquids and glasses. J. Chem. Phys. 137, 080901 (2012).
Franz, S., Maimbourg, T., Parisi, G. & Scardicchio, A. Impact of jamming criticality on low-temperature anomalies in structural glasses. Proc. Natl. Acad. Sci. USA 116, 13768 (2019).
Ramos, M. A. (ed.). Low-Temperature and Vibrational Properties of Disordered Solids: A Half-Century of “Anomalies” of Glasses (World Scientific, Singapore, 2022).
Goldstein, M. Viscous liquids and the glass transition: a potential energy barrier picture. J. Chem. Phys. 51, 3728 (2003).
Stillinger, F. H. A topographic view of supercooled liquids and glass formation. Science 267, 1935 (1995).
Rodríguez-Tinoco, C., González-Silveira, M., Ramos, M. A. & Rodríguez-Viejo, J. Ultrastable glasses: new perspectives for an old problem. Riv. Nuovo Cim. 45, 325 (2022).
Kauzmann, W. The nature of the glassy state and the behavior of liquids at low temperatures. Chem. Rev. 43, 219 (1948).
Ramos, M. A. Are universal “anomalous” properties of glasses at low temperatures truly universal? Low. Temp. Phys. 46, 104 (2020).
Zink, B. L., Pietri, R. & Hellman, F. Thermal conductivity and specific heat of thin-film amorphous silicon. Phys. Rev. Lett. 96, 055902 (2006).
Queen, D. R., Liu, X., Karel, J., Metcalf, T. H. & Hellman, F. Excess specific heat in evaporated amorphous silicon. Phys. Rev. Lett. 110, 135901 (2013).
Liu, X., Queen, D. R., Metcalf, T. H., Karel, J. E. & Hellman, F. Hydrogen-free amorphous silicon with no tunneling states. Phys. Rev. Lett. 113, 025503 (2014).
Swallen, S. F. et al. Organic glasses with exceptional thermodynamic and kinetic stability. Science 315, 353–356 (2007).
Leon-Gutierrez, E., Sepúlveda, A., Garcia, G., Clavaguera-Mora, M. T. & Rodríguez-Viejo, J. Stability of thin film glasses of toluene and ethylbenzene formed by vapor deposition: an in situ nanocalorimetric study. Phys. Chem. Chem. Phys. 12, 14693–14698 (2010).
Leon-Gutierrez, E., Sepúlveda, A., Garcia, G., Clavaguera-Mora, M. T. & Rodríguez-Viejo, J. Correction: Stability of thin film glasses of toluene and ethylbenzene formed by vapor deposition: an in situ nanocalorimetric study. Phys. Chem. Chem. Phys. 18, 8244–8245 (2016).
Ediger, M. D. Perspective: Highly stable vapor-deposited glasses. J. Chem. Phys. 147, 210901 (2017).
Pérez-Castañeda, T., Rodríguez-Tinoco, C., Rodríguez-Viejo, J. & Ramos, M. A. Suppression of tunneling two-level systems in ultrastable glasses of indomethacin. Proc. Natl. Acad. Sci. USA 111, 11275 (2014).
Khomenko, D., Scalliet, C., Berthier, L., Reichman, D. R. & Zamponi, F. Depletion of two-level systems in ultrastable computer-generated glasses. Phys. Rev. Lett. 124, 225901 (2020).
Mocanu, F. C. et al. Microscopic observation of two-level systems in a metallic glass model. J. Chem. Phys. 158, 014501 (2023).
Pérez-Castañeda, T., Jiménez-Riobóo, R. J. & Ramos, M. A. Low-temperature thermal properties of a hyperaged geological glass. J. Phys.: Cond. Matter 25, 295402 (2013).
Pérez-Castañeda, T., Jiménez-Riobóo, R. J. & Ramos, M. A. Two-level systems and boson peak remain stable in 110-million-year-old amber glass. Phys. Rev. Lett. 112, 165901 (2014).
Pérez-Castañeda, T., Jiménez-Riobóo, R. J. & Ramos, M. A. Do two-level systems and boson peak persist or vanish in hyperaged geological glasses of amber? Philos. Mag. 96, 774–787 (2016).
Rodríguez-Tinoco, C., González-Silveira, M., Ràfols-Ribé, J., García, G. & Rodríguez-Viejo, J. Highly stable glasses of celecoxib: influence on thermo-kinetic properties, microstructure and response towards crystal growth. J. Non-Cryst. Solids 407, 256−261 (2015).
Liu, T. et al. Birefringent stable glass with predominantly isotropic molecular orientation. Phys. Rev. Lett. 119, 095502 (2017).
Ediger, M. D., de Pablo, J. & Yu, L. Anisotropic vapor-deposited glasses: hybrid organic solids. Acc. Chem. Res. 52, 407 (2019).
Fiori, M. E., Bagchi, K., Toney, M. F. & Ediger, M. D. Surface equilibration mechanism controls the molecular packing of glassy molecular semiconductors at organic interfaces. Proc. Natl. Acad. Sci. USA 118, e2111988118 (2021).
Rodríguez-Tinoco, C., González-Silveira, M., Ràfols-Ribé, J., Lopeandía, A. F. & Rodríguez-Viejo, J. Transformation kinetics of vapor-deposited thin film organic glasses: the role of stability and molecular packing anisotropy. Phys. Chem. Chem. Phys. 17, 31195−31201 (2015).
Esaki, Y., Komino, T., Matsushima, T. & Adachi, C. Enhanced electrical properties and air stability of amorphous organic thin films by engineering film density. J. Phys. Chem. Lett. 8, 5891–5897 (2017).
Antony, L. W. et al. Influence of vapor deposition on structural and charge transport properties of Ethylbenzene films. ACS Cent. Sci. 3, 415–424 (2017).
Rodríguez-Tinoco, C., Rams-Baron, M., Rodríguez-Viejo, J. & Paluch, M. Emergence of a substrate-temperature-dependent dielectric process in a prototypical vapor deposited hole-transport glass. Sci. Rep. 8, 1380 (2018).
Ràfols-Ribé, J. et al. Evidence of thermal transport anisotropy in stable glasses of vapor deposited organic molecules. Phys. Rev. Mater. 2, 035603 (2018).
Wolf, S. E. et al. Role of molecular layering in the enhanced mechanical properties of stable glasses. J. Phys. Chem. Lett. 13, 3360–3368 (2022).
Clarke, J. & Wilhelm, F. K. Superconducting quantum bits. Nature 453, 1031–1042 (2008).
Devoret, M. H. & Schoelkopf, R. J. Superconducting circuits for quantum information: an outlook. Science 339, 1169–1174 (2013).
Müller, C., Cole, J. H. & Lisenfeld, J. Towards understanding two-level-systems in amorphous solids: insights from quantum circuits. Rep. Prog. Phys. 82, 124501 (2019).
Meissner, A. et al. Acoustic properties of metallic glasses at low temperatures: tunneling systems and their dephasing. Phys. Rev. B 103, 224209 (2021).
Stephens, R. & Liu, X. Low Energy Excitations in Disordered Solids Ch. 9 (World Scientific, Singapore, 2021).
Ràfols-Ribé, J. et al. Kinetic arrest of front transformation to gain access to the bulk glass transition in ultrathin films of vapour-deposited glasses. Phys. Chem. Chem. Phys. 20, 29989–29995 (2018).
Vila-Costa, A., González-Silveira, M., Rodríguez-Tinoco, C., Rodríguez-López, M. & Rodríguez-Viejo, J. Emergence of equilibrated liquid regions within the glass. Nat. Phys. 19, 114–119 (2023).
Gujral, A., O’Hara, K. A., Toney, M. F., Chabinyc, M. L. & Ediger, M. D. Structural characterization of vapor-deposited glasses of an organic hole transport material with X-ray scattering. Chem. Mater. 27, 3341 (2015).
Vragović, I., Calzado, E. M. & Díaz García, M. A. The structure and energetics of TPD ground and excited states. Chem. Phys. 332, 48 (2007).
Scholz, R. et al. Asymmetry between absorption and photoluminescence line shapes of TPD: spectroscopic fingerprint of the twisted biphenyl core. J. Phys. Chem. A 113, 315 (2009).
Ward, I. M. Structure and Properties of Oriented Polymers, 2nd edn, Ch. 1 (Springer, Berlin, 1997).
Yokoyama, D. Molecular orientation in small-molecule organic light-emitting diodes. J. Mater. Chem. 21, 19187 (2011).
Dalal, S. S., Walters, D. M., Lyubimov, I., de Pablo, J. J. & Ediger, M. D. Tunable molecular orientation and elevated thermal stability of vapor-deposited organic semiconductors. Proc. Natl. Acad. Sci. USA. 112, 4227–4232 (2015).
Sakai, Y., Shibata, M. & Yokoyama, D. Simple model-free estimation of orientation order parameters of vacuum-deposited and spin-coated amorphous films used in organic light-emitting diodes. Appl. Phys. Express 8, 096601 (2015).
Ramos, M. A. Are the calorimetric and elastic Debye temperatures of glasses really different? Philos. Mag. 84, 1313 (2004).
Ramos, M. A. Low-temperature specific heat of glasses and disordered crystals. in Low-Temperature and Vibrational Properties of Disordered Solids: A Half-Century of “Anomalies” of Glasses (ed. Ramos, M. A.) Ch.2 (World Scientific, Singapore, 2022).
Walters, D. M., Antony, L., de Pablo, J. J. & Ediger, M. D. Influence of molecular shape on the thermal stability and molecular orientation of vapor-deposited organic semiconductors. J. Phys. Chem. Lett. 8, 3380–3386 (2017).
Krüger, J. K., Ems, J., Brierley, J. & Jiménez Riobóo, R. J. A new Brillouin scattering technique for the investigation of acoustic and opto-acoustic properties: application to polymers. J. Phys. D. 31, 1913 (1998).
Bachmann, R. et al. Heat capacity measurements on small samples at low temperatures. Rev. Sci. Instrum. 43, 205 (1972).
Pérez-Enciso, E. & Ramos, M. A. Low-temperature calorimetry on molecular glasses and crystals. Thermochim. Acta 461, 50 (2007).
Pérez-Castañeda, T. et al. Low-temperature specific heat of graphite and CeSb2: validation of a quasi-adiabatic continuous method. J. Low. Temp. Phys. 173, 4 (2013).
Acknowledgements
M.M. and M.A.R. are grateful to J. G. Rodrigo and J. M. Castilla for unvaluable help with the 3He cryostat. M.M. and M.A.R. acknowledge financial support from PID2021-127498NB-I00/AEI/FEDER/10.13039/501100011033, also from MCIN/AEI/10.13039/ 501100011033 through the “María de Maeztu” Program for Units of Excellence in R&D (CEX2018-000805-M), as well as from the Autonomous Community of Madrid through program S2018/NMT-4321 (NANOMAGCOST-CM). J.R.V., C.R.T. and M.R.L. acknowledge Grant PID2020-117409RB-I00, funded by MCIN/AEI/10.13039/ 501100011033. C.R.T. is a Serra Hunter Fellow. The ICN2 is funded by the CERCA program/Generalitat de Catalunya. The ICN2 was supported by the “Severo Ochoa” Centres of Excellence Program, funded by the Spanish Research Agency (AEI, grant no. CEX2021-001214-S). R.J.J.R. received funds from the PID2021-127033OB-C21/MCIN/AEI/10.13039/501100011033 research project of the Spanish Ministerio de Ciencia e Innovación.
Author information
Authors and Affiliations
Contributions
J.R.V. and M.A.R. conceived the idea and proposed the experiments. M.M. implemented the experimental setups for low-temperature calorimetry under the supervision of M.A.R., M.R.L. prepared the samples. M.R.L. and C.R.T. performed the calorimetric and structural characterizations and their data analysis. R.J.J.R. conducted the Brillouin light scattering measurements and obtained the sound velocity data. M.M. conducted the specific-heat measurements at low temperature and their data analysis with the input of M.A.R. M.A.R. and J.R.V. wrote the original manuscript draft. All authors contributed to the writing and editing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks Xiao Liu, and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Moratalla, M., Rodríguez-López, M., Rodríguez-Tinoco, C. et al. Depletion of two-level systems in highly stable glasses with different molecular ordering. Commun Phys 6, 274 (2023). https://doi.org/10.1038/s42005-023-01398-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-023-01398-4
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.