Abstract
Hybridization is one of the most fundamental quantum mechanical phenomena, with the text book example of binding two hydrogen atoms in a hydrogen molecule. Here we report tunnel spectroscopy experiments illustrating the hybridization of another type of discrete quantum states, namely of superconducting subgap states that form in segments of a semiconducting nanowire in contact with superconducting reservoirs. We discuss a collection of intermediate states with unique (tunnel) spectroscopic fingerprints in the process of merging well-known individual bound states, hybridized by a central quantum dot and eventually coherently linking the reservoirs, carrying a Josephson current. These coupled and fused Andreev bound states can be seen as superconducting analogues to atomic and molecular single electron states in nature, and explain a variety of recent bound state spectra, with specific fingerprints that will have to be winnowed in future Majorana fusion experiments.
Similar content being viewed by others
Introduction
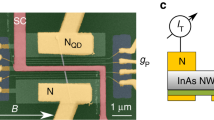
For non-interacting confined electrons, single particle quantum states can be viewed as standing waves at discrete energies. Similarly, with a superconductor as a boundary, two-particle standing waves can form due to Andreev reflection, as illustrated in Fig. 1. Such discrete Andreev bound states (ABSs), or Andreev atoms, can form in a semiconductor with one1,2, two3,4, or potentially with multiple superconducting contacts5. We use the term ABS also for the conceptually similar Yu-Shiba-Rusinov (YSR) subgap states4,6,7 and specify only when necessary. ABSs are the topologically trivial next of kin to the topologically non-trivial Majorana bound states (MBSs), currently a major research topic due to the promise of topologically protected quantum information processing8. Merging MBSs in a process called fusion will be a first step in probing the nature of MBSs9,10. Disputes over recent MBS experiments11,12,13,14 highlight the need for sharp and sufficiently high tunnel barriers15,16, while prospective MBS fusion experiments require gate-tunable barriers to hybridize different well-defined nanowire (NW) segments. To obtain such well-defined structures, we have grown zincblende InAs NWs with integrated wurtzite tunnel barriers forming a central QD17,18, and fabricated superconducting contacts, S1,2, at each end of the NW, forming lead segments (LSs) adjacent to the QD. The ABSs under investigation form in these LSs19,20. An energy level diagram and a colored scanning electron micrograph of such a device are shown in Fig. 2a and b, respectively, including the experimental setup.
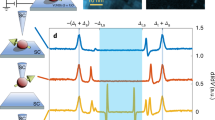
a Individual discrete Andreev bound states (ABSs, red and light blue arrows) form in the two lead segments LS1,2 coupled to the superconducting reservoirs S1,2 (blue), with Andreev reflections at the S - LS interfaces. Discrete single particle bound states form on the central quantum dot (QD) between the barriers (grey). b With increasing tunnel coupling (black arrows), the ABSs of both lead segments hybridize individually with the QD, forming a molecular state between single and two-particle bound states. c If the coupling becomes strong enough, the ABSs of all segments fuse into two (time resolved) extended ABSs, eventually carrying a Josephson current.
a Schematic energy level diagram for the three nanowire (NW) segments, including superconducting contacts S1,2 (blue), Andreev bound states ABS1,2 (light blue) and the quantum dot (QD, red), corresponding to the scanning electron micrograph of a representative device in b. The device consists of a zincblende InAs NW with two 30 nm wurtzite tunnel barriers (grey) forming gate tunable tunnel barriers17 - 19,30. The central NW segment (~25 nm) forms a QD, while the left and right NW lead segments, LS1,2 of lengths ℓ1 < ℓ2, are coupled to the superconducting contacts S1,2. The scalebar is 100 nm. In the experiments, we measure the modulation of the electrical current I at the grounded drain terminal (S2) and record the differential conductance G = dI/dVSD = IAC/VAC as a function of the backgate voltage VBG and the bias voltage VSD applied to the source contact (S1). c G as a function of VSD for low backgate voltages VBG close to the NW depletion, showing essentially a single Coulomb blockade resonance. d At large VBG, we find the Josephson effect, demonstrated here as a plot of the differential resistance as a function of the current bias, with the Josephson critical current Ic indicated for one gate voltage.
We present spectroscopy experiments that show intermediate states in the process of fusing such sub-gap states, as illustrated in Fig. 1: an increase in the gate voltage increases the tunnel coupling19,21, so that the ABSs of each LS hybridize with the QD, forming one of the possible Andreev molecules22,23,24. For even lower barriers, ABSs extend over the complete device, eventually generating a Josephson current. In analogy to the fusion of hydrogen atoms, one might call this state Andreev helium.
Results and discussion
In most of the presented experiments we measure the differential conductance G, as discussed in the Methods section. The basic characterization of the central QD with the contacts in the normal state (B = 50 mT) is shown in Supplementary Figs. 1 and 2, with addition energies around 8 meV, level spacing of 0.5 meV to 2 meV, and a resonance broadening of ΓQD ≈ 50 μeV at low gate voltages, all increasing for larger gate voltages18,19,21. Experiments on the two well-known limiting cases are shown in Fig. 2: at very low backgate voltages, shown in Fig. 2c, we find Coulomb blockade (CB) resonances similar as in the normal state, with a replica of the QD resonance with positive slope labeled \(\overline{{{{{{{{\rm{QD}}}}}}}}}\), consistent with a QD state aligning with an increased quasi particle density of states (DoS) at an energy Δ* ≈ 160 μeV in LS1 (or in S1)19,25. For a QD directly, but weakly tunnel coupled to two fully gaped superconducting reservoirs, one might expect a transport gap for e∣ΔVSD∣ < 2Δ* and no shift of the CB diamonds in gate voltage25. These seemingly contradictory findings can be immediately understood by noting that the integrated barriers allow us to go to very low gate voltages, resulting in a small and homoegeneous Fermi velocity vF, so that the ABSs in the LSs are in the long-junction limit (ℓLS > ℏvF/Δ*), with energies distributed and broadened continuously across the energy gap19. The replica resonance \(\overline{{{{{{{{\rm{QD}}}}}}}}}\) we attribute to some ABSs already moving towards Δ* in the shorter LS1. We note that without the experiments below showing a clean superconducting gap at larger gate voltages, this mechanism is difficult to distinguish from a residual single particle DoS in the superconducting reservoirs19,26, or from resonant Cooper pair tunneling25. The second limiting case is the Josephson effect, which we find well developed at very large gate voltages. In Fig. 2d we plot a current bias measurement of the differential resistance, demonstrating a gate tunable Josephson effect. In this limit, the barriers are very low and ABSs extend between the two superconducting reservoirs, carrying the zero-resistance current. Additional tunnel spectroscopy data for VBG between 1 V and 7.5 V can be found in Supplementary Fig. 4, where the subgap conductance becomes larger than above the gap due to high-transmission Andreev reflection, while Supplementary Fig. 5 shows additional current bias experiments for VBG between 10 V and 16 V, showing an increasing, gate voltage modulated Josephson current27,28, up to ~0.5 nA. The latter value seems small, compatible with the large distance and tunnel barriers between the reservoirs. Our main results are experiments in between these two limits, when individual, discrete ABSs form on the two LSs, and discrete single electron states on the QD. These states can be brought to hybridize in a controlled way with relatively small changes in the gate voltage, as shown in the series of experiments plotted in Fig. 3. All plots show G as a function of the bias and gate voltages, centered on different charge degeneracy points of the QD, with the reservoirs in the superconducting state (B = 0). Larger scale data and similar resonances in between are shown in Supplementary Figs. 2 and 3, respectively.
a–c G vs. VBG and VSD in the superconducting state (B = 0) for gate voltage intervals around different charge degeneracy points of the central QD. d–f corresponding model results. a, d: Here, both lead segments (LSs) carry a discrete, gate voltage independent Andreev bound state (ABS) at the gap energy Δ* (Andreev atoms), resulting in conductance peaks at ∣VSD∣ ≈ Δ*/e and 2Δ*/e. In addition, the ABS on LS1 hybridizes with the quantum dot (QD, two-atom Andreev molecule), resulting in the avoided crossing (cyan arrows). b, e Discrete ABSs in both LSs, both hybridizing with the QD state at different bias and gate voltage settings. c, f The QD now strongly hybridizes with the ABS in LS2 forming a Yu-Shiba-Rusinov state. The cyan arrows point out the onset of a Josephson current carried by the fused ABSs. The model parameters are given in Supplementary table 1.
Figure 3 a shows discrete, weak ABS resonances at constant VSD ≈ ± Δ*/e (ABS2), and stronger ones at VSD = ± 2Δ*/e labeled \({\overline{{{{{{{{\rm{ABS}}}}}}}}}}_{2}\). The QD resonances forming a Coulomb diamond with shifted low-bias tips are characteristic for a QD weakly coupled to a superconductor25. The ABSs in the LSs becoming discrete (‘Andreev atoms’) with increasing gate voltage is consistent with an increase in the Fermi velocity and a correspondingly larger level spacings19,21. Due to the Andreev reflection processes, the ABSs in the LSs are pinned to the source or drain electrochemical potentials, resulting in horizontal resonances as long as the voltage drop occurs mainly across the QD. Most prominently, Fig. 3a shows a strong avoided crossing of the horizontal ABS resonances \({\overline{{{{{{{{\rm{ABS}}}}}}}}}}_{2}\) (and less visibly for ABS2), with the CB resonance of positive slope, pointed out by cyan arrows. This avoided crossing can be directly identified as the hybridization of an ABS in LS2 with a QD state, thus forming the equivalent of a ‘two-atom heteronuclear molecular state’, similar to a CO molecule in chemistry. This hybrid state is mapped by energy selective tunneling of electrons from an ABS in LS1 (or alternatively from the superconducting BCS coherence peaks in S1). Since each ABS is pinned to the respective reservoir, the ABS of the avoided crossings in Fig. 3a is necessarily located in LS2. An avoided crossing suggests an increased coupling between the LSs and the QD, consistent with an increase in the normal state QD broadening, from ΓQD ≈ 50 μeV for Fig. 2c at the lowest gate voltages, to ΓQD ≈ 150 μeV for Fig. 3a19,21. The negative differential conductance near the ABS resonances and near the avoided crossings are due to the non-monotonic DoS in the LSs carrying ABSs, or in the superconductor. In addition, we find two more resonances, labeled I and II, that follow the curvature of the avoided crossing discussed above. Intuitively, I corresponds to aligning the ABS-QD hybrid state to a residual single particle DoS in LS1, or in S1. The slightly shifted resonance II we tentatively attribute to an additional ABS in LS2. In Fig. 3b, at a slightly larger backgate voltage, we find such avoided crossings almost symmetrically around the centre of the original CB diamond, as pointed out by green and cyan arrows at negative bias. Following a similar argument as above, one now finds that discrete ABSs form on both LSs, each hybridizing with the QD state when the energies align, i.e. not at the same gate voltage and bias values. This situation corresponds to two CO molecules in chemistry, either of which forms depending on the external parameters, here the gate and bias voltages. Now the CB diamonds at opposite bias are not shifted with respect to each other, and we find two resonances that cross zero bias, replicating the respective avoided crossings due to a finite background DoS. Data over another QD charge degeneracy point at again slightly higher backgate voltages are shown in Fig. 3c, for which we extract a QD broadening in the normal state of ΓQD ≈ 400 μeV > Δ*. Here, we find two strongly, but continuously curved and strongly broadened resonances, essentially mirror symmetric for negative biases. These resonances oscillate roughly between the biases Δ*/e and 2Δ*/e when increasing the gate voltage, opening a gap in the transport characteristics, reminiscent of a gate tunable ABS mapped by superconducting reservoirs3. Due to the reduced barrier height, one might expect that the ABSs in the LSs hybridize and form another type of molecular Andreev state hybridizing all three sites simultaneously, similar to a ‘three-atom heteronuclear molecular state’ like CO2 in chemistry. However, the simple model discussed below rather suggests that the QD region becomes coupled to S2 strongly enough to develop an independent, now gate tunable ABS. We further point out two small conductance peaks at zero bias (cyan arrows), which we tentatively attribute to the onset of the Josephson effect, since similar structures were found in other NW Josephson junctions14,29. A Josephson effect can be understood as ABSs ‘fusing’ across the complete NW length, forming an ABS spanning across all three NW segments, as illustrated in Fig. 1c transmitting coherent Cooper pairs. These peaks correspond to Josephson currents of a few ten fA, too small to be investigated in current bias experiments in our setups.
To illustrate the formation of intermediate states in the ABS fusion process, we use a basic three-site model, described in the supporting information, with simple electron (and hole) states at originally constant energies in each LS, mimicking ABSs, and with a single QD state in the center, tunnel coupled to both LSs. The conductance we obtain as the product of the transmissions through the individual sites. The main results are plotted in Fig. 3d–f, while the model is described in more detail in the Methods section. We note explicitly that this model is mainly for illustration and does not aim to model the physical system from first principles. First, we reproduce the experiment in Fig. 2c, for which we use a constant transmission in the LSs and a BCS DoS with a constant background in S1 and a constant DoS in S2, mimicking the long junction limit in LS2. These assumptions result in plots reproducing Fig. 2c, including a replica \(\overline{{{{{{{{\rm{QD}}}}}}}}}\) of the QD resonance due to the BCS coherence peaks in S1 (see Ref. 19). Next, Fig. 3d shows the case of one discrete state in LS2, tunnel coupled to the QD, and both reservoirs with a BCS DoS with a small background. As discussed for the data in Fig. 3a, we find horizontal resonances (\({\overline{{{{{{{{\rm{ABS}}}}}}}}}}_{2}\)) and an avoided crossing at ± 2Δ*/e, with replicas (ABS2) due to a background transmission in the LSs, or a residual DoS in S1. Similarly, adding a discrete tunnel coupled ABS as well in LS1, we obtain Fig. 3e, with a qualitatively similar pattern as in Fig. 3b, especially the additional avoided crossings with the QD resonance of negative slope. Surprisingly, simply increasing the tunnel coupling strengths between the sites in this model does not reproduce the experiments in Fig. 3c, especially the continuously curved ABS gate dependence. However, if we insert a standard, gate tunable YSR state on the QD site at the drain electrochemical potential, that is mapped by the the ABS in LS1 (or the BCS DoS in S1), we obtain Fig. 3f, which qualitatively reproduces the experiments, especially the two-lobed structure between Δ*/e and 2Δ*/e3. Here, we explicitly use the expressions for YSR states with energies continuously approaching the small energy gap Δ for gate voltages detuned from the charge degeneracy point, as seen in the experiment. This suggests that for low enough barriers, the QD resonance becomes broadened beyond Γ ≈ Δ*, allowing electrons and holes to be transmitted simultaneously. At the same time, the segment becomes coupled to the superconductor S2, mediated by ABSs in LS2, which results in a proximity effect on the QD in the form of a YSR state. In the model, we added a small background in the reservoirs to render the original YSR resonances around zero bias visible, illustrating that the large amplitude features labeled \(\overline{{{{{{{{\rm{YSR}}}}}}}}}\) are replicas of the original YSR resonances mapped by ABS1. Interestingly, the originally horizontal ABS2 in LS2 now exhibits an avoided crossing with the YSR feature, best visible in the replica pointed out by green arrows. This hybridization constitutes yet another type of superconducting molecular bound state. The onset of the Josephson effect we find roughly where the YSR resonances cross zero bias, possibly because in this situation the NW transmission is at a maximum and the bias as a decoherence factor at a minimum. We note that to obtain this spectrum, we had to reduce the lever arm of the central QD region by 80%, suggesting that the bias drop occurs partially at other sites, probably mainly across barrier 1, which makes microscopic modeling rather difficult.
In summary, we present transport spectroscopy measurements of intermediate states that occur when ‘fusing’ individual ABSs in NW segments coupled to a central QD, ultimately forming subgap states reaching across the entire NW. We show the evolution from discrete Andreev atoms to different types of Andreev molecules and the fusion of individual states to ‘Andreev helium’, ultimately carrying a Josephson current. We qualitatively reproduce the experimental data with a simple model, which supports our qualitative understanding. Surprisingly, the model requires a gate tunable YSR state on the QD to reproduce the data, suggesting a proximity effect on the QD mediated by the ABSs in the LSs, which can be viewed as a physical implementation of the zero bandwidth model6. We expect that such transitions could be observed on the same CB resonance when controlling the LS and QD states individually by separate sidegates, which can, for example, be used to perform fusion experiments with topologically non-trivial subgap states, and later for Majorana braiding experiments.
Methods
Sample preparation
The InAs nanowires were grown by metal-organic-vapor-phase epitaxy (MOVPE) and have an average diameter of 70 nm. Two segments of wurtzite crystal phase (thickness: 30 nm) are in-situ grown inside the NW. These segments act as atomically precise hard-wall tunnel barriers for electrons, because the ZB and WZ bandstructure align with a conduction band offset of ~ 100 meV18,30. The ZB segment in between, which defines the QD, has a width of 25 nm.
The nanowires were transferred mechanically from the growth substrate to a degenerately p-doped silicon substrate with a SiO2 capping layer (400 nm). The substrate is used as a global back gate. For the electron beam lithography we employ pre-defined markers and contact pads, The superconducting contacts consist of evaporated titanium/aluminium (Ti/Al: 5 nm/80 nm). Before the evaporation step, the native oxide of the NW is removed by an Argon ion sputtering. The total length of the junction is ≈ 450 nm and the QD is located closer to one of the superconducting contacts S1 (L1 ~ 50 nm) than to the other superconducting contact S2 (L2 ~ 320 nm). All measurements were carried out in a dilution refrigerator at a base temperature of 20 mK. Differential conductance has been measured using standard lock-in techniques with a bias voltage modulation of Vac = 10 μVrms at a frequency of fac = 278 Hz.
Description of the three-site model
To illustrate the formation of intermediate states in the ABS fusion process, we use a simple toy model with three sites, namely the two LSs (LS1 and LS2) and the QD, with the tunnel couplings in between as a perturbation, resulting in the strongly simplified Hamiltonian
with \({H}_{{{{{{{{{\rm{LS}}}}}}}}}_{j}}={\sum }_{k}{\epsilon }_{j,k}{s}_{j,k}^{{{{\dagger}}} }{s}_{j,k}\) and \({s}_{j,k}^{({{{\dagger}}} )}\) the LS Hamiltonians, with the annihilation (creation) operator for the two resonances, k ∈ {1, 2}, in the uncoupled LSj. For simplicity, we assume identical bound states in the two LSs pinned to the electrochemical potential of the respective reservoir, ϵj,k = μj + (−1)kEBS, with EBS a constant bound state energy, i.e. with a negligible gate capacitance compared to the ones to source and drain. Hd = ϵdd†d describes the single QD eigenstate at the energy ϵd = − eαSdVS − eαDdVD − eαBGdVBG, with the lever arms αℓd to the respective reservoir, ℓ ∈ {S, D, BG}, and d(†) the annihilation (creation) operator on the QD. The hybridization between the sites we describe by the hopping terms between LSj and the QD, \({H}_{{{{{{{{{\rm{LS}}}}}}}}}_{j}-{{{{{{{\rm{d}}}}}}}}}={\sum }_{k}\left[{t}_{dj}({s}_{jk}^{{{{\dagger}}} }d+c.c.)\right]\), with the hopping parameter tdj, which we choose identically between all sites. More advanced theoretical treatments of multiple NW segments were published recently31,32,33. To roughly reproduce the experiments shown in Fig. 3f, we replace the single QD resonance above by two bias-symmetric subgap resonances on the QD segment, for which we chose the form of YSR states34, where ϵd of the QD enters the YSR resonance energy \({E}_{{{{{{{{\rm{YSR}}}}}}}}}=\pm {\Delta }^{* }\frac{1-{g}^{2}+{w}^{2}}{\sqrt{{(1-{g}^{2}+{w}^{2})}^{2}+4* {g}^{2}}}\) using \(g=\frac{4\pi {D}_{N}{t}^{2}}{U(1-{x}^{2})}\), w = 0.5gx and x = 1 + 2ϵd/U, with t the tunnel coupling strength to the LSs, U the QD charging energy and DN the normal state DoS. To obtain the electrical current I, we simply assume an identical Lorentzian transmission \({{{{{{{\mathcal{L}}}}}}}}(E)\) for all cases, with identical and constant broadening for each eigenstate n, centered at the eigenenergy En, and with an amplitude \({A}_{j}^{(n)}\) given by the weights on site j, yielding the transmission through the three sites T(E) = T1TdT2 with \({T}_{j}={\sum }_{n}| {A}_{j}^{(n)}{| }^{2}{{{{{{{\mathcal{L}}}}}}}}(E-{E}_{n})\), and the current25,35
with f1,2 the Fermi distribution functions and D1,2 the single particle DoS in the respective reservoirs. For the latter we use the standard BCS expression with a small broadening described by the Dynes parameter19,36 and an additional constant background.
Data availability
All data in this publication are available in numerical form at https://doi.org/10.5281/zenodo.3558308. Further information on this study is available from the corresponding author on reasonable request.
References
Lee, E. J. H. et al. Spin-resolved andreev levels and parity crossings in hybrid superconductor–semiconductor nanostructures. Nat. Nanotechnol. 9, 79–84 (2013).
Gramich, J., Baumgartner, A. & Schönenberger, C. Andreev bound states probed in three-terminal quantum dots. Phys. Rev. B 96, 195418 (2017).
Pillet, J.-D. et al. Andreev bound states in supercurrent-carrying carbon nanotubes revealed. Nat. Phys. 6, 965–969 (2010).
Prada, E. et al. From andreev to majorana bound states in hybrid superconductor–semiconductor nanowires. Nat. Rev. Phys. 2, 575–594 (2020).
Riwar, R.-P., Houzet, M., Meyer, J. S. & Nazarov, Y. V. Multi-terminal josephson junctions as topological matter. Nat. Commun. 7, 11167 (2016).
Grove-Rasmussen, K. et al. Yu–shiba–rusinov screening of spins in double quantum dots. Nat. Commun. 9, 2376 (2018).
Scherübl, Z. et al. Large spatial extension of the zero-energy yu–shiba–rusinov state in a magnetic field. Nat. Commun. 11, 1834 (2020).
O’Farrell, E. et al. Hybridization of subgap states in one-dimensional superconductor-semiconductor coulomb islands. Phys. Rev. Lett. 121, 256803 (2018).
Alicea, J., Oreg, Y., Refael, G., von Oppen, F. & Fisher, M. P. A. Non-abelian statistics and topological quantum information processing in 1d wire networks. Nat. Phys. 7, 412–417 (2011).
Zhang, H., Liu, D. E., Wimmer, M. & Kouwenhoven, L. P. Next steps of quantum transport in majorana nanowire devices. Nat. Commun. 10, 5128 (2019).
Mourik, V. et al. Signatures of majorana fermions in hybrid superconductor-semiconductor nanowire devices. Science 336, 1003–1007 (2012).
Albrecht, S. M. et al. Exponential protection of zero modes in majorana islands. Nature 531, 206–209 (2016).
Nichele, F. et al. Relating andreev bound states and supercurrents in hybrid josephson junctions. Phys. Rev. Lett. 124, 226801 (2020).
Razmadze, D., O’Farrell, E., Krogstrup, P. & Marcus, C. Quantum dot parity effects in trivial and topological josephson junctions. Phys. Rev. Lett. 125, 116803 (2020).
Reeg, C., Dmytruk, O., Chevallier, D., Loss, D. & Klinovaja, J. Zero-energy andreev bound states from quantum dots in proximitized rashba nanowires. Phys. Rev. B 98, 245407 (2018).
Kells, G., Meidan, D. & Brouwer, P. W. Near-zero-energy end states in topologically trivial spin-orbit coupled superconducting nanowires with a smooth confinement. Phys. Rev. B 86, 100503 (2012).
Lehmann, S., Wallentin, J., Jacobsson, D., Deppert, K. & Dick, K. A. A general approach for sharp crystal phase switching in InAs, GaAs, InP, and GaP nanowires using only group v flow. Nano Lett. 13, 4099–4105 (2013).
Nilsson, M. et al. Single-electron transport in InAs nanowire quantum dots formed by crystal phase engineering. Phys. Rev. B 93, 195422 (2016).
Jünger, C. et al. Spectroscopy of the superconducting proximity effect in nanowires using integrated quantum dots. Commun. Phys. 2, 76 (2019).
Jünger, C. et al. Magnetic-field-independent subgap states in hybrid rashba nanowires. Phys. Rev. Lett. 125, 017701 (2020).
Thomas, F. S. et al. Highly symmetric and tunable tunnel couplings in InAs/InP nanowire heterostructure quantum dots. Nanotechnology 31, 135003 (2020).
Su, Z. et al. Andreev molecules in semiconductor nanowire double quantum dots. Nat. Commun. 8, 585 (2017).
Scherübl, Z., Pályi, A. & Csonka, S. Transport signatures of an andreev molecule in a quantum dot–superconductor–quantum dot setup. Beilstein J. Nanotechnol. 10, 363–378 (2019).
Pillet, J.-D., Benzoni, V., Griesmar, J., Smirr, J.-L. & Girit, Ç. Nonlocal josephson effect in andreev molecules. Nano Lett. 19, 7138–7143 (2019).
Gramich, J., Baumgartner, A. & Schönenberger, C. Resonant and inelastic andreev tunneling observed on a carbon nanotube quantum dot. Phys. Rev. Lett. 115, 216801 (2015).
Su, Z. et al. Mirage andreev spectra generated by mesoscopic leads in nanowire quantum dots. Phys. Rev. Lett. 121, 127705 (2018).
Doh, Y.-J. et al. Tunable supercurrent through semiconductor nanowires. Science 309, 272–275 (2005).
Nilsson, H. A., Samuelsson, P., Caroff, P. & Xu, H. Q. Supercurrent and multiple andreev reflections in an InSb nanowire josephson junction. Nano Lett. 12, 228–233 (2011).
Saldaña, J. E. et al. Supercurrent in a double quantum dot. Phys. Rev. Lett. 121, 257701 (2018).
Chen, I.-J. et al. Conduction band offset and polarization effects in InAs nanowire polytype junctions. Nano Lett. 17, 902–908 (2017).
Villas, A. et al. Tunneling processes between yu-shiba-rusinov bound states. Phys. Rev. B 103, 155407 (2021).
Hess, R., Legg, H. F., Loss, D. & Klinovaja, J. Local and nonlocal quantum transport due to andreev bound states in finite rashba nanowires with superconducting and normal sections. Phys. Rev. B 104, 075405 (2021).
Steffensen, G. O. et al. Direct transport between superconducting subgap states in a double quantum dot. arXiv:2105.06815 (2021).
Kiršanskas, G., Goldstein, M., Flensberg, K., Glazman, L. I. & Paaske, J. Yu-shiba-rusinov states in phase-biased superconductor-quantum dot-superconductor junctions. Phys. Rev. B 92, 235422 (2015).
Yeyati, A. L., Cuevas, J. C., López-Dávalos, A. & Martín-Rodero, A. Resonant tunneling through a small quantum dot coupled to superconducting leads. Phys. Rev. B 55, R6137–R6140 (1997).
Dynes, R. C., Narayanamurti, V. & Garno, J. P. Direct measurement of quasiparticle-lifetime broadening in a strong-coupled superconductor. Phys. Rev. Lett. 41, 1509–1512 (1978).
Acknowledgements
The authors thank R. Delagrange, D. Chevallier, C. Reeg, S. Hoffman, J. Klinovaja and D. Loss for useful discussions and A. Mettenleiter for the help with the illustrations. This work was supported by the Swiss National Science Foundation by (a) the project “Quantum Transport in Nanowires” granted to CS, grant agreement No 192027, (b) the National Center of Competence in Research Quantum Science and Technology (QSIT), and (c) the QuantEra project SuperTop, grant agreement No 175341. We further acknowledge funding from the European Union’s Horizon 2020 research and innovation program under grant agreement No 828948, project AndQC, the project QUSTEC, as well as the Swiss Nanoscience Institute (SNI). S.L., K.A.D. and C.T. acknowledge financial support by the Knut and Alice Wallenberg Foundation (KAW) and the Swedish Research Council (VR).
Author information
Authors and Affiliations
Contributions
C.J. fabricated the devices and performed the measurements. A.B. and C.J. analyzed the data. A.B. implemented the three-site model. S.L., K.A.D. and C.T. developed the nanowire structure. C.S. and A.B. planned and designed the experiments, and participated in all discussions. All authors contributed to the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jünger, C., Lehmann, S., Dick, K.A. et al. Intermediate states in Andreev bound state fusion. Commun Phys 6, 190 (2023). https://doi.org/10.1038/s42005-023-01273-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-023-01273-2
This article is cited by
-
Phase-dependent Andreev molecules and superconducting gap closing in coherently-coupled Josephson junctions
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.