Abstract
Recently, porphyrin units have been attached to graphene nanoribbons (Por-GNR) enabling a multitude of structures. Here we report first-principles calculations of two prototypical, experimentally feasible, Por-GNR hybrids, one of which displays a small band gap relevant as electrodes in devices. Embedding a Fe atom in the porphyrin causes spin-polarized ground state (S = 1). Using density functional theory and nonequilibrium Green’s function, we examine a 2-terminal setup involving a Fe-Por-GNR between small band gap, Por-GNR electrodes. The coupling between the Fe-d and GNR band states results in a Fano anti-resonance feature in the spin transport, making the conductance highly sensitive to the Fe spin state. We demonstrate how mechanical strain or chemical adsorption on the Fe give rise to spin-crossover to S = 2 and S = 0, directly reflected in the transmission. Our results provide a deep understanding which can open an avenue for carbon-based spintronics and chemical sensing.
Similar content being viewed by others
Introduction
Graphene nanoribbons (GNRs) with extensive π-delocalized electrons have attracted attention due to their electronic properties like width-dependent band gaps, edge states and long spin relaxation time, turning these one-dimensional (1D) materials into promising building blocks for nanoelectronic and spintronic devices in the carbon family1,2,3,4,5. One of the most significant pigments in nature, porphyrin, exhibits tunable spin properties in its conjugated arrays, depending on the central metal ion and the surrounding ligand field6,7,8. Therefore, it would be a highly appealing strategy to synthesize porphyrin-graphene nanoribbon (Por-GNR) hybrids with well-ordered atomic arrangements and possibilities of tailoring the band gap, topological phases, and detecting magnetic signals in transport.
During the last decade, on-surface synthesis has become a powerful technique to form atomically precise nanostructures by linking small precursor molecules9,10,11,12 or porphyrin building blocks13,14 in a bottom-up approach. This makes the fabrication of quasi 1D Por-GNR hybrids feasible, avoiding problems such as random molecular placement and metal clusters formation15,16. Recently, several research groups have attempted to expand the synthetic 1D complexes including porphyrin cores in different ways17,18. The structures considered so far, both in experimental and theoretical works, have mainly been porphyrin oligomers/polymers19, or porphyrin nanotapes20, which lack the GNRs segments as a backbone. Only finite nanostructures with two metal-free (H2) Pors connected by a short GNR segment have been synthesized on surface by Mateo et al.21. Interestingly, the charge transport properties of the nickel Pors nanoribbons (nanotapes) devices with graphene electrodes show the quantum interference phenomena22. This naturally poses the question of how electronic transport takes places in GNRs with incorporated Pors, and especially spin transport for Pors with magnetic centers.
In this letter, we propose two Por-GNR hybrids which might be experimentally feasible using two existing carbon-based precursor molecules23,24 and a porphyrin center. Combining such molecular units gives rise to the straight hybrid1 and “S-shape” hybrid2 structures shown in Fig. 1. Our first principles calculations reveal that hybrid2 has a small electronic band-gap ( ~ 0.1 − 0.2 eV), which is highly desirable for potential spintronic devices. Embedding an iron atom in the porphyrin center in both 1D nanostructures gives rise to spin polarization with a spin ground state of S = 1. Employing the nonequilibrium Green’s function (NEGF) formalism, we consider a 2-terminal device setup including one Fe-hybrid2 linked between two H2-hybrid2. The coupling between the electronic states of the GNR segments and those states with matching symmetry in the Fe-porphyrin center, leads to spin-polarized Fano anti-resonances close to the Fermi energy in the transmission. A switching of the spin-state to S = 2 can be achieved by mechanical strain, while the adsorption of a CO molecule on top of the Fe center fully quenches the magnetism. Our work highlights the potential of Por-GNRs as a highly tunable and flexible platform for spintronics and sensing applications.
Results and discussion
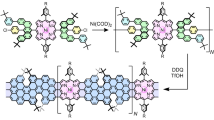
Figure 1a and b show two existing carbon-based precursor units (1,2) and the porphyrin building block, respectively, with M representing either a metal-free (H2) or a metallized (e.g., with a Fe atom) unit. The precursors we select here have already been synthesized and successfully used to grow atomically precise 7-AGNRs (unit 1)25 and 13-AGNRs26 (unit 2) on surface. In Fig. 1c we show how the combination of Por with units 1 or 2 can give rise to a quasi 1D Por-GNR structure which may be repeated periodically or joined by additional “pristine” 1 or 2 units, respectively. Moreover, the different precursors produce GNR segments of distinct morphology, resulting in a straight-shaped hybrid1 and a “S-shaped” hybrid2. The previous successful bottom-up synthesis of GNRs and Por-GNR connections indicates that these proposed systems should be feasible.
The DFT optimized structures in Fig. 2a are planar for the two periodically repeated H2-Por-GNR hybrids, and both are non-spin polarized, as seen in the band structures in Fig. 2b. Besides, the bands shown in the left and middle panels in Fig. 2b indicate that different edge conformations lead to different frontier bands and, importantly, reveal a band gap closing in hybrid2 at the Y-point (zone-boundary). Although this result depends on the DFT exchange functional employed, the trend is the same: the straight hybrid1 has a larger gap of 0.75 eV for PBE and 0.9 eV for HSE06, whereas the “S-shape” hybrid2 displays a small electronic gap of 0.1 eV for PBE and 0.25 eV for HSE06. The functional HSE06 is commonly used for GNRs, and can improve the description of band gaps within the framework of DFT27,28. This band-gap “closing” is likely to be caused by the presence of wider GNR segments in hybrid2, as the band gap of the pristine 13-AGNRs is around 1 eV larger than that of 7-AGNRs26. The small band gap exhibited by hybrid2 would be highly useful for potential applications in quantum transport nanodevices. To gain a deeper insight into the properties of the Por-GNR hybrids, we calculate the \({{\mathbb{Z}}}_{{{\mbox{2}}}}\) topological invariant for non-metallized hybrid1 and hybrid2, using the supercells shown in the left and middle panels of Fig. 2a. We obtain \({{\mathbb{Z}}}_{{{\mbox{2}}}}\) = 1 for both structures, indicating that they are both in a topologically non-trivial phase and that localized end states at the interface to vacuum are be expected. Moreover, as shown in Supplementary Fig. 1, we do not observe any symmetry inversion when inspecting the wavefunctions of the conduction and valence bands at Γ and Y for both Por-GNR structures, also confirming that such two hybrids belong to the same topological family.
a The optimized structures of 1D Por-GNR hybrids. The gray, blue, white and yellow balls represent C, N, H, and Fe atoms, respectively. b The corresponding band structure as obtained with the PBE functional. Here, EF is the Fermi level. For Fe-Por-GNR hybrid2, the black solid and dash lines represent the spin up and spin down states, respectively, and the red dash line is labeled the spin down state of Fe-dxz. S is the total spin angular momentum.
In an attempt to realize future spintronics in these novel nanostructures, we embed an iron atom in the porphyrin center in hybrid2 (Fe-hybrid2). This gives rise to spin polarization, the ground state being the S = 1 solution. The atomic structure of D4h symmetry remains planar and the four equivalent Fe-N bonds have a length of 2 Å. For comparison, we also introduce a Fe atom into hybrid1 and the relaxed flat structure has the same occupation of Fe-3d orbitals as Fe-hybrid2 (see Supplementary Fig. 2), with a slightly decrease Fe-N bond length of 1.97 Å. The ground state of the isolated iron tetraphenyl porphyrin (FeTPP), which contains the same central macrocycle, has a S = 1 ground state (3A2g) and the occupancy of the 3d shell is \({({d}_{{x}^{2}-{y}^{2}})}^{2}{({d}_{{z}^{2}})}^{2}{({d}_{xz})}^{1}{({d}_{yz})}^{1}\), where the last two orbitals are degenerate as a consequence of the molecular symmetry29,30. However, for the ground state of the hybrid2 we obtain the 3Eg electronic configuration, in which the 3d occupation is \({({d}_{{x}^{2}-{y}^{2}})}^{2}({d}_{{z}^{2}}){({d}_{xz})}^{2}{({d}_{yz})}^{1}\), despite the total spin moment being still 2 μB. It is the breaking of symmetry and the coupling of the GNR band states to the Fe-porphyrin states with matching symmetry which results in this change. The right panel in Fig. 2b illustrates the electronic band structure of Fe-Por-GNR hybrid2, with the occupied spin down state of Fe-dxz (marked in red) very close to the Fermi level (at ≈ -0.15 eV). The DOS projected on Fe-3d orbitals in a larger energy range for the Fe-Por-GNR hybrid2 (Supplementary Fig. 3) is shown in Supplementary Fig. 3c. Most of them are below -2 eV or above 2 eV, which are far from the Fermi level. In addition, we obtain a meta-stable state with the occupation corresponding to 3A2g, at a modest energy expense of 0.1 eV (see Supplementary Fig. 4). For the isolated Fe-porphyrin molecule, the energy difference between 3A2g and 3Eg is always very small ~ 10 meV30. This implies that the spin state of the central iron atom can be stabilized by coupling with the GNRs segments, revealing one of the distinct advantages of the proposed 1D hybrids. Indeed, the spin-multiplet energetics of nearly degenerate spin-states is a difficulty for this research area at least from the theoretical perspective30,31,32.
Motivated by this understanding, we now consider the electronic transport properties of the 1D Por-GNR hybrid2. We create a two-terminal setup in order to access the spin-dependent transport of one isolated Fe-hybrid2 unit sandwiched between two H2-hybrid2 in the device region, the latter being repeated in the semi-infinite left/right directions acting as electrodes, as shown in Fig. 3a. Since we employ pristine H2-hybrid2 as electrodes, there is a small gap of 0.1 eV at the Fermi level in the zero-bias transmission function (see Fig. 3b). Figure 3c describes the 3d level occupation of the Fe atom in the device region, which is the same as for the Fe atom in the periodical Fe-Por-GNR hybrid2 (3Eg). Interestingly, a zero-bias transmission dip occurs for spin down channel (red line in Fig. 3b) at -0.15 eV related to the 3dxz orbital of Fe atom. The interference between waves involving the 3d state on the Fe atom, and waves directly transmitted in band states not involving the Fe states, yields a Fano resonance33. We further plot the real part of the source-to-drain eigen channel scattering state34,35 for the energy corresponding to the dip (-0.15 eV) in Fig. 3d. The wavefunction for the spin up state goes through the device region, while it is fully reflected and therefore vanishing on the top side for the spin down state. From the sign and shape of the wavefunctions we can identify the orbitals involved in the transport (dxz on Fe).
a Two-terminal transport setup. The shaded areas (Source and Drain) are the electrodes. b Zero-bias transmission (T). The black and red lines represent the spin up and spin down states, respectively. c Occupation of Fe d-orbitals in the S = 1 state in the device. d The real part of the (source-to-drain) eigenchannel scattering states at -0.15 eV. Both spin up and spin down channels in the scattering region are shown. Red and blue clouds indicate the positive and negative sign of the wavefunction, respectively. Isosurfaces with values of ± 0.01 e bohr-3 are shown. EF is the Fermi level and S is the total spin angular momentum.
The Fe porphyrin-based nanomaterials, presenting an open d-shell, allow for various possible electronic configurations and different spin-multiples. This can result in a spin-crossover (SCO) behavior controlled by the environment and external stimuli. In Fig. 4 we demonstrate how we may manipulate the spin state of the 1D device discussed above, either by mechanical strain along the GNR backbones, or by chemical adsorption of a CO molecule on the Fe center. Figure 4a shows the mechanically strained SCO device and the resulting spin transition from S = 1 to S = 2 obtained by applying 3% uniaxial strain. The four Fe-N bond lengths in the stretched flat geometry increase from 2 to 2.10 Å, leading to the variation of the Fe-d occupation and spin state, as shown in Fig. 4e. Here, we keep the d-orbital sequence used in Fig. 3c, representing the corresponding variations of the d configurations in a simple way36. Similar results also observed by S. Bhandary et al. in the system of a strain-induced spin crossover of a Fe-porphyrin molecule bridging zigzag GNRs: spin switching by 2.5% strain37. This variation results in a drastic change in transport, specially in the valence band where the Fano feature disappears, when compared to the unstrained case in Fig. 3b. The strain results in almost equal spin up and spin down transmissions in the energy range from −0.5 to 0.5 eV, as shown in Fig. 4c. Thus our proposed Por-GNR hybrid2 device is a good candidate for a mechanically driven spin filter device.
a Schematic diagram of strain effect on the Fe atom in 1D Por-GNR hybrid2 device. b Schematic diagram of CO on top of the Fe atom in Fe-Por-GNR hybrid2 device. The corresponding zero-bias transmission (T) are shown c, d. EF is the Fermi level and S is the total spin angular momentum. The occupation of Fe d-orbitals e in the S = 2 state and f in the S = 0 state in the device. Here, we keep the d-orbital sequence used in Fig. 3c, representing the corresponding variations of the d configurations in a simple way. EF is the Fermi level.
Another way to change the spin state in the same device setup is the adsorption of a CO molecule on top of the Fe atom, with a binding energy of 2.03 eV. In this case the total magnetic moment varies from 2 to 0 μB due to the strong covalent binding. In detail, the Fe-CO bond length is 1.73 Å and the C-O distance is 1.16 Å (see Fig. 4b). Interestingly, the Fe-N bond length remains 2 Å and there is also little vertical displacement of the Fe atom. The Mulliken charge analysis shows that upon adsorption only 0.2 electrons are transferred from CO to the Fe-3d system, and the density of states projected on the 3d orbitals of the Fe atom displays a stronger crystal-field splitting (see Supplementary Fig. 5). The corresponding transmission and the Fe-d occupation are shown in Fig. 4d, f. Here the change of the crystal field from a square planar to a square pyramidal symmetry is responsible for the spin transition. Such results are in an agreement with previous works38,39,40. This indicates that our proposed Por-GNR hybrid2 device would be a promising material for next-generation chemical sensing41.
It is worth emphasizing that such hybrid nanoarchitectures are normally synthesized on metallic surfaces, and the spin could be quenched by the substrate. However, we note that the conductance properties of 1D magnetic nanoarchitectures have already been addressed experimentally by their attachment and subsequently lifting using an STM tip42. Furthermore, in some cases ribbons and even 2D materials formed by their lateral fusion can be transferred onto insulating substrates sand function as free-standing-like systems in the devices43,44. Under any of these scenarios, the spin properties demonstrated in this paper would be preserved.
Conclusion
We have performed first principles DFT-NEGF calculations to study the electronic and transport properties of two proposed metal-free Por-GNR hybrids based on already synthesized precursors. The 1D dimensional “S-shaped” Por-GNR system (hybrid2) reveals a small band gap, and is therefore interesting as a device electrode candidate. Embedding an iron atom in the porphyrin center causes spin polarization with 3Eg ground state, due to the coupling of the GNR band states to the Fe-porphyrin. A feasible 2-terminal transport setup including one Fe-hybrid2 is considered, and a Fano anti-resonance dip appears in the zero-bias transmission of the spin down channel close to the Fermi energy. We demonstrate how this prominent feature and the resulting transmission around the Fermi level can be manipulated by external stimuli that change the spin state, such as an applied mechanical strain (S = 2 @ 3% strain), or the adsorption of a CO molecule which quench the magnetic moment (S = 0). In light of potential applications in spintronics, it is worth exploring possible magnetic properties including the surface effect (Kondo resonance), topological quantum phase45, spin–spin interaction46 and the possibility of the 2D structures47 in the desirable, spin-hosting Por-GNRs hybrids, which will be pursued in future investigations.
Method
Computational procedures
We employed the SIESTA/TransSIESTA code, GGA-PBE48 for exchange-correlation, and a DZP basis-set49,50,51. The energy cutoff of 400 Ry was used to define the real-space grid. All the calculations were carried out with a low electronic temperature of 50 K and spin polarization was also included. The k-point mesh of 1 × 6 × 1 was used and a 25 Å thick vacuum layer for the slab model was introduced. Importantly, all atoms were allowed to relax until the forces on each atom were smaller than 0.01 eV/Å. Moreover, we considered the mean-field correction of the Hubbard U = 3 eV for Fe 3d orbitals52. The computational parameters used in the equilibrium calculations were checked carefully for convergence and reproduced accurately the trends obtained by the Vienna ab initio simulation package (VASP)53 with PBE48 and HSE0627 functionals. Subsequently, physical quantities like the density of states, transmission, current and spin density were extracted using SISL54. Zak phases were obtained from the electronic contributions to the macroscopic electric polarization values calculated with the SIESTA code49,55.
Data availability
The data that support this work can be found in the Manuscript and Supplementary Information. Additional data will be available from the corresponding author upon reasonable request.
References
Gröning, O. et al. Engineering of robust topological quantum phases in graphene nanoribbons. Nature 560, 209–213 (2018).
Zhao, F., Cao, T. & Louie, S. G. Topological phases in graphene nanoribbons tuned by electric fields. Phys. Rev. Lett. 127, 166401 (2021).
Cao, T., Zhao, F. & Louie, S. G. Topological phases in graphene nanoribbons: junction states, spin centers, and quantum spin chains. Phys. Rev. Lett. 119, 076401 (2017).
Kim, W. Y. & Kim, K. S. Prediction of very large values of magnetoresistance in a graphene nanoribbon device. Nat. Nanotechnol. 3, 408–412 (2008).
de Oteyza, D. G. & Frederiksen, T. Carbon-based nanostructures as a versatile platform for tunable π-magnetism. J. Phys.: Condens. Matter 34, 443001 (2022).
Hiroto, S., Miyake, Y. & Shinokubo, H. Synthesis and functionalization of porphyrins through organometallic methodologies. Chem. Rev. 117, 2910–3043 (2017).
Tanaka, T. & Osuka, A. Conjugated porphyrin arrays: synthesis, properties and applications for functional materials. Chem. Soc. Rev. 44, 943–969 (2015).
Jurow, M., Schuckman, A. E., Batteas, J. D. & Drain, C. M. Porphyrins as molecular electronic components of functional devices. Coord. Chem. Rev. 254, 2297–2310 (2010).
Cai, J. et al. Atomically precise bottom-up fabrication of graphene nanoribbons. Nature 466, 470–473 (2010).
Ruffieux, P. et al. On-surface synthesis of graphene nanoribbons with zigzag edge topology. Nature 531, 489–492 (2016).
Narita, A. et al. Synthesis of structurally well-defined and liquid-phase-processable graphene nanoribbons. Nat. Chem. 6, 126–132 (2014).
Jacobse, P. H. et al. Bottom-up assembly of nanoporous graphene with emergent electronic states. J. Am. Chem. Soc. 142, 13507–13514 (2020).
Tanaka, T. & Osuka, A. Conjugated porphyrin arrays: synthesis, properties and applications for functional materials. Chem. Soc. Rev. 44, 943–969 (2015).
Li, J. et al. Survival of spin state in magnetic porphyrins contacted by graphene nanoribbons. Sci. Adv. 4, eaaq0582 (2018).
Sun, Q., Wang, Q., Jena, P. & Kawazoe, Y. Clustering of ti on a c60 surface and its effect on hydrogen storage. J. Am. Chem. Soc. 127, 14582–14583 (2005).
Gao, F., Ding, Z. & Meng, S. Three-dimensional metal-intercalated covalent organic frameworks for near-ambient energy storage. Sci. Rep. 3, 1–9 (2013).
Kawai, S. et al. On-surface synthesis of porphyrin-complex multi-block co-oligomers by defluorinative coupling. Angew. Chem. 134, e202114697 (2022).
Mallada, B. et al. On-surface synthesis of one-dimensional coordination polymers with tailored magnetic anisotropy. ACS Appl. Mater. Interfaces 13, 32393–32401 (2021).
Deyerling, J. et al. On-surface synthesis of rigid benzenoid-and nonbenzenoid-coupled porphyrin–graphene nanoribbon hybrids. J. Phys. Chem. C 126, 8467 (2022).
Sun, Q. et al. Bottom-up fabrication and atomic-scale characterization of triply linked, laterally π-extended porphyrin nanotapes. Angew. Chem. 133, 16344–16350 (2021).
Mateo, L. M. et al. On-surface synthesis and characterization of triply fused porphyrin–graphene nanoribbon hybrids. Angew. Chem. 132, 1350–1355 (2020).
Chen, Z. et al. Phase-coherent charge transport through a porphyrin nanoribbon-graphene junction. arXiv preprint arXiv:2205.08499 (2022).
Cai, J. et al. Atomically precise bottom-up fabrication of graphene nanoribbons. Nature 466, 470–473 (2010).
Talirz, L., Ruffieux, P. & Fasel, R. On-surface synthesis of atomically precise graphene nanoribbons. Adv. Mater. 28, 6222–6231 (2016).
Talirz, L. et al. Termini of bottom-up fabricated graphene nanoribbons. J. Am. Chem. Soc. 135, 2060–2063 (2013).
Chen, Y.-C. et al. Tuning the band gap of graphene nanoribbons synthesized from molecular precursors. ACS nano 7, 6123–6128 (2013).
Krukau, A. V., Vydrov, O. A., Izmaylov, A. F. & Scuseria, G. E. Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 125, 224106 (2006).
Jain, M., Chelikowsky, J. R. & Louie, S. G. Reliability of hybrid functionals in predicting band gaps. Phys. Rev. Lett. 107, 216806 (2011).
Liao, M.-S. & Scheiner, S. Electronic structure and bonding in metal porphyrins, metal= fe, co, ni, cu, zn. J. Chem. Phys. 117, 205–219 (2002).
Bouatou, M. et al. Intraconfigurational transition due to surface-induced symmetry breaking in noncovalently bonded molecules. J. Phys. Chem. Lett. 11, 9329–9335 (2020).
Li Manni, G. & Alavi, A. Understanding the mechanism stabilizing intermediate spin states in fe (ii)-porphyrin. J. Phys. Chem. A 122, 4935–4947 (2018).
Liao, M.-S., Watts, J. D. & Huang, M.-J. Electronic structure of some substituted iron (ii) porphyrins. are they intermediate or high spin? J. Phys. Chem. A 111, 5927–5935 (2007).
Wang, Z.-Q. et al. Modulation of spin thermoelectric properties in transition metal porphyrin single-molecule spin caloritronic devices by fano resonance. Phys. E: Low.-Dimens Syst. Nanostruct. 121, 114129 (2020).
Fürst, J. A., Brandbyge, M., Jauho, A.-P. & Stokbro, K. Ab initio study of spin-dependent transport in carbon nanotubes with iron and vanadium adatoms. Phys. Rev. B 78, 195405 (2008).
Paulsson, M. & Brandbyge, M. Transmission eigenchannels from nonequilibrium green’s functions. Phys. Rev. B 76, 115117 (2007).
Meng, X. et al. Controlling the spin states of fetbrpp on au (111). ACS nano 17, 1268 (2023).
Bhandary, S., Tomczak, J. M. & Valli, A. Designing a mechanically driven spin-crossover molecular switch via organic embedding. Nanoscale Adv. 3, 4990–4995 (2021).
Falahati, K., Tamura, H., Burghardt, I. & Huix-Rotllant, M. Ultrafast carbon monoxide photolysis and heme spin-crossover in myoglobin via nonadiabatic quantum dynamics. Nat. Commun. 9, 4502 (2018).
Ammar, H. & Badran, H. Effect of co adsorption on properties of transition metal doped porphyrin: a dft and td-dft study. Heliyon 5, e02545 (2019).
Abdurahman, A. & Renger, T. Density functional studies of iron-porphyrin cation with small ligands x (x: O, co, no, o2, n2, h2o, n2o, co2). J. Phys. Chem. A 113, 9202–9206 (2009).
Hu, X. et al. What is the real origin of the activity of fe–n–c electrocatalysts in the o2 reduction reaction? critical roles of coordinating pyrrolic n and axially adsorbing species. J. Am. Chem. Soc. 144, 18144–18152 (2022).
Friedrich, N. et al. Magnetism of topological boundary states induced by boron substitution in graphene nanoribbons. Phys. Rev. Lett. 125, 146801 (2020).
Chen, Z. et al. Synthesis of graphene nanoribbons by ambient-pressure chemical vapor deposition and device integration. J. Am. Chem. Soc. 138, 15488–15496 (2016).
Moreno, C. et al. Bottom-up synthesis of multifunctional nanoporous graphene. Science 360, 199–203 (2018).
Gröning, O. et al. Engineering of robust topological quantum phases in graphene nanoribbons. Nature 560, 209–213 (2018).
Van Raden, J. M. et al. Singly and triply linked magnetic porphyrin lanthanide arrays. J. Am. Chem. Soc. 144, 8693 (2022).
Zhou, J. & Sun, Q. Magnetism of phthalocyanine-based organometallic single porous sheet. J. Am. Chem. Soc. 133, 15113–15119 (2011).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Soler, J. M. et al. The siesta method for ab initio order-n materials simulation. J. Phys.: Condens. Matter 14, 2745 (2002).
Brandbyge, M., Mozos, J.-L., Ordejón, P., Taylor, J. & Stokbro, K. Density-functional method for nonequilibrium electron transport. Phys. Rev. B 65, 165401 (2002).
Papior, N., Lorente, N., Frederiksen, T., García, A. & Brandbyge, M. Improvements on non-equilibrium and transport green function techniques: the next-generation transiesta. Comput. Phys. Commun. 212, 8–24 (2017).
Dudarev, S. L., Botton, G. A., Savrasov, S. Y., Humphreys, C. & Sutton, A. P. Electron-energy-loss spectra and the structural stability of nickel oxide: an lsda+ u study. Phys. Rev. B 57, 1505 (1998).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558 (1993).
Papior, N. sisl: v0.9.4, 2018.
King-Smith, R. D. & Vanderbilt, D. Theory of polarization of crystalline solids. Phys. Rev. B 47, 1651–1654 (1993).
Acknowledgements
We thank Aitor Mugarza and Diego Peña for fruitful discussions and highly valuable input. This project received funding from the EU Horizon 2020 under Grant No. 766726 and funding from Villum fonden (VIL 13340). We gratefully acknowledge financial support from Grant PID2019-107338RB-C66 funded by MCIN/AEI/10.13039/501100011033, Grant No. TED2021-132388B-C41 funded by MCIN/AEI/10.13039/501100011033 and the European Union NextGenerationEU/PRTR, the European Union (EU) H2020 program through the FET Open project SPRING (Grant Agreement No. 863098). The authors also acknowledge the financial support received from the IKUR Strategy under the collaboration agreement between Ikerbasque Foundation and DIPC on behalf of the Department of Education of the Basque Government.
Author information
Authors and Affiliations
Contributions
A.G.-L. and M.B. conceived the idea. F.G. performed most of the ab initio calculations and analyzed the data. R.E.M. carried out some numerical simulations for Zak phases. F.G., A.G.-L., and M.B. wrote the manuscript; All authors discussed the results and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
All other authors declare no competing interest.
Peer review
Peer review information
Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gao, F., Menchón, R.E., Garcia-Lekue, A. et al. Tunable spin and conductance in porphyrin-graphene nanoribbon hybrids. Commun Phys 6, 115 (2023). https://doi.org/10.1038/s42005-023-01231-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-023-01231-y
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.