Abstract
Explaining the properties and functions of materials in terms of their atomic arrangements and inhomogeneous structures is a fundamental challenge for the development of ferroelectric oxides. Dielectric response, a fundamental property of matter, can be explained by long-wavelength polar lattice vibrations and dipole relaxations capable of responding to electrical bias; therefore spectroscopic methods, such as Raman spectroscopy, can be used to investigate its origin. Herein, we used angle-resolved polarized Raman mapping to investigate how phase boundaries and giant dielectric responses are related in a relaxor-Pb(Mg1/3Nb2/3)O3–ferroelectric-PbTiO3 (PMN-xPT) solid-solution system using a compositionally graded crystal, with gradual changes in polarization direction visualized by Raman mapping. The variation of the width of quasielastic light scattering with position reveals the following: The huge dielectric response observed in PMN-xPT is ascribable to the slowing down of a relaxation related to mesoscopic ferroelectric domains near the phase boundary, which is characteristic of relaxor–ferroelectric solid-solution systems and differentiates them from other ferroelectrics.
Similar content being viewed by others
Introduction
The properties of a functional crystal are not always explained by its atomic arrangement (i.e., crystal structure). For example, local symmetry breaking sometimes leads to the “forbidden” enhancement of material properties. Perovskite ABO3-type ferroelectrics are typical functional materials with a large response to electric fields and show large dielectric or piezoelectric properties; these large responses are closely associated with polar inhomogeneity (i.e., regions in which local symmetry breaks). For example, local symmetry breaking due to polar correlation along [111]C in BaTiO3 has been observed over several nanometers in an average tetragonal structure, with polar correlation through reorientation of the local dipoles leading to large dielectric responses1,2,3,4,5,6,7,8,9. Pb-based B-site complex perovskites, such as Pb(Mg1/3Nb2/3)O3, which are referred to as “relaxors”, exhibit dielectric responses that are one order of magnitude larger than those of BaTiO3 due to its more complex structure10,11,12,13,14. Relaxors are characterized by several types of local symmetry breaking. One involves one-to-two nanometer cation disorder at B-sites that are referred to as “chemical ordered regions” (CORs) that lead to random electric and elastic fields15,16. Random fields induce polar nanoregions (PNRs) that are several nanometers in size, depending on the temperature, and PNR arrays form micrometer-scale ferroelectric domains17,18,19,20,21,22,23. In addition, micrometer-scale ferroelectric domains are arranged according to the electric poling direction24,25,26,27. Therefore, achieving a unique understanding of relaxors is challenging because inhomogeneous structures and their dynamics are widely spread across various length and time scales.
Furthermore, piezoelectric and dielectric responses are enhanced near morphotropic phase boundaries (MPBs) that are parallel to the temperature axis in the composition–temperature phase diagram of a relaxor-ferroelectric solid-solution single crystal22,28,29,30. A relaxor-Pb(Mg1/3Nb2/3)O3–ferroelectric-PbTiO3 (PMN-xPT) solid solution (mixing ratio = 100−x:x; x mol%) exhibits an MPB between a ferroelectric rhombohedral (R: R3m) phase in a Ti-poor region and a ferroelectric tetragonal (T: P4mm) phase in a Ti-rich region at an x value of approximately 30 mol%. Monoclinic B (MB: Cm) and C (MC: Pm) phases are widely recognized to form bridges that connect R and T phases, as shown in Fig. 1a31,32. The energy states of every phase compete around the MPB, and relaxor-ferroelectric solid-solution single crystals become unstable to external electric fields. The “ease of polarization rotation via monoclinic phases” concept, which is based on phenomenological and first-principles calculations, has been proposed around MPBs to explain the large responses of relaxor-ferroelectric solid solutions by considering the instabilities of ferroelectric phases33,34. Here, spontaneous polarization can easily rotate in the (\(10\bar{1}\)) planes in the MB phase and in the (010) planes in the MC phase. In addition to the polarization rotation mechanism, several qualitative mechanisms have been proposed, including the “critical phenomenon in composition–temperature–electric field phase diagram”, “adaptive domain structure”, and “domain engineering” mechanisms, among others24,29,35.
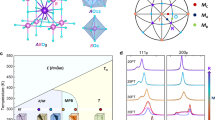
a Phase diagram of PMN-xPT obtained by X-ray powder diffraction31,32. C, R, MB, MC, and T denote cubic, rhombohedral, monoclinic (type B), monoclinic (type C), and tetragonal crystal structures, respectively. The horizontal red thick line at 396K indicates the compositional range of a Ti-composition-gradient PMN-xPT crystal used in this study. b Optical image and Ti-Kα and Nb-Kα X-ray fluorescence mapping of PMN-xPT with Ti composition gradient. Relative composition could be evaluated by measuring X-ray fluorescence from each element using an X-ray analytical microscope. c Position dependence of x in PMN-xPT crystal obtained by synchrotron X-ray fluorescence. d Schematics of sample setting in Raman microscope with relationships between average crystal structure and polarization direction. It also shows how the polarization direction of light is controlled by a half-wave plate.
The science in the vicinity of an MPB is complex and still under debate because several crystal structures share the same energy state, and show aspects that depend on their morphology (such as crystals, ceramics, and thin films) and the experimental technique used (such as X-ray and neutron diffractometry) near the MPB. For example, X-rays and neutrons with different degrees of penetration produce different Bragg diffractions from Pb(Zn1/3Nb2/3)O3 and (1 − x)Pb(Zn1/3Nb2/3)O3-xPbTiO3 (PZN-xPT: x = 4.5 and 8.0 mol%) crystals because the surface has a higher crystal symmetry than the interior36. Consequently, a systematic study involving the preparation of many crystal samples with different compositions is essential when investigating the origins of electrical responses near the MPB. Instead of preparing multiple crystals, we investigated a single PMN-xPT crystal with a Ti composition gradient37 that ranges between x = 29.0 and 37.7 mol% using X-ray diffraction38 and inelastic X-ray scattering mapping39 techniques. The crystal coherence length, determined by the pseudo-cubic (400) Bragg reflection width, is smallest just below the MPB composition, leading to nano-domains (i.e., static PNRs) that rotate more easily, and enhanced electric responses near the MPB38. From a dynamics viewpoint, the transverse acoustic phonon perpendicular to the spontaneous polarization was found to become unstable in the MC phase39.
Since long-wavelength lattice vibrations are associated with ferroelectric interactions, Raman scattering techniques, which probe much longer wavelengths than inelastic X-ray and neutron scattering methods, have revealed instabilities near phase transitions from a dynamics viewpoint40. Raman spectroscopy also provides information on crystal symmetry because Raman scattering from a crystal depends on the Raman tensors derived from the point symmetry of the crystal41. Our angle-resolved polarized Raman spectroscopy technique effectively uses Raman tensor information: The relationship between Raman peak intensity and the angle between the polarization direction of the incident and scattered light, θ, provides information about the crystal sample, such as the point group and optical axis direction, in addition to the frequencies and damping constants associated with lattice vibrations obtained by usual Raman spectroscopy42,43. Here, mapping the Ti-composition-gradient PMN-xPT crystal is expected to provide information about lattice vibrations in the vicinity of the MPB. In this study, we added a mapping device to this spectroscopic method. Angle-resolved polarized Raman spectra were acquired at each position of the Ti-composition-gradient PMN-xPT crystal to understand the dielectric response in terms of the atomic arrangements and inhomogeneous structures present. This experiment clarified the spatial arrangement of polarization and relaxation dynamics, and the origin of the giant dielectric response in the vicinity of the MPB was discussed.
Results and discussion
Evaluating a Ti-composition-gradient PMN-xPT crystal and its placement in the Raman microscope
An as-grown Ti-composition-gradient PMN-xPT crystal was cut to provide a 62.7 × 15.0 × 0.3 mm {100} plane, of which two large surfaces were optically polished37. Figure 1b shows an optical image and Ti-Kα and Nb-Kα X-ray fluorescence intensity maps of the crystal acquired by analytical X-ray microscopy. The Ti-Kα and Nb-Kα fluorescence intensity are uniform in the longitudinal direction. In contrast, the Ti-Kα fluorescence intensity increases, and the Nb-Kα fluorescence intensity decreases toward the right-hand side of the image. In the same way, Pb was determined to be uniformly distributed. To quantitatively determine the composition, x, of the Ti-composition-gradient PMN-xPT crystal in the transverse direction, Ti fluorescence (Kα: 4.51 keV) intensities were examined together with those of reference PMN-xPT samples with x = 0 and 38.7 mol%. Figure 1c shows the positional dependence of x, with x observed to change from 27.0 to 38.0 mol% over the 62.7-mm sample length. The relationship between the composition range of the sample and the phase diagram is also represented in Fig. 1a. The space groups within the crystal confirmed in our previous studies are shown in Fig. 1d38. The cloudy-to-transparent change in appearance in the optical image corresponds to the boundary between MB and MC phases. The crystal was positioned on the Raman microscope such that the boundary between the two phases was placed at X = 13 mm on the stage, after which angle-resolved polarized Raman mapping was performed.
Probing static properties by Raman mapping
Raman spectra were collected at various spatial positions (X, Y) at a constant light polarization angle θ. Figure 2a shows one spectrum obtained at X = 2 mm (in the MB phase), Y = 7 mm, and θ = 131°, indicating Stokes and anti-Stokes scattering, and several characteristic peaks can be seen. The origin of the peaks has been considered in various ways, including local and average structures, some of which will be discussed later based on their light polarization angle dependence. As a first step in the analysis of the spectra, the corresponding X-Y Raman image of the crystal is shown in Fig. 2b. The spectrum obtained at each position is reduced to only one value for the corresponding area around the peak at 50 cm−1 to represent the spatial distribution of the peak intensity. This figure contains both spectral and spatial information. Discontinuous colors are seen at phase boundaries at X values of ~13.2 and ~39.9 mm that correspond to x = ~29.2 and 34.5 mol%, respectively31,32. The weak scattering intensity area observed at the bottom of the figure is not intrinsic and is due to the Kapton tape used to fix the specimen. Determining the origin of each peak is difficult due to average and various local structures. Nevertheless, the apparent anomalies observed at the two-phase boundaries indicate that while such mapping provides average structural information, it does not detect details related to changes in polarization, local structure, or dynamics in phases near the MPB.
a Raman spectrum in the monoclinic (type B, MB) phase acquired at a polarization direction of the incident light, θ, equal to 131° with a backward-scattering geometry with vertical to horizontal (VH) polarization. b X-Y Raman map colored by the intensity in the area around 50 cm−1 in the spectra acquired at θ = 131°. c Angle-resolved polarized Raman spectra at X = 2 mm and Y ~ 7 mm, shown at three θ values (upper) and as a contour plot colored by intensity (lower). d X-θ Raman map colored by the intensity in the area around 750 cm−1 of the spectra acquired at Y ~ 7 mm. e Relationship between the direction of spontaneous polarization and the pseudo-cubic axis in each ferroelectric phase (average structure). R, O, T, and MC in the figure represent the rhombohedral, orthorhombic, tetragonal, and monoclinic (type C, MC) phases, respectively. f X dependence of the spontaneous polarization in the MB phase, as interpreted in panel d.
The spontaneous polarization direction in the Ti-composition-gradient PMN-xPT crystal should rotate continuously with changing positions in the MB and MC phases. Consequently, Raman tensor information acquired by angle-resolved polarized Raman spectroscopy is expected to be important because Raman spectra obtained from a crystal are usually dependent on the polarization direction of the light. Angle-resolved polarized Raman spectra obtained at different θ values at constant position (X = 2 mm, Y = ~ 7 mm) are shown in Fig. 2c, which reveals that the shape of the spectrum is θ-dependent. The Raman spectrum at each angle is shown along the horizontal direction of this contour map, whereas the angular dependence of each frequency shift is displayed in the vertical direction. The prominent peaks located at −49 and 49 cm−1 are most intense at θ = 0° and 90°, with minimum values of almost zero observed at θ = 45° and 135°. These two peaks are anti-Stokes and Stokes Raman scattering, originating from the same origin. According to previous studies on Raman spectroscopy of PMN, the peaks observed for PMN are mainly attributable to CORs with 1:1 Mg: Nb chemical ordering and Fm\(\bar{3}\)m symmetry44,45,46 (the x-dependence of this peak for PZN-xPT is discussed in detail by Kanagawa et al.47). In a similar manner, the peak at around 750 cm−1 is attributable to light scattering from the R3m crystal structure, which is related to local PNR structures19 and the average structure of the R phase of PMN44. Based on the pair distribution functions of PMN19,48 and PZN-xPT49, the average structures of the relaxor-ferroelectric solid solutions are determined by the arrangement of the PNRs (R3m): For example, a fractional combination of local polarization along [111]C and that along [1\(\bar{1}\)1]C can reproduce polarization direction in the MB phase. Thus, peaks from the average PMN-xPT structures (MB, MC, and T phases) also overlap with those from PNRs (R3m) and CORs (Fm\(\bar{3}\)m) at room temperature50, which is more complicated than the PMN situation at room temperature; although this idea has not reached settlement yet, the PMN mode assignment44,45,46 is very helpful in interpreting spectra in this study.
We performed angle-resolved polarization Raman mapping (X-θ mapping), which was developed by incorporating θ information into the Raman mapping process using a rotating half-waveplate placed in the microscope (Fig. 1d). The contour map for the peak at 750 cm−1 is shown in Fig. 2d (other peak-intensity maps are shown in Supplementary Fig. S1 in Supplementary Note 1). The following relationship between θ and intensity at each X was observed: θmax, the angle corresponding to the maximum value in the angular-dependent Raman peak-intensity map (shown in red in Fig. 2d), is almost constant at each X in the MC (13 mm < X < 40 mm) and T (40 mm < X) phases, whereas it changes continuously with X in the MB phase (X < 13 mm). While θmax was observed to decrease linearly (from 88° to 74°) with increasing X (from 4.6 to 7.1 mm), θmax changed abruptly from 74° at X = 4.6mm to 35° at X = 5.6 mm, and then back to 74° at X = 7.1 mm; it increased linearly (from 74° to 89°) as X was increased 7.1–11.6 mm.
The relationship between θ and Raman peak intensity associated with changes in the direction of spontaneous polarization is shown in the Supplementary Information (Supplementary Figs. S2–S5 in Supplementary Note 2). The observation that θmax is independent of X (X > 13 mm in Fig. 2d) is well-reproduced when the polarization directions in the MC and T phases change, as shown in Fig. 2e. However, θmax should increase or decrease monotonically when the polarization in the MB phase rotates from the R phase to the O phase, as shown in Fig. 2e, which is not observed for X < 13 mm in Fig. 2d. The polarization direction must change by about 90° when viewed from above to explain the experimentally observed decreasing-to-increasing shift in θmax at X = 5.6 mm. The direction in which polarization rotates reverses in moving from the R phase to the O phase (See MB phase in Fig. 2e); as a result, the X-dependent θmax switches from a decreasing trend to an increasing one. While the switching θmax trend can be reproduced as shown in Supplementary Figs. S2 and S3, the magnitude of the change cannot be explained here since a simple polarization rotation in the MB phase would only change θmax by 30°. Therefore, we suggest that the polarization rotation shown in Fig 2f, which connects the change in the polarization direction by about 90°, is required to explain the abrupt shift in θmax observed in the 4.6–7.1 mm X range. Analyzing the relationship between X and θmax is complicated using the Raman tensor in the polarization-rotation process shown here because the crystal structure is different from that of MB or MC. However, the crystal structure is expected to be identical to that of the MC phase when polarization is oriented horizontally during rotation; θmax changes toward 0° at X = 5.6 mm in Fig. 2d, which is the same as that of the MC phase. We consider that the experimental results also support our interpretation, as shown in Fig. 2f.
No anomalies were observed at X = 5.6 mm in our previous XRD mapping of the same crystal38, which implies that the average crystal structure maintains MB-phase symmetry. Therefore, local polarization in the average crystal structure of MB exists as a set of dipoles smaller than the laser focus (about 10 micrometers in diameter), such as static PNRs, and the local polarization positionally rotates as shown in Fig. 2f. Uncertainty still exists when determining the polarization configuration in the depth direction; therefore, complementary experiments, such as Raman spectroscopy in other scattering configurations and crystal structure analyses, are necessary. However, the excellent progress afforded by angle-resolved polarized Raman spectroscopy can be used to study polarization-rotation behavior at about 2.5 mm, from X = 4.6 to 7.1 mm, which cannot be examined using ordinary Raman mapping techniques (Fig. 2b), polarized light microscopy, or optical microscopy.
Probing lattice dynamics around the MPB
Typically, spectra are acquired at each position at constant θ when studying the positional dependence of lattice vibrations in a single crystalline sample, with positional dependence compared. However, comparing spectra acquired from the Ti-composition-gradient PMN-xPT at constant θ is difficult because the θ-dependence of spectra changes in the MB phase, as shown in Fig. 2d. Therefore, this angle-resolved polarized Raman spectroscopic method, which acquires spectra at various θ values, is decisive for comparing dynamics at each position. Since angle-resolved polarized Raman data composed of 20 spectra were obtained at each position in this study, extracting a spectrum (or a few spectra) that are representative of a single position is necessary. For this reason, we used the multivariate curve resolution-alternating least squares (MCR) matrix-factorization technique, a schematic of which is displayed in Fig. 3a, which shows that a matrix with polarization angle as the vertical axis and frequency shift as the horizontal axis is decomposed into two angular profiles and two spectra51. The number of decompositions (i.e., two) was determined by singular value decomposition and is the same for all positions in the MB phase. In this decomposition, the number of decompositions was also tried in the case of three, but the third component was not properly identified. Therefore, it was confirmed that the decomposition with two components was accomplished without excesses or deficiencies. The contour map displayed in Fig. 3b shows angle-resolved polarized Raman spectral data at X = 5 mm, with the MCR results shown in Fig. 3c. Here, two spectra, I1(ν) and I2(ν), and two angle profiles, p1(θ) and p2(θ), are the features of the contour map. p1(θ) and p2(θ) are numbers representing the proportion of I1(ν) and I2(ν), respectively, in the spectra at each θ; consequently, the sum of I1(ν)・p1(θ) and I2(ν)・p2(θ) approximately reproduces the initial contour-map matrix. Here, p1(θ) clearly shows maxima at 60° and 150° and minima at 10° and 110°, whereas p2(θ) is characterized by maxima at 5° and 100°, and minima at 50° and 140°. The peak at 49 cm−1 is the most remarkable feature of I2(ν) because it reveals that it contains significant COR scattering. On the other hand, I1(ν) shows various peaks, such as the peak at 750 cm−1 that reflects ferroelectric fluctuations of BO6 oxygen octahedra in the average crystal structure (MB symmetry) containing static PNRs (R symmetry).
a Multivariate curve resolution (MCR) concept for angle-resolved polarized Raman spectroscopy, where the number of components, k, was determined to be two in the monoclinic (type B, MB) phase by singular-value decomposition (SVD). The data consist of a 20 × 1024 matrix, which can be decomposed into a 20 × 2 matrix (two angle profiles, p1(θ) and p2(θ)) and a 2 × 1024 matrix (two base spectra, I1(ν) and I2(ν)). b Angle-resolved polarized Raman spectra at X = 5 mm and Y ~ 7 mm, shown as a contour plot colored by intensity. c MCR data showing that p1(θ) and p2(θ) are numbers representing the proportion of I1(ν) and I2(ν), respectively, in the spectra at each θ.
Figure 4a, b displays the X-dependences of p1(θ) and p2(θ) and reveal that p1(θ) exhibits the same polarization-rotation behavior discussed above, while p2(θ) is independent of X, which means that I1(ν) in Fig. 4c reflects ferroelectric instability and I2(ν) in Fig. 4d reflects nonpolar vibrations, including those in the CORs. The observation that the peak at ±49 cm−1, which corresponds to the COR contribution44,45,46, dominates I2(ν) (Figs. 3c and 4d) supports this interpretation. The enlargement of the low-frequency region displayed in Fig. 4c shows that I1(ν) is significantly more dependent on X in the region near 0 cm−1 at an X value of ~10 mm, while an abrupt change is observed at X = 13.6 mm at the MPB. Since changes in low-frequency polar vibrations are closely related to the electric field response, the low-frequency regions of the spectra were least-squares fitted by assuming five damped harmonic oscillators and one Lorentzian function centered at 0 cm−1 that represents Debye-type relaxation (Fig. 4e). The X-dependences of the determined parameters of each peak are shown in Fig. 4f, which reveals that the frequency shifts of the four modes do not change. On the other hand, the width of the Lorentzian function (Δν), which represents quasielastic scattering, shows a minimum at X = 10.0 mm; this position corresponds to PMN-28.6PT, which has a lower PbTiO3 concentration than the MPB (PMN-29.0PT). Electric-dipole relaxation is responsible for the quasielastic scattering observed for a relaxor ferroelectric52,53,54,55,56,57,58. Peak narrowing corresponds to slower polarization relaxation as determined using: π·Δν·τ = 1 assuming Debye relaxation with relaxation time τ. The determined values τ are shown in Fig. 5a, with a possible electric-dipole relaxation process shown in Fig. 5b, which is based on the ease of polarization rotation in the MB phase. Such slow relaxation might reflect competing mesoscopic domains formed by the arrangements of static PNRs. Mesoscopic domain relaxation increases the dielectric response at this position (composition). Our previous diffraction experiments38 showed that the correlation length, determined from the width of the Bragg peak, is the smallest (~70 nm) at the exact location, which suggests that smaller mesoscopic domains can readily fluctuate compared with larger domains, thereby enhancing the electric field response. The mechanism responsible for how compositional changes affect correlation length and relaxation time remains to be solved. One possible interpretation of the short correlation and slow relaxation at the MPB involves phase instability due to competing MB-phase and MC-phase energy states. Because the ferroelectric domains become smaller and fluctuate more slowly when the temperature approaches the ferroelectric transition temperature –due to competing energy states between paraelectric and ferroelectric phases–, the mesoscopic domains in the MB phase of our Ti-composition-gradient PMN-xPT crystal become smaller and relax more slowly as the composition approaches the MPB. Here, the MB/MC phase boundary is unique in that it is easily polarized in various directions and is more unstable to external electric fields than other phase boundaries.
a–d X dependence of two angle profiles (p1(θ) and p2(θ)) and two base spectra (I1(ν) and I2(ν)). The low-frequency regions related to the dielectric constant are expanded for I1(ν) and I2(ν). e I1(ν) fitted to determine peak anomalies induced by changing X. f Fitted results. The full width at half maximum (FWHM) of the quasielastic scattering clearly shows narrowing at X ~ 10 mm. The error bars represent standard errors determined by least-squares fitting.
Butterfly-shaped diffuse scattering at the Brillouin zone center (q = 0), a cut of the diffuse scattering in the reciprocal lattice (HK0) plane59,60,61,62, has been reported to arise from complex mesoscopic domains and to exhibit a maximum intensity at around the MPB composition (PMN-30PT)63, which indicates that this diffuse scattering is related to a significant electric field response; however, the static nature of diffuse scattering itself cannot explain the electric field response41. Our findings on I1(ν) relaxation provide a dynamic perspective on polar mesoscopic domains and establish a link between the existence of mesoscopic domains and (di)electric responses.
Conclusions
Angle-resolved polarized Raman mapping of a Ti-composition-gradient PMN-xPT crystal revealed positional changes in spontaneous polarization direction and the relaxation dynamics in the MB phase. By acquiring Raman spectra of various light polarization directions at each position, in addition to the usual X-Y mapping, subtle changes in spontaneous polarization direction could be detected, and a positional polarization rotation is suggested. Furthermore, by simplifying the 20 spectra at one position with MCR, the relaxation time of polarization fluctuations could be extracted from the quasielastic light scattering. The position dependence of the relaxation time shows the slowing down in the MB phase as it approaches the MPB. And the following consistent and straightforward story that connects the local structure with the dielectric response is provided: Local polarization relaxes more slowly, leading to an enhanced dielectric response because the mesoscopic domains become smaller near the MPB.
These experimental results and their interpretation deepen our understanding of the relationship between the complex structure of a crystal and its material properties, and can be applied to other ferroelectric relaxor systems.
Methods
Evaluating a Ti-composition-gradient PMN-xPT crystal
An as-grown Ti-composition-gradient PMN-xPT crystal was provided by JFE Mineral37 and cut to provide a 62.7 × 15.0 × 0.3 mm {100} plane in which two large surfaces were optically polished. Compositional mapping was qualitatively performed using X-ray fluorescence spectroscopy with an analytical X-ray microscope (XGT-5000, Horiba), and quantitatively using a 200 × 100 μm X-ray beam at the BL22XU beamline of the SPring-8 facility using reference PMN and PMN-38.7PT crystals.
Angle-resolved polarized Raman mapping
Raman scattering data were acquired using our system, which comprises a polarization rotation system installed in a microscope42,43. A Ti-composition-gradient PMN-xPT crystal was placed on an XYZ mapping stage (Tokyo Instruments) installed in the microscope (BH-2, Olympus). Linearly polarized incident light from a 200-mW single-frequency diode-pumped solid-state laser (Spectra Physics) operating at 532 nm was passed to the sample through a polarization rotation device (Sigma Koki) equipped with a broadband half-waveplate (Kogakugiken) in the microscope. Using a 10× objective lens, the focus was about 10 μm in diameter on the sample. Two-volume Bragg gratings (i.e., ultra-narrow-band notch filters; OptiGrate) were used to eliminate strong elastic scattering. The inelastically scattered light was dispersed by a single monochromator (Lucir), and the dispersed component was detected using a charge-coupled device (Andor). A crossed-Nicols polarization (vertical–horizontal: VH) backscattering geometry was adopted because a vertical–vertical configuration includes quasielastic scattering from thermal diffusion unrelated to polarization relaxation64. A schematic of the system has previously been reported43.
The obtained contour maps contained shot noise, which was eliminated using the median filter.
Matrix factorization (multivariate curve resolution, MCR)65,66,67,68
MCR was performed using the Unscrambler X multivariate statistical analysis software (Camo Analytics). MCR is a matrix factorization technique that uses linear combinations of a prescribed number, k, of spectral components and their constrained angle dependence. An m × n nonnegative data matrix containing Raman spectra acquired at different θ values at constant position X is decomposable into an m × k matrix (k base spectra) and a k × n matrix (k angle profiles) under the condition that the matrix elements are nonnegative51. The prescribed number, k, is determined by singular value decomposition. The data matrix was also analyzed by assuming k ± 1 to ascertain possible excesses or deficiencies in the base spectra and angle profiles to reproduce the data matrix.
Data availability
The datasets generated during the current study are available from the corresponding author (S.T.) on reasonable request.
References
Takahashi, H. A note on the theory of barium titanate. J. Phys. Soc. Jpn. 16, 1685–1689 (1961).
Comes, R., Lambert, M. & Guinier, A. The chain structure of BaTiO3 and KNbO3. Solid State Commun. 6, 715–719 (1968).
Lambert, M. & Comes, R. The chain structure and phase transition of BaTiO3 and KNbO3. Solid State Commun. 7, 305–308 (1969).
Burns, G. & Dacol, F. H. The index of refraction of BaTiO3 above TC. Ferroelectr. 37, 661–664 (1981).
Bencan, A. et al. Atomic scale symmetry and polar nanoclusters in the paraelectric phase of ferroelectric materials. Nat. Commun. 12, 3509 (2021).
Tsuda, K. & Tanaka, M. Direct observation of the symmetry breaking of the nanometer-scale local structure in the paraelectric cubic phase of BaTiO3 using convergent-beam electron diffraction. Appl. Phys. Express 9, 071501 (2016).
Ko, J. H. et al. Elastic softening and central peaks in BaTiO3 single crystals above the cubic-tetragonal phase-transition temperature. Appl. Phys. Lett. 93, 23–25 (2008).
Lee, J. W., Ko, J. H., Roleder, K. & Rytz, D. Complete determination of elastic stiffness coefficients and local symmetry breaking in the paraelectric barium titanate. Appl. Phys. Lett. 114, 072901 (2019).
Tsukada, S., Ohwada, K., Kojima, S. & Akishige, Y. Local linear coupling between polarization and strain in KF-substituted barium titanate crystals probed by brillouin scattering and dielectric properties. J. Phys. Soc. Jpn. 89, 124702 (2020).
Smolensky, G. Physical phenomena in ferroelectrics with diffused phase transition. J. Phys. Soc. Jpn. 28, Suppl. 26–37 (1970).
Vieland, D., Jang, S. J., Cross, L. E. & Wuttig, M. Freezing of the polarization fluctuations in lead magnesium niobate relaxors. J. Appl. Phys. 68, 2916–2921 (1990).
Fu, D. et al. Relaxor Pb(Mg1/3Nb2/3)O3: a ferroelectric with multiple inhomogeneities. Phys. Rev. Lett. 103, 207601 (2009).
Blinc, R. Advanced ferroelectricity (Oxford University Press, 2011).
Takenaka, H., Grinberg, I., Liu, S. & Rappe, A. M. Slush-like polar structures in single-crystal relaxors. Nature 546, 391 (2017).
Hilton, A. D., Barber, D. J., Randall, C. A. & Shrout, T. R. On short range ordering in the perovskite lead magnesium niobate. J. Mater. Sci. 25, 3461–3466 (1990).
Randall, C. A. & Bhalla, A. S. Nanostructural-property relations in complex lead perovskites. Jpn. J. Appl. Phys. 29, 327–333 (1990).
Burns, G. & Scott, B. A. Index of Refraction in ‘Dirty’ displacive ferroelectrics. Solid State Commun. 13, 423–426 (1973).
Viehland, D., Jang, S. J., Cross, L. E. & Wuttig, M. Local polar configurations in lead magnesium niobate relaxors. J. Appl. Phys. 69, 414–419 (1991).
Jeong, I. et al. Direct observation of the formation of polar nanoregions in Pb(Mg1/3Nb2/3)O3. Phys. Rev. Lett. 94, 147602 (2005).
Roth, M., Mojaev, E., Dul’kin, E., Gemeiner, P. & Dkhil, B. Phase transition at a nanometer scale detected by acoustic emission within the cubic phase Pb(Zn1/3Nb2/3)O3-xPbTiO3 relaxor ferroelectrics. Phys. Rev. Lett. 98, 265701 (2007).
Manley, M. E. et al. Phonon localization drives polar nanoregions in a relaxor ferroelectric. Nat. Commun. 5, 3683 (2014).
Li, F. et al. The origin of ultrahigh piezoelectricity in relaxor-ferroelectric solid solution crystals. Nat. Commun. 7, 13807 (2016).
Manley, M. E. et al. Giant electromechanical coupling of relaxor ferroelectrics controlled by polar nanoregion vibrations. Sci. Adv. 2, e1501814 (2016).
Park, S.-E. & Shrout, T. R. Ultrahigh strain and piezoelectric behavior in relaxor based ferroelectric single crystals. J. Appl. Phys. 82, 1804 (1997).
Qiu, C. et al. Transparent ferroelectric crystals with ultrahigh piezoelectricity. Nature 577, 350–354 (2020).
Sun, Y., Karaki, T., Fujii, T. & Yamashita, Y. Enhanced electric property of relaxor ferroelectric crystals with low AC voltage high-temperature poling. Jpn. J. Appl. Phys. 59, SPPD08 (2020).
Luo, C., Karaki, T., Sun, Y., Yamashita, Y. J. & Xu, J. Effect of field cooling AC poling on electrical and physical properties for Pb (Mg1/3Nb2/3)O3-PbTiO3 -based single crystals manufactured by a continuous-feeding Bridgman process. Jpn. J. Appl. Phys. 59, SPPD07 (2020).
Bokov, A. A. & Ye, Z. G. Recent progress in relaxor ferroelectrics with perovskite structure. J. Mater. Sci. 41, 31–52 (2006).
Kutnjak, Z., Petzelt, J. & Blinc, R. The giant electromechanical response in ferroelectric relaxors as a critical phenomenon. Nature 441, 956–959 (2006).
Li, F., Zhang, S., Damjanovic, D., Chen, L. Q. & Shrout, T. R. Local structural heterogeneity and electromechanical responses of ferroelectrics: learning from relaxor ferroelectrics. Adv. Funct. Mater. 28, 1801504 (2018).
Singh, A. K., Pandey, D. & Zaharko, O. Powder neutron diffraction study of phase transitions in and a phase diagram of (1-x) [Pb(Mg1/3Nb2/3)O3] -xPbTiO3. Phys. Rev. B 74, 024101 (2006).
Singh, A. K. & Pandey, D. Evidence for MB and MC phases in the morphotropic phase boundary region of (1-x)[Pb(Mg1/3Nb2/3)O3]-xPbTiO3: A Rietveld study. Phys. Rev. B 67, 064102 (2003).
Vanderbilt, D. & Cohen, M. H. Monoclinic and triclinic phases in higher-order Devonshire theory. Phys. Rev. B 63, 094108 (2001).
Fu, H. & Cohen, R. E. Polarization rotation mechanism for ultrahigh electromechanical response in single-crystal piezoelectrics. Nature 403, 281–283 (2000).
Jin, Y. M., Wang, Y. U., Khachaturyan, A. G., Li, J. F. & Viehland, D. Conformal miniaturization of domains with low domain-wall energy: Monoclinic ferroelectric states near the morphotropic phase boundaries. Phys. Rev. Lett. 91, 197601 (2003).
Xu, G., Hiraka, H., Shirane, G. & Ohwada, K. Dual structures in (1-x)Pb(Zn 1/3Nb2/3)O3-xPbTiO3 ferroelectric relaxors. Appl. Phys. Lett. 84, 3975–3977 (2004).
Matsushita, M., Tachi, Y. & Iwasaki, Y. Development of large diameter piezo-single crystal PMN-PT with high energy conversion efficiency. JFE Tech. Rep. 6, 46–53 (2005).
Shimizu, D. et al. Negative correlation between electrical response and domain size in a Ti-composition-gradient Pb[(Mg1/3Nb2/3)1-xTix]O3 crystal near the morphotropic phase boundary. Phys. Rev. B 92, 174121 (2015).
Ohwada, K. et al. Polarization rotation associated with phonon dynamics in monoclinic C phase near morphotropic phase boundary studied by diffuse and inelastic X-ray scattering from a Ti-composition-gradient Pb[(Mg1/3Nb2/3)1-xTix]O3 single crystal. Ferroelectrics 532, 100–110 (2018).
Scott, J. F. Soft-mode spectroscopy: experimental studies of structural phase transitions. Rev. Mod. Phys. 46, 83–128 (1974).
Blinc, R. & Žekš, B. Soft modes in ferroelectrics and antiferroelectrics (North-Holland Pub. Co., 1974).
Fujii, Y. et al. Raman tensor analysis of crystalline lead titanate by quantitative polarized spectroscopy. Ferroelectrics 462, 8–13 (2014).
Tsukada, S. et al. Raman scattering study of the ferroelectric phase transition in BaTi2O5. Phys. Rev. B 97, 024116 (2018).
Prosandeev, S. A. et al. Lattice dynamics in PbMg1/3Nb2/3O3. Phys. Rev. B 70, 134110 (2004).
Taniguchi, H., Itoh, M. & Fu, D. Raman scattering study of the soft mode in Pb(Mg1/3Nb2/3)O3. J. Raman Spectrosc. 42, 706–714 (2011).
Svitelskiy, O., Toulouse, J., Yong, G. & Ye, Z. G. Polarized Raman study of the phonon dynamics in Pb(Mg1/3Nb2/3)O3 crystal. Phys. Rev. B 68, 104107 (2003).
Kanagawa, A., Fujii, Y., Ohwada, K., Akishige, Y. & Tsukada, S. Morphotropic phase boundaries of (1−x)Pb(Zn1/3Nb2/3)O3–xPbTiO3 probed by Raman spectroscopy at high temperature. Jpn. J. Appl. Phys. 60, SFFA04 (2021).
Egami, T. A. Local Structure and Dynamics of Ferroelectric Solids. In Ferro- and antiferroelectricity: order/disorder versus displacive (eds. Dalal, N. S. & Bussmann-Holder, A.) 69–88 (Springer Berlin Heidelberg, 2007). https://doi.org/10.1007/430_2006_047
Jeong, I. K. Temperature evolution of short- and medium-range ionic correlations in relaxor ferroelectric [Pb(Zn1/3Nb2/3)O3]1-x[PbTiO3]x (x=0.05, 0.12). Phys. Rev. B 79, 052101 (2009).
Ohwa, H., Iwata, M., Orihara, H., Yasuda, N. & Ishibashi, Y. Raman scattering in (1 - x)Pb(Mg1/3Nb2/3)O3 -xPbTiO3. J. Phys. Soc. Jpn. 70, 3149–3154 (2001).
Tsukada, S. & Fujii, Y. Multivariate curve resolution for angle-resolved polarized Raman spectroscopy of ferroelectric crystals. Jpn. J. Appl. Phys. 59, SKKA03 (2020).
Siny, I., Lushnikov, S., Katiyar, R. & Rogacheva, E. Central peak in light scattering from the relaxor ferroelectric PbMg1/3Nb2/3O3. Phys. Rev. B 56, 7962 (1997).
Lushnikov, S. G., Gvasaliya, S. N. & Siny, I. G. Phonons and fractons in the vibration spectrum of the relaxor ferroelectric PbMg1/3Nb2/3O3. Phys. B 263–264, 286–289 (1999).
Tsukada, S. et al. Relation between Fractal Inhomogeneity and In / Nb- Arrangement in Pb(In1/2Nb1/2)O3. Sci. Rep. 7, 17508 (2017).
Helal, M. A., Aftabuzzaman, M., Tsukada, S. & Kojima, S. Role of polar nanoregions with weak random fields in Pb-based perovskite ferroelectrics. Sci. Rep. 7, 44448 (2017).
Tsukada, S. & Kojima, S. Broadband light scattering of two relaxation processes in relaxor ferroelectric 0.93Pb(Zn1/3Nb2/3)O3-0.07PbTiO3 single crystals. Phys. Rev. B 78, 144106 (2008).
Tsukada, S. et al. Broadband inelastic light scattering of a relaxor ferroelectric 0.71 Pb(Ni1/3Nb2/3)O 3-0.29PbTiO3. Appl. Phys. Lett. 89, 212903 (2006).
Ko, J. H., Kim, D. H. & Kojima, S. Central peaks, acoustic modes, and the dynamics of polar nanoregions in Pb [(Zn1/3Nb2/3)xTi1-x]O3 single crystals studied by Brillouin spectroscopy. Phys. Rev. B 77, 104110 (2008).
Xu, G., Zhong, Z., Hiraka, H. & Shirane, G. Three-dimensional mapping of diffuse scattering in Pb(Zn1/3Nb2/3)O3-xPbTiO3. Phys. Rev. B 70, 174109 (2004).
Xu, G., Zhong, Z., Bing, Y., Ye, Z. G. & Shirane, G. Electric-field-induced redistribution of polar nano-regions in a relaxor ferroelectric. Nat. Mater. 5, 134–140 (2006).
Hiraka, H., Lee, S. H., Gehring, P. M., Xu, G. & Shirane, G. Cold neutron study on the diffuse scattering and phonon excitations in the relaxor Pb(Mg1/3Nb2/3)O3. Phys. Rev. B 70, 184105 (2004).
Hirota, K., Wakimoto, S. & Cox, D. E. Neutron and X-ray scattering studies of relaxors. J. Phys. Soc. Jpn. 75, 111006 (2006).
Krogstad, M. J. et al. The relation of local order to material properties in relaxor ferroelectrics. Nat. Mater. 17, 718–724 (2018).
Koreeda, A., Nagano, T., Ohno, S. & Saikan, S. Quasielastic light scattering in rutile, ZnSe, silicon, and SrTiO3. Phys. Rev. B 73, 024303 (2006).
de Juan, A. & Tauler, R. Multivariate curve resolution-alternating least squares for spectroscopic data. Data Handl. Sci. Technol. 30, 5–51 (2016).
Garrido, M., Rius, F. X. & Larrechi, M. S. Multivariate curve resolution-alternating least squares (MCR-ALS) applied to spectroscopic data from monitoring chemical reactions processes. Anal. Bioanal. Chem. 390, 2059–2066 (2008).
Wehrens, R. Chemometrics with R. chemometrics with R- multivariate data analysis in the natural sciences and life sciences (Springer, 2011). https://doi.org/10.1007/978-3-642-17841-2
Noothalapati, H., Iwasaki, K. & Yamamoto, T. Biological and medical applications of multivariate curve resolution assisted raman spectroscopy. Anal. Sci. 33, 15–22 (2017).
Acknowledgements
We would like to thank Akira Tsujimoto of Shimane University for compositional analysis assistance using the analytical X-ray microscope. This study was partly supported by JSPS KAKENHI Grant Nos. 19H02618, 19K05252, 21H01018, and 22H01976, and Shimane University Internal Competitive Grants of FY2021. Sample evaluations using synchrotron radiation were performed at the BL22XU beamline of the SPring-8 facility with the approval of the Japan Synchrotron Radiation Research Institute (JASRI) (Proposals No. 2012A3713 and No. 2013A3713).
Author information
Authors and Affiliations
Contributions
S.T. and K.O. initiated and supervised the project. S.T. and A.K. performed the Raman scattering experiments. S.T. and Y.F. analyzed the Raman scattering data. S.T. and K.O. evaluated the positional dependence of the crystal composition. S.T. wrote the manuscript. All authors discussed the obtained results and approved the final manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks Elena Buixaderas and Jae-Hyeon Ko for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tsukada, S., Fujii, Y., Kanagawa, A. et al. Polarization behavior in a compositionally graded relaxor–ferroelectric crystal visualized by angle-resolved polarized Raman mapping. Commun Phys 6, 107 (2023). https://doi.org/10.1038/s42005-023-01219-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-023-01219-8
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.