Abstract
The typical approaches to generate heralded single photons rely on parametric processes, with the advantage of generating highly entangled states at the price of a random pair emission. To overcome this limit, degenerate spontaneous Four-Wave-Mixing is a reliable technique which combines two pump photons into a pair of signal and idler photons via Kerr nonlinear optical effect. By exploiting the intrinsic small confinement volume and thermally tuning the resonances of a 20 μm-long Photonic Crystal cavity, we efficiently generate time-energy entangled photon pairs and heralded single photons at a large maximum on-chip rate of 22 MHz, using 36 μW of pump power. We measure time-energy entanglement with net visibility up to 96.6 % using 1 second integration time constant. Our measurements demonstrate the viability of Photonic Crystal cavities to act as an alternative and efficient photon pair source for quantum photonics.
Similar content being viewed by others
Introduction
The development of quantum technologies promises a paradigm change in the way we process and encode information, leading to a great leap towards encryption safety1,2 and exponential computational advantage3,4,5. Integrated photonics can provide solutions to address the generation and manipulation of entangled states of light on-chip and at room temperature6,7. Single photons can serve as the fundamental photonic qubit, or can be manipulated to construct more general entangled states; therefore, efficient single photon sources (SPSs) are required. Different routes have been explored in this regard, for example, the emission of defects in diamonds or semiconductors8,9,10, artificial solid-state quantum emitters such as quantum dots11,12,13, and parametric processes exploiting intrinsic material nonlinearity. Correlated photon pairs spontaneously generated via parametric processes can be used to build heralded SPSs14,15,16,17,18, in which the detection of one photon in one input channel heralds the presence of its twin photon in the other. Such processes can provide highly coherent entangled states but, relying on spontaneous processes, the pair emission is random and the source is probabilistic, making it crucial to achieve the highest generation efficiency. Our system exploits degenerate spontaneous four-wave-mixing (FWM) that is an ultrafast Kerr optical nonlinear effect where two pump photons (at frequency νp) are converted into a pair of signal (νs) and idler (νi) photons. Because of energy conservation (Fig. 1a), 2hνp = hνs + hνi, signal and idler photons are emitted symmetrically relative to the pump, as in Fig. 1b. As a consequence, resonant enhancement can only be achieved if at least three resonances of the cavity (at frequencies ν−, ν0 and ν+) are strictly equispaced. This is called the triply resonant configuration and under this condition, the internal pair generation rate (number of pairs generated per second) scales as19,20\(R\propto ({n}_{2}^{2}{Q}^{3}/{V}^{2}){P}^{2}\); with n2 the Kerr nonlinear index, Q the average quality factor of the three modes defined as \({Q}^{3}={Q}_{0}^{2}\sqrt{{Q}_{-}{Q}_{+}}\), V the volume of the resonator, and P the pump power delivered to the cavity. Ring resonators have gained huge interest for quantum optics as they own the adequate properties (high Q-factor, equispaced modes, ...) for triply resonant FWM and are now easily integrated on-chip. Time-energy entangled photon pairs have already been demonstrated in silicon photonics21 and III–V semiconductors as InP22 and recently AlGaAs23. This last material has shown efficiency R/P2 as large as 20 GHz/mW2 mainly due to a very large Q-factor up to 1.24 × 106, making it the current state-of-the-art integrated photon pair source based on semiconductors via FWM. Larger efficiency is reachable by increasing the Q-factor or further decreasing the volume of the cavity, but bending losses set a lower bound to the size of the ring.
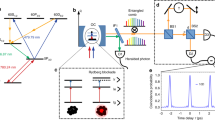
a Schematic of the energy diagram for degenerate FWM, where two pump photons are converted into a signal and idler photons. Frequencies (νp,νs, and νi) are dictated by energy conservation 2νp = νs + νi and h is Planck constant. b Corresponding schematic of the emission spectra, showing emission at νs and νi symmetrical to νp. c SEM image of the cavity describing the different elements of the design. a and a' are the periods of the holes. Pin is for the input power in the waveguide. White and orange arrows guide the eyes to see the shift of the lines of holes forming the reflector. d Reflection spectrum (measured with OCT) of the cavity limited to the first three modes of frequencies ν−,ν0, and ν+ used here for photon pair generation. The corresponding spatial profile of the modes ∣Ey∣2 are given above. Q is the Q-factor e Thermal tuning, the evolution of the Free Spectral Range ν0 − ν− (red points) and ν+ − ν0 (blue points) as a function of the pump offset \({{{\Delta }}}_{0}={\nu }_{p}-{\overline{\nu }}_{0}\). Colored circles are measured with pump-probe OCT and continuous lines are linear fit of the data. Equispaced configuration is reached at Δ0 = 31 GHz.
Yet, whether entangled photons can be generated using a radically different kind of resonator where the field is strongly localized within the scale of the wavelength, has not been investigated at all to the best of our knowledge. We consider a photonic crystal (PhC) cavity where the very large index contrast leads to a very strong confinement of light24. Moreover, the generation of time-correlated photons has just been reported25. PhC are dielectric sub-wavelength structures where Bragg scattering inhibits the propagation of light within a large angular and spectral range. This enables the strong localization of the field26 to the scale of the wavelength. This is a fundamental difference with respect to other dielectric structures, which is appreciated when considering the possibility of manipulating each single mode. This gives superior control on the parametric processes, either desired or undesired, and represents a considerable advantage when each emitted photon counts. Practical PhC are one or two-dimensional periodic structures with imperfect bandgap, yet they are still able to confine a small number of non-degenerate modes within a volume ≈ (λ/2n)3 (λ being the wavelength and n the index of the medium) while ensuring a large Q-factor27, up to 10 million on silicon28 and one million in III–V semiconductors29. Considering the strong dependence of the photon pair generation efficiency on these parameters, PhC cavities are very attractive for quantum light generation via FWM25, provided that the free spectral range is controlled with very high accuracy. The first demonstration of spontaneous emission via FWM was reported by Azzini et al.30 by coupling three identical nanobeam cavities with Q-factor ≈ 5 × 103, which in the tight-binding approximation, would lead to three symmetrically spaced resonances. Unfortunately, the dispersive nature of the coupling in PhC31 and ring resonators32 fundamentally leaves a non-zero dispersion Δ2 = (ν+ − ν0) − (ν0 − ν−). This effect is not severe if the Q-factor is moderate (e.g. ≈ 5 × 103) but absolutely needs to be controlled if a much larger Q is to be harnessed. We consider another approach that consists in designing a cavity which, by construction, results in evenly spaced modes29. However, fabrication tolerances contribute with additional random frequency shift, affecting inhomogeneously the different resonances due to their non-degenerate nature. It can be corrected with post-fabrication trimming, like in Silicon33. Owing to a self-tuning technique, we demonstrated time-correlated photon pairs25 and optical parametric oscillations34 with pump power in the tens of microWatt level. Here, we will show that our triply resonant PhC cavity generates correlated photon pairs with very large efficiency, that are time-energy entangled and allow heralded single-photon emission.
Results
Bichromatic photonic crystal resonator
The resonator design is based on the so-called bichromatic lattice35 and is shown in Fig. 1c. Details on the cavity are given in Methods: Sample design, fabrication, and characterization. The purpose of this design is to create an effective parabolic potential for the optical field. Analogously to the quantum harmonic oscillator, modes are equispaced in frequencies as desired for triply resonant FWM; and their spatial profiles are described in good approximation by Hermite–Gauss functions.
The field distributions for the first three modes of the resonator, that will be used in the following are shown in Fig. 1d, along with the reflection spectrum of the resonator. This is measured using optical coherent tomography (OCT), a coherent spectral technique providing the phase and the amplitude of the spectrum. The parameters of the triplet of resonances are extracted following the procedure in ref. 29. In the specific case of the resonator considered here, the Q-factors of the signal and idler modes are different: Q− = 3.8 × 104 and Q+ = 2.4 × 105, giving an average (defined above) of 2.09 × 105. The free spectral range is not constant, leading to a deviation from the required frequency matching condition defined as Δ2 = (ν+ − ν0) − (ν0 − ν−) = −5 GHz. This mismatch is comparable with the largest linewidth of the triplet (≈5 GHz); therefore, either post-fabrication tuning33 or dynamic tuning are necessary to bring the cavity to the triply resonant configuration.
In the present work, we resort to the latter option, more precisely, self-thermal tuning. This technique has already been discussed and detailed in refs. 25,34,36. It is based on the differential thermo-optic effect that originates from the inhomogeneous spatial distribution of the mode profiles and their consequently different overlaps with a thermal gradient. The aftermath of inhomogeneous temperature in the cavity is a different frequency shift for each mode. Here, the thermal gradient is generated via residual linear absorption through the pump mode. Experimentally, the frequency νp of a CW pump laser is gradually shifted to get on resonance with the pump mode at frequency \({\overline{\nu }}_{0}\) (“ \({\bar {\,\!}}\) ” indicates the frequency without thermal tuning). We introduce the pump offset \({{{\Delta }}}_{0}={\nu }_{p}-{\overline{\nu }}_{0}\) to express the shift of the pump laser. As Δ0 < 0, the laser starts to be partially resonant with the pump mode allowing energy transfer from the laser to the cavity via the pump mode. The effect of the differential spectral shift of the modes is that as Δ0 changes, ν0 − ν− and ν+ − ν0 eventually equalize, which is shown in Fig. 1e using the pump-probe OCT25,29 technique. We note that the cavity is kept in the upper (on resonance) branch of the thermal bistable cycle, which closes when Δ0 = Δb. This condition, not shown in this particular plot, represents a non-equilibrium point where any additional spectral shift is no longer sustained by the thermo-refractive effect. Consequently, aligning the modes requires a minimum pump power (estimated here to be ≈20 μW) that increases with the initial mismatch. It is then possible to operate at low power only when using resonance triplets with a low initial mismatch.
Internal generation rate
First and foremost, the internal pair generation rate R is measured (see Methods: Experimental setups). Indeed, the pump laser used for thermal tuning is also used to generate the photon pairs via spontaneous FWM (SFWM). They are collected by the same lensed fiber and split into two different channels using Dense Wavelength Division Multiplexing, whose frequencies are aligned with the signal and idler ones. For that, the temperature of the sample is set to 32 ∘C. Each of them is followed by a cascaded bandpass filter with a central frequency matching signal or idler frequency in order to gain additional filtering of the remaining pump photons. Detection is accomplished using superconducting nanowire single-photon detectors, with a quantum efficiency of ≈85%, connected to a time correlator. Photons’ arrival times are measured and represented in a typical histogram shown in Fig. 2a, after 1 s of integration. It clearly exhibits a main peak corresponding to photon pairs arriving at the detectors over a wideband background, which can be the result of broken signal/idler pairs, the emission of multiple pairs or parasitic processes like Raman scattering in the input waveguide or in the filtering stage21. This coincidence peak is not symmetric, that we account for the unbalanced Q-factors. In order to prove that, the coincidence peak is fitted using a model taking into account these unbalanced Q-factors, from which we clearly recover the shape of the peak with the exact Q-factors (see Methods: Coincidence peak fitting). The number of coincidences per second, Rdet, is extracted by integrating over the full-width-half-maximum (FWHM) of the peak. Taking into account the losses between the output of the cavity and detectors (αs and αi), estimated to be 12 and 12.84 dB (see Methods: Experimental setups), we infer the internal pair generation rate20 R = Rdet/(αsαi). This measurement has been performed for different values of the pump offset Δ0. As shown in Fig. 2b, the internal pair generation rate increases as the modes are tuned to the triply resonant configuration, up to a maximum of 22 MHz, corresponding to a large measured coincidence rate of 70 kHz. We note that the maximum of generation rate does not exactly correspond to the triply resonant condition (details in ref. 25). We can also infer the amount of effective pump power (Fig. 2c) transferred to the cavity P0, with the power in the waveguide Pc and the pump offset at which the bistable jump occurs Δb : P = (Δ0/Δb)Pc. This effective power can be interpreted as the necessary amount of power required to obtain the corresponding internal generation rate. In order to resolve the entire evolution, Pc = 56 μW have been sent in the waveguide. Finally, we calculate the efficiency. The maximum internal generation rate is obtained for P = 36 μW, that gives a maximal efficiency R/P2 of 16 ± 1 GHz/mW2.
a Coincidence histogram (blue squares) obtained for an effective pump power in the cavity of P0 ≈ 30 μW after Tint = 1 s of integration. Δ0 is the pump offset. The main peak is thus fitted (black line) using the model (detailed in Methods: Coincidence peak fitting) to extract the number of coincidences. b On-chip pair generation rate R and the corresponding coincidence rate Rdet as a function of Δ0. Vertical lines denote the point of triply resonant configuration (TRP) and bistable jump. The black arrow indicates the maximal measured internal generation rate Rmax. Error bars are due to uncertainty on the measured coincidence rate, namely a Poisson distribution. c Evolution of the effective pump power P0 as a function of the pump offset Δ0.
Time-energy entanglement
The original idea to exploit energy and time correlation to test non-local quantum correlations was suggested in ref. 37. In this seminal paper, two photons emitted in an atomic cascade process are used to test Bell’s inequality. Nowadays, systems based on parametric processes, like the one presented in this work, are most commonly exploited20,22,23. The nonlinear medium in the PhC cavity is pumped with a highly coherent (τcoh ≃ 10 μs) laser at a central frequency νp. Photon pairs are simultaneously generated via SFWM, but their emission time is undetermined within the coherence time of the pump, because the coherence time associated with the targeted resonances, 210 and 48 ps for ν− and ν+ respectively, is much shorter than the pump one. If the pairs encounter an unbalanced Mach–Zehnder interferometer, the output state of the pair can be written on the path basis, being \(\left\vert L\right\rangle\) and \(\left\vert S\right\rangle\) the single photon long and short path state, respectively. When the photons of the pair take different paths, \(\left\vert LS\right\rangle\) or \(\left\vert SL\right\rangle\), they can be distinguished from their time correlations and the states are separable. If, conversely, the two photons take the same path in the interferometer, the state is described by the entangled state \(\left\vert \psi \right\rangle =(\left\vert SS\right\rangle +\exp [i({\varphi }_{s}+{\varphi }_{i})]\, \left\vert LL\right\rangle )/\sqrt{2}\), where φs and φi are the additional phase acquired for each photon of the pair in the long arm of the interferometer, respectively. As the photons result from a parametric conversion, this phase inherits the coherence of the pump. As a result, it will yield an interference in the count rates with a global phase dependence, φs+i = φs + φi, even though the interferometer unbalance is larger than the coherence time associated with the resonances of the pair.
Time-energy entangled photon pairs have been measured for three different pump powers. Figure 3 shows the results for P0 = 15 μW, corresponding to an internal generation rate R = 3 MHz. Four coincidence histograms for different values of the relative signal and idler photon phase φs+i are displayed in Fig. 3a–d obtained after only 1 s of integration. On the one hand, the side peaks that correspond to photons taking \(\left\vert SL\right\rangle\) or \(\left\vert LS\right\rangle\) path sequence are indeed independent of the phase. On the other hand, the number of coincidences in the central peak, due to photons taking indistinguishable paths (\(\left\vert SS\right\rangle\) and \(\left\vert LL\right\rangle\)), is oscillating with the phase. In Fig. 3e, independent phase evolution of the side peaks is confirmed, while oscillations of the central one are clear over more than 2π in Fig. 3f. The data are fitted using a sinusoidal function (see Methods: Bell curve data extraction), from which the raw visibility Vraw is extracted. In Fig. 3f, it is measured to be Vraw = 93.88 ± 4.07%, violating Bell inequalities by 5.7 standard deviations, proving the entangled nature of the photon pairs. As the pair generation rate R increases, the visibility decreases and drops to 79.81 ± 1.98% at maximum efficiency due to large increase in the background scaling with P4, which is a fundamental limitation due to the statistical properties of the emission process. Finally, the raw visibility is corrected using the one of the interferometer \({{{{{{{\mathcal{V}}}}}}}}\). It is directly measured by introducing the pump laser in the Mach–Zehnder and measuring first-order interference visibility. Here, \({{{{{{{\mathcal{V}}}}}}}}=0.972\pm 0.001\) and so the net visibility is \({V}_{{{{{{\mathrm{net}}}}}}}={V}_{{{{{{\mathrm{raw}}}}}}}/{{{{{{{\mathcal{V}}}}}}}}\). Results are summarized in Table 1, including also the result obtained with a PhC nanobeam cavity on a different experimental setup (See Supplementary Note 1) and whose photon pair emission properties are detailed in ref. 25. Time-energy entangled photon pairs have thus been demonstrated with net visibility as high as Vnet = 96.6% with 15 μW pump power.
a–d Coincidence histograms after Tint = 1 s integration for different values of the phase acquired by the signal and idler photons in the interferometer φs + φi. The paths of the photons are shown in the first histogram (S short and L long). e, f Coincidence rate for the side peaks (green and red circles) and for the central peak (blue circles), respectively, as a function of φs + φi. The black curve is fitted with a sinusoidal function to extract the visibility of the fringes caused by two-photon interference. This measurement is obtained for P0 = 15 μW of pump power. Vertical error bars refer to the standard deviation of a Poisson distribution and horizontal ones to uncertainty on the photon pair phase.
Heralded single-photon emission
In order to show that the entangled photons are emitted as single pairs, the heralded second-order correlation function \({g}_{h}^{(2)}\) has been measured. The channel with the higher emission rate, νi, has been chosen as the herald, and on the other channel is performed a conditioned Hanbury Brown–Twiss experiment (see Methods: Experimental setups), feeding light to a 50:50 beam-splitter and sending the output to two distinct Superconducting nanowire single-photon detectors. The \({g}_{h}^{(2)}\) can be written in terms of coincidence rate38
Ri12(τ) being the rate of triple coincidences at delay τ, and Ri1, Ri2 the number of double coincidences between the idler photon and the signal photon in arm 1 or 2 of the Hanbury Brown–Twiss setup, respectively. The expression in eq. (1) can be averaged in time and expressed in terms of measured counts. In this work, a 3-h-long integration leads to the curve depicted in Fig. 4 where the value of the \({g}_{h}^{(2)}(0)\simeq 0.17\pm 0.02\) is a clear sign of the antibunched statistic of the emitted state. Yet, the \({g}_{h}^{(2)}(0)\) is not as low as achieved in other systems (see Table 2). The reason is that we measured \({g}_{h}^{(2)}(0)\) with the pump power level set for maximum pair emission rate, which was dictated by the need to limit the measurement time to a few hours. In this condition, the probability of multiple pairs emission is high, which also explains the low measured CAR ≈10. To gain more insight, we have measured the second-order self-correlation g(2)(0) of the heralded channel (See Supplementary Note 2), which is directly linked to the purity P and the Schmidt number K:
As we measure g(2)(0) = 1.58, the purity is 58 ± 1.7%, which confirms multiple pairs emission. Hence, lower \({g}_{h}^{(2)}(0)\) is expected by repeating the measurement at a lower pair emission rate, as shown in ref. 39.
Discussion
This work shows that PhC cavities are a different and competitive platform for the generation of quantum states of light. First, the performances of our InGaP PhC source are compared to other semiconductor-based microresonators for photon pair generation via SFWM as shown in Fig. 5. The figure compares the performances as a photon pair source of the nanobeam cavity introduced in ref. 25 and the bichromatic cavity discussed here with some landmark results reported in the literature. We consider the generation efficiency R/P2, the ratio of the internal pair generation rate over the square of the on-chip pump power as a function of a figure of merit \(M\propto ({n}_{2}^{2}{Q}^{3})/{V}^{2}\) which represents the expected scaling with the material nonlinearity, the Q-factor and the nonlinear interaction volume. This figure of merit is normalized to the value corresponding to the performances of the AlGaAs nonlinear ring23. The Q-factors and other parameters differ considerably, yet the expected scaling with the figure of merit M is followed rather well. A large on-chip generation efficiency, up to 16 GHz/mW2, is achieved with the PhC cavity, which is very close to the current state-of-the-art, AlGaAs ring resonator (20 GHz/mW2) and so, much higher than the other sources. We point out that the smaller Q-factor in the PhC (2.09 × 105, to be compared with 1.24 × 106 in the AlGaAs ring resonator) and the smaller nonlinearity of our material InGaP are compensated by the much smaller nonlinear volume of the cavity (5.7 μm3, see ref. 34). Thus, the self-tuning technique used here allows to systematically achieve the maximum efficiency, consistently with the scaling. This implies that a further order of magnitude increase in the efficiency is expected, considering Q-factors are twofold larger than in this sample (7 × 105, as reported in ref. 36). Still, in order to access the ultra-low pump power limit, it is necessary to have samples with a minimal mismatch; otherwise the minimum pump power will be set by the amount of dissipation required to compensate for it.
Efficiency R/P2 vs. the normalized figure of merit \(M\propto ({n}_{2}^{2}{Q}^{3})/{V}^{2}\) (being 1 for the AlGaAs ring), with Q the Q-factor, V the resonator volume, and n2 the Kerr nonlinear index. Q and V are deduced from the articles as described in ref. 25. Here, we use n2 = 0.6 × 10−17 m2/W for InGaP/Si, 2.7 × 10−17 m2/W for InP, 0.025 × 10−17 m2/W for Si3N451 and 4 × 10−17 m2/W for AlGaAs. For PhC cavities, N refers to Nanobeam and B to a bichromatic cavity.
Besides resonant SFWM, we also consider spontaneous parametric down-conversion (SPDC) in Table 2. Relevant figures are the visibility of the Franson fringes and the heralded second-order correlation function at τ = 0 : \({g}_{h}^{(2)}(0)\). Since it is based on second-order nonlinearity, the SPDC process is intrinsically much stronger than SFWM, which is based on a higher-order process. Related to that is also the fact that the scaling with the pump power is different; therefore, a comparison is possible only when fixing either the pump power or the pair generation rate. Here we have chosen the former, consistent with the literature.
First, the data in Table 2 reveal that SFWM sources are almost on par with SPDC. This is essentially due to the fact that the former have lower volumes and higher Q-factors. Yet, exceptionally large SPDC efficiency has been reported in InGaP (the same material as here) rings40. This leaves an open question, namely whether the superior intrinsic efficiency of SPDC offsets the additional complexity: phase matching over one octave, handling very different wavelengths and the tensor nature of second-order processes.
Let us now consider entanglement. From a more practical standpoint, reduced insertion losses and the use of superconducting detectors compared to previous settings25 have considerably improved the detected rate of coincidences (up to 70 kHz), which allows to measure a large amount of entangled photon pairs with integration time as low as 1 s or below. The table reports the net visibility, which does not depend on the interferometer used for the experiment, therefore providing a rather fair comparison of the sources. We report visibility up to 96.6%, which is close to the value measured with the AlGaAs ring23, yet smaller than in refs. 41,42, where efficiency is much lower.
As for the purity of the heralded photon state, we note that the measurement of the second-order correlation reveals that \({g}_{h}^{(2)}(0)\) is not very small. The main reason was that the source was operated at maximal efficiency in order to keep the integration time below three hours. It is well known that single-pair purity decreases when the generation rate increases39 and this is why better results reported elsewhere have been obtained at a much lower generation rate.
Overall, both the visibility of Franson fringes and the purity of the heralded single-photon state are limited by the cavity-detectors losses and unequal Q-factors for the signal and idler modes, which eventually leads to a different count rate on each detector, increasing the background. Substantial improvement is possible by reducing these insertion losses, which are essentially related to the signal and idler separation, and pump suppression. This can be achieved by integrating on-chip these passive linear functions. Another obvious improvement relies on the choice of similar escape rates (loaded Q-factors) for the idler and signal cavity modes. Integration in a complete quantum circuit, as currently pursued with the AlGaAs platform43, is also our perspective; therefore, this engineering work will squarely be addressed in future work.
On a more fundamental standpoint, the demonstration that a PhC resonant parametric source allows entanglement and heralding unlocks the possibility of using photonic bandgap engineering to suppress unwanted photons to a degree which is not accessible to other kind of resonators. In fact, we have shown that it is very easy to operate a PhC resonator such that only the required modes are able to interact through FWM. All the other interactions are strongly suppressed as they correspond to a very low density of optical states. This has many benefits, for instance, more efficient power conversion in OPOs36, which is more difficult to achieve in ring resonators and requires nontrivial engineering44,45,46. The suppression of unwanted interactions is also critical for the generation of squeezed light47. All these issues are solved using PhC resonators. As a final note, PhC cavities have the lowest footprint (Table 2), which is a direct consequence of the strong confinement. This is an important asset for scalability and the integration of multiple sources on a single chip for photonic computing tasks.
In conclusion, we demonstrated the very efficient generation of time-energy entangled photon pairs using an InGaP photonic crystal cavity. Large efficiency is achieved by operating at low power and scales well compared to most semiconductor-based ring resonators due to a smaller volume. This work proves that PhC cavities are an adequate, different, and competitive candidate for the generation of quantum states of light and can play an important role in integrated quantum optics.
Methods
Sample design, fabrication, and characterization
The samples have been fabricated in the Centre de Nanosciences et de Nanotechnologies (C2N). They consist of an array of 2 × 11 PhC cavities, fabricated by patterning a suspended membrane of In0.5Ga0.5P lattice-matched to GaAs following the same process as in previous studies29. The layout is transferred using e-beam lithography and then inductively coupled plasma etching (ICP), while wet etching is used to remove the material underlying the membrane.
The cavity, depicted in Fig. 1c, consists of a 2D array of holes with constant period a, except for two lines with a slightly reduced period \({a}^{{\prime} }\) where the cavity is located. A missing line of holes constitutes a waveguide where photons can propagate and are evanescently coupled to the cavity. A mode adapter is placed on the edge of the waveguide to realize an adiabatic transition from the mode of the waveguide to that of the lensed fiber. A reflector is constructed on the other side by shifting inwards two lines of holes.
High-resolution (20 MHz) linear optical spectra are measured using optical coherent tomography (OCT), as detailed in ref. 29. Based on the linear characterization, among the different devices with the proper spectral alignment usable for SFWM, the one with the best trade-off between Q-factors, efficiencies, and spectral misalignment has been selected for nonlinear and quantum measurements.
Experimental setups
The experimental setup for the state generation is depicted in Fig. 6a. A fiber-coupled tunable laser source (Santec TSL-710) is used to pump the process. The sample is stabilized in temperature and accessed through a fiber optical circulator. A lensed fiber is used to couple light in and out of the resonator and the emitted photons, as well as the reflected pump, are collected via the circulator reflection channel. The input polarization is optimized with a polarization controller monitoring the reflected power. When measuring double coincidences to retrieve the internal generation rate, the experimental setup used is in Fig. 6b. The emitted photons are spectrally filtered to attenuate the pump field. The filtering stage consists of a telecom dense wavelength division multiplexing with 3.6 dB of insertion losses and a rejection of 85 dB, and then a tunable bandpass filter per channel, with 3.4 and 4.2 dB of insertion losses, respectively. To measure time correlations, the collected photons are directed into two superconducting nanowire single-photon detectors with a quantum efficiency greater than 85% and a 37 ps time jitter. Details of all the encountered losses by the photons are given in Table 3.
a Experimental setup for the generation of the photon pairs in the PhC cavity. PC stands for polarization controller. The blue and red arrows denote signal and idler photons. b Time-correlation measurement setup. DWDM stands for dense wavelength division multiplexing, BPF for bandpass filter, and SPD for single-photon detector. c Time-energy entanglement measurement setup. PS stands for phase shifter, MZI for Mach–Zehnder interferometer. d Heralding single-photon emission measurement setup. BS stands for beam-splitter, here with a ratio of 50:50.
When measuring time-energy entanglement (Fig. 6c), the photons encounter a Franson interferometer. It is a single, fibered, heavily unbalanced Mach–Zehnder interferometer, in which the difference in length between the two arms is L = 2 m. The unbalance has to be larger than the coherence length of each of the photons of the emitted pairs \({L}_{{{{{{\mathrm{single}}}}}}}^{{{{{{\mathrm{coh}}}}}}}\) (on the order of 10 cm for this device), to wash out classical first-order interference; but simultaneously shorter than the coherence length of the pair, that, in this experiment, is given by the coherence length of the continuous-wave pump laser \({L}_{{{{{{\mathrm{pair}}}}}}}^{{{{{{\mathrm{coh}}}}}}}\) (~1 km).
The phase is actively stabilized on an ultra-stable laser (Orbits Lightwave Ethernal) with a feedback correction signal sent to a fiber phase shifter. Changing the offset voltage of the phase shifter allows to change the relative phase of the two arms within an estimated error of less than 10∘. After leaving the interferometer, the photons encounter the same filtering stage as before. Figure 6d show the Hanbury Brown–Twiss setup for heralding single photons measurement.
Coincidence peak fitting
We illustrate the heuristic model we adopted to fit the asymmetric coincidence histogram measured in the experimental configurations depicted in Fig. 6b, c. We assume that the emission time of each photon pair is a Poisson point process, but with an average time constant τi that is different for the signal and idler channel, respectively
where Θ(t) is the Heaviside step function. To take into account the time jitter of the detector, we assume a Gaussian time response gjitt(t0 = 0, σ) with σ = 37 ps, as characterized by the manufacturer. The probability pi(t) of measuring a photon at delay t for the signal or idler channel after measuring no photons in the time interval [0, t] is then proportional to the convolution
The probability of a coincidence at zero delay is then proportional to the convolution of the probabilities of the independent signal and idler events
that is, the lineshape used to fit the coincidence histogram. In Supplementary Note 3 are shown the values of τs and τi given by the fitting procedure, that correspond to the dwelling times retrievable from the linewidth of the resonances measured with spectroscopic techniques.
Bell curve data extraction
Using the experimental setup depicted in Fig. 6c, a number of histograms have been acquired for different values of the phase φs + φi. The same process detailed in section Coincidence peak fitting is used to extract the number of coincidences in each of the three peaks in a typical histogram (see Fig. 3a). The error on the coincidences is assumed here to be Poissonian. The dependence of the coincidence rate Rdet with φs + φi is fitted using the following sinusoidal function as in ref. 21 :
with f0, A, and φ0 are fit parameters. As a consequence, if Rc is the number of coincidence rate of the central peak, the raw visibility defined as Vraw = (Rc,max − Rc,min)/(Rc,max + Rc,min) can be directly extracted from the fit parameters using eq. (6) : Vraw = A/f0. The error on each fit parameter is obtained from the covariance matrix giving the standard deviation on the visibility:
Finally, we can deduce the number of standard deviations from which the Bell inequality is violated, knowing entanglement is proved if Vraw > 70.71%.
Data availability
All essential data were available in the paper. Additional data were given in the supplementary file. Further supporting data can be provided from the corresponding author upon request.
References
Wehner, S., Elkouss, D. & Hanson, R. Quantum internet: a vision for the road ahead. Science 362, eaam9288 (2018).
Ekert, A. K. Quantum cryptography based on bell’s theorem. Phys. Rev. Lett. 67, 661–663 (1991).
Madsen, L. S. et al. Quantum computational advantage with a programmable photonic processor. Nature 606, 75–81 (2022).
Slussarenko, S. & Pryde, G. J. Photonic quantum information processing: a concise review. Appl. Phys. Rev. 6, 041303 (2019).
Bernien, H. et al. Probing many-body dynamics on a 51-atom quantum simulator. Nature 551, 579–584 (2017).
Arrazola, J. M. et al. Quantum circuits with many photons on a programmable nanophotonic chip. Nature 591, 54–60 (2021).
Vigliar, C. et al. Error-protected qubits in a silicon photonic chip. Nat. Phys. 17, 1137–1143 (2021).
Martínez, J. A. et al. Photonic indistinguishability of the tin-vacancy center in nanostructured diamond. Phys. Rev. Lett. 129, 173603 (2022).
Siampour, H. et al. Ultrabright single-photon emission from germanium-vacancy zero-phonon lines: deterministic emitter-waveguide interfacing at plasmonic hot spots. Nanophotonics 9, 953–962 (2020).
Wu, C. et al. Room-temperature on-chip orbital angular momentum single-photon sources. Sci. Adv. 8, eabk3075 (2022).
Uppu, R. et al. Scalable integrated single-photon source. Sci. Adv. 6, eabc8268 (2020).
da Silva, S. F. C. Gaas quantum dots grown by droplet etching epitaxy as quantum light sources. Appl. Phys. Lett. 119, 120502 (2021).
Liu, F. et al. High purcell factor generation of indistinguishable on-chip single photons. Nat. Nanotechnol. 13, 835–840 (2018).
Borghi, M. et al. Superspontaneous four-wave mixing in an array of silicon microresonators. Phys. Rev. Appl. 18, 034007 (2022).
Sabattoli, F. A. et al. Suppression of parasitic nonlinear processes in spontaneous four-wave mixing with linearly uncoupled resonators. Phys. Rev. Lett. 127, 033901 (2021).
Jin, B., Mishra, D. & Argyropoulos, C. Efficient single-photon pair generation by spontaneous parametric down-conversion in nonlinear plasmonic metasurfaces. Nanoscale 13, 19903–19914 (2021).
Chuprina, I., Perminov, N., Tarankova, D. Y. & Kalachev, A. Generating pure single-photon states via spontaneous four-wave mixing in a system of coupled microresonators. Laser Phys. Lett. 15, 105104 (2018).
Signorini, S. et al. A silicon source of heralded single photons at 2 μ m. APL Photonics 6, 126103 (2021).
Helt, L. G., Liscidini, M. & Sipe, J. E. How does it scale? Comparing quantum and classical nonlinear optical processes in integrated devices. JOSA B 29, 2199–2212 (2012).
Azzini, S. et al. Ultra-low power generation of twin photons in a compact silicon ring resonator. Opt. Express 20, 23100–23107 (2012).
Grassani, D. et al. Micrometer-scale integrated silicon source of time-energy entangled photons. Optica 2, 88–94 (2015).
Kumar, R. R., Raevskaia, M., Pogoretskii, V., Jiao, Y. & Tsang, H. K. Entangled photon pair generation from an InP membrane micro-ring resonator. Appl. Phys. Lett. 114, 021104 (2019).
Steiner, T. J. et al. Ultrabright entangled-photon-pair generation from an al ga as-on-insulator microring resonator. PRX Quantum 2, 010337 (2021).
Foresi, J. Photonic-bandgap microcavities in optical waveguides. Nature 390, 143–145 (1997).
Chopin, A. et al. Time-correlated photons from an in0.5ga0.5p photonic crystal cavity on a silicon chip. Phys. Rev. Res. 4, 043132 (2022).
John, S. Strong localization of photons in certain disordered dielectric superlattices. Phys. Rev. Lett. 58, 2486–2489 (1987).
Akahane, Y., Asano, T., Song, B.-S. & Noda, S. High-Q photonic nanocavity in a two-dimensional photonic crystal. Nature 425, 944–947 (2003).
Asano, T., Ochi, Y., Takahashi, Y., Kishimoto, K. & Noda, S. Photonic crystal nanocavity with a Q factor exceeding eleven million. Opt. Express 25, 1769 (2017).
Combrié, S., Lehoucq, G., Moille, G., Martin, A. & De Rossi, A. Comb of high-Q resonances in a compact photonic cavity. Laser Photonics Rev. 11, 1700099 (2017).
Azzini, S. et al. Stimulated and spontaneous four-wave mixing in silicon-on-insulator coupled photonic wire nano-cavities. Appl. Phys. Lett. 103, 031117 (2013).
Lian, J. et al. Dispersion of coupled mode-gap cavities. Opt. Lett. 40, 4488–4491 (2015).
Popović, M. A., Manolatou, C. & Watts, M. R. Coupling-induced resonance frequency shifts in coupled dielectric multi-cavity filters. Opt. Express 14, 1208–1222 (2006).
Clementi, M., Barone, A., Fromherz, T., Gerace, D. & Galli, M. Selective tuning of optical modes in a silicon comb-like photonic crystal cavity. Nanophotonics 9, 205–210 (2020).
Marty, G., Combrié, S., Raineri, F. & De Rossi, A. Photonic crystal optical parametric oscillator. Nat. Photonics 15, 53–58 (2021).
Alpeggiani, F., Andreani, L. C. & Gerace, D. Effective bichromatic potential for ultra-high Q-factor photonic crystal slab cavities. Appl. Phys. Lett. 107, 261110 (2015).
Chopin, A. et al. Canonical four-wave-mixing in photonic crystal resonators: tuning, tolerances and scaling. IEEE Journal of Selected Topics in Quantum Electronics, 29, 1,1-13 (2022).
Franson, J. D. Bell inequality for position and time. Phys. Rev. Lett. 62, 2205 (1989).
Signorini, S. & Pavesi, L. On-chip heralded single photon sources. AVS Quantum Sci. 2, 041701 (2020).
Ma, Z. Ultrabright quantum photon sources on chip. Phys. Rev. Lett. 125, 263602 (2020).
Zhao, M. & Fang, K. Ingap quantum nanophotonic integrated circuits with 1.5 nonlinearity-to-loss ratio. Optica 9, 258–263 (2022).
Ma, C. et al. Silicon photonic entangled photon-pair and heralded single photon generation with car> 12,000 and g(2)(0)< 0.006. Opt. Express 25, 32995–33006 (2017).
Oser, D. et al. High-quality photonic entanglement out of a stand-alone silicon chip. npj Quantum Inf. 6, 31 (2020).
Castro, J. E. et al. Expanding the quantum photonic toolbox in algaasoi. APL Photonics 7, 096103 (2022).
Stone, J. R., Moille, G., Lu, X. & Srinivasan, K. Conversion efficiency in kerr-microresonator optical parametric oscillators: From three modes to many modes. Phys. Rev. Appl. 17, 024038 (2022).
Nigro, D., Clementi, M., Brés, C.-S., Liscidini, M. & Gerace, D. Single-photon nonlinearities and blockade from a strongly driven photonic molecule. Opt. Lett. 47, 5348–5351 (2022).
Perez, E.F. et al. High-performance Kerr microresonator optical parametric oscillator on a silicon chip. Nat. Communications, 14, 242 (2023).
Zhang, Y. et al. Squeezed light from a nanophotonic molecule. Nat. Commun. 12, 1–6 (2021).
Xu, B.-Y. et al. Spectrally multiplexed and bright entangled photon pairs in a lithium niobate microresonator. Sci. China Phys. Mech. Astron. 65, 1–7 (2022).
Guo, X. et al. Parametric down-conversion photon-pair source on a nanophotonic chip. Light. Sci. Appl. 6, e16249–e16249 (2017).
Ramelow, S. et al. Silicon-nitride platform for narrowband entangled photon generation. Preprint at arXiv:1508.04358 (2015).
Moody, G., Chang, L., Steiner, T. J. & Bowers, J. E. Chip-scale nonlinear photonics for quantum light generation. AVS Quantum Sci. 2, 041702 (2020).
Acknowledgements
The authors thank Dario Gerace for enlightening discussions and for having encouraged this collaboration. A.D.R. thanks Mikkel Heuck, K. Bensheick, I. Sagnes, and T. Debuisschert for stimulating discussions. This work was funded by the Agence nationale de la recherche (ANR) under the contract COLOURS (ANR-21-CE24-0024) and by Ministero dell’Istruzione, dell’Università e della Ricerca [MIUR grant Dipartimenti di Eccellenza 2018-2022 (F11I18000680001)]. This work was partly supported by the French Renatech network.
Author information
Authors and Affiliations
Contributions
A.C. and A.B. equally contributed to the measurements, analysed the data, and wrote the manuscript with the contributions of all the authors. I.G. contributed to the preliminary linear measurements. S.C. contributed to the fabrication of the sample and developed the optical characterization facilities used in TRT. D.B. helped during the quantum experiments. F.R. fabricated the sample. A.D.R., M.G., and F.R. equally supervised the work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chopin, A., Barone, A., Ghorbel, I. et al. Ultra-efficient generation of time-energy entangled photon pairs in an InGaP photonic crystal cavity. Commun Phys 6, 77 (2023). https://doi.org/10.1038/s42005-023-01189-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-023-01189-x
This article is cited by
-
Entangled photon pair generation in an integrated SiC platform
Light: Science & Applications (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.